将军饮马练习

“将军饮马”常见模型及18道典型习题何为将军饮马？2000多年以前。

古希腊的亚历山大城里住着一位睿智的数学家海伦。

一天，城里来了一位将军，听闻海伦盛名，特来向他请教一个问题。

将军说，每天早上，他都骑着马儿从营帐出发，到河边让马儿饮水，然后，再去河岸同一侧的一块草地上带着马儿去吃草，问题时，在河岸的哪个具体位置喝水，行程最短？海伦略做沉思，给出了将军最佳方案。

此之谓“将军饮马”。

最佳方案为何？且阅下文：一、将军饮马常见的5种模型：1、一动两定（和最小）：如图，点A是将军和马居住的营帐，点B是一块指定的草地，一条小河L潺潺流过，P是将军带着马儿喝水的地方，P点在何处时，将军和马儿走过的路PA+PB的值最小？解析：做A点关于L的对称点A’，连接A’B，与L的交点即为P点。

为什么这时PA+PB最小？假设L上有一点M（与P点不重合）。

∵A点与A’关于L对称∴AP=A’P；AM=A’M；∴AP + BP =A’P +BP =A’B而AM + BM = A’M +MB在△A’MB中，两边之和大于第三边∴A’B < A’M +MB；而M为L上任一点（与P点不重合）。

∴动点P在A’B与L交点处时AP+BP最小。

2、一定两动：如图，点A是将军和马居住的营帐，小河L1依然像上题中一样潺潺流过，P是将军带着马儿喝水的地方，不同的是，这次吃草的地方不在是一个指定的点，而是L2所代表的一片草地，Q则是将军骑马吃草的地方，水足草饱以后，将军和马儿会再回到营帐。

那么，P点、Q点在何处时，将军走过的路AP+PQ+QA的值最小？解析：做A点关于L1的对称点A’；做A点关于L2的对称点A‘’；连接A’A‘’，与L1和L2的交点即为P、Q。

为什么此时，AP+PQ+AQ的和最小？假设L1上有点M（不与P重合）、L2上有点N（不与Q重合）。

∵A点与A’关于L1对称；A点与A‘’关于L2对称。

∴AP=A’P；AQ=A”Q；AM=A’M；AN=A”N；∴AP+PQ+AQ = A’P+PQ+A”Q =A’A”；AM+MN+AN = A’M+MN+A”N在四边形A’MNA”中：A’M+MN+A”N >A’A”∴P、Q位于A’A”与L1和L2的交点处时，AP+PQ+AQ的和最小。

初二将军饮马练习题及答案题目一：将军饮马练习阅读下面的短文，然后根据短文内容回答问题。

春秋时期，楚国的将军薛将军因在战场上立下赫赫战功，受到国王的嘉奖，被封为将军。

薛将军深感自己取得的成就来之不易，为了更好地提升自己的军事才能，他经常利用业余时间练习骑射。

一天，他饮酒之后，心血来潮，决定骑马练习。

他醉醺醺地骑在马背上，手握弓箭，身姿挺拔。

突然，他抬头目视远方的鹰，大声喊道：“马儿，你好生奔放，将你的速度发挥到极致。

”马儿似乎听懂了薛将军的话，使出浑身解数奔驰起来。

薛将军稳稳地坐在马背上，准备放箭。

问题：1. 薛将军为什么经常练习骑射？2. 为什么薛将军喊马儿将速度发挥到极致？3. 薛将军的骑射练习中有哪些亮点？答案：1. 薛将军经常练习骑射是为了提升自己的军事才能。

2. 薛将军喊马儿将速度发挥到极致是为了更好地测试自己的骑射技巧。

3. 薛将军的骑射练习中的亮点包括：饮酒后决定进行练习，以更高难度的状态来挑战自己；喊马儿将速度发挥到极致，考验自己的射击准确性和反应能力。

题目二：将军饮马练习答案解析问题：1. 薛将军为什么经常练习骑射？答案解析：薛将军经常练习骑射是为了更好地提升自己的军事才能。

他深感自己在战场上立下的赫赫战功来之不易，因此希望通过练习骑射来增强自己的战斗力。

2. 为什么薛将军喊马儿将速度发挥到极致？答案解析：薛将军喊马儿将速度发挥到极致是为了更好地测试自己的骑射技巧。

他希望在马儿飞驰的情况下，能够准确地射箭，展现出自己的高超技艺。

3. 薛将军的骑射练习中有哪些亮点？答案解析：薛将军的骑射练习中的亮点包括：a) 饮酒后决定进行练习：饮酒之后，薛将军心血来潮，决定骑马练习。

这展现了他的勇气和自信，也体现了他对自己技艺的自豪感。

b) 喊马儿将速度发挥到极致：薛将军对马儿的速度要求极高，希望它能够发挥出最快的速度。

这要求他自己的反应能力和射击准确性都必须达到非常高的水平。

总结：薛将军通过练习骑射来提升自己的军事才能，展示了他在战场上立下的赫赫战功所带来的成就感。

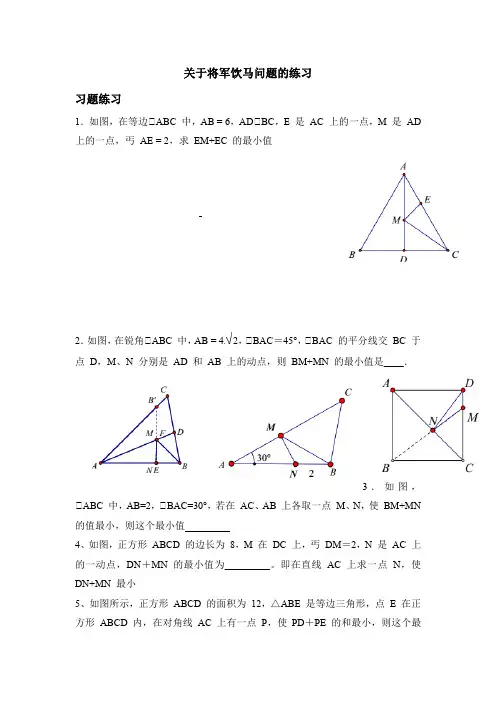
关于将军饮马问题的练习习题练习1．如图，在等边△ABC 中，AB = 6，AD△BC，E 是AC 上的一点，M 是AD 上的一点，丐AE = 2，求EM+EC 的最小值2．如图，在锐角△ABC 中，AB = 42，△BAC＝45°，△BAC 的平分线交BC 于点D，M、N 分别是AD 和AB 上的动点，则BM+MN 的最小值是____．3．如图，△ABC 中，AB=2，△BAC=30°，若在AC、AB 上各取一点M、N，使BM+MN 的值最小，则这个最小值4、如图，正方形ABCD 的边长为8，M 在DC 上，丐DM＝2，N 是AC 上的一动点，DN＋MN 的最小值为_________。

即在直线AC 上求一点N，使DN+MN 最小5、如图所示，正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P，使PD＋PE 的和最小，则这个最小值为6、在边长为2 ㎝的正方形ABCD 中，点Q 为BC 边的中点，点P 为对角线AC 上一动点，连接PB、PQ，则△PBQ 周长的最小值为____________㎝（结果不取近似值）.7、如图，四边形ABCD 是正方形，AB = 10cm，E 为边BC 的中点，P 为BD 上的一个动点，求PC+PE 的最小值；模拟检测8．如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AE PQ的周长取最小值时，四边形AEPQ的面积是9.如图，在矩形OABC 中，已知A ，C 两点的坐标分别为A （4，0），C （0，2），D 为OA 的中点．设点P 是∠AOC 平分线上的一个动点（不与点O 重合）．（1）试证明：无论点P 运动到何处，PC 总与PD 相等；（2）当点P 运动到与点B 的距离最小时，求P 的坐标；（3）已知E （1，﹣1），当点P 运动到何处时，△PDE 的周长最小？求出此时点P 的坐标和△PDE 的周长．10.如图，在平面直角坐标系中，直线 分别交x 轴,y 轴于A ，B 两点，点C 为0B 的中点,点D 在第二象限，且四边形AOCD 为矩形.动点P 从点C 出发,沿线段CD 向终点D 运动，过点P 作PH 丄OA ，垂足为H.点Q 是点B 关于点A 的对称点，求BP+PH+HQ 的最小值.434+=x y。

将军饮马18道典型习题将军饮马"是一个古希腊数学问题，源于2000多年前。

当时，一位将军向城里的著名数学家海伦请教：他每天早上都要骑马到河边让马喝水，然后到河岸同一侧的一块草地上让马吃草。

将军想知道，在河岸的哪个具体位置让马喝水，可以让他和马儿走的路程最短。

经过思考，海伦给出了答案，这就是"将军饮马"问题。

以下是"将军饮马"问题的五种常见模型：1.一动两定（和最小）模型：假设点A是将军和马儿居住的营帐，点B是指定的草地，小河L在两点之间流过。

问题是，将军和马儿在哪个具体位置喝水，可以让他们走的路程最短？解决方法是，做A点关于L的对称点A'，连接A'B，与L的交点即为P点。

这时，PA+PB最小。

为什么呢？因为在L 上任意取一点M（不与P重合），根据几何原理，PA+PB=A'P+PB=A'B，AM+MB>A'B，所以动点P在A'B与L 交点处时，PA+PB最小。

2.一定两动模型：假设点A和小河L1与第一种模型一样，但是这次，草地不是指定的点，而是由L2代表的一片草地。

问题是，在哪个具体位置喝水和吃草，可以让将军和马儿走的路程最短？解决方法是，做A点关于L1的对称点A'，做A点关于L2的对称点A''，连接A'A''，与L1和L2的交点即为P、Q。

这时，AP+PQ+QA的和最小。

为什么呢？因为在L1上取点M（不与P重合），在L2上取点N（不与Q重合），根据几何原理，AP+PQ+AQ=A'P+PQ+A''Q=A'A''，AM+MN+AN>A'A''，所以动点P和Q在A'A''与L1、L2的交点处时，AP+PQ+QA的和最小。

3.两动一定模型：假设点A和小河L1与第一种模型一样，但是这次，将军要骑马到L2代表的一片草地吃草，然后再回到营帐。

将军饮马练习题姓名：__________ 指导：__________ 日期：__________将军饮马问题1．(2016秋·北京十三中·期中)如图，等边三角形ABC，D为BC边的中点，AD=12，P为AC的中点，问在AD是否存在一点Q，使CQ+PQ最小，如果存在，写出作图思路，画出Q的位置，并求出这个最小值；如果不存在，说明理由.2.(2016秋·吉林吉化九中·期中)如图，四边形ABCD中，∠A=∠B=90°，∠C=60°，CD=2AD.AB=4（1）在AB边上求作点P，使PC+PD最小.（2）求出（1）中PC+PD的最小值.3.(2016秋·南京二十九中·期中)如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点.若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（）.A.6B.8C.10D.124．(2016秋·天津河西·期末)如图，已知点P在锐角∠AOB内部，∠AOB=α，在OB边上存在一点D，在OA边上存在一点C，能使PD+DC最小，此时∠PDC=.5．(2016秋·北京159中·期中)如图，MN是正方形ABCD的一条对称轴，点P 是直线MN上的一个动点，当PC+PD最小时，∠PCD=°.6．(2015·乐乐课堂·练习)如图，已知正方形ABCD的边长为10，点P是对角线BD上的一个动点，M、N分别是BC、CD边上的中点，则PM+PN的最小值是．7．(2015·乐乐课堂·练习)如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为cm．8．(2015·乐乐课堂·练习)如图，正方形ABCD的边长为2，M、N分别为AB、AD的中点，在对角线BD上找一点P，使△MNP的周长最小，则此时PM+PN=．9．(2015·乐乐课堂·练习)已知如图所示，∠MON=40°，P为∠MON内一点，A 为OM上一点，B为ON上一点，则当△PAB的周长取最小值时，∠APB的度数为°．10.如图，点P在∠AOB内，且OP=15cm，点E、F是OA、OB上任意一点，若∠AOB=30°，则△PEF的周长最小值是cm．11如图，已知∠AOB=30°，点P为∠AOB内一点，OP=10cm，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，则△PMN 的周长为cm．12如图，已知∠MON=50°，P为∠MON内一定点，点A为OM上的点，B为ON上的点，当△PAB的周长取最小值时，则∠APB度数是°．13．(2016秋·天津宁河·期中)如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，∠AOB=30°则△PMN周长的最小值=。

最短路径问题（将军饮马）专项训练一、单选题1．如图，在ABC 中，AB AC =，10BC =，60ABC S =△，D 是BC 中点，EF 垂直平分AB ，交AB 于点E ，交AC 于点F ，在EF 上确定一点P ，使PB PD +最小，则这个最小值为( )A ．10B ．11C ．12D ．132．如图方格纸中每个小正方形的边长均为1，线段AC 的两个端点均在小正方形的顶点上，点P 也在小正方形的顶点上．某人从点P 出发，沿图中已有的格点所连线段走一周（即不能直接走线段AC 且要回到P ），则这个人所走的路程最少是（ ）A ．7B ．14C ．10D ．不确定3．如图，在等边△ABC 中，AB ＝2，N 为AB 上一点，且AN ＝1，AD ＝3，∠BAC 的平分线交BC 于点D ，M 是AD 上的动点，连接BM 、MN ，则BM+MN 的最小值是（ ）A ．3B ．2C ．1D ．34．如图，在△ABC 中，∠C=90°，∠BAC=30°，AB=12，AD 平分∠BAC ，点PQ 分别是AB 、AD 边上的动点，则BQ+QP 的最小值是（ ）A．4 B．5 C．6 D．75．如图，在△ABC中，点D、E分别是边AB、AC的中点，∠B=50°，∠A=26°，将△ABC沿DE折叠，点A的对应点是点A′，则∠AEA′的度数是（）A．145°B．152°C．158°D．160°6．图1为某四边形ABCD纸片，其中∠B=70°，∠C=80°．若将CD迭合在AB上，出现折线MN，再将纸片展开后，M、N两点分别在AD、BC上，如图2所示，则∠MNB的度数为（）度.A．90 B．95 C．100 D．1057．如图，在△ABC中，∠ACB＝90°，以AC为底边在△ABC外作等腰△ACD，过点D作∠ADC的平分线分别交AB，AC于点E，F．若AC＝12，BC＝5，△ABC的周长为30，点P是直线DE上的一个动点，则△PBC周长的最小值为（）A．15 B．17 C．18 D．208．平面直角坐标系xOy中，已知A(－1，0)，B(3，0)，C(0，－1)三点，D(1，m)是一个动点，当△ACD 的周长最小时，则△ABD的面积为（）A．13B．23C．43D．839．如图，等边△ABC的边长为4，AD是边BC上的中线，F是边AD上的动点，E是边AC上一点，若AE=2，则EF+CF取得最小值时，∠ECF的度数为（）A ．15°B ．22.5°C ．30°D ．45°10．如图，在△ABC 中，∠C =90°，∠BAC =30°，AB =8，AD 平分∠BAC ，点PQ 分别是AB 、AD 边上的动点，则PQ +BQ 的最小值是A ．4B ．5C ．6D ．711．如图，锐角三角形ABC 中，∠C ＝45°，N 为BC 上一点，NC ＝5，BN ＝2，M 为边AC 上的一个动点，则BM ＋MN 的最小值是（ ）A ．29B ．21C ．74D ．4512．如图是一块长，宽，高分别是6cm ，4cm 和3cm 的长方体纸盒子，一只老鼠要从长方体纸盒子的一个顶点A 处，沿着长方体的表面到长方体上和A 相对的顶点B 处吃食物，那么它需要爬行的最短路径的长是（ ）A ．(3213cm +B 85cmC 97cmD 109cm13．如图，ABC ∆是等边三角形，2AB =，AD 是BC 边上的高，E 是AC 的中点，P 是AD 上的一个动点，则PE PC +的最小值为（ ）A ．1B ．2C ．3D ．2314．如图，在锐角△ABC 中，AB ＝42，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM ＋MN 的最小值是（ ）A ．3B ．4C ．5D ．615．如图，A 、B 是两个居民小区，快递公司准备在公路l 上选取点P 处建一个服务中心，使P A +PB 最短．下面四种选址方案符合要求的是（ ）A ．B ．C ．D ．16．已知：如图，在Rt △ABC 中，∠ACB=90°，∠A ＜∠B ，CM 是斜边AB 上的中线，将△ACM 沿直线CM 折叠，点A 落在点A 1处，CA 1与AB 交于点N ，且AN=AC ，则∠A 的度数是（ ）A ．30°B ．36°C ．50°D ．60°17．如图，在ABC 中，90BCA ∠=︒，3BC =，4CA =，AD 平分BAC ∠，点M N 、分别为AD AC 、上的动点，则CM MN +的最小值是（ ）A ．1.2B ．2C ．2.4D ．518．在平面直角坐标系中，点A 、B 的坐标分别为（ 2，0 ），（4，0），点C 的坐标为（m ，3 m ）（m 为非负数），则CA ＋CB 的最小值是（ ）A ．6B ．37C ．27D ．5二、填空题 19．如图，在等边ABC ∆中，D 是BC 的中点，E 是AB 的中点，H 是AD 上任意一点．如果10AB AC BC ===，53AD =，那么HE HB +的最小值是 ．20．如图，在ABC 中，10AB AC cm ==，8BC cm =，AB 的垂直平分线交AB 于点M ，交AC 于点N ，在直线MN 上存在一点P ，使P 、B 、C 三点构成的PBC 的周长最小，则PBC 的周长最小值为______．21．如图，等腰三角形ABC 的底边BC 长为6，面积是36，腰AC 的垂直平分线EF 分别交AC ，AB 边于E ，F 点，若点D 为BC 边的中点，点M 为线段EF 上一动点，则CDM ∆周长的最小值____．22．如图，P 是AOB ∠内一定点，点M ，N 分别在边OA ，OB 上运动，若30AOB ∠=︒，3OP =，则PMN 的周长的最小值为___________.23．等边三角形ABC中，∠BPC＝150°，BP＝3，PC＝4，M、N分别为AB，AC上两点，且AM＝AN，则PM+PN的最小值为__．24．如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=4，M是AB边上一动点，N是AC边上的一动点，则MN+MC的最小值为_____．25．如图，四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN 周长最小时，则∠AMN+∠ANM的度数为____．26．如图所示，在边长为2的等边三角形ABC中，G为BC的中点，D为AG的中点，过点D作EF∥BC 交AB于E，交AC于F，P是线段EF上一个动点，连接BP，GP，则△BPG的周长的最小值是________．27．已知∠AOB=30°，点P、Q分别是边OA、OB上的定点，OP=3，OQ=4，点M、N是分别是边OA、OB上的动点，则折线P-N -M -Q长度的最小值是___________.28．如图，在等边三角形ABC中，BC边上的中线4AD=，E是AD上的一个动点，F是边AB上的一个动点，在点E、F运动的过程中，EB EF+的最小值是______．29．如图，∠AOB=30°，∠AOB内有一定点P，且OP=12，在OA上有一点Q，OB上有一点R，若△PQR 周长最小，则最小周长是_____30．如图，在△ABC中，AB＝AC＝5，BC＝6，AD是∠BAC的平分线，AD＝4．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是_____．31．如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，AB=4，点D是BC上一动点，以BD为边在BC 的右侧作等边△BDE，F是DE的中点，连结AF，CF，则AF+CF的最小值是_____.32．如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（6，0）是OB上的一定点，点M是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为_____．33．某市为解决农村燃气困难，在P处建立了一个燃气站，从P站分别向A、B、C村铺设燃气管道。

“将军饮马”常见模型及18道典型习题何为将军饮马？2000多年以前。

古希腊的亚历山大城里住着一位睿智的数学家海伦。

一天，城里来了一位将军，听闻海伦盛名，特来向他请教一个问题。

将军说，每天早上，他都骑着马儿从营帐出发，到河边让马儿饮水，然后，再去河岸同一侧的一块草地上带着马儿去吃草，问题时，在河岸的哪个具体位置喝水，行程最短？海伦略做沉思，给出了将军最佳方案。

此之谓“将军饮马”。

最佳方案为何？且阅下文：一、将军饮马常见的5种模型：1、一动两定（和最小）：如图，点A是将军和马居住的营帐，点B是一块指定的草地，一条小河L潺潺流过，P是将军带着马儿喝水的地方，P点在何处时，将军和马儿走过的路PA+PB的值最小？解析：做A点关于L的对称点A’，连接A’B，与L的交点即为P点。

为什么这时PA+PB最小？假设L上有一点M（与P点不重合）。

∵A点与A’关于L对称∴AP=A’P；AM=A’M；∴AP + BP =A’P +BP =A’B而AM + BM = A’M +MB在△A’MB中，两边之和大于第三边∴A’B < A’M +MB；而M为L上任一点（与P点不重合）。

∴动点P在A’B与L交点处时AP+BP最小。

2、一定两动：如图，点A是将军和马居住的营帐，小河L1依然像上题中一样潺潺流过，P是将军带着马儿喝水的地方，不同的是，这次吃草的地方不在是一个指定的点，而是L2所代表的一片草地，Q则是将军骑马吃草的地方，水足草饱以后，将军和马儿会再回到营帐。

那么，P点、Q点在何处时，将军走过的路AP+PQ+QA的值最小？解析：做A点关于L1的对称点A’；做A点关于L2的对称点A‘’；连接A’A‘’，与L1和L2的交点即为P、Q。

为什么此时，AP+PQ+AQ的和最小？假设L1上有点M（不与P重合）、L2上有点N（不与Q重合）。

∵A点与A’关于L1对称；A点与A‘’关于L2对称。

∴AP=A’P；AQ=A”Q；AM=A’M；AN=A”N；∴AP+PQ+AQ = A’P+PQ+A”Q =A’A”；AM+MN+AN = A’M+MN+A”N在四边形A’MNA”中：A’M+MN+A”N >A’A”∴P、Q位于A’A”与L1和L2的交点处时，AP+PQ+AQ的和最小。

初中将军饮马问题题型总结(全)题型一：将军饮马之单动点1.三角形中的将军饮马题目描述：在等腰三角形ABC中，AB=AC，AD、CE是三角形ABC的两条中线，P是AD上的一个动点，则下列线段的长度等于BP+EP最小值的是()解析：连接PC，由于AB=AC，BD=CD，AD垂直于BC，所以PB=PC。

因此，PB+PE=PC+PE，PE+PC>CE，当P、C、E共线时，PB+PE的值最小，最小值为CE的长度，故选B．2.等边三角形中的将军饮马题目描述：在等边三角形ABC中，AB=2，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，则PE+PC的最小值为()解析：连接BE交AD于点P'，AD、BE分别是等边三角形ABC边BC、AC的垂直平分线，P'B=P'C，P'E+P'C=P'E+P'B=BE。

根据两点之间线段最短，点P在点P'时，PE+PC有最小值，最小值即为BE的长。

因此，BE=BC/2-CE/2=3，所以P'E+P'C的最小值为3，故选C．3.等腰三角形中的将军饮马题目描述：在等腰三角形ABC中，AB=AC，BC=4，面积是16，AC的垂直平分线EF分别交AC、AB边于E、F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为()解析：连接AD、AM，由于△ABC是等腰三角形，点D是BC边的中点，AD垂直于BC，所以S△ABC=1/2×4×AD=16，解得AD=8.EF是线段AC的垂直平分线，所以点C关于直线EF的对称点为点A，MA=MC，AD=AM+MD，因此AD的长为CM+MD的最小值。

且AC6，BM3，因为BM AD，故BM AC，所以BM是AC的中线，故CM3。

又因为AC是菱形的对角线，所以AC平分DAB，即DAM30。

又因为AM MD，所以ADM75。

将军饮马问题专项训练一、基本模型古希腊有一个著名的“将军饮马问题”，大致内容如下：古希腊一位将军，每天都要巡查河岸侧的两个军营A、B，他总是先去A营，再到河边饮马，之后再去B营，如图，他时常想，怎么走才能使每天的路程之和最短呢？大数学家海伦曾用轴对称的方法巧妙的解决了这问题．二、实战演练1．如图所示，如果将军从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB 上的某一位置Q，然后立即返回校场N．请为将军重新设计一条路线（即选择点P和Q），使得总路程MP PQ QN++最短．【变式】如图所示，将军希望从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB上的某一位置Q．请为将军设计一条路线（即选择点P和Q），使得总路程MP PQ＋最短．2．将军要检阅一队士兵，要求(如图所示)：队伍长为a ，沿河OB 排开（从点P 到点Q ）；将军从马棚M 出发到达队头P ，从P 至Q 检阅队伍后再赶到校场N ．请问：在什么位置列队（即选择点P 和Q ），可以使得将军走的总路程MP PQ QN ++最短?3．如图，点M 在锐角AOB ∠内部，在OB 边上求作一点P ，使点P 到点M 的距离与点P 到OA 边的距离之和最小．4．已知MON ∠内有一点P ，P 关于OM ，ON 的对称点分别是1P 和2P ，12P P 分别交OM ，ON 于点A 、B ，已知1215PP =，则△PAB 的周长为（ ）． A. 15 B 7.5 C. 10 D. 245．已知AOB ∠，试在AOB ∠内确定一点P ，如图，使P 到OA 、OB 的距离相等，并且到M 、N 两点的距离也相等．6．已知40MON ∠=︒，P 为MON ∠内一定点，OM 上有一点A ，ON 上有一点B ，当△P AB 的周长取最小值时，求APB ∠的度数．7．如图，在四边形ABCD 中，90A ∠=︒，4AD =，连接BD ，BD ⊥CD ，ADB C ∠=∠．若P 是BC 边上一动点，则DP 长的最小值为________．8．已知点A 在直线l 外，点P 为直线l 上的一个动点，探究是否存在一个定点B ，当点P 在直线l 上运动时，点P 与A 、B 两点的距离总相等，如果存在，请作出定点B ；若不存在，请说明理由．9．如图，在公路a 的同旁有两个仓库A 、B ，现需要建一货物中转站，要求到A 、B 两仓库的距离和最短，这个中转站M 应建在公路旁的哪个位置比较合理?aBA10．已知：A 、B 两点在直线l 的同侧， 在l 上求作一点M ，使得||AM BM -最小．11．如图，正方形ABCD 中，8AB =，M 是DC 上的一点，且2DM =，N 是AC 上的一动点，求DN MN+的最小值与最大值．NMD CB A12．如图，已知AOB ∠内有一点P ，试分别在边OA 和OB 上各找一点E 、F ，使得△PEF的周长最小．试画出图形，并说明理由．13．如图，直角坐标系中有两点A 、B ，在坐标轴上找两点C 、D ，使得四边形ABCD 的周长最小．14．如图，村庄A 、B 位于一条小河的两侧，若河岸a 、b 彼此平行，现在要建设一座与河岸垂直的桥CD ，问桥址应如何选择，才能使A 村到B 村的路程最近?15．221(9)4y x x =++-+，试判断：当x 为何值时，y 的值最小，并求出这个最小值．16．如图，在等腰梯形ABCD 中，2AB CD AD ===，120D ∠=︒，点E 、F 是底边AD 与BC 的中点，连接EF ，在线段EF 上找一点P ，使BP+AP 最短．. A. B17．已知P 是△ABC 的边BC 上的点，你能在AB 、AC 上分别确定一点Q 和R ，使△PQR 的周长最短吗?18．如图，A 和B 两地在一条河的两岸，现要在河上造一座桥MN ．乔早在何处才能使从A 到B 的路径AMNB最短?（假定河的两岸是平行的直线，桥要与河垂直）19．某课题组在探究“将军饮马问题”时抽象出数学模型：直线l 同旁有两个定点A 、B ，在直线l 上存在点P ，使得PA PB +的值最小．解法：作点A 关于直线l 的对称点A′，连接A′B ，则A′B 与直线l 的交点即为P ，且P A P B +的最小值为A B '．请利用上述模型解决下列问题：（1）几何应用：如图1，等腰直角三角形ABC 的直角边长为2，E 是斜边 AB 的中点，P 是AC 边上的一动点，则PB PE +的最小值为________；（2）几何拓展：如图2，△ABC 中，2AB =，30BAC ∠=︒，若在AC 、AB 上各取一点M 、N 使BM+MN 的值最小，求这个最小值；（3）代数应用：求代数式221(4)4x x ++-+（0≤x ≤4）的最小值．。

难关必刷03轴对称之将军饮马模型（3种类型30题专练）【模型梳理】如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？B军营河如图，在直线上找一点P使得PA+PB最小？这个问题的难点在于PA+PB是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．【模型解析】作点A关于直线的对称点A’，连接PA’，则PA’=PA，所以PA+PB=PA’+PB当A’、P、B三点共线的时候，PA’+PB=A’B ，此时为最小值（两点之间线段最短）类型一：两定一动在OA 、OB 上分别取点M 、N ，使得△PMN 周长最小．此处M 、N 均为折点，分别作点P 关于OA （折点M 所在直线）、OB （折点N 所在直线）的对称点，化折线段PM +MN +NP 为P ’M +MN +NP ’’，当P ’、M 、N 、P ’’共线时，△PMN 周长最小．类型二：两定两动在OA 、OB 上分别取点M 、N 使得四边形PMNQ 的周长最小。

考虑PQ 是条定线段，故只需考虑PM +MN +NQ 最小值即可，类似，分别作点P 、Q 关于OA 、OB 对称，化折线段PM +MN +NQ 为P ’M +MN +NQ ’，当P ’、M 、N 、Q ’共线时，四边形PMNQ 的周长最小。

类型三：一定两动在OA 、OB 上分别取M 、N 使得PM +MN 最小。

此处M 点为折点，作点P 关于OA 对称的点P ’，将折线段PM +MN 转化为P ’M +MN ，即过点P ’作OB 垂线分别交OA 、OB 于点M 、N ，得PM +MN 最小值（点到直线的连线中，垂线段最短）BBBBBB【题型讲解】类型一：两定一动【例1】如图，在中，，是的两条中线，是上一个动点，则下列线段的长度等于最小值的是（ ）A ．B ．C ．D ．【答案】B 【详解】在中，，AD 是的中线，可得点B 和点D 关于直线AD 对称，连结CE ，交AD 于点P ，此时最小，为EC 的长，故选B.【变式】如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值为___________．【分析】△PMN 周长即PM +PN +MN 的最小值，此处M 、N 均为折点，分别作点P 关于OB 、OA 对称点P ’、P ’’，化PM +PN +MN 为P ’N +MN +P ’’M ．当P ’、N 、M 、P ’’共线时，得△PMN 周长的最小值，即线段P ’P ’’长，连接OP ’、OP ’’，可得△OP ’P ’’为等边三角形，所以P ’P ’’=OP ’=OP =8．P OBAMNA类型二：两定两动【例2】如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为 A ．3B ．4C ．D ．【分析】此处E 点为折点，可作点C 关于AD 的对称，对称点C ’在AB 上且在AB 中点，化折线段CE +EF 为C ’E +EF ，当C ’、E 、F 共线时得最小值，C ’F 为CB 的一半，故选C ．【变式】如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是 A()E AFCDB()NMDCBAAB ．2C ．D ．4【分析】此处M 点为折点，作点N 关于BD 的对称点，恰好在AB 上，化折线CM +MN 为CM+MN ’．因为M 、N 皆为动点，所以过点C 作AB 的垂线，可得最小值，选C ．类型三：一定两动【例3】点P 是定点，在OA 、OB 上分别取M 、N ，使得PM+MN 最小。