解一元一次方程的方法和步骤()

初一上册数学解一元一次方程解一元一次方程是初中数学的基础内容。

下面是解一元一次方程的步骤：
1. 将方程整理成标准形式：ax + b = 0，其中a和b是已知常数。

2. 移项：将b移到方程的另一侧，得到ax = -b。

3. 消去系数a：如果a不等于0，则将方程两边都除以a，得到x = -b/a。

这是方程的唯一解。

4. 如果a等于0，那么方程就变成了bx = 0。

这种情况下，方程有无穷多解，即任何实数都可以作为方程的解。

总结起来，解一元一次方程的关键是将方程整理成标准形式，然后通过移项和消去系数的操作得到解。

如果a不等于0，则方程有唯一解；如果a等于0，则方程有无穷多解。

1。

一次方程的求解方法一次方程作为方程中最基础的形式，应用广泛，需要熟练掌握。

在管综考试中，涉及到的一次方程包含一元一次方程和二元一次方程组。

一、一元一次方程的求解一元一次方程求解的一般步骤：1、去分母：在方程两边同乘以各分母的最小公倍数，注意每项都要乘。

2、去括号：依据乘法分配律和去括号法则，注意变号，防止漏乘。

3、移项：把含有未知数的项移到方程的一边，常数项移到另一边，注意移项要变号。

5、系数化为1：方程两边同时除以未知数的系数或者乘以系数的倒数。

在求解具体的题目时，上述步骤不一定全部用到，同学们要根据具体的题目进行选择。

二、二元一次方程组的求解消元是解二元一次方程组的基本思路，所谓消元就是减少未知数的个数，使多元方程最终转化为一元方程再进行求解。

常用的消元方法有：代入消元法（简称代入法）和加减消元法（简称加减法）。

一般情况下，当未知数的系数为1时，选择代入消元法更快，同一未知数的系数出现相同或者互为相反数时，选择加减消元法更快。

如果这两种情况都不符合，一般会利用等式的性质，将某一未知数的系数化为相同或者相反数，再用加减消元法进行求解。

三、一次方程的应用在应用题中，利用一次方程求解的一般步骤是：1、审：审题，找准等量关系。

2、设：设未知数，一般求谁设谁。

3、列：根据等量关系列出方程。

4、解：根据前面所学方法求解方程。

在例3中，我们利用了二元一次方程组进行求解，列出方程后，由于方程中系数有分数，可以先去掉分母以后再进行求解。

例4的解题关键在于分析出每个竖式无盖箱子与横式无盖箱子需要几块正方形木板和长方形木板，从而找准等量关系，列出方程组。

在解方程组时，不同于例3，这道题目可以用选项代入验证，同学们可以结合自身掌握程度灵活选取。

含分母的一元一次方程解法步骤含分母的一元一次方程是指方程中存在形如1/x的项，解这种方程需要特别的方法。

下面将介绍一种解法步骤。

解法步骤如下：1. 清除分母。

首先，我们需要将方程中的分母消去，以便得到一个等价的无分母方程。

为了实现这一点，我们可以将方程两边乘以分母的最小公倍数，这样就可以消去分母。

假设方程中有两个分母为a和b的项，那么我们可以将方程两边乘以ab来消去分母。

如果方程中有多个分母项，那么我们需要找到它们的最小公倍数来进行消去。

2. 整理方程。

在消去分母后，我们得到一个等价的无分母方程。

现在，我们需要整理方程，将所有项移到等号的一侧，并将方程化简为标准形式ax + b = 0，其中a和b是已知的系数。

3. 求解方程。

根据一元一次方程的定义，我们知道方程的解就是使得方程成立的变量的取值。

对于标准形式的一元一次方程，我们可以通过移项的方法求解。

首先，我们将常数项b移到等号的另一侧，得到ax = -b。

然后，我们可以通过除以系数a来求解x的值，即x = -b/a。

这就是方程的解。

4. 验证解。

最后，我们需要验证求得的解是否符合原始方程。

将求得的解代入原始方程中，计算两边的值是否相等。

如果相等，那么解是正确的。

如果不相等，那么解是错误的，我们需要重新检查解的求解过程。

以上就是含分母的一元一次方程解法的步骤。

通过清除分母、整理方程、求解方程和验证解，我们可以准确地求解这类方程。

这种解法在实际问题中也具有一定的应用，可以帮助我们解决含有分母的一元一次方程。

解一元一次方程的方法
解一元一次方程可以采用以下方法：
1. 两边加减同一个数：对于方程ax + b = c，可以将b的相反
数加到两边，得到ax = c - b。

2. 两边乘除同一个数：对于方程ax = c，可以将方程两边同时
除以a，得到x = c/a。

要注意a不能为零。

3. 移项：对于方程ax + b = c，可以将b移动到等式的另一边，得到ax = c - b。

再根据上述方法继续求解x。

4. 合并同类项：对于方程ax + bx + c = d，可以将同类项ax和bx相加，得到(a + b)x + c = d。

再根据上述方法继续求解x。

5. 解方程应用逆运算：对于方程3x - 5 = 4，可以通过逆运算
来求解。

首先将-5移动到等式的另一边，得到3x = 4 + 5。

然
后再除以3，得到x = 9/3。

所以方程的解为x = 3。

以上是解一元一次方程的一些常用方法，根据具体情况选择合适的方法来解方程。

注意要进行合理的运算步骤，并在求解过程中保持等式的平衡。

求解一元一次方程的步骤一元一次方程是数学中最基本也是最简单的方程形式。

求解一元一次方程的方法可以通过反复运用等式性质和运算法则，从而得出方程的解。

本文将详细介绍求解一元一次方程的步骤，帮助读者更好地理解和应用这一方法。

一、方程的基本形式及含义一元一次方程的基本形式是：ax + b = 0，其中a和b是已知数，x是待求解的未知数。

在这个方程中，a称为方程的系数，b称为方程的常数项。

方程的解即为使等式成立的未知数的值。

二、求解一元一次方程的步骤1. 化简方程：根据方程的基本形式，将方程中的任何常数项或系数项进行合并、化简，使方程形式更简单。

比如消去常数项b。

2. 移项：把含有未知数x的项移到方程一侧，含有常数项的项移到方程另一侧，使方程变形为ax = -b的形式。

这一步可以通过等式两侧加减法完成。

3. 化简方程：根据需要，可以进一步化简方程，使其形式更加简洁明了。

例如，可以通过除以系数a来将方程转化为最简形式x = -b/a。

4. 检验解：将求得的解代入原方程中进行检验。

若代入后等式成立，则解是正确的；若代入后等式不成立，则需要重新检查步骤，排查错误。

三、求解一元一次方程的示例为了更好地说明上述求解步骤，下面举例说明。

例题：求解方程2x + 3 = 7。

1. 化简方程：方程已经是最简形式，无需化简。

2. 移项：将常数项3移到方程另一侧，得到2x = 7 - 3。

3. 化简方程：计算右侧等式得4，所以方程变为2x = 4。

4. 求解：将方程两侧除以系数2，得到x = 2。

这个结果即为方程的解。

使用这个解验证原方程，将x = 2代入原方程得到2 * 2 + 3 = 7，等式左侧为7，右侧也为7，两侧相等，说明解是正确的。

通过以上示例，我们可以看到，求解一元一次方程的步骤是简单直观的。

无论是在学校的数学课堂上，还是在实际生活中，一元一次方程都有重要的应用价值。

掌握求解一元一次方程的方法能够帮助我们更好地解决问题，提高解决实际困境的能力。

一元一次方程应用题解题技巧一元一次方程是数学中的一种基本方程，广泛应用于解决实际问题。

掌握一元一次方程的应用，对于提高数学解题能力具有重要意义。

本文将介绍一元一次方程应用题的基本概念、解题步骤和技巧。

一、基本概念一元一次方程是指未知数最高次数为1的方程，其形式为ax+b=0（a≠0）。

在实际应用中，一元一次方程常用来描述简单的一次性量与变量之间的关系，如速度与时间的关系、销售量与价格的关系等。

二、解题步骤1. 审题：仔细阅读题目，理解题意，找出题目中的等量关系。

2. 设未知数：根据题目中的等量关系，设定未知数。

3. 列方程：根据等量关系，列出方程。

4. 解方程：求出方程的解。

5. 检验：将解代入原方程，检验是否符合题意。

三、解题技巧1. 寻找等量关系：在应用题中，等量关系往往隐藏在题目中，需要仔细寻找。

常见的等量关系有速度相等、价格相等、数量相等等。

找到等量关系是解决应用题的关键。

2. 画图辅助：对于较为复杂的应用题，可以借助图形来辅助解题。

如行程问题中的路程图、销售问题中的价格走势图等。

通过图形，可以更加直观地理解题目中的信息。

3. 灵活运用未知数：在一元一次方程中，未知数的个数是有限的，可以通过设定不同的未知数来列出不同的方程，从而得到多个解。

但在实际问题中，有些解是不符合实际情况的，需要加以排除。

因此，在解题时要注意灵活运用未知数，不要盲目求解。

4. 利用公式法求解：对于一些特殊的一元一次方程，可以利用公式法求解。

如利用韦达定理求解一元二次方程的解。

对于一些特定的题目，利用公式法可以更加简便地得到答案。

四、例题解析【例题】某公司生产一种产品，每件成本为20元，售价为30元。

公司每天的人工、电费、设备折旧等固定成本为2000元。

为了降低成本并提高利润，公司决定采用新技术降低每件产品的成本。

如果新技术的成本每件降低5元，则每天的净收入可增加200元。

问是否需要采用新技术？【解析】设采用新技术后每天的生产量为x件，则采用新技术前每天的生产量为(x-1)件。

一元一次方程的应用题的解题步骤
在数学学习中，一元一次方程是一个非常基础且常见的概念。

通过学习一元一
次方程的应用题，我们可以更好地理解数学知识在实际问题中的应用。

解决一元一次方程的应用题需要遵循一定的步骤，下面将详细介绍解题的过程。

步骤一：审题
在解决一元一次方程的应用题时，首先要认真阅读题目，理解问题的意义和要求。

需要清楚问题中给出的已知条件和需要求解的未知数，确保对问题的整体把握。

步骤二：建立方程
根据问题的描述，利用代数式建立方程。

在建立方程时，要仔细分析问题的逻
辑关系，将问题中的信息转化为数学表达式。

步骤三：化简方程
将建立的方程进行整理和化简，消除无关项，最终得到标准的一元一次方程形
式ax+b=c。

步骤四：解方程
通过适当的运算和规律，解出方程中的未知数的值。

常用的解方程方法有逆运
算法、等价方程法和植入法等。

步骤五：验证解答
对求得的未知数进行验证，将其代入原方程，确保方程两边相等。

步骤六：给出答案
根据最终验证的结果，得出问题的解答。

通常将解答进行简要描述或总结，回
答问题的要求。

以上是解决一元一次方程应用题的基本步骤。

通过不断练习和掌握这些方法，
可以提高解题效率和准确性，帮助我们在数学学习中取得更好的成绩。

希望这些步骤能帮助你更好地理解和应用一元一次方程的知识。

解一元一次方程的一般步骤及根据：
1.去分母——等式的性质2
2.去括号——分配律
3.移项——等式的性质1
4.合并——分配律
5.系数化为1——等式的性质2
6.验根——把根分别代入方程的左右边看求得的值是否相等
注意事项：
（1）分母是小数时，根据分数的基本性质，把分母转化为整数；
（2）去分母时，方程两边各项都乘各分母的最小公倍数，此时不含分母的项切勿漏乘，分数线相当于括号，去分母后分子各项应加括号；
（3）去括号时，不要漏乘括号内的项，不要弄错符号；
（4）移项时，切记要变号，不要丢项，有时先合并再移项，以免丢项；
（5）系数化为1时，方程两边同乘以系数的倒数或同除以系数，不要弄错符号；
（6）不要生搬硬套解方程的步骤，具体问题具体分析，，找到最佳解法。

（7）分、小数运算时不能嫌麻烦。

（8）不要跳步，一步步仔细算。

[。

一元一次方程应用解题方法和技巧总结一元一次方程是数学中的一个基本概念，在实际生活中有着广泛的应用。

掌握一元一次方程的解法和应用技巧，对于解决实际问题具有重要的意义。

本文将介绍一元一次方程应用解题方法和技巧总结。

1. 一元一次方程的定义和特点一元一次方程是指未知数最高次数为1次的整式方程，其一般形式为ax+b=0(a,b为常数且a≠0)。

一元一次方程的特点是未知数最高次数为1次，且只含有一个未知数。

2. 一元一次方程的解法一元一次方程的解法通常采用移项、系数化为1和开方等步骤。

具体步骤如下：(1)移项：将方程的左侧移项右侧，使方程只含有一个未知数；(2)系数化为1：将方程的未知数系数化为1，常数项化为0；(3)开方：如果方程有根，则对其进行开方运算，得到方程的解。

3. 一元一次方程的应用技巧一元一次方程在实际生活中有着广泛的应用，例如在销售、工程、医学等领域。

掌握一元一次方程的应用技巧，可以帮助我们解决实际问题。

以下是一些常见的一元一次方程应用技巧：(1)代数式转换：将实际问题中的数学问题转换为代数式，并使用一元一次方程求解；(2)分析法：通过分析问题中的变量关系，列出方程求解；(3)试算法：通过试错法逐步逼近方程的解。

4. 举例以下是一元一次方程应用的一个例子：某工厂生产一批零件，共有10个不同规格的零件，每个零件的长度(单位：毫米)如下：29、31、32、33、34、35、36、37、38、39。

这批零件中，有且只有一个尺寸超过了公称尺寸40毫米，求公称尺寸的最大值和最小值。

分析：本题可以将问题转化为一个一元一次方程的应用问题。

设公称尺寸的最大值为x，则有以下情况：(1)29个零件长度都小于x，则有x-29u003c0，解得xu003c29；(2)29个零件长度都大于x，则有x+29u003e40，解得xu003e11；(3)有一个零件长度大于x，则有x+该零件长度-40u003e0，解得xu003e5.该零件长度小于x+29，解得xu003e7.5。

人教版六年级上册数学知识点归纳解一元一次方程的基本步骤在数学学习中，一元一次方程是我们常见的一种方程类型。

学习解一元一次方程的基本步骤对于巩固和提高我们的数学能力至关重要。

在本文中，我们将归纳总结人教版六年级上册数学中解一元一次方程的基本步骤。

一、方程的定义和概念方程是数学中用等号连接的含有未知数的算术或代数式。

一元一次方程是指只含有一个未知数，并且该未知数的最高次数为1的方程。

二、解一元一次方程的基本步骤解一元一次方程的基本步骤主要包括以下几个方面：1. 观察方程并确定未知数：首先，仔细观察方程，确定方程中的未知数是什么。

一元一次方程通常以字母表示未知数，如x、y等。

2. 移项：将含有未知数的项全部移动到方程的一边，将常数项移动到另一边，以使方程变成x=常数的形式。

在移项过程中，要注意保持等式两边的平衡。

3. 合并同类项：将等式两边的同类项进行合并，得到简化的方程。

4. 系数化为1：将未知数的系数化为1，使得方程变为x=常数的形式。

若未知数的系数不为1，则将方程两边同时除以未知数的系数。

5. 检验解：将求得的解代入原方程进行验证，确保解满足原方程。

三、解一元一次方程的示例以下通过一个具体的例子来演示解一元一次方程的基本步骤：例题：2x + 3 = 11步骤1：观察方程并确定未知数：方程中的未知数为x。

步骤2：移项：将3移到方程的另一边，得到2x = 11 - 3，即2x = 8。

步骤3：合并同类项：无需合并同类项。

步骤4：系数化为1：将未知数x的系数2化为1，得到x = 8 ÷ 2，即x = 4。

步骤5：检验解：将求得的解x = 4代入原方程，2x + 3 = 2(4) + 3 = 8 + 3 = 11，等式成立。

通过以上步骤，我们成功地解出了一元一次方程2x + 3 = 11的解为x = 4。

四、总结解一元一次方程的基本步骤是观察方程并确定未知数，移项，合并同类项，系数化为1，以及检验解。

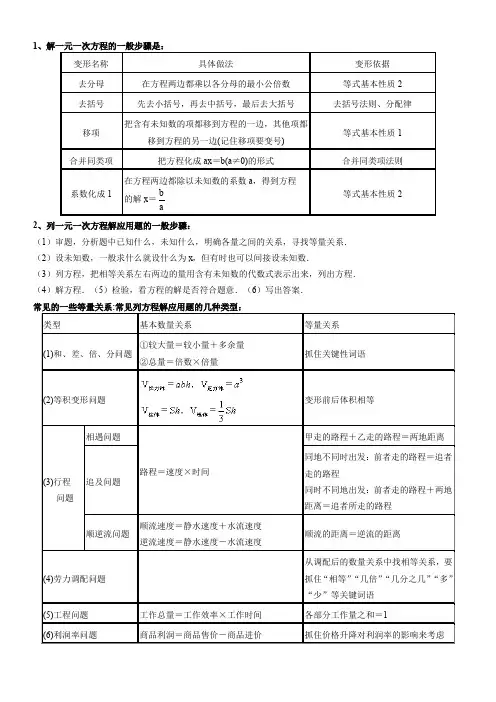
12、列一元一次方程解应用题的一般步骤：（1）审题，分析题中已知什么，未知什么，明确各量之间的关系，寻找等量关系．（2）设未知数，一般求什么就设什么为x，但有时也可以间接设未知数．（3）列方程，把相等关系左右两边的量用含有未知数的代数式表示出来，列出方程．（4）解方程．（5）检验，看方程的解是否符合题意．（6）写出答案．商品利润率＝1.商品销售此类问题主要涉及的关键量：进价，标价，实际售价，利润，利润率。

熟记这些量间的基本关系式：商品的利润=商品的实际售价-商品的进价.（这里不考虑其它因素）商品的利润率=商品打折后的售价=商品的标价÷10×折扣数.另外在解决商品的利润率的问题中，还涉及如下关系式.注意会由基本关系式推出式子的变形，以便于解决问题.例：由×100%=利润率，可得商品的实际售价=商品的进价×(1+利润率).例1、商店里的皮上衣每件标价为2200元，在一次促销活动中，它打八折销售，结果仍获利10%，求此商品的进价.分析：题中的相等关系是商品的进价×(1+利润率)=商品的实际售价.解：设此商品的进价为x元，依题意(1+10%)x=2200×0.8.解这个方程，得x=1600.答：此商品的进价为1600元.例2、以现价销售一件商品的利润率为30%，如果商家在现有的价格基础上先提价40%，后降价50%的方法进行销售，商家还能有利润吗？为什么？依题意其后来折扣后的售价为(1+30%)a×(1+40%)(1-50%)=0.91a.∵0.91a-a=-0.09a,∴×100%=-9%.答：商家不仅没有利润，而且亏损的利润率为9%.2.银行存贷款例3、夏老师欲购买一辆汽车，销售商告诉夏老师，若采取分期付款方式：一种付款方式是第一月付4万元，以后每月付款一万元；另一种付款方式是前一半时间每月付款1万四千元，后一半时间，每月付款1万1千元；两种付款方式中付款钱数和付款时间都相同。

一元一次方程的解法一元一次方程是指形如ax + b = 0的方程，其中a和b为已知数，x 为未知数。

解一元一次方程是求出方程中未知数x的值。

在解这类方程时，可以采用以下几种方法来求解。

1. 逐步代入法：逐步代入法是一种比较简单易懂的解法，适用于简单的一元一次方程。

具体的步骤如下：Step 1: 将方程中的x替换为一个变量（例如使用y）。

Step 2: 使用代入法将方程中的y的值逐步代入，求解y的值。

Step 3: 将求得的y的值代回方程，求解出x的值。

Step 4: 验证求解的结果是否符合原方程。

例如，对于方程2x + 3 = 7，可以使用逐步代入法进行求解：Step 1: 将x替换为y，得到2y + 3 = 7。

Step 2: 将y的值代入，得到2 * 2 + 3 = 7，即4 + 3 = 7。

Step 3: 求解出y的值，得到y = 2。

Step 4: 将y的值代回原方程，得到2x + 3 = 7，将y替换为2得到2x + 3 = 7。

继续求解，得到2x = 7 - 3，即2x = 4。

最终求解出x的值，得到x = 2。

2. 相等原则法：相等原则法是一种常用的解法，适用于各种形式的一元一次方程。

具体的步骤如下：Step 1: 将方程中的等号左右两边的式子进行化简。

Step 2: 将化简后的等式右侧的常数项移到左侧，同时移变量项到右侧，得到标准形式方程。

Step 3: 根据相等原则，使等式两侧的值相等，同时进行运算得到未知数的值。

Step 4: 验证求解的结果是否符合原方程。

例如，对于方程5x - 2 = 13，可以使用相等原则法进行求解：Step 1: 化简方程，得到5x = 15。

Step 2: 将常数项移到左侧，移动变量项到右侧，得到5x - 15 = 0。

Step 3: 根据相等原则，等式两侧的值相等，进行运算得到x的值，即5 * x = 15，解得x = 3。

Step 4: 验证结果，将x代入原方程，得到5 * 3 - 2 = 13，验证结果符合原方程。

解一元一次方程的一般步骤一、等式：用等号表示相等关系的式子叫等式。

等式性质 1 等式两边加上（或减去）同一个数（或式子），结果仍相等。

等式性质 2 等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。

等式性质 3 等式两边同时乘方（或开方），两边依然相等。

等式性质 4 等式具有对称性。

若a=b,则b=a。

等式性质 5 等式具有对传递性。

如果a=b且b=c,那么a=c。

注意：（1）、等式中一定含有等号；（2）、等式两边除以一个数时，这个数必须不为0；（3）、对等式变形必须同时进行，且是同一个数或式。

二、一元一次方程的概念：只含有一个未知数（元）且未知数的指数是1（次）的方程叫做一元一次方程。

解方程就是求出使方程中等号左右两边相等的未知数的值，能使方程左右两边相等的未知数的值，叫做方程的解1、写出一个满足下列条件的一元一次方程：①某个未知数的系数是2；②方程的解是3；这样的方程是。

2、若关于x的方程（k－1）x2+x－1=0是一元一次方程，则k= 。

三、列一元一次方程解应用题的一般步骤：1、审题：弄清题意．2、找出等量关系：找出能够表示本题含义的相等关系．3、设出未知数，列出方程：设出未知数后，表示出有关的含字母的式子，然后利用已找出的等量关系列出方程。

（1）、直接设元法，求什么设什么，方程的解就是问题的答案；（2）、间接设元法，不是求什么设什么，方程的解并不是问题的答案，需要根据问题中的数量关系求出最后的答案。

4、解方程：解所列的方程，求出未知数的值．5、检验并作答：检验所求出的未知数的值是否是方程的解，是否符合实际，检验后写出答案。

四、解一元一次方程的一般步骤和注意事项：1、去分母：在方程两边都乘分母的最小公倍数。

（1）、没有分母的项不要漏乘（尤其整数项）。

也可以说方程中的每一项都要乘以分母的最小公分母。

（2)、去分母时，应把分子作为一个整体加上括号。

2、去括号：先去小括号,再去中括号,最后去大括号，注意：括号外面是负号时，去括号后，括号内的每一项都要变号。

初中数学解一元一次方程的基本步骤一、引言解一元一次方程是初中数学中的基本内容之一，也是进一步学习代数和方程的基础。

掌握解一元一次方程的基本步骤对于提高数学解题能力至关重要。

二、方程的定义和基本形式一元一次方程是由一个未知数和系数组成的等式。

其一般形式表示为：ax + b = 0，其中，a和b为已知常数，x为未知数。

三、解一元一次方程的基本步骤解一元一次方程的基本步骤如下：1. 去括号：如果方程中有括号，根据分配律进行去括号运算；2. 合并同类项：合并方程中的同类项，即将具有相同变量的项进行简化；3. 移项：将含有未知数的项移到方程的一边，将常数项移到方程的另一边；4. 化简：对于方程两边进行合并、消去或简化，使方程的形式变为ax = b的形式；5. 求解：根据解一元一次方程的性质，将解代入方程中进行验证；6. 得出结论：根据情况得出方程的解或者无解的结论。

四、实例演示为了更好地理解解一元一次方程的基本步骤，我们来看一个实际的例子：例1：解方程2x + 5 = 11解：第一步，去括号：方程中没有括号，跳过此步骤；第二步，合并同类项：方程中的同类项为2x，简化后方程为2x + 5 = 11；第三步，移项：将常数项5移到方程的另一边，得到2x = 11 - 5；第四步，化简：计算得到2x = 6；第五步，求解：将解x = 3代入方程2x + 5 = 11进行验证，验证结果为2 × 3 + 5 = 11，方程成立；第六步，得出结论：方程的解为x = 3。

五、解一元一次方程的注意事项在解一元一次方程时，还需要注意以下几点：1. 若方程两边是完全相同的多项式，则方程有无穷多个解；2. 若方程两边是完全不同的多项式，则方程没有解；3. 若方程两边是完全相同的非零常数，则方程没有解。

六、解一元一次方程的应用解一元一次方程的方法在日常生活和其他学科中都有广泛的应用。

例如，在商业中解方程可以帮助我们计算商品折扣率、利润和成本；在物理学中解方程可以求解速度和加速度等问题。

一元一次解方程及步骤
嘿，朋友们！咱今儿来聊聊一元一次解方程呀！这可是数学里挺重
要的一块儿呢！
你看啊，一元一次方程就像是一个小小的谜团，等着我们去解开它。

比如说，给你个方程 3x+5=14，那怎么解呢？其实啊，就跟咱玩解谜
游戏似的。

首先呢，咱得想法子把那个带着 x 的项单独拎出来。

就好比是要把
藏在一堆东西里的宝贝给找出来。

在这个例子里，咱就先把 5 给挪到
等号右边去，这一挪，符号可就得变喽，变成3x=14-5，也就是3x=9。

接下来呀，就该求出 x 到底是多少啦。

这就好像是已经知道了宝藏
的线索，就差临门一脚找到它啦。

那怎么找呢？简单，把 3 除过去，x 不就等于 9÷3 嘛，那 x 就是 3 呀！你说神奇不神奇？
再举个例子，2x-7=5，这又咋解呢？还是老办法呀，先把 7 移到等
号右边，变成 2x=5+7，也就是 2x=12。

然后呢，除以 2，x 就等于 6 啦！
解一元一次方程就像是走一条路，每一步都得走得稳稳当当的。

你
可别小瞧了这些步骤，少一步都不行呢！就好像建房子，少块砖房子
都不结实呀！
咱平时生活里其实也经常会碰到类似解方程的事儿呢。

比如说，你
知道买一个东西花了多少钱，又知道总共花了多少钱，那不就能算出
买了几个嘛，这和解方程不是一个道理嘛！
学一元一次解方程啊，不仅能让咱在数学考试里拿高分，还能让咱
脑子更灵活，更会思考问题呢！所以啊，大家可得好好学，别觉得它
难就退缩啦！加油哦，朋友们，相信你们都能轻松搞定一元一次方程！就这么简单的事儿，咱肯定能行！。