管理运筹学作业 韩伯棠第3版高等教育出版社课后答案
- 格式:doc
- 大小:476.00 KB
- 文档页数:31


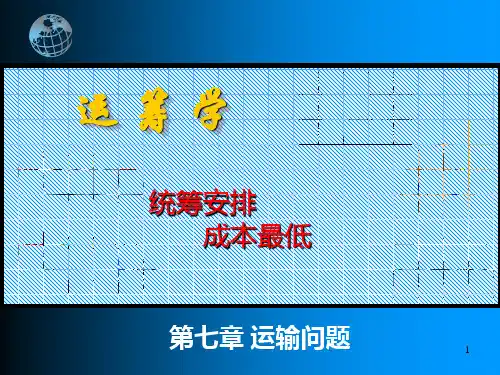
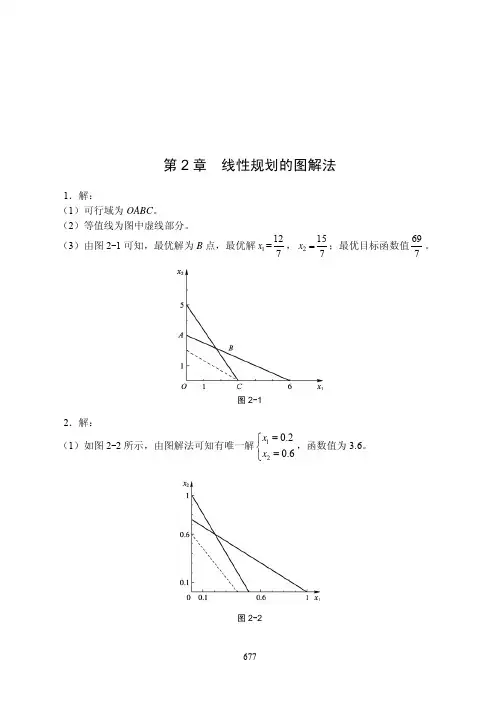
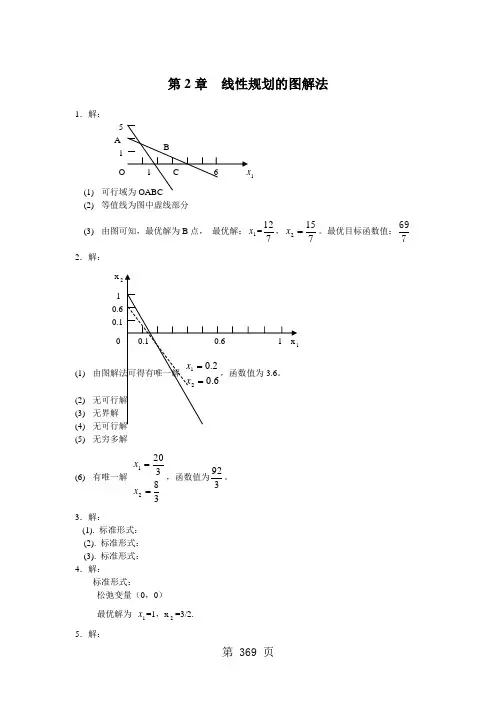
第2章 线性规划的图解法1.解: 5 A 11 (1) (2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 1 0(1) (2) (3) 无界解 (4) (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式: (2). 标准形式:(3). 标准形式: 4.解:标准形式:松弛变量(0,0) 最优解为 1x =1,x 2=3/2. 5.解:标准形式:剩余变量(0.0.13) 最优解为 x 1=1,x 2=5. 6.解:(1) 最优解为 x 1=3,x 2=7. (2) 最优解为 x 1=8,x 2=0. (3) 不变化。
因为当斜率31121-≤-≤-c c ,最优解不变,变化后斜率为1,所以最优解不变. 7.解:模型:(1) 1501=x ,702=x ,即目标函数最优值是103000 (2) 2,4有剩余,分别是330,15,均为松弛变量. (3) 50,0,200,0。
(4) 在[]500,0变化,最优解不变。
在400到正无穷变化,最优解不变. (5) 因为143045021-≤-=-c c ,所以原来的最优产品组合不变. 8.解:(1) 模型:b a x x f 38min +=基金a,b 分别为4000,10000,回报率为60000。
(2) 模型变为:b a x x z 45max +=推导出:180001=x 30002=x ,故基金a 投资90万,基金b 投资30万。
第3章 线性规划问题的计算机求解1.解:(1) 1501=x ,702=x 。
目标函数最优值103000。
(2) 1,3车间的加工工时已使用完;2,4车间的加工工时没用完;没用完的加工工时数为2车间330小时,4车间15小时. (3) 50,0,200,0含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
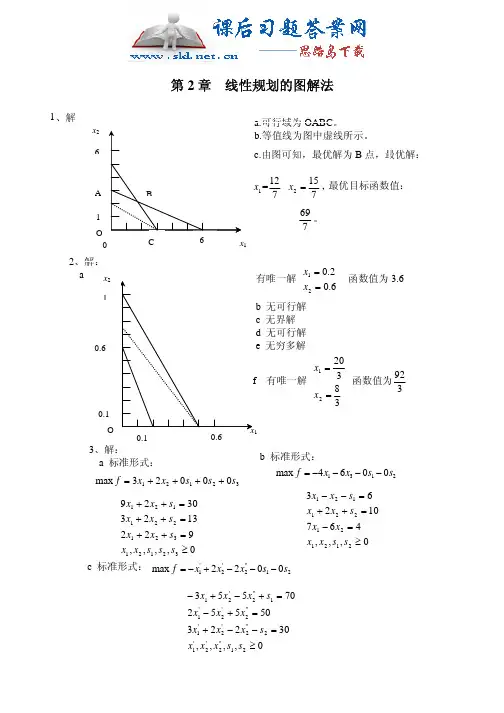

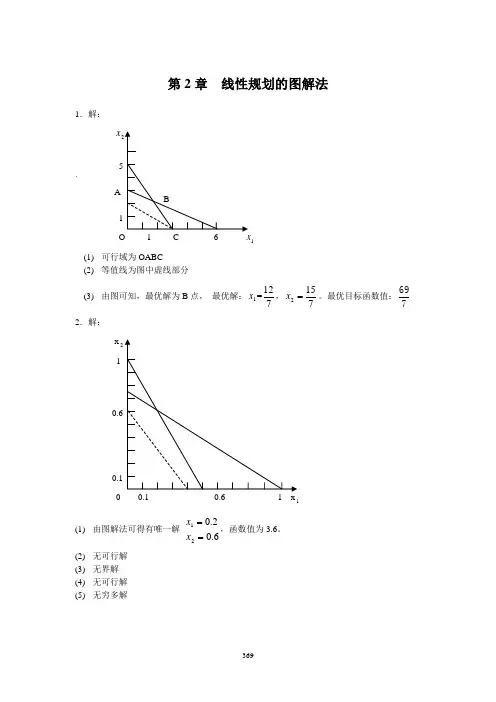
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023max s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064min s s x x f +++= 0,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022min s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510max s s x x z +++= 0,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811min s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。


一、管理运筹学的定义运筹学(Operational Research,简称OR) ,英文直译为“运作研究”。
管理运筹学是应用分析、试验、量化的方法,对经济管理系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
——《中国企业管理百科全书》绪论二、管理运筹学Ⅰ的主要分支线性规划(Linear Programming,简称LP)整数规划(Integral Programming,简称IP)目标规划(Objective Programming,简称OP)动态规划(Dynamic Programming,简称DP)图与网络(Graph and Network)三、管理运筹学的工作步骤提出问题、分析问题建立模型求解解的检验、控制、实施四、运筹学方法的特点1. 最优化方法2. 定量的方法线性规划(LP)一、问题的提出1.生产计划安排问题:合理利用人力、物力、财力等,在资源有限的约束条件下,寻求使得获利最大的最优生产计划方案。
2.人力资源分配的问题:在满足工作的需要的条件下,寻求使用最少的劳动力的最优分配方案。
3.套裁下料问题:在保证正常生产,完成生产任务的条件下,寻求使用原料最省的最优下料方案。
4.投资问题:在投资额限制的条件下,从多个投资项目中选取使得投资回报最大的最优投资方案。
5.运输问题:寻求使得总运费最小的最优调运方案。
二、建模1.一般步骤:分析问题,设出决策变量根据所提问题列出目标函数根据已知条件列出所有约束条件数学模型的一般形式★矩阵形式:假设有n个决策变量,m个约束条件。
目标函数:Max (Min)z = CX约束条件:AX ≤(=, ≥)b.X≥0其中,C=(c1 , c2 , …, cn )(价值向量)X= (x1 , x2 , …, xn )T(决策变量向量)b=(b1 , b2 , …, bm )T (限定向量)a11 a12 (1)a21 a22 …a2n (约束条件系数矩阵) Am×n = ……am1 am2 …amn数学模型的特点(1)由目标函数和约束条件构成;(2)目标函数只有两种情况:求极小或求极大。
第 4 章线性规划在工商管理中的应用1、解:为了用最少的原材料得到 10 台锅炉,需要混合使用 14 种下料方案设按 14 种方案下料的原材料的根数分别为 x 1,x 2,x 3,x 4,x 5,x 6,x 7,x 8,x 9, x 10,x 11,x 12,x 13,x 14,则可列出下面的数学模型: min f =x 1+x 2+x 3+x 4+x 5+x 6+x 7+x 8+x 9+x 10+x 11+x 12+x 13+x 14 s .t . 2x 1+x 2+x 3+x 4 ≥ 80x 2+3x 5+2x 6+2x 7+x 8+x 9+x 10≥ 350 x 3+x 6+2x 8+x 9+3x 11+x 12+x 13≥ 420x 4+x 7+x 9+2x 10+x 12+2x 13+3x 14 ≥ 10x 1,x 2,x 3,x 4,x 5,x 6,x 7,x 8,x 9,x 10,x 11,x 12,x 13,x 14≥ 0 用管理运筹学软件我们可以求得此问题的解为:x 1=40,x 2=0,x 3=0,x 4=0,x 5=116.667,x 6=0,x 7=0,x 8=0, x 9=0,x 10=0,x 11=140,x 12=0,x 13=0,x 14=3.333 最优值为 300。
2、解:从上午 11 时到下午 10 时分成 11 个班次,设 x i 表示第 i 班次安排的临时工的人数,则可列出下面的数学模型:min f=16(x 1+x 2+x 3+x 4+x 5+x 6+x 7+x 8+x 9+x 10+x 11) s .t . x 1+1 ≥ 9x 1+x 2+1 ≥ 9x 1+x 2+x 3+2 ≥ 9x 1+x 2+x 3+x 4+2 ≥ 3x 2+x 3+x 4+x 5+1 ≥ 3 x 3+x 4+x 5+x 6+2 ≥ 3 x 4+x 5+x 6+x 7+1 ≥ 6 x 5+x 6+x 7+x 8+2 ≥ 12 x 6+x 7+x 8+x 9+2 ≥ 12 x 7+x 8+x 9+x 10+1 ≥ 7 x 8+x 9+x 10+x 11+1 ≥ 7x 1,x 2,x 3,x 4,x 5,x 6,x 7,x 8,x 9,x 10,x 11≥ 0 用管理运筹学软件我们可以求得此问题的解为:x 1=8,x 2=0,x 3=1,x 4=1,x 5=0,x 6=4,x 7=0,x 8=6,x 9=0,x 10=0,x 11=0 最优值为 320。
运筹学第三版习题答案
《运筹学第三版习题答案》
运筹学是一门研究如何有效地组织和管理资源,以达到最优解的学科。
第三版习题答案是这门学科的重要参考资料,它包含了大量的问题和答案,帮助学生更好地理解和掌握运筹学的知识。
在运筹学中,我们需要运用数学和逻辑推理来解决各种实际问题,比如资源分配、生产计划、物流管理等。
通过对这些问题的分析和建模,可以找到最优的解决方案,从而提高效率和降低成本。
而第三版习题答案则为我们提供了一系列实例和解决方法,帮助我们更好地理解和应用运筹学的理论。
在学习运筹学的过程中,我们常常会遇到各种各样的问题,有些问题可能会让我们感到困惑和无从下手。
而第三版习题答案则为我们提供了宝贵的参考,帮助我们更好地理解问题的本质,掌握解决问题的方法。
通过对习题答案的学习和思考,我们可以提高自己的分析和解决问题的能力,为将来的实际工作做好准备。
除此之外,第三版习题答案还可以帮助我们检验自己的学习成果。
通过做习题和对照答案,我们可以及时发现自己的不足之处,及时调整学习方法和提高学习效率。
这对于我们的学习和成长都是非常有益的。
总的来说,第三版习题答案是运筹学学习过程中的重要工具,它不仅可以帮助我们更好地理解和掌握运筹学的知识,还可以帮助我们提高解决问题的能力和检验学习成果。
希望大家在学习运筹学的过程中,能够善加利用这份宝贵的资料,不断提高自己的能力和水平。
课程:管理运筹学管理运筹学作业第二章线性规划的图解法P23:Q2:(1)-(6);Q3:(2)Q2:用图解法求解下列线性规划问题,并指出哪个问题具有唯一最优解,无穷多最优解,无界解或无可行解。
(1)Min f=6X1+4X2约束条件:2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下:如图1Min f=3.6X1=0.2, X2=0.6本题具有唯一最优解。
图1(2)Max z=4X1+8X2约束条件:2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下:如图2:Max Z 无可行解。
图2(3) Max z =X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下:如图3: Max Z=有无界解。
图3(4) Max Z =3X1-2X2 约束条件:X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下:如图4: Max Z 无可行解。
图4(5)Max Z=3X1+9X2 约束条件:X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下:如图5:Max Z =66;X1=4 X2=6本题有唯一最优解。
图5(6)Max Z=3X1+4X2 约束条件:-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下:如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。
图6Q3:将线性规划问题转化为标准形式(2)min f=4X1+6X2约束条件:3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下:1)目标函数求最小值化为求最大值:目标函数等式左边min改为max,等式右边各项均改变正负号。
2)决策变量非负化:若Xi≤0,令Xi=-Xia,(Xia≥0);若Xi无约束,令Xi=Xia-Xib,(Xia≥0,Xib≥0);将上述替换变量代入目标函数和约束条件。
3)约束条件不等式化为等式:不等号为≤的,不等式左边加松弛变量;不等号为≥的,不等式左边减剩余变量。
4)常数项为非负。
本题标准化如下:令:z=-f,则:Max z=min (-f)= -4X1-6X2+0X3+0X4所以:Max z=-4X1-6X2+0X3+0X4约束条件:3X1-2X2-X3+0X4=6X1+2X2+0X3-X4=107X1-6X2+0X3+0X4=4X1,X2,X3,X4>=0第三章线性规划问题的计算机求解P37: Q4; P38:Q5Q4:考虑下面的线性规划问题:Max Z=2X1+X2-X3+X4约束条件:X1-X2+2X3+X4>=2X1-3X2+X3-X3-X4<=42X2+X3+2X4<=3X1,X2,X3,X4>=0计算机结果输出如下:**********************最优解如下*************************目标函数最优值为: 18.5变量最优解相差值------- -------- --------x1 8.5 0x2 1.5 0x3 0 4.5x4 0 4约束松弛/剩余变量对偶价格------- ------------- --------1 5 02 0 23 0 3.5目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 .2 2 无上限x2 -3 1 无上限x3 无下限 1 5.5x4 无下限 1 5常数项数范围:约束下限当前值上限------- -------- -------- --------1 无下限2 72 -1 4 无上限3 0 3 无上限回答下列问题:(1)请指出其最优解及其最优目标值。
(2)那些约束条件起到了约束作用,它们的对偶价格各为多少,请给予说明。
(3)如果请你选择一个约束条件,将它的常数项增加一个单位,你将选择哪一个约束条件,这时候最优目标函数值是多少?(4)请问在目标函数中X3的系数在什么范围内变化时,其最优解不变,这时其最优目标函数值是否会发生变化,为什么?(5)请问在目标函数中X1的系数在什么范围内变化时,其最优解不变,这时其最优目标函数值是否会发生变化,为什么?解题如下:答:(1)其最优解是X1=8.5;X2=1.5;X3=0;X4=0;最优目标值是MaxZ=18.5(2)约束条件2、3起到了约束的作用,它们的对偶价格分别为2和3.5。
(3)因为求目标函数值MaxZ,因选择约束条件3的对偶价格为3.5,当该约束条件改善一个单位时,目标函数最大值改善3.5。
这时目标函数最大值为18.5+3.5=22。
(4)计算机输出结果可知,当X3的系数在(-∞,5.5)范围内变化时,其最优解不变。
且这时其最优目标函数值不会发生变化。
因为输出结果中X3=0。
(5)计算机输出结果可知,当X1的系数在(0.2,∞)范围内变化时,其最优解不变。
因X1=8.5为最优解,因此目标函数值会随着X1的变化而改变。
Q5、考虑下面线性规划问题:MinZ=16X1+16X2+17X3;约束条件:X1+X2<=300.5X1-X2+6X3>=153X1+4X2-X3>=20X1,X2,X3>=0计算机输出结果如下:**********************最优解如下*************************目标函数最优值为: 148.916变量最优解相差值------- -------- --------x1 7.297 0x2 0 .703x3 1.892 0约束松弛/剩余变量对偶价格------- ------------- --------1 22.703 02 0 -3.6223 0 -4.73目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 1.417 16 16.565x2 15.297 16 无上限x3 14.4 17 192常数项数范围:约束下限当前值上限------- -------- -------- --------1 7.297 30 无上限2 3.333 15 4353 -2.5 20 90回答如下问题:(1)第二个约束方程的对偶价格是一个负数(-3.622),它的含义是什么?(2)X2的相差值为0.703,它的含义是什么。
(3)当目标函数中X1的系数从16降为15,而X2的系数从16升为18时,最优解是否会发生变化?会发生变化。
(4)当第一个约束条件的常数项从30变为15,而第二个常数项从15变为80时,你能断定其对偶价格是否会发生变化,为什么?会。
384.32解题如下:答:(1)第二个约束方程的对偶价格是一个负数(-3.622),其含义是如果把约束条件2的下限15增加1,那么最优目标函数值将增加3.622。
即148.916+3.622=152.538 (2)决策变量最优解非零,则相差值为0;决策变量最优解为零,则存在正数相差值。
相差值表示为使得相应的决策变量参加最优生产组合(最优解取正),其价值系数至少需要增加的量(max型目标函数)或其价值系数至少需要减少的量(min型目标函数)。
X2的相差值为0.703,它的含义是X2的系统需要减少0.703,即16-0.703=15.297,此时的目标函数值为148.919.(3) 当目标函数中X1的系数从16降为15,而X2的系数从16升为18时,最优解不会发生变化,但是目标函数最优值会发生变化。
因为X1在(1.417, 16.565)和X2在(15.297, )范围内变化时,最优解不会发生变化。
只是会影响目标函数最优值变化。
(4)当第一个约束条件的常数项从30变为15,而第二个常数项从15变为80时,对偶价格不会发生变化。
对偶价格是某种资源在最佳生产组合的基础上,每增加一个单位产生的最优目标值的改进量。
常数项的变化只对目标函数最优解产生影响,对偶价格不会产生变化。
第四章线性规划在工商管理中的应用作业:P57-58,Q2,Q3Q2:某快餐店座落在一个旅游景点中。
该景点远离市区,平时顾客不多,而在每个周六顾客猛增。
该店主要为顾客提供低价位的快餐服务。
该店雇佣2名正式工,每天工作8小时。
其余工作由临时工担任,临时工每天工作4小时。
周六营业时间11:00a.m-22:00p.m。
根据就餐情况,在周六每个营业小时所需的职工数如表(包括正式工和临时工)。
已知一名正式工从11点上班,工作4小时后休息1小时,而后在工作4小时。
另外一名正式工13点上班,工作4小时后,休息1小时,在工作4小时。
又知临时工每小时工资4元。
(1)、满足对职工需求的条件下,如何安排临时工的班次,使得临时工成本最小。
(2)、这时付给临时工的工资总额是多少,一共需要安排多少临时工班次。
请用剩余变量来说明应该安排一些临时工的3小时工作时间的班次,可使得总成本更小。
(3)、如果临时工每班工作时间可以是3小时,也可以是4小时,那么如何安排临时工的班次,使得临时工总成本最小。
这样比(1)节省多少费用,这时要安排多少临时工班次。
解题如下:(1)临时工的工作时间为4小时,正式工的工作时间也是4小时,则第五个小时需要新招人员,临时工只要招用,无论工作多长时间,都按照4小时给予工资。
每位临时工招用以后,就需要支付16元工资。
从上午11时到晚上10时共计11个班次,则设Xi(i=1,2,…,11)个班次招用的临时工数量,如下为最小成本:minf=16(X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11)两位正式工一个在11-15点上班,在15-16点休息,然后在16-20点上班。
另外一个在13-17点上班,在17-18点休息,18-22点上班。
则各项约束条件如下:X1+1>=9X1+X2+1>=9X1+X2+X3+2>=9X1+X2+X3+X4+2>=3X2+X3+X4+X5+1>=3X3+X4+X5+X6+2>=3X4+X5+X6+X7+2>=6X5+X6+X7+X8+1>=12X6+X7+X8+X9+2>=12X7+X8+X9+X10+1>=7X8+X9+X10+X11+1>=7Xi>=0(i=1,2, (11)运用计算机解题,结果输出如下;**********************最优解如下*************************目标函数最优值为: 320变量最优解相差值------- -------- --------x1 8 0x2 0 0x3 1 0x4 0 0x5 1 0x6 4 0x7 0 0x8 6 0x9 0 0x10 0 1x11 0 1目标函数最优值为: 320这时候临时工的安排为:变量班次临时工班次时间------- -------- --------x1 8 11:00-12:00x2 0 12:00-13:00x3 1 13:00-14:00x4 0 14:00-15:00x5 1 15:00-16:00x6 4 16:00-17:00x7 0 17:00-18:00x8 6 18:00-19:00x9 0 19:00-20:00x10 0 20:00-21:00x11 0 21:00-22:00(2)付出工资总额为:Minf=16(X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11)=16(8+0+1+0+1+4+0+6+0+0+0)=320元共需要安排20个临时工班次。