物理几何光学竞赛讲解及试题精品
- 格式:ppt
- 大小:427.50 KB
- 文档页数:26
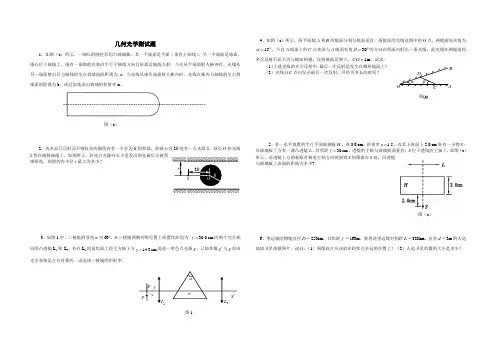
几何光学测试题1、如图(a )所示,一细长的圆柱形均匀玻璃棒,其一个端面是平面(垂直于轴线),另一个端面是球面,球心位于轴线上.现有一很细的光束沿平行于轴线方向且很靠近轴线人射.当光从平端面射人棒内时,光线从另一端面射出后与轴线的交点到球面的距离为a ;当光线从球形端面射人棒内时,光线在棒内与轴线的交点到球面的距离为b .试近似地求出玻璃的折射率n 。
2、内表面只反射而不吸收光的圆筒内有一半径为R 的黑球,距球心为2R 处有一点光源S ,球心O 和光源S 皆在圆筒轴线上,如图所示.若使点光源向右半边发出的光最后全被黑球吸收,则筒的内半径r 最大为多少?3、如图1中,三棱镜的顶角α为60︒,在三棱镜两侧对称位置上放置焦距均为 30.0cm f =的两个完全相同的凸透镜L 1和 L 2.若在L 1的前焦面上距主光轴下方14.3cm y =处放一单色点光源S ,已知其像S '与S 对该光学系统是左右对称的.试求该三棱镜的折射率.4、如图(a )所示,两平面镜A 和B 的镜面分别与纸面垂直,两镜面的交线过图中的O 点,两镜面间夹角为︒=15α,今自A 镜面上的C 点处沿与A 镜面夹角︒=30β的方向在纸面内射出一条光线,此光线在两镜面经多次反射后而不再与镜面相遇。
设两镜面足够大,1=CO m 。
试求:(1)上述光线的多次反射中,最后一次反射是发生在哪块镜面上? (2)光线自C 点出发至最后一次反射,共经历多长的时间?5、有一水平放置的平行平面玻璃板H ,厚3.0 cm ,折射率 1.5n =。
在其下表面下2.0 cm 处有一小物S ;在玻璃扳上方有一薄凸透镜L ,其焦距30cm f =,透镜的主轴与玻璃板面垂直;S 位于透镜的主轴上,如图(a )所示。
若透镜上方的观察者顺着主轴方向观察到S 的像就在S 处,问透镜与玻璃板上表面的距离为多少?6、望远镜的物镜直径D =250cm ,其焦距f =160m 。

【预赛 三一 自招】高中物理竞赛模拟专题之《几何光学》1 如图所示,一储油圆桶,底面直径与桶高均为d .当桶内无油时,从某点A 恰能看到桶底边缘上的某点B .当桶内油的深度等于桶高一半时,在A 点沿AB 方向看去,看到桶底上的C 点,C 、B 相距.4d由此可得油的折射率以及光在油中传播的速度为() (A)17s m 10106,102-⋅⨯ (B) 17s m 10106,210-⋅⨯ (C)18s m 10105.1,210-⋅⨯ (D) 18s m 10105.1,102-⋅⨯ 分析与解 如图所示,C 点发出的光线经O 点折射后射向A 点,则由折射定律r n i n sin sin 0=(n 为油的折射率,0n 为空气的折射率),可知油的折射率210/45sin sin sin ===OC CD i r n .光在折射率为n 的介质中速度n c v =,因而可进一步求得光在油中传播的速度1718s m 10106s m 2/10103--⋅⨯=⋅⨯==n c v .故选(B ).题 13-1 图2 在水中的鱼看来,水面上和岸上的所有景物,都出现在一倒立圆锥里,其顶角为( ) (A )48.8(B )41.2(C )97.6(D )82.4分析与解 本题是一个全反射的应用题.根据水的折射率,光线从空气射入水中时反射光的临界角 8.481arcsin≈=ni c,其中n =1.33为水的折射率.如图所示,当光线以90 的最大入射角射入水中时,折射角为r ,故所有射入水中的光线的折射角均小于r ,根据空间旋转对称,水面上所有的景物都落在顶角为 6.9722c==i r 的锥面内.故选(C ).题 13-2 图3 一远视眼的近点在1 m 处,要看清楚眼前10 cm 处的物体,应佩戴怎样的眼镜() (A ) 焦距为10 cm 的凸透镜 (B ) 焦距为10 cm 的凹透镜 (C ) 焦距为11 cm 的凸透镜 (D ) 焦距为11 cm 的凹透镜 分析与解 根据薄透镜的成像公式f p p '=-'111,可由物距p 和像距p '计算透镜的像方焦距f '.根据题意,物距p =-0.1 m ,像距p '=-1 m ,则代入公式可求得像方焦距cm 11m 11.0=≈'f .像方焦距为正数,故为凸透镜.正确答案为(C )4 一平行超声波束入射于水中的平凸有机玻璃透镜的平的一面,球面的曲率半径为10 cm ,试求在水中时透镜的焦距.假设超声波在水中的速度为11s m 1470-⋅=u ,在有机玻璃中的速度为12s m 2680-⋅=u .分析 薄透镜的像方焦距公式为210r n n r n n n f Li L i---=',弄清公式中各值代表的物理意义即可求解本题.这里i n n 、0分别为透镜前后介质的折射率,由题意透镜前后介质均为水,故水n n n i ==0;L n 为透镜的折射率;1r 为透镜平的一面的曲率半径,即∞=1r ;2r 为透镜凸的一面的曲率半径,即2r = - 10 cm.解 由上述分析可得cm 1.2211212122221112-=-=-=---='u u rn n r r n n r n n n f i5 将一根短金属丝置于焦距为35 cm 的会聚透镜的主轴上,离开透镜的光心为50 cm处,如图所示. (1) 试绘出成像光路图;(2)求金属丝的成像位置.分析 (1) 凸透镜的成像图只需画出两条特殊光线就可确定像的位置.为此作出以下两条特殊光线:过光心的入射光线折射后方向不变;过物方焦点的入射光线通过透镜入射后平行于主光轴.(2)在已知透镜像方焦距f '和物距p 时,利用薄透镜的成像公式f p p '=-'111即可求得像的位置.解 (1)根据分析中所述方法作成像光路图如图所示. (2) 由成像公式可得成像位置为cm 117cm 355035)50(=+-⨯-='+'='f p f p p题 13-5 图6 一架显微镜的物镜和目镜相距为 20 cm ,物镜焦距为7 mm ,目镜的焦距为 5 mm ,把物镜和目镜均看做是薄透镜.试求:(1)被观察物到物镜的距离;(2)物镜的横向放大率;(3)显微镜的视角放大率.分析 (1)图示为显微镜的工作原理图.使用显微镜观察物体时,是将物体置于物镜物方焦点o f 外侧附近.调节物镜与目镜的间距d ,使物体经物镜放大成实像(显微镜的中间像)在目镜物方焦点e f 附近.由题意,图中d 和e f 已知,可以求得中间像到物镜的距离,即物体对物镜的像距ef d p -='.则利用薄透镜成像公式就可求得物体到物镜的距离p .(2)物镜的横向放大率可由公式pp V'=直接求出.而显微镜的视角放大率由公式e o 0f f s M ∆-=计算.其中∆为物镜像方焦点到目镜物方焦点的距离.解 (1)由分析可知,显微镜的中间像对物镜的距离(像距)为cm 195e =-='f d p而像方焦距f '=7 mm ,则由薄透镜成像公式f p p '=-'111可得观察物到物镜的距离为 mm -7.3mm 19571957=-⨯='-'''=p f p f p(2)物镜的横向放大率为7.26-='=pp V (3)由分析知mm 188mm 57200e o =--=--=∆)(f f d,则显微镜的视角放大率)5()7(188250-⨯-⨯-=M 1343-≈题 13-6 图7 一天文望远镜,物镜与目镜相距90 cm ,放大倍数为 8⨯(即8倍),求物镜和目镜的焦距.分析 望远镜的放大率为e o f f M''--=,其中o f '和e f '分别为物镜和目镜的像方焦距.而通常物镜的像方焦点和目镜的物方焦点几乎重合,即目镜和物镜的间距为两者焦距之和,而题中已知o f '+e f '=90 cm ,由此可求o f '和e f '.解 由分析可知8e o =''=f f M ,又o f '+e f '=90 cm ,则得物镜和目镜的像方焦距为⎩⎨⎧='='cm10cm80e o f f。



1如图,三角形ABC 为某透明介质的横截面,O 为BC 边的中点,位于截面所在平面内的一束光线自O 以角i 入射,第一次到达AB 边恰好发生全反射。
已知θ=15°,BC 边长为2L,该介质的折射率为2。
求:①入射角i;②从入射到发生第一次全反射所用的时间(设光在真空中的速度为c,可能用到:6sin 75=tan152=-1【解析】①根据全反射规律可知,光线在AB 边上某点P 的入射角等于临界角C,由折射定律得1sin C n=① 代入数据得C=45°②设光线在BC 边上的折射角为r,由几何关系得 r=30°③ 由折射定律得sin sin inr=④ 联立③④式,代入数据得 i=45°⑤②在△OPB 中,根据正弦定律得00sin 75sin 45OP L=⑥设所用时间为t,光线在介质中的速度为v,得OP=vt ⑦c v v=⑧ 联立⑥⑦⑧式,代入数据得t =2一半径为 6 m 的半圆柱玻璃砖,上方有平行横截面直径AB 的固定直轨道,轨道上有一小车,车上固定一与轨道成45°角的激光笔,发出的细激光束始终在与横截面平行的平面上.打开激光笔,并使小车从左侧足够远的地方以恒定速度向右运动,结果在半圆柱玻璃砖的弧面有激光射出的时间持续了1 s .不考虑光在AB 面上的反射,已知该激光在该玻璃砖中的折射率为 2 ,光在空气中的传播速度大小为c .求: ①该激光在玻璃砖中传播的速度大小; ②小车向右匀速运动的速度v 0的大小.7、①由n =v c得,激光在玻璃中的传播速度为v =n c = 22c (2分)②激光从玻璃射向空气,发生全反射的临界角为 C =arcsin n 1=45°(1分) n =sin θsin 45°,θ=30°(2分)设激光射到M 、N 两点时,折射光线恰好在弧面发生全反射,激光从M 点到N 点的过程弧面有激光射出 由正弦定理得sin 45°MO =sin 60°R ,得MO = 36R (1分) 同理可得ON =36R (1分)又t =v0MN(2分) 可得v 0=4 m/s(1分)3一个半圆柱形玻璃砖,其横截面是半径为R 的半圆,AB 为半圆的直径,O 为圆心,如图所示。

最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改几何光学 §1几何光学基础1、光的直线传播:光在同一均匀介质中沿直线传播。
2、光的独立传播:几束光在交错时互不妨碍,仍按原来各自的方向传播。
3、光的反射定律:①反射光线、入射光线和法线在同一平面内;②反射光线和入射光线分居法线两侧;③反射角等于入射角。
4、光的折射定律:①折射光线、入射光线和法线在同一平面内;②折射光线和入射光线分居法线两侧;③入射角1i 与折射角2i 满足2211sin sin i n i n =;④当光由光密介质向光疏介质中传播,且入射角大于临界角C 时,将发生全面反射现象(折射率为1n 的光密介质对折射率为2n 的光疏介质的临界角12sin n n C =)。
几何光学 §2光的反射2.1组合平面镜成像组合平面镜:由两个以上的平面镜组成的光学系统叫做组合平面镜,射向组合平面镜的光线往往要在平面镜之间发生多次反射,因而会出现生成复像的现象。
先看一种较简单的现象,两面互相垂直的平面镜(交于O 点)镜间放一点光源S (图1),S 发出的光线经过两个平面镜反射后形成了1S 、2S 、3S 三个虚像。
用几何的方法不难证明:这三个虚像都位于以O 为圆心、OS 为半径的圆上,而且S 和1S 、S 和2S 、1S 和3S 、2S 和3S 之间都以平面镜(或它们的延长线)保持着对称关系。
用这个方法我们可以容易地确定较复杂的情况中复像的个数和位置。
S S 2图1两面平面镜AO 和BO 成60º角放置(图2),用上述规律,很容易确定像的位置:①以O 为圆心、OS 为半径作圆;②过S 做AO 和BO 的垂线与圆交于1S 和2S ;③过1S 和2S 作BO 和AO 的垂线与圆交于3S 和4S ;④过3S 和4S 作AO 和BO 的垂线与圆交于5S ,51~S S 便是S 在两平面镜中的5个像。
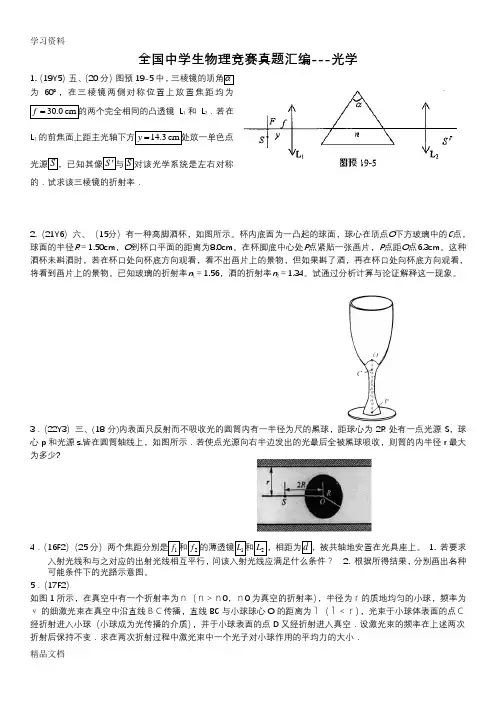
全国中学生物理竞赛真题汇编---光学1.(19Y5)五、(20分)图预19-5中,三棱镜的顶角α为60︒,在三棱镜两侧对称位置上放置焦距均为30.0cmf=的两个完全相同的凸透镜L1和L2.若在y=处放一单色点L1的前焦面上距主光轴下方14.3cm光源S,已知其像S'与S对该光学系统是左右对称的.试求该三棱镜的折射率.2.(21Y6)六、(15分)有一种高脚酒杯,如图所示。
杯内底面为一凸起的球面,球心在顶点O下方玻璃中的C点,球面的半径R=1.50cm,O到杯口平面的距离为8.0cm。
在杯脚底中心处P点紧贴一张画片,P点距O点6.3cm。
这种酒杯未斟酒时,若在杯口处向杯底方向观看,看不出画片上的景物,但如果斟了酒,再在杯口处向杯底方向观看,将看到画片上的景物。
已知玻璃的折射率n1=1.56,酒的折射率n2=1.34。
试通过分析计算与论证解释这一现象。
3.(22Y3)三、(18分)内表面只反射而不吸收光的圆筒内有一半径为尺的黑球,距球心为2R处有一点光源S,球心p和光源s.皆在圆筒轴线上,如图所示.若使点光源向右半边发出的光最后全被黑球吸收,则筒的内半径r最大为多少?4.(16F2)(25分)两个焦距分别是1f和2f的薄透镜1L和2L,相距为d,被共轴地安置在光具座上。
1. 若要求2. 根据所得结果,分别画出各种可能条件下的光路示意图。
5.(17F2)如图1所示,在真空中有一个折射率为n(n>n0,n0为真空的折射率),半径为r的质地均匀的小球,频率为ν的细激光束在真空中沿直线BC传播,直线BC与小球球心O的距离为l(l<r),光束于小球体表面的点C经折射进入小球(小球成为光传播的介质),并于小球表面的点D又经折射进入真空.设激光束的频率在上述两次折射后保持不变.求在两次折射过程中激光束中一个光子对小球作用的平均力的大小.图16.(17F6)、普通光纤是一种可传输光的圆柱形细丝,由具有圆形截面的纤芯A和包层B组成,B的折射率小于A的折射率,光纤的端面和圆柱体的轴垂直,由一端面射入的光在很长的光纤中传播时,在纤芯A和包层B的分界面上发生多次全反射.现在利用普通光纤测量流体F 的折射率.实验方法如下:让光纤的一端(出射端)浸在流体F 中.令与光纤轴平行的单色平行光束经凸透镜折射后会聚光纤入射端面的中心O,经端面折射进入光纤,在光纤中传播.由点O出发的光束为圆锥形,已知其边缘光线和轴的夹角为α0,如图3甲所示.最后光从另一端面出射进入流体F.在距出射端面h1处放置一垂直于光纤轴的毛玻璃屏D,在D上出现一圆形光斑,测出其直径为d1,然后移动光屏D至距光纤出射端面h2处,再测出圆形光斑的直径d2,如图3乙所示.图31.若已知A和B的折射率分别为nA与nB,求被测流体F 的折射率nF的表达式.2.若nA、nB和α0均为未知量,如何通过进一步的实验以测出nF的值?7.(18F1)(22分)有一放在空气中的玻璃棒,折射率 1.5n =,中心轴线长45cm L =,一端是半径为110cm R =的凸球面.1.要使玻璃棒的作用相当于一架理想的天文望远镜(使主光轴上无限远处物成像于主光轴上无限远处的望远系统),取中心轴线为主光轴,玻璃棒另一端应磨成什么样的球面?2.对于这个玻璃棒,由无限远物点射来的平行入射光柬与玻璃棒的主光轴成小角度1φ时,从棒射出的平行光束与主光轴成小角度,求21/φφ(此比值等于此玻璃棒望远系统的视角放大率).8.(19F5)(20分)薄凸透镜放在空气中,两侧焦点和透镜中心的距离相等。

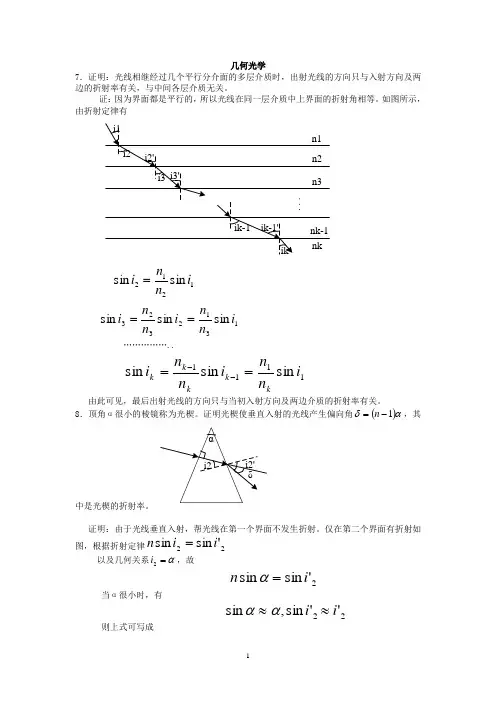


D 几何光学训练题1.对于下列光现象的说法中,正确的是( )A .夏天烈日照射下公路远望像洒了一层水一样,这是光的全反射现象B .通过玻璃三棱镜看到的像比物体实际位置要低C .光导纤维是利用光的全反射现象制成的D .手术台上的无影灯消除影子是由于光没直线传播的形成的 2.对于光的传播,下列说法中正确的是( ). A.一定颜色的光传播度大小由媒质决定B.不同颜色的光在同一种媒质中传播时,波长越短的光传播速度越快C.同一频率的光在不同媒质波长不同,而在真空中的波长最长D.同一色光的频率随传播速度不同而改变3.简易潜望镜中的两块平面镜中心点之间的距离为L,通过潜望镜观察水平正前方的物体,看到像的位置比物体的实际位置( ).A.水平方向远L,竖直方向低LB.水平方向远L,竖直方向高LC.水平方向近L,竖直方向高LD.水平方向近L,竖直方向低L4.某一单色光在折射率为n 1的媒质中传播时,它的波长、频率和波速分别用λ1、γ1和υ1表示,在折射度为n 2的媒质中,分别用λ2、γ2和υ2表示,以上这些物理量存在如下的关系( ).5.在两束频率相同的单色光的交点前放一块平行的玻璃砖后,则交点的位置与不放玻璃砖前相比( ).(如图7-2-4所示)A.不变B.向左C.向右D.向左还是向右由光的频率大小决定6.点光源S 通过带有圆孔的挡板N ,照射到屏M 上,形成直径为d 的亮圆.如果在挡 板靠近光屏一侧放上一块厚玻璃砖,如图20-14所示,这时点光源通过圆孔和玻璃,在屏上形成直径为D 的亮圆.则直径D 和d 的大小关系为 ( )A .d >DB .d =DC .d <D D .无法确定7.如图所示,任意一条光线射向夹角为ϕ的两平面镜的相对镜面上,相继经两镜面反射后,最后射出线与最初入射线的方向间夹角应为( )(A) ϕ (B)2ϕ (C)3ϕ (D)4ϕ8.某同学为了研究光的色散,设计了如下实验:在墙角放置一个盛水 的容器,其中有一块与水平面成45°角放置的平面镜M ,如图所示,一细束白光斜射向水面,经水折射向平面镜,被平面镜反射经 水面折射后照在墙上,该同学可在墙上看到 ( ) A .上紫下红的彩色光带 B .上红下紫的彩色光带 C .外红内紫的环状光带 D .一片白光 9.如图所示,两个同种玻璃制成的棱镜,顶角α1 略大于α2 ,两单色光1和2分别垂直入射三棱镜,其出射光线与第二界面的夹角β1 =β2 ,则A 、在棱镜中1光的折射率比2光小B 、在光谱中,1光比较靠近红光C 、在棱镜中1光的传播速度比2光的小D 、把此两光由水中射向空气,产生全反射时,1光的临界角比2光的临界角大。
光学竞赛题光学竞赛题一、选择题1.(3分)细心的小明同学注意到这样一个问题:如果打开窗户,直接看远处的高架电线,电线呈规则的下弯弧形;而如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,而且,轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.产生这种现象的原因是()A.玻璃上不同部位对视线的阻挡情况不同B.玻璃各部分的透光度不均匀C.玻璃各部分的厚度不均匀D.玻璃上不同部位对光的反射不一样2.(3分)如图所示,平面镜OM与ON的夹角为θ,一条平行于平面ON的光线经过两个平面镜的多次反射后,能够沿着原来的光路返回,则两平面镜之间的夹角不可能是()A.20°B.15°C.10°D.5°3.(3分)在探究凸透镜成像规律的实验中,我们发现像距v和物距u是一一对应的,在如图所示的四个图线中,能正确反映凸透镜成像规律的应该是()A.图线A B.图线B C.图线C D.图线D4.(3分)如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像5.(3分)如图所示,P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、O2是过圆孔中心O垂直于Q的直线,已知P和Q都足够大,现在直线O1O2上光屏P左侧5厘米处放置一点光源S,则平面镜上的反射光在屏上形成的亮斑面积为()A.米2B.米2C.米2D.米26.(3分)如图(a)所示,平面镜OM与ON夹角为θ,光线AB经过平面镜的两次反射后出射光线为CD.现将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,而入射光线不变,如图(b)所示.此时经过平面镜的两次反射后的出射光线将()A.与原先的出射光线CD平行B.与原先的出射光线CD重合C.与原先的出射光线CD之间的夹角为2βD.与原先的出射光线CD之间的夹角为β7.(3分)小明坐在前排听讲座时,用照相机把由投影仪投影在银幕上的彩色图象拍摄下来.由于会场比较暗,他使用了闪光灯.这样拍出来的照片()A.比不用闪光灯清楚多了B.与不用闪光灯的效果一样C.看不清投影到屏幕上的图象D.色彩被“闪”掉了,拍到的仅有黑色的字和线条8.(3分)如果不慎在照相机的镜头上沾上了一个小墨点,则照出的相片上()A.有一个放大的墨点像B.有一个缩小的墨点像C.一片漆黑D.没有墨点的像9.(3分)如图所示,水池的宽度为L,在水池右侧距离池底高度H处有一激光束,水池内无水时恰好在水池的左下角产生一个光斑.已知L=H,现向水池内注水,水面匀速上升,则光斑()A.匀速向右移动,且移动速度小于水面上升的速度B.匀速向右移动,且移动速度大于水面上升的速度C.减速向右移动,但速度始终大于水面上升的速度D.加速向右移动,但速度始终小于水面上升的速度10.(3分)如图所示,两平面镜OA、OB夹角为θ,位于镜前P 点的某人分别在OA、OB镜内看到自己像的个数为()A.1;1 B.2;1 C.2;0 D.1;011.(3分)如图所示,凸透镜竖直放置,凸透镜焦距f,现有一点光源S在凸透镜左侧以凸透镜两倍焦距处为圆心,在经过主光轴的竖直平面内做顺时针圆周运动,直径为D,且f<D<2f,则在下列关于点光源所成的像的运动轨迹的各图中,正确的是()A.B.C.D.12.(3分)(2011•西宁)在皮鞋擦过鞋油,还要用鞋刷或软布反复擦几下,越擦越亮,这是由于()A.反复擦可增加漫反射效果B.反复擦可使鞋油填平皮革表面的凹坑,增加表面光滑程度,增加镜面反射效果C.鞋油反光性能比皮革好,反复擦可使鞋油均匀分布,增加漫反射效果D.鞋油的颜色比皮革鲜艳,可增加镜面反射效果13.(3分)在光具座上自左向右依次竖直放置一个凹透镜、凸透镜和平面镜,两个透镜的主光轴重合,凸透镜的焦距为f,此时两个透镜之间的距离为L.在凹透镜的左侧有一水平平行光束通过两个透镜后入射到平面镜上,经平面镜反射后,反射光恰能沿原来的光路返回,据此可判断凹透镜的焦距为()A.f B.L C.f+L D.f﹣L14.(3分)用转动八面镜法可以测光速,实验装置示意图如图所示.S为发光点,T为望远镜,平面镜O与凹面镜B构成了反射系统.八面镜M距反射系统的距离AB为L(L可长达几十千米),且远大于OB以及S和T到八面镜的距离.调整八面镜的位置直到通过望远镜能看到发光点S,然后使八面镜转动起来,并缓慢增大其转速(1秒内转过的圈数),当转速达到n0时,恰能在望远镜中再一次看见发光点S,由此得到光速c的表达式是()A.c=4Ln o B.c=8Ln o C.c=16Ln o D.c=32Ln o16.(3分)照相时,通过选择不同的“光圈”可以控制镜头的进光面积;选择不同的快门速度,可以控制镜头的进光时间.两者结合的目的是使底片受到的光照能量保持一定而得到好照片,下表中列出了照相机光圈与快门的几种正确组合.在“快门”一行中,“25”表示快门打开的时间是秒.在“光圈”一行中,“15”表示镜头透光部分的直径等于镜头焦距的.那么快门“50”对应的“光圈”应该是()光圈20 15 12 6 3 2快门9 16 25 50 100 400 900A.7B.7.5 C.8D.8.517.(3分)如图所示,OO'为凸透镜的主光轴,将点光源放在A点时,像在B点;将点光源放在B点时,像在C 点.当将点光源放在C点时,则()A.一定在B点成一个实像B.一定在A点的左侧成一个虚像C.可能在B、C之间成一个实像D.可能在C点的右侧成一个虚像18.(3分)如图所示,光线AB经过某凸透镜的一个焦点,B点在薄透镜上.已知F是该透镜的另一个焦点.若使用圆规和刻度尺来确定透镜的位置,则还需知道的条件是()A.光线AB经过的焦点位置B.透镜光心的位置C.光线AB经透镜后的折射光线D.不需要任何条件19.(3分)夜晚,人们仰望天空,有时能看到闪烁的人造地球卫星.地球赤道处有一观察者,在日落4小时后看到一颗人造地球卫星从赤道正上方高空中经过,设地球半径为R,则这颗人造地球卫星距赤道地面的高度至少为()A.R/2 B.R C.2R D.4R20.(3分)如图所示,平面镜OM与ON镜面之间夹角为α,在两平面镜角平分线上有一个点光源S,如果要保证S发出的任意一条光线最多只能产生两次反射,则α的最小值是()A.120°B.90°C.72°D.6021.(3分)如图所示,位于凸透镜主光轴上某发光点P发出红、黄、绿三色复光,当用与主光轴相垂直的毛玻璃屏从透镜附近沿轴方向向远移动时,在屏上将依次看到()A.红、黄、绿亮点B.红、绿、黄亮点C.黄、红、绿亮点D.绿、黄、红亮点22.(3分)如图所示,有一圆柱形玻璃体,在它的中心轴线上有一球形气泡,柱体低面是磨砂的毛面,当平行光沿柱轴方向向下照射时,在磨砂的毛面上可能会看到()A.圆形亮斑B.圆型暗斑C.圆形暗斑且中心有一亮点D.圆形亮斑且中心有一暗点23.(3分)电影画面每隔秒更换一次,由于人的眼睛存在反应时间,所以会出现“眼见未必为实”的奇怪现象.如图所示,屏幕上出现的一辆匀速行驶汽车的车轮(车轮有6根对称分布的相同辐条),则下列现象中不符合此时人感觉的是()A.若在秒内每根辐条转过60°,则人觉得车轮是不转的B.若在秒内每根辐条转过355°,则人觉得车轮是倒转的C.若在秒内每根辐条转过360°,则人觉得车轮是不转的D.若在秒内每根辐条转过365°,则人觉得车轮是不转的24.(3分)(2013•宜春模拟)如图所示,凸透镜的焦距为5厘米,在透镜左侧10厘米处,有一个与主光轴垂直的物体AB,在透镜右侧15厘米处放一个平面镜,镜面与凸透镜的主光轴垂直,则该光具组中,物体AB的成像情况是()A.一个正立实像,一个倒立实像,一个正立虚像B.一个正立实像,一个正立虚像,一个倒立虚像C.一个倒立实像,一个正立虚像,一个倒立虚像D.一个正立实像,一个倒立实像,一个倒立虚像25.(3分)如图所示,平面镜OM与ON垂直放置,在它们的角平分线上P点处,放有一个球形放光物体,左半部分为浅色,右半部分为深色,在P点左侧较远的地方放有一架照相机,不考虑照相机本身在镜中的成像情况,则拍出照片的示意图正确的是()A.B.C.D.26.(3分)在一张白纸上用红色水彩笔写上红色的“E”字.当你通过红色玻璃观察写在这张白纸上的“E”字时,观察到的现象是()A.清晰的红色“F”字B.清晰的黑色“F”字C.清晰的红底白色“E”字D.几乎看不出“E”字27.(3分)一焦距为f的凸透镜.主轴和水平x轴重合,透镜左侧x轴上有一点光源.点光源到透镜的距离大于f 而小于2f,若将此透镜沿x轴向右平移2f的距离,则在此过程中点光源经透镜所成的像将()A.一直向右移动B.一直向左移动C.先向右移动.接着向左移动D.先向左移动,接着向右移动28.(3分)如图所示,一点光源位于凸透镜的主轴上,凸透镜位置固定.当点光源位于A点时,它的像在B点;当点光源位于B点时,它的像在C点.则凸透镜位于()A.A的左侧B.A B之间C.B C之间D.C的右侧29.(3分)早在公元前305年,著名天文家埃拉托色尼就已经测量出了地球的周长,与现代科学公认的地球周长的真实值相差不到0.1%.他在研究中发现,每年夏至这天,塞恩城(今埃及阿斯旺)正午的太阳光正好直射到城内一口深井的底部,而远在S千米以外的亚历山大城,夏至这天正午的太阳光却会使物体在地面上留下一条影子,他测得太阳光方向与竖直方向之间的夹角为θ°,由此得出地球的周长为()A.千米B.千米C.千米D.千米30.(3分)如图所示,房间内一墙角处相临两墙面挂了两个平面镜,两平面镜相互垂直,在该墙角紧靠镜面处放有一个脸盆,盆内有水.某同学通过镜面和水面最多能看到自己像的个数为()A.3个B.6个C.9个D.无穷31.(3分)如图所示,两平面镜垂直放置,某光线PA以入射角α入射到镜面M上,经平面镜M和N两次反射后反射光线BQ与PA平行.现将两平面镜以过O点且垂直于纸面的直线为轴同时逆时针旋转一个角度β(β<α),假设镜面足够大,则入射光线与反射光线之间的距离将()A.增大B.减小C.不变D.无法判断32.(3分)如图所示,两平面镜A和B之间的夹角为9°自平面镜B上的某点P射出一条与B镜面成β角的光线,在β角由0°至180°范围内(不包括0°)连续变化的过程中,发现当β取某角度时,光线经镜面一次或多次反射后,恰好能返回到P点,则符合该要求的β的个数有()A.1个B.4个C.6个D.9个33.(3分)如图所示,有一正方形的不透光的房间,在其中的一面墙上开有一个圆形小孔.在这面墙的对面有一个正方形的平面镜.在房间里有一个人靠在与平面镜垂直的一侧墙面上,当有一束垂直于圆孔的平行光通过圆孔射到平面镜上时,他能看到的是()A.镜面上有一个圆形的亮斑B.整个正方形镜子的形状C.整个房间的各处都是亮的D.感到整个房间是一片黑暗34.(3分)(2013•顺义区二模)如图为潜望镜工作原理图.若现有一军舰位于S点处,则潜水艇中的人通过潜望镜看到的像的位置()A.在图中的A处B.在图中的B处C.在图中的C处D.在图中的D处35.一束光线经过某光学元件后的出射光线如图所示,则方框内放置的光学元件()A.只能是平面镜或凸透镜B.只能是凸透镜或凹透镜C.只能是凹透镜或平面镜D.平面镜、凸透镜和凹透镜均可36.如图所示,在空气中平行于玻璃凸透镜主光轴的光线经凸透镜会聚于主光轴的一点S,若把凸透镜浸没在水中,会聚点S′()A.在S的上方B.在S的下方C.与S重合D.条件不足,无法判断37.如图所示,M、N为某一透镜的主光轴,若将点光源置于A点,则成像于B点,若将点光源置于B点,则成像于C点,已知AB>BC,则以下有关透镜的种类和位置的说法中正确的是()A.透镜是凸透镜,位于A点左侧B.透镜是凹透镜,位于C点右侧C.透镜是凸透镜,位于C点右侧D.透镜是凹透镜,位于A点左侧38.无云的晴天里,某同学在操场上竖立一根直杆,地面上OA是这根杆在太阳光下的投影,过了一段时间后,影子的位置移到了OB,且OA=OB,如图所示.则AB所指的方向是()A.东B.西C.南D.北39.如图所示,在竖直平面xoy内,人眼位于P(0,4)位置处,平面镜MN竖直放置其两端M、N的坐标分别为(3,1)和(3,0),某发光点S在该竖直平面y轴的右半部分某一区域内自由移动时,此人恰好都能通过平面镜看见S的像,则该区域的最大面积为()(图中长度单位为:米)A.0.5米2B.3.5米2C.4米2D.4.5米240.(3分)用一支可以写出红颜色字的笔在一张白纸上写一行字,则下列说法中正确的是()A.白纸上的这一行字,在阳光下会吸收白光中的红色光,所以这一行字是红色的B.白纸上的这一行字,在阳光下会反射白光中的红色光,所以这一行字是红色的C.白纸上的这一行字,由于它能发出红光,所以这一行字是红色的D.白纸上的这一行字,如果只用绿色光照射上去,这一行字就会是绿色的二、填空题41.(3分)如图所示,一点光源位于金属圆筒内部轴线上A点.圆筒轴线与凸透镜主光轴重合,光屏与圆筒轴线垂直且距离透镜足够远.此时,点光源正好在光屏上形成一个清晰的像,测出此时凸透镜与圆筒右端面的距离为L;向右移动凸透镜到适当位置,光屏上再次出现了清晰的像.由于光源位于圆筒的内部,无法直接测量出A与筒右端面的距离d,为了求出d的大小,在上述过程中还需要测量出的一个物理是_________;如果用N来表示该物理量的大小,则可以得出d为_________.42.(3分)如图所示,水平地面上有一不透光的边长为X的正方体物块.在正方体正左方有一点光源S,点光源和正方体物块的距离也为X.若在点光源S的上方距离为H处水平放置平面镜,H大小固定不变,平面镜足够大.不考虑其他光源的存在,那么在正方体的另一侧水平面上,将会由于点光源S发出的光线经平面镜反射而被照亮,现改变X的大小,当X增大到_________时,照亮区域将消失.光学竞赛题参考答案与试题解析一、选择题1.(3分)细心的小明同学注意到这样一个问题:如果打开窗户,直接看远处的高架电线,电线呈规则的下弯弧形;而如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,而且,轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.产生这种现象的原因是()A.玻璃上不同部位对视线的阻挡情况不同B.玻璃各部分的透光度不均匀C.玻璃各部分的厚度不均匀D.玻璃上不同部位对光的反射不一样考点:光的折射现象及其应用.专题:应用题.分析:根据光的折射现象,从玻璃上不同部位因厚度不同对光的折射情况不同这一角度入手,然后再对各个选项逐一分析即可.解答:解:A、如果隔着窗玻璃看,玻璃上不同部位对光的折射程度不同,而不是玻璃上不同部位对视线的阻挡情况不同,故本选项错误;B、因玻璃上不同部位透过光的颜色是相同的,都是透过白色光,故本选项错误;C、因玻璃上不同部位因厚度不同对光的折射情况不同,所以如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,当轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.故本选项正确;D、因如果隔着窗玻璃看,玻璃上不同部位对光的折射情况不同,而不是反射情况不同.故选C.点评:此题主要考查学生对光的折射现象及其应用,而且此题的中现象对学生来说并不陌生,但是要从光的折射角度来解释这一现象,尤其是“因玻璃上不同部位因厚度不同对光的折射情况不同”这一点,对学生来说就增加了一定的难度,因平时的练习题目,只是简单地折射定律,因此,此题属于难题.2.(3分)如图所示,平面镜OM与ON的夹角为θ,一条平行于平面ON的光线经过两个平面镜的多次反射后,能够沿着原来的光路返回,则两平面镜之间的夹角不可能是()A.20°B.15°C.10°D.5°考点:光的反射定律.专题:光的传播和反射、平面镜成像.分析:要解决此题首先要明确下面两点:(1)做出光的反射光路图,根据光路图可以确定每次入射时入射角两个平面镜夹角θ的关系.(2)光线原路返回的含义:必须是经过多次反射后,最后的一次入射是垂直于其中的一个平面镜,即入射角等于零.解答:解:画光的反射光路图如下图所示,由图知:光线第一次反射的入射角为:90°﹣θ;第二次入射时的入射角为:90°﹣2θ;第三次的入射角为:90°﹣3θ;第N次的入射角为:90°﹣Nθ.要想延原来光路返回需要光线某次反射的入射角为零所以有90°﹣Nθ=0,解得:N=由于N为自然数,所以θ不能等于20°.故选A.点评:(1)此题考查了光的反射定律并结合了几何方面的知识.(2)明确此题中每一次反射,入射角与两平面镜之间夹角θ的关系是解决此题的一个难点,它利用了几何中三角形的外角等于不相邻的内角和的知识.3.(3分)在探究凸透镜成像规律的实验中,我们发现像距v和物距u是一一对应的,在如图所示的四个图线中,能正确反映凸透镜成像规律的应该是()A.图线A B.图线B C.图线C D.图线D考点:凸透镜成像规律及其探究实验.专题:图析法.分析:①首先看清图象中的横轴表示物距,纵轴表示像距,根据凸透镜成像规律中的u=2f时,物距v=2f,求出其焦距.②凸透镜成像时,像距、物距和焦距三者之间是有一定的联系的,若用一个公式表示,就是:+=(其中u表示物距,v表示像距,f表示焦距),③将ABCD4个图线中的物距、像距数值,分别代入+=逐一分析即可得出结论.解答:解:A、因为A图线中,物距和像距始终相等,不符合凸透镜成像规律中的物距和像距的关系.故本选项不能正确反映凸透镜成像规律;B、B图线中,随着物距的不断增大,像距在不断减小,不符合凸透镜成像规律中的物距和像距的关系.故本选项不能正确反映凸透镜成像规律;C、图线C,当物距为15cm时,像距为15cm,由凸透镜成像规律可知,u=2f,v=2f,此时f=7.5cm,当物距为35cm时,像距为5cm,代入+≠,故本选项不能正确反映凸透镜成像规律;D、图线D,当物距为10cm时,像距为10cm,由凸透镜成像规律可知,u=2f,v=2f,此时f=5cm,当物距为30cm时,像距为6cm,代入+=,故本选项能正确反映凸透镜成像规律.故选D.点评:此题主要考查学生对凸透镜成像规律的理解和掌握,此题对学生的要求比较高,第一,要求学生看懂图象,第二要求学生根据图象求出各自的焦距,第三,要求学生知道凸透镜成像时,像距、物距和焦距三者之间的关系,即+=,总之,此题难度较大,属于难题.4.(3分)如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像考点:凸透镜成像的应用.专题:应用题.分析:(1)平面镜成像的规律:虚像、物体和像大小相等、物体和像到镜面的距离相等,物体和像的连线与镜面垂直;(2)凸透镜成像规律:当物体位于凸透镜的2倍焦距处,成倒立、等大的实像.解答:解:①按题意,AB在凸透镜右侧距离透镜2f处成一个倒立的等大的实像.②由于成像后的光线是射向右下方的,所以不能在平面镜上成像(平面镜只在主光轴的上方),所以只能成一个实像.③如果平面镜足够大,则“AB在凸透镜右侧距离透镜2f处成一个倒立的等大的实像”又会在平面镜上成一个等大的虚像,平面像反射后的光线又会经凸透镜成一个缩小的倒立的实像(成在凸透镜左侧f与2f之间.此时相当于物距为4f.当然,也要满足凸透镜是足够大了才有此种情况).故选D.点评:此题主要考查凸透镜成像规律及其应用,此题的突破点是,AB只有在主光轴上的那点折射后入MN,其它均没有,故只有一个实像.5.(3分)如图所示,P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、O2是过圆孔中心O垂直于Q的直线,已知P和Q都足够大,现在直线O1O2上光屏P左侧5厘米处放置一点光源S,则平面镜上的反射光在屏上形成的亮斑面积为()A.米2B.米2C.米2D.米2考点:平面镜成像的特点、原理、现象及其实验方案;光的反射定律.专题:光的传播和反射、平面镜成像.分析:设出圆孔的半径与光斑的半径,通过画图找出二者之间的大小关系,再运用面积的计算公式进行计算即可.解答:解:设圆孔的半径为d,亮斑的半径为r.作出光的传播路线图,由三角形的知识可得:r:d=25:5=5:1而亮斑的面积:S=πr2﹣πd2=π(r2﹣d2)=π[(5d)2﹣d2]=π24d2=π24×(2.5cm)2=π150cm2=0.015πm2=m2.故选C.点评:此题虽然是一道光学题,但难不在光学知识,却是数学知识,画出图形,通过三角形的关系找出两个圆的半径关系是解决问题最关键的一步.6.(3分)如图(a)所示,平面镜OM与ON夹角为θ,光线AB经过平面镜的两次反射后出射光线为CD.现将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,而入射光线不变,如图(b)所示.此时经过平面镜的两次反射后的出射光线将()A.与原先的出射光线CD平行B.与原先的出射光线CD重合C.与原先的出射光线CD之间的夹角为2βD.与原先的出射光线CD之间的夹角为β考点:作光的反射光路图.专题:图析法.分析:若将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,可知入射角增大或减小的度数,进而可知反射角增大或减小的度数,从而可知第一次反射的光线偏转的角度,因平面镜M1和M2一起以B 为轴沿纸面转动时,保持α角不变,所以第二次反射的光线方向不变.解答:解:因为保持θ角不变,将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,则入射角增大或减小β,反射角也增大或减小β,所以反射光线与入射光线的夹角是2β,即反射的光线偏转2β角,因为平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β时,两平面镜OM与ON互成θ角的角度没变,所以第二次反射的光线方向不变.又因为入射光线不变,所以此时经过平面镜的两次反射后的出射光线将与原先的出射光线CD重合.故选B.点评:此题主要考查了有关光的反射定律的应用,首先要掌握定律的内容,特别是反射角与入射角的关系,同时要掌握反射角与入射角的概念,知道这些角都是光线与法线的夹角.7.(3分)小明坐在前排听讲座时,用照相机把由投影仪投影在银幕上的彩色图象拍摄下来.由于会场比较暗,他使用了闪光灯.这样拍出来的照片()A.比不用闪光灯清楚多了B.与不用闪光灯的效果一样C.看不清投影到屏幕上的图象D.色彩被“闪”掉了,拍到的仅有黑色的字和线条考点:镜面反射.专题:应用题.分析:闪光灯的光比投影仪的光强,白光盖过了投影仪的光.就像白天看星星一样,看不到的.银幕反射彩色的光本来就是漫反射,光很弱.如果用闪光灯,银幕反射白光强度大,只拍出白色银幕或者上面的污点.彩色图片被冲淡,拍不出了.解答:解:闪光灯的光照射到物体上,可以使物体表面的亮度增大,但闪光灯照射到银幕上以后,只能增加银幕的亮度,而不能增加图象的亮度,相反,图象的亮度和清晰度明显减弱,所以反而看不清银幕上的图象,而银幕上的污渍更加清晰了,银幕上的黑色的字和纸条实际上就是投影片上不透明物体的影子,即黑暗区域.因此不用闪光灯拍摄的效果好.综上所述,只有选项C正确.故选C.点评:此题不仅仅是考查凸透镜成像的规律,而主要考查光的反射和漫反射,有一定的拔高难度,属于难题.8.(3分)如果不慎在照相机的镜头上沾上了一个小墨点,则照出的相片上()A.有一个放大的墨点像B.有一个缩小的墨点像C.一片漆黑D.没有墨点的像考点:凸透镜成像的应用.专题:应用题.分析:照相机的镜头是一个凸透镜.物体有无数点组成,物体上任一点射向照相机镜头有无数条光线,经凸透镜折射后,有无数条折射光线会聚成该点的像.当照相机的镜头上沾上一个墨点,还有另外的部分光线,经凸透镜折射会聚成像.解答:解:当照相机的镜头上沾上一个墨点,还有另外的部分光线,经凸透镜折射会聚成像,像的大小不发生变化,折射光线减少,会聚成的像变暗.。
光学竞赛题光学竞赛题一、选择题1.(3分)细心的小明同学注意到这样一个问题:如果打开窗户,直接看远处的高架电线,电线呈规则的下弯弧形;而如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,而且,轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.产生这种现象的原因是()A.玻璃上不同部位对视线的阻挡情况不同B.玻璃各部分的透光度不均匀C.玻璃各部分的厚度不均匀D.玻璃上不同部位对光的反射不一样2.(3分)如图所示,平面镜OM与ON的夹角为θ,一条平行于平面ON的光线经过两个平面镜的多次反射后,能够沿着原来的光路返回,则两平面镜之间的夹角不可能是()A.20°B.15°C.10°D.5°3.(3分)在探究凸透镜成像规律的实验中,我们发现像距v和物距u是一一对应的,在如图所示的四个图线中,能正确反映凸透镜成像规律的应该是()A.图线A B.图线B C.图线C D.图线D4.(3分)如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像5.(3分)如图所示,P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、O2是过圆孔中心O垂直于Q的直线,已知P和Q都足够大,现在直线O1O2上光屏P左侧5厘米处放置一点光源S,则平面镜上的反射光在屏上形成的亮斑面积为()A.米2B.米2C.米2D.米26.(3分)如图(a)所示,平面镜OM与ON夹角为θ,光线AB经过平面镜的两次反射后出射光线为CD.现将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,而入射光线不变,如图(b)所示.此时经过平面镜的两次反射后的出射光线将()A.与原先的出射光线CD平行B.与原先的出射光线CD重合C.与原先的出射光线CD之间的夹角为2βD.与原先的出射光线CD之间的夹角为β7.(3分)小明坐在前排听讲座时,用照相机把由投影仪投影在银幕上的彩色图象拍摄下来.由于会场比较暗,他使用了闪光灯.这样拍出来的照片()A.比不用闪光灯清楚多了B.与不用闪光灯的效果一样C.看不清投影到屏幕上的图象D.色彩被“闪”掉了,拍到的仅有黑色的字和线条8.(3分)如果不慎在照相机的镜头上沾上了一个小墨点,则照出的相片上()A.有一个放大的墨点像B.有一个缩小的墨点像C.一片漆黑D.没有墨点的像9.(3分)如图所示,水池的宽度为L,在水池右侧距离池底高度H处有一激光束,水池内无水时恰好在水池的左下角产生一个光斑.已知L=H,现向水池内注水,水面匀速上升,则光斑()A.匀速向右移动,且移动速度小于水面上升的速度B.匀速向右移动,且移动速度大于水面上升的速度C.减速向右移动,但速度始终大于水面上升的速度D.加速向右移动,但速度始终小于水面上升的速度10.(3分)如图所示,两平面镜OA、OB夹角为θ,位于镜前P 点的某人分别在OA、OB镜内看到自己像的个数为()A.1;1 B.2;1 C.2;0 D.1;011.(3分)如图所示,凸透镜竖直放置,凸透镜焦距f,现有一点光源S在凸透镜左侧以凸透镜两倍焦距处为圆心,在经过主光轴的竖直平面内做顺时针圆周运动,直径为D,且f<D<2f,则在下列关于点光源所成的像的运动轨迹的各图中,正确的是()A.B.C.D.12.(3分)(2011•西宁)在皮鞋擦过鞋油,还要用鞋刷或软布反复擦几下,越擦越亮,这是由于()A.反复擦可增加漫反射效果B.反复擦可使鞋油填平皮革表面的凹坑,增加表面光滑程度,增加镜面反射效果C.鞋油反光性能比皮革好,反复擦可使鞋油均匀分布,增加漫反射效果D.鞋油的颜色比皮革鲜艳,可增加镜面反射效果13.(3分)在光具座上自左向右依次竖直放置一个凹透镜、凸透镜和平面镜,两个透镜的主光轴重合,凸透镜的焦距为f,此时两个透镜之间的距离为L.在凹透镜的左侧有一水平平行光束通过两个透镜后入射到平面镜上,经平面镜反射后,反射光恰能沿原来的光路返回,据此可判断凹透镜的焦距为()A.f B.L C.f+L D.f﹣L14.(3分)用转动八面镜法可以测光速,实验装置示意图如图所示.S为发光点,T为望远镜,平面镜O与凹面镜B构成了反射系统.八面镜M距反射系统的距离AB为L(L可长达几十千米),且远大于OB以及S和T到八面镜的距离.调整八面镜的位置直到通过望远镜能看到发光点S,然后使八面镜转动起来,并缓慢增大其转速(1秒内转过的圈数),当转速达到n0时,恰能在望远镜中再一次看见发光点S,由此得到光速c的表达式是()A.c=4Ln o B.c=8Ln o C.c=16Ln o D.c=32Ln o16.(3分)照相时,通过选择不同的“光圈”可以控制镜头的进光面积;选择不同的快门速度,可以控制镜头的进光时间.两者结合的目的是使底片受到的光照能量保持一定而得到好照片,下表中列出了照相机光圈与快门的几种正确组合.在“快门”一行中,“25”表示快门打开的时间是秒.在“光圈”一行中,“15”表示镜头透光部分的直径等于镜头焦距的.那么快门“50”对应的“光圈”应该是()光圈20 15 12 6 3 2快门9 16 25 50 100 400 900A.7B.7.5 C.8D.8.517.(3分)如图所示,OO'为凸透镜的主光轴,将点光源放在A点时,像在B点;将点光源放在B点时,像在C 点.当将点光源放在C点时,则()A.一定在B点成一个实像B.一定在A点的左侧成一个虚像C.可能在B、C之间成一个实像D.可能在C点的右侧成一个虚像18.(3分)如图所示,光线AB经过某凸透镜的一个焦点,B点在薄透镜上.已知F是该透镜的另一个焦点.若使用圆规和刻度尺来确定透镜的位置,则还需知道的条件是()A.光线AB经过的焦点位置B.透镜光心的位置C.光线AB经透镜后的折射光线D.不需要任何条件19.(3分)夜晚,人们仰望天空,有时能看到闪烁的人造地球卫星.地球赤道处有一观察者,在日落4小时后看到一颗人造地球卫星从赤道正上方高空中经过,设地球半径为R,则这颗人造地球卫星距赤道地面的高度至少为()A.R/2 B.R C.2R D.4R20.(3分)如图所示,平面镜OM与ON镜面之间夹角为α,在两平面镜角平分线上有一个点光源S,如果要保证S发出的任意一条光线最多只能产生两次反射,则α的最小值是()A.120°B.90°C.72°D.6021.(3分)如图所示,位于凸透镜主光轴上某发光点P发出红、黄、绿三色复光,当用与主光轴相垂直的毛玻璃屏从透镜附近沿轴方向向远移动时,在屏上将依次看到()A.红、黄、绿亮点B.红、绿、黄亮点C.黄、红、绿亮点D.绿、黄、红亮点22.(3分)如图所示,有一圆柱形玻璃体,在它的中心轴线上有一球形气泡,柱体低面是磨砂的毛面,当平行光沿柱轴方向向下照射时,在磨砂的毛面上可能会看到()A.圆形亮斑B.圆型暗斑C.圆形暗斑且中心有一亮点D.圆形亮斑且中心有一暗点23.(3分)电影画面每隔秒更换一次,由于人的眼睛存在反应时间,所以会出现“眼见未必为实”的奇怪现象.如图所示,屏幕上出现的一辆匀速行驶汽车的车轮(车轮有6根对称分布的相同辐条),则下列现象中不符合此时人感觉的是()A.若在秒内每根辐条转过60°,则人觉得车轮是不转的B.若在秒内每根辐条转过355°,则人觉得车轮是倒转的C.若在秒内每根辐条转过360°,则人觉得车轮是不转的D.若在秒内每根辐条转过365°,则人觉得车轮是不转的24.(3分)(2013•宜春模拟)如图所示,凸透镜的焦距为5厘米,在透镜左侧10厘米处,有一个与主光轴垂直的物体AB,在透镜右侧15厘米处放一个平面镜,镜面与凸透镜的主光轴垂直,则该光具组中,物体AB的成像情况是()A.一个正立实像,一个倒立实像,一个正立虚像B.一个正立实像,一个正立虚像,一个倒立虚像C.一个倒立实像,一个正立虚像,一个倒立虚像D.一个正立实像,一个倒立实像,一个倒立虚像25.(3分)如图所示,平面镜OM与ON垂直放置,在它们的角平分线上P点处,放有一个球形放光物体,左半部分为浅色,右半部分为深色,在P点左侧较远的地方放有一架照相机,不考虑照相机本身在镜中的成像情况,则拍出照片的示意图正确的是()A.B.C.D.26.(3分)在一张白纸上用红色水彩笔写上红色的“E”字.当你通过红色玻璃观察写在这张白纸上的“E”字时,观察到的现象是()A.清晰的红色“F”字B.清晰的黑色“F”字C.清晰的红底白色“E”字D.几乎看不出“E”字27.(3分)一焦距为f的凸透镜.主轴和水平x轴重合,透镜左侧x轴上有一点光源.点光源到透镜的距离大于f 而小于2f,若将此透镜沿x轴向右平移2f的距离,则在此过程中点光源经透镜所成的像将()A.一直向右移动B.一直向左移动C.先向右移动.接着向左移动D.先向左移动,接着向右移动28.(3分)如图所示,一点光源位于凸透镜的主轴上,凸透镜位置固定.当点光源位于A点时,它的像在B点;当点光源位于B点时,它的像在C点.则凸透镜位于()A.A的左侧B.A B之间C.B C之间D.C的右侧29.(3分)早在公元前305年,著名天文家埃拉托色尼就已经测量出了地球的周长,与现代科学公认的地球周长的真实值相差不到0.1%.他在研究中发现,每年夏至这天,塞恩城(今埃及阿斯旺)正午的太阳光正好直射到城内一口深井的底部,而远在S千米以外的亚历山大城,夏至这天正午的太阳光却会使物体在地面上留下一条影子,他测得太阳光方向与竖直方向之间的夹角为θ°,由此得出地球的周长为()A.千米B.千米C.千米D.千米30.(3分)如图所示,房间内一墙角处相临两墙面挂了两个平面镜,两平面镜相互垂直,在该墙角紧靠镜面处放有一个脸盆,盆内有水.某同学通过镜面和水面最多能看到自己像的个数为()A.3个B.6个C.9个D.无穷31.(3分)如图所示,两平面镜垂直放置,某光线PA以入射角α入射到镜面M上,经平面镜M和N两次反射后反射光线BQ与PA平行.现将两平面镜以过O点且垂直于纸面的直线为轴同时逆时针旋转一个角度β(β<α),假设镜面足够大,则入射光线与反射光线之间的距离将()A.增大B.减小C.不变D.无法判断32.(3分)如图所示,两平面镜A和B之间的夹角为9°自平面镜B上的某点P射出一条与B镜面成β角的光线,在β角由0°至180°范围内(不包括0°)连续变化的过程中,发现当β取某角度时,光线经镜面一次或多次反射后,恰好能返回到P点,则符合该要求的β的个数有()A.1个B.4个C.6个D.9个33.(3分)如图所示,有一正方形的不透光的房间,在其中的一面墙上开有一个圆形小孔.在这面墙的对面有一个正方形的平面镜.在房间里有一个人靠在与平面镜垂直的一侧墙面上,当有一束垂直于圆孔的平行光通过圆孔射到平面镜上时,他能看到的是()A.镜面上有一个圆形的亮斑B.整个正方形镜子的形状C.整个房间的各处都是亮的D.感到整个房间是一片黑暗34.(3分)(2013•顺义区二模)如图为潜望镜工作原理图.若现有一军舰位于S点处,则潜水艇中的人通过潜望镜看到的像的位置()A.在图中的A处B.在图中的B处C.在图中的C处D.在图中的D处35.一束光线经过某光学元件后的出射光线如图所示,则方框内放置的光学元件()A.只能是平面镜或凸透镜B.只能是凸透镜或凹透镜C.只能是凹透镜或平面镜D.平面镜、凸透镜和凹透镜均可36.如图所示,在空气中平行于玻璃凸透镜主光轴的光线经凸透镜会聚于主光轴的一点S,若把凸透镜浸没在水中,会聚点S′()A.在S的上方B.在S的下方C.与S重合D.条件不足,无法判断37.如图所示,M、N为某一透镜的主光轴,若将点光源置于A点,则成像于B点,若将点光源置于B点,则成像于C点,已知AB>BC,则以下有关透镜的种类和位置的说法中正确的是()A.透镜是凸透镜,位于A点左侧B.透镜是凹透镜,位于C点右侧C.透镜是凸透镜,位于C点右侧D.透镜是凹透镜,位于A点左侧38.无云的晴天里,某同学在操场上竖立一根直杆,地面上OA是这根杆在太阳光下的投影,过了一段时间后,影子的位置移到了OB,且OA=OB,如图所示.则AB所指的方向是()A.东B.西C.南D.北39.如图所示,在竖直平面xoy内,人眼位于P(0,4)位置处,平面镜MN竖直放置其两端M、N的坐标分别为(3,1)和(3,0),某发光点S在该竖直平面y轴的右半部分某一区域内自由移动时,此人恰好都能通过平面镜看见S的像,则该区域的最大面积为()(图中长度单位为:米)A.0.5米2B.3.5米2C.4米2D.4.5米240.(3分)用一支可以写出红颜色字的笔在一张白纸上写一行字,则下列说法中正确的是()A.白纸上的这一行字,在阳光下会吸收白光中的红色光,所以这一行字是红色的B.白纸上的这一行字,在阳光下会反射白光中的红色光,所以这一行字是红色的C.白纸上的这一行字,由于它能发出红光,所以这一行字是红色的D.白纸上的这一行字,如果只用绿色光照射上去,这一行字就会是绿色的二、填空题41.(3分)如图所示,一点光源位于金属圆筒内部轴线上A点.圆筒轴线与凸透镜主光轴重合,光屏与圆筒轴线垂直且距离透镜足够远.此时,点光源正好在光屏上形成一个清晰的像,测出此时凸透镜与圆筒右端面的距离为L;向右移动凸透镜到适当位置,光屏上再次出现了清晰的像.由于光源位于圆筒的内部,无法直接测量出A与筒右端面的距离d,为了求出d的大小,在上述过程中还需要测量出的一个物理是_________;如果用N来表示该物理量的大小,则可以得出d为_________.42.(3分)如图所示,水平地面上有一不透光的边长为X的正方体物块.在正方体正左方有一点光源S,点光源和正方体物块的距离也为X.若在点光源S的上方距离为H处水平放置平面镜,H大小固定不变,平面镜足够大.不考虑其他光源的存在,那么在正方体的另一侧水平面上,将会由于点光源S发出的光线经平面镜反射而被照亮,现改变X的大小,当X增大到_________时,照亮区域将消失.光学竞赛题参考答案与试题解析一、选择题1.(3分)细心的小明同学注意到这样一个问题:如果打开窗户,直接看远处的高架电线,电线呈规则的下弯弧形;而如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,而且,轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.产生这种现象的原因是()A.玻璃上不同部位对视线的阻挡情况不同B.玻璃各部分的透光度不均匀C.玻璃各部分的厚度不均匀D.玻璃上不同部位对光的反射不一样考点:光的折射现象及其应用.专题:应用题.分析:根据光的折射现象,从玻璃上不同部位因厚度不同对光的折射情况不同这一角度入手,然后再对各个选项逐一分析即可.解答:解:A、如果隔着窗玻璃看,玻璃上不同部位对光的折射程度不同,而不是玻璃上不同部位对视线的阻挡情况不同,故本选项错误;B、因玻璃上不同部位透过光的颜色是相同的,都是透过白色光,故本选项错误;C、因玻璃上不同部位因厚度不同对光的折射情况不同,所以如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,当轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.故本选项正确;D、因如果隔着窗玻璃看,玻璃上不同部位对光的折射情况不同,而不是反射情况不同.故选C.点评:此题主要考查学生对光的折射现象及其应用,而且此题的中现象对学生来说并不陌生,但是要从光的折射角度来解释这一现象,尤其是“因玻璃上不同部位因厚度不同对光的折射情况不同”这一点,对学生来说就增加了一定的难度,因平时的练习题目,只是简单地折射定律,因此,此题属于难题.2.(3分)如图所示,平面镜OM与ON的夹角为θ,一条平行于平面ON的光线经过两个平面镜的多次反射后,能够沿着原来的光路返回,则两平面镜之间的夹角不可能是()A.20°B.15°C.10°D.5°考点:光的反射定律.专题:光的传播和反射、平面镜成像.分析:要解决此题首先要明确下面两点:(1)做出光的反射光路图,根据光路图可以确定每次入射时入射角两个平面镜夹角θ的关系.(2)光线原路返回的含义:必须是经过多次反射后,最后的一次入射是垂直于其中的一个平面镜,即入射角等于零.解答:解:画光的反射光路图如下图所示,由图知:光线第一次反射的入射角为:90°﹣θ;第二次入射时的入射角为:90°﹣2θ;第三次的入射角为:90°﹣3θ;第N次的入射角为:90°﹣Nθ.要想延原来光路返回需要光线某次反射的入射角为零所以有90°﹣Nθ=0,解得:N=由于N为自然数,所以θ不能等于20°.故选A.点评:(1)此题考查了光的反射定律并结合了几何方面的知识.(2)明确此题中每一次反射,入射角与两平面镜之间夹角θ的关系是解决此题的一个难点,它利用了几何中三角形的外角等于不相邻的内角和的知识.3.(3分)在探究凸透镜成像规律的实验中,我们发现像距v和物距u是一一对应的,在如图所示的四个图线中,能正确反映凸透镜成像规律的应该是()A.图线A B.图线B C.图线C D.图线D考点:凸透镜成像规律及其探究实验.专题:图析法.分析:①首先看清图象中的横轴表示物距,纵轴表示像距,根据凸透镜成像规律中的u=2f时,物距v=2f,求出其焦距.②凸透镜成像时,像距、物距和焦距三者之间是有一定的联系的,若用一个公式表示,就是:+=(其中u表示物距,v表示像距,f表示焦距),③将ABCD4个图线中的物距、像距数值,分别代入+=逐一分析即可得出结论.解答:解:A、因为A图线中,物距和像距始终相等,不符合凸透镜成像规律中的物距和像距的关系.故本选项不能正确反映凸透镜成像规律;B、B图线中,随着物距的不断增大,像距在不断减小,不符合凸透镜成像规律中的物距和像距的关系.故本选项不能正确反映凸透镜成像规律;C、图线C,当物距为15cm时,像距为15cm,由凸透镜成像规律可知,u=2f,v=2f,此时f=7.5cm,当物距为35cm时,像距为5cm,代入+≠,故本选项不能正确反映凸透镜成像规律;D、图线D,当物距为10cm时,像距为10cm,由凸透镜成像规律可知,u=2f,v=2f,此时f=5cm,当物距为30cm时,像距为6cm,代入+=,故本选项能正确反映凸透镜成像规律.故选D.点评:此题主要考查学生对凸透镜成像规律的理解和掌握,此题对学生的要求比较高,第一,要求学生看懂图象,第二要求学生根据图象求出各自的焦距,第三,要求学生知道凸透镜成像时,像距、物距和焦距三者之间的关系,即+=,总之,此题难度较大,属于难题.4.(3分)如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像考点:凸透镜成像的应用.专题:应用题.分析:(1)平面镜成像的规律:虚像、物体和像大小相等、物体和像到镜面的距离相等,物体和像的连线与镜面垂直;(2)凸透镜成像规律:当物体位于凸透镜的2倍焦距处,成倒立、等大的实像.解答:解:①按题意,AB在凸透镜右侧距离透镜2f处成一个倒立的等大的实像.②由于成像后的光线是射向右下方的,所以不能在平面镜上成像(平面镜只在主光轴的上方),所以只能成一个实像.③如果平面镜足够大,则“AB在凸透镜右侧距离透镜2f处成一个倒立的等大的实像”又会在平面镜上成一个等大的虚像,平面像反射后的光线又会经凸透镜成一个缩小的倒立的实像(成在凸透镜左侧f与2f之间.此时相当于物距为4f.当然,也要满足凸透镜是足够大了才有此种情况).故选D.点评:此题主要考查凸透镜成像规律及其应用,此题的突破点是,AB只有在主光轴上的那点折射后入MN,其它均没有,故只有一个实像.5.(3分)如图所示,P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、O2是过圆孔中心O垂直于Q的直线,已知P和Q都足够大,现在直线O1O2上光屏P左侧5厘米处放置一点光源S,则平面镜上的反射光在屏上形成的亮斑面积为()A.米2B.米2C.米2D.米2考点:平面镜成像的特点、原理、现象及其实验方案;光的反射定律.专题:光的传播和反射、平面镜成像.分析:设出圆孔的半径与光斑的半径,通过画图找出二者之间的大小关系,再运用面积的计算公式进行计算即可.解答:解:设圆孔的半径为d,亮斑的半径为r.作出光的传播路线图,由三角形的知识可得:r:d=25:5=5:1而亮斑的面积:S=πr2﹣πd2=π(r2﹣d2)=π[(5d)2﹣d2]=π24d2=π24×(2.5cm)2=π150cm2=0.015πm2=m2.故选C.点评:此题虽然是一道光学题,但难不在光学知识,却是数学知识,画出图形,通过三角形的关系找出两个圆的半径关系是解决问题最关键的一步.6.(3分)如图(a)所示,平面镜OM与ON夹角为θ,光线AB经过平面镜的两次反射后出射光线为CD.现将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,而入射光线不变,如图(b)所示.此时经过平面镜的两次反射后的出射光线将()A.与原先的出射光线CD平行B.与原先的出射光线CD重合C.与原先的出射光线CD之间的夹角为2βD.与原先的出射光线CD之间的夹角为β考点:作光的反射光路图.专题:图析法.分析:若将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,可知入射角增大或减小的度数,进而可知反射角增大或减小的度数,从而可知第一次反射的光线偏转的角度,因平面镜M1和M2一起以B 为轴沿纸面转动时,保持α角不变,所以第二次反射的光线方向不变.解答:解:因为保持θ角不变,将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,则入射角增大或减小β,反射角也增大或减小β,所以反射光线与入射光线的夹角是2β,即反射的光线偏转2β角,因为平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β时,两平面镜OM与ON互成θ角的角度没变,所以第二次反射的光线方向不变.又因为入射光线不变,所以此时经过平面镜的两次反射后的出射光线将与原先的出射光线CD重合.故选B.点评:此题主要考查了有关光的反射定律的应用,首先要掌握定律的内容,特别是反射角与入射角的关系,同时要掌握反射角与入射角的概念,知道这些角都是光线与法线的夹角.7.(3分)小明坐在前排听讲座时,用照相机把由投影仪投影在银幕上的彩色图象拍摄下来.由于会场比较暗,他使用了闪光灯.这样拍出来的照片()A.比不用闪光灯清楚多了B.与不用闪光灯的效果一样C.看不清投影到屏幕上的图象D.色彩被“闪”掉了,拍到的仅有黑色的字和线条考点:镜面反射.专题:应用题.分析:闪光灯的光比投影仪的光强,白光盖过了投影仪的光.就像白天看星星一样,看不到的.银幕反射彩色的光本来就是漫反射,光很弱.如果用闪光灯,银幕反射白光强度大,只拍出白色银幕或者上面的污点.彩色图片被冲淡,拍不出了.解答:解:闪光灯的光照射到物体上,可以使物体表面的亮度增大,但闪光灯照射到银幕上以后,只能增加银幕的亮度,而不能增加图象的亮度,相反,图象的亮度和清晰度明显减弱,所以反而看不清银幕上的图象,而银幕上的污渍更加清晰了,银幕上的黑色的字和纸条实际上就是投影片上不透明物体的影子,即黑暗区域.因此不用闪光灯拍摄的效果好.综上所述,只有选项C正确.故选C.点评:此题不仅仅是考查凸透镜成像的规律,而主要考查光的反射和漫反射,有一定的拔高难度,属于难题.8.(3分)如果不慎在照相机的镜头上沾上了一个小墨点,则照出的相片上()A.有一个放大的墨点像B.有一个缩小的墨点像C.一片漆黑D.没有墨点的像考点:凸透镜成像的应用.专题:应用题.分析:照相机的镜头是一个凸透镜.物体有无数点组成,物体上任一点射向照相机镜头有无数条光线,经凸透镜折射后,有无数条折射光线会聚成该点的像.当照相机的镜头上沾上一个墨点,还有另外的部分光线,经凸透镜折射会聚成像.解答:解:当照相机的镜头上沾上一个墨点,还有另外的部分光线,经凸透镜折射会聚成像,像的大小不发生变化,折射光线减少,会聚成的像变暗.。
高二物理竞赛(9)几何光学和波动光学班级:_____________ 姓名:_________________ 座号:_____________一、一平凸透镜焦距为f,其平面上镀了银,现在其凸面一侧距它2f处,垂直于主轴放置一高为H的物,其下端在透镜的主轴上(如图所示)。
(1)用作图法画出物经镀银透镜所成的像,并标明该像是虚、是实;(2)用计算法求出此像的位置和大小。
二、有一水平放置的平行平面玻璃板H,厚3.0cm,折射率n=1.5。
在其下表面下2.0cm处有一小物S;在玻璃扳上方有一薄凸透镜L,其焦距f=30cm,透镜的主轴与玻璃板面垂直;S位于透镜的主轴上,如图所示。
若透镜上方的观察者顺着主轴方向观察到S的像就在S处,问透镜与玻璃板上表面的距离为多少?三、一束平行光沿薄平凸透镜的主光轴入射,经透镜折射后,会聚于透镜f=48cm处,透镜的折射率n=1.5。
若将此透镜的凸面镀银,物置于平面前12cm处,求最后所成像的位置。
四、图中,三棱镜的顶角α为60°,在三棱镜两侧对称位置上放置焦距均为f=30.0cm的两个完全相同的凸透镜L1和L2。
若在L1的前焦面上距主光轴下方y=14.3cm处放一单色点光源S,已知其像S 与S对该光学系统是左右对称的。
试求该三棱镜的折射率。
五、两个薄透镜L1和L2共轴放置,如图所示。
已知L1的焦距f1=f,L2的焦距f2=-f,两透镜间距离也是f。
小物体位于物面P上,物距u1=3f。
(1)小物体经这两个透镜所成的像在L2的__________边,到L2的距离为_________,是__________倍(虚或实)、____________像(正或倒),放大率为_________________;(2)现在把两透镜位置调换,若还要给定的原物体在原像处成像,两透镜作为整体应沿光轴向____________边移动距离_______________。
这个新的像是____________像(虚或实)、______________像(正或倒),放大率为________________。
D 几何光学训练题1.对于下列光现象的说法中,正确的是 ( )A .夏天烈日照射下公路远望像洒了一层水一样,这是光的全反射现象B .通过玻璃三棱镜看到的像比物体实际位置要低C .光导纤维是利用光的全反射现象制成的D .手术台上的无影灯消除影子是由于光没直线传播的形成的 2.对于光的传播,下列说法中正确的是( ). A.一定颜色的光传播度大小由媒质决定B.不同颜色的光在同一种媒质中传播时,波长越短的光传播速度越快C.同一频率的光在不同媒质波长不同,而在真空中的波长最长D.同一色光的频率随传播速度不同而改变3.简易潜望镜中的两块平面镜中心点之间的距离为L,通过潜望镜观察水平正前方的物体,看到像的位置比物体的实际位置( ).A.水平方向远L,竖直方向低LB.水平方向远L,竖直方向高LC.水平方向近L,竖直方向高LD.水平方向近L,竖直方向低L4.某一单色光在折射率为n 1的媒质中传播时,它的波长、频率和波速分别用λ1、γ1和υ1表示,在折射度为n 2的媒质中,分别用λ2、γ2和υ2表示,以上这些物理量存在如下的关系( ).5.在两束频率相同的单色光的交点前放一块平行的玻璃砖后,则交点的位置与不放玻璃砖前相比( ).(如图7-2-4所示)A.不变B.向左C.向右D.向左还是向右由光的频率大小决定6.点光源S 通过带有圆孔的挡板N ,照射到屏M 上,形成直径为d 的亮圆.如果在挡 板靠近光屏一侧放上一块厚玻璃砖,如图20-14所示,这时点光源通过圆孔和玻璃,在屏上形成直径为D 的亮圆.则直径D 和d 的大小关系为 ( )A .d >DB .d =DC .d <D D .无法确定7.如图所示,任意一条光线射向夹角为ϕ的两平面镜的相对镜面上,相继经两镜面反射后,最后射出线与最初入射线的方向间夹角应为( )(A) ϕ (B)2ϕ (C)3ϕ (D)4ϕ8.某同学为了研究光的色散,设计了如下实验:在墙角放置一个盛水 的容器,其中有一块与水平面成45°角放置的平面镜M ,如图所示,一细束白光斜射向水面,经水折射向平面镜,被平面镜反射经 水面折射后照在墙上,该同学可在墙上看到 ( ) A .上紫下红的彩色光带 B .上红下紫的彩色光带 C .外红内紫的环状光带 D .一片白光 9.如图所示,两个同种玻璃制成的棱镜,顶角α1 略大于α2 ,两单色光1和2分别垂直入射三棱镜,其出射光线与第二界面的夹角β1 =β2 ,则A 、在棱镜中1光的折射率比2光小B 、在光谱中,1光比较靠近红光C 、在棱镜中1光的传播速度比2光的小D 、把此两光由水中射向空气,产生全反射时,1光的临界角比2光的临界角大。
光学竞赛题一、选择题1.(3分)细心的小明同学注意到这样一个问题:如果打开窗户,直接看远处的高架电线,电线呈规则的下弯弧形;而如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,而且,轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.产生这种现象的原因是()A.玻璃上不同部位对视线的阻挡情况不同B.玻璃各部分的透光度不均匀C.玻璃各部分的厚度不均匀D.玻璃上不同部位对光的反射不一样2.(3分)如图所示,平面镜OM与ON的夹角为θ,一条平行于平面ON的光线经过两个平面镜的多次反射后,能够沿着原来的光路返回,则两平面镜之间的夹角不可能是()A.20°B.15°C.10°D.5°3.(3分)在探究凸透镜成像规律的实验中,我们发现像距v和物距u是一一对应的,在如图所示的四个图线中,能正确反映凸透镜成像规律的应该是()A.图线A B.图线B C.图线C D.图线D4.(3分)如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像5.(3分)如图所示,P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、O2是过圆孔中心O垂直于Q的直线,已知P和Q都足够大,现在直线O1O2上光屏P左侧5厘米处放置一点光源S,则平面镜上的反射光在屏上形成的亮斑面积为()A.米2B.米2C.米2D.米2光学竞赛题6.(3分)如图(a)所示,平面镜OM与ON夹角为θ,光线AB经过平面镜的两次反射后出射光线为CD.现将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,而入射光线不变,如图(b)所示.此时经过平面镜的两次反射后的出射光线将()A.与原先的出射光线CD平行B.与原先的出射光线CD重合C.与原先的出射光线CD之间的夹角为2βD.与原先的出射光线CD之间的夹角为β7.(3分)小明坐在前排听讲座时,用照相机把由投影仪投影在银幕上的彩色图象拍摄下来.由于会场比较暗,他使用了闪光灯.这样拍出来的照片()A.比不用闪光灯清楚多了B.与不用闪光灯的效果一样C.看不清投影到屏幕上的图象D.色彩被“闪”掉了,拍到的仅有黑色的字和线条8.(3分)如果不慎在照相机的镜头上沾上了一个小墨点,则照出的相片上()A.有一个放大的墨点像B.有一个缩小的墨点像C.一片漆黑D.没有墨点的像9.(3分)如图所示,水池的宽度为L,在水池右侧距离池底高度H处有一激光束,水池内无水时恰好在水池的左下角产生一个光斑.已知L=H,现向水池内注水,水面匀速上升,则光斑()A.匀速向右移动,且移动速度小于水面上升的速度B.匀速向右移动,且移动速度大于水面上升的速度C.减速向右移动,但速度始终大于水面上升的速度D.加速向右移动,但速度始终小于水面上升的速度10.(3分)如图所示,两平面镜OA、OB夹角为θ,位于镜前P点的某人分别在OA、OB镜内看到自己像的个数为()A.1;1B.2;1C.2;0D.1;011.(3分)如图所示,凸透镜竖直放置,凸透镜焦距f,现有一点光源S在凸透镜左侧以凸透镜两倍焦距处为圆心,在经过主光轴的竖直平面内做顺时针圆周运动,直径为D,且f<D<2f,则在下列关于点光源所成的像的运动轨迹的各图中,正确的是()A.B.C.D.12.(3分)(2011西宁)在皮鞋擦过鞋油,还要用鞋刷或软布反复擦几下,越擦越亮,这是由于()A.反复擦可增加漫反射效果B.反复擦可使鞋油填平皮革表面的凹坑,增加表面光滑程度,增加镜面反射效果C.鞋油反光性能比皮革好,反复擦可使鞋油均匀分布,增加漫反射效果D.鞋油的颜色比皮革鲜艳,可增加镜面反射效果13.(3分)在光具座上自左向右依次竖直放置一个凹透镜、凸透镜和平面镜,两个透镜的主光轴重合,凸透镜的焦距为f,此时两个透镜之间的距离为L.在凹透镜的左侧有一水平平行光束通过两个透镜后入射到平面镜上,经平面镜反射后,反射光恰能沿原来的光路返回,据此可判断凹透镜的焦距为()A.f B.L C.f+L D.f﹣L14.(3分)用转动八面镜法可以测光速,实验装置示意图如图所示.S为发光点,T为望远镜,平面镜O与凹面镜B构成了反射系统.八面镜M距反射系统的距离AB为L(L可长达几十千米),且远大于OB以及S和T到八面镜的距离.调整八面镜的位置直到通过望远镜能看到发光点S,然后使八面镜转动起来,并缓慢增大其转速(1秒内转过的圈数),当转速达到n0时,恰能在望远镜中再一次看见发光点S,由此得到光速c的表达式是()A.c=4Lno B.c=8LnoC.c=16LnoD.c=32Lno16.(3分)照相时,通过选择不同的“光圈”可以控制镜头的进光面积;选择不同的快门速度,可以控制镜头的进光时间.两者结合的目的是使底片受到的光照能量保持一定而得到好照片,下表中列出了照相机光圈与快门的几种正确组合.在“快门”一行中,“25”表示快门打开的时间是秒.在“光圈”一行中,“15”表示镜头透光部分的直径等于镜头焦距的.那么快门“50”对应的“光圈”应该是()光圈201512632快门9162550100400900A.7B.C.8D.17.(3分)如图所示,OO'为凸透镜的主光轴,将点光源放在A点时,像在B点;将点光源放在B点时,像在C点.当将点光源放在C点时,则()A.一定在B点成一个实像B.一定在A点的左侧成一个虚像C.可能在B、C之间成一个实像D.可能在C点的右侧成一个虚像18.(3分)如图所示,光线AB经过某凸透镜的一个焦点,B点在薄透镜上.已知F是该透镜的另一个焦点.若使用圆规和刻度尺来确定透镜的位置,则还需知道的条件是()A.光线AB经过的焦点位置B.透镜光心的位置C.光线AB经透镜后的折射光线D.不需要任何条件19.(3分)夜晚,人们仰望天空,有时能看到闪烁的人造地球卫星.地球赤道处有一观察者,在日落4小时后看到一颗人造地球卫星从赤道正上方高空中经过,设地球半径为R,则这颗人造地球卫星距赤道地面的高度至少为()A.R/2B.R C.2R D.4R20.(3分)如图所示,平面镜OM与ON镜面之间夹角为α,在两平面镜角平分线上有一个点光源S,如果要保证S发出的任意一条光线最多只能产生两次反射,则α的最小值是()A.120°B.90°C.72°D.6021.(3分)如图所示,位于凸透镜主光轴上某发光点P发出红、黄、绿三色复光,当用与主光轴相垂直的毛玻璃屏从透镜附近沿轴方向向远移动时,在屏上将依次看到()A.红、黄、绿亮点B.红、绿、黄亮点C.黄、红、绿亮点D.绿、黄、红亮点22.(3分)如图所示,有一圆柱形玻璃体,在它的中心轴线上有一球形气泡,柱体低面是磨砂的毛面,当平行光沿柱轴方向向下照射时,在磨砂的毛面上可能会看到()A.圆形亮斑B.圆型暗斑C.圆形暗斑且中心有一亮点D.圆形亮斑且中心有一暗点23.(3分)电影画面每隔秒更换一次,由于人的眼睛存在反应时间,所以会出现“眼见未必为实”的奇怪现象.如图所示,屏幕上出现的一辆匀速行驶汽车的车轮(车轮有6根对称分布的相同辐条),则下列现象中不符合此时人感觉的是()A.若在秒内每根辐条转过60°,则人觉得车轮是不转的B.若在秒内每根辐条转过355°,则人觉得车轮是倒转的C.若在秒内每根辐条转过360°,则人觉得车轮是不转的D.若在秒内每根辐条转过365°,则人觉得车轮是不转的24.(3分)(2013宜春模拟)如图所示,凸透镜的焦距为5厘米,在透镜左侧10厘米处,有一个与主光轴垂直的物体AB,在透镜右侧15厘米处放一个平面镜,镜面与凸透镜的主光轴垂直,则该光具组中,物体AB的成像情况是()A.一个正立实像,一个倒立实像,一个正立虚像B.一个正立实像,一个正立虚像,一个倒立虚像C.一个倒立实像,一个正立虚像,一个倒立虚像D.一个正立实像,一个倒立实像,一个倒立虚像25.(3分)如图所示,平面镜OM与ON垂直放置,在它们的角平分线上P点处,放有一个球形放光物体,左半部分为浅色,右半部分为深色,在P点左侧较远的地方放有一架照相机,不考虑照相机本身在镜中的成像情况,则拍出照片的示意图正确的是()A.B.C.D.26.(3分)在一张白纸上用红色水彩笔写上红色的“E”字.当你通过红色玻璃观察写在这张白纸上的“E”字时,观察到的现象是()A.清晰的红色“F”字B.清晰的黑色“F”字C.清晰的红底白色“E”字D.几乎看不出“E”字27.(3分)一焦距为f的凸透镜.主轴和水平x轴重合,透镜左侧x轴上有一点光源.点光源到透镜的距离大于f而小于2f,若将此透镜沿x轴向右平移2f的距离,则在此过程中点光源经透镜所成的像将()A.一直向右移动B.一直向左移动C.先向右移动.接着向左移动D.先向左移动,接着向右移动28.(3分)如图所示,一点光源位于凸透镜的主轴上,凸透镜位置固定.当点光源位于A点时,它的像在B点;当点光源位于B点时,它的像在C点.则凸透镜位于()A.A的左侧B.A B之间C.B C之间D.C的右侧29.(3分)早在公元前305年,着名天文家埃拉托色尼就已经测量出了地球的周长,与现代科学公认的地球周长的真实值相差不到%.他在研究中发现,每年夏至这天,塞恩城(今埃及阿斯旺)正午的太阳光正好直射到城内一口深井的底部,而远在S千米以外的亚历山大城,夏至这天正午的太阳光却会使物体在地面上留下一条影子,他测得太阳光方向与竖直方向之间的夹角为θ°,由此得出地球的周长为()A.千米B.千米C.千米D.千米30.(3分)如图所示,房间内一墙角处相临两墙面挂了两个平面镜,两平面镜相互垂直,在该墙角紧靠镜面处放有一个脸盆,盆内有水.某同学通过镜面和水面最多能看到自己像的个数为()A.3个B.6个C.9个D.无穷31.(3分)如图所示,两平面镜垂直放置,某光线PA以入射角α入射到镜面M上,经平面镜M和N 两次反射后反射光线BQ与PA平行.现将两平面镜以过O点且垂直于纸面的直线为轴同时逆时针旋转一个角度β(β<α),假设镜面足够大,则入射光线与反射光线之间的距离将()A.增大B.减小C.不变D.无法判断32.(3分)如图所示,两平面镜A和B之间的夹角为9°自平面镜B上的某点P射出一条与B镜面成β角的光线,在β角由0°至180°范围内(不包括0°)连续变化的过程中,发现当β取某角度时,光线经镜面一次或多次反射后,恰好能返回到P点,则符合该要求的β的个数有()A.1个B.4个C.6个D.9个33.(3分)如图所示,有一正方形的不透光的房间,在其中的一面墙上开有一个圆形小孔.在这面墙的对面有一个正方形的平面镜.在房间里有一个人靠在与平面镜垂直的一侧墙面上,当有一束垂直于圆孔的平行光通过圆孔射到平面镜上时,他能看到的是()A.镜面上有一个圆形的亮斑B.整个正方形镜子的形状C.整个房间的各处都是亮的D.感到整个房间是一片黑暗34.(3分)(2013顺义区二模)如图为潜望镜工作原理图.若现有一军舰位于S点处,则潜水艇中的人通过潜望镜看到的像的位置()A.在图中的A处B.在图中的B处C.在图中的C处D.在图中的D处35.一束光线经过某光学元件后的出射光线如图所示,则方框内放置的光学元件()A.只能是平面镜或凸透镜B.只能是凸透镜或凹透镜C.只能是凹透镜或平面镜D.平面镜、凸透镜和凹透镜均可36.如图所示,在空气中平行于玻璃凸透镜主光轴的光线经凸透镜会聚于主光轴的一点S,若把凸透镜浸没在水中,会聚点S′()A.在S的上方B.在S的下方C.与S重合D.条件不足,无法判断37.如图所示,M、N为某一透镜的主光轴,若将点光源置于A点,则成像于B点,若将点光源置于B 点,则成像于C点,已知AB>BC,则以下有关透镜的种类和位置的说法中正确的是()A.透镜是凸透镜,位于A点左侧B.透镜是凹透镜,位于C点右侧C.透镜是凸透镜,位于C点右侧D.透镜是凹透镜,位于A点左侧38.无云的晴天里,某同学在操场上竖立一根直杆,地面上OA是这根杆在太阳光下的投影,过了一段时间后,影子的位置移到了OB,且OA=OB,如图所示.则AB所指的方向是()A.东B.西C.南D.北39.如图所示,在竖直平面xoy内,人眼位于P(0,4)位置处,平面镜MN竖直放置其两端M、N的坐标分别为(3,1)和(3,0),某发光点S在该竖直平面y轴的右半部分某一区域内自由移动时,此人恰好都能通过平面镜看见S的像,则该区域的最大面积为()(图中长度单位为:米)A.米2B.米2C.4米2D.米240.(3分)用一支可以写出红颜色字的笔在一张白纸上写一行字,则下列说法中正确的是()A.白纸上的这一行字,在阳光下会吸收白光中的红色光,所以这一行字是红色的B.白纸上的这一行字,在阳光下会反射白光中的红色光,所以这一行字是红色的C.白纸上的这一行字,由于它能发出红光,所以这一行字是红色的D.白纸上的这一行字,如果只用绿色光照射上去,这一行字就会是绿色的二、填空题41.(3分)如图所示,一点光源位于金属圆筒内部轴线上A点.圆筒轴线与凸透镜主光轴重合,光屏与圆筒轴线垂直且距离透镜足够远.此时,点光源正好在光屏上形成一个清晰的像,测出此时凸透镜与圆筒右端面的距离为L;向右移动凸透镜到适当位置,光屏上再次出现了清晰的像.由于光源位于圆筒的内部,无法直接测量出A与筒右端面的距离d,为了求出d的大小,在上述过程中还需要测量出的一个物理是_________ ;如果用N来表示该物理量的大小,则可以得出d为_________ .42.(3分)如图所示,水平地面上有一不透光的边长为X的正方体物块.在正方体正左方有一点光源S,点光源和正方体物块的距离也为X.若在点光源S的上方距离为H处水平放置平面镜,H大小固定不变,平面镜足够大.不考虑其他光源的存在,那么在正方体的另一侧水平面上,将会由于点光源S发出的光线经平面镜反射而被照亮,现改变X的大小,当X增大到_________ 时,照亮区域将消失.光学竞赛题参考答案与试题解析一、选择题1.(3分)细心的小明同学注意到这样一个问题:如果打开窗户,直接看远处的高架电线,电线呈规则的下弯弧形;而如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,而且,轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.产生这种现象的原因是()A.玻璃上不同部位对视线的阻挡情况不同B.玻璃各部分的透光度不均匀C.玻璃各部分的厚度不均匀D.玻璃上不同部位对光的反射不一样考点:光的折射现象及其应用.专题:应用题.分析:根据光的折射现象,从玻璃上不同部位因厚度不同对光的折射情况不同这一角度入手,然后再对各个选项逐一分析即可.解答:解:A、如果隔着窗玻璃看,玻璃上不同部位对光的折射程度不同,而不是玻璃上不同部位对视线的阻挡情况不同,故本选项错误;B、因玻璃上不同部位透过光的颜色是相同的,都是透过白色光,故本选项错误;C、因玻璃上不同部位因厚度不同对光的折射情况不同,所以如果隔着窗玻璃看,电线虽然整体上也呈弧形,但电线上的不同部位有明显的不规则弯曲,当轻微摆动头部让视线移动时,电线上的不规则弯曲情景也在移动.故本选项正确;D、因如果隔着窗玻璃看,玻璃上不同部位对光的折射情况不同,而不是反射情况不同.故选C.点评:此题主要考查学生对光的折射现象及其应用,而且此题的中现象对学生来说并不陌生,但是要从光的折射角度来解释这一现象,尤其是“因玻璃上不同部位因厚度不同对光的折射情况不同”这一点,对学生来说就增加了一定的难度,因平时的练习题目,只是简单地折射定律,因此,此题属于难题.2.(3分)如图所示,平面镜OM与ON的夹角为θ,一条平行于平面ON的光线经过两个平面镜的多次反射后,能够沿着原来的光路返回,则两平面镜之间的夹角不可能是()A.20°B.15°C.10°D.5°考点:光的反射定律.专题:光的传播和反射、平面镜成像.分析:要解决此题首先要明确下面两点:(1)做出光的反射光路图,根据光路图可以确定每次入射时入射角两个平面镜夹角θ的关系.(2)光线原路返回的含义:必须是经过多次反射后,最后的一次入射是垂直于其中的一个平面镜,即入射角等于零.解答:解:画光的反射光路图如下图所示,由图知:光线第一次反射的入射角为:90°﹣θ;第二次入射时的入射角为:90°﹣2θ;第三次的入射角为:90°﹣3θ;第N次的入射角为:90°﹣Nθ.要想延原来光路返回需要光线某次反射的入射角为零所以有90°﹣Nθ=0,解得:N=由于N为自然数,所以θ不能等于20°.故选A.点评:(1)此题考查了光的反射定律并结合了几何方面的知识.(2)明确此题中每一次反射,入射角与两平面镜之间夹角θ的关系是解决此题的一个难点,它利用了几何中三角形的外角等于不相邻的内角和的知识.3.(3分)在探究凸透镜成像规律的实验中,我们发现像距v和物距u是一一对应的,在如图所示的四个图线中,能正确反映凸透镜成像规律的应该是()A.图线A B.图线B C.图线C D.图线D考点:凸透镜成像规律及其探究实验.专题:图析法.分析:①首先看清图象中的横轴表示物距,纵轴表示像距,根据凸透镜成像规律中的u=2f时,物距v=2f,求出其焦距.②凸透镜成像时,像距、物距和焦距三者之间是有一定的联系的,若用一个公式表示,就是:+=(其中u表示物距,v表示像距,f表示焦距),③将ABCD4个图线中的物距、像距数值,分别代入+=逐一分析即可得出结论.解答:解:A、因为A图线中,物距和像距始终相等,不符合凸透镜成像规律中的物距和像距的关系.故本选项不能正确反映凸透镜成像规律;B、B图线中,随着物距的不断增大,像距在不断减小,不符合凸透镜成像规律中的物距和像距的关系.故本选项不能正确反映凸透镜成像规律;C、图线C,当物距为15cm时,像距为15cm,由凸透镜成像规律可知,u=2f,v=2f,此时f=,当物距为35cm时,像距为5cm,代入+≠,故本选项不能正确反映凸透镜成像规律;D、图线D,当物距为10cm时,像距为10cm,由凸透镜成像规律可知,u=2f,v=2f,此时f=5cm,当物距为30cm时,像距为6cm,代入+=,故本选项能正确反映凸透镜成像规律.故选D.点评:此题主要考查学生对凸透镜成像规律的理解和掌握,此题对学生的要求比较高,第一,要求学生看懂图象,第二要求学生根据图象求出各自的焦距,第三,要求学生知道凸透镜成像时,像距、物距和焦距三者之间的关系,即+=,总之,此题难度较大,属于难题.4.(3分)如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像考点:凸透镜成像的应用.专题:应用题.分析:(1)平面镜成像的规律:虚像、物体和像大小相等、物体和像到镜面的距离相等,物体和像的连线与镜面垂直;(2)凸透镜成像规律:当物体位于凸透镜的2倍焦距处,成倒立、等大的实像.解答:解:①按题意,AB在凸透镜右侧距离透镜2f处成一个倒立的等大的实像.②由于成像后的光线是射向右下方的,所以不能在平面镜上成像(平面镜只在主光轴的上方),所以只能成一个实像.③如果平面镜足够大,则“AB在凸透镜右侧距离透镜2f处成一个倒立的等大的实像”又会在平面镜上成一个等大的虚像,平面像反射后的光线又会经凸透镜成一个缩小的倒立的实像(成在凸透镜左侧f与2f之间.此时相当于物距为4f.当然,也要满足凸透镜是足够大了才有此种情况).故选D.点评:此题主要考查凸透镜成像规律及其应用,此题的突破点是,AB只有在主光轴上的那点折射后入MN,其它均没有,故只有一个实像.5.(3分)如图所示,P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、O2是过圆孔中心O垂直于Q的直线,已知P和Q都足够大,现在直线O1O2上光屏P左侧5厘米处放置一点光源S,则平面镜上的反射光在屏上形成的亮斑面积为()A.米2B.米2C.米2D.米2考点:平面镜成像的特点、原理、现象及其实验方案;光的反射定律.专题:光的传播和反射、平面镜成像.分析:设出圆孔的半径与光斑的半径,通过画图找出二者之间的大小关系,再运用面积的计算公式进行计算即可.解解:设圆孔的半径为d,亮斑的半径为r.答:作出光的传播路线图,由三角形的知识可得:r:d=25:5=5:1而亮斑的面积:S=πr2﹣πd2=π(r2﹣d2)=π[(5d)2﹣d2]=π24d2=π24×()2=π150cm2=πm2=m2.故选C.点评:此题虽然是一道光学题,但难不在光学知识,却是数学知识,画出图形,通过三角形的关系找出两个圆的半径关系是解决问题最关键的一步.6.(3分)如图(a)所示,平面镜OM与ON夹角为θ,光线AB经过平面镜的两次反射后出射光线为CD.现将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,而入射光线不变,如图(b)所示.此时经过平面镜的两次反射后的出射光线将()A.与原先的出射光线CD平行B.与原先的出射光线CD重合C.与原先的出射光线CD之间的夹角为2βD.与原先的出射光线CD之间的夹角为β考点:作光的反射光路图.专题:图析法.分析:若将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,可知入射角增大或减小的度数,进而可知反射角增大或减小的度数,从而可知第一次反射的光线偏转的角度,因平面镜M1和M2一起以B为轴沿纸面转动时,保持α角不变,所以第二次反射的光线方向不变.解答:解:因为保持θ角不变,将平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β,则入射角增大或减小β,反射角也增大或减小β,所以反射光线与入射光线的夹角是2β,即反射的光线偏转2β角,因为平面镜OM与ON同时绕垂直纸面过0点的轴转过一个较小的角度β时,两平面镜OM与ON互成θ角的角度没变,所以第二次反射的光线方向不变.又因为入射光线不变,所以此时经过平面镜的两次反射后的出射光线将与原先的出射光线CD重合.故选B.点评:此题主要考查了有关光的反射定律的应用,首先要掌握定律的内容,特别是反射角与入射角的关系,同时要掌握反射角与入射角的概念,知道这些角都是光线与法线的夹角.7.(3分)小明坐在前排听讲座时,用照相机把由投影仪投影在银幕上的彩色图象拍摄下来.由于会场比较暗,他使用了闪光灯.这样拍出来的照片()A.比不用闪光灯清楚多了B.与不用闪光灯的效果一样。