下载文档原格式
电容传感器动态特性实验报告电容传感器动态特性实验报告引言：电容传感器是一种常见的传感器，广泛应用于工业自动化、仪器仪表、医疗设备等领域。
了解电容传感器的动态特性对于优化传感器的工作性能和提高测量精度具有重要意义。
本实验旨在通过实际操作和数据分析，研究电容传感器的动态特性。
实验装置：本次实验所使用的电容传感器为平行板电容传感器。
实验装置包括电容传感器、信号发生器、示波器、数据采集卡等设备。
实验步骤：1. 连接电路：将信号发生器的输出端与电容传感器的输入端相连，将示波器的输入端与电容传感器的输出端相连，使用数据采集卡将示波器的输出信号记录下来。
2. 设置信号参数：通过信号发生器设置不同的频率和幅值，以模拟实际工作环境下的电容传感器。
3. 数据采集：使用数据采集卡记录示波器输出信号的振幅和相位差。
4. 数据分析：根据采集到的数据，分析电容传感器的动态特性，包括频率响应、幅频特性、相频特性等。
实验结果与分析：1. 频率响应：通过改变信号发生器的频率，记录示波器输出信号的振幅变化。
实验结果显示，电容传感器的输出信号随着频率的增加而逐渐减小，说明电容传感器在高频率下的灵敏度较低。
2. 幅频特性：保持信号发生器的频率不变，改变信号发生器的幅值，记录示波器输出信号的振幅变化。
实验结果显示，电容传感器的输出信号随着信号幅值的增加而线性增加，但当信号幅值达到一定值后，电容传感器的输出信号增加速度变慢，出现饱和现象。
3. 相频特性：通过改变信号发生器的频率，记录示波器输出信号的相位差变化。
实验结果显示，电容传感器的输出信号相位差随着频率的增加而逐渐增大，说明电容传感器的相位响应较慢。
实验讨论：1. 频率响应与幅频特性：电容传感器的频率响应和幅频特性受到传感器自身特性和外部环境的影响。
传感器本身的结构和材料会影响传感器的频率响应和幅频特性，而外部环境的温度、湿度等因素也会对传感器的动态特性产生影响。
2. 相频特性：电容传感器的相频特性与传感器的响应速度有关。
控制工程实训课程学习总结基于MATLAB 的系统建模与仿真实验报告摘要：本报告以控制工程实训课程学习为背景，基于MATLAB软件进行系统建模与仿真实验。
通过对实验过程的总结，详细阐述了系统建模与仿真的步骤及关键技巧，并结合实际案例进行了实验验证。
本次实训课程的学习使我深入理解了控制工程的基础理论，并掌握了利用MATLAB进行系统建模与仿真的方法。
1. 引言控制工程是一门应用广泛的学科，具有重要的理论和实践意义。
在控制工程实训课程中，学生通过实验来加深对控制系统的理解，并运用所学知识进行系统建模与仿真。
本次实训课程主要基于MATLAB软件进行，本文将对实验过程进行总结与报告。
2. 系统建模与仿真步骤2.1 确定系统模型在进行系统建模与仿真实验之前，首先需要确定系统的数学模型。
根据实际问题，可以选择线性或非线性模型，并利用控制理论进行建模。
在这个步骤中，需要深入理解系统的特性与工作原理，并将其用数学方程表示出来。
2.2 参数识别与估计参数识别与估计是系统建模的关键，它的准确性直接影响到后续仿真结果的可靠性。
通过实际实验数据，利用系统辨识方法对系统的未知参数进行估计。
在MATLAB中，可以使用系统辨识工具包来进行参数辨识。
2.3 选择仿真方法系统建模与仿真中，需要选择合适的仿真方法。
在部分情况下，可以使用传统的数值积分方法进行仿真；而在其他复杂的系统中，可以采用基于物理原理的仿真方法，如基于有限元法或多体动力学仿真等。
2.4 仿真结果分析仿真结果的分析能够直观地反映系统的动态响应特性。
在仿真过程中，需对系统的稳态误差、动态响应、鲁棒性等进行综合分析与评价。
通过与理论期望值的比较，可以对系统的性能进行评估，并进行进一步的优化设计。
3. 实验案例及仿真验证以PID控制器为例，说明系统建模与仿真的步骤。
首先，根据PID控制器的原理以及被控对象的特性，建立数学模型。
然后，通过实际实验数据对PID参数进行辨识和估计。
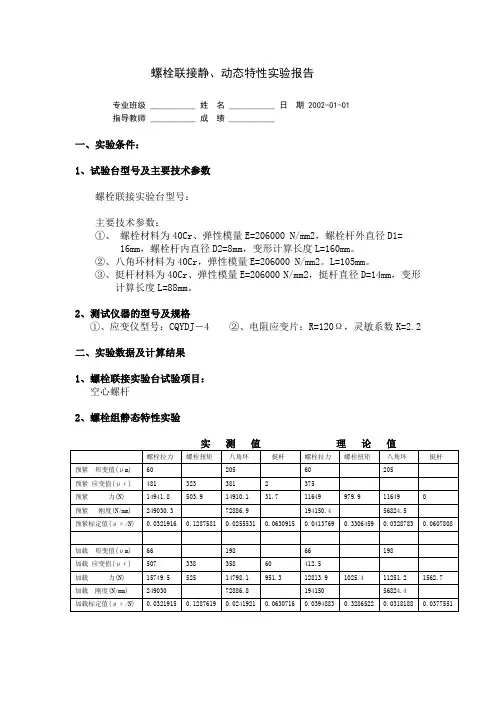
螺栓联接静、动态特性实验报告
专业班级 ___________ 姓名 ___________ 日期 2002-01-01
指导教师 ___________ 成绩 ___________
一、实验条件：
1、试验台型号及主要技术参数
螺栓联接实验台型号：
主要技术参数：
①、螺栓材料为40Cr、弹性模量E=206000 N/mm2，螺栓杆外直径D1=
16mm，螺栓杆内直径D2=8mm，变形计算长度L=160mm。
②、八角环材料为40Cr，弹性模量E=206000 N/mm2。
L=105mm。
③、挺杆材料为40Cr、弹性模量E=206000 N/mm2，挺杆直径D=14mm，变形
计算长度L=88mm。
2、测试仪器的型号及规格
①、应变仪型号：CQYDJ－4 ②、电阻应变片：R=120Ω，灵敏系数K=2.2
二、实验数据及计算结果
1、螺栓联接实验台试验项目：
空心螺杆
2、螺栓组静态特性实验
3、螺栓联接静、动特性应力分布曲线图 (空心螺杆)
三、实验结果分析。
机械工程学院研究生研究型课程考试答卷课程名称：材料动态特性实验（SHPB实验）考试形式：□专题研究报告□论文√大作业□综合考试评阅人：时间：年月日材料动态特性实验实验目的：1、了解霍普金森杆的实验原理和实验步骤；2、会用霍普金森杆测试材料动态力学性能。
1.SHPB 组成：Kolsky 在Hopkinson 压杆技术的基础上提出采用分离式 Hop-kinson 压杆 SHPB )技术来测定材料在一定应变率范围的动态应力 ── 应变行为 ,该实验的理论基础是一维应力波理论, 它通过测定压杆上的应变来推导试样材料的应力 ── 应变关系, 是研究材料动态力学性能最基本的实验方法之一。
为了测出A3钢（又称Q235钢）的屈服极限、弹性模量以及其他性能参数。
用SHPB 实验就行数据测量。
SHPB 的实现装置如下图：分离式Hopkinson 压杆装置示意图它由压缩气枪、撞击杆、测时仪、输入杆（入射杆）、超动态应变仪、试件、透射杆、吸收杆、阻尼器和数据处理系统组成。
2.实验原理：SHPB 技术建立在两个基本假定的前提上：（1）杆中应力波是一维波；（2）试件应力/应变沿其长度均匀分布。
根据垂直入射应力波在界面出的反射、透射原理和上述假定由：应力相等：)()()(t t t T R I σσσ=+ (1)应变相等：)()()(t t t T R I εεε=+ (2)式中()I t σ和()R t σ分别为入射杆的入射应力和反射应力，()T t σ为透射杆的透射应力，()I t ε和()R t ε为入射杆的入射应变和反射应变，()Tt ε为透射杆的透射应变。
图1 输入杆-试件-输出杆相对位置如图2所示，在满足一维应力波假定的条件下，一旦测得试件与输入杆的界面X 1处的应力，可理论推导得： []112()(,)(,)(,)2S I R T SA t X t X t X t A σσσσ=++ （3） SR I T S S L t X v t X v t X v L t X v t X v t ),(),(),(),(),()(11212--=-=ε （4） []⎰⎰--==t R I T S t S S dt t X v t X v t X v L dt t 01120),(),(),(1)(εε （5）式中：A 为压杆的横截面积，s A 为试件的横截面积，S L 为试件的长度。
实验一 典型环节的MATLAB 仿真 一、实验目的1．熟悉MATLAB 桌面和命令窗口，初步了解SIMULINK 功能模块的使用方法。
2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。
3．定性了解各参数变化对典型环节动态特性的影响。
二、实验内容① 比例环节1)(1=s G 和2)(1=s G ；Simulink 图形实现：示波器显示结果：② 惯性环节11)(1+=s s G 和15.01)(2+=s s GSimulink 图形实现：示波器显示结果：③ 积分环节s s G 1)(1Simulink 图形实现：示波器显示结果：④ 微分环节s s G )(1Simulink 图形实现：波器显示结果：⑤ 比例+微分环节（PD ）2)(1+=s s G 和1)(2+=s s G1）、G1（s ）=s+2Simulink 图形实现：示波器显示结果：2）、G2（s）=s+1 Simulink图形实现：示波器显示结果：⑥ 比例+积分环节（PI ）s s G 11)(1+=和s s G 211)(2+=1）、G1（1）=1+1/sSimulink 图形实现：示波器显示结果：2）G2（s）=1+1/2s Simulink图形实现：示波器显示结果：三、心得体会通过这次实验我学到了很多，对课本内容加深了理解，熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法，加深对各典型环节响应曲线的理解，这为对课程的学习打下了一定基础。
实验二线性系统时域响应分析一、实验目的1．熟练掌握step( )函数和impulse( )函数的使用方法，研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。
2．通过响应曲线观测特征参量ζ和nω对二阶系统性能的影响。
3．熟练掌握系统的稳定性的判断方法。
二、实验内容1．观察函数step( )的调用格式，假设系统的传递函数模型为243237()4641s s G s s s s s ++=++++绘制出系统的阶跃响应曲线？2．对典型二阶系统222()2n n n G s s s ωζωω=++1）分别绘出2(/)n rad s ω=，ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线，分析参数ζ对系统的影响，并计算ζ=0.25时的时域性能指标,,,,p r p s ss t t t e σ。
自动控制原理实验报告实验名称：二阶系统的动态特性与稳定性分析班级：姓名：学号：实验二 二阶系统的动态特性与稳定性分析一、实验目的1、 掌握二阶系统的电路模拟方法及其动态性能指标的测试技术过阻尼、临界阻尼、欠阻尼状态2、 分析二阶系统特征参量（ξω，n ）对系统动态性能的影响；3、 分析系统参数变化对系统稳定性的影响，加深理解“线性系统稳定性至于其结构和参数有关，与外作用无关”的性质；4、 了解掌握典型三阶系统的稳定状态、临界稳定、不稳定状态；5、 学习二阶控制系统及其阶跃响应的Matlab 仿真和simulink 实现方法。
二、实验内容1、 构成各二阶控制系统模拟电路，计算传递函数，明确各参数物理意义。
2、 用Matlab 和simulink 仿真，分析其阶跃响应动态性能，得出性能指标。
3、 搭建典型二阶系统，观测各个参数下的阶跃响应曲线，并记录阶跃响应曲线的超调量%σ、峰值时间tp 以及调节时间ts ，研究其参数变化对典型二阶系统动态性能和稳定性的影响；4、 搭建典型三阶系统，观测各个参数下的阶跃响应曲线，并记录阶跃响应曲线的超调量%σ、峰值时间tp 以及调节时间ts ，研究其参数变化对典型三阶系统动态性能和稳定性的影响；5、 将软件仿真结果与模拟电路观测的结果做比较。
三、实验步骤1、 二阶系统的模拟电路实现原理 将二阶系统：ωωξω22)(22nn s G s s n++=可分解为一个比例环节，一个惯性环节和一个积分环节ωωξω)()()()(2C C C C s C C 22262154232154232154215426316320nn s s s s s G s s s C R R R R R R R R R R R R C R R R R R R R R R U U n i ++=++=++== 2、 研究特征参量ξ对二阶系统性能的影响将二阶系统固有频率5.12n =ω保持不变，测试阻尼系数ξ不同时系统的特性，搭建模拟电路，改变电阻R6可改变ξ的值当R6=50K 时，二阶系统阻尼系数ξ=0.8 当R6=100K 时，二阶系统阻尼系数ξ=0.4 当R6=200K 时，二阶系统阻尼系数ξ=0.2（1）用Matlab 软件仿真实现二阶系统的阶跃响应，计算超调量%σ、峰值时间tp 以及调节时间ts 。
控制系统仿真实验报告一、实验目的本次控制系统仿真实验的主要目的是通过使用仿真软件对控制系统进行建模、分析和设计，深入理解控制系统的工作原理和性能特点，掌握控制系统的分析和设计方法，提高解决实际控制问题的能力。
二、实验设备与软件1、计算机一台2、 MATLAB 仿真软件三、实验原理控制系统是由控制对象、控制器和反馈环节组成的一个闭环系统。
其工作原理是通过传感器测量控制对象的输出，将其与期望的输出进行比较，得到误差信号，控制器根据误差信号产生控制信号，驱动控制对象，使系统的输出逐渐接近期望的输出。
在仿真实验中，我们使用数学模型来描述控制对象和控制器的动态特性。
常见的数学模型包括传递函数、状态空间方程等。
通过对这些数学模型进行数值求解，可以得到系统的输出响应，从而对系统的性能进行分析和评估。
四、实验内容1、一阶系统的仿真建立一阶系统的数学模型，如一阶惯性环节。
使用 MATLAB 绘制系统的单位阶跃响应曲线，分析系统的响应时间和稳态误差。
2、二阶系统的仿真建立二阶系统的数学模型，如典型的二阶振荡环节。
改变系统的阻尼比和自然频率，观察系统的阶跃响应曲线，分析系统的稳定性、超调量和调节时间。
3、控制器的设计与仿真设计比例控制器（P 控制器）、比例积分控制器（PI 控制器）和比例积分微分控制器（PID 控制器）。
对给定的控制系统，分别使用不同的控制器进行仿真，比较系统的性能指标，如稳态误差、响应速度等。
4、复杂控制系统的仿真建立包含多个环节的复杂控制系统模型，如串级控制系统、前馈控制系统等。
分析系统在不同输入信号下的响应，评估系统的控制效果。
五、实验步骤1、打开 MATLAB 软件，新建脚本文件。
2、根据实验内容，定义系统的数学模型和参数。
3、使用 MATLAB 中的函数，如 step(）函数绘制系统的阶跃响应曲线。
4、对响应曲线进行分析，计算系统的性能指标，如超调量、调节时间、稳态误差等。
5、设计控制器，修改系统模型，重新进行仿真，比较系统性能的改善情况。
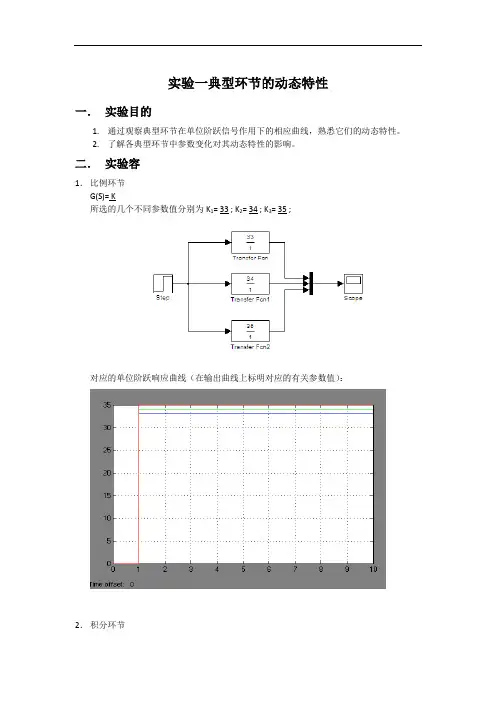
实验一典型环节的动态特性一．实验目的1.通过观察典型环节在单位阶跃信号作用下的相应曲线，熟悉它们的动态特性。
2.了解各典型环节中参数变化对其动态特性的影响。
二．实验容1．比例环节G(S)= K所选的几个不同参数值分别为K1= 33 ; K2= 34 ; K3= 35 ;对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：2．积分环节G(S)=S Ti1所选的几个不同参数值分别为T i1= 33 ; T i2= 33 ; T i3= 35 :对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：3．一阶惯性环节G(S)=STKc1令K不变（取K= 33 ），改变T c取值：T c1=12；T c2=14；T c3=16；对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：4． 实际微分环节G(S)=ST ST K D D D 1令K D 不变（取K D =33），改变T D 取值：T D 1=10；T D 2=12；T D 3=14；对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：5．纯迟延环节G(S)=S eτ-所选的几个不同参数值分别为τ1=2；τ2=5；τ3=8；对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：6． 典型二阶环节G(S)=222nn nS S K ωξωω++令K 不变（取K =33）①令ωn =1，ξ取不同值：ξ1=0；ξ2=0.2,ξ3=0.4（0<ξ<1）；ξ4=1；ξ5=3（ξ≥1）；对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：②令ξ=0，ωn 取不同值：ωn 1=1；ωn 2=2；对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：③令ξ=0.216，ωn取不同值：ωn1=3；ωn 2=4；对应的单位阶跃响应曲线（在输出曲线上标明对应的有关参数值）：。
测试装置动态特性仿真实验
班级：7391 学号：2009301828 姓名：张志鹏
一、实验目的
1、加深对一阶测量装置和二阶测量装置的幅频特性与相频特性的理解；
2、加深理解时间常数变化对一阶系统动态特性影响；
3、加深理解频率比和阻尼比变化对二阶系统动态特性影响；
4、使学生了解允许的测量误差与最优阻尼比的关系。
二、实验原理
1、 一阶测量装置动态特性
一阶测量装置是它的输入和输出关系可用一阶微分方程描述。
一阶测量装置的频率响应函数为：
式中：S S 为测量装置的静态灵敏度；τ为测量装置的时间常数。
一阶测量装置的幅频特性和相频特性分别为：
可知，在规定S S =1的条件下，A （ω）就是测量装置的动态灵敏度。
当给定一个一阶测量装置，若时间常数τ确定，如果规定一个允许的幅值误差ε，则允许测量的信号最高频率ωH 也相应地确定。
为了恰当的选择一阶测量装置，必须首先对被测信号的幅值变化范围和频率成分有个初步了解。
有根据地选择测量装置的时间常数τ，以保证A （ω）≥1-ε 能够满足。
2、二阶测量装置动态特性
二阶测量装置的幅频特性与相频特性如下：
幅频特性202220)/(4))/(1(/1)(ωωξωωω--=A
相频特性2200))/(1/()/(2()(ωωωωξφ--=arctg w
Α（ω）是ξ和ω/0ω的函数，即具有不同的阻尼比ξ的测试装置当输入信⎥⎦⎤⎢⎣⎡ωτ+ωτ-ωτ+=ωτ+=ω22s s )(1j )
(11S j 11S )j (H ()()2
11
A ωτ+=ω()ωτ
-=ωφarctan
号频率相同时，应具有不同的幅值响应，反之，当不同的频率的简谐信号送入同一测试装置时它们的幅值响应也不相同，同理具有不同的阻尼比ξ的测试装置当输入信号频率相同时，应有不同的相位差。
(1).当ω=0时，Α（ω）=1;(2).当ω→∞，A （ω）=0;(3).当ξ≥0.707时随着输入信号频率的加大，Α（ω）单调的下降, ξ＜0.707时Α（ω）的特性曲线上出现峰值点;(4)如果ξ=0，))/(1/(1))/(1(/1)(202
20ωωωωω-=-=A ，显然，其峰值点出现在ω=0ω处。
其值为“∞”，当ξ从0向0.707变化过程中随着的加大其峰值点逐渐左移，并不断减小。
对以上二阶环节的幅频特性的结论论证如下：
(1).当ω=0时A(ω)=1
(2).当ω→∞时,A(ω)=0 (3).要想得到A(ω)的峰值就要使202220)/(4))/(1(/1)(A ωωξ-ωω-=ω 中的202220)/(4))/(1(ωωξωω--取最小值。
令:t=20)/(ωω
t t t f 224)1()(ξ+-=
对其求导可得t=1-22ξ时,f(t)取最小值.由于t=20)/(ωω≥0,所以1-22ξ≥0, 2ξ必须小于1/2时,f(t)才有最小值,即ξ>2/2时，A(ω)不出现峰值点;当ξ＜2/2时4244)(ξξ-=t f ,f(t)对ξ求导得)21(82ξξ-，可以看出f(t):
ξ属于[0，
2/2]时单调递增，于是得A(ω)的峰值点A 为4244/1)(/1ξξ-=t f ; 在ξ属于[0，2/2]递减。
(4).当ξ=0时 A=∞，t=20)/(ωω，ω/0ω=1,即ξ=0时A(ω)的峰值为∞，且必出现在ω/0ω=1时，当ξ=2/2时,t=0→ω=0，A(ω)=1. 还可以看出，在ξ属于[0，2/2]增大时t=1-22ξ就减小，即f(t)的峰值左平移。
（二）阻尼比的优化
在测量系统中，无论是一阶还是二阶系统的幅频特性都不能满足将信号中的所有频率都成比例的放大。
于是希望测量装置的幅频特性在一段尽可能宽的范围内最接近于1。
根据给定的测量误差，来选择最优的阻尼比。
首先设允许的测量误差，由第一部分可知，存在一个ξ使得A(w)峰值接近于 1+△A ，即直线A=1+△A 与A(w)相切，且切与A(w)的峰值点。
设这个峰值点为0ξ，
（1）当0＜ξ＜0ξ时 ，A(w)与直线A=1+△A 有两个交点为A,B
（2）当ξ＞0ξ时无交点。
（3）无论取何值，A(w)与A=1-△A 只有一个交点。
从图中可以看出，0＜ξ＜0ξ时,环节的通频带为（0，0/ωωA ）;ξ＞0ξ时,通频带为（0，0/ωωD ）.此时找出两种情况下的最宽的通频带，在进一步比较两个通频带，其中宽的就是误差为△A 时的最宽的通频带。
由于ξ=0ξ时,A(w)与直线A=1+△A 相切,于是可解的: 2/]))1/(111[20A ∆+--=ξ
令)()/(),()/(2020ξωωξωωY X D A ==,于是: 2
)])1/(1(1[4)24(42)(2222A X ∆+-----=ξξξ 2
)])1/(1(1[4)24(42)(2222A Y ∆----+-=ξξξ 分别以)(ξX 和)(ξY 为目标函数,以0＜ξ＜0ξ和ξ≥0ξ为约束条件，用0.618法求)(ξX 和)(ξY 的最大值。
由于求目标函数的极大化就等于求函数- f(t)的极小化，于是求)(ξX 和)(ξY 的极大化就等于求函数-)(ξX 和-)(ξY 的极小化。
它们可以分别写成:
)2
)])1/(1(1[4)24(42()](min[2222A X ∆+------=-ξξξ
其中0＜ξ＜0ξ，)(ξX ＞0
)2
)])1/(1(1[4)24(42()](min[2222A Y ∆----+--=-ξξξ 其中ξ≥0ξ，)(ξY ＞0 。
对以上两个数学模型用0.618法得到最优解分别为（1max ,ξX ），（2m a x ,ξY ）.
三、实验内容
1、一阶测量装置的动态特性仿真
选择虚拟的一阶测量装置，分别在不同的输入信号：周期性信号（正弦波、方波、三角波、锯齿波等）、冲击信号、正弦扫描信号、及采样函数信号等情况下，改变时间常数，观察和分析一阶测量装置的动态特性变化情况。
根据给定的幅值测量误差，选择最优的时间常数，确定有效的频率测量范围。
2、 二
选择虚拟的二阶测量装置，分别在不同的输入信号：周期性信号（正弦波、方波、三角波、锯齿波等）、冲击信号、正弦扫描信号、及采样函数信号等情况下，改变频率比和阻尼比，观察和分析二阶测量装置的动态特性变化。
根据给定的幅值测量误差，选择最优的频率比和阻尼比，确定有效的频率测量范围。
四、实验报告
(1).总结一阶测量装置的幅频特性与时间常数τ之间的关系，与课本中的结论相比较，看是否正确;
当t=0.01
当t=0.37
(2)、绘出一阶测量装置的三条幅频曲线验证你从计算机上所得的最优时间常数 ；
(3).总结二阶测量装置的幅频特性与阻尼比ξ之间的关系，与课本中的结论相比较，看是否正确;
0.7
0.707。
