圆提升专题(十一)

2022-2023学年人教版中考数学复习《圆综合压轴题》专题提升训练（附答案）1．锐角三角形△ABC的外心为O，外接圆直径为d，延长AO，BO，CO，分别与对边BC，CA，AB交于D，E，F．（1）求的值；（2）求证：．2．如图，AB是⊙O的直径，点C在⊙O上，CP是⊙O的切线．点P在AB的延长线上．（1）求证：∠COB＝2∠PCB；（2）若M是弧AB的中点，CM交AB于点N，若AB＝6．求MC•MN的值．3．如图，AC为⊙O的直径，CF切⊙O于点C，AF交⊙O于点D，点B在DF上，BC交⊙O于点E，且∠CAF＝2∠BCF，BG⊥CF于点G，连接AE．（1）求∠AEB的度数；（2）求证：△CBG∽△ABE；（3）若∠F＝60°，GF＝2，求⊙O的半径长．4．如图，△ABC内接于⊙O，BC是⊙O的直径，E是上一点，弦BE交AC于点F，弦AD⊥BE于点G，连接CD、CG，且∠CBE＝∠ACG．（1）求证：∠CAG＝∠ABE；（2）求证：CG＝CD；（3）若AB＝4，BC＝2，求GF的长．5．如图，△ABC为⊙O的内接三角形，AD⊥BC，垂足为D，直径AE平分∠BAD，交BC于点F，连结BE．（1）求证：∠AEB＝∠AFD；（2）若AB＝10，BF＝5，求DF的长；（3）若点G为AB的中点，连结DG，若点O在DG上，求BF：FC的值．6．如图，△ABC为⊙O的内接等腰三角形，AB＝AC，CD为⊙O的直径，DF∥AC交AB、BC于点E、F．（1）求证：DE＝EF；（2）若sin∠B＝，⊙O的半径为5，求CF的长．7．如图，⊙O为△ABC的外接圆，AB为⊙O直径，AC＝BC，点D在劣弧BC上，CE⊥CD交AD于E，连接BD．（1）求证：△ACE≌△BCD．（2）若CD＝2，BD＝3，求⊙O的半径．8．如图，在△ABC中，∠ACB＝90°，点D在BC边上（不包括端点B，C），过A，C，D三点的⊙O交AB于另一点E，连接AD，DE，CE，且CE⊥AD于点G，过点C作CF∥DE交AD于点F，连接EF．（1）求证：四边形DCFE是菱形；（2）当tan∠AEF＝，AC＝4时，求⊙O的直径长．9．如图，在△ABC中，以AB为直径的⊙O交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，且DH是⊙O的切线，连接DE交AB于点F，连接BE．（1）求证：DC＝DE；（2）若AE＝4，．求：①BE的长；②cos∠BDF的值．10．如图，AB是半圆的直径，AC为半圆的切线，AC＝AB、在半圆上任取一点D，作DE⊥CD，交直线AB 于点F，BF⊥AB，交线段AD的延长线于点F．（1）设是x°的弧，并要使点E在线段BA的延长线上，则x的取值范围是；（2）不论D点取在半圆什么位置，图中除AB＝AC外，还有两条线段一定相等，指出这两条相等的线段，并予证明．11．如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接P A，PB，AB，已知∠PBA＝∠C．（1）求证：PB是⊙O的切线；（2）连接OP，若OP∥BC，且OP＝8，⊙O的半径为2，求BC的长．12．如图，点C是以AB为直径的圆O上一点，直线AC与过B点的切线相交于D，点E是BD的中点，直线CE交直线AB于点F．（1）求证：CF是⊙O的切线；（2）若ED＝3，cos F＝，求⊙O的半径．13．如图①，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE＝CB．（1）求证：BC为⊙O的切线；（2）连接AE并延长与BC的延长线交于点G（如图②所示）．若AB＝，CD＝9，求线段BC和EG 的长．14．如图，AB为⊙O的直径，AB＝10，C为⊙O上一点，AD⊥CD，垂足为D，且交⊙O于E，C是的中点．（1）求证：DC是⊙O的切线；（2）若AC＝8，请直接写出CD的长．（3）若DC+DE＝6，求AE的长．15．如图，AB为⊙O的直径，点P是⊙O外一点，PD与⊙O相切于点C，与BA的延长线交于点D，DE ⊥PO，交PO的延长线于点E，连接PB，∠EDB＝∠EPB．（1）求证：PB是⊙O的切线；（2）若PB＝3，DB＝4，求⊙O的半径．16．如图，点P是⊙O外一点，P A切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O 于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD＝cm，AC＝8cm，点E是的中点，连接CE，求CE的长．17．如图，点O是等腰△ABC的外心，AD是圆O的切线，切点为A，过点C作CD∥AB，交AD于点D．连接AO并延长交BC于点M，连接AD，交过点C的直线于点P，且∠BCP＝∠ACD．（1）判断直线PC与⊙O的位置关系，并说明理由；（2）若AB＝12，BC＝8．求PC的长．18．如图，在Rt△ABC中，∠C＝90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．（1）求证：ED为⊙O的切线；（2）如果⊙O的半径为，ED＝2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．19．如图1，AB是圆O的直径，O为圆心，AD、BD是半圆的弦，且∠PDA＝∠PBD．延长PD交圆的切线BE于点E（1）判断直线PD是否为⊙O的切线，并说明理由；（2）如图2，如果∠BED＝60°，PD＝，求P A的长．20．如图，AB是⊙O的直径，点C是的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且＝，CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH．（1）求证：BD是⊙O的切线；（2）当OB＝2时，求BH的长．21．如图，AB是⊙O的直径，延长BA至点P，过点P作⊙O的切线PC，切点为C，过点B向PC的延长线作垂线BE交该延长线于点E，BE交⊙O于点D，已知P A＝1，PC＝OC，（1）求BE的长；（2）连接DO，延长DO交⊙O于F，连接PF，①求DE的长；②求证：PF是⊙O的切线．参考答案1．（1）解：由于AD，BE，CF交于点O，∴＝，＝，＝，∴++＝1；（2）证明：如图，延长AD交⊙O于M，设R为△ABC的外接圆半径，AD，BE，CF交于点O．∵＝＝1﹣＝1﹣，同理有：＝1﹣，＝1﹣，代入++＝1，得（1﹣）+（1﹣）+（1﹣）＝1，∴++＝2，∴++＝＝．2．（1）证明：∵CP是⊙O的切线，∴OC⊥CP，∴∠PCB+∠OCB＝90°，∵AB是⊙O的直径，∴∠ACO+∠OCB＝90°，∴∠ACO＝∠PCB，∵OA＝OC，∴∠A＝∠ACO，∵∠PCB＝∠A，∴∠COB＝2∠A＝2∠PCB；（2）解：如图2中，连接MA．∵点M是弧AB的中点，∴＝，∴∠ACM＝∠BAM，∵∠AMC＝∠AMN，∴△AMC∽△NMA，∴＝，∴AM2＝MC•MN，∵AB是⊙O的直径，∴∠AMB＝90°，∵AM＝BM，AB＝6．∴2AM2＝62，∴AM2＝18，∴MC•MN＝18．3．解：（1）如图，∵AC是⊙O的直径，∴∠AEC＝∠AEB＝90°．（2）如图∵CF与⊙O相切，∴∠ACF＝90°．∴∠BCF＝90°﹣∠ACE＝∠CAE．∵∠CAF＝2∠BCF．∴∠CAF＝2∠CAE．∴∠CAE＝∠BAE．∴∠BCF＝∠BAE．∵BG⊥BF，AE⊥BC，∴∠CGB＝∠AEB＝90°．∵∠BCF＝∠BAE，∠CGB＝∠AEB，∴△CBG∽△ABE．（3）连接BD，如图2所示．∵∠DAE＝∠DCE，∠DAE＝∠BCF，∴∠DCE＝∠BCF．∵AC是⊙O的直径，∴∠ADC＝90°．∴CD⊥AF．∵∠DCB＝∠BCF，CD⊥AF，BGCBF，∴BD＝BG．∵∠F＝60°，GF＝2，∠BGF＝90°，∴tan∠F＝＝BG＝tan60°＝，∵BG＝2，∴BD＝BG＝2．∵∠AFC＝60°，∠ACF＝90°，∴∠CAF＝30°．∵∠ADC＝90°，∠CAF＝30°，∴AC＝2CD．∵∠CAE＝∠BAE，∠AEC＝∠AEB，∴∠ACE＝∠ABE．∴AB＝AC．设⊙O的半径为r，则AC＝AB＝2r，CD＝r．∵∠ADC＝90°，∴AD＝r．∴DB＝AB﹣AD＝2r﹣r＝（2﹣）r＝2．∴r＝4+6．∴⊙O的半径长为4+6．4．（1）证明：∵BC是⊙O的直径，∴∠CAB＝90°，∴∠CAG+∠BAG＝90°，∵AD⊥BE，∴∠AGB＝90°，∴∠BAG+∠ABE＝90°，∴∠CAG＝∠ABE；（2）证明：∵∠CGD＝∠CAG+∠ACG，∠ABC＝∠ABE+∠CBE，由（1）知，∠CAG＝∠ABE，∵∠CBE＝∠ACG，∴∠CGD＝∠ABC，∵∠ABC＝∠D，∴∠DGC＝∠D，∴CG＝CD；（3）解：连接AE、CE，∵BC是直径，∴∠BEC＝90°，∴∠AGE＝∠BEC，∴AD∥CE，∵∠CAE＝∠EBC，∠ACG＝∠EBC，∴∠CAE＝∠ACG，∴AE∥CG，∴四边形AGCE是平行四边形，∴AF＝AC，∵AC2＝BC2﹣AB2，∴AC2＝﹣42，∴AC＝6，∴AF＝×6＝3，∵BF2＝AF2+AB2，∴BF2＝32+42，∴BF＝5，∵∠ABG＝∠ABF，∠AGB＝∠BAF，∴△BAG∽△BF A，∴BA：BF＝BG：BA，∴4：5＝BG：4，∴BG＝，∵FG＝BF﹣BG，∴FG＝5﹣＝．5．（1）证明：∵AE为⊙O的直径，∴∠ABE＝90°，∴∠BAE+∠AEB＝90°，∵AD⊥BC，∴∠ADF＝90°，∴∠AFD+∠F AD＝90°，∵AE平分∠BAD，∴∠BAE＝∠F AD，∴∠AEB＝∠AFD；（2）解：如图1，过点F作BM⊥AB于点M．则∠AMF＝90°，∵∠AFD＝∠BFE，∠AFD＝∠AEB，∴∠BFE＝∠AEB，∴BF＝BE＝5，∵∠ABE＝∠AMF＝90°，∠BAE＝∠MAF，∴△AMF∽△ABE，∴，即，设MF＝x，则AM＝2x，∴BM＝10﹣2x，∵BM2+MF2＝BF2，∴（10﹣2x）2+x2＝52，解得x＝3，即MF＝3，∵AE平分∠ABD，AD⊥BC，∴DF＝MF＝3；（3）解：∵∠ADB＝90°，G为AB的中点，∴AG＝DG＝BG，OG⊥AB，∴∠BGD＝∠AGD＝90°，∴△ADG为等腰直角三角形，∴∠GAD＝45°，∴∠ABD＝45°，过点F作FH⊥AB于点H，如图2，∵AF平分∠BAD，∴FD＝FH，∵∠ABD＝45°，∴BF＝FH＝FD，∵∠AFD＝∠AEB，∠AEB＝∠C，∴∠AFD＝∠C，∴AF＝AC，又∵AD⊥BC，∴FD＝DC，设FD＝DC＝x，则BF＝x，∴．6．（1）证明：如图，连接DB，∵CD为⊙O的直径，∴∠DBC＝90°，∵DF∥AC，AB＝AC，∴∠ABC＝∠ACB＝∠DFB，∴EB＝EF，∵∠DBF＝90°，∴∠DBE+∠EBF＝∠EDB+∠EFB，∴∠DBE＝∠EDB，∴DE＝EB，∴DE＝EF；（2）解：如图，连接AO，EO，延长AO交BC于点G，∵AB＝AC，∴AG⊥BC，∵OC＝OD，DE＝EF，∴OE∥FC，FC＝2OE，∴∠AEO＝∠B，∵OE⊥OA，在Rt△AEO中，sin∠AEO＝，∵sin∠B＝，⊙O的半径为5，∴＝，∴AE＝，∴OE＝＝＝．∴CF＝2OE＝．7．解：（1）证明：∵AB为⊙O直径，∴∠ACB＝90°，∵CE⊥CD，∴∠ECD＝90°，∴∠ACE＝90°﹣∠ECB＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（ASA）；（2）∵△ACE≌△BCD，∴CE＝CD，AE＝BD，∵CE⊥CD，∴△ECD是等腰直角三角形，∵CD＝2，BD＝3,∴DE＝2，AE＝3，∴AD＝5，∵AB为⊙O直径，∴∠ADB＝90°，∴AB＝＝2，∴⊙O的半径为．8．解：（1）证明：∵CE⊥AD，∴EG＝CG，∵CF∥DE，∴∠DEG＝∠FCG，∵∠FGC＝∠DGE，∴△DEG≌△FCG（ASA），∴ED＝FC，∴四边形DCFE为平行四边形，又∵CE⊥DF，∴四边形DCFE是菱形；（2）∵AG⊥EC，EG＝CG，∴AE＝AC＝4，∵四边形AEDC内接于⊙O，∴∠BED＝∠BCA＝90°，∵四边形DCFE是菱形，∴EF∥DC，DE＝DC，∴∠AEF＝∠ABC，∴tan∠ABC＝tan∠AEF＝，在Rt△BED中，设DE＝3a，则BE＝4a，∴DC＝3a，BD＝＝5a，∵BC2+AC2＝AB2，∴（5a+3a）2+42＝（4a+4）2，解得a＝或a＝0（舍去），∴DE＝DC＝2，∴AD＝＝＝2．即⊙O的直径长为2．9．解：（1）证明：连接OD，BE，∵OD⊥AC，且DH是⊙O的切线，∴∠ODH＝∠DHA＝90°，∴OD∥CA，∴∠C＝∠ODB，∵OD＝OB，∴∠OBD＝∠ODB，∴∠OBD＝∠C，∵∠OBD＝∠DEC，∴∠C＝∠DEC，∴DC＝DE；（2）①由（1）可知：OD∥AC，∴∠AEF＝∠ODF，∴∠AFE＝∠OFD，∴△AFE∽△OFD，∴，∵AE＝4，∴OD＝6，∵AB为⊙O的直径，∴；∴BE的长为8；②在Rt△AEB中，，∵∠BDF＝∠BAE，∴．10．解：（1）0＜x＜90，（2）连接BD，可证△BDF∽△ADB，得＝，∵∠DBE＝∠DAC，∴∠BDE＝∠ADC＝90°﹣∠ADE，∴△BDE∽△ADC，∴＝，∴＝，∴BE＝BF．11．（1）证明：连接OB，如图所示：∵AC是⊙O的直径，∴∠ABC＝90°，∴∠C+∠BAC＝90°，∵OA＝OB，∴∠BAC＝∠OBA，∵∠PBA＝∠C，∴∠PBA+∠OBA＝90°，即PB⊥OB，∴PB是⊙O的切线；（2）解：∵⊙O的半径为2，∴OB＝2，AC＝4，∵OP∥BC，∴∠C＝∠BOP，又∵∠ABC＝∠PBO＝90°，∴△ABC∽△PBO，∴＝，即＝，∴BC＝2．12．（1）证明：连CB、OC，如图，∵BD为⊙O的切线，∴DB⊥AB，∴∠ABD＝90°，∵AB是直径，∴∠ACB＝90°，∴∠BCD＝90°，∵E为BD的中点，∴CE＝BE，∴∠BCE＝∠CBE，而∠OCB＝∠OBC，∴∠OBC+∠CBE＝∠OCB+∠BCE＝90°，∴OC⊥CF，∴CF是⊙O的切线；（2）解：CE＝BE＝DE＝3，在Rt△BFE中，cos F＝，tan F＝＝，∴BF＝4，∴EF＝＝5，∴CF＝CE+EF＝8，在Rt△OCF中，tan F＝＝，∴OC＝6，即⊙O的半径为6．13．（1）证明：如图1，连接OE，OC；∵CB＝CE，OB＝OE，OC＝OC∴△OEC≌△OBC（SSS）∴∠OBC＝∠OEC又∵DE与⊙O相切于点E∴∠OEC＝90°∴∠OBC＝90°∴BC为⊙O的切线．（2）解：如图2，过点D作DF⊥BC于点F，则四边形ABFD是矩形，∵AD，DC，BG分别切⊙O于点A，E，B∴DA＝DE，CE＝CB，在Rt△DFC中，CF＝＝1，设AD＝DE＝BF＝x，则x+x+1＝9，x＝4，∵AD∥BG，∴∠DAE＝∠EGC，∵DA＝DE，∴∠DAE＝∠AED；∵AD∥BG，∵∠AED＝∠CEG，∴∠EGC＝∠CEG，∴CG＝CE＝CB＝5，∴BG＝10，在Rt△ABG中，AG＝＝6，∵AD∥CG，∴＝＝，∴EG＝×6＝．14．（1）证明：连接OC．∵C是的中点，∴AC平分∠DAB，∴∠DAC＝∠OAC，∵OA＝OC，∴∠OCA＝∠OAC，∴∠DAC＝∠OCA，∴DA∥OC，∵AD⊥DC，∴∠ADC＝90°，∴∠OCD＝90°，即OC⊥DC，∵OC为半径，∴DC为⊙O的切线．（2）解：∵AB是⊙O的直径，∴AB＝10，∠ACB＝90°＝∠ADC，∴BC＝＝6，又∵∠DAC＝∠OAC，∴△ACD∽△ABC，∴＝，即＝，解得：CD＝4.8．（3）如图，连接EC，作CF⊥AB于F．∵CA平分∠BAD，CD⊥AD，CF⊥AB，∴CD＝CF，∵＝，∴CE＝BC，∴Rt△CDE≌Rt△CFB，∴DE＝BF，∴CF+BF＝CD+DE＝6，设BF＝x，则CF＝6﹣x，由△ACF∽△CBF，可得CF2＝AF•BF，∴（6﹣x）2＝（10﹣x）•x，解得x＝2或9（舍弃），∴BF＝DE＝2，CD＝CF＝4，易证AF＝AD＝8，∴AE＝AD﹣DE＝6．15．（1）证明：∵∠EDB＝∠EPB，∠DOE＝∠POB，∴∠DEO＝∠PBO，∵DE⊥PE，∴∠DEO＝90°，∴∠PBO＝90°，∴PB是⊙O的切线；（2）由（1）知，PB是⊙O的切线，∴∠PBD＝90°，∵PB＝3，DB＝4，∴PD＝5，∵PC和PB都是⊙O的切线，∴PC＝PB＝3，∠OCD＝90°，∴CD＝2，设⊙O的半径为x，则OC＝x，OD＝4﹣x，则22+x2＝（4﹣x）2，解得，x＝，即⊙O的半径是．16．（1）证明：如图，连接OC，∵P A切⊙O于A．∴OA⊥P A，∴∠P AO＝90°，∵OP∥BC，∴∠AOP＝∠OBC，∠COP＝∠OCB，∵OC＝OB，∴∠OBC＝∠OCB，∴∠AOP＝∠COP，在△P AO和△PCO中，∴△P AO≌△PCO（SAS），∴∠P AO＝∠PCO＝90°，∴OC⊥PC，∴PC是⊙O的切线；（2）解：连接EA、EB，作BH⊥CE于H，如图，∵AB是⊙O的直径，∴∠ACB＝∠AEB＝90°，∵OP∥BC，∴PO⊥AC，∴AD＝CD＝AC＝4，在Rt△P AD中，P A＝＝＝，∵∠APO＝∠DP A，∴Rt△P AD∽Rt△POA，∴P A：PO＝PD：P A，即：PO＝：，解得PO＝，∴OD＝PO﹣PD＝3，∵AO＝BO，OD∥BC，∴BC＝2OD＝6，在Rt△ACB中，AB＝＝10，∵点E是的中点，∴∠BCE＝∠ACE＝∠ACB＝45°，∴AE＝BE，∴△BCH和△ABE都是等腰直角三角形，∴CH＝BH＝BC＝3，BE＝AB＝5，在Rt△BEH中，EH＝＝4，∴CE＝CH+EH＝3+4＝7．17．解：（1）直线PC与圆O相切，理由为：过C点作直径CE，连接EB，如图，∵CE为直径，∴∠EBC＝90°，即∠E+∠BCE＝90°，∵AB∥DC，∴∠ACD＝∠BAC，∵∠BAC＝∠E，∠BCP＝∠ACD．∴∠E＝∠BCP，∴∠BCP+∠BCE＝90°，即∠PCE＝90°，∴CE⊥PC，∴PC与圆O相切；（2）∵AD是⊙O的切线，切点为A，∴OA⊥AD，∵BC∥AD，∴AM⊥BC，∴BM＝CM＝BC＝4，∴AC＝AB＝12，在Rt△AMC中，AM＝＝8，设圆O的半径为r，则OC＝r，OM＝AM﹣r＝8﹣r，在Rt△OCM中，OM2+CM2＝OC2，即42+（8﹣r）2＝r2，解得：r＝，∴CE＝2r＝＝9，OM＝8﹣＝，∴BE＝2OM＝7，∵∠E＝∠MCP，∴Rt△PCM∽Rt△CEB，∴＝，即＝∴PC＝．18．解：（1）证明：连接OD，∵OE∥AB，∴∠COE＝∠CAD，∠EOD＝∠ODA，∵OA＝OD，∴∠OAD＝∠ODA，∴∠COE＝∠DOE，在△COE和△DOE中，，∴△COE≌△DOE（SAS），∴∠ODE＝∠OCE＝90°，∴ED⊥OD，∴ED是圆O的切线；（2）连接CD，交OE于M，在Rt△ODE中，∵OD＝，DE＝2，∴OE＝＝＝，∵OE∥AB，∴△COE∽△CAB，∴＝，∴AB＝5，∵AC是直径，∴∠ADC＝90°，∴cos∠BAC＝＝＝，∴AD＝，∴CD＝＝，∵EF∥AB，∴，∴CM＝DM＝CD＝，∴EF＝OE+OF＝4，BD＝AB﹣AD＝5﹣＝，∴S△ADF＝S梯形ABEF﹣S梯形DBEF＝（AB+EF）•DM﹣（BD+EF）•DM＝×（5+4）×﹣×（+4）×＝．∴△ADF的面积为．19．解：（1）直线PD是否为⊙O的切线．理由如下：连接OD，如图1，∵OD＝OB，∴∠1＝∠OBD，∵∠PDA＝∠PBD，∴∠1＝∠PDA，∵AB为直径，∴∠ADB＝90°，即∠2+∠1＝90°，∴∠PDA+∠2＝90°，即∠PDO＝90°，∴OD⊥PD，∴PD为⊙O的切线；（2）如图2，连接OD，∵ED和EB为⊙O的切线，∴ED＝EB，而∠BED＝60°，∴△EDB为等边三角形，∴∠EBD＝60°，∴∠PBD＝30°，∴∠PDA＝30°，而∠ADB＝90°，∴∠P＝30°，在Rt△OAD中，OD＝PD＝×＝1，OP＝2OD＝2，∴P A＝PO﹣OA＝2﹣1＝1．20．证明：（1）连接OC，∵AB是⊙O的直径，点C是的中点，∴∠AOC＝90°，∵OA＝OB，CD＝AC，∴OC是△ABD是中位线，∴OC∥BD，∴∠ABD＝∠AOC＝90°，∴AB⊥BD，∵点B在⊙O上，∴BD是⊙O的切线；解：（2）由（1）知，OC∥BD，∴△OCE∽△BFE，∴，∵OB＝2，∴OC＝OB＝2，AB＝4，，∴，∴BF＝3，在Rt△ABF中，∠ABF＝90°，根据勾股定理得，AF＝5，∵S△ABF＝AB•BF＝AF•BH，∴AB•BF＝AF•BH，∴4×3＝5BH，∴BH＝．21．解：（1）设圆的半径是r，则OP＝P A+r＝1+r，OC＝r，PC＝r．∵PC是圆的切线，∴∠PCO＝90°，∴在直角△PCO中，PC2+OC2＝OP2，即（r）2+r2＝（1+r）2，解得：r＝1或r＝﹣（舍去负值）．在直角△OPC中，cos∠POC＝＝，∴∠POC＝60°，∵∠PCO＝90°，BE⊥BC，∴BE∥OC，∴△OPC∽△BPE，∠B＝∠POC＝60°，∴＝＝，∴BE＝OC＝；（2）①在△OBD中，OB＝OD，∠B＝60°，∴△OBD是等边三角形，BD＝OB＝1，∠BOD＝60°．∴DE＝BE﹣BD＝﹣1＝；②∵在△OPC和△OPF中，，∴△OPC≌△OPF（SAS），∴∠OFP＝∠OCP＝90°，∴PF是⊙O的切线．。

2022-2023学年九年级数学中考复习《圆综合压轴题》解答题专题提升训练（附答案）1．如图，以线段AB为直径作⊙O，交射线AC于点C，AD平分∠CAB交⊙O于点D，过点D作直线DE⊥AC于点E，交AB的延长线于点F．连接BD并延长交AC于点M．（1）求证：直线DE是⊙O的切线；（2）求证：AB＝AM；（3）若ME＝1，∠F＝30°，求BF的长．2．如图，在⊙O中，AB为⊙O的直径，点E在⊙O上，D为的中点，连接AE，BD并延长交于点C．连接OD，在OD的延长线上取一点F，连接BF，使∠CBF＝∠BAC．（1）求证：BF为⊙O的切线；（2）若AE＝4，OF＝，求⊙O的半径．3．已知：如图，AB为⊙O的直径，CD与⊙O相切于点C，交AB延长线于点D，连接AC，BC，∠D＝30°，CE平分∠ACB交⊙O于点E，过点B作BF⊥CE，垂足为F．（1）求证：CA＝CD；（2）若AB＝12，求线段BF的长．4．如图，在半径为10cm的⊙O中，AB是⊙O的直径，CD是过⊙O上一点C的直线，且AD⊥DC于点D，AC平分∠BAD，点E是BC的中点，OE＝6cm．（1）求证：CD是⊙O的切线；（2）求AD的长．5．如图，在△ABC中，AB＝AC．以AB为直径的⊙O与线段BC交于点D，过点D作DE ⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．（1）求证：直线PE是⊙O的切线；（2）若⊙O的半径为6，∠P＝30°，求CE的长．6．如图，点O是△ABC的边AC上一点，以点O为圆心，OA为半径作⊙O，与BC相切于点E，交AB于点D，连接OE，连接OD并延长交CB的延长线于点F，∠AOD＝∠EOD．（1）连接AF，求证：AF是⊙O的切线；（2）若FC＝10，AC＝6，求FD的长．7．如图，P为⊙O外一点，P A、PB为⊙O的切线，切点分别为A、B，直线PO交⊙O于点D、E，交AB于点C．（1）求证：∠ADE＝∠P AE．（2）若∠ADE＝30°，求证：AE＝PE．（3）若PE＝4，CD＝6，求CE的长．8．如图，△ABC中，AB＝AC，D为AC上一点，以CD为直径的⊙O与AB相切于点E，交BC于点F，FG⊥AB，垂足为G．（1）求证：FG是⊙O的切线；（2）若BG＝1，BF＝3，求CF的长．9．如图，AB为⊙O的直径，过圆上一点D作⊙O的切线CD交BA的延长线于点C，过点O作OE∥AD交CD于点E，连接BE．（1）直线BE与⊙O相切吗？并说明理由；（2）若CA＝2，CD＝4，求DE的长．10．如图，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD，垂足是点H，过点C作直线分别与AB，AD的延长线交于点E，F，且∠ECD＝2∠BAD．（1）求证：CF是⊙O的切线；（2）如果AB＝10，CD＝6，①求AE的长；②求△AEF的面积．11．如图，DP是⊙O的切线，D为切点，弦AB∥DP，连接BO并延长，与⊙O交于点C，与DP交于点E，连接AC并延长，与DP交于点F，连接OD．（1）求证：AF∥OD；（2）若OD＝5，AB＝8，求线段EF的长．12．如图，△ABC内接于⊙O，AB＝AC，AD是⊙O的直径，交BC于点E，过点D作DF ∥BC，交AB的延长线于点F，连接BD．（1）求证：DF是⊙O的切线；（2）已知AC＝12，AF＝15，求DF的长．13．如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点C作CE⊥AD交AD的延长线于点E，延长EC，AB交于点F，∠ECD＝∠BCF．（1）求证：CE为⊙O的切线；（2）若DE＝1，CD＝3，求⊙O的半径．14．如图，已知：AB为⊙O的直径，⊙O分别交△ABC的边AC、BC于点D、E，点F为AC的延长线上一点，且∠CBF＝∠BOE．（1）求证：BF是⊙O的切线；（2）若AB＝4，∠CBF＝45°，BE＝2EC，求AD和CF的长．15．如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，点D是的中点，DE∥BC交AC的延长线于点E．（1）求证：直线DE与⊙O相切；（2）若⊙O的直径是10，∠A＝45°，求CE的长．16．如图，以等边三角形ABC的BC边为直径画圆，交AC于点D，DF⊥AB于点F，连接OF，且AF＝1．（1）求证：DF是⊙O的切线；（2）求线段OF的长度．17．如图，已知△ABC内接于⊙O，AB是⊙O的直径，∠CAB的平分线交BC于点D，交⊙O于点E，连接EB，作∠BEF＝∠CAE，交AB的延长线于点F．（1）求证：EF是⊙O的切线；（2）若BF＝10，EF＝20，求⊙O的半径和AD的长．18．如图，AB为⊙O直径，D为⊙O上一点，BC⊥CD于点C，交⊙O于点E，CD与BA 的延长线交于点F，BD平分∠ABC．（1）求证：CD是⊙O的切线；（2）若AB＝10，CE＝1，求CD和DF的长．19．如图，在Rt△ABC中，∠ACB＝90°，延长CA到点D，以AD为直径作⊙O，交BA 的延长线于点E，延长BC到点F，使BF＝EF．（1）求证：EF是⊙O的切线；（2）若OC＝9，AC＝4，AE＝8，求BF的长．20．如图，在Rt△ABC中，∠C＝90°，D是AB上的一点，以AD为直径的⊙O与BC相切于点E，连接AE，DE．（1）求证：AE平分∠BAC；（2）若∠B＝30°，求的值．参考答案1．（1）证明：连接OD，则OD＝OA，∴∠ODA＝∠OAD，∵AD平分∠CAB，∴∠OAD＝∠DAC，∴∠ODA＝∠DAC，∴OD∥AC，∵DE⊥AC，∴∠ODF＝∠AED＝90°，∵OD是⊙O的半径，且DE⊥OD，∴直线DE是⊙O的切线．（2）证明：∵线段AB是⊙O的直径，∴∠ADB＝90°，∴∠ADM＝180°﹣∠ADB＝90°，∴∠M+∠DAM＝90°，∠ABM+∠DAB＝90°，∵∠DAM＝∠DAB，∴∠M＝∠ABM，∴AB＝AM．（3）解：∵∠AEF＝90°，∠F＝30°，∴∠BAM＝60°，∴△ABM是等边三角形，∴∠M＝60°，∵∠DEM＝90°，ME＝1，∴∠EDM＝30°，∴MD＝2ME＝2，∴BD＝MD＝2，∵∠BDF＝∠EDM＝30°，∴∠BDF＝∠F，∴BF＝BD＝2．2．（1）证明：如图，连接AD，AB是圆的直径，则∠ADB＝90°，D为的中点，则∠BAD＝∠CAD＝∠BAC，∵，∴∠CBF＝∠BAD，∵∠BAD+∠ABD＝90°，∴∠ABF＝∠ABD+∠CBF＝90°，∴AB⊥BF，∵OB是⊙O的半径，∴BF是⊙O的切线；（2）解：如图，连接BE，AB是圆的直径，则∠AEB＝90°，∵∠BOD＝2∠BAD，∠BAC＝2∠BAD，∴∠BOD＝∠BAC，又∵∠ABF＝∠AEB＝90°，∴△OBF∽△AEB，∴OB：AE＝OF：AB，∴OB：4＝：2OB，OB2＝9，OB＞0，则OB＝3，∴⊙O的半径为3．3．（1）证明：连接OC，∵CD与⊙O相切于点C，∴∠OCD＝90°，∵∠D＝30°，∴∠COD＝90°﹣∠D＝60°，∴∠A＝∠COD＝30°，∴∠A＝∠D＝30°，∴CA＝CD；（2）解：∵AB为⊙O的直径，∴∠ACB＝90°，∵∠A＝30°，AB＝12，∴BC＝AB＝6，∵CE平分∠ACB，∴∠BCE＝∠ACB＝45°，∵BF⊥CE，∴∠BFC＝90°，∴BF＝BC•sin45°＝6×＝3，∴线段BF的长为3．4．（1）证明：连接OC，如图：∵AC平分∠BAD，∴∠DAC＝∠CAO，∵OA＝OC，∴∠CAO＝∠OCA，∴∠DAC＝∠OCA，∴AD∥OC，∵AD⊥DC，∴CO⊥DC，∵OC是⊙O的半径，∴CD是⊙O的切线；（2）解：∵E是BC的中点，且OA＝OB，∴OE是△ABC的中位线，AC＝2OE，∵OE＝6cm，∴AC＝12cm，∵AB是⊙O的直径，∴∠ACB＝90°＝∠ADC，又∠DAC＝∠CAB，∴△DAC∽△CAB，∴，即＝，∴AD＝cm．5．（1）证明：连接OD，如图：∵AB＝AC，∴∠ABC＝∠ACB，∵OB＝OD，∴∠ABC＝∠ODB，∴∠ACB＝∠ODB，∴OD∥AC，∵DE⊥AC，∴DE⊥OD，即PE⊥OD，∵OD是⊙O的半径，∴PE是⊙O的切线；（2）解：连接AD，连接OD，如图：∵DE⊥AC，∴∠AEP＝90°，∵∠P＝30°，∴∠P AE＝60°，∵AB＝AC，∴△ABC是等边三角形，∴∠C＝60°，∵⊙O的半径为6，∴BC＝AB＝12，∵AB是⊙O的直径，∴∠ADB＝90°，∴BD＝CD＝BC＝6，在Rt△CDE中，CE＝CD•cos C＝6×cos60°＝3，答：CE的长是3．6．（1）证明：在△AOF和△EOF中，，∴△AOF≌△EOF（SAS），∴∠OAF＝∠OEF，∵BC与⊙O相切，∴OE⊥FC，∴∠OAF＝∠OEF＝90°，即OA⊥AF，∵OA是⊙O的半径，∴AF是⊙O的切线；（2）解：在Rt△CAF中，∠CAF＝90°，FC＝10，AC＝6，∴AF＝＝8，∵∠OCE＝∠FCA，∠OEC＝∠F AC＝90°，∴△OEC∽△F AC，∴，设⊙O的半径为r，则，解得r＝，在Rt△F AO中，∠F AO＝90°，AF＝8，AO＝，∴OF＝＝，∴FD＝OF﹣OD＝﹣，即FD的长为﹣．7．（1）证明：连接OA，如图，∵P A为⊙O的切线，∴AO⊥P A，∴∠OAE+∠P AE＝90°．∵DE是⊙O的直径，∴∠DAE＝90°，∴∠ADE+∠AED＝90°．∵OA＝OE，∴∠OAE＝∠AED，∴∠ADE＝∠P AE；（2）证明：由（1）知：∠ADE＝∠P AE＝30°，∵∠DAE＝90°，∴∠AED＝90°﹣∠ADE＝60°．∵∠AED＝∠P AE+∠APE，∴∠APE＝∠P AE＝30°，∴AE＝PE；（3）解：设CE＝x，则DE＝CD+CE＝6+x，∴OA＝OE＝，∴OC＝OE﹣CE＝，OP＝OE+PE＝．∵P A、PB为⊙O的切线，∴P A＝PB，PO平分∠APB，∴PO⊥AB．∵P A为⊙O的切线，∴AO⊥P A，∴△OAC∽△OP A，∴，∴，即：x2+10x﹣24＝0．解得：x＝2或﹣12（不合题意，舍去），∴CE＝2．8．（1）证明：如图，连接OF，∵AB＝AC，∴∠B＝∠C，∵OF＝OC，∴∠C＝∠OFC，∴∠OFC＝∠B，∴OF∥AB，∵FG⊥AB，∴FG⊥OF，又∵OF是半径，∴GF是⊙O的切线；（2）解：如图，连接OE，过点O作OH⊥CF于H，∵BG＝1，BF＝3，∠BGF＝90°，∴FG＝＝＝2，∵⊙O与AB相切于点E，∴OE⊥AB，又∵AB⊥GF，OF⊥GF，∴四边形GFOE是矩形，∴OE＝GF＝2，∴OF＝OC＝2，又∵OH⊥CF，∴CH＝FH，∵cos C＝cos B＝，∴，∴CH＝，∴CF＝．9．解：（1）直线BE与⊙O相切，理由：连接OD，∵CD与⊙O相切于点D，∴∠ODE＝90°，∵AD∥OE，∴∠ADO＝∠DOE，∠DAO＝∠EOB，∵OD＝OA，∴∠ADO＝∠DAO，∴∠DOE＝∠EOB，∵OD＝OB，OE＝OE，∴△DOE≌△BOE（SAS），∴∠OBE＝∠ODE＝90°，∵OB是⊙O的半径，∴直线BE与⊙O相切；（2）解法一：设⊙O的半径为r，在Rt△ODC中，OD2+DC2＝OC2，∴r2+42＝（r+2）2，∴r＝3，∴AB＝2r＝6，∴BC＝AC+AB＝2+6＝8，由（1）得：△DOE≌△BOE，∴DE＝BE，在Rt△BCE中，BC2+BE2＝CE2，∴82+BE2＝（4+DE）2，∴64+DE2＝（4+DE）2，∴DE＝6；解法二：设⊙O的半径为r，在Rt△ODC中，OD2+DC2＝OC2，∴r2+42＝（r+2）2，∴r＝3，∴OA＝3，∵AD∥OE，∴＝，∴＝，∴DE＝6，∴DE的长为6．10．（1）证明：连接OC，如图，∵AB是⊙O的直径，AB⊥CD，∴，∴∠CAB＝∠DAB．∵∠COB＝2∠CAB，∴∠COB＝2∠BAD．∵∠ECD＝2∠BAD，∴∠ECD＝∠COB．∵AB⊥CD，∴∠COB+∠OCH＝90°，∴∠OCH+∠ECD＝90°，∴∠OCE＝90°．∴OC⊥CF．∵OC是⊙O的半径，∴CF是⊙O的切线；（2）解：①∵AB＝10，∴OA＝OB＝OC＝5，∵AB是⊙O的直径，AB⊥CD，∴CH＝DH＝CD＝3．∴OH＝＝4，∵OC⊥CF，CH⊥OE，∴△OCH∽△OEC，∴，∴，∴OE＝．∴AE＝OA+OE＝5+＝；②过点F作FG⊥AB，交AB的延长线于点G，如图，∵∠OCF＝∠FGE＝90°，∠CEO＝∠GEF，∴△OCE∽△FGE．∴，设FG＝4k，则FE＝5k，∴EG＝＝3k，∵DH⊥AB，FG⊥AB，∴DH∥FG．∴，∴，解得：k＝．∴FG＝4k＝5．∴△AEF的面积＝×AE•FG＝．11．（1）证明：延长DO交AB于点H，∵DP是⊙O的切线，∴OD⊥DP，∵AB∥DP，∴HD⊥AB，∵BC为⊙O的直径，∴∠BAC＝90°，∴AF∥OD；（2）∵OH⊥AB，AB＝8，∴BH＝AH＝4，∴OH＝＝＝3，∵BH∥ED，∴△BOH∽△EOD，∴＝，即＝，解得：ED＝，∵∠BAC＝90°，DH⊥AB，DH⊥DP，∴四边形AFDH为矩形，∴DF＝AH＝4，∴EF＝ED﹣DF＝﹣4＝．12．（1）证明：∵AD是⊙O的直径，∴∠ABD＝90°，即∠ABC+∠CBD＝90°，∵AB＝AC，∴∠ABC＝∠C，∵∠ADB＝∠C，∴∠ABC＝∠ADB，∵BC∥DF，∴∠CBD＝∠FDB，∴∠ADB+∠FDB＝90°，即∠ADF＝90°，∴AD⊥DF，又∵OD是⊙O的半径，∴DF是⊙O的切线；（2）解：∵AB＝AC＝12，AF＝15，∴BF＝AF﹣AB＝3，∵∠F＝∠F，∠FBD＝∠FDA＝90°，∴△FBD∽△FDA，∴BF：DF＝DF：AF，∴DF2＝BF×AF＝3×15＝45，∴DF＝＝3．13．（1）证明：如图1，连接OC，∵OB＝OC，∴∠OCB＝∠OBC，∵四边形ABCD内接于⊙O，∴∠CDE＝∠OBC，∵CE⊥AD，∴∠E＝∠CDE+∠ECD＝90°，∵∠ECD＝∠BCF，∴∠OCB+∠BCF＝90°，∴∠OCE＝90°，即OC⊥EF，∵OC是⊙O的半径，∴CE为⊙O的切线；（2）解：如图2，过点O作OG⊥AE于G，连接OC，OD，则∠OGE＝90°，∵∠E＝∠OCE＝90°，∴四边形OGEC是矩形，∴OC＝EG，OG＝EC，设⊙O的半径为x，Rt△CDE中，CD＝3，DE＝1，∴EC＝＝2，∴OG＝2，GD＝x﹣1，OD＝x，由勾股定理得：OD2＝OG2+DG2，∴x2＝（2）2+（x﹣1）2，解得：x＝4.5，∴⊙O的半径是4.5．14．（1）证明：连结AE，OE，∵∠BAE＝∠BOE，∠CBF＝∠BOE，∴∠BAE＝∠CBF，∵AB为⊙O的直径，∴∠AEB＝90°，∴∠BAE+∠ABE＝90°，∴∠ABE+∠CBF＝90°，即∠ABF＝90°，∴BF⊥AB，∴BF是⊙O的切线；（2）解：过点C作CG⊥BF于点G，连结BD，∵∠CBF＝45°，∴∠ABE＝90°﹣∠CBF＝45°，在Rt△ABE中，AB＝4，∴AE＝BE＝4×sin45°＝4，∵BE＝2EC，∴EC＝2，BC＝6，在Rt△CBG中，∠CBG＝45°，BC＝6，∴CG＝BG＝3，∵CG⊥BF，BF⊥AB，∴AB∥CG，∴△FCG∽△F AB，∴＝，∴＝，∴FG＝9，∴BF＝12，在Rt△FCG中，CF＝＝6，在Rt△ABF中，AF＝＝8，∵AB为⊙O的直径，∴∠ADB＝90°，又∵∠BAD＝∠BAF，∴cos∠BAD＝cos∠BAF，即＝，∴＝，∴AD＝．15．（1）证明：连接OD，如图，∵点D是的中点，∴OD⊥BC，∵DE∥BC，∴OD⊥DE，∴直线DE与⊙O相切；（2）解：∵AC是⊙O的直径，∴∠B＝90°，∵∠A＝45°，∴∠ACB＝45°，∵BC∥DE，∴∠E＝45°，而∠ODE＝90°，∴△ODE为等腰直角三角形，∴OE＝OD＝5，∴CE＝OE﹣OC＝5﹣5．16．（1）证明：连接OD，∵△ABC是等边三角形，∴∠C＝∠A＝60o，∵OC＝OD，∴△OCD是等边三角形，∴∠CDO＝∠A＝60o，∴OD∥AB，∵DF⊥AB，∴∠FDO＝∠AFD＝90°，∴OD⊥DF，∴DF是⊙O的切线；（2）解：∵OD∥AB，OC＝OB，∴OD是△ABC的中位线，∵∠AFD＝90°，∠A＝60o，∴∠ADF＝30°，∵AF＝1∴CD＝OD＝AD＝2AF＝2，在Rt△ADF中，由勾股定理得DF2＝AD2﹣AF2＝3，在Rt△ODF中，由勾股定理得OF＝，∴线段OF的长为．17．（1）证明：连接OE，∵AB是⊙O的直径，∴∠AEB＝90°，即∠AEO+∠OEB＝90°，∵AE平分∠CAB，∴∠CAE＝∠BAE，∵∠BEF＝∠CAE，∴∠BEF＝∠BAE，∵OA＝OE，∴∠BAE＝∠AEO，∴∠BEF＝∠AEO，∴∠BEF+∠OEB＝90°，∴∠OEF＝90°，∴OE⊥EF，∵OE是⊙O的半径，∴EF是⊙O的切线；（2）解：如图，设⊙O的半径为x，则OE＝OB＝x，∴OF＝x+10，在Rt△OEF中，由勾股定理得：OE2+EF2＝OF2，∴x2+202＝（x+10）2，解得：x＝15，∴⊙O的半径为15；∵∠BEF＝∠BAE，∠F＝∠F，∴△EBF∽△AEF，∴＝＝，设BE＝a，则AE＝2a，由勾股定理得：AE2+BE2＝AB2，即a2+（2a）2＝302，解得：a＝6，∴AE＝2a＝12，∵∠CAE＝∠BAE，∴，∴OE⊥BC，∵OE⊥EF，∴BC∥EF，∴，即，∴AD＝9．18．（1）证明：连接OD，∵BD平分∠ABC．∴∠ABD＝∠DBC，又∵OB＝OD，∴∠OBD＝∠ODB，∴∠DBC＝∠ODB，又∵BC⊥CD，∴∠C＝90°，∴∠DBC+∠BDC＝90°，∴∠ODB+∠BDC＝90°，即OD⊥DC，∴CD是⊙O的切线；（2）解：连接AE交OD于点H，∵AB为⊙O直径，∴∠AEB＝90°，∴∠HEC＝90°，∵BC⊥CD，OD⊥DC，∴∠ODC＝∠C＝90°，∴四边形HECD是矩形，∴DH＝CE＝1，HE＝CD，∠EHD＝90°，HE∥CD，∴OD⊥AE，∴AH＝HE，∵AB＝10，∴OA＝OD＝5，∴OH＝OD﹣DH＝5﹣1＝4，∴AH＝，∴HE＝AH＝3，∴CD＝HE＝3，∵HE∥CD，∴△OAH∽△OFD，∴，∴，∴DF＝．19．证明：（1）连接OE，∵OA＝OE，∴∠OEA＝∠OAE，在Rt△ABC中，∠ACB＝90°，∴∠BAC+∠B＝90°，∵BF＝EF，∴∠B＝∠BEF，∵∠OAE＝∠BAC，∴∠OEA＝∠BAC，∴∠OEF＝∠OEA+∠BEF＝∠BAC+∠B＝90°，∴OE⊥EF，∵OE是⊙O的半径，∴EF是⊙O的切线；（2）解：连接DE，∵OC＝9，AC＝4，∴OA＝OC﹣AC＝5，∵AD＝2OA，∴AD＝10，∵AD是⊙O的直径，∴∠AED＝90°，在Rt△ADE中，∵DE＝＝＝6，∴cos∠DAE＝＝＝，在Rt△ABC中，cos∠BAC＝＝，∵∠BAC＝∠DAE，∴＝，∴AB＝5，∴BE＝AB+AE＝5+8＝13，∵OD＝OE，∴∠ODE＝∠OED，∵EF是⊙O的切线，∴∠FEO＝90°，∵∠OED+∠OEA＝90°，∠FEB+∠OEA＝90°，∴∠FEB＝∠OED，∴∠B＝∠FEB＝∠OED＝∠ODE，∴△FBE∽△ODE，∴＝，∴＝，∴BF＝．方法二：解：连接DE，∵OC＝9，AC＝4，∴OA＝OC﹣AC＝5，∵AD＝2OA，∴AD＝10，∵AD是⊙O的直径，∴∠AED＝90°，在Rt△ADE中，∵DE＝＝＝6，∴cos∠DAE＝＝＝，在Rt△ABC中，cos∠BAC＝＝，∵∠BAC＝∠DAE，∴＝，∴AB＝5，∴BE＝AB+AE＝5+8＝13，过F作FH⊥BE于F，则BH＝6.5，∵∠B的余弦等于0.6，∴BF＝6.5÷0.6＝．20．（1）证明：连接OE，∵BC是⊙O的切线，∴OE⊥BC，即∠OEB＝90°，∵∠C＝90°，∴OE∥AC，∴∠OEA＝∠EAC，∵OE＝OA，∴∠OEA＝∠OAE，∴∠OAE＝∠EAC，即AE平分∠BAC；（2）解：∵AD为⊙O的直径，∴∠AED＝90°，∵∠OAE＝∠EAC，∠C＝90°，∴△DAE∽△EAC，∴＝，∵∠C＝90°，∠B＝30°，∴∠BAC＝90°﹣30°＝60°，∴∠DAE＝∠BAC＝30°，∵cos∠DAE＝，cos30°＝，∴＝＝．。

专题十一 立体几何中的内切外接问题知识点一 棱锥外接问题外接问题常见于球的计算，而一部分棱锥的外接球的问题，常转化为棱锥外接棱柱的外接球问题或将三棱锥补为长方体，本节就先来探究特殊三棱锥的内外接问题.(1)三组对棱分别相等的四面体必内接于唯一的长方体，且四面体的棱分别为长方体的面对角线;(2)正四面体P ABC -内接于正方体且正方体的棱长a =;(3)若四面体有三条棱两两互相垂直.则可将其放入某个长方体内，其中三条互相垂直的棱也为长方体的棱; (4)若四面体的四个面均是直角三角形，该四面体为鳖臑，则可将其放入某个长方体内，其中三条互相垂直的棱也为长方体的棱;(5)三组对棱分别相等的四面体的棱长A B BC A C ''''、、必构成锐角三角形，即为外接长方体的三个面对角线构成的三角形;(6)任一四面体均内接于唯一的平行六面体.每条棱均为平行六面体的面对角线，且四面体体积是平行六面体体积的三分之一;(7)连接两组对棱的中点可组成平行四边形EGFH ，且另一组对棱与该面距离相等，此时平行四边形EGFH 平行于四面体内接平行六面体的一对平行平面;(8)过一组对棱(AB 与CD )中点()E F ，连线的任一平面(E G F H 、、、共面)必平分其()A BCD V -体积，即AC BGFH BD BD BZFH V V V --=-;（9）由正方体性质可知(i)1BD ⊥平面11AC D ，1BD ⊥平面1ACB . (ii)F 为平面11A C D 的中心，E 为平面1ACB 的中心. (iii)E ，F 为1BD 的三等分点.则正方体内接正四面体C AB D 11-高为E D 1，即正方体体对角线的23.【例1】(2009·江西卷)如图所示.在四面体ABCD 中.截面PQMN 是正方形.则在下列命题中.错误的为（ ）A.AC BD ⊥B.AC 平行于截面PQMNC.AC BD = D .异面直线PM 与BD 所成的角为45【例2】(重庆市七校联考)(多选)如图，在边长为2的正方体1111ABCD A B C D -中，点E ,F 分别是棱1BB ，11B C 的中点，G 是棱1CC 上的动点，则下列说法正确的是（ ） A.当G 为中点时，直线AG ∥面1A EFB.当G 为中点时，直线AG 与EF 所成的角为30C.若H 是棱AA 上的动点，且1C G AH =，则平面ACD ⊥平面1B HGD.当G 在1CC 上运动时，直线AG 与平面11AA D D 所成的角的最大值为45︒知识点二 与球有关的内切、外接问题与球有关的内切、外接问题是立体几何的一个重点(切、接问题的解题思路类似，此处以多面体的外接球为例).研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，并且还要特别注意多面体的有关几何元素与球的半径之间的关系.一．长方体切割体的外接球设长方体相邻的三条边棱长分别为a ，b ，c ．图1墙角体 图2鳖臑 图3挖墙角体 图4对角线相等的四面体图1与图2有重垂线，三视图都是三个直角三角形，图3无重垂线，俯视图是一矩形，AC 为虚线，主视图和左视图为直角三角形，外接球半径均为长方体体对角线一半，R =．图4中2222222222222222222a b BC AD BC AB CD b c AC a b c R AC BD c a AB ααβγβγ⎧+===⎫⎪++⎪=⇒+==⇒++=⇒=⎬⎨⎪⎪=+==⎭⎩abc abc abc V BCD A 31461=⨯-=-．外接球问题遇到墙角体就十分好处理，遇到以下墙角体性质的问题，就可以直接套用公式. 墙角体性质：(1)2222222()AB BC CA a b c ++=++.图 1【解析】如图1，因为Rt PAB △，Rt PBC △，Rt PCA △，所以222222222AB a b BC b c CA a c ⎧=+⎪=+⎨⎪=+⎩，故2222222()AB BC CA a b c ++=++.(2)顶点P 在底面上的投影H 恰为ABC △的垂心.如图 2【解析】如图2，因为Rt PAB △，Rt PBC △，Rt PCA △，又PA ⊥平面PBC ，所以PA BC ⊥. 因为PH ⊥平面ABC ，所以PH BC ⊥，故平面PAH BC ⊥，从而AH BC ⊥. 同理CH BA ⊥，BH AC ⊥，所以H 为ABC △的垂心.(3)设三个侧面和底面的面积分别为ABP S △，BCP S △，CAP S △，ABC S △，则 ①ABP S △是ABH S △与ABC S △的比例中项; ②BCP S △是CBH S △与ABC S △的比例中项; ③CAP S △是CAH S △与ABC S △的比例中项;④2222ABP BCP CAP ABC S S S S ++=△△△△.【解析】因为12BCP S BC PD =⋅△，12CBH S BC HD =⋅△，12ABC S BC AD =⋅△. 在Rt PDA △中，2PD HD AD =⋅.所以2BCP CBH ABC S S S =⋅△△△，所以BCP S △是CBH S △与ABC S △的比例中项. 同理，ABP S △是ABH S △与ABC S △的比例中项. CAP S △是CAH S △与ABC S △的比例中项.2BCP CBH ABC S S S =⋅△△△，2BCP ABH ABC S S S =⋅△△△，2CAP CAH ABC S S S =⋅△△△.三式相加，得222BCP ABP CAP CBH ABC ABH ABC CAH ABC S S S S S S S S S ++=⋅+⋅+⋅△△△△△△△△△2()CBH ABH CAH ABC ABC S S S S S =++⋅=△△△△△.【例3】在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直，且a PC PB PA ===,则这个球的表面积是 ．【例4】(张家口期末)在《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑 (bi ē n ào)．如图，三棱锥D ABC -为一个鳖臑，其中DA ⊥平面ABC ，AB BC ⊥，2DA AB BC ===，AM DC ⊥，M 为垂足，则（ ）A ．AM ⊥平面BCDB ．DC 为三棱锥D ABC -的外接球的直径C ．三棱锥M ABD -的外接球体积为D ．三棱锥M ABC -的外接球体积与三棱锥M ABD -的外接球体积相等 【例5】(市中区校级模拟)在直角梯形ABCD 中，AB CD ∥，AD AB ⊥，22AB DC ==，E 为AD 的中点．将EAB △和ECD △分别沿EB ，EC 折起，使得点A ，D 重合于点F ，构成四面体FBCE ．若四面体FBCE 的四个面均为直角三角形，则其外接球的半径为 ． 【例6】(江西模拟)在三棱锥P ABC -中，PA ⊥底面ABC ，AB AC ⊥，6AB =，8AC =，D 是线段AC 上一点，且3AD DC =．三棱锥P ABC -的各个顶点都在球O 表面上，过点D 作球O 的截面，若所得截面圆的面积的最大值与最小值之差为16π，则球O 的表面积为（ ）A ．72πB ．86πC ．112πD ．128π【例7】四面体BCD A -中，5==CD AB ，34==BD AC ，41==BC AD ，则四面体BCD A -外接球的表面积为（ ） A ．π50B ．π100C ．π150D ．π200【例8】(辽宁期末)粽子，古时北方也称“角黍”，是由粽叶包裹糯米、泰米等馅料蒸煮制成的食品，是中国汉族传统节庆食物之一．端午食粽的风俗，千百年来在中国盛行不衰．粽子形状多样，馅料种类繁多，南北方风味各有不同．某四角蛋黄粽可近似看成一个正四面体，蛋黄近似看成一个球体，且每个粽子里仅包裹一个蛋黄．若粽子的棱长为9cm ，则其内可包裹的蛋黄的最大体积约为（ ）（参考数据：6 2.45≈，3.14)π≈A ．320cmB ．322cmC ．326cmD ．330cm【解析】蛋黄近似看成一个棱长为9cm 的正四面体ABCD 的内切球，正四面体为ABCD ，设四面体的内切 【例9】(遵义期末)已知三棱锥P ABC -的顶点P 在底面的射影O 与ABC ∆的垂心重合，且ABC PBCPBC OBCS S S S =△△△△．若三棱锥P ABC -的外接球半径为3，则PAB PBC PAC S S S ++△△△的最大值为（ ） A ．6 B ．8 C ．10D ．12二． 三棱柱的切割体的外接球⇒图1立着放的模型 图2躺着放的模型图1：立着放的模型一定有重垂线，且重垂线在底面的射影一定位于底面三个顶点中的一个，底面三角形非直角三角形，将重垂线长度设为h ，底面三角形外接圆半径设为r ，A a r sin 2=可以求出，则222⎪⎭⎫⎝⎛+=h r R ； 图2：躺着放的模型，底面是直角三角形或者矩形，侧面非直角三角形，底面一条棱垂直于侧面，222⎪⎭⎫⎝⎛+=h r R ．【例10】如图，三棱锥的所有顶点都在一个球面上，在ABC △中，3=AB ，︒=∠60ACB ，︒=∠90BCD ，AB CD ⊥，22=CD ，则该球的体积为 ．【例11】(莱西市期末)已知球O 是正三棱锥A BCD -(底面是正三角形，顶点在底面的射影为底面中心)的外接球，3BC =，23AB =，点E 在线段BD 上，且3BD BE =．过点E 作球O 的截面，则所得截面面积的最小值是（ ） A ．2πB ．3πC ．4πD ．5π三、切瓜模型(两个平面互相垂直，最大高和最小高问题)图1,PAC BAC AB BC ⊥⊥面面 图2底面ABC 固定，P 在球面上运动，ABC P V -最值问题图1：由图可知，小圆ABC 直径AC 长可以求出，平面PAC 必在大圆上，由APCR sin 2=，解出R ．图2：先根据ABCr sin 2=求出底面圆的直径MN ，再根据几何性质求出球大圆的直径，最后根据垂径定理算出P 到底面距离的最大值和最小值．双半径单交线公式：4222212l R R R -+=2122212122D O E O D O OO OD R +=+==2222222222121121()()24l O C CE O D O C BC O D R R =-+=-+=+-注意：常见的切瓜模型中，一旦出现21l R =或22lR =时，则2R R =或1R R =．双半径单交线公式适合所有的直二面角模型，两个半平面的外接圆半径分别为1R 和2R ，两半平面交线长度为l ，此公式属于一种开挂般的存在，在前面的直三棱柱切割体模型当中也可以使用，一旦两个半平面的二面角不是︒90时，此公式将不再适用．【例12】(柴桑区校级期末)球O 为三棱锥P ABC -的外接球，ABC △和PBC △都是边长为23的正三角形，平面PBC ⊥平面ABC ，则球的表面积为（ ） A ．28π B ．20π C ．18π D ．16π【解析】【例13】(驻马店期末)已知平面图形PABCD ，ABCD 为矩形，4AB =，PAD 是以P 为顶点的等腰直角三角形，如图所示，将PAD △沿着AD 翻折至△P AD '，当四棱锥P ABCD '-体积的最大值为163，此时四棱锥P ABCD '-外接球的表面积为（ ）A ．12πB ．16πC ．24πD ．32π四、含二面角的外接球终极公式双距离单交线公式：4sin cos 222222l mn n m R +-+=αα如图，若空间四边形ABCD 中，二面角D AB C --的平面角大小为α，ABD 的外接圆圆心为1O ，ABC 的外接圆圆心为2O ，E 为公共弦AB 中点，则α=∠21EO O ，m E O =1，n E O =2，2lAE =，R OA =，由于21O E O O 、、、四点共圆，且αsin 221O O R OE ='=，根据余弦定理αcos 222221mn n m O O -+=，4sin cos 22222222l mn n m AE OE R +-+=+=αα．(当C ∠与D ∠均为钝角时，外接圆圆心在半平面的另一侧，21EO O ∠为二面角的对顶角，公式不变；当C ∠与D ∠为钝角时，21EO O ∠为二面角的补角，只需将公式中的角α转化为απ-，即4-sin -cos 222222l mn n m R +-+=）（）（απαπ) 注意：此公式最好配合剖面图，需要求出两个半平面的外接圆半径，和外接圆圆心到公共弦的距离，通常是，剖面图能很快判断出两条相等弦的优先使用公式()2tan 2222αr h r R -+=．【例14】(亳州模拟)已知空间四边形ABCD ，CD BD ⊥，3CD =，3AB BD AD ===，二面角A BD C --是120︒，若A 、B 、C 、D 四点在同一球面上，则该球的表面积是（ ） A ．15π B ．18π C ．21π D ．24π 【例15】(北碚区校级期末)如图，在四边形ABCD 中，AD BC ∥，2AD AB ==，45BCD ∠=︒，90BAD ∠=︒，将ABD △沿BD 进行翻折，在这一翻折过程中，下列说法正确的是（ ）A ．始终有AC BD ⊥B ．当平面ABD ⊥平面BCD 时，平面ABD ⊥平面ACDC ．当平面ABD ⊥平面BCD 时，直线BC 与平面ABD 成45︒角D ．当二面角A BD C --的大小为120︒时，三棱锥A BCD -外接球表面积为563π 【例16】在四面体S ABC -中，AB BC ⊥，AB BC =，SAC △为等边三角形，二面角S AC B --的余弦值为，则四面体S ABC -的外接球表面积为 ．知识点三 内切球1、内切球的基本概念 (1)内切球定义：①球心到多面体各面距离相等且等于半径的球；②与圆柱两底面以及每条母线都相切的球；③与圆锥底面和各母线都相切的球；④与圆台上下两底面以及每条母线都相切的球. (2)正多面体的内切球和外接球球心重合.(3)正棱锥的内切球和外接球球心都在高线上，除正四面体外，均不重合.(4)任意四面体都有内切球，面数超过四的凸多面体需利用定义判断是否存在内切球. 2、多面体和旋转体的内切球 (1)棱锥内切球半径：①等体积法：由球心到各面距离相等，多面体体积可表示为：123123111111333333n n V rS rS rS rS rS rS ++++=++++==表，所以3V r S =表. ②相似法求解正棱锥内切球半径：（以下以正三棱锥为例）如图，由正三棱锥内切球球心O 在高线上，则球与侧面的切点E 在侧面的高线PD 上，与底面的切点H 为高线垂足，易知POE PDH△∽△，故利用OE PODH PD=，可解出内切球半径R .(2)旋转体内切球半径：（可按照轴截面的内切圆半径计算，外接球同理）如图，已知圆锥高为h ，底面半径为r ，利用两个直角三角形ABD △和AOE △相似可得OE BDAE AD=，故rh=，所以rR rh=（）.注：圆柱、圆台同样以轴截面的方式处理.(3)常见几何体内切球、外接球半径：棱长为a的正方体：内切球半径2aR=，外接球半径R=.棱长为a的正四面体：内切球半径R，外接球半径R.柱体侧棱长a，底面外接圆半径r：柱体可能不存在内切球，柱体中最大的球的半径min{}2aR r=，.【例17】(昌江区校级期末)正方体的外接球体积与内切球体积的比为（）A．3B．C D．2【例18】(山东一模)如图，三棱锥V ABC-中，VA⊥底面ABC，90BAC∠=︒，2AB AC AV===，则该三棱锥的内切球和外接球的半径之比为（）A．(2:1B．3):1C．1):3D．1):2【例19】(南京模拟)如图，正三棱柱111ABC A B C-，底面边长为2，D，E，F，M，N分别为棱AC，AB，BC，11A C，11B C的中点，P为线段MN上的动点，则三棱锥P DEF-内切球半径的最大值为．【例20】(青岛开学)已知圆台的上下底面半径分别为1和2，侧面积为，则该圆台的外接球半径为（）A B C D【例21】(重庆月考)若正三棱柱111ABC A B C -既有外接球，又有内切球，记该三棱柱的外接球和内切球的半径分别为1R 、2R ，则212()R R =（ ） A ．5 B ．4 C ．92D ．103同步训练1.在三棱锥A BCD -中，侧棱AB 、AC 、AD 两两垂直，ABC △、ACD △、ADB △、，则三棱锥A BCD -的外接球的体积为（ ）A B ． C ． D ．2．(凤阳县校级三模)已知正方形123APP P 的边长为4，点B ，C 分别是边12P P ，23P P 的中点，沿AB ，BC ，CA 折叠成一个三棱锥P ABC -（使1P ，2P ，3P 重合于点)P ，则三棱锥P ABC -的外接球的体积为（ ）A ．24πB ．C ．D ．4π3．(瑶海区月考)已知三棱锥P ABC -的顶点P 在底面的射影O 为ABC △的垂心，若2ABC OBC PBC S S S ⋅=△△△，且三棱锥P ABC -的外接球半径为3，则PAB PBC PAC S S S ++△△△的最大值为（ ） A ．8B ．10C ．18D ．224.已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足AB BC =3AC =，若该三棱，则其外接球的半径为（ ）A ．1B ．2C ．3D ．235．(河南模拟)在四面体ABCD 中，ABD △与BDC △都是边长为2的等边三角形，且平面ABD ⊥平面BDC ，则该四面体外接球的体积为 ．6．(怀化二模)已知空间四边形ABCD 中，2AB BD AD ===，1BC =，CD 若平面ABD ⊥平面BCD ，则该几何体的外接球表面积为 ．7．(江西月考)已知空间四边形ABCD 中，2AB BD AD ===，1BC =，CD ，若二面角A BD C --的大小是120︒，则该几何体的外接球表面积是 ．8．(葫芦岛模拟)已知空间四边形ABCD 中，2AB BD AD ===，1BC =，CD ，若二面角A BD C--的取值范围为2[]43ππ，，则该几何体的外接球表面积的取值范围为 ．9.(全国四模)已知三棱锥D ABC -所有顶点都在球O 的球面上，ABC △为边长为ABD △是以BD 为斜边的直角三角形，且2AD =，二面角C AB D --为120︒，则球O 的表面积为（ ）A ．1483π B ．28π C ．373π D ．36π10.(江门月考)已知三棱锥P ABC -三条侧棱PA ，PB ，PC 两两互相垂直，且2PA PB PC ===，M ，N分别为该三棱锥的内切球和外接球上的动点，则M ，N 两点间距离的最小值为（ ）A ．2B 1C ．2D 2-11.(和平区二模)已知圆锥底面圆的直径为3，该圆锥的内切球也是棱长为a 的正四面体的外接球，则此正四面体的棱长a 为（ ）A B C ．3 D ．9212.(山西月考)P ABC -的外接球和内切球的半径分别为1R 和2R ，则12R R -的值为（ ）A ．4BCD ．1 13．(大武口区校级三模)正方形ABCD 中，E ，F 分别为线段AB ，BC 的中点，连接DE ，DF ，EF ，将ADE △，CDF △，BEF △分别沿DE ，DF ，EF 折起，使A ，B ，C 三点重合，得到三棱锥O DEF -，则该三棱锥外接球半径R 与内切球半径r 的比值为 ．14．(南开区模拟)如果一个八面体各个面都是全等的正三角形，如图所示，则这个几何体叫正八面体，则棱长为4的正八面体的内切球半径是 ．15．(黄冈期末)若圆锥的内切球（球面与圆锥的侧面以及底面都相切）的半径为1，当该圆锥体积是球体积两倍时，该圆锥的高为（ ）A ．2B ．4CD ．16．(胶州市期末)在三棱柱111ABC A B C -中，上下底面均为等腰直角三角形，且AB ==1AA ⊥平面ABC ，若该三棱柱存在内切球，则1AA =（ ）A ．2B ．2C ．2D。

期末填空专项训练（6）1．把一个圆分成若干等份，剪开后拼成一个近似的长方形，这个长方形的长是6.28分米，这个圆的面积是平方分米，周长是分米。

2．把一个圆平均分成若干份，剪拼成一个近似长方形，周长增加10厘米，原来圆的周长是厘米，面积是平方厘米。

3．有位特别爱动脑筋的李明同学，他是这样推导圆面积公式的：把圆平均分成8份，12份，16份，……得到若干个完全一样的小块，再把它们拼成一个近似的三角形，（分的份数越多，拼成的图形就越近似一个三角形）。

如图是他把圆等分成份后拼成的图形，如果圆的半径用r来表示，那么三角形的底可以表示成，高可以表示成，则三角形的面积S＝×÷2，由此可以得到圆的面积S＝。

4．如图，阴影部分的面积是25cm2，圆环的面积是cm2。

（π取3.14）5．如图，把一个圆剪拼成一个近似的长方形，已知长方形的周长是16.56厘米，则阴影部分的面积是平方厘米。

6．如图，长方形里有两个圆，涂色部分的面积是14cm2，那么一个圆的面积是cm2。

7．如图，将一个圆沿半径剪开，拼成一个近似的长方形，长方形的周长比原来圆的周长长20cm，那么原来圆的周长是厘米，圆面积是平方厘米。

8．从一个长10cm，宽6cm的长方形中剪一个最大的半圆，这个半圆的周长是，面积是。

9．如图所示，正方形的面积是12cm2，圆的面积是πcm210．如图，小圆与大圆的半径比是；已知阴影部分的面积是7.2dm2，小圆面积是dm2。

11．把一个圆剪拼成一个近似的长方形，长方形的周长是33.12厘米，则圆的面积是平方厘米。

12．在一个半径4米的圆形花圃周围铺上一条1米宽的鹅卵石路，鹅卵石路的面积是平方米。

在鹅卵石路上走一圈，至少走米，最多走米。

13．向阳广场中间有一个周长是62.8米的圆形喷水池，这个喷水池的半径是米，面积是平方米。

现在要把这个喷水池扩宽，扩宽后的半径比原来增加了，扩宽后的喷水池的周长是米，面积比原来增加了平方米。

九年级数学上册圆几何综合（提升篇）（Word版含解析）一、初三数学圆易错题压轴题（难）1．在直角坐标系中，A（0，4），B（4，0）．点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动，同时点D从点A出发沿AO方向以每秒1个单位的速度向点O 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点C、D运动的时间是t秒(t>0)．过点C作CE⊥BO于点E，连结CD、DE．⑴当t为何值时，线段CD的长为4；⑵当线段DE与以点O为圆心，半径为的⊙O有两个公共交点时，求t的取值范围；⑶当t为何值时，以C为圆心、CB为半径的⊙C与⑵中的⊙O相切？【答案】(1); (2) 4-＜t≤; (3)或．【解析】试题分析：（1）过点C作CF⊥AD于点F，则CF，DF即可利用t表示出来，在Rt△CFD中利用勾股定理即可得到一个关于t的方程，从而求得t的值；（2）易证四边形ADEC是平行四边形，过点O作OG⊥DE于点G，当线段DE与⊙O相切时，则OG=，在直角△OEG中，OE可以利用t表示，则OG也可以利用t表示出来，当OG＜时，直线与圆相交，据此即可求得t的范围；（3）分两圆外切与内切两种情况进行讨论，当外切时，圆心距等于两半径的和，当内切时，圆心距等于圆C的半径减去圆O的半径，列出方程即可求得t的值．（1）过点C作CF⊥AD于点F，在Rt△AOB中，OA=4，OB=4，∴∠ABO=30°，由题意得：BC=2t，AD=t，∵CE⊥BO，∴在Rt△CEB中，CE=t，EB=t，∵CF⊥AD，AO⊥BO，∴四边形CFOE是矩形，∴OF=CE=t，OE=CF=4-t，在Rt△CFD中，DF2+CF2=CD2，∴（4-t-t）2+（4-t）2=42，即7t2-40t+48=0，解得：t=，t=4，∵0＜t＜4，∴当t=时，线段CD的长是4；（2）过点O作OG⊥DE于点G（如图2），∵AD∥CE，AD=CE=t∴四边形ADEC是平行四边形，∴DE∥AB∴∠GEO=30°，∴OG=OE=（4-t）当线段DE与⊙O相切时，则OG=，∴当（4-t）＜，且t≤4-时，线段DE与⊙O有两个公共交点．∴当 4-＜t≤时，线段DE与⊙O有两个公共交点；（3）当⊙C与⊙O外切时，t=；当⊙C与⊙O内切时，t=；∴当t=或秒时，两圆相切．考点：圆的综合题．2．已知：图1 图2 图3 （1）初步思考：如图1， 在PCB ∆中，已知2PB =，BC=4，N 为BC 上一点且1BN =，试说明：12PN PC =（2）问题提出：如图2，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC +的最小值．（3）推广运用：如图3，已知菱形ABCD 的边长为4，∠B ﹦60°，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC -的最大值．【答案】（1）详见解析；（2）5；（3）最大值37DG =【解析】 【分析】（1）利用两边成比例，夹角相等，证明BPN ∆∽BCP ∆，得到PN BNPC BP=，即可得到结论成立；（2）在BC 上取一点G ，使得BG=1，由△PBG ∽△CBP ，得到12PG PC =，当D 、P 、G 共线时，12PD PC +的值最小，即可得到答案； （3）在BC 上取一点G ，使得BG=1，作DF ⊥BC 于F ，与（2）同理得到12PG PC =，当点P 在DG 的延长线上时，12PD PC -的值最大，即可得到答案. 【详解】（1）证明：∵2,1,4PB BN BC ===， ∴24,4PB BN BC =⋅=， ∴2PB BN BC =⋅，∴BN BPBP BC =， ∵B B ∠=∠，∴BPN BCP ∆∆∽， ∴12PN BN PC BP ==， ∴12PN PC =； （2）解：如图，在BC 上取一点G ，使得BG=1，∵242,212PB BC BG PB ====， ∴,PB BCPBG PBC BG PB=∠=∠， ∴PBG CBP ∆∆∽， ∴12PG BG PC PB ==， ∴12PG PC =， ∴12PD PC DP PG +=+； ∵DP PG DG +≥， ∴当D 、P 、G 共线时，12PD PC +的值最小， ∴最小值为：22435DG =+=；（3）如图，在BC 上取一点G ，使得BG=1，作DF ⊥BC 于F ，与（2）同理，可证12PG PC=，在Rt△CDF中，∠DCF=60°，CD=4，∴DF=CD•sin60°=23，CF=2，在Rt△GDF中，DG=22(23)537+=，∴12PD PC PD PG DG -=-≤，当点P在DG的延长线上时，12PD PC-的值最大，∴最大值为：37DG=.【点睛】本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识，解题的关键是学会构建相似三角形解决问题，学会用转化的思想思考问题，把问题转化为两点之间线段最短解决，题目比较难，属于中考压轴题．3．选做题：从甲乙两题中选作一题，如果两题都做，只以甲题计分题甲：已知矩形两邻边的长、是方程的两根.（1）求的取值范围；（2）当矩形的对角线长为时，求的值；（3）当为何值时，矩形变为正方形？题乙：如图，是直径，于点，交于点，且．（1）判断直线和的位置关系，并给出证明；（2）当，时，求的面积．【答案】题甲（1）（2）（3）题乙：（1）BD是切线；证明所以OB⊥BD，BD是切线（2）S=【解析】试题分析：题甲：（1）、是方程的两根，则其；由得（2）矩形两邻边的长、，矩形的对角线的平方=；矩形两邻边的长、是方程的两根，则；因为，所以；解得由得（3）矩形变为正方形，则a=b；、是方程的两根，所以方程有两个相等的实数根，即，由得题乙：（1）BD是切线；如图所示，是弧AC所对的圆周角，；因为，所以；于点，，所以，，在三角形OBD中，所以OB⊥BD；BD是切线（2），AB是圆的直径，所以OB=5；于点，交于点，F是BC的中点；，BF=4；在直角三角形OBF中由勾股定理得OF=；根据题意，，则，所以，从而，解得DF=，的面积=考点：直线与圆相切，相似三角形点评：本题考查直线与圆相切，相似三角形；解本题的关键是会判断直线与圆是否相切，能判定两个三角形相似4．如图，△ABC内接于⊙O，点D在AB边上，CD与OB交于点E，∠ACD＝∠OBC；（1）如图1，求证：CD⊥AB；（2）如图2，当∠BAC＝∠OBC+∠BCD时，求证：BO平分∠ABC；（3）如图3，在（2）的条件下，作OF⊥BC于点F，交CD于点G，作OH⊥CD于点H，连接FH并延长，交OB于点P，交AB边于点M．若OF＝3，MH＝5，求AC边的长．【答案】（1）见解析；（2）见解析；（3）AC＝48 5【解析】【分析】（1）根据直径所对的圆周角是直角，得出∠FCB=90°，再根据“同弧所对的圆周角相等”得出∠A=∠F，再根据已知条件得∠3=90°，得CD⊥AB；（2）延长BO交AC于K，由已知可得∠A=∠5，由∠A+∠2=90°得∠5+∠2=90°，根据三角形的内角和定理及外角定理得出∠9=∠1得出BO平分∠ABC；（3）延长BO交AC于点K，延长CD交⊙O于点N，联结BN，由条件可得CH=NH，BF=CF，从而HF是△CBN的中位线，HF∥BN，得出∠OEH=∠EHM又由∠OEH+∠EOH=∠EHM+∠OHP=90°可得HM=OB=5，在Rt△OBF中，根据勾股定理可得BF=4，解出BC=8，sin∠OBC=35，所以可得AC=2CK，CK=BC•sin∠OBC=245得AC=48 5.【详解】解：（1）如图1，令∠OBC＝∠1，∠ACD＝∠2延长BO交⊙O于F，连接CF．∵BF是⊙O的直径，∴∠FCB＝90°∴∠1+∠F＝90°，∵弧BC＝弧BC，∴∠A＝∠F又∵∠1＝∠2，∴∠2+∠A＝90°，∴∠3＝90°，∴CD⊥AB（2）如图2，令∠OBC＝∠1，∠BCD＝∠4延长BO交AC于K∵∠A＝∠1+∠4，∠5＝∠1+∠4，∴∠A＝∠5，∵∠A+∠2＝90°，∴∠5+∠2＝90°，∴∠6＝90°∵∠7＝180°﹣∠3＝90°，∴∠6＝∠7，又∵∠5＝∠8，∴∠9＝∠2∵∠2＝∠1，∴∠9＝∠1，∴BO平分∠ABC（3）如图3，延长BO交AC于点K，延长CD交⊙O于点N，联结BN∵OH⊥CN，OF⊥BC∴CH＝NH，BF＝CF∴HF是△CBN的中位线，HF∥BN∴∠FHC＝∠BNC＝∠BAC∵∠BAC＝∠OEH，∠FHC＝∠EHM∴∠OEH＝∠EHM设EM、OE交于点P∵∠OEH+∠EOH＝∠EHM+∠OHP＝90°∴∠EOH＝∠OHP∴OP＝PH∵∠ADC＝∠OHC＝90°∴AD∥OH∴∠PBM＝∠EOH，∠BMP＝∠OHP∴PM＝PB∴PM+PH＝PB+OP∴HM＝OB＝5在Rt△OBF中，根据勾股定理可得BF＝4∴BC＝8，sin∠OBC＝3 5∵∠A+∠ABO＝∠DEB+∠ABO＝90°∴∠AKB+∠CKB＝90°∴OK⊥ACAC＝2CK，CK＝BC•sin∠OBC＝24 5∴AC＝48 5【点睛】此题主要考查了圆的综合应用以及三角形的内角和定理及外角定理和勾股定理、三角函数等知识，理解同弧所对的圆周角相等是解题关键．5．在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，点P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：过圆心C的任意直线CP与⊙C交于点A，B，若满足|PA﹣PB|＝2，则称点P为⊙C的“完美点”，如图点P为⊙C的一个“完美点”．(1)当⊙O的半径为2时①点M(32，0)⊙O的“完美点”，点(﹣32，﹣12)⊙O的“完美点”；(填“是”或者“不是”)②若⊙O的“完美点”P在直线y＝34x上，求PO的长及点P的坐标；(2)设圆心C的坐标为(s，t)，且在直线y＝﹣2x+1上，⊙C半径为r，若y轴上存在⊙C的“完美点”，求t的取值范围．【答案】(1)①不是，是；②PO的长为1，点P的坐标为(45，35)或(﹣45，﹣35)；(2)t的取值范围为﹣1≤t≤3．【解析】【分析】（1）①利用圆的“完美点”的定义直接判断即可得出结论.②先确定出满足圆的“完美点”的OP的长度，然后分情况讨论计算即可得出结论；（2）先判断出圆的“完美点”的轨迹，然后确定出取极值时OC与y轴的位置关系即可得出结论.【详解】解：(1)①∵点M(32，0)，∴设⊙O与x轴的交点为A，B，∵⊙O的半径为2，∴取A(﹣2，0)，B(2，0)，∴|MA﹣MB|＝|(32+2)﹣(2﹣32)|＝3≠2，∴点M不是⊙O的“完美点”，同理：点(﹣32，﹣12)是⊙O的“完美点”．故答案为不是，是．②如图1，根据题意，|PA﹣PB|＝2，∴|OP+2﹣(2﹣OP)|＝2，∴OP＝1．若点P在第一象限内，作PQ⊥x轴于点Q，∵点P在直线y＝34x上，OP＝1，∴43,55 OQ PQ==．∴P(43,55)．若点P在第三象限内，根据对称性可知其坐标为(﹣45，﹣35)．综上所述，PO的长为1，点P的坐标为(43,55)或（43,55--）)．(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|＝2，∴|CP+r﹣(r﹣CP)|＝2．∴CP＝1．∴对于任意的点P，满足CP＝1，都有|CP+r﹣(r﹣CP)|＝2，∴|PA﹣PB|＝2，故此时点P为⊙C的“完美点”．因此，⊙C的“完美点”是以点C为圆心，1为半径的圆．设直线y＝﹣2x+1与y轴交于点D，如图2，当⊙C移动到与y轴相切且切点在点D的上方时，t的值最大．设切点为E，连接CE，∵⊙C的圆心在直线y＝﹣2x+1上，∴此直线和y轴，x轴的交点D(0，1)，F(12，0)，∴OF＝12，OD＝1，∵CE∥OF，∴△DOF∽△DEC，∴OD OF DE CE=，∴112 DE=，∴DE＝2，∴OE＝3，t的最大值为3，当⊙C移动到与y轴相切且切点在点D的下方时，t的值最小．同理可得t的最小值为﹣1．综上所述，t 的取值范围为﹣1≤t ≤3．【点睛】此题是圆的综合题，主要考查了新定义，相似三角形的性质和判定，直线和圆的位置关系，解本题的关键是理解新定义的基础上，会用新定义，是一道比中等难度的中考常考题.6．已知ABD △内接于圆O ，点C 为弧BD 上一点，连接BC AC AC 、，交BD 于点E ，CED ABC ∠=∠．（1）如图1，求证：弧AB =弧AD ；（2）如图2，过B 作BF AC ⊥于点F ，交圆O 点G ，连接AG 交BD 于点H ，且222EH BE DH =+，求CAG ∠的度数；（3）如图3，在（2）的条件下，圆O 上一点M 与点C 关于BD 对称，连接ME ，交AB 于点N ，点P 为弧AD 上一点，PQ BG ∥交AD 于点Q ，交BD 的延长线于点R ，AQ BN =，ANE 的周长为20，52DR =O 半径．【答案】（1）见解析；（2）∠CAG=45°；（3）r=62【解析】【分析】（1）证∠ABD=∠ACB 可得；（2）如下图，△AHD 绕点A 旋转至△ALE 处，使得点D 与点B 重合，证△ALE ≌△AHE ，利用勾股定理逆定理推导角度；（3）如下图，延长QR 交AB 于点T ，分别过点N 、Q 作BD 的垂线，交于点V ，I ，取QU=AE ，过点U 作UK 垂直BD.先证△AEN ≌△QUD ，再证△NVE ≌△RKU ，可得到NV=KR=DK ，进而求得OB 的长.【详解】（1）∵∠CED 是△BEC 的外角，∴∠CED=∠EBC+∠BCA∵∠ABC=∠ABD+∠EBC又∵∠CED=∠ABC∴∠ABD=∠ACB∴弧AB=弧AD（2）如下图，△AHD 绕点A 旋转至△ALE 处，使得点D 与点B 重合∵△ALB是△AHD旋转所得∴∠ABL=∠ADB，AL=AH设∠CAG=a，则∠CBG=a∵BG⊥AC∴∠BCA=90°-a，∴∠ADB=∠ABD=90°-a∴在△BAD中，BAE+∠HAD=180-a-(90°-a)-(90°-a)=a∴∠LAE=∠EAH=a∵LA=AH，AE=AE∴△ALE≌△AHE，∴LE=EH∵HD=LB，222=+EH BE DH∴△LBE为直角三角形∴∠LBE=(90°-a)+(90°-a)=90°，解得：a=45°∴∠CAG=45°（3）如下图，延长QR交AB于点T，分别过点N、Q作BD的垂线，交于点V，I，取QU=AE，过点U作UK垂直BD由（2）得∠BAD=90°∴点O在BD上设∠R=n，则∠SER=∠BEC=∠MEB=90°-n∴∠AEN=2n∵SQ⊥AC∴∠TAS=∠AQS=∠DQR，AN=QD∵QU=AE∴△AEN ≌△QUD∴∠QUD=∠AEN=2n∴UD=UR=NE ，∵△ANE 的周长为20∴QD+QR=20在△DQR 中，QD=7∵∠ENR=∠UDK=∠R=n∴△NVE ≌△RKU∴NV=KR=DK=522∴BN=5∴BD=122，OB=62r =【点睛】本题考查了圆的证明，涉及到全等、旋转和勾股定理，解题关键是结合图形特点，适当构造全等三角形7．已知：AB 为⊙O 直径，弦CD ⊥AB ，垂足为H ，点E 为⊙O 上一点，AE BE =，BE 与CD 交于点F ．（1）如图1，求证：BH ＝FH ；（2）如图2，过点F 作FG ⊥BE ，分别交AC 、AB 于点G 、N ，连接EG ，求证：EB ＝EG ； （3）如图3，在（2）的条件下，延长EG 交⊙O 于M ，连接CM 、BG ，若ON ＝1，△CMG 的面积为6，求线段BG 的长．【答案】（1）见解析；（2）见解析；（3）10 ．【解析】【分析】（1）连接AE ，根据直径所对圆周角等于90°及弧与弦的关系即可得解；（2）根据题意，过点C 作CQ FG CS FB ⊥⊥，，连接CE BC 、，通过证明Rt CGQ Rt CBS ∆≅∆，CBE CGE ∆≅∆即可得解；（3）根据题意，过点G 作GT CD ⊥于T ，连接CN ，设CAB α∠＝，证明()CMG CNG AAS ∆≅∆，再由面积法及勾股定理进行计算求解即可.【详解】解：（1）如下图，连接AE∵AB 为直径∴90AEB =︒∠∵AE BE =∴AE BE =∴45B ∠=︒又∵CD AB ⊥于H ∴45HFB ∠=︒∴HF HB =；（2）如下图，过点C 作CQ FG CS FB ⊥⊥，，连接CE BC 、AB 为直径，∴90ACB QCS ∠=∠=︒∴GCQ BCS ∠=∠∴()Rt CGQ Rt CBS AAS ∆≅∆∴CG CB =同理()CBE CGE SAS ∆≅∆∴EG EB =；（3）如下图，过点G 作GT CD ⊥于T ，连接CN设CAB α∠=由（2）知：CM CB =∴CM CB =∵HB HF =∴45HBF HFB ∠=∠=︒∵GF BE ⊥∴45NFH NH BH CN BC ∠=︒∴=∴=，，∴CM CB CN ==则：2MEB α∠=902AEG α∠=︒-∴45EAG EGA α∠=∠=︒+∴45M MGC α∠=∠=︒+∴()CMG CNG AAS ∆≅∆∵CMG ∆面积为6∴6CAN GAN S S -=设2122BH NH x OA OB x AN x ====+=+，，则()CGT BCH AAS ∆≅∆∴C BH x ==∴6AN CH AN TH ⋅-⋅=∴1(22)62x CT +⋅= 解得：2x =∵2BC BH BA =⋅∴2210BC =⨯，则25BC ＝∴2210BG BC ＝＝．【点睛】本题主要考查了圆和三角形的综合问题，熟练掌握圆及三角形的各项重要性质及判定方法是解决本题的关键.8．如图，PA ，PB 分别与O 相切于点A 和点B ，点C 为弧AB 上一点，连接PC 并延长交O 于点F ，D 为弧AF 上的一点，连接BD 交FC 于点E ，连接AD ，且2180APB PEB ∠+∠=︒．（1）如图1，求证：//PF AD ；（2）如图2，连接AE ，若90APB ∠=︒，求证：PE 平分AEB ∠；（3）如图3，在（2）的条件下，连接AB 交PE 于点H ，连接OE ，8AD =，4sin 5ABD ∠=，求PH 的长． 【答案】（1）见解析；（2）见解析；（3）257 【解析】【分析】（1）连接OA 、OB ，由切线的性质可得90OAP OBP ∠=∠=︒，由四边形内角和是360︒，得180∠+∠=︒P AOB ，由同弧所对的圆心角是圆周角的一半，得到2AOB ADB ∠=∠，等量代换得到ADB PEB ∠=∠，由同位角相等两直线平行，得到//PF AD ；（2）过点P 做PK PF ⊥交EB 延长线于点K ，由90APB ∠=︒得290PEB ∠=︒，从而45PEB ∠=︒，由切线的性质，得PA PB =，由PK PE ⊥，45PEK ∠=︒，得PE PK =，从而90APE EPB ︒∠=-∠，进而APE BPK ∠=∠，即可证得APE BPK ∆∆≌由此45K AEP ∠=∠=︒，得到AEP PEB ∠=∠，即可证得PE 平分AEB ∠；（3）连接AO 并延长交圆O 于点M ，连接OB 、OH 、OP 、OD 、DM ，由45ADE ∠=︒，90AED ∠=︒，可得DE AE =，由OA 、OD 为半径，可得OA OD =，即可证出DEO AEO ∆∆≌，由直径所对的圆周角是直角，可得90ADM ∠=︒，在Rt ADM ∆中，由正弦定义可得10AM =，由此5OA OB ==，由OAPB 为正方形，对角线AB 垂直平分OP ，从而，OH PH =.在Rt OAP ∆中，252OP OA ==.延长EO 交AD 于K ，在Rt OEP ∆中，由勾股定理得7PE =，在Rt OEH ∆中，由勾股定理得257PH =. 【详解】 （1）连接OA 、OB∵PA 、PB 与圆O 相切于点A 、B ，且OA 、OB 为半径，∴OA AP ⊥，OB BP ⊥，∴90OAP OBP ∠=∠=︒，∴在四边形AOBP 中，360180180P AOB ∠+∠=︒-︒=︒，∵AB AB =，∴2AOB ADB ∠=∠，∴2180P ADB ∠+∠=︒，∵2180P PEB ∠+∠=︒，∴ADB PEB ∠=∠，∴//PF AD（2）过点P 做PK PF ⊥交EB 延长线于点K∵90APB ∠=︒，∴21809090PEB ∠=︒-︒=︒，∴45PEB ∠=︒，∵PA 、PB 为圆O 的切线，∴PA PB =，∵PK PE ⊥，45PEK ∠=︒，∴PE PK = ，∵9090APE EPB KPB EPB ︒︒∠=-∠=∠=-∠，∴APE BPK ∠=∠，∴APE BPK ∆∆≌，∴45K AEP ∠=∠=︒，∴AEP PEB ∠=∠，∴PE 平分AEB ∠；（3）连接AO 并延长交圆O 于点M ，连接OB 、OH 、OP 、OD 、DM∵45ADE ∠=︒，90AED ∠=︒，∴DE AE =，∵OA 、OD 为半径，∴OA OD =，∵OE OE =，∴DEO AEO ∆∆≌，∴1452AEO OED AED ∠=∠=∠=︒， ∴90OEP ∠=︒，∵AM 为圆O 的直径，∴90ADM ∠=︒，∵弧AD =弧AD ，∴ABD AMD ∠=∠，在Rt ADM ∆中，8AD =，4sin 5AMD ∠=，则10AM =， ∴5OA OB ==，由题易证四边形OAPB 为正方形，∴对角线AB 垂直平分OP ，AB OP =，∵H 在AB 上，∴OH PH =，在Rt OAP ∆中，252OP OA ==，延长EO 交AD 于K ，∵DE AE =，可证OK AD ⊥，DOK ABD ∠=∠，∴4DK KE ==，3OK =，1OE =∴在Rt OEP ∆中，227PE OP OE =-=在Rt OEH ∆中，222OH OE EH =+∵OH PH =，7EH PE HP PH =-=-∴()22217PH PH =+- ∴257PH =． 【点睛】 本题考查了圆的综合题，圆的性质，等腰三角形的性质，相交弦定理，正弦定理，勾股定理，灵活运用这些性质定理解决问题是本题的关键．9．如图，在梯形ABCD 中，AD//BC ，AB=CD=AD=5，cos 45B =，点O 是边BC 上的动点，以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ，联结AM ，作∠CMN=∠BAM ，射线MN 与边AD 、射线CD 分别交于点F 、N ．（1）当点E 为边AB 的中点时，求DF 的长；（2）分别联结AN 、MD ，当AN//MD 时，求MN 的长；（3）将O 绕着点M 旋转180°得到'O ，如果以点N 为圆心的N 与'O 都内切，求O 的半径长．【答案】（1）DF 的长为158；（2）MN 的长为5；（3）O 的半径长为258． 【解析】【分析】 （1）作EH BM ⊥于H ，根据中位线定理得出四边形BMFA 是平行四边形，从而利用cos 45B =解直角三角形即可求算半径，再根据平行四边形的性质求FD 即可；（2）先证AMB CNM ∠=∠，再证MAD CNM ∠=∠，从而证明AFM NFD ∆~∆，得到AF MF AF DF NF MF NF DF=⇒=，再通过平行证明AFN DFM ∆~∆，从而得到AF NF AF MF NF DF DF MF=⇒=，通过两式相乘得出AF NF =再根据平行得出NF DF =， 从而得出答案．（3）通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒，再利用cos 45B =解三角函数即可得出答案． 【详解】 （1）如图，作EH BM ⊥于H ：∵E 为AB 中点，45,cos 5AB AD DC B ==== ∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ，在Rt OEH ∆中： ()222322r r ⎛⎫=-+ ⎪⎝⎭解得：2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形∴2528AF BM r ===∴2515588FD AD AF =-=-= （2）如图：连接MD AN ，∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN∴AFN DFM ∆~∆ ∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5；（3）作如图：∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ，圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上∴54cos 5AB B BM BM === 解得：254BM =O 的半径长为258【点睛】 本题是一道圆的综合题目，难度较大，掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键．10．在O 中，AB 为直径，CD 与AB 相较于点H ，弧AC=弧AD（1）如图1，求证：CD AB ⊥;（2）如图2，弧BC 上有一点E ，若弧CD=弧CE ，求证：3EBA ABD ∠=∠;（3）如图3，在（2）的条件下，点F 在上，连接,//FH FH DE ，延长FO 交DE 于点K ，若165,55FK DB BE ==，求AB ．【答案】（1）证明见解析；（2）证明见解析；（3）185AB =．【解析】【分析】（1）连接,OC OD,根据AC AD=得出COA DOA∠=再根据OC OD=得出OCD ODC∠=∠，从而得证；（2）连接,BC BD,根据AC AD=得出,BC BD BA CD=⊥，CBA ABD∠=∠，再根据CE CD=,得出CBE CBD∠=∠,从而得出结论；（3）作,CM DB CN BE⊥⊥，过点P作,PT BE PS BD⊥⊥，,5BE BP a DB a===先证CDM CEN∆≅∆，DM EN=，再证,CMB CNB BM BN∆≅∆=，设DM b=，得出2b a=，再算出,CM CD得出CPD∆为等腰三角形，再根据BP是角平分线利用角平分线定理得出BCPEBPS DP BDS PE BE∆==，从而算出,PE DE,再根据三角函数值算出BG,,,,AB r OG OH，再根据//FH DE得出HO OFGO OK=，从而计算AB．【详解】（1）连接OC，CD因为AC AD=，所以COA DOA∠=∠OC OD=，,OA CD CD AB∴⊥∴⊥;(2)连接BC，,BC BD BA CD=⊥所以AB平分CBD∠，设ABD ABCα∠=∠=2CBDα∴∠=CD CE∴=2CBE CBDα∴∠=∠=，3EBAα∴∠=3EBA ABD∴∠=∠．(3) 2,90EBC BPE PEB αα︒∠=∠=∠=-设,5BE BP a DB a ===作,CM DB CN BE ⊥⊥，可证：CDM CEN ∆≅∆，DM EN =，再证：,CMB CNB BM BN ∆≅∆=设,5,2DM EN b a b a b b a ==+=-∴=在CBM ∆中勾股4CM a =在CDM ∆中勾股25CD a =得CPD ∆为等腰三角形25DP DC a ==因为BP 为角平分线，过点P 作,PT BE PS BD ⊥⊥ 可证：5BCP EBP S DP BD S PE BE∆=== 2525,53PE a DE a ∴== 14tan ,tan 223αα== 2555,32BG a AB a ∴== 557535,,4124r a OG a OH a === //FH DE97HO OF GO OK ∴== 99518516OF KF AB ===【点睛】本题是一道圆的综合题目，难度较大，考查了圆相关的性质以及与三角形综合，掌握相关的线段与角度转化是解题关键．。

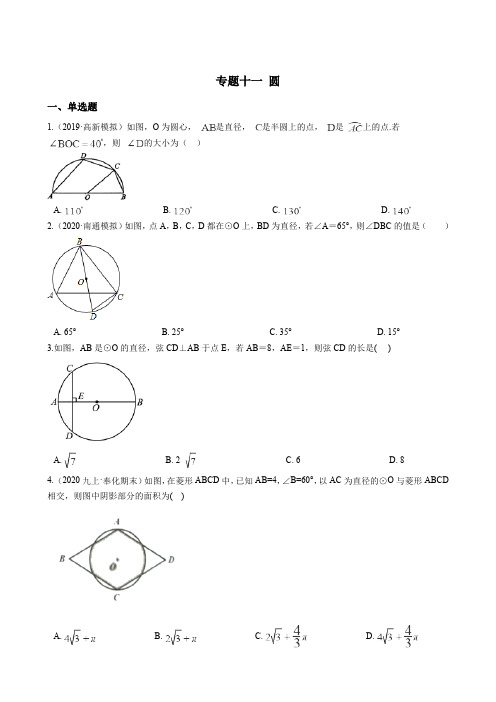
专题十一圆一、单选题1.（2019·高新模拟）如图，O为圆心，是直径，是半圆上的点，是上的点.若，则的大小为（）A. B. C. D.2.（2020·南通模拟）如图，点A，B，C，D都在⊙O上，BD为直径，若∠A＝65°，则∠DBC的值是（ ）A. 65°B. 25°C. 35°D. 15°3.如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是( )A. B. 2 C. 6 D. 84.（2020九上·奉化期末）如图，在菱形ABCD中，已知AB=4，∠B=60°，以AC为直径的⊙O与菱形ABCD 相交，则图中阴影部分的面积为( )A. B. C. D.5.（2019九上·温州月考）如图，△ABC内接于⊙O中，AB=AC，=60°，则∠B=( )A. 30°B. 45°C. 60°D. 75°6.（2020九上·中山期末）如图，AD是半圆的直径，点C是弧BD的中点，∠ADC=55°，则∠BAD等于（）A. 50°B. 55°C. 65°D. 70°7.（2020九上·海曙期末）平面直角坐标系中，⊙P的圆心坐标为(-4，-5)，半径为5，那么⊙P与y轴的位置关系是（）A. 相交B. 相离C. 相切D. 以上都不是8.（2019九上·驻马店期末）如图，直径AB为3的半圆，绕A点逆时针旋转60°，此时点B到了点B′处，则图中阴影部分的面积是（）A. 3πB.C. 6πD. 24π9.（2020九上·北仑期末）下列四个结论，不正确的是（）①过三点可以作一个圆；②圆内接四边形对角相等③平分弦的直径垂直于弦；④相等的圆周角所对的弧也相等A. ②③B. ①③④C. ①②④D. ①②③④10.（2020九上·诸暨期末）如图，是圆内接四边形的一条对角线，点关于的对称点在边上，连接.若，则的度数为（）A. 106°B. 116°C. 126°D. 136°11.（2019九上·武汉月考）如图，O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB 于点C，则△ABC的最大面积是（）A. B. C. D.12.如图，在⊙O中，点C在优弧AB上，将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为，AB=8，则BC的长是（）A. B. C. D.13.（2019九上·如皋期末）如图，▱ABCD中，，，，是边AB上的两点，半径为2的过点A，半径为1的过点、E、F分别是边CD，和上的动点则的最小值等于A. B. 6 C. D. 914.（2019·武汉模拟）点G为△ABC的重心（△ABC三条中线的交点），以点G为圆心作⊙G与边AB，AC相切，与边BC相交于点H，K，若AB＝4，BC＝6，则HK的长为（）A. B. C. D.15.（2019·武汉模拟）如图，⊙O内切于正方形ABCD，边AD，CD分别与⊙O切于点E，F，点M、N 分别在线段DE，DF上，且MN与⊙O相切，若△MBN的面积为8，则⊙O的半径为（）A. B. 2 C. D. 216.（2020·长兴模拟）如图，AB为☉O的直径，P为弦BC上的点，∠ABC=30°，过点P作PD⊥OP交☉O 于点D，过点D作DE∥AB交AB的延长线于点E.若点C恰好是的中点，BE=6，则PC的长是（）A. -8B. -3C. 2D. 12-17.（2019九上·宜兴月考）在平面直角坐标系中，直线经过点A（－3，0），点B（0，），点P的坐标为（1，0），与轴相切于点O，若将⊙P沿轴向左平移，平移后得到（点P的对应点为点P′），当⊙P′与直线相交时，横坐标为整数的点P′共有（）A. 1个B. 2个C. 3个D. 4个18.（2019·海州模拟）如图，菱形ABCD的边AB=5，面积为20，∠BAD＜90°，⊙O与边AB、AD都相切，AO=2，则⊙O的半径长等于（）A. B. C. D.19.（2019·高台模拟）如图，AB与⊙O相切于点C，OA＝OB，⊙O的直径为6cm，AB＝6 cm，则阴影部分的面积为（）A. B. C. D.20.（2019九下·深圳月考）如图，△ABC内接于圆O，∠BOC=120°，AD为圆O的直径．AD交BC于P 点且PB=1，PC=2，则AC的长为( )A. B. C. 3 D. 2二、填空题21.（2019·嘉定模拟）如图，的半径长为5cm，内接于，圆心O在的内部，如果，cm，那么的面积为________cm22.（2019九上·黄石期末）如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠BAC=25°.求∠P的度数________.23.（2020九上·东台期末）如图，⊙O是△ABC的外接圆，已知∠ABO=40°，则∠ACB的大小为________．24.（2019·台江模拟）如图，⊙O是Rt△ABC的外接圆，∠ACB＝90°，∠A＝25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是________．25.（2019九上·道里期末）如图，已知，在中，，，，是ABC的内切圆，则这个圆的半径是________．26.（2020九上·北仑期末）如图，四边形ABCD中，∠BAD=∠BCD=90°，∠B=45°，DE⊥AC于E交AB 于F，若BC=2CD，AE=2，则线段BF=________。

专题十一：古诗词鉴赏（一）古诗文阅读闻王昌龄左迁龙标遥有此寄李白[来源:]杨花落尽子规啼，闻道龙标过五溪。

我寄愁心与明月，随风直到夜郎西。

1.诗人在“杨花落尽子规啼”—句里写了哪些景物？渲染了怎样的气氛？2.从“我寄愁心与明月，随风直到夜郎西”两句中，你解读出了诗人哪些情感？（二）阅读下面的宋词，完成1-2题。

清平乐独宿博山王氏庵辛弃疾绕床饥鼠，蝙蝠翻灯舞。

屋上松风吹急雨，破纸窗间自语。

平生塞北江南，归来华发苍颜。

布被秋宵梦觉，眼前万里江山。

（1）请简要赏析上片“破纸窗间自语”一句。

答：__________________________________________________________________（2）全词抒发了词人怎样的思想感情？请概括作答。

答：_______________________________________________________________________ (三)阅读《江城子•密州出猎》一词，完成1—2题.老夫聊发少年狂，左牵黄，右擎苍，锦帽貂裘，千骑卷平冈。

为报倾城随太守，亲射虎，看孙郎。

酒酣胸胆尚开张。

鬓微霜，又何妨!持节云中，何日遣冯唐?会挽雕弓如满月，西北望，射天狼。

17.用简明的语言概括词的上阕、下阕的内容。

上阕：下阕：18.下面对该词的理解品味有误的一项是：（）A. 此词是苏轼的第一首最具豪放风格的作品，表现他决心抗击辽、夏侵略的爱国壮志。

自此，他树起了“自是一家”的旗帜，提高了词品，扩大了词的界境。

B. 开篇着一“聊”一“狂”两字，更见作者的潇洒豪放，也隐约透露出怨愤之情;再用一个“卷”字，写出众多人马像疾风一样驰骋山冈的壮观的出猎场面。

C. 用典故是古诗词创作常用艺术手法之一，用典故能含蓄委婉地表情达意。

词中下阕采用冯唐持节赦免魏尚的典故，表达了作者希望朝廷悯恤年老，免去罪名的愿望。

D. 结尾三句卒章显志，表明作者想要驰骋沙场、为国杀敌、一展宏图的强烈愿望和远大的志向，其耿耿忠心溢于言表，凸显了刚强威武的英雄气概。

完美的图形—圆1、从树木的年轮,我们可以清楚地看出树木的生长年龄,如果一棵20年树龄的红杉树的树干直径是23厘米,你知道这棵红杉树的半径平均每年增加多少厘米吗?解析:20年树龄的树干直径是23厘米,我们可以根据在同一个圆中直径是半径的2倍关系求出半径,然后再求出平均每年半径增加的厘米数。

解答:23÷2÷20=0.575(厘米)答:这棵红杉树的半径平均每年增加0.575厘米。

2、将两个大小相同的圆形铁片平放在桌面上,一个固定不动,另一个沿着不动铁片的边缘滚动,则滚动铁片的圆心转一周后所形成的圆的半径是铁片半径的几倍?若圆形铁片的半径是1厘米,则形成的大圆的半径是多少厘米?解析：由图知，两个圆形铁片大小相同，滚动铁片的圆心转一周后所形成的圆就是虚线画的圆，虚线的圆的半径是铁片半径的2倍，如果圆形铁片的半径是1厘米,则形成的大圆的半径就是2个铁片半径，也就是2厘米。

解答：滚动铁片的圆心转一周后所形成的圆的半径是铁片半径的2倍，若圆形铁片的半径是1厘米,则形成的大圆的半径是2厘米。

3、在一张边长是2厘米的正方形纸上画一个最大的扇形。

解析:扇形是由两条半径和圆上的一段弧线组成的,在边长是2厘米的正方形中画出一个最大的扇形,需要考虑扇形的圆心角要最大,因此需要把正方形的一个顶点为圆心,边长为半径作弧,这样就可以找到最大的扇形。

解答:4、下面扇形的圆心角各是多少度?解析:因为一个周角是360°，12圆的圆心角就是360°的一半，也就是180°；14圆的圆心角就是360°的14，也就是90°；15圆的圆心角就是360°的15，也就是72°。

解答: 180° 90° 72°5、下图中大圆的直径是6厘米,小圆的直径是4厘米,你知道阴影部分的宽是多少吗?解析：根据题意可知大圆的直径是6厘米,则半径就是3厘米；小圆的直径是4厘米，则半径就是2厘米。

2023年春九年级数学中考复习《圆综合压轴解答题》专题提升训练（附答案）1．如图，已知四边形ACBD内接于⊙O，AB是⊙O的直径，AB＝10，点D是半圆的中点，连接CD，点I是CD上一点，且DI＝DB．（1）求证：点I是△ABC的内心；（2）若BC＝6，求△BIC的面积；（3）随着点C的变化，点I的位置也发生改变，请探求CI长度的取值范围．2．如图，在△ABC中，AB＝4，以AB为直径作⊙O，分别交BC于点D，交CA的延长线于点E，过点D作⊙O的切线DH交AC于点H，且DH⊥AC，连接DE与AB交于点G．（1）求证：AB＝AC；（2）填空：①当BD＝时，四边形EODA为菱形；②若∠EGA＝∠EAG，则GO 的长为．3．如图，AB是⊙O的直径，点D在⊙O上，连接AD并延长至点C，连接BC交⊙O于点E，AB＝BC＝10，AC＝12，过点D作DF⊥BC于点F．（1）求证：直线DF是⊙O的切线；（2）连接DE，设△CDE的面积为S1，四边形ADEB的面积为S2，求的值；（3）点P在上，且的长为，点Q为线段BD上一动点，连接PQ，求的最小值．4．（1）如图①，在△ABC中，∠BAC＝90°，AB＝4，AC＝3，若AD平分∠BAC交CB于点D，那么点D到AC的距离为；（2）如图②，四边形ABCD内接于⊙O，AC为直径，点B是半圆AC的三等分点（弧AB＜弧BC），连接BD，若BD平分∠ABC，且BD＝8，求四边形ABCD的面积．（3）如图③，有一块半径为1的⊙O，若⊙O的内接四边形ABCD满足∠ABC＝60°，AB＝AD，且AD+DC＝2，求AB的长．5．如图1，△ABC内接于⊙O，弦AE交BC于点D，连接BO，且∠ABO＝∠DAC．（1）求证：AE⊥BC；（2）如图2，点F在弧AC上，连接CF、BF，BF交AE于点M，若∠ACF＝∠OBC，求证：MD＝ED；（3）如图3，在（2）的条件下，∠BFC＝3∠EAC，若BM＝，AM＝3时，求弦CF 的长．6．如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，连接BO并延长交边AC于点D．（1）如图1，求证：∠BAC＝2∠ABD；（2）如图2，过点B作BH⊥AC于点H，延长BH交⊙O于点G，连接OC，CG，OC 交BG于点F，求证：BF＝2HG；（3）如图3，在（2）的条件下，若AD＝2，CD＝3，求线段BF的长．7．如图，等边△ABC内接于⊙O，点D是弧AC上一点，连接BD交AC于E．（1）如图1，求证∠ADB＝∠CDB；（2）如图2，点F为线段BD上一点，连接CF，若∠BCF＝2∠ABD时，求证：BF＝DE+AD；（3）在（2）的条件下，作∠BCF的平分线交⊙O于M，在CM上取点R，连接AR交CF于点T，若TR＝1，MR＝5，∠CAT＝3∠ACD，求AT的长．8．如图，在△ABC中，∠C＝90°，AC＝BC＝2．（1）若点D、E、F分别在AB，AC，BC边上（如图1），连接DE，DF，EF，且∠EDF ＝90°，DE＝DF．①四边形DECF的四个顶点是否在同一个圆上，并说明你的理由；②EF最小值为；四边形CEDF的面积是；（请直接写出答案）③点C到线段EF的最大距离为；（请直接写出答案）（2）若点D、E、F分别在AC，BC，AB边上（如图2），连接DE，DF，EF，且∠EDF ＝90°，DE＝DF，求EF的最小值．9．已知，△ABC内接于⊙O，AD⊥BC于点G，连接AO．（1）如图1，求证：∠BAO＝∠CAD；（2）如图2，过点O作ON⊥BC于N，过点B作BH⊥AC于H，交AD于点E，交⊙O 于点F，求证：AE＝2ON；（3）如图3，在（2）的条件下，直线OE交AB于点P，交AC于点Q，若HC：EF＝：2，BP＝11，CQ＝2，求线段AD的长．10．（1）如图1，P是半径为5的⊙O上一点，直线l与⊙O交于A、B两点，AB＝8，则点P到直线l的距离的最大值为．问题探究：（2）如图2，在等腰△ABC中，BA＝BC，∠ABC＝45°，F是高AD和高BE的交点，求S△ABF：S△BFD的值．问题解决：（3）如图3，四边形ABCD是某区的一处景观示意图，AD∥BC，∠ABC＝60°，∠BCD ＝90°，AB＝60m，BC＝80m，M是AB上一点，且AM＝20m．按设计师要求，需在四边形区域内确定一个点N，修建花坛△AMN和草坪△BCN，且需DN＝25m．已知花坛的造价是每平米400元，草坪的造价是每平米200元，请帮设计师算算修好花坛和草坪预算最少需要多少元？11．如图，AB是⊙O的直径，P为AB上一点，弦CD与弦EF交于点P，PB平分∠DPF，连DF交AB于点G．（1）求证：CD＝EF；（2）若∠DPF＝60°，PE：PF＝1：3，AB＝2，求OG的长．12．已知⊙O是△ABC的外接圆，BC为⊙O的直径，弧AB上一点D满足DB＝DA，连结CD交AB于点E．（1）求∠AED+∠ABC的值．（2）求证：AC•BC＝CE•CD；（3）连接OE，若∠BOE＝∠BEO，求△BEO与△BED的面积比．13．【基础巩固】（1）如图1，点A，F，B在同一直线上，若∠A＝∠B＝∠EFC，求证：△AFE∼△BCF；【尝试应用】（2）如图2，AB是半圆⊙O的直径，弦长AC＝BC＝4，E，F分别是AC，AB上的一点，∠CFE＝45°，若设AE＝y，BF＝x，求出y与x的函数关系及y的最大值．【拓展提高】（3）已知D是等边△ABC边AB上的一点，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上．如图3，如果AD：BD＝1：2，求CE：CF的值．14．如图1，▱ABCD为⊙O的内接四边形，已知，以A为顶点作∠P AZ＝45°，交BC于P，交CD于Z．（1）求证：四边形ABCD为正方形；（2）若BC＝4BP，求DZ：CZ的值；（3）如图2，过P作PQ⊥AD于Q，过Z作ZX⊥AB于X，交PQ于Y．若，求四边形ZYPC的面积．15．如图1，在Rt△ABC中，∠C＝90°，AC＝16cm，AB＝20cm，动点D由点C向点A 以每秒1cm速度在边AC上运动，动点E由点C向点B以每秒cm速度在边BC上运动，若点D、点E从点C同时出发，运动t秒（t＞0），联结DE．（1）求证：△DCE∽△BCA；（2）如图2，设经过点D、C、E三点的圆为⊙P；①当⊙P与边AB相切时，求t的值；②在点D、点E运动过程中，若⊙P与边AB交于点F、G（点F在点G左侧，如图3），联结CP并延长交边AB于点M，连接PF，当△PFM与△CDE相似时，求CE的长．16．问题解决：（1）如图①，半圆O的直径AB＝6，点P是半圆O上的一个动点，则△P AB的面积最大值是．（2）如图②，在扇形OAB中，∠AOB＝90°，OA＝6，点C、D分别在OA和OB上，且AC＝2，D是OB的中点，点E在弧AB上．连接CE、DE，四边形CODE的面积是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．（3）如图③，四边形ABCD中，AB＝AD＝6，∠BAD＝60°，∠BCD＝120°，四边形ABCD的面积是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．17．给出定义：有两个内角分别是它们对角的两倍的四边形叫做倍对角四边形．（1）如图1，在倍对角四边形ABCD中，∠D＝2∠B，∠A＝2∠C，求∠B与∠C的度数之和；（2）如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO，∠OBA 的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．求证：四边形DBCF是倍对角四边形；（3）如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当4DH＝3BG时，求△BGH与△ABC的面积之比．18．【概念提出】圆心到弦的距离叫作该弦的弦心距．【数学理解】如图①，在⊙O中，AB是弦，OP⊥AB，垂足为P，则OP的长是弦AB的弦心距．（1）若⊙O的半径为5，OP的长为3，则AB的长为．（2）若⊙O的半径确定，下列关于AB的长随着OP的长的变化而变化的结论：①AB的长随着OP的长的增大而增大；②AB的长随着OP的长的增大而减小；③AB的长随着OP的长的确定而确定；④AB的长与OP的长无关．其中所有正确结论的序号是．【问题解决】如图②，已知线段EF，MN，点Q是⊙O内一定点．（3）用直尺和圆规过点Q作弦AB，满足AB＝EF；（保留作图痕迹，不写作法）（4）若弦AB，CD都过点Q，AB+CD＝MN，且AB⊥CD．设⊙O的半径为r，OQ的长为d，MN的长为l．①求AB，CD的长（用含r，d，l的代数式表示）；②写出作AB，CD的思路．19．阅读，然后解答问题：我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形．（1）根据“奇异三角形”的定义，请你证明：“三边分别为3，，5的三角形是奇异三角形；（2）在Rt△ABC中，AB＝c，AC＝b，BC＝1，且c＞b＞1，若Rt△ABC是奇异三角形，求b和c；（3）如图，AB是⊙的直径，C是⊙O上一点（不与点A、B重合），D是半圆的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE＝AD，CB＝CE．①求证：△ACE是奇异三角形；②当△ACE是直角三角形时，求∠AOC的度数．20．问题情境：如图1，P是⊙O外的一点，直线PO分别交⊙O于点A，B，则P A是点P 到⊙O上的点的最短距离．（1）探究证明：如图2，在⊙O上任取一点C（不与点A，B重合），连接PC，OC．求证：P A＜PC．（2）直接应用：如图3，在Rt△ABC中，∠ACB＝90°，AC＝BC＝3，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是．（3）构造运用：如图4，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A1MN，连接A1B，则A1B 长度的最小值为．（4）综合应用：如图5，平面直角坐标系中，分别以点A（﹣2，3），B（4，5）为圆心，以1，2为半径作⊙A，⊙B，M，N分别是⊙A，⊙B上的动点，P为x轴上的动点，直接写出PM+PN的最小值为．参考答案1．（1）如图1，证明：∵点D是半圆的中点，∴∠ACD＝∠ABD＝∠BCD＝∠DAB，∵DI＝DB．∴∠DIB＝∠DBI，∴∠DCB+∠CBI＝∠ABD+∠ABI，∴∠CBI＝∠ABI，∴点I是△ABC的内心；（2）如图2，作AE⊥CD于E，∵AB是⊙O的直径，∴∠ACB＝∠ADB＝90°，∴∠ACD＝∠ABD＝∠BCD＝∠DAB＝45°，在Rt△ABC中，BC＝6，AB＝10，∴AC＝8，在Rt△ACE中，AE＝CE＝AC＝4，在Rt△ADE中，AE＝4，BD＝AD＝＝5，∴DE＝3，∴CD＝CE+DE＝7，∵DI＝BI＝5，∴CI＝2，作IJ⊥BC于J，∴IJ＝CI＝2，∴S△BIC＝＝＝6；（3）如图3，∵DI＝BD＝5，∴I在以D为圆心，5为半径的圆上一段弧上运动，作⊙O的直径DC′与⊙D交于点I′，当C与C′重合，I与I′重合时，IC最大，C′I′＝10﹣5，∴0＜CI≤10﹣52．（1）证明：连接OD，∵DH为⊙O的切线，D为切点，∴OD⊥DH，∵DH⊥AC，∴∠ODH＝∠DHC＝90°，∴OD∥AC，∴∠ODB＝∠C，∵OB＝OD，∴∠OBD＝∠ODB，∴∠OBD＝∠C，∴AB＝AC；（2）解：①如图，连接AD、OD、EO，∵四边形EODA为菱形，∴AD＝OD＝AB＝2，∵AB为⊙O的直径，∴∠ADB＝90°，∴BD＝，故答案为：2；②∵∠EGA＝∠EAG，∴∠EAG＝∠OGD，∵AE∥OD，∴∠CED＝∠ODE，∠EAG＝∠AOD，∴∠OGD＝∠GOD，∴OD＝DG，∵∠B＝∠AED，∴∠ODE＝∠B，又∵∠OGD＝∠DGB，∴△OGD∽△DGB，设OG＝x，∴，∴，∵x＞0，∴x＝﹣1，∴OG＝﹣1，故答案为：﹣1．3．（1）证明：连接OD，∵AO＝OD，∴∠OAD＝∠ODA，∵AB＝BC，∴∠OAD＝∠C．∴OD∥BC，∵DF⊥BC，∴DF⊥OD，∵OD是⊙O的半径，∴直线DF是⊙O的切线；（2）解：∵AB是⊙O的直径，∴∠ADB＝90°，∵AB＝BC，∴AD＝DC＝6，∵四边形ADEB是⊙O的内接四边形，∴∠ADE+∠ABE＝180°，∵∠ADE+∠CDE＝180°，∴∠CDE＝∠ABC，∵∠C＝∠C，∴△CDE∽△CBA，∴＝，∴；（3）如图，过点Q作QG⊥AB于点G，∵sin∠ABD＝，∴QG＝BQ，∴PQ+BQ＝PQ+QG，∴当P，Q，G三点共线时，PQ+BQ有最小值为PG，∵的弧长为π，∴，∴∠POB＝60°，∴PG＝OP•sin60°＝，∴PQ+BQ的最小值为．4．解：（1）如图1，作DE⊥AC于E，作DF⊥AB于F，∵AD平分∠BAC，∴DE＝DF，由S△ABC＝S△ABD+S△ACD得，AB•AC＝，∴4×3＝4•DE+3DE，∴DE＝，故答案是；（2）如图2，作CE⊥BD于E，作AF⊥BD于F，∵AC是直径，∴∠ABC＝90°，∵BD平分∠ABC，∴∠DBC＝∠ABD＝，∴＝，∠ECB＝90°﹣∠DBC＝45°＝∠DBC，∴AD＝CD，BE＝CE，∵点B是半圆AC的三等分点（弧AB＜弧BC），∴的度数是60°，的度数是120°，∴∠ADB＝30°，∠BDC＝60°，∴∠ADB＝∠DCE＝30°，∴△ADF≌△DCE（AAS），∴AF＝DE，∴AF+CE＝DE+BE＝8，∴S四边形ABCD＝S△ABD＝＝＝＝＝32；（3）如图3连接AC，延长CD至E，使DE＝AD，连接AE，∵AB＝AD，∴＝，∴∠ACB＝∠ACE，∵四边形ABCD内接于⊙O，∴∠ADE＝∠ABC＝60°，∴△ADE是等边三角形，∴∠E＝60°，∴∠B＝∠E，又∵AC＝AC，∴△ABC≌△AEC（AAS），∴BC＝CE，∵CE＝DE+CD＝AD+CD＝2，∴BC＝2．∵⊙O的半径是1，∴BC是⊙O的直径，∴∠BAC＝90°，∴AB＝BC•cos60°＝1．5．（1）证明：延长BO交⊙O于G，连接AG，如图：∵＝，∴∠G＝∠C，∵∠ABO＝∠DAC，∴∠G+∠ABO＝∠C+∠DAC，∵BG为⊙O直径，∴∠BAG＝90°，∴∠G+∠ABO＝∠C+∠DAC＝90°，∴∠ADC＝90°，∴AE⊥BC；（2）证明：设BF交AC于N，延长BO交⊙O于G，连接CG，BE，如图：∵BG为⊙O直径，∴∠BCG＝90°，∴∠G+∠OBC＝90°，∵∠G＝∠BFC，∠OBC＝∠ACF，∴∠BFC+∠ACF＝90°，∴∠CNF＝90°，∴∠NBC+∠NCB＝90°，由（1）知：AE⊥BC有∠DAC+∠NCB＝90°，∴∠NBC＝∠DAC，∵＝，∴∠DAC＝∠DBE，∴∠NBC＝∠DBE，又∠BDM＝∠BDE＝90°，BD＝BD，∴△BDM≌△BDE（ASA），∴MD＝ED；（3）解：连接AF、BE，如图：∵＝，∴∠BFC＝∠BAC，∵∠BFC＝3∠EAC，∴∠BAC＝3∠EAC，∴∠BAE＝2∠EAC，由（2）知∠EAC＝∠DBE＝∠DBM，BE＝BM＝，∴∠EBM＝2∠EAC，∴∠EBM＝∠BAE，又∠BEM＝∠AEB，∴△BEM∽△AEB，∴＝＝，∵AM＝3，∴＝＝，解得：EM＝2，AB＝5，在Rt△AMN中，MN2+AN2＝AM2＝9（Ⅰ），在Rt△ABN中，（+MN）2+AN2＝AB2＝25（Ⅱ），由（Ⅰ）、（Ⅱ）可得：MN＝，AN＝，∵∠AMF＝∠BME，∠AFM＝∠BEM，∴△BEM∽△AFM，∴＝，即＝，∴MF＝，∴NF＝MF﹣MN＝，∵cos∠BAC＝cos∠BFC，∴＝，即＝，∴CF＝．6．（1）如图1，证明：连接OA，OC，∴OB＝OC，又AB＝AC，OA＝OA，∴△AOB≌△AOC（SSS），∴∠OAC＝∠OAB，∴∠BAC＝2∠OAB，∵OA＝OB，∴∠ABD＝∠OAB，∴∠BAC＝2∠ABD；（2）如图2，证明：连接AG，OG，延长AO交BG于M，交BC于P，交⊙O于N，由（1）知，∠BAO＝∠CAO，∴＝，∵AB＝AC，∴AP⊥BC，∵BH⊥AC，∠AMH＝∠BMP，∴∠CBG＝∠CAO，∵＝，∴∠CAG＝∠CBG，∴∠CAG＝∠CAO，∴AM＝AG，＝，∴GM＝2GH，∠BON＝∠COG，∵OB＝OG，∴∠OBG＝∠OGB，∴△BOM≌△GOF（ASA），∴BM＝GF，∴BM+MF＝GF+MF，即BF＝MG＝2GH；（3）如图3，解：设∠ABD＝α，由（1）（2）知，∠BAC＝2∠ABD＝2α，∠CAG＝，连接AG，作DT⊥AB于T，截取TK＝AT，∴AD＝DK＝2，∴∠DKA＝∠DAK＝2α，∵∠BDK＝∠AKD﹣∠ABD＝2α﹣α＝α，∴BK＝DK＝2，∴AK＝AB﹣BK＝3，∴AT＝KT＝＝，∴DT＝＝＝，∴cos2α＝＝＝，tanα＝＝，在Rt△ABH中，AH＝AB•cos2α＝5×＝，在Rt△AHG中，GH＝AH•tanα＝＝，∴BF＝2GH＝．7．解：（1）证明：∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∴＝，∴∠ADB＝∠CDB；（2）证明：如图，作∠BCF的角平分线，交BD于点G，设∠ACD＝α，∵＝，∴∠ABD＝∠ACD＝α，∵∠BCF＝2∠ABD，∴∠FCG＝∠BCG＝∠ACD＝α，∵△ABC是等边三角形，∴BC＝AC，∵＝，∴∠DAC＝∠DBC，在△ADC与△BGC中，，∴△ADC≌△BGC（SAS），∴BG＝AD，DC＝GC，∵＝，∴∠BDC＝∠BAC＝60°，∴△DGC是等边三角形，∴∠FGC＝∠EDC＝60°，在△CED与△CFG中，，∴△CED≌△CFG（ASA），∴ED＝FG，∴BF＝BG+GF＝AD+DE，即BF＝DE+AD；（3）解：设∠ACD＝α，则∠CAT＝3∠ACD＝3α，如图，延长CF交⊙O点P，交AM于N点，连接P A，过M点作MQ∥AP，交AR于Q 点，连接PM，∵CM是∠BCF的平分线，由（2）得∠FCG＝∠BCG＝∠ACD＝α，∴∠ACP＝∠ACB﹣∠BCF＝60°﹣2α，∠BAT＝∠BAC﹣∠CAT＝60°﹣3α，∵＝，＝，∴∠MAB＝∠BCG＝α，∠MAP＝∠FCG＝α，∴∠MAC＝∠BAC+∠BAM＝60°+α，∴∠MAT＝∠MAC﹣∠CAT＝60°+α﹣3α＝60°﹣2α，∠P AT＝∠MAT+∠MAP＝60°﹣2α+α＝60°﹣α，∵＝，∴∠AMP＝∠ACP＝60°﹣2α，∴∠AMP＝∠MAT＝60°﹣2α，∴MP∥AR，∴∠AMQ＝∠MAP＝α，∠MQT＝∠P AR＝60°﹣α，∵＝，∴∠AMC＝∠ABC＝60°，∴∠QMR＝∠AMC﹣∠AMQ＝60°﹣α，∴∠QMR＝∠MQR＝60°﹣α，∴QR＝MR＝5，∵设MP＝AQ＝m，则QT＝QR﹣TR＝5﹣1＝4，∴AT＝QT+AQ＝4+m，∵＝，∴∠MPC＝∠MAC＝60°+α，又∵∠MNP＝∠ANT＝∠APC+∠P AM＝60°+α，∠ATN＝∠ACP+∠CAT＝60°﹣2α+3α＝60°+α，∴∠MNP＝∠MPC＝∠ANT＝∠ATN＝60°+α，∴MP＝MN，AN＝AT，∴AM＝MN+AN＝MP+AT＝m+4+m＝4+2m，在△AMR中，∠AMR＝60°，AM＝4+2m，MR＝5，AR＝5+m，如图，过R点作AM边的高HR，∴∠MRH＝30°，∴MH＝MR＝，HR＝＝MR＝，∴AH＝AM﹣MH＝+2m，在Rt△AHR中，HR2+AH2＝AR2，∴（）2+（+2m）2＝（5+m）2，解得：m＝2或﹣（舍去），∴AT＝4+m＝6．8．解：（1）①取EF中点P，连接CP，DP，∵点P为EF中点，∴PE＝PF＝EF．∵∠ACB＝∠EDF＝90°，∴CP＝DP＝AC，∴PE＝PF＝PC＝PD，∴点E、D、F、C在以P为圆心，EF为半径的同一个圆上；②当DE⊥AC时，DE的长度最小，此时EF最短，∵∠A＝45°，AD＝，∴DE＝1，∵DE＝DF，∴EF＝＝；∵D是AB的中点，∴AD＝BD＝CD＝，CD⊥AB，∠BCD＝45°，∵DE⊥DF，∴∠EDF＝90°，∴∠ADE＝∠CDF，在△ADE和△CDF中，，∴△ADE≌△CDF（ASA），∴S△ADE＝S△CDF，∴S四边形DECF＝S△DEC+S△DCF＝S△DEC+S△ADE＝S△ADC＝××＝1；故答案为；1．③由②可知当EF取最小值时，点C到线段EF的最大距离为EF＝．故答案为．（2）过点F分别作FG⊥CA于点G，设DC＝a，CE＝b，∵∠CDE+∠GDF＝∠GDF+∠DFG＝90°，∴∠CDE＝∠DFG，∵∠C＝∠DGF，DE＝DF，∴△DCE≌△FGD（AAS），∴FG＝DC＝a，GD＝CE＝b，则2a+b＝2，a2+b2＝DF2，∴DF2＝a2+（2﹣2a）2，＝5a2_8a+4＝5，当a＝时，DF2最小，此时EF2最小，∴EF的最小值为．9．（1）证：如图1，作直径AE，连接BE，∴∠ABE＝90°，∴∠BAO＝90°﹣∠E，∵＝，∴∠E＝∠C，∴∠BAO＝90°﹣∠C，∵AD⊥BC，∴∠AGC＝90°，∴∠CAD＝90°﹣∠C，∴∠BAO＝∠CAD；（2）证：如图2，∵ON⊥BC，∴BC＝2CN，作直径CM，连接BM，AM，∴MB⊥BC，∵ON⊥BC，∴ON∥BM，∴△CON∽△CMB，∴＝＝2，∴BM＝2ON，∵＝，∴∠BAM＝∠BCM，∴∠BAM＝∠BCM＝90°﹣∠BMC，∵＝，∴∠BMC＝∠BAC，∴∠BAM＝90°﹣∠BAC，∵∠AHB＝90°，∴∠ABH＝90°﹣∠BAC，∴∠BAM＝∠ABH，∴BE∥AM，∴四边形AMBE是平行四边形，∴AE＝BM，∴AE＝2ON；（3）解：如图3，连接AF，CF，连接CE并延长交AB于I，连接OB、OC和BD，作OJ⊥AB于J，∵AG⊥BC，BH⊥AC，∴CI⊥AB，又∵∠AEH＝∠BEG，∴∠GBE＝∠EAH，∵＝，∴∠F AC＝∠GBE，∴∠F AC＝∠EAH，∵∠AHF＝∠AHE＝90°，AH＝AH，∴△AHE≌△AHF（ASA），∴EH＝FH，∴FH＝，同理可得：EG＝DG＝，∴tan∠BFC＝＝＝，∴∠BFC＝60°，∵＝，∴∠BAC＝∠BFC＝60°，∴∠BOC＝2∠BAC＝120°，∵OB＝OC，ON⊥BC，∴∠BON＝＝60°，∴OA＝OB＝2ON，∵AE＝2ON，∴AO＝AE，∴∠AOE＝∠AEO，∴∠AOP＝∠AEQ，∵∠BAO＝∠CAD，∵△AOP≌△AEQ（ASA），∴AP＝AQ，∴△APQ是等边三角形，∴∠APQ＝60°，∵∠AEH＝90°﹣∠BAC＝30°，∴∠AEH＝∠ABH＝30°，∴PE＝PB＝11，设AP＝AQ＝PQ＝x∴OP＝EQ＝PQ﹣PE＝x﹣11，AC＝AQ+CQ＝x+2，在Rt△AIC中，∠BAC＝60°，AC＝x+2，∴AI＝AC＝（x+2），CI＝（x+2），∴BI＝AB﹣AI＝（x+11）﹣（x+2）＝+10，在Rt△BIC中，BC2＝BI2+CI2，＝（）2+[（x+2）]2，在Rt△POJ中，∠APH＝60°，OP＝x﹣11，∴PJ＝（x﹣11），OJ＝（x﹣11），∴AJ＝AP﹣PJ＝x﹣（x﹣11）＝，在Rt△AOJ中，OA2＝OJ2+AJ2＝[（x﹣11）]2+（）2，∴OB2＝[（x﹣11）]2+（）2，∵BN＝OB，∴BC＝2BN＝OB，∴BC2＝3OB2＝3•[（x﹣11）]2+（）2，∴3•[（x﹣11）]2+（）2＝（）2+[（x+2）]2，化简，得，x2﹣23x+130＝0，∴x1＝13，x2＝10（舍去），∴AB＝x+11＝24，AC＝x+2＝15，∴BH＝AB＝12，AH＝12，∴CH＝AC﹣AH＝3，∴BC＝＝21，∵∠CAD＝∠CBH，∠AGC＝∠BHC＝90°，∴△ACG∽△BCH，△BGE∽△AGC，∴＝＝，＝∴＝＝＝，∴AG＝，CG＝，∴BG＝BC﹣CG，＝21﹣＝，∴＝，∴DG＝EG＝，∴AD＝AG+DG＝+＝．10．解：（1）点P到直线l距离的最大值，即过圆心O向直线l作垂线交圆O于点P，连接OA，∵AB＝8，OC⊥AB，∴AC＝4，由勾股定理得：OC＝3，∴PC＝8，故答案为：8；（2）过点F作FG⊥AB，∵∠ABC＝45°，AD⊥BC，∴△ABD为等腰直角三角形，∴AB＝BD，又∵△ABC为等腰三角形，且AB＝BC，BE⊥AC，∴BE平分∠ABC，又∵FD⊥BC，FG⊥AB，∴FG＝FD，∴S△ABF＝×AB×FG，S△BDF＝×BD×DF，∴；（3）连接MC，过点A作AP⊥BC于点P，∵∠ABC＝60°，AB＝60，∴BP＝30，AP＝30，∴CD＝30，设总费用为W元，∴W＝400S△AMN+200S△BNC，∴W＝200（2S△AMN+S△BNC），∴当2S△AMN+S△BNC最小时，总费用最小，又∵AM＝20米，BM＝40米，∴2S△AMN＝S△BMN，∴当S△BMN+S△BNC最小时，费用最小，即S四边形BMNC最小时，费用最小，又∵S四边形BMNC＝S△BMC+S△CMN，过点M作MH⊥BC，垂足为H，∵∠ABC＝60°，BM＝40米，∴BH＝20米，MH＝20米，MC＝40米，∴∠BCM＝30°，∴∠DCM＝60°，∴S△BMC＝＝800（平方米），∴当S△CMN最小时，费用最小，∴S△CMN＝×NQ＝20NQ，∴当NQ最小时，费用最小，∵ND＝25米，∴N点在以D为圆心，25为半径的圆上运动，过圆心D向MC作垂线交⊙D于N点，交MC于Q，即此时NQ最小，∵CQ＝15米，DQ＝45米，∴NQ＝45﹣25＝20（米），∴S△MNC最小值＝×20＝400（平方米），∴S四边形BMNC最小值＝1200（平方米）∴W最小值＝200×1200＝240000（元），11．（1）证明：如图，过点O作OM⊥EF于点M，ON⊥CD于点N，连接OF、OD，则∠OMF＝∠OND＝90°，∵PB平分∠DPF，OM⊥EF，ON⊥CD，∴OM＝ON，在Rt△OFM和Rt△ODN中，，∴Rt△OFM≌Rt△ODN（HL），∴FM＝DN，∵OM⊥EF，ON⊥CD，∴EF＝2FM，CD＝2DN，∴CD＝EF；（2）∵PE：PF＝1：3，∴设PE＝x，PF＝3x，则EF＝PE+PF＝4x，∵OM⊥EF，∴EM＝FM＝EF＝2x，∴PM＝EM﹣PE＝2x﹣x＝x，∵PB平分∠DPF，∠DPF＝60°，∴∠FPB＝DPB＝DPF＝30°，∴OM＝x，OP＝x，在Rt△OPM和Rt△OPN中，，∴Rt△OPM≌Rt△OPN（HL），∴PM＝PN，由（1）知：FM＝DN，∴PM+FM＝PN+DN，∴PF＝PD，∵∠DPF＝60°，∴△PDF是等边三角形，∵PB平分∠DPF，∴PB⊥DF，垂足为G，∴DF＝PF＝3x，FG＝DF＝，∴PG＝＝＝，∴OG＝PG﹣OP＝﹣x＝，∵AB＝2，∴OF＝AB＝，在Rt△OFG中，根据勾股定理，得OG2+FG2＝OF2，∴（）2+（）2＝（）2，整理，得x2＝3，解得x＝±（负值舍去），∴x＝，∴OG＝＝＝．12．（1）解：∵BC是直径，∴∠CAB＝90°，∴∠ACB+∠ABC＝90°，∴∠ACB+∠ABC＝45°，∵BD＝AD，∴＝，∴∠ACD＝∠BCD，∵∠AED＝∠ACD+∠CAE，∴∠AED+∠ABC＝90°+∠ACB+∠ABC＝135°；（2）证明：∵＝，∴∠ACD＝∠BCE，∵∠CBE＝∠ADC，∴△CBE∽△CDA，∴＝，∴AC•BC＝CE•CD；（3）解：如图，过点B作BT⊥OE交CD于点T，连接OT．∵BO＝BE，∴BO垂直平分线段OE，TB平分∠ABC，∴TO＝TE，∴TB平分∠OTE，∵CE平分∠ACB，∴∠BTD＝∠TCB+∠TBC＝（∠ACB+∠ABC）＝45°，∴∠OTE＝90°，∴OT⊥CD，∴CT＝TD，∵BC是直径，∴∠BDT＝90°，∴∠BTD＝∠DBT＝45°，∴BD＝DT＝CT，∵CO＝OB，CT＝TD，∴BD＝2OT，∴DT＝CT＝2ET，∴CE＝3DE，∴S△BEC＝3S△ADE，∵BO＝OC，∴S△BEC＝2S△BEO，∴2S△BEO＝3S△DEB，∴＝．13．（1）证明：∵∠A＝∠EFC，∴∠E+∠EF A＝∠EF A+∠CFB，∴∠E＝∠CFB，∵∠A＝∠B，∴△AFE∽△BCF；（2）解：∵AB是⊙O的直径，∴∠ACB＝90°，∴AB＝＝8，∵AC＝BC，∴∠A＝∠B＝45°，∴∠A＝∠B＝∠CFE＝45°，由（1）可得△AFE∽△BCF，∴，即，∴y＝﹣x2+x（0≤x≤8），∴当x＝4时，y最大＝2；（3）解：连接DE，DF，∵△EFC与△EFD关于EF对称，∴∠EDF＝∠ECF＝60°，EC＝ED，FC＝FD，∵∠BDF+∠EDF＝∠BDE＝∠A+∠DEA，∵∠EDF＝∠A＝60°，∴∠BDF＝∠DEA，∴△ADE∽△BFD，设AD＝x，CE＝DE＝a，CF＝DF＝b，∵AD：BD＝1：2，∴DB＝2x，∴AB＝3x＝AC＝BC，∴AE＝3x﹣a，BF＝3x﹣b，∵△ADE∽△BFD，∴，∴，由前两项得，2ax＝b（3x﹣a），由后两项得，（3x﹣a）（3x﹣b）＝2x2，即：3x（3x﹣a）﹣b（3x﹣a）＝2x2，∴3x（3x﹣a）﹣2ax＝2x2，∴a＝x，∴，∴CE：CF＝4：5．14．（1）∵四边形ABCD为平行四边形，∴∠B＝∠D．又∵∠B+∠D＝180°，∴∠B＝∠D＝90°．∴四边形ABCD为矩形，∵，∴AB＝AD．∴四边形ABCD为正方形．（2）延长CD至点Q，使得DQ＝BP，连接AQ，如图，∵四边形ABCD为正方形，∴∠ABP＝∠ADQ＝90°．在△ABP和△ADQ中，，∴△ABP≌△ADQ（SAS），∴AP＝AQ，∠BAP＝∠DAQ．∵∠BAD＝90°，∴∠DAP+∠BAD＝90°．∴∠DAP+∠QAD＝90°．∴∠QAP＝90°．∵∠P AZ＝45°，∴∠P AZ＝∠QAZ＝45°．在△APZ和△AQZ中，，∴△APZ≌△AQZ（SAS）．∴PZ＝QZ．设AB＝4a，DZ＝t，则BP＝a，ZC＝4a﹣t，ZP＝t+a，在Rt△CPZ中，∵ZC2+CP2＝ZP2，∴（4a﹣t）2+（3a）2＝（t+a）2．解得：t＝．∴DZ＝a，CZ＝a，∴DZ：CZ＝3：2．（3）∵四边形ABCD为正方形，PQ⊥AD，ZX⊥AB，∴四边形AXYQ，AXZD，XBPY，XBCZ均为矩形．设AB＝a，AX＝m，AQ＝n，则mn＝．由（2）可知，PZ＝DZ+BP＝m+n，CZ＝XB＝a﹣m，CP＝DQ＝a﹣n．在Rt△CPZ中，∵ZC2+PC2＝PZ2，∴（a﹣m）2+（a﹣n）2＝（m+n）2．化简得：a2﹣（m+n）a＝mn．∴S四边形ZYPC＝（a﹣m）（a﹣n）＝a2﹣（m+n）a+mn＝2mn＝2×＝5．15．（1）证明：∵∠C＝90°，AC＝16，AB＝20，∴BC＝＝12，∴＝，∵＝＝，∴＝，∵∠C＝∠C，∴△DCE∽△BCA；（2）解：①如图1，作PG⊥AC于G，PF⊥BC于F，作PH⊥AB于H，设CD＝3a，CE＝4a，DE＝5a，由题意得，PH＝PC＝DE＝，PF＝CG＝CD＝a，FG＝2a，∵S△ABC＝S△APB+S△PBC+S△P AC，∴BC•AC＝AB•PH++，∴12×16＝20×a+12×a+16×2a，∴a＝，∴t＝3a＝；②如图2，设CD＝3a，CE＝4a，DE＝5a，∴PF＝DE＝a，由（1）知，△DCE∽△BCA，当△PMF∽△DCE时，∴△PMF∽△BCA，＝＝，∴PM＝a，FM＝2a，由S△ABC＝得20•CM＝12×16，∴CM＝，∵CP+PM＝CM，∴a+a＝，∴4a＝，即CE＝，当△PMF∽△ECD时，类比上可得，a+2a＝，∴4a＝，∴CE＝，综上所述：CE＝或．16．解：（1）点P运动至半圆O的中点时，如图1：此时底边AB上的高最大，即P'O＝r＝3，△P AB的面积最大值，∴S△P'AB＝×3×6＝9，故答案为：9；（2）四边形CODE的面积存在最大值，作OG⊥CD，垂足为G，延长OG交弧AB于点E′，则此时△CDE'的面积最大，如图2：∵OA＝OB＝6，AC＝2，点D为OB的中点，∴OC＝4，OD＝3，在Rt△COD中，CD＝5，OG＝2.4，∴GE′＝6﹣2.4＝3.6，∴四边形CODE'面积为S△CDO+S△CDE′＝×3×4+×5×3.6＝15，∴四边形CODE的面积的最大值为15；（3）四边形ABCD的面积存在最大值，连接BD，作△ABD的外接圆O，过A作AE⊥BD于E，如图3：∵∠DAB＝60°，∠DCB＝120°，∴∠DAB+∠DCB＝180°，∴A、B、C、D四点共圆，即C在⊙O上，∵AD＝AB，∠DAB＝60°，∴△ADB是等边三角形，有BD＝AB＝AD＝6，在Rt△ABE中，BE＝AB＝3，AE＝BE＝3，∴S△ABD＝BD•AE＝×6×3＝9，当C为中点，即A、E、C共线时，△BDC的面积最大，此时∠ACB＝∠ADB＝60°，AC为⊙O直径，∴∠CAB＝30°，∴AC＝＝4，∴CE＝AC﹣AE＝，∴S△BDC＝BD•CE＝×6×＝3，∴S四边形ABCD＝S△ABD+S△BDC＝12，即四边形ABCD的面积的最大值是12．17．（1）解：在倍对角四边形ABCD中，∠D＝2∠B，∠A＝2∠C，∵∠A+∠B+∠C+∠D＝360°，∴3∠B+∠3∠C＝360°，∴∠B+∠C＝120°，∴∠B与∠C的度数之和为120°；（2）证明：在△BED与△BEO中，，∴△BED≌△BEO（SAS），∴∠BDE＝∠BEO，∵∠BOE＝2∠BCF，∴∠BDE＝2∠BCF连接OC，设∠EAF＝α，则∠AFE＝2α，∴∠EFC＝180°﹣∠AFE＝180°﹣2α，∵OA＝OC，∴∠OAC＝∠OCA＝α，∴∠AOC＝180°﹣∠OAC﹣∠OCA＝180°﹣2α，∴∠EFC＝∠AOC＝2∠ABC，∴四边形DBCF是倍对角四边形；（3）解：过点O作OM⊥BC于M，∵四边形DBCF是倍对角四边形，∴∠ABC+∠ACB＝120°，∴∠BAC＝60°，∴∠BOC＝2∠BAC＝120°，∵OB＝OC，∴∠OBC＝∠OCB＝30°，∴BC＝2BM＝BO＝BD，∵DG⊥OB，∴∠HGB＝∠BAC＝60°，∵∠DBG＝∠CBA，∴△DBG∽△CBA，∴＝＝，∵4DH＝3BG，BG＝2HG，∴DG＝，∴＝＝，∴＝．18．解：（1）连接OA，∵OP⊥AB，∴AP＝，∵OA＝5，OP＝3，∴AP＝＝4，∴AB＝2AP＝8，故答案为：8；（2）设半径为r不变，∴AB＝2AP＝2，当r不变，OP的长增大时，AB减小；OP长确定时，AB也确定，故选：②③；（3）如图，利用△MPF和△OP'B全等，首先作EF的垂直平分线，再取FM＝r，然后以点O为圆心，MP为半径画圆，再以OQ为直径画圆，两圆交点为P'，从而画出线段AB，如图，线段AB即为所求；（4）①解：设AB＝2m，CD＝2n，如图，可得：，解得：，∴AB＝，CD＝，②作图思路：先作斜边为4r，一条直角边为2，另一条直角边为的直角三角形；再作斜边为，一条直角边为l，另一条直角边为的直角三角形；再在⊙O中作出长为的弦，再如（3）中作法，过点Q作弦AB；最后过点Q作AB的垂直弦CD．19．（1）证明：在△ABC中，三边长分别是3，和5，∵32+52＝2（）2，。

六年级数学上册-圆的认识-提升练习含答案3套全一、我会填。

1、圆中心的一点叫( )，通常用字母( )表示，它决定了圆的( )。

2、通过( )，并且两端都在圆上的( )，叫作圆的直径，用字母( )表示。

直径是圆内两端都在圆上的所有线段中( )的一条。

3、从( )到圆上( )一点的线段叫作圆的半径，用字母( )表示，它决定了圆的( )。

4、时钟的分针转动一周形成的图形是( )，分针的长度是这个图形的( )。

5、在同圆或等圆内，( )的长度是( )长度的2倍，我们字母表示( )。

6、( )决定圆的大小，( )决定圆的位置。

7、画圆时，圆规两脚之间的距离为4厘米，那么这个圆的直径是（）厘米。

8、在一个边长为4分米的正方形里，画一个最大的圆，这个圆的直径为( )分米，半径为( )分米。

二、我会辩一辩。

1、圆的直径都相等。

( )2、同一个圆上所有的点到圆心的距离都相等。

( )3、直径一定比半径长。

( )4、半径是射线，直径是直线。

( )5、画圆时，圆规两脚间的距离就是圆的直径。

( )6、直径总比半径长。

（）7、通过圆心的线段，叫做直径。

（）三、我会选。

(每题2分，共10分)1、一个圆有( )条直径。

A、1B、2C、无数2、在一个边长是5㎝的正方形内，画一个最大的圆。

它的半径是( )。

A、5㎝B、10㎝C、任意长D、2.5㎝3、圆的直径是半径的( )。

A、2倍B、C、1.2倍4、直径和半径都是( )。

A、射线B、直线C、线段5、画圆时，圆规两脚分开4㎝，所画的圆的直径是( )㎝。

A、2.5B、4C、8四、我会算。

五、我会画。

(每题5分，共20分)1、半径是2㎝的圆。

2、直径是3㎝的圆。

参考答案答案：一、1. 圆心，O，位置2.圆心，线段，d,最长3.圆心，任意，r，大小4. 圆，半径1.直径，半径，d=2r 6.半径，圆心7. 8cm 8. 4，2二、×√×××××三、C D A C C四、4 ，0.6,4.5,14,2.4,3一、填空题。

专题能力提升训练(十一)非选择题(本题共6小题)1．(2022·临汾模拟)总订单数已经超过1 000架的国产大飞机C919预定在今年交付，其制造使用了较多含硼材料(如硼纤维、氮化硼等)，多项技术打破了外国垄断。

(1)原子的能量由核电荷数、电子数、 电子(运动)状态 三个因素共同决定；基态B 原子的核外电子填充在 3 个轨道中。

(2)耐高温材料立方BN 制备流程中用到NH 3、BCl 3和触媒剂Ca 3B 2N 4。

①Ca、B 、N 三种元素电负性从大到小的顺序为 N>B>Ca 。

②BCl 3中B 原子的 sp 2杂化 轨道与Cl 原子的 3p 轨道形成σ键；形成BCl 3过程中基态B 原子价电子层电子先激发，再杂化，激发后B 原子的价电子排布图为 。

③BCl 3在四氯化碳中的溶解度远大于NH 3，原因是 BCl 3和四氯化碳均为非极性分子，而氨气属于极性分子，相似相溶 。

(3)硼砂是非常重要的含硼矿物。

一种硼砂阴离子的结构如图1所示，则1 mol 该阴离子存在的配位键物质的量为 2 mol ，n ＝ 2 。

(4)制造硼合金的原料硼化钙(CaB 6)晶胞结构如图2所示，硼原子全部组成B 6正八面体，各个顶点通过B —B 键互相连接成三维骨架。

已知该晶体晶胞参数为a pm ，B 6八面体中B —B 键的键长为d pm ，M 点原子的坐标参数为⎝ ⎛⎭⎪⎫12，12，12，则N 点原子的坐标参数为⎝ ⎛⎭⎪⎫ 2d 2a ，1，0。

【解析】 (1)整个原子的能量由核电荷数、电子数和电子(运动)状态三个因素共同决定；基态B 原子的电子排布式为1s 22s 22p 1，故其核外电子填充在1s ，2s ，2p 三个轨道中；(2)①金属的电负性较小，另外，同周期元素电负性从左向右在增大，故Ca 、B 、N 三种元素电负性从大到小的顺序为N>B>Ca ；②BCl 3中B原子的价层电子对数为3，其杂化方式为sp2，故BCl3中B原子的sp2杂化轨道与Cl原子的3p轨道形成σ键；基态B原子价电子层上的电子先进行激发，再进行杂化，说明B原子激发后的三个轨道能量相同，故激发时B原子的价电子排布图为：③极性相似的物质溶解度较大，BCl3和四氯化碳为非极性分子，氨气为极性分子，故原因是：BCl3和四氯化碳均为非极性分子，而氨气属于极性分子，相似相溶；(3)由图1可知，图中形成4个键的B原子含有配位键，故1 mol该阴离子存在的配位键物质的量为2 mol，在该阴离子中B显＋3价，O显－2价，H显＋1价，根据化合价的关系可知，n ＝2；(4)将8个正八面体的中心连接呈晶胞的立方晶系图，由M点坐标知该原子位于晶胞的中心，且每个坐标系的单位长度都记为1，已知B6八面体中B—B键的键长为d pm，晶胞参数为a pm，则八面体中心到顶点的距离为22d，则N点在棱的2d2a处，其坐标为⎝⎛⎭⎪⎫2d2a，1，0。