当前位置：文档之家 › 碳纤维布加固混凝土梁截面刚度计算

碳纤维布加固混凝土梁截面刚度计算

  • 格式：doc
  • 大小：200.50 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

碳纤维布梁加固计算书

碳纤维布梁加固计算书

碳纤维梁加固计算书一、基本资料1．设计依据:《碳纤维片材加固混凝土结构技术规程》（CECS 146:2003）（以下简称规程）《混凝土结构设计规范》（GB50010—2002）（以下简称规范）《混凝土结构加固技术规范》（GB 50367-2006）（以下简称加固规范）图纸所提供的相关数据2．问题类型:因荷载增加原有混凝土梁承载力不足，需进行加固处理，加固方式采用碳纤维布。

3．梁底受拉碳纤维片材参数:碳纤维布等级：Ⅰ级弹性模量E cf = 2.30 × 105 MPa (见加固规范表9.1.6-1)抗拉强度设计值f f = 2300.00 MPa (见加固规范表9.1.6-1)单层厚度t cfv = 0.167 mm重量：300g/m2不考虑二次受力二、计算结果1. KL3梁荷载增加后缺筋面积为750mm2，采用等强代换原则换算碳纤维布粘贴尺寸：HRB400钢筋抗拉强度设计值：360N/mm2碳纤维布抗拉强度设计值：2300 N/mm2缺筋面积*钢筋抗拉强度设计值≤碳纤维布厚度*宽度*碳纤维布抗拉强度设计值750*360≤0.167*宽度*2300宽度≥702.94KL3梁截面尺寸为400*900，结构梁宽度为400不能满足碳纤维布粘贴宽度，考虑粘贴双层碳纤维布，计算碳纤维布多层粘贴折减系数：（见加固规范9.2.4-2）折减系数=1.16-(粘贴层数*弹性模量设计值*单层厚度)/308000≤0.9=1.16-(2*230000*0.167)/308000=0.91折减系数=0.9750*360≤0.167*宽度*2300*0.9宽度≥781.05KL3梁宽度为400mm，碳纤维布粘贴双层面积：2*400=800≥781.05，满足强度要求。

碳纤维加固计算,典型框架梁计算书

碳纤维加固计算,典型框架梁计算书

碳纤维矩形受弯构件正截面加固计算一、工程信息工程名称: 浙江长征化工有限公司构件编号: 2/B-D,3/B-D梁设计人: 上海杰固建筑科技有限公司校对人:审定人: 负责人:日期: 2011年11月9日加固原因: 梁混凝土严重碳化腐蚀，梁钢筋锈蚀严重，需恢复原结构承载力，消除结构病害。

二、依据规范《混凝土结构设计规范》(GB50010－2002)①《混凝土结构加固设计规范》(GB50367－2006)②三、示意图四、计算信息1. 原构件信息截面宽度: b＝300mm截面高度: h＝900mm混凝土等级: C20受拉钢筋等级: HPB235受压钢筋等级: HPB235受拉钢筋面积: A so＝2946mm2受压钢筋面积: A so'＝226mm2受拉钢筋合力点到边缘距离a＝35mm受压钢筋合力点到边缘距离a'＝35mm受拉钢筋排数1排2. 加固信息纤维名称: 织物二级结构等级: 重要构件纤维厚度: t f＝0.167mm纤维层数: n f＝3层板材类型: 现场粘贴板梁两侧粘贴纤维高度: h c ＝9003. 荷载信息是否考虑二次受力: 计算初始弯矩: M ok ＝50kN.m设计弯矩值: M ＝500kN.m五、计算系数1. 受拉钢筋抗拉强度 f yo ＝210N/mm 2受压钢筋抗拉强度 f yo '＝210N/mm 2受拉钢筋弹性模量 E s ＝210000N/mm 22. 混凝土抗压强度 f co ＝9.60N/mm 2混凝土计算系数 α1＝1.03. 碳纤维复合材设计计算指标纤维抗拉强度设计值 f f ＝1600M pa纤维弹性模量 E f ＝230000M pa纤维抗拉应变设计值 εf ＝0.007M pa4. 混凝土净高 h o ＝865mm六、计算1. 原受弯构件加固前相对受压区高度ξb ＝β11＋f yo E s εcu ＝0.6142. 原混凝土受压区高度 【7.2.1－2】①x ＝A so f yo －A so ' f yo 'α1 f co b ＝2946×210－226×2101.00×9.6×300＝198.33mm3. 判断原结构是否需要加固 【7.2.1－1】①M 1＝α1 f co b x (h o －x 2)＋f yo ' A so ' (h －a ')＝1.0×9.6×300×198.33×(865－198.332)＋210×226×(900－35) ＝478.50kN.m ＜M ＝500.00kN.m需要加固4. 混凝土受拉截面面积 【8.1.2－1】①A te ＝0.5 b h ＝0.5×300×900＝135000mm 25. 综合考虑受弯构件裂缝截面内力臂变化、钢筋拉应变不均匀以及钢筋排列影响等的计算系数ρte ＝A so A te ＝2946.00135000.00＝0.022 σ0＝M ok 0.87×A so ×h o ＝0.00 αf ＝1.04查表【9.2.8】②6. 判断是否计算二次应力和计算εfo 取值εfo ＝αf M ok E s A so h o ＝ 1.04×50000000.00210000.00×2946.00×865＝0.00017. 纤维复合材厚度折减系数采用现场粘贴, 根据【9.2.4－2】②K m ＝1.16－n f E f t f 308000＝1.16－3×230000×0.17308000＝0.798. 纤维布折算面积A fb ＝2 h c n f t f ＝2×900×3×0.167＝901.80mm 2A fl ＝ηf A fb ＝0.00×901.80＝0.00mm 2A f ＝b n f t f ＋A fl ＝300×3×0.167＋0.00＝150.30mm 2A fe ＝A f K m ＝150.30×0.79＝118.12mm 29. 加固后受压区高度和纤维实际应变联立下列规范公式求出加固后受压区高度和纤维实际应变M ≦α1 f co b x (h －x 2)＋f yo ' A so ' (h －a')－f yo A so (h －h o ) 【9.2.3－1】②α1 f co b x ＝f yo A so ＋ψf f f A fe －f yo ' A so ' 【9.2.3－2】②(0.8εcu h x)－εcu －εfo εf ) 【9.2.3－3】②x ≧2a' 【9.2.3－4】② εf '＝0.008ψf ＝0.8 εcu h εcu ＋εf '＋εfo ＝0.8×0.0033×9000.0033＋0.008＋0.0001＝207.06≧2 a _＝2×35.00＝70.00满足要求10. 根据受压区高度判断梁的破坏形态 【9.2.3－3】x h ＝207.06900.00＝0.23≦ξbψf ＝εf 'εf ＝0.0080.007＝1.15＞1.0 准适筋梁, 建议重新设计11. 加固后最大承载力 【9.2.3－1】②M u2＝αf f co b x (h －x 2)＋f yo ' A so ' (h o －a ')＋E f εf ' A fe (h －h o )＝1.04×9.6×300×207.06×(900－207.062)＋210×226×(865－35)＋230000×0.007×118×(900－865)＝541.52kN.m M u2≧M 弯矩满足12. 纤维复合材粘贴延伸长度b f＝b×n f＝300×3＝900mml c＝f f A ff fv b f＋200＝1600.00×150.300.44×900＋200＝807.27mm七、结论原结构承载力M ok＝50.00kN.m 设计弯矩M＝500.00kN.m 加固后弯矩承载力M u2＝541.52kN.m 加固后梁破坏类型准适筋梁粘贴纤维截面面积A fe＝118.12mm2加固是否满足要求满足。

碳纤维布加固梁刚度计算

碳纤维布加固梁刚度计算

其中 ， ， ， ， 为裂缝 间受压混凝土 、 受拉钢筋 、 受拉碳纤维 应 变不均匀系数 。 ２ 物理 （ 构 ） 系 ： 混凝 土受 压应力—应 变曲线 、 ） 本 关 对 钢筋 应
力一应变计算 曲线 、 Ｆ Ｐ应力一应变计算 曲线 ， ＣＲ 可根据材料 的性
质 和强度等级选取合理 的方程 。考 虑混凝土 塑性 变形性能 ， 在此
体现出来。第 Ⅱ阶段 中加 固梁 的剐度 比普通 混凝 土梁 的剐度提 ２ ２ 构件 截 面平均 刚度 的计 算 ． 高较大 ， 这是 因为加 固用碳纤维布对混凝 土受拉 区起 到了约束作 １几何 （ ） 变形 ） 条件 ： 试验 证 明， 面 的平均应 变符合 线性分 截 用， 虽然碳纤维布不能 阻止混 凝土 开裂 ， 但能 使受拉 区混凝 土开 布 ， 中和轴距截面顶面如 ， 截面的平均 曲率用式（） １计算 。 裂后裂缝扩展的趋势受 到抑制 。第 Ⅲ阶段 中加 固梁 的 剐度 比普 其中 ， 混凝土 的平均压应力取 ｅ＝ ， 由于顶面混凝 土压应 通梁的剐度 有较 大提 高 ， 通梁在这一阶段 中 由于截面 塑性 发展 变 的变化 幅度较小 ， 普 近似取 ： 很大使得 刚度下 降较快 ， 而加固梁中 的碳纤维 材料本身直 到破断 ＝１ ｅ＝ ， 前都是弹性性质 的， 纤维布对混凝 土裂缝 的约束使得裂缝 开展 碳
受压变形塑性系数 ， 即任～应 变 （ ） 力 时的割线 弹性 模量 （Ｅ 与 ２ ）
文 中引用 的是均质 、 弹性 材料 的刚度计算 方法。其主要原 理 初始弹性模量的 比值 ， 也是 弹性应 变（ ｅ） 总应 变 的比值 ， 与 由应 其数 值 随应变 的增加 而单调 减少 ， 是将截面上 的钢筋 、 碳纤维布 ， 通过弹性模量值折 换 ， 到等 效的 力一 应变曲线方程计算 确定 ， 得 １： 均质材料换算截面 ， 推导并建立相应 的计算公式 。碳纤 维布钢筋 计算 公式如下… 混凝土受弯构件 ， 受拉 区裂 缝 出现 的前 后有不 同的换算 截面 ， 在

碳纤维布提高钢筋混凝土梁刚度的试验研究与计算

碳纤维布提高钢筋混凝土梁刚度的试验研究与计算
粘贴数 量 的增加 而 增加 ， 果 以此 衡蹙 ， 如 则粘 贴碳 纤维 布 可 以提 高构 ｆ－ 延性 ． 于碳纤维 布 在拉 断之 ｔ 的 由
前一 直保持严 格 的 线弹性 ， 故构 件 的破 坏 较 突然 ， 以 ， 于粘贴 碳纤 维 布使 构 件 的 延性增杏 不能 考虑 所 对 碡
合． 可供 设计 参考． 一
关键 词 ： 碳纤维布； 混凝土梁； 刚度
中 图分类 号 ： Ｕ３７ ． ；Ｕ ７． ４ 文献 标识 码 ： Ｔ １ ２Ｔ ３ ７９ ． Ａ
Ｏ ｇ 言 ｌ
混 凝 ・梁 经碳纤 维 （ ａｂ ｎＦｂｒ ｉｆｒｅ ｌｙ ｒ ｈｅ ， ｛ ： Ｃ ｒｏ ｉｅ ｎｏｃｄＰｏ ｍｅ ｅｔ简称 Ｃ Ｒ Ｓ ｆ…后 川 度得到 提 Ｒｅ Ｓ Ｆ Ｐ ）Ｉ Ｊ １ 高． 使用阶段 的 变 形减 小． 文 试验 的 基础 对 底 面粘 贴 碳 纤维 布混 凝 梁 的 川 度进 行 ＿推 导研 存 本 ｒ ＿
物 理 关 系
。 。
一
， 一
（ ４）
’
…
一ｆ ５ Ｉ ｆ
－ ＝－＝ ＝＝
鑫
’
（ ５）
（ ６）
‘ 、ｌ 是裂缝 截 面处 碳纤 维 布的 应 变 、 凝 ｔ的 应 变 、 筋的 托 应变 ． ，Ｅ、 混 钢
、
是碳纤 维 布 、 凝 十、 筋 的腹 力应 变不 均匀 系数 ． 混 钢
图１ 所示 为三 种试验 梁的荷载 ． 度曲线， 挠 其中
Ｂ０为对 比梁 ， １ 不粘碳 纤 维 ，Ｉ １ 底 粘 层 ， Ｉ Ｂ １１梁 １ Ｆ Ｂ ２在 梁底粘 两 层 ， 以上二 种 试 件的 截 面均 为 ： ｂ＊ｈ ｌＯ＊ Ｏ
２０梁底纵筋均 为２ 『； ｉ ， ０． ｊ８Ｂｌ 截面与Ｂ 相同， ２ ｌ Ｉ 纵筋为２ １， ２梁底 粘贴 …层 碳纤维 ， ｝每种 Ｊ况 都准 备两根 以

碳纤维布加固钢筋混凝土桥梁正截面强度计算

碳纤维布加固钢筋混凝土桥梁正截面强度计算
得到刘 宝琛院士基金资助。 周 爱军 ，女 ，副教授 ，硕士。
土屈服应变 ，《 路桥规》 取 ０ ０２ … 为混凝 公 ．０ ； 土极限压应变 ，《 公路桥规》取 ０ ０３ ．０ 。 （ ）碳纤维 布的应力应变关系满足线弹性关 ５ 系 ，碳纤维的应力等于碳纤维弹性模量与其相应应 变的乘积 ，即 ｏｆ Ｅｆ。 ｒ＝ 。 ｆ 。 。 （ ） 由于外 贴 的碳纤 维 布 很薄 ，近 似认 为 ６ ＣＲ Ｆ Ｐ布中心离梁顶的距离与梁高相等。 （ ）在 达到 受 弯 承 载 力 极 限状 态 前 ，碳 纤 维 ７ 与混凝土之间粘结可靠 ，不发生粘结剥离破坏 。
维普资讯
．
３ Ｏ・
全 国中文核心期刊
路基工程
２０ ０ ６年第 ５期 （ 总第 １８期 ） ２
碳纤维布加 固钢筋混凝 土桥 梁正截 面强度计算 术
周 爱 军 于 晓
（ 鲁东 大学 土木工程学 院 山东烟台 ２４ ２ ） ６ ０ ５
摘 要 针对碳 纤维布加 固桥 梁时的受力机 理和破坏形式 ，以 《 公路钢 筋混凝 土及预应力 混凝土桥 涵设计规范》 （Ｔ ６ ２０ ）为依据 ，提 出了 纤维布加 固桥 梁的抗弯承载力计算 ＪＧ Ｄ ２— ０４ 碳 公式和应满足的条件 ，可应用于桥 梁的加 固设计计算。 关键词 碳 纤 维布 桥 梁加 固 正截 面 强度 仅达到其极限抗拉强度 的 １１ ／０左右 ，该种破坏形 态必 须避 免 ，可通 过 限制 碳 纤 维 最 大用 量 来 控 制 ； 第 （ ）、（ ）种剥离破坏都具有明显的脆性 ，一 ４ ５ 般可通过构造和锚 固措施予以保证。 １ ２ 基本假 定 ． 根据 《 公路桥规》及国内外 Ｃ Ｒ Ｆ Ｐ布加固钢筋 混凝土梁的试验结果 ，抗弯承载能力计算采用如下

梁碳纤维加固计算书

梁碳纤维加固计算书

碳纤维梁加固计算书项目名称_____________构件编号_____________日期_____________设计_____________校对_____________审核_____________一、基本资料1．设计依据:《碳纤维片材加固混凝土结构技术规程》（CECS 146:2003）（以下简称规程）《混凝土结构设计规范》（GB50010—2002）（以下简称规范）2．问题类型:根据碳纤维片材求承载力3．截面参数:截面宽度: b = 300.00 mm截面高度: h = 500.00 mm受拉钢筋面积A s = 1017.88 mm2受拉钢筋合力点至截面近边缘的距离a = 25.00 mm受拉筋: HPB235(Q235), 受拉筋抗拉强度设计值f y = 210.00 N/mm2受压钢筋面积A's = 0.00 mm2受压钢筋合力点至截面近边缘的距离a' = 20.00 mm受压筋: HPB235(Q235), 受压筋抗拉强度设计值f 'y = 210.00 N/mm2混凝土: C15轴心抗压强度设计值f c = 7.2 N/mm2轴心抗拉强度设计值f t = 0.91 N/mm2轴心抗拉强度标准值f tk = 1.27 N/mm24．梁底受拉碳纤维片材参数:弹性模量E cf= 1.40 × 105 MPa抗拉强度标准值f c f k = 2000.00 MPa粘贴层数n cf = 1单层厚度t cf = 0.111 mm梁底碳纤维片材的宽度 = 300.00 mm梁底碳纤维片材的截面面积A cf = 33.30 mm2考虑二次受力, 加固前计算截面上实际作用的初始弯矩M i= 20.00 kN·m 5．梁侧受剪碳纤维片材参数:粘贴层数n cfv = 1单层厚度t cfv = 0.111 mm弹性模量E cfv= 1.40 × 105 MPa条带宽度w cf = 100.00 mm条带净间距s cf = 100.00 mm侧面粘贴高度h cf = 100.00 mm加固方式: 封闭粘贴, 碳纤维片材受剪加固形式系数 取1.00荷载形式: 集中荷载(包括集中荷载对支座截面或节点边缘所产生的剪力值占总剪力值的75%以上的情况),集中荷载至支座距离为600.00mm 6．箍筋参数: 箍筋直径 6mm 箍筋肢数 1箍筋间距 150.00mm箍筋: HPB235(Q235), 箍筋抗拉强度设计值 f yv = 210.00 N/mm 27．弯起筋参数: 弯起筋直径 6mm 弯起筋根数 0 弯起角度 45二、计算结果1．加固前构件在初始弯矩作用下, 截面受拉边缘混凝土的初始应变 i:考虑二次受力, i 按规程4.3.4中各式计算: h 0 = h - a = 500.00 - 25.00 = 475.00 mmsi =M iA s · h 0 = 20.00×1061017.88 × 0.87 × 475.00= 47.55 N/mm 2受拉钢筋拉应变不均匀系数:= 1.1 - 0.65f tksite= 1.1 - 0.65 × 1.2747.55 × 0.0136 = -0.179< 0.2根据《GB50010-2002》8.1.2的规定, 当 < 0.2 时, 取 = 0.2。

碳纤维片材局部粘结加固梁的刚度计算分析

碳纤维片材局部粘结加固梁的刚度计算分析

筋混 凝 土梁截 面刚度 的变 化规 律 ，对正 常使 用 阶段
第一 阶段 ， 混凝 土没 出现 裂缝 前 。在这 一 阶段 ， 荷载 较小 ， 中 的弯矩也 较小 。 凝土 的应 力与 应变 梁 混 呈线性 变化 ．荷 载一 挠度 曲线 或弯 矩一 曲率 曲线 为直
梁 的截 面 刚度 进行 分 析 ， 于 文献 『１ 验 资料 分 析 基 １试
线 ， 时截 面 刚度 保 持不 变 ， 面表 现 为 弹性性 质 ， 这 截
这 与普 通混凝 土梁 的性质 一致 。 二 阶段 ， 第 混凝 土开 裂 至纵 向钢筋 屈服 。在 这一 阶段 受 拉 区混凝 土 出现 裂缝 ， 弯矩 与 曲率 曲线 出现 拐点 ， 曲线 的斜率 减 小 ， 但 随后 曲线 的斜率 基本 保持 不变 。这 一 阶段 的变化 与普 通混 凝土梁 的 变化 一致 ，截 面也表 现 为弹性 性
提 出用 截 面刚度综 合 变化 系数表 达各 种 因素 对碳纤 维片材 加 固钢筋 混凝 土梁截 面刚 度 的影 响 ，并 由此 提 出推 导碳纤 维 片材加 固钢 筋混 凝土 梁截 面 刚度 的 简化计算 公式 。该公 式 在表达 方式 上 与普 通钢 筋混 凝 土梁 的截 面刚度计 算公 式相 似 。与试 验结 果相 比
阶 段 的 刚度 较 普通 混 凝 土 梁 的刚 度还 是 有所 增 加 。 当粘 结层具 有 非连续 性 的时候 ，加 固梁 的刚度 如何
反应 ， 面用 具体 的实例来 说 明这个 问题 。 下
钢 筋 混 凝 土 的 简支 梁 ，梁 的跨 度 为 １０ ０ ｍ． ０ｍ
Ｆ Ｐ 片 材 端 部 离 支 座 的 距 离 ５ ｒｍ，梁 的 弹 性 模 量 Ｒ ０ ａ
２。

碳纤维布加固RC梁正截面强度计算理论

碳纤维布加固RC梁正截面强度计算理论

碳纤维布加固RC梁正截面强度计算理论李英勇1王松根1王苏岩 2(1山东省交通厅公路局，山东济南 250002；2大连理工大学土木水利学院，辽宁大连 116024)摘要：为建立与现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）相衔接的碳纤维布加固钢筋混凝土桥梁正截面强度计算理论，结合CFRP加固钢筋混凝土抗弯构件的研究成果，对加固后截面承载能力极限状态、界限破坏状态、界限加固量以及混凝土受压区界限高度系数进行了合理的界定，最后，针对原《公桥钢筋混凝土及预应力混凝土桥涵设计规范》（JTJ 023-85）、现行《公桥钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）与《混凝土结构设计规范》（GB50010-2002）的不同要求，提出了粘贴碳纤维布加固钢筋混凝土桥梁正截面强度计算公式。

通过与室内试验数据比较，碳纤维布贡献计算值与试验值吻合良好，所提公式可用于实际桥梁粘贴碳纤维布的加固计算。

关键词：碳纤维复合材料（CFRP）；桥梁；加固；受弯承载力Design Philosophy of Reinforced Concrete Beams with externallyBonded CFRP SheetsLi ying-yong1 Wang Song-gen1Wang Su-yan2（1 Highway Bureau of Shandong Province，Shandong Jinan 250002 China；2 School of Civil and hydraulic Engineering, Dalian University of Technology，liaoning Dalian 116024 China）Abstract：The method to define the ultimate limit state of carrying capacity, critical failure, critical strengthened quantity and critical height coefficient of concrete compressive region is suggested. Design algorithms in Code for Design of Highway Reinforced Concrete and prestressed Bridges and Culverts（JTJ 023-85） and （JTG D62-2004）format as well as Code for Design of Concrete Structures（GB50010-2002）format are proposed to predict the capacity of available beams strengthened in flexure with CFRP sheets. The effectiveness of the design approach is then validated by comparing the experimental results with the calculated flexural capacity. Results showed that the proposed design approach is conservative and acceptable.Key words：Carbon fiber reinforced polymer（CFRP）；Bridge；strengthening；Flexural capacity0 前言粘贴碳纤维布加固混凝土结构技术是一项新型、简捷、有效的混凝土桥梁加固技术。

碳布加固计算公式

碳布加固计算公式

碳布加固计算公式
碳布加固计算公式通常使用以下公式：
弯曲刚度（Flexural stiffness） = (力乘以臂长) / (挠度乘以曲率)
弹性模量（Modulus of elasticity） = 弯矩 / (弯曲应力乘以横截面积)
弯曲应力（Bending stress） = 力乘以臂长 / (惯性矩乘以横截
面距离)
其中，力是施加在结构上的力，臂长是力施加点到结构横截面的距离，挠度是结构受力形变产生的弯曲度，曲率是曲线的弯曲程度，弯矩是力在结构上造成的弯曲力矩，横截面积是结构横截面的面积，惯性矩是结构横截面对某一轴的惯性度量，横截面距离是结构横截面上某点到某一轴的最短距离。

这里提供的公式是一般的碳布加固计算公式，具体计算还需要根据实际情况进行适当的调整和修正，以确保计算结果的准确性和可靠性。

碳纤维布梁加固计算书

碳纤维布梁加固计算书

碳纤维梁加固计算书一、基本资料1．设计依据:《碳纤维片材加固混凝土结构技术规程》（CECS 146:2003）（以下简称规程）《混凝土结构设计规范》（GB50010—2002）（以下简称规范）《混凝土结构加固技术规范》（GB 50367-2006）（以下简称加固规范）图纸所提供的相关数据2．问题类型:因荷载增加原有混凝土梁承载力不足，需进行加固处理，加固方式采用碳纤维布。

3．梁底受拉碳纤维片材参数:碳纤维布等级：Ⅰ级弹性模量E cf = 2.30 × 105 MPa (见加固规范表9.1.6-1)抗拉强度设计值f f = 2300.00 MPa (见加固规范表9.1.6-1)单层厚度t cfv = 0.167 mm重量：300g/m2不考虑二次受力二、计算结果1. KL3梁荷载增加后缺筋面积为750mm2，采用等强代换原则换算碳纤维布粘贴尺寸：HRB400钢筋抗拉强度设计值：360N/mm2碳纤维布抗拉强度设计值：2300 N/mm2缺筋面积*钢筋抗拉强度设计值≤碳纤维布厚度*宽度*碳纤维布抗拉强度设计值750*360≤0.167*宽度*2300宽度≥702.94KL3梁截面尺寸为400*900，结构梁宽度为400不能满足碳纤维布粘贴宽度，考虑粘贴双层碳纤维布，计算碳纤维布多层粘贴折减系数：（见加固规范9.2.4-2）折减系数=1.16-(粘贴层数*弹性模量设计值*单层厚度)/308000≤0.9=1.16-(2*230000*0.167)/308000=0.91折减系数=0.9750*360≤0.167*宽度*2300*0.9宽度≥781.05KL3梁宽度为400mm，碳纤维布粘贴双层面积：2*400=800≥781.05，满足强度要求。

梁抗弯加固计算(粘贴碳纤维布)

梁抗弯加固计算(粘贴碳纤维布)
梁抗弯粘贴碳纤维布 加固计算
碳纤维布 层数计算 （反复调 整实际层 数nf取 值，直到 OK）
延伸长度 计算
【混凝土结构加固设计规范 GB50367-2013 第10.2节】 F1-KL1跨中 碳纤维布采用高强度Ⅰ级，构件按重要构件 600 【梁高】 h= mm 300 【梁宽】 b= mm 35 【受拉钢筋距砼面】 as= mm 565 【截面有效高度】 ho= mm 14.3 【砼抗压强度设计值】 fco= N/mm² 360 【受拉钢筋强度设计值】 fyo= N/mm² 200000 【受拉钢筋弹性模量】 Es= N/mm² 628 【梁宽b的受拉筋面积】 Aso= mm² 1.00 【砼规6.2.6条】 α 1= 100.0 【梁宽b的原弯矩标准值，按原构件计算结果】 Mok= kN·m 170.0 【梁宽b的新弯矩设计值，按新构件计算结果】 M= kN·m 1600 【查表4.3.4-1】 布强度设计值ff= MPa 230000 【查表4.3.5】 布弹性模量Ef= MPa 7.913E+06 fyoAso(h-ho)= α 1fcobx(h-x/2)=M+fyoAso(h-ho)= 1.779E+08 0.440 ξ b,f=0.85ξ b= 计算过程 248.77 xb=ξ b,fho= 73.6 砼受压区高度x= 89827 ψ fffAfe=α 1fcobx-fyoAso= 1.00 ψ f=((0.8ε cuh/x)-ε cu-ε fo)/ε f= 其中： 0.0033 其中： ε cu= 0.00174 ρ te=0.5Aso/b/h= 计算过程 0.70 【查表10.2.8】 α f= ε fo=α fMok/(EsAsho)= 0.00099 0.0070 【碳布拉应变设计值，查表4.3.5】 ε f= Afe= 56.14 mm² 【受力计算确定的梁宽b需要的碳布截面面积】 梁宽b范围碳布条数： 1 【输入，一般为1条，梁宽较宽时可多条】 每条碳布各层总面积Afe1= 56.14 mm² 每条宽度： 200 mm 【设计确定的每条碳纤维布宽度】 每条碳布需要的总厚度= 0.281 mm 单层碳纤维布厚度tf= 0.167 mm 【300g/m²：0.167，200g/m²：0.111】 预估碳布层数= 1.6809 取 2 【输入整数，且应不小于左侧计算值】 0.900 km=1.16-nfEftf/30800= 62.38 【考虑km后，每条碳布各层总面积】 Af1=Afe1/km= 计算需要最少层数nf= 1.87 【未超输入的预估层数，OK】 延伸长度lc=ffAf/(ff,vbf)+200= 1134 mm 【第10.2.5条】 0.572 其中： ff,v=max(0.4,min(0.7,0.4*ft))= 1.43 N/mm² 【砼抗拉强度设计值】 ft=

CFRP加固钢筋混凝土梁裂缝宽度与刚度的计算方法

CFRP加固钢筋混凝土梁裂缝宽度与刚度的计算方法
摘要 ： 科 学技 术的快速发展给 工程建设提供 了强大的技 术支持 ，新材料 以及新工 艺的不断涌现极 大地促进 了工程建设的发展 ，
●
在水利工程以及土木工程 建设 中，纤维复合材料 以其轻便 、抗腐蚀 等优 点得到 了广泛的运用。如何采 用纤维复合材料进行 混凝土结 构＿ 加 固一直是 国内外的研 究热点，有 关裂缝宽度与刚度的计算方法也在 不断完善与进步。
较快 。
巍 ＾
２ ． ３裂缝宽度的计算方法 分析纵向受拉钢筋的应力时可假设混凝土梁被破坏的过程 中，混凝土 、钢 筋
２ Ｃ Ｆ Ｒ Ｐ加 固钢筋混凝土梁裂缝间距和宽度 的计算 方 法
２ ． １ 碳纤维布厚度折减系数
及碳纤维布的应变始终保持在一个平面上 ，同时排除混凝土抗拉强度 的影 响。碳 纤维布加 固钢筋混凝土梁的平均裂缝宽度应为平均裂缝间距范 围内钢筋伸长量 与 混凝土伸长量之间的差 ，大量试验研究表明 ，混凝土 的受拉平均应变 比纵 向
： 串
霉 ≮
： ； ：
图 １ 裂缝间距计算简化模型 根据已有裂缝和即将出现裂缝之间的构件截面力平衡 、结合 《 混凝土结构设 计规范 》所以及钢筋混凝土平均裂缝间距的计算方法 ，同时引入加 固影 响系数 和 粘结影响系数得 到碳纤维 布加 固钢筋混凝土梁平均裂缝间距 ｒ与普通钢筋混凝
针对碳纤维布厚度折减系数 ｋ ，国内外学者进行 了诸多研究 ，并立足于各 自
也不 会影 响建筑物的使用空 间，同时 ，碳纤 维复合材 料具有很 好的耐久性和耐腐 蚀性 ，化 学性质很稳定 ，能够解决其他加 固方法所 面ｌ 临的化学腐蚀问题。除此之 外， 碳纤 维复合材料还具有很好 的弹性 ，能够很好地 限制混凝 土裂缝的开展 ，同

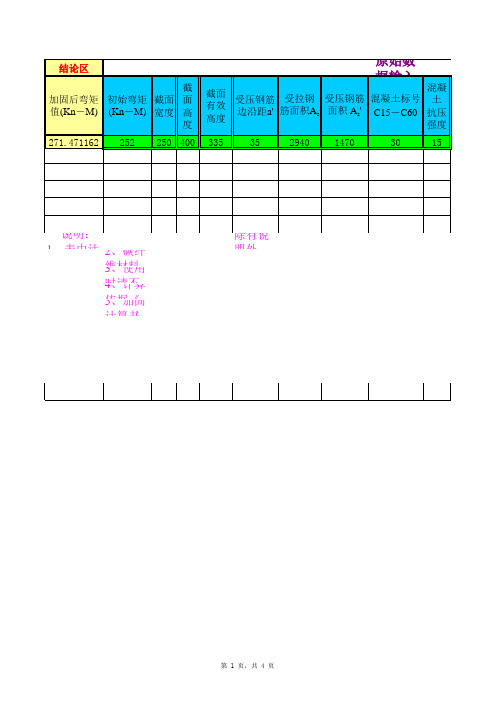
碳纤维加固计算

碳纤维加固计算

，面积为平方毫米。
》（报批稿） 断采用的计算公式。土受 拉边沿 压区高度 压区高度 计算公式 混凝土 x x2 初始应 变ε i 131.058 0.0606217 1 0.001
计算碳纤 碳纤维 计算相 中间变量 维允许拉 厚度折 对受压 混凝土抗 应变 减系数 区高度 压强度 0.01 0.9093 0.173 0
结论区 截 加固后弯矩 初始弯矩 截面 面 值(Kn－M) (Kn－M) 宽度 高 度 271.471162 252 250 400
原始数据输入区
混凝 截面 受压钢筋 受拉钢 受压钢筋 混凝土标号 土 有效 边沿距a' 筋面积As 面积 As' C15－C60 抗压 高度 强度 335 35 2940 1470 30 15
中间 变量 混凝 土抗 拉强 0
第 3 页，共 4 页
中间变量区（请勿修改）
中间变 量混凝 土弹性 模量 0 fyAsfy'As' 455700 Ecf Acf ε cu＋ε i fcb
数据输入区
受压翼缘 受压翼缘 宽度 高度
9519000
0.0043
3750
第 4 页，共 4 页
说明： 1、表中计算采用单位， 除有说明外，长度宽度均为毫米，面积为平方毫米。 2、碳纤维材料选择类型见“混凝土与碳纤维材料技术参数。 3、使用时请不要修改非数据输入部分数据。 4、计算依据《碳纤维片材加固修复混凝土结构技术规程》（报批稿） 5、加固计算书按照规范要求，以混凝土受压区高度来判断采用的计算公式。
第 1 页，共 4 页
考虑二次受 碳纤维类型 力 1否则取0 1、2或3 1 2
碳纤维 碳纤维 碳纤维极 碳纤 碳纤维宽 碳纤维拉 碳纤维拉 厚度 弹模 限应变 维层 度bcf 应变ε cf 应变ε cf2 数ncf cfu tcf Ecf 0.167 228000 0.0155 1 250 0.003757 0.003757

碳纤维片材加固计算

碳纤维片材加固计算

一、梁基本数据梁结构类型： 重要构件混凝土抗压强度设计值fc： 11.9 (n/mm2)梁钢筋级别： HRB400钢筋抗拉/抗压强度设计值： 360 (n/mm2)梁受压区钢筋排数： 1 排梁受压区钢筋排数： 1 排二、梁加固设计数据初始弯距： 200 (KN.m)进行二次受力影响计算查GB50367－2006表9.2.8 αf= 0.7εf0=αf×M0k/(Es×As×H0)= 0.00218采用碳纤维片材类型： 高强Ⅰ级碳布碳纤维片材拉应变设计值： 0.007碳纤维片材设计强度： 1600 (n/mm2)试算碳纤维片材层数： 2 层梁正截面抗弯加固计算书混凝土标号： C25梁截面尺寸： 240 × 500 (mm)选用碳纤维片材厚度： 0.167 (mm)三、计算过程ρte=As/Ate= 0.005设计弯矩值： 302 (KN.m)二次受力影响： 考虑碳纤维片材弹模设计值： 230000 (Mpa)根据（9.2.3-1）式解出XX= 173.14 (mm),代入（9.2.3-3）式ψf= 0.31 取ψf= 0.31 代入（9.2.3-3）式按（9.2.4-2）计算 km= 0.93428 (mm)选用2层0.167mm厚3428mm宽的高强Ⅰ级碳布，满足计算要求。

so yofe f f so yo co A f A f A f bx f a ′′−+=ψ1)()(2(1o so yo so yo co h h A f a h A f x h bx f a M −−′−′′+−≤ffocu cu f x h εεεεψ−−=)/8.0(fe fe fe fe n t b A ××==××=mf fe f fe k n t A b e f A=m fe f k A A /=。

碳纤维布加固混凝土梁截面刚度计算

碳纤维布加固混凝土梁截面刚度计算

加固混凝土梁截面刚度计算碳纤维布加固混凝土梁在结构工程加固应用中已极为普遍，相应的实验研究功效也比较多，目前国内外对碳纤维布加固混凝土梁的承载力研究已比较成熟[1-5]，对裂痕、变形和刚度等也有许多实验资料。

实验结果说明，用碳纤维布加固梁的截面刚度比未加固梁的截面刚度有所提高，但关于加固梁刚度的计算目前尚没有成熟的研究功效。

本文通过解析分析，成立了基于实验资料的碳纤维布加固钢筋混凝土梁截面刚度简化计算公式，实验资料验证结果说明，该计算公式能够用于碳纤维布加固钢筋混凝土梁的截面刚度计算。

1 加固梁截面刚度转变规律实验现象国内外大量的实验结果说明，碳纤维布加固混凝土梁的刚度转变与一般混凝土梁的刚度转变趋势是一致的，都与混凝土中裂痕的显现和进展有关，从整体上看，碳纤维布加固梁的截面刚度比一般混凝土梁的截面刚度大，即挠度比相应的一般混凝土梁的挠度要小，其刚度转变进程也能够分为3个时期，如图1所示。

图1 碳纤维布加固梁典型弯矩－曲率曲线第Ⅰ时期：混凝土开裂以前。

该时期中弯矩很小，混凝土的应力与应变成正比，荷载-挠度曲线（或弯矩-曲率曲线）为直线，即截面刚度维持不变，截面表现出较好的弹性性质，与一般混凝土梁的性质相同，而曲线斜率稍大，即刚度值较对照一般混凝土梁的刚度值略有提高。

第Ⅱ时期：混凝土开裂至纵向受力钢筋屈服。

受拉区混凝土开裂时，弯矩-曲率曲线上显现拐点，曲线斜率减小，但随后曲线斜率大体不变。

那个时期中加固梁截面刚度转变也与一般混凝土梁的表现相似，截面大体上仍表现为弹性性质，但相应刚度值也较对照一般混凝土梁的刚度值大一些，即曲线斜率更大一些。

第Ⅲ时期：纵向受力钢筋屈服钢筋后至极限状态。

纵向受力钢筋屈服时弯矩-曲率曲线上又有一个明显的拐点，曲线斜率又一次减小（这时碳纤维布的应变也有突然增大现象），即截面刚度进一步下降，挠度增加，直到极限状态。

但从整体上看，本时期加固梁刚度较对照一般混凝土梁的刚度有较大的提高。

碳纤维布加固混凝土T形梁正截面强度程序化计算

碳纤维布加固混凝土T形梁正截面强度程序化计算

（ ）截 面应变 符合平 截面 假定 ； １ （ ）钢 筋的应 力一 变关 系 ， 用完全 弹塑性 模型 ； ２ 应 采
一
Ｅ ｅ （ ｓｓ ｏ
ｅ） Ｏ ； ＂ ＿ （ ｓ一 ， ｅ
ｅ ０ ｏ ） ５ ． １
式 中 ： 钢筋设 计强度 对应 的拉 应变 ， 为钢 筋的 弹性模 量． ￡ （ ）混凝土 的应 力一 ３ 应变 关 系 ， 不考 虑受 拉 区混 凝土抗 拉强 度 ；
系㈣， 界限受 压区 Ｘ 高度 ： 一０ ８ ， ． ｘ 由此可 得 Ｔ 形梁在 钢筋 屈服 、 压 区边缘 混凝 土达 到极 限压应变 、 受
一
ｎ ｏ
碳纤维 布达到 允许拉 应变 时 ， 限相 对受 压 区高度 为 ： ＝ 一 界
． 当受 压 区高度 ， ＜￡ 时 Ｔ
１２ Ｃ Ｒ ． Ｆ Ｐ粘 贴量 的确 定 ＣＲ Ｆ Ｐ粘贴 量主 要是 依据 钢 筋强度 补 偿系数 （ 减系数 ） 补 偿钢 筋强 度 ， 折 “” 按未粘 贴 碳纤维 布加
固前 ， Ｔ形 梁构件 受压 区高 度 ｘ与其界 限受 压 区高 度 的 比值确 定． 于 的破 坏形 式为钢 筋屈 服 、 压 基 受
图3计算流程图图4信息接收j万方数据第4期闰长旺等碳纤维布加固混凝土t形梁正截面强度程序化计算307计算方法的实验验证根据文献8所进行的试验数据按照本文所提出的计算方法和基于visualbasic的可视化计算程序进行可转换为t形截面的混凝土构件正截面强度计算方法的实验验证
内 蒙古 工业 大 学 学报
性和较好的可靠性．
关键 词 ： 碳纤维布； 钢筋混凝土Ｔ形梁 ； 可视化程序
中图分类 号 ： Ｕ ２．； Ｕ ２．８ 文献标 识码 ： Ｔ ３０２Ｔ ５８５２ Ａ

(完整word版)粘碳纤维加固计算书(word文档良心出品)

(完整word版)粘碳纤维加固计算书(word文档良心出品)

梁粘贴碳纤维布加固计算书：1、计算缺少受拉钢筋面积A s0=980mm2,受拉钢筋强度f y0=360Mpa。

粘贴碳纤维布强度ff=2800Mpa。

1）当粘贴碳纤维布层数nf=2，厚度t=0.167mm，宽度b'=400mm。

实际粘贴碳纤维布层数折减系数km =0.95，实际粘贴碳纤维布截面积Afe'=126.92 mm2。

按强度等效，如下：碳纤维强度2800X126.92=355376>缺少钢筋强度360X980=352800(满足要求)2）当粘贴碳纤维布层数nf=3，厚度t=0.167mm，宽度b'=300mm。

实际粘贴碳纤维布层数折减系数km =0.85，实际粘贴碳纤维布截面积Afe'=127.755 mm2。

按强度等效，如下：碳纤维强度2800X127.755=357714>缺少钢筋强度360X980=352800(满足要求)2、计算缺少受拉钢筋面积A s0=2454mm2,受拉钢筋强度f y0=360Mpa。

粘贴碳纤维板强度ff=2000Mpa。

1）当粘贴碳纤维板时，厚度t=1.4mm，宽度b'=400mm。

实际粘贴碳纤维板截面积Afe'=560mm2。

按强度等效，如下：碳纤维强度2000X560=1120000>缺少钢筋强度360X2454=883440(满足要求)板粘贴碳纤维布加固计算书：1、计算缺少受拉钢筋面积As0=393mm2／m,受拉钢筋强度fy0=360Mpa。

粘贴碳纤维布强度ff=2800Mpa。

1）当粘贴碳纤维布层数nf=1，厚度t=0.167mm，宽度b'=200mm,间距200。

实际粘贴碳纤维布截面积Afe'=66.8 mm2／m。

按强度等效，如下：碳纤维强度2800X66.8=187040>缺少钢筋强度360X393=141480(满足要求)2、计算缺少受拉钢筋面积As0=565mm2／m,受拉钢筋强度fy0=360Mpa。

二次受力碳纤维布加固钢筋混凝土梁短期刚度的计算

二次受力碳纤维布加固钢筋混凝土梁短期刚度的计算

二次受力碳纤维布加固钢筋混凝土梁短期刚度的计算黄楠;李辉【摘要】In this paper the flexural behavior of six reinforced concrete beams strengthened by carbon fiber sheets is tested. Using the weights and lever loading system, the tests have simulated the condition of secondary load on the reinforced concrete beams strengthened by carbon fiber sheets, and obtained the typical load-displacement curve of the reinforced concrete beams. Based on analysis of the stiffness changes on the cross-section of the reinforced concrete beams, and using both theoretical and experimental statistics, this paper proposes the method of calculating the short-term stiffness on the rectangular section of the reinforced concrete beams. The accuracy is validated by comparing the experimental results with those obtained from generic calculation methods.%进行了6根碳纤维布加固钢筋混凝土梁的抗弯性能试验研究。

碳纤维布加固混凝土梁截面刚度计算

碳纤维布加固混凝土梁截面刚度计算

碳纤维布加固混凝土梁截面刚度计算摘要:本文对碳纤维布加固钢筋混凝土梁的刚度进行了研究，针对钢筋是否屈服的两种不同情况，分别讨论碳纤维布加固后梁的刚度的计算公式。

采用解析分析方法，较系统地建立了碳纤维布加固混凝土梁各种受力状态的截面刚度的简化计算公式。

该公式与《碳纤维片材加固混凝土结构技术规程》相配套，有利完善加固工程设计。

关键词:碳纤维布；混凝土梁刚度；变形条件；本构关系0 引言碳纤维布加固混凝土梁在结构工程加固应用中己极为广泛，相应的试验研究成果也比较多，目前国内外对碳纤维布加固混凝土梁的承载能力研究已比较成熟，对裂缝、变形和刚度等也有许多试验资料。

在我国《混凝土结构设计规范》中对普通混凝土梁的刚度的计算方法进行了规定，规定对等截面构件在钢筋屈服前用最大弯矩处的刚度进行计算。

但是，对用碳纤维布加固的梁其刚度的提高主要是在钢筋屈服后。

由于屈服前后构件的截面承载力性能是不同的，因此本文在参照《混凝土结构设计规范》中普通混凝土梁刚度计算方法的基础上，研究了碳纤维布加固后梁的刚度。

1 基本假设1．混凝土应力—应变关系采用《混凝土结构设计规范》中推荐的混凝土应力—应变设计曲线。

2．钢筋的应力—应变关系为经典的弹塑性关系。

3．碳纤维布直到破坏前都保持为线性。

4．混凝土开裂前截面惯性矩为整个截面的换算惯性矩I0，而且在开裂前截面的刚度保持不变。

5．碳纤维布满跨粘贴，在支座处截断，忽略未加固的支座处的额外的变形。

6．碳纤维布和混凝土梁之间为完全粘结，不考虑碳纤维布和混凝土之间的粘结滑移。

2加固梁的刚度大量试验证明，用碳纤维布加固的梁，当荷载小于屈服荷载的时候，其刚度呈下凸曲线规律单调递减，与未加固梁的刚度变化规律极其相似；钢筋屈服后，则随着碳纤维布加固层数的增加，其刚度退化越来越缓慢，构件在屈服后仍然能维持一定的刚度继续承载，直到碳纤维布突然拉断或者混凝土突然压碎，而且碳纤维布的加固层数越多，刚度的提高越明显。

梁粘贴纤维法正截面加固计算书

梁粘贴纤维法正截面加固计算书

梁粘贴纤维法正截面加固计算书
1、已知条件
梁截面宽度b=240㎜，截面高度h=550㎜,受压钢筋合力点至截面近边缘距离a s=30㎜，受拉钢筋合力点至截面近边缘距离
as=30㎜，混凝土强度等级C15，受拉钢筋强度设计值f y=300Mpa,受压钢筋强度设计值f y=300Mpa,纤维抗拉强度设计值f f=2300Mpa 纤维设计拉应变εf=0.007，受拉钢筋面积As=1018㎜²,受压钢筋面积As=509㎜²,3级抗震，非地震组合，设计截面位于框架梁梁中，弯矩设计值M=170kN·m,地震组合折减系数ˇRa=0.85。

2、加固计算
混凝土抗压强度设计值
f c=7.2Mpa
截面相对界限受压区高度
£b=0.413
当£=£b时，截面所能承受的最大弯矩
M max=233.57kN·m
Mmax>M，经计算可求得截面受压区高度和受拉纤维有效截面面积 x=118.14㎜
A fe=21.95㎜²
故300g碳纤维布宽度为b=21.95÷0.167≈131.4mm
加固时采用。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

碳纤维布加固混凝土梁截面刚度计算摘要:本文对碳纤维布加固钢筋混凝土梁的刚度进行了研究，针对钢筋是否屈服的两种不同情况，分别讨论碳纤维布加固后梁的刚度的计算公式。

采用解析分析方法，较系统地建立了碳纤维布加固混凝土梁各种受力状态的截面刚度的简化计算公式。

该公式与《碳纤维片材加固混凝土结构技术规程》相配套，有利完善加固工程设计。

关键词:碳纤维布；混凝土梁刚度；变形条件；本构关系0 引言碳纤维布加固混凝土梁在结构工程加固应用中己极为广泛，相应的试验研究成果也比较多，目前国内外对碳纤维布加固混凝土梁的承载能力研究已比较成熟，对裂缝、变形和刚度等也有许多试验资料。

在我国《混凝土结构设计规范》中对普通混凝土梁的刚度的计算方法进行了规定，规定对等截面构件在钢筋屈服前用最大弯矩处的刚度进行计算。

但是，对用碳纤维布加固的梁其刚度的提高主要是在钢筋屈服后。

由于屈服前后构件的截面承载力性能是不同的，因此本文在参照《混凝土结构设计规范》中普通混凝土梁刚度计算方法的基础上，研究了碳纤维布加固后梁的刚度。

1 基本假设1．混凝土应力—应变关系采用《混凝土结构设计规范》中推荐的混凝土应力—应变设计曲线。

2．钢筋的应力—应变关系为经典的弹塑性关系。

3．碳纤维布直到破坏前都保持为线性。

4．混凝土开裂前截面惯性矩为整个截面的换算惯性矩I0，而且在开裂前截面的刚度保持不变。

5．碳纤维布满跨粘贴，在支座处截断，忽略未加固的支座处的额外的变形。

6．碳纤维布和混凝土梁之间为完全粘结，不考虑碳纤维布和混凝土之间的粘结滑移。

2加固梁的刚度大量试验证明，用碳纤维布加固的梁，当荷载小于屈服荷载的时候，其刚度呈下凸曲线规律单调递减，与未加固梁的刚度变化规律极其相似；钢筋屈服后，则随着碳纤维布加固层数的增加，其刚度退化越来越缓慢，构件在屈服后仍然能维持一定的刚度继续承载，直到碳纤维布突然拉断或者混凝土突然压碎，而且碳纤维布的加固层数越多，刚度的提高越明显。

大量的研究证明，碳纤维布加固混凝土梁的截面刚度随着弯矩值的增大而减小，但是在各个阶段中，截面的刚度变化并不显著，如图1所示。

杨勇新、岳清瑞等对用碳纤维布加固后梁的刚度进行了理论研究，但是在他们的分析过程中钢筋没有屈服，是通过将得到的公式中的参数利用试验数据进行统计分析得到的，且得到的为二次曲线的形式，在工程中应用起来不方便。

本文在参考其分析过程的基础上，考虑了采用碳纤维布加固的梁在钢筋屈服前后两种不同情况下的刚度计算，并且由于混凝土达到峰值应变前后的图形完整系数和受压变形塑性系数的表达式是不同的，因此，将整个计算刚度的过程分为四个部分。

第一部分，混凝土开裂前：混凝土开裂前，整个梁都处于弹性阶段，利用弹性理论计算梁的刚度，00.85C B E I =⨯ （1） 其中，E c 为混凝土的弹性模量，0.85为折减系数，I 0为换算截面惯性矩。

将构件和碳纤维布的弹性模量按照与混凝土弹性模量的比值进行换算得到惯性矩，()()()()b s S cf cf I h A h A h χχαχαχ0⎡⎤=⨯⨯+-+-⨯⨯-+⨯-⎣⎦22330000113（2） ()()2001b 12b 1cf cf s S s S cf cfh A h A h h A A ααχαα⨯⨯+⨯⨯+-⨯⨯=⨯+-⨯+⨯ （3）上面各个表达式中各参数的含意分别为,0cf cf E E α=,0ss E E α=, cf E 为碳纤维布的弹性模量，s E 为钢筋的弹性模量，0E 为混凝土的弹性模量，cf A 为碳纤维布的横截面积，S A 为钢筋截面积，b 为梁的宽度，h 为梁的高度。

第二部分，混凝土开裂至钢筋发生屈服：混凝土开裂后退出工作，钢筋和碳纤维布的应力突然增加。

以此阶段裂缝截面为研究对象，在这个平面上满足三个条件：变形条件、本构关系和平衡条件。

变形条件：由平截面假定，截面的平均曲率可以表示为：01cf c cf c sh h hεεεεεϕρχχχ+=====-- （4） 碳纤维布的平均应变cf ε为：cf cf εψε= （5） 钢筋的平均应变s ε为：s s εψε= （6） 混凝土的平均应变c ε为：c c εε= （7） 本构关系：在本阶段，裂缝处受压区混凝土、钢筋和碳纤维布的应力分别按照下式进行计算：c c c c c E E σενεν=⨯⨯=⨯⨯ （8） /cf cf cf cf cf E E σεεψ=⨯=⨯ （9） 其中，ν为混凝土的受压变形塑性系数：()200/,0.002,0.0020.0033c c c cc c c c f E f E εεενενεε⎧⨯2/-⎪=≤⎪⎨⎪=<≤⎪⨯⎩（10） ψ为钢筋和碳纤维布的不均匀系数，通过下式进行计算：0.651.1 1.10.5b cr cssM f A Mhψσ⨯⎛⎫=⨯1-=- ⎪⎝⎭⨯⨯⨯ （11）可以看出：构件刚开裂时，钢筋不均匀系数ψ最小，随着弯矩的增大，ψ值渐增，达到屈服弯矩后钢筋屈服，ψ值接近于1.0。

由于碳纤维布的作用为约束混凝土与钢筋的变形，因此可以认为裂缝处碳纤维和混凝土变形的不均匀程度相当，即碳纤维布的不均匀系数也取为ψ，对于混凝土的不均匀系数，因为混凝土发生破坏的时候应变比较小，因此取1.0。

由平截面假定可以得到碳纤维布应力和钢筋应力之间的关系：0s s cf cf h E h E ψσσψ⨯⨯=⨯⨯⨯ （12）平衡条件：裂缝截面混凝土的拉应力为零，裂缝截面的应力分布如图2所示，建立截面的力的平衡方程，对受压混凝土的合力中心取矩：()()0s s cf cf M A h Y A h Y σχσχ=⨯⨯-++⨯⨯-+ （13） 其中，2/31/4/11/3/c c Y εεχεε-⨯=⨯-⨯ （14）对钢筋中心取矩：()0cf cf M C h Y A χσ=⨯-++⨯⨯α （15） 其中，20001b b 3c c c C εεσωχσχεε⎡⎤⎛⎫⎢⎥=⨯⨯⨯=-⨯⨯⨯ ⎪⎢⎥⎝⎭⎣⎦（16）式(16)中的ω为受压区混凝土应力图形完整系数：0000/,0.00211/3//,0.0020.003311/3/c c c c cc εεωεεεεεωεεε2/3-1/6⨯⎧=≤⎪-⨯⎪⎨1-1/2⨯⎪=<≤⎪-⨯⎩（17） 由式（13）、（15）可求得cf σ、cf ε、c σ、c ε。

cf ε、c ε代入（4）式得：000000/1/3/1/311/3/11/3/1c c s s cf cfc c h E A h h E A h M B Kεεεεχχεεεερ⎛⎫⎛⎫1/12⨯-1/12⨯-⨯⨯⨯+⨯+⨯⨯⨯+⨯ ⎪ ⎪-⨯-⨯⎝⎭⎝⎭==其中，K 称为截面刚度综合变化系数，它随着s s cf cf αραρ+的增大而逐渐增大，通过对刚度B 中的系数K 进行数学分析，并利用编程的方法，可以看出000/1/311/3/c c h h εεχεε1/12⨯-+⨯-⨯、00/1/311/3/c c h h εεχεε1/12⨯-+⨯-⨯围绕0.9上下浮动，变化不是很大，故取其为0.9，同理0h χνω⨯⨯取为0. 0015。

这样钢筋屈服前用碳纤维布加固后梁的刚度可以写为：220200.910.0015s s cf cf s s cf cf h E A h E A MB h h αραρρψ⨯⨯+⨯⨯==⨯⎛⎫⨯+⨯ ⎪⎝⎭+（18） 第三部分，钢筋屈服后：因为在混凝土达到峰值应变的前后，其受压变形塑性系数ν和应力图形完整系数的表达式不同。

因此将本阶段分为两个部分：I 混凝土应变小于峰值应变，II 混凝土应变大于峰值应变。

在这两个不同阶段有下面的区别：00002/31/4/,0.00211/3/1/21/12/,0.0020.003311/3/c c c c cc Y Y εεχεεεεεχεεε-⨯⎧=⨯≤⎪-⨯⎪⎨-⨯⎪=⨯<≤⎪-⨯⎩（19） ()200/,0.002,0.0020.0033c c c cc c c c f E f E εεενενεε⎧⨯2/-⎪=≤⎪⎨⎪=<≤⎪⨯⎩（20）变形条件：变形条件表达式同钢筋屈服前的式(4)、 (5)、(7)。

本构关系：混凝土和碳纤维的应力应变关系同钢筋屈服前的式(8)、(9)，只有钢筋的应力—应变关系发生了变化：s y σσ= （21） 由平截面假定可以得到碳纤维布应变和混凝土应变之间的关系： cf c h χεεχ-=⨯（22）平衡条件：裂缝截面混凝土的拉应力为零，裂缝截面的应力分布如图2所示，在此隔离体上力的平衡方程为， 对受压混凝土的合力中心取矩：()()0y s cf cf M A h Y A h Y σχσχ=⨯⨯-++⨯⨯-+ （23）其中，Y 根据混凝土的受压应变情况，按照式（19）取值。

对受拉钢筋取矩：()0b c cf cf M h Y A σωχχσ=⨯⨯⨯⨯-++⨯⨯α （24）由式（23）、（24）可求得cf σ、cf ε、c σ、c ε。

cf ε、c ε代入（4）式得：()1cf cfh h Y E A M B Kχρ⨯-+⨯⨯==（25）其中，01s cf s s cf cf cf y s cf cf hK A h Y h A h Y σχααραρωνσσχχωνσχ⨯⨯+⨯+⨯⨯=⎛⎫⨯-+⨯⨯⨯⨯+ ⎪⎪⨯-+⎝⎭称为截面刚度综合变化系数，对刚度B 中的系数K 进行数学分析，并利用编程的方法，可以看出h Yhχ-+围绕0.9上下浮动，变化不是很大，故取其为0.9；0h Yh Yχχ-+-+取为0.83；因为混凝土是否达到峰值应变，其压区应力图形完整系数以及压区变形塑性系数是不同的，故在混凝土的应变小于峰值应变时h χων⨯⨯取0.11；混凝土应变介于峰值应变和极限应变时极限应变时hχων⨯⨯取0.06。

因此把钢筋屈服前后碳纤维布加固后梁的刚度系数写为取0.06。

因此把钢筋屈服前后碳纤维布加固后梁的刚度系数写为：0.11,0.0020.110.8310.06,,0.0020.00330.060.831y cf s cf cf cf c y s cf cf y cf s cf cf cfc y s cf cf K A A K A A σαραρσεσσσαραρσεσσ⎧⨯⨯+⨯+⎪⎪=≤⎪⎛⎫⨯⨯⨯+⎪ ⎪ ⎪⨯⎪⎝⎭⎨⎪⨯⨯+⨯+⎪=<≤⎪⎛⎫⨯⎪⨯⨯+ ⎪⎪ ⎪⨯⎝⎭⎩（26）在混凝土开裂前，碳纤维布加固梁的刚度与普通混凝土梁的刚度差别不大。

这是由于本阶段中梁受力还比较小，混凝土、钢筋和碳纤维布都处于弹性阶段，截面整体上表现出较好的弹性性质，碳纤维布与钢筋的作用完全相同，只是碳纤维布的约束使得截面的弹性性质较未加固梁更充分。