《电工学》秦曾煌第六版上下册课后答案(1)
- 格式:doc
- 大小:6.79 MB
- 文档页数:211
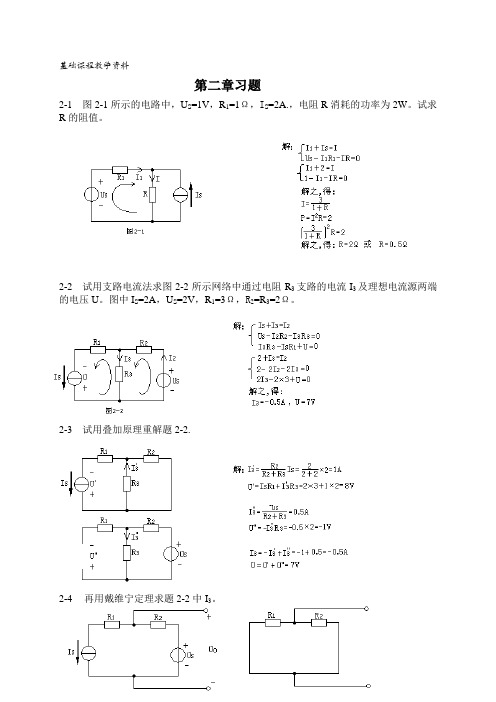
基础课程教学资料第二章习题2-1 图2-1所示的电路中,U S=1V,R1=1Ω,I S=2A.,电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中I S=2A,U S=2V,R1=3Ω,R2=R3=2Ω。
2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。
2-5 图2-3所示电路中,已知U S1=6V,R1=2Ω,I S=5A,U S2=5V,R2=1Ω,求电流I。
2-6 图2-4所示电路中,U S1=30V,U S2=10V,U S3=20V,R1=5kΩ,R2=2kΩ,R3=10kΩ,I S=5mA。
求开关S在位置1和位置2两种情况下,电流I分别为多少?2-7 图2-5所示电路中,已知U AB=0,试用叠加原理求U S的值。
2-8 电路如图2-6所示,试用叠加原理求电流I。
2-9 电路如图2-7所示,试用叠加原理求电阻R4上电压U的表达式。
2-10电路如图2-8所示,已知R1=Ω,R2=R3=2Ω,U S=1V,欲使I=0,试用叠加原理确定电流源I S的值。
2-11 画出图2-9所示电路的戴维宁等效电路。
2-12 图2-10所示的电路接线性负载时,U 的最大值和I的最大值分别是多少?2-13 电路如图2-11所示,假定电压表的内阻无穷大,电流表的内阻为零。
当开关S处于位置1时,电压表的读数为10V,当S处于位置2时,电流表的读数为5mA。
试问当S处于位置3SHI 4,电压表和电流表的读数各为多少?2-14 图2-12所示电路中,各电源的大小和方向均未知,只知每个电阻均为6Ω,又知当R=6Ω时,电流I=5A。
今欲使R支路电流I=3A,则R应该多大?2-15 图2-13所示电路中,N为线性有源二端网络,测得AB之间电压为9V,见图(a);若连接如图(b)所示,可测得电流I=1A。
现连接如图(c)所示形式,问电流I为多少?2-16 电路如图2-14所示,已知R1=5Ω时获得的功率最大,试问电阻R是多大?本章小结1、支路电流法是分析和计算电路的基本方法,适用于任何电路。

图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V电工学秦曾煌课后答案全解 doc格式1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。
电流和电压的参考方向如图中所示。
今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。
2 判断哪些元件是电源?哪些是负载?3 计算各元件的功率,电源发出的功率和负载取用的功率是否平衡?[解]:2 元件1,2为电源;3,4,5为负载。
3 P1 = U1I1 = 140 ×(−4)W = −560WP2 = U2I2 = (−90) ×6W = −540WP3 = U3I3 = 60 ×10W = 600WP4 = U4I1 = (−80) ×(−4)W =320W P5 = U5I2 = 30 ×6W = 180W P1 + P2 = 1100W 负载取用功率P = P3 + P4 + P5 = 1100W 两者平衡电源发出功率P=E1.5.2在图2中,已知I= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端1,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
电压U3[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图−I1 + I2 −I3= 0−3 + 1 −I3= 0可求得I3= −2mA, I3的实际方向与图中的参考方向相反。
根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V = 60V 其次确定电源还是负载:1 从电压和电流的实际方向判定:电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出,故为电源;电流I1从“+”端流出,故为负载。

学习-----好资料1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。
电流和电压的参考方向如图中所示。
今通过实验测量得知图1.5.1图1: 习题?I= 6A I= 10A A = I43 2 1 ?= UU= 60V V = 140U23 1 =90V U?5 = U4 30V 80V 1 试标出各电流的实际方向和各电压的实际极性。
判断哪些元件是电源?哪些是负载?2计算各元件的功率,电源发出的功率和负载取用的功率是否平衡?3]:解[为负载。
,5,2为电源;3,42 元件1电源发出功率P= ??×W (=4)= UI140 W 5603P= E 1 1 1??×W 5406W (IP= U= = 90) 2 2 2×W= I= PU= 60 60010W 3 3 3??×= 80) 4)W (IP= U= (1 4 4×30 IP320W = U= WW 6= 1802 5 5P+ P= 1100W 2 1负载取用功率P = P+ P+ P= 1100W 5 4 3两者平衡1.5.2在图2中,已知I和其两端I中的电流试确定电路元件mA= ImA= 3,1.33 12更多精品文档.学习-----好资料电压U,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
3更多精品文档.学习-----好资料[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图?? = 0 + III 2 1 3?? = 0 I1 3 + 3可求得I的实际方向与图中的参考方向相反。
?I2mA, = 33根据基尔霍夫电流定律可得?3 3 ×××)10V = 60V = U(30 + 10 103 3其次确定电源还是负载:从电压和电流的实际方向判定:1电路元件3 电流I从“+”端流出,故为电源; 3电流I从“+”端流出,故为电源;80V元件2电流I从“+”端流出,故为负载。

1 电路的基本概念与定律电源有载工作、开路与短路电源发出功率P E =在图2中,已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
[解] 首先根据基尔霍夫电流定律列出图 2: 习题图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。
根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V= 60V其次确定电源还是负载:1 从电压和电流的实际方向判定:电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出,故为电源;电流I1从“+”端流出,故为负载。
2 从电压和电流的参考方向判别:电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W =−120 ×10−3W (负值),故为电源;80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10−3W =80 ×10−3W (正值),故为电源;30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10−3 W =90 ×10−3W (正值),故为负载。
两者结果一致。
最后校验功率平衡:电阻消耗功率:2 2P R= R1I= 10 ×3 mW = 90mW12 2P R= R2I= 20 ×1 mW = 20mW2电源发出功率:P E = U2I2 + U3I3 = (80 + 120)mW =200mW负载取用和电阻损耗功率:P = U1I1 + R1 I2 + R2I2 = (90 + 90 + 20)mW =200mW1 2两者平衡基尔霍夫定律试求图6所示部分电路中电流I、I1和电阻R,设U ab = 0。

晶体管起放大作用的外部条件,发射结必须正向偏置,集电结反向偏置。
晶体管放大作用的实质是利用晶体管工作在放大区的电流分配关系实现能量转换。
2.晶体管的电流分配关系晶体管工作在放大区时,其各极电流关系如下:C B I I β≈(1)E B C B I I I I β=+=+C C BB I I I I ββ∆==∆3.晶体管的特性曲线和三个工作区域 (1)晶体管的输入特性曲线:晶体管的输入特性曲线反映了当UCE 等于某个电压时,B I 和BE U 之间的关系。
晶体管的输入特性也存在一个死区电压。
当发射结处于的正向偏压大于死区电压时,晶体管才会出现B I ,且B I 随BE U 线性变化。
(2)晶体管的输出特性曲线:晶体管的输出特性曲线反映当B I 为某个值时,C I 随CE U 变化的关系曲线。
在不同的B I 下,输出特性曲线是一组曲线。
B I =0以下区域为截止区,当CE U 比较小的区域为饱和区。
输出特性曲线近于水平部分为放大区。
(3)晶体管的三个区域:晶体管的发射结正偏,集电结反偏,晶体管工作在放大区。
此时,C I =b I β,C I 与b I 成线性正比关系,对应于曲线簇平行等距的部分。
晶体管发射结正偏压小于开启电压,或者反偏压,集电结反偏压,晶体管处于截止工作状态,对应输出特性曲线的截止区。
此时,B I =0,C I =CEO I 。
晶体管发射结和集电结都处于正向偏置,即CE U 很小时,晶体管工作在饱和区。
此时,C I 虽然很大,但C I ≠b I β。
即晶体管处于失控状态,集电极电流C I 不受输入基极电流B I 的控制。
14.3 典型例题例14.1 二极管电路如例14.1图所示,试判断二极管是导通还是截止,并确定各电路的输出电压值。
设二极管导通电压D U =。
25610VD1(a)(b)(c)(d)例图解:○1图(a )电路中的二极管所加正偏压为2V ,大于DU =,二极管处于导通状态,则输出电压0U =A U —D U =2V —=。

1 电路的基本概念与定律1.5 电源有载工作、开路与短路电源发出功率P E =1.5.2在图2中,已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。
根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V= 60V其次确定电源还是负载:1 从电压和电流的实际方向判定:电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出,故为电源;电流I1从“+”端流出,故为负载。
2 从电压和电流的参考方向判别:电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W =−120 ×10−3W (负值),故为电源;80V 元 件 U 2 和I 2的 参 考 方 向 相 反P = U 2I 2 = 80 × 1 ×10−3W = 80 × 10−3W (正值),故为电源;30V 元件 U 1 和I 1参考方向相同P = U 1I 1 = 30 × 3 × 10−3 W =90 ×10−3W (正值),故为负载。
两者结果一致。
最后校验功率平衡: 电阻消耗功率:2 2P R 1 = R 1I 1 = 10 × 3 mW = 90mW 2 2P R 2 = R 2I 2 = 20 × 1 mW = 20mW电源发出功率:P E = U 2 I 2 + U 3 I 3 = (80 + 120)mW =200mW负载取用和电阻损耗功率:P = U 1I 1 + R 1 I 2 + R 2I 2 = (90 + 90 + 20)mW = 200mW1 2两者平衡1.6 基尔霍夫定律1.6.2试求图6所示部分电路中电流I 、I 1 和电阻R ,设U ab = 0。
图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V电工学秦曾煌课后答案全解 doc格式1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。
电流和电压的参考方向如图中所示。
今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。
2 判断哪些元件是电源?哪些是负载?3 计算各元件的功率,电源发出的功率和负载取用的功率是否平衡?[解]:2 元件1,2为电源;3,4,5为负载。
3 P1 = U1I1 = 140 ×(−4)W = −560WP2 = U2I2 = (−90) ×6W = −540WP3 = U3I3 = 60 ×10W = 600W P4 = U4I1 = (−80) ×(−4)W = 320W P5 = U5I2 =130 ×6W = 180WP1 + P2 = 1100W负载取用功率P = P3+ P4 + P5 = 1100W 两者平衡电源发出功率PE=1.5.2在图2中,已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
2[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图−I1 + I2 −I3= 0−3 + 1 −I3= 0可求得I3= −2mA, I3的实际方向与图中的参考方向相反。
根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V = 60V 其次确定电源还是负载:1 从电压和电流的实际方向判定:电路元件380V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出,故为电源;电流I1从“+”端流出,故为负载。
图 1: 习题1.5.1图I1 = 4A U1 = 140V U4 = 80V I2 = 6AU2 = 90VU5 = 30VI3 = 10AU3 = 60V1 电路的基本概念与定律电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。
电流和电压的参考方向如图中所示。
今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。
2 判断哪些元件是电源哪些是负载3 计算各元件的功率,电源发出的功率和负载取用的功率是否平衡[解]:2 元件1,2为电源;3,4,5为负载。
3 P1 = U1I1 = 140 ×(4)W = 560W P2 =U2I2 = (90) ×6W = 540W P3 = U3I3 =60 ×10W = 600WP4 = U4I1 = (80) ×(4)W = 320W P5 =U5I2 = 30 ×6W = 180WP1 + P2 = 1100W负载取用功率P = P3 + P4 + P5 = 1100W两者平衡电源发出功率P E =1.5.2在图2中,已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图I1 + I2 I3= 03 + 1 I3= 0可求得I3= 2mA, I3的实际方向与图中的参考方向相反。
根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×103 )V = 60V 其次确定电源还是负载:1 从电压和电流的实际方向判定:电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出,故为电源;电流I1从“+”端流出,故为负载。
2 从电压和电流的参考方向判别:电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(2) ×103W = 120 ×103W (负值),故为电源;80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×103W =80 ×103W (正值),故为电源;30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×103 W = 90 ×103W (正值),故为负载。
14 二极管和晶体管二极管在图1所示的各电路图中,E = 5V ,u i = 10 sin ωtV ,二极管D的正向压降可忽略不计,试分别画出输出电压u0 的波形。
[ 解]图 1: 习题图(a) u i为正半周时,u i> E,D导通;u i < E,D截止。
u i为负半周时,D截止。
D导通时,u0 = E;D截止时,u o = u i。
(b)u i为正半周时;u i > E,D导通;u i < E,D截止。
u i为负半周时,D截止。
D导通时,u0 = u i;D截止时,u0 = E。
u0的波形分别如图2(a)和(b)所示。
图 2: 习题图××3在图3中,试求下列几种情况下输出端电位V Y 及各元件中通过的电流。
(1)V A= +10V ,V B= 0V ;(2)V A = +6V ,V B = +;(3)V A = V B = +5V .设二极管的正向电阻为零,反向电阻为无穷大。
[解]图 3: 习题图(1) 二极管D A优先导通,则10V Y = 9 ×1 + 9V = 9VV Y 9I D= I R == A = 1 10R 9 ×103A = 1mAD B反向偏置,截止,I D= 0(2) 设D A和D B两管都导通,应用结点电压法计算V Y :V Y =6+1 11 1 1 V =×9V = < ++191 1 9可见D B管也确能导通。
I D=6A = ×1031 ×103A =I D= A = ×1031 ×103A =I R= A = 1039 ×103A =×3 (3) D A 和D B 两管都能导通5 5 + V Y = 1 1 1 1 1 V = + + 1 1 9V Y I R = = A = 10 R 9 × 103A =I D = I D =I R = 2mA =2稳压二极管有两个稳压二极管D Z 1和D Z 2,其稳定电压分别为 和 ,正向压降都 是 。
优秀学习资料欢迎下载14.3.2 在图14.02 的各电路图中,E=5V,u i=10si nωt,二极管的正向压降可忽略不计,试分别画出输出电压u o 的波形。
u u(a)(b)(c)(d)【解】:图14.02 习题14.3.2的图(a) 电路的输出波形14.3.5 在图14.05 中,试求下列几种情况下输出端电位V F 及各元件中通过的电流:(1)V A=+10V,V B=0V;优秀学习资料欢迎下载3(2)V A=+6V,V B=+5.8V;(3)V A=V B=+5V,设二极管的正向电阻为零,反向电阻无穷大。
【解】:(1)D A 优先导通9V AVF=1+ 9×10VV= 9V9V B FIDA= IR= F =R9 ×103A = 1mA图14.05 习题14.3.5的图D B 截止,I DB=0(2)设D A 和D B 两管都导通,应用节点电压法计算V F6+5.81 1,V F = 1 1++1 11V = 5.59V < 5.8V9可见D B 管的确都导通。
IDA=6 −5.591×103A = 0.41mA,IDB= 5.8 −5.91×103A = 0.21mA,IR= 5.599×10A = 0.62mA(3)D A 和D B 两管都能导通5+5V = 1 1 V= 4.47V , I=VF =4.47A = 0.53mAF 1 1 1++1 1 9R R 9 ×10 3IDA= IDB=IR2=0.53mA = 0.26mA214.4.2 有两个稳压管D Z1 和D Z2,其稳定电压分别为5.5V 和8.5V,正向压降都是0.5V。
如果要得到0.5V、3V、6V、9V 和14V 几种稳定电压,这两个稳压管(还有限流电阻)应该如何联结?画出各个电路。
【解】:++5V+6V---++9V6V-14.3.2在图1所示的各电路图中,E = 5V ,u i = 10 sin ωtV ,二极管D的正向压降可忽略不计,试分别画出输出电压u0 的波形。
图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。
电流和电压的参考方向如图中所示。
今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。
2 判断哪些元件是电源?哪些是负载?3 计算各元件的功率,电源发出的功率和负载取用的功率是否平衡?[解]:2 元件1,2为电源;3,4,5为负载。
3 P1 = U1I1 = 140 ×(−4)W = −560WP2 = U2I2 = (−90) ×6W = −540WP3 = U3I3 = 60 ×10W = 600WP4 = U4I1 = (−80) ×(−4)W =320W P5 = U5I2 = 30 ×6W = 180WP1 + P2 = 1100W负载取用功率P = P3+ P4 + P5 = 1100W 两者平衡电源发出功率PE=1.5.2在图2中,已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3,并说明它是电源还是负载。
校验整个电路的功率是否平衡。
[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图−I1 + I2 −I3= 0−3 + 1 −I3= 0可求得I3= −2mA, I3的实际方向与图中的参考方向相反。
根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V = 60V 其次确定电源还是负载:1 从电压和电流的实际方向判定:电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出,故为电源;电流I1从“+”端流出,故为负载。
2 从电压和电流的参考方向判别:电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W =−120 ×10−3W (负值),故为电源;80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10−3W = 80 ×10−3W (正值),故为电源;30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10−3 W = 90 ×10−3W (正值),故为负载。
两者结果一致。
最后校验功率平衡:电阻消耗功率:2 2P R1= R1I1 = 10 ×3 mW = 90mW2 2P R2= R2I2 = 20 ×1 mW = 20mW电源发出功率:P E = U2I2 + U3I3 = (80 + 120)mW = 200mW负载取用和电阻损耗功率:P = U1I1 + R1 I2 + R2I2 = (90 + 90 + 20)mW = 200mW1 2两者平衡1.5.3有一直流电源,其额定功率PN= 200W ,额定电压U N= 50V 。
内阻R0 =0.5Ω,负载电阻R可以调节。
其电路如教材图1.5.1所示试求:1 额定工作状态下的电流及负载电阻;2 开路状态下的电源端电压;3 电源短路状态下的电流。
[解]P N (1) 额定电流I N =U N200=50A = 4A, 负载电阻R =U NI N50== 12.5Ω4(2) 电源开路电压U0 = E = U N + I N R0 = (50 + 4 ×0.5)V = 52VE (3) 电源短路电流I S=R052=0.5A = 104A1.5.4有一台直流稳压电源,其额定输出电压为30V ,额定输出电流为2A,从空载到额定负载,其输出电压的变化率为千分之一(即∆U= U0 −U NU N = 0.1%),试求该电源的内阻。
[解] 电源空载电压U0即为其电动势E,故可先求出U0 ,而后由U = E −R0I,求内阻R。
由此得U0 −U NU NU0 −3030= ∆U= 0.1 % U0 = E = 30.03VU N N 再由U = E − R 0I30 = 30.03 − R 0 × 2得出R 0 = 0.015Ω1.5.6一只110V 、8W 的指示灯,现在要接在380V 的电源上,问要串多大阻值的 电阻?该电阻应选多大瓦数的?[解] 由指示灯的额定值求额定状态下的电流I N 和电阻R N :I =P N N 8U N = A = 0.073A R N = 110I N 110= Ω = 1507Ω 0.073在380V 电源上指示灯仍保持110V 额定电压,所串电阻其额定功率R = U − U N I N =380 − 110 0.073 Ω = 3700ΩP N = R I 2 = 3700 × (0.073)2W = 19.6W故可选用额定值为3.7K Ω、20W 的电阻。
1.5.8图3所示的是用变阻器R 调节直流电机励磁电流I f 的电路。
设电机励磁绕组 的电阻为315Ω,其额定电压为220V ,如果要求励磁电流在0.35 ∼ 0.7A 的范围内变 动,试在下列三个变阻器中选用一个合适的:(1) 1000Ω、0.5A ;(2) 200Ω、1A ;(3) 350Ω、1A 。
[解] 当R = 0时当I = 0.35A 时220I =315= 0.7AR + 315 = 220 0.35= 630ΩR = (630 − 315) = 315Ω因此,只能选用350Ω、1A 的变阻器。
图 3: 习题1.5.8图1.5.11图4所示的是电阻应变仪中测量电桥的原理电路。
R x 是电阻应变片,粘附 在被测零件上。
当零件发生变形(伸长或缩短)时,R x 的阻值随之而改变,这 反映在输出信号U o 上。
在测量前如果把各个电阻调节到R x = 100Ω,R 1 = R 2 =R x200Ω,R 3 = 100Ω,这时满足 R 3 时,如果测出:= R 1 R 2的电桥平衡条件,U o = 0。
在进行测量(1) U o = +1mV ;(2) U o = −1mV ;试计算两种情况下的∆R x 。
U o 极性的改 变反映了什么?设电源电压U 是直流3V 。
[解] (1) U o = +1mV图 4: 习题1.5.11图应用基尔霍夫电压定律可列出:U ab + U bd + U da = 0 U ab + U o − U ad = 0或U R x + R 3 UR x + U o − 2= 03R x R x + 100+ 0.001 − 1.5 = 0解之得R x = 99.867 Ω因零件缩短而使Rx阻值减小,即(2) U o = −1mV同理∆R x = (99.867 −100)Ω= −0.133 Ω3RxR x + 100−0.001 −1.5 = 0R x = 100.133 Ω因零件伸长而使Rx阻值增大,即∆R x = (100.133 −100) Ω= +0.133 ΩU o 极性的变化反映了零件的伸长和缩短。
1.5.12图5是电源有载工作的电路。
电源的电动势E = 220V ,内阻R= 0.2Ω;负载电阻R1= 10Ω,R2 = 6.67Ω;线路电阻R l = 0.1Ω。
试求负载电阻R2并联前后:(1)电路中电流I;(2)电源端电压U1和负载端电压U2;(3)负载功率P 。
当负载增大时,总的负载电阻、线路中电流、负载功率、电源端和负载端的电压是如何变化的?[解] R2并联前,电路总电阻图5: 习题1.5.12图R = R0 + 2R l + R1 = (0.2 + 2 ×0.1 + 10) Ω= 10.4 Ω(1) 电路中电流EI ==R 22010.4A = 21.2A× R R (2) 电源端电压U 1 = E − R 0I = (220 − 0.2 × 21.2)V = 216V负载端电压(3) 负载功率U 2 = R 1I = 10 × 21.2V = 212VP = U 2I = 212 × 21.2W = 4490W = 4.49k WR 2 并联后,电路总电阻R 1R 2 10 × 6.67 R = R 0 + 2R l + 1(1) 电路中电流+ R 2 = (0.2 + 2 × 0.1 + 10 + 6.67 = 4.4 Ω(2) 电源端电压E I = =R 220 4.4A = 50AU 1 = E − R 0I = (220 − 0.2 × 50)V = 210V负载端电压R 1 R 210 × 6.67(3) 负载功率U 2 =1+ R 2I = 50V = 200V 10 + 6.67P = U 2I = 200 × 50W = 10000W = 10kW可见,当负载增大后,电路总电阻减小,电路中电流增大,负载功率增大,电 源端电压和负载端电压均降低。
1.6 基尔霍夫定律1.6.2试求图6所示部分电路中电流I 、I 1 和电阻R ,设U ab = 0。
[解] 由基尔霍夫电流定律可知,I = 6A 。
由于设U ab = 0,可得I 1 = −1A6I 2 = I 3 = 2A = 3A图 6: 习题1.6.2图并得出I 4 = I 1 + I 3 = (−1 + 3)A = 2A I 5 = I − I 4 = (6 − 2)A = 4A因I 5R = I 4 × 1得R =I 4 I 5 2= = 0.5Ω 41.7 电路中电位的概念及计算1.7.4[解]在图7中,求A 点电位V A 。
图 7: 习题1.7.4图I 1 − I 2 − I 3 = 0(1) 50 − V AI 1 =(2) 10I 2 =V A − (−50) (3) 5V A将式(2)、(3)、(4)代入式(1),得I 3 =(4)2050 − V A V A + 50 V A10− 5 − 20 = 0V A = −14.3V目录第2章电路的分析方法 3 第2.1节电阻串并联接的等效变换. . . . . . . . . . . . . . . . . . . . . 3第2.1.1题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 第2.1.2题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 第2.1.3题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 第2.1.5题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 第2.1.6题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 第2.1.7题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 第2.1.8题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 第2.3节电源的两种模型及其等效变换. . . . . . . . . . . . . . . . . . 8第2.3.1题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 第2.3.2题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 第2.3.4题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 第2.4节支路电流法. . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 第2.4.1题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 第2.4.2题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 第2.5节结点电压法. . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 第2.5.1题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 第2.5.2题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 第2.5.3题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 第2.6节叠加定理. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 第2.6.1题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 第2.6.2题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 第2.6.3题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 第2.6.4题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 第2.7节戴维南定理与诺顿定理. . . . . . . . . . . . . . . . . . . . . . 19第2.7.1题 (19)第2.7.2题 (19)第2.7.5题 (20)第2.7.7题 (21)第2.7.8题 (22)第2.7.9题 (22)第2.7.10题 (23)第2.7.11题 (24)List of Figures1习题2.1.1图 (3)2习题2.1.2图 (4)3习题2.1.3图 (4)4习题2.1.5图 (6)5习题2.1.7图 (7)6习题2.1.8图 (7)7习题2.3.1图 (8)8习题2.3.2图 (9)9习题2.3.4图 (9)10习题2.4.1图 (10)11习题2.4.2图 (11)12习题2.5.1图 (13)13习题2.5.2图 (13)14习题2.5.3图 (14)15习题2.6.1图 (15)16习题2.6.2图 (16)17习题2.6.3图 (17)18习题2.6.4图 (18)19习题2.6.4图 (18)20习题2.7.1图 (19)21习题2.7.2图 (20)22习题2.7.5图 (20)23习题2.7.7图 (21)24习题2.7.8图 (22)25习题2.7.9图 (23)26习题2.7.10图 (23)27习题2.7.11图 (24)× R R R 2 电路的分析方法2.1 电阻串并联接的等效变换2.1.1在 图1所 示 的 电 路 中 ,E = 6V ,R 1 = 6Ω,R 2 = 3Ω,R 3 = 4Ω,R 4 = 3Ω,R 5 = 1Ω,试求I 3 和I 4。