巧解机车启动问题

高中物理：机车的启动问题汽车之类的交通工具靠发动机对外做功，发动机的额定功率认为是其最大输出功率，实际工作的功率范围在0－P额之间.1、机车以恒定功率启动设机车在运动过程中所受的阻力F f保持不变，由F－F f =ma及F=P／v知，随着速度v的增大，F将减小，加速度a减小，所以机车做变加速运动，当a=0时，机车速度达到最大值v m=P／F f，以后机车将做匀速直线运动，v－t图如图所示.2、以恒定加速度a启动要维持机车的加速度恒定，则牵引力应为恒力. 由P=F v知，汽车的输出功率必将越来越大，而输出功率的增大是有限的，当输出功率达到额定功率以后，机车只能再以恒定的功率（额定功率）行驶，此后，随着速度v的继续增大，牵引力F将减小，加速度a将减小，当a=0时，速度达到最大值v m=P／F f，以后机车做匀速运动. 其v－t图如图所示. 图中的v0是匀加速过程能达到的最大速度，而v m是全过程所能达到的最大速度，两者不能混淆.例、图示为修建高层建筑常用的塔式起重机。

在起重机将质量m=5×103 kg的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加速度a=0.2 m/s2，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做v m=1.02 m/s的匀速运动。

取g=10 m/s2，不计额外功。

求：（1）起重机允许输出的最大功率。

（2）重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。

解析：（1）设起重机允许输出的最大功率为P0，重物达到最大速度时，拉力F0等于重力。

P0＝F0v m ①F0＝mg ②代入数据，有：P0＝5.1×104W ③（2）匀加速运动结束时，起重机达到允许输出的最大功率，设此时重物受到的拉力为F，速度为v1，匀加速运动经历时间为t1，有：P0＝F0v1 ④F－mg＝ma ⑤V1＝at1 ⑥由③④⑤⑥，代入数据，得：t1＝5 s ⑦T＝2 s时，重物处于匀加速运动阶段，设此时速度为v2，输出功率为P，则v2＝at ⑧P＝Fv2 ⑨由⑤⑧⑨，代入数据，得：P＝2.04×104W。

机车起动的两种方式分析机车起动问题是指汽车、火车、轮船、摩托等动力机械的起动问题，而起动过程分为以恒定功率起动和恒力起动（先匀加速起动至额定功率后再变加速运动）两种情况，因起动过程中各物理量相互关联而又发生变化，过程比较复杂，有一定的难度．1．以恒定功率起动在此过程中，机车不断加速，因为开始时机车已经达到额定功率，根据P=Fv 可知在速度v 不断增大的时候，牵引力F 会不断减小，加速度F-f=ma （f 表示机车运动过程中受到的阻力）也不断减小，但因为加速度的方向和速度的方向相同，所以无论加速度a 怎样小，速度v 也是增加的．即机车一直做加速度减小的加速运动，直到F f =时，达到最大速度m P P v F f==，此后以v m 做匀速直线运动．起动过程结束的标志就是“速度不变”． 例1．汽车发动机的额定功率为60kw,汽车质量为5t,汽车在水平路面上行驶时，阻力是车中的0.1倍，g=10m/s 2问（1）汽车保持以额定功率从静止启动能达到的最大速度是多少？解析：由P =F·v 可知，汽车在额定功率下行驶，牵引力与速度成反比．速度增大，牵引力减小，当汽车的牵引力与所受阻力相等时，速度达到最大．所以v m =P /F f=60000/0.1×5000×10m/s = 12m/s ． 说明：此类问题主要把握住机车作加速度减小的加速运动，最终匀速的运动特点，利用F f =时，达到最大速度m P P v F f==来解题． 2．先以恒力起动至额定功率后再恒功率起动该起动过程分为两个阶段：阶段１是匀加速过程，在此过程中，速度v 由零开始不断增加，功率P 也由零开始逐渐增加；由F-f=ma ，因为加速度a 是不变的，所以在此过程中牵引力F 也是不变的．此过程的结束就是第二个过程的开始，以“功率P 达到最大即额定功率，但速度没有达到最大”为标志．阶段２中因为还有加速度的存在，所以速度v 会继续增加，在功率P 不变的情况下，根据P =Fv ，可知牵引力F 不断减小，加速度a 也相应减小．第二过程结束的标志就是“机车的功率P 最大，速度v 也是最大”，到此为止，整个起动过程结束．再以后，机车将以v m 做匀速直线运动，功率不变．例2．汽车发动机的额定功率为60 kW ，汽车的质量为4 t ，当它行驶在坡度为0.02的长直公路上时，如图１，所受阻力为车重的0.1倍(g ＝10 m/s 2)，求：⑴汽车所能达到的最大速度v m =？⑵若汽车从静止开始以0.6 m/s 2的加速度做匀加速直线运动，则此过程能维持多长时间？解析： ⑴汽车在坡路上行驶，所受阻力由两部分构成，即f ＝kmg ＋mg sin α=4000＋800N=4800 N ． 又因为F ＝f 时达到最大速度，且P =f·v m ，所以36010/12.5/sin 4800m P v m s m s kmg mg α⨯===+． ⑵汽车从静止开始，以a =0.6 m/s 2匀加速行驶，由F ＝ma ，有F ′－f －mg sin α＝ma ．故 3sin 7.210F kmg mg ma N α'=++=⨯ 保持这一牵引力，汽车匀加速行驶到速度mv '，此时达到额定功率，据P Fv =有图１8.33/m m P v m s F '=='． 由运动学规律可以求出匀加速行驶的时间8.3313.90.6m v t s s a '===． 说明：此后汽车将做加速度减小的加速运动，直到达到12.5m/s,而后匀速直线运动． ３．两种启动方式的共同点对同一机车，在相同条件下，两种启动方式最终都是F =f ，匀速时的速度v m 相同．v -t 图像如图２所示．例3．电动机通过一绳子吊起质量为8 kg 的物体，绳的拉力不能超过120 N ，电动机的功率不能超过1200 W ，要将此物体由静止起用最快的方式吊高90 m （已知此物体在被吊高接近90 m 时，已开始以最大速度匀速上升）试分析应如何吊起物体？达到最大功率的最短时间是多少？匀速时的速度是多少？解析： 此题可以采用机车起动类问题的思路，即将物体吊高分为两个过程处理：第一过程是以绳所能承受的最大拉力拉物体，使物体匀加速上升，第一个过程结束时，电动机刚达到最大功率．第二个过程是电动机一直以最大功率拉物体，拉力逐渐减小，当拉力等于重力时，物体开始匀速上升.在匀加速运动过程中加速度为a =8108120m ⨯-=-m mg F m/s 2=5 m/s 2 末速度v t =1201200=m m F P =10 m/s 上升的时间t 1=510=a v t s=2 s 此即达到最大功率的最短时间．在功率恒定的过程中，最后匀速运动的速率为v m =1081200⨯==mg F F P m m =15 m/s 说明：本题考查对机车启动两类问题的理解及迁移应用的创新能力．同学们往往对整个过程分析不透，若开始即以最大功率拉，绳会被拉断．v v 2。

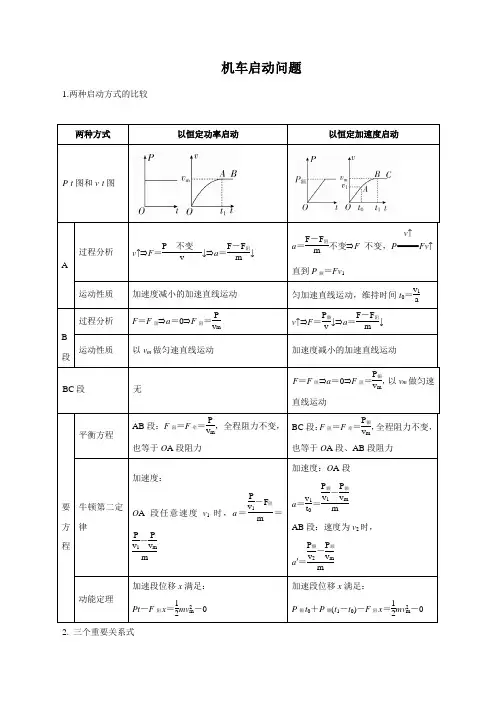
机车启动问题1.两种启动方式的比较两种方式以恒定功率启动以恒定加速度启动P -t 图和v -t 图OA段过程分析 v ↑⇒F ＝P不变v ↓⇒a ＝F －F 阻m↓ a ＝F －F 阻m 不变⇒F 不变，P =====v ↑Fv ↑直到P 额＝Fv 1运动性质 加速度减小的加速直线运动 匀加速直线运动，维持时间t 0＝v 1aA B 段过程分析 F ＝F 阻⇒a ＝0⇒F 阻＝Pv mv ↑⇒F ＝P 额v ↓⇒a ＝F －F 阻m↓运动性质以v m 做匀速直线运动加速度减小的加速直线运动BC 段 无F ＝F 阻⇒a ＝0⇒F 阻＝P 额v m ，以v m 做匀速直线运动重要方程平衡方程AB 段：F 阻＝F 牵＝P v m ，全程阻力不变，也等于O A 段阻力 BC 段：F 阻＝F 牵＝P 额v m，全程阻力不变，也等于O A 段、AB 段阻力 牛顿第二定律 加速度：O A 段任意速度v 1时，a ＝Pv 1－F 阻m ＝P v 1－P v mm加速度：O A 段 a ＝v 1t 0＝P 额v 1－P 额v m mAB 段：速度为v 2时， a ′＝P 额v 2－P 额v m m动能定理加速段位移x 满足：Pt －F 阻x ＝12mv 2m－0加速段位移x 满足：P 额t 0＋P 额(t 1－t 0)－F 阻x ＝12mv 2m－02. 三个重要关系式(1) 无论哪种启动过程，机车的最大速度都等于其匀速运动时的速度，即v m ＝PF 阻。

(2) 机车以恒定加速度启动时，匀加速过程结束后功率最大，速度不是最大，即v ＝P F <v m ＝PF 阻。

(3) 机车以恒定功率运行时，牵引力做的功W ＝Pt ，由动能定理得Pt －F 阻x ＝ΔE k ，此式经常用于求解机车以恒定功率启动过程的位移或速度。

【典例】一列火车总质量m ＝500 t ，发动机的额定功率P ＝6×105 W ，在水平轨道上行驶时，轨道对火车的阻力f 是车重的0.01倍，g 取10 m/s 2。

机车启动问题一、机车的两种启动问题当机车从静止开始沿水平面加速运动时，有两种不同的加速过程，但分析时采用的基本公式都是P Fv =和F f ma -=。

为使问题简化，假定机车所受阻力大小恒定。

1．恒定功率的加速问题由公式P Fv =和F f ma -=知，由于P 恒定，随着v 的增大，F 必将减小，a 也必将减小，机车做加速度不断减小的加速运动，直到F f =，a =0，这时v 达到最大值：m P P v F f==，可见恒定功率的加速运动一定不是匀加速运动.这种加速过程发动机做的功只能用W=Pt 计算，不能用W Fs =计算（因为F 为变力）。

以上机车的启动过程可用如图所示的v-t 图像来表示。

2．恒定牵引力的加速问题由公式P Fv =和F f ma -=知，由于F 恒定，所以a 恒定，机车做匀加速运动，而随着v 的增大，功率也将不断增大，直到功率达到额定功率P ，功率不能再增大了。

这时匀加速运动结束，其最大速度为1=m P P v v F f=＜，此后机车要想继续加速就只能做恒定功率的变加速运动了。

可见当机车做恒定牵引力的加速运动时功率一定不恒定。

这种加速过程发动机做的功只能用W=F·s计算，不能用W=P·t计算（因为P为变功率）。

以上机车的启动过程可用如图所示的v-t图像来概括说明。

0~t1时间内，机车从静止开始匀加速运动，牵引力F恒定，机车的输出功率P=Fv不断变大，t1时刻达到额定功率（匀加速阶段结束）；t1~t2时间内，机车以恒定功率继续加速，牵引力和加速度不断减小（加速度减小的加速运动），对应图像中曲线部分；t2时刻加速度减为零，F=f，机车匀速前进（对应图像中水平直线部分），此时达到最大速度m Pvf。

例题1. 一新型赛车在水平专用测试道上进行测试，该车总质量为m=1×103 kg，由静止开始沿水平测试道运动，用传感设备记录其运动的v-t图像如图所示。

机车启动问题典型例题摘要：1.机车启动问题的概念和背景2.机车启动问题的典型例题3.机车启动问题的解决方法和策略4.总结和展望正文：一、机车启动问题的概念和背景机车启动问题是指在铁路运输系统中，机车从静止状态开始加速行驶，直至达到目标速度的过程中所涉及的各种技术问题。

机车启动问题在铁路运输领域具有重要的实践意义，因为它关系到铁路运输的安全、高效和节能。

二、机车启动问题的典型例题以下是一道典型的机车启动问题例题：已知某型号机车的最大牵引力为F_max，最大速度为v_max，机车的质量为m，阻力为f。

问从静止开始，机车达到最大速度所需的最小启动时间、最大平均速度以及最小能量消耗。

三、机车启动问题的解决方法和策略1.机车启动过程的分析机车启动过程中，机车受到牵引力、阻力、重力和摩擦力等力的作用。

为了使机车达到最大速度，需要分析各种力的变化情况，找到合适的启动策略。

2.机车启动的最小启动时间为了使机车达到最大速度，需要尽可能缩短启动时间。

根据运动学公式，机车达到最大速度所需的最小启动时间为t_min = v_max / a，其中a 为机车的加速度。

3.机车启动的最大平均速度在机车启动过程中，机车的平均速度可以通过以下公式计算：v_avg = (v_0 + v_max) / 2，其中v_0 为机车启动时的速度。

为了使机车的平均速度最大，需要使v_0 接近0。

4.机车启动的最小能量消耗机车启动过程中的能量消耗与机车的牵引力、速度和时间有关。

为了使能量消耗最小，需要选择合适的启动策略，使机车的牵引力尽可能小。

四、总结和展望机车启动问题是铁路运输领域的一个重要问题，涉及到机车的安全、高效和节能。

通过对机车启动问题的研究，可以为铁路运输提供理论依据和技术支持。

机车的两种启动方式机车启动是高中物理教材功能部分的一个重要题型。

主要是两类题型：一是恒定功率启动；二是恒定加速度启动。

对于学生而言常见问题求速度、阻力、牵引力、功率、或匀加速运动的时间是，这些难度都不算大。

难度最大的是运用动能定理求变加速阶段的运动时间或位移。

在这个练习中给出了相关的练习题目，非常适合学生拔高练习 。

一、以额定功率启动（1）0～t 1时间内，功率P 不变 ，速度v 增加 ，牵引力F 减小 ，合力F 合 减小 ，加速度a 减小 ；（2）t 1时刻以后，功率P 不变 ，速度v 不变 ， 牵引力F =f ，合力F 合 =0 ，加速度a =0 ；（3）t 1时刻速度达到 最大 值，此时牵引力F 与阻力f 相等 ，v m =； （4）0～t 1时间内，汽车做 加速度逐渐减小的加速 运动； （5）t 1时刻以后，汽车做 匀速直线 运动。

（6）0～t 1时间内的位移的求解方法：动能定理 （上式是机车启动问题的难点，需要学生和教师特别重视，反复练习才能达到透彻理解，并熟练掌握。

） 二、以恒定加速度启动（1）0～t 1时间内，功率P 增大 ，速度v 增大 ，牵引力F 不变 ， 合力F 合 不变 ，加速度a 不变 ；（2）t 1～t 2时间内，功率P 不变 ，速度v 增大 ，牵引力F 减小 ， 合力F 合 减小 ，加速度a 减小 ；（3）t 2时刻以后，功率P 不变 ，速度v 不变 ，牵引力F 等于阻力 ， 合力F 合 =0 ，加速度a =0 ；（4）t 1时刻的速度v 1为 匀加速 运动的 最大 速度，v 1= at 1 ；v 1（5）t 2时刻的速度v m 为 整个过程的最大 速度，v m =； （5）t 1时刻 功率 达到最大值； （5）t 2时刻 速度 达到最大值；（6）0～t 1时间内，汽车做 匀加速直线 运动；（7）t 1～t 2时间内，汽车做 加速度逐渐减小的加速运动；（8）t 2时刻以后，汽车做 匀速直线 运动。

机车启动问题典型例题
有一辆机车启动问题的典型例题如下：
问题描述：小明有一辆机车，最近发现启动困难，有时需要多次尝试才能成功启动。

请帮助小明分析可能的原因以及解决方法。

解决思路：
1. 电池失效：检查电池是否充电正常，电池是否老化损坏，如果电池电量低或电池老化，需要更换电池。

2. 燃油供应问题：检查燃油是否充足，燃油泵是否正常工作。

如果燃油不足或燃油泵损坏，需要添加燃油或更换燃油泵。

3. 点火系统问题：检查点火线圈和火花塞是否正常，如果出现线圈故障或火花塞脏污，需要修理或更换。

4. 发动机问题：检查发动机是否正常运转，如有异常声音或震动等，需要检修发动机。

以上是机车启动问题的典型原因和解决方法，具体问题具体分析，建议小明根据实际情况逐个排查，或者请专业人士进行检修。

机车起动问题的分析及处理策略时间：2021.03.02 创作：欧阳数1. 两个起动方式机车起动问题中有两种运动模式，即机车以恒定功率（通常为额定功率）和以恒定加速度a起动。

如何分析这两种方式的起动过程及相关问题的处理，这是教与学中经常碰到的问题。

2. 两个基本关系“”和“”是分析与处理机车起动过程的两个重要的、基本的关系式。

它反映了机车瞬时状态的各量间的关系。

下图是机车在工作状态下的受力情况，应当明确P为机车的瞬时功率；F为机车的牵引力，而不是机车受的合力；v 为机车的瞬时速度；a为瞬时加速度；f为机车所受的阻力（通常机车所受阻力设为恒力）；m是机车的质量。

在实践中，我们只要抓住两个基本关系式，相关问题则会迎刃而解。

3. 两个最值速度3.1额定功率起动的情形由和可知，因功率P保持不变，速度增大，则机车的牵引力F必然减小，也就不难看出机车的加速度a因此而减小，所以该过程是一个加速度逐渐减小的运动。

显然当牵引力F减小到等于机车所受阻力f时，即F=f，其加速度a=0，则机车的速度达到最大值。

如下图所示，额定功率下起动过程的两个阶段，即从为加速度逐渐减小的加速运动；此后以速度作匀速直线运动。

3.2恒定加速度起动的情形初速度为0的匀加速起动的过程，同样根据知，由于加速度a恒定，则牵引力F不变（通常设定机车所受阻力f恒定）。

因此随着速度v增大，其机车的瞬时功率P随之增大，当P增大到额定功率时，此刻速度便是匀加速运动过程的最大速度，其大小为。

应当注意到是匀加速运动的末状态，此刻机车的功率刚好等于额定功率，而此时此刻牵引力仍为F，且F，再由两个基本关系式，容易分析出，在功率不变的情况下，速度还会继续增大，牵引力随之减小，所以此后过程是加速度逐渐减小的加速运动，直到加速度时，机车的速度达到最终的最大速度。

如下图所示，恒定加速度起动的过程的三个阶段，即从为匀加速运动阶段；为加速度逐渐减小的加速运动；此后以速度作匀速直线运动。

机车启动问题（阻力恒为f ）② v = at ② F-f = ma③ P = Fv 1 ③ P = fv m④ P = fv m⑤ 12mv m 2 - 12mv 12 = P (t 2-t 1) - fx ④ 12mv m 2=Pt – fx1. 汽车以恒定功率P 由静止出发，沿平直路面行驶，最大速度为v ，则下列判断正确的是 （ ）A ．汽车先做匀加速运动，最后做匀速运动B ．汽车先做加速度越来越大的加速运动，最后做匀速运动C ．汽车先做加速度越来越小的加速运动，最后做匀速运动D ．汽车先做加速运动，再做减速运动，最后做匀速运动2. 质量为m 的汽车，以恒定功率P 在平直马路上行驶，所受阻力恒定，匀速行驶时的速度为v 1，则汽车的速度为v 2时（v 2<v 1）的加速度为 （ ）A ．B ．C ．D ．3. 汽车发动机的功率为60kW ，汽车的质量为4t ，当它行驶在坡度为0.02的长直公路上时，所受阻力为车重的0.1倍(g 取10m ／s 2)，问:（1）汽车所能达到的最大速度v max 多大?（2）若汽车从静止开始以0.6m ／s 2的加速度作匀加速直线运动，则此过程能维持多长时间? （3）当汽车匀加速行驶的速度达到最大值时，汽车做功多少?（4）在10s 末汽车的即时功率为多大?2mv P 1mv P 2121)(v mv v v P -)(221mv mv P +4.额定功率为80kW、质量是2.0×103kg的汽车，在平直公路上行驶，在发动机保持额定功率的情况下，汽车行驶的最大速度是40m/s。

如果汽车从静止开始做匀加速直线运动，加速度的大小是2.0m/s2，运动过程中受到的阻力不变。

求：（1）汽车受到的阻力大小；（2）4.0s末汽车发动机的瞬时功率。

5.一辆摩托车在平直的公路上以恒定的加速度启动，已知摩托车的额定功率为10kw，人和车的总质量为200kg。

设行使中受到的阻力为人和车重的0.1倍并保持不变，摩托车由静止开始匀加速运动的前8秒内的位移为64m，求：（g取10m/s2）（1）摩托车做匀加速运动时加速度的大小及发动机牵引力的大小；（2）摩托车能达到的最大速率；（3）若摩托车达到最大速度时紧急制动，设车紧急制动时的制动力为车重的0.5倍，且其它阻力不计，求车滑行的距离。