山东建筑大学机械控制课件第二章
- 格式：ppt
- 大小：762.50 KB
- 文档页数：46
文档推荐
-
第六讲 机器人运动学逆解.页数:49
-
机电产品大赛报名表页数:11
-
山东大学机械工程学院2019考研复试方案页数:4
-
山东大学认识实习报告页数:11
下载文档原格式
合集下载
机械电气控制(第二章)ppt课件
精选PPT课件
10
精选PPT课件
11
三. 电器设备接线图
它是根据原理图，配合安装要求来绘制的， 用来表示各电器元件之间实际接线情况。
电器设备接线图为各电器元件的配线、检 修和施工提供了方便，实际工作时一般要与电 器控制原理图配合使用。
精选PPT课件
12
绘制电器设备接线图的主要规定:
⑴同一电器元件的各个部件应画在一起; ⑵不在同一控制柜或配电屏上的电器元件的电气连
精选PPT课件
6
2.控制线路的全部触点都要按“平常” (即未通电或未受外力作用时)状态绘出。
3. 同一电器元件的各部分分别绘在它
们完成作用的地方，但需用同一文字符号标
出。若有多个同一种类的电器元件，可在文 字符号的后面加上数字序号的下标，如KM1 、 KM2等。
精选PPT课件
7
4.对具有循环运动的机构，应给出工 作循环图，如行程开关等应绘出动作程序 和动作位置。
QF KM
M 3~
精选PPT课件
18
2. 过电流保护
对于直流电动机和绕线 式异步电动机的限流起动， 过流保护元件是过流继电器 KA，串联于主电路的隔离开 关QS与接触器KM的主触点之 间。KA的动作值一般定为1.2 倍的电动机起动电流。
精选PPT课件
19
3. 过载保护
当电动机长期超载运行时, 其绕组的温升将超 过允许值而损坏，所以应设过载保护环节，此保护 元件多采用热继电器。
热继电器具有反时限特性,但因热惯性的关系,热继 电器不会受短路电流的冲击而瞬时动作。例如当有8-10 倍的额定电流通过热继电器时,需经1-3秒的时间才能动 作,这样在热继电器动作前,就可能使热继电器的发热元 件先烧坏。所以在使用热继电器作过载保护时，还必须 将熔断器与热继电器配合使用。
机械控制工程(董玉红 第二版)—第二章 系统的数学模型
*
模型类型（与物理性能、分析、设计方法有关） 系统允许的误差条件（在允许的条件下尽可能取简单的模型形式）
Ui(S)
U0(S)
1/R
R1
CS
R2
I1(S)
I2(S)
I(S)
+
-
U0(S)
+
一、机械系统的 微分方程
1、机械平动系统 平动即直线运动，其主要元件为质量、弹簧、阻尼器。
（一）机械系统 机械系统分为平动系统和旋转系统，其数学模型的建立主要应用牛顿定理来列写。
数学模型：描述系统输入、输出变量以及内部各变 量之间关系的数学表达式。 数学模型的主要形式 ：
引言
数学模型
微分方程
传递函数
频率特性
结构框图
信号流图
复域
时域
※
L
L-1
频域
*
主要解决的问题： 为什么要建立系统的数学模型 什么是数学模型 对系统数学模型的基本要求
*
为什么要建立控制系统的数学模型?
预备知识
电容两端电压为：
解：设电路中电流为 i(t)
整理得:
例2.3 无源电器网如图2-3所示， 为输入电压， 为输出电压，列写其关于输入输出微分方程模型。
图2-3
uo(t)
Ui(t)
C
L
R
机械系统（a）和电系统（b）具有相同的数学 模型，故这些物理系统为相似系统。（即电系 统为机械系统的等效网络） 物理本质不同的系统可有相似的数学模型，同 一数学模型可以描述不同的系统。 我们可以利用简单易实现的系统（如电的系统） 去模拟其它难于实现的系统（机械系统）......
机械控制工程基础
第二章 系统的数学模型
模型类型（与物理性能、分析、设计方法有关） 系统允许的误差条件（在允许的条件下尽可能取简单的模型形式）
Ui(S)
U0(S)
1/R
R1
CS
R2
I1(S)
I2(S)
I(S)
+
-
U0(S)
+
一、机械系统的 微分方程
1、机械平动系统 平动即直线运动，其主要元件为质量、弹簧、阻尼器。
（一）机械系统 机械系统分为平动系统和旋转系统，其数学模型的建立主要应用牛顿定理来列写。
数学模型：描述系统输入、输出变量以及内部各变 量之间关系的数学表达式。 数学模型的主要形式 ：
引言
数学模型
微分方程
传递函数
频率特性
结构框图
信号流图
复域
时域
※
L
L-1
频域
*
主要解决的问题： 为什么要建立系统的数学模型 什么是数学模型 对系统数学模型的基本要求
*
为什么要建立控制系统的数学模型?
预备知识
电容两端电压为：
解：设电路中电流为 i(t)
整理得:
例2.3 无源电器网如图2-3所示， 为输入电压， 为输出电压，列写其关于输入输出微分方程模型。
图2-3
uo(t)
Ui(t)
C
L
R
机械系统（a）和电系统（b）具有相同的数学 模型，故这些物理系统为相似系统。（即电系 统为机械系统的等效网络） 物理本质不同的系统可有相似的数学模型，同 一数学模型可以描述不同的系统。 我们可以利用简单易实现的系统（如电的系统） 去模拟其它难于实现的系统（机械系统）......
机械控制工程基础
第二章 系统的数学模型
机械控制.pptx
H. Hazen
机械控制理论
第一章 绪 论
(5) 英国A. M. Turine提出图灵计算机的设想(1937) (6) 在贝尔实验室Bode领导的火炮控制系统研究小组工作的C. Shannon 提出继电器逻辑自动化理论(1938)，随后，发表专著《通信的数字理论》 (The Mathematical Theory of Communication)，奠定了信息论的基础
西汉漏壶
第一章 绪 论
(2) 亚历山大的希罗发明开闭庙门和分发圣水等自动装置(100年)
(3) 中国张衡发明水运浑象，研制出自动测量地震的候风地动仪(132年)
机械控制理论
机械控制理论
第一章 绪 论
(4) 中国马钧研制出用齿轮传动的自动指示方向的指南车(235年)
(5) 中国明代宋应星所著《天工开物》 记载有程序控制思想(CNC)的提花织 机结构图(1637年)
Lan J. Chu
(8) 美国W. Evans提出根轨迹法(Root Locus Method) (1948)，以单 输入线性系统为对象的经典控制研究工作完成。
V. Bush
机械控制理论
第一章 绪 论
(4) 美国H.S. Black提出放大器性能的负反馈方法(Negative Feedback Amplifier) (1927)
H. S. Black
第一章 绪 论
(5) 自动控制的基础为闭环控制。控制论的奠基人N.Wiener 给出的定义为：
“Feedback is a method of controlling a system by inserting into it the result of its past performance”
机械控制理论
第一章 绪 论
(5) 英国A. M. Turine提出图灵计算机的设想(1937) (6) 在贝尔实验室Bode领导的火炮控制系统研究小组工作的C. Shannon 提出继电器逻辑自动化理论(1938)，随后，发表专著《通信的数字理论》 (The Mathematical Theory of Communication)，奠定了信息论的基础
西汉漏壶
第一章 绪 论
(2) 亚历山大的希罗发明开闭庙门和分发圣水等自动装置(100年)
(3) 中国张衡发明水运浑象，研制出自动测量地震的候风地动仪(132年)
机械控制理论
机械控制理论
第一章 绪 论
(4) 中国马钧研制出用齿轮传动的自动指示方向的指南车(235年)
(5) 中国明代宋应星所著《天工开物》 记载有程序控制思想(CNC)的提花织 机结构图(1637年)
Lan J. Chu
(8) 美国W. Evans提出根轨迹法(Root Locus Method) (1948)，以单 输入线性系统为对象的经典控制研究工作完成。
V. Bush
机械控制理论
第一章 绪 论
(4) 美国H.S. Black提出放大器性能的负反馈方法(Negative Feedback Amplifier) (1927)
H. S. Black
第一章 绪 论
(5) 自动控制的基础为闭环控制。控制论的奠基人N.Wiener 给出的定义为：
“Feedback is a method of controlling a system by inserting into it the result of its past performance”
机械工程控制基础课件(第2章宋文强)
实部
虚部
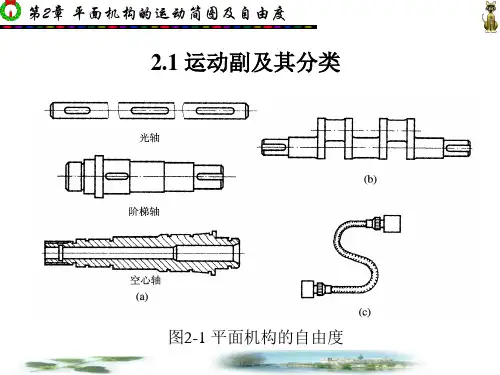
复变函数的一般表示形式
若有复变函数
K ( s z1 )(s z 2 ) ( s z m ) G( s) ( s p1 )(s p2 ) ( s pn )
当s=z1,z2,……,zm时，G(s)=0,则称z1,z2,……,zm 为G(s)的零点
当s=p1,p2,……,pn时，G(s)=∞,则称p1,p2,……,pn 为G(s)的极点
L[e
at
的拉氏变换
sin t ]
( s a) 2 2
同理可求得
sa ( s a) 2 2 n! at n L[e t ] ( s a) n 1 L[e at cost ]
4. 微分定理
若时间函数f(t)的拉氏变换为F(s)，且其一阶导数 f’(t)存在，则
f (t ) Me
at
式中，M,a均为实常数，这一个条件使拉氏变换的被 积函数的绝对值收敛
由于
f (t )e
所以
st
f (t ) e
st
f (t ) e
t
f (t )e st Me at e t Me ( a ) t
只要在复平面上对于Re(s)>a的所有复数s，都能 使前式的积分绝对收敛，则Re(s)>a为拉氏变换的 定义域，a称为收敛坐标
2. 实数域的位移定理（滞后定理）
若f(t)的拉氏变换为F(s)，则对任意正实数a，有
L[ f (t a)] e
as
F ( s)
f(t-a)是函数f(t)在时间上滞后了a秒的延时函数。 当t<a时，f(t-a)=0 证明(令 t-a = τ )
L[ f (t a )] f (t a )e st dt
《机械控制技术》PPT课件
停止： 按下停止按钮SB21 KM因线圈断电而释放
KM动合辅助触点断开 KM主触点断开 电动机M停转
编辑ppt
17
连续控制电路的保护功能：
欠压保护 接触器本身自带欠压保护功能，当电动机运行 时，电源电压下降到工作电压的85%以下时，接触器的磁通 变弱，电磁铁吸力不足，衔铁在反力弹簧的作用下释放，自 锁触点断开，失去自锁，同时主触点断开，电机停转。
电气接线图的绘制原则是：
1）各电气元件 均按实际安装位置 绘出，元件所占图 面按实际尺寸以统 一比例绘制。
2）一个元件中所 有的带电部件均画 在一起，并用点划 线框起来，即采用 集中表示法。
编辑ppt
8
3）各电气元件的图形符号和文字符号必须与电气 原理图一致，并符合国家标准。
4）各电气元件上凡是需接线的部件端子都应绘出， 并予以编号，各接线端子的编号必须与电气原理图上 的导线编号相一致。
2．电气控制线路分为主电路和控制电路。 主电路用粗线画出，控制电路用细线画出。 一般主电路画在左侧，控制电路画在右侧
3．同一电气的各导电部件用同一文字表示 4．电气控制线路中的全部触点都按“常态”绘出。
编辑ppt
3
5．原理图的绘制要层次分明，各电器元件及 触头的安排要合理，既要做到所用元件、触头 最少，耗能最少，又要保证电路运行可靠，节 省连接导线以及安装、维修方便。
一、三相异步电动机单向旋转控制线路
（一） 点动控制
点动控制是指按下按钮，电动机就得电运行；松开 按钮，电动机就失电停转。
编辑ppt
11
点动控制原理图
起动：按下按钮SB 接触器线圈KM得电 主触点KM闭合 电动机M起动运转
停止：松开按钮SB 接触器线圈KM失电 主触点KM分断
机械控制工程基础(第二章)ppt课件
dt
a0x0t
bm
dmxi t
dtm
bm1
dm1xi t
d tm1
b1
d xi t
dt
b0xi
t
在初始条件为零时，对上式进行拉氏变换
ansnan 1sn 1 a 1sa0X 0s b m smb m 1sm 1 b 1sb 0X i s
故得系统（或环节）的传递函数为
G sX X 0 is sb a m n s sm n a b n m 精 1 1 选s sn Pm P 1 T1 课 件 a b 1 1 s s a b 0 0
x0(t)Txi(t)
精选PPT课件
16
例 下图是简化了的直流发电机组。激磁电压 v恒i 定，磁通不变。
此时电枢电压 与转v速0 成正比•。若 为输入，输出是电压 ，
试v求0此系统的传递函数。
R
•
解：v 0 T
vi i
LM
式中 T——常数
v0 VsT s s 0
GsV 0ssTs
即直流发电机作为测速发电机时，可认为是微分环节。
2
x0
0
精选PPT课件
xi
3
x• 0
0
精选PPT课件
xi
4பைடு நூலகம்
F
0
x?
F
0
x?
精选PPT课件
5
线性化方法：
利用台劳公式 f(x)k n 1 0f(k k )!(a)(xa)kR n(x)
f(a)k n 1 1f(k k )!(a)(x a)kR n(x)
f( x ) f( x 0 ) f( x 0 )x ( x 0 )
物理系统的数学模型
及传递函数
a0x0t
bm
dmxi t
dtm
bm1
dm1xi t
d tm1
b1
d xi t
dt
b0xi
t
在初始条件为零时，对上式进行拉氏变换
ansnan 1sn 1 a 1sa0X 0s b m smb m 1sm 1 b 1sb 0X i s
故得系统（或环节）的传递函数为
G sX X 0 is sb a m n s sm n a b n m 精 1 1 选s sn Pm P 1 T1 课 件 a b 1 1 s s a b 0 0
x0(t)Txi(t)
精选PPT课件
16
例 下图是简化了的直流发电机组。激磁电压 v恒i 定，磁通不变。
此时电枢电压 与转v速0 成正比•。若 为输入，输出是电压 ，
试v求0此系统的传递函数。
R
•
解：v 0 T
vi i
LM
式中 T——常数
v0 VsT s s 0
GsV 0ssTs
即直流发电机作为测速发电机时，可认为是微分环节。
2
x0
0
精选PPT课件
xi
3
x• 0
0
精选PPT课件
xi
4பைடு நூலகம்
F
0
x?
F
0
x?
精选PPT课件
5
线性化方法：
利用台劳公式 f(x)k n 1 0f(k k )!(a)(xa)kR n(x)
f(a)k n 1 1f(k k )!(a)(x a)kR n(x)
f( x ) f( x 0 ) f( x 0 )x ( x 0 )
物理系统的数学模型
及传递函数
机械工程控制基础(第二章)杨叔子 第五版
Kx，
其中： K
df (x) dx
x
x0
上式即为非线性系统的线性化模型，称为增量
方程。y0 = f (x0)称为系统的静态方程；
23
增量方程的数学含义就是将参考坐标的原点移到系统 或元件的平衡工作点上，对于实际系统就是以正常工 作状态为研究系统运动的起始点，这时，系统所有的 初始条件均为零。
对多变量系统，如：y = f (x1, x2)，同样可采用泰勒级 数展开获得线性化的增量方程。
estdt
0
称为拉普拉氏积分；
F(s)称为函数f(t)的拉普拉氏变换或象函数， 它是一个复变函数；f(t)称为F(s)的原函数；
L为拉氏变换的符号。
2、拉氏反变换
f (t) L1
F (s)
1
2j
j j
F
(s)e
st
ds
,
t 0
L－1为拉氏反变换的符号。
33
3、几种典型函数的拉氏变换
单位阶跃函数1(t) f(t)
1
3、数学模型的形式
➢ 时间域：微分方程（一阶微分方程组）、差 分方程、状态方程
➢ 复数域：传递函数、结构图
➢ 频率域：频率特性 二、系统的微分方程
1、定义：时域中描述系统动态特性的数学模型。
2、 建立数学模型的一般步骤
➢ 分析系统工作原理和信号传递变换的过程，
确定系统和各元件的输入、输出量；
2
➢ 从输入端开始，按照信号传递变换过程，依据 各变量遵循的物理学定律，依次列写出各元件、 部件的动态微分方程；
R
dt
即：
RC
duo (t) dt
ui
(t)
14
例：列写下图所示机械系统的微分方程
机械设计基础课件第2章
F=3n-2pL-pH=3×4-2×6-0=0
第2章 平面机构的运动简图及自由度 图2-16 机车车轮联动机构中的虚约束
第2章 平面机构的运动简图及自由度
按照上述计算结果，一般而论，这类机构是不能运动的。 但在某些特定的几何条件下，出现了虚约束，机构就能够产生 运动。
为了便于分析，将构件4及回转副E、F拆除，得图（c）所 示机构运动图。又由题中给定的构件长度关系可知，ABCD为 一平行四边形，BC始终平行于AD，所以连杆BC作平动，其上 任一点的轨迹形状相同，连杆上E点的轨迹是以F为中心，EF为 半径的圆弧。显然，无论构件4及回转副E、F是否存在对整个 机构的运动都不发生影响。也可以说，构件4和回转副E、F引 入的一个约束不起限制作用，是虚约束。
各构件之间的联接方式如下：5和6， 7和8之间构成高副； 1和4，8和4之间构成移动副；7和4， 2和1， 2和3， 3和4之间均 为相对转动， 构成回转副。
第2章 平面机构的运动简图及自由度 图2-9 内燃机及其机构运动简图
第2章 平面机构的运动简图及自由度
2.3 平面机构的自由度
2.3.1 平面运动的自由构件具有三个自由度。当两个构件组成运
第2章 平面机构的运动简图及自由度
2.1 运动副及其分类
图2-1 平面机构的自由度
第2章 平面机构的运动简图及自由度
2.1.1
1.
若组成运动副的两个构件只能在一个平面内作相对转动， 这种运动副称为回转副，或称铰链。如图2-2(a)所示的轴承1与轴 2组成的回转副，它有一个构件是固定的，故称为固定铰链。图 2-2(b)所示构件1与构件2也组成了回转副，它的两个构件都未固 定，故称为活动铰链。例如图1-1中曲轴与气缸体所组成的回转 副是固定铰链，活塞与连杆、连杆与曲轴所组成的回转副是活动 铰链。
第2章 平面机构的运动简图及自由度 图2-16 机车车轮联动机构中的虚约束
第2章 平面机构的运动简图及自由度
按照上述计算结果，一般而论，这类机构是不能运动的。 但在某些特定的几何条件下，出现了虚约束，机构就能够产生 运动。
为了便于分析，将构件4及回转副E、F拆除，得图（c）所 示机构运动图。又由题中给定的构件长度关系可知，ABCD为 一平行四边形，BC始终平行于AD，所以连杆BC作平动，其上 任一点的轨迹形状相同，连杆上E点的轨迹是以F为中心，EF为 半径的圆弧。显然，无论构件4及回转副E、F是否存在对整个 机构的运动都不发生影响。也可以说，构件4和回转副E、F引 入的一个约束不起限制作用，是虚约束。
各构件之间的联接方式如下：5和6， 7和8之间构成高副； 1和4，8和4之间构成移动副；7和4， 2和1， 2和3， 3和4之间均 为相对转动， 构成回转副。
第2章 平面机构的运动简图及自由度 图2-9 内燃机及其机构运动简图
第2章 平面机构的运动简图及自由度
2.3 平面机构的自由度
2.3.1 平面运动的自由构件具有三个自由度。当两个构件组成运
第2章 平面机构的运动简图及自由度
2.1 运动副及其分类
图2-1 平面机构的自由度
第2章 平面机构的运动简图及自由度
2.1.1
1.
若组成运动副的两个构件只能在一个平面内作相对转动， 这种运动副称为回转副，或称铰链。如图2-2(a)所示的轴承1与轴 2组成的回转副，它有一个构件是固定的，故称为固定铰链。图 2-2(b)所示构件1与构件2也组成了回转副，它的两个构件都未固 定，故称为活动铰链。例如图1-1中曲轴与气缸体所组成的回转 副是固定铰链，活塞与连杆、连杆与曲轴所组成的回转副是活动 铰链。
机械工程控制基础ppt课件
16
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
五、本课程参考书
杨叔子主编 版社
朱骥北主编 胡寿松主编 董景新编著
王积伟编著
《机械工程控制基础》
《机械控制工程基础》 《自动控制原理》 《控制工程基础》 《控制工程基础》
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
机械设计制造(教材)
第一章 第二章 第三章 第四章 第五章 第六章 第七章
绪论 拉普拉斯变换的数学方法 系统的数学模型 系统的瞬态响应与误差分析 系统的频率特性 系统的稳定性分析 机械工程控制系统的校正与设计
二、控制理论的发展
控制理论发展大体可分三个阶段： 第一阶段： 20世纪40～50年代为经典控制论发展时期。经
典控制论的内容是以微分方程、传递函数为基 础，主要研究单输入、单输出控制系统的分析 和设计问题，对线性定常系统，这种方法是成 熟而有效的。
12
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
实现控制的三个基本步骤
•不论采用人工控制还是自动控制都具有以下的共同点： •一是要检测被控制量的实际值； •二是被控制量的实际值要与给定值进行比较得出 偏差值； •三是要用偏差值产生控制调节作用再去消除偏差。
• 总结：检测偏差，消除偏差
23
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
五、本课程参考书
杨叔子主编 版社
朱骥北主编 胡寿松主编 董景新编著
王积伟编著
《机械工程控制基础》
《机械控制工程基础》 《自动控制原理》 《控制工程基础》 《控制工程基础》
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
机械设计制造(教材)
第一章 第二章 第三章 第四章 第五章 第六章 第七章
绪论 拉普拉斯变换的数学方法 系统的数学模型 系统的瞬态响应与误差分析 系统的频率特性 系统的稳定性分析 机械工程控制系统的校正与设计
二、控制理论的发展
控制理论发展大体可分三个阶段： 第一阶段： 20世纪40～50年代为经典控制论发展时期。经
典控制论的内容是以微分方程、传递函数为基 础，主要研究单输入、单输出控制系统的分析 和设计问题，对线性定常系统，这种方法是成 熟而有效的。
12
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
实现控制的三个基本步骤
•不论采用人工控制还是自动控制都具有以下的共同点： •一是要检测被控制量的实际值； •二是被控制量的实际值要与给定值进行比较得出 偏差值； •三是要用偏差值产生控制调节作用再去消除偏差。
• 总结：检测偏差，消除偏差
23
为 了 规 范 事 业单位 聘用关 系，建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度， 保障用 人单位 和职工 的合法 权益
山东建筑大学机械控制课件
第 二 节 串 联 校 正
工程实例
采用Bode图对雕刻机的控制系统进行 相位滞后校正
第八章 系统的性能校正
采 用 波 德 图 进 行 相 位 滞 后 校 正
相位滞后校正
第 二 节 串 联 校 正
雕刻机x轴位置控制系统
第八章 系统的性能校正
相位滞后校正
第 二 节 串 联 校 正
采 用 波 德 图 进 行 相 位 滞 后 校 正
T 1 m 。为 T
，可得零
第7步
画出系统校正后的Bode图，验算相角稳定裕度，如不满足 要求可增大 从步骤（3）重新计算，直到满足要求。
第8步
校验其他性能指标。
第八章 系统的性能校正
相位滞后校正
第 二 节 串 联 校 正
相 位 滞 后 校 正
相 位 滞 后 校 正
相位滞后校正
采 用 波 德 图 进 行 相 位 滞 后 校 正
第八章 系统的性能校正
相位滞后校正
第 二 节 串 联 校 正
采 用 波 德 图 进 行 相 位 滞 后 校 正
（5）确定滞后校正环节的转角频率。
第八章 系统的性能校正
相位滞后校正
第 二 节 串 联 校 正
采 用 波 德 图 进 行 相 位 滞 后 校 正
PD
1
PD控制规律
PD控制规律时域方程
PD控制传递函数
第八章 系统的性能校正
PD调节器
第 调 节 三 器 节 PID 校 正
PD
1
PD控制规律
PD调节器控制框图
PD调节器Bode图
第八章 系统的性能校正
PD调节器
第 调 节 三 器 节 PID 校 正
机械原理课件 山东建筑大学 刘会英 第二版
束”。
第二章 机构的组成和结构分析 机构的结构分析 第二章
机构中为什么要使用虚约束?
a.使受力状态更合理 b.使机构平衡
使用虚约束时要注意什么问题?
保证满足虚约束存在的几何条件，在机械设计中使用 虚约束时，机械制造的精度要提高。 作业：2-2 a b c d
第二章 机构的组成和结构分析 机构的结构分析 第二章 第四节 平面机构的组成原理与结构分析
例2-9
+
+
=
综上所述，把若干个自由度为零的基本杆组依次连接到原动件和机架上，就可 组成一个新的机构，其自由度数与原动件数目相等。上图表示了根据机构组成原理 组成机构的过程。首先把Ⅱ级杆组BCD通过其外副B、D连接到基本机构上形成四杆 机构ABCD。再把Ⅲ级杆组通过外副E、I、J依次与Ⅱ级杆组及机架连接，组成图示
第二章 机构的组成和结构分析 机构的结构分析 第二章
第三节 机构自由度的计算
机构的自由度——机构所具有的独立运动的数目。
转动副构件
移动副构件
高副构件
结论：
平面低副具有两个约束，平面高副具有一个约束。
第二章 机构的组成和结构分析 机构的结构分析 第二章
一、机构自由度计算公式
设机构有N个构件，N-1=n个活动构件，用PL个低副，PH个高副连接 后，机构的3n个自由度，受到2PL+PH个约束，则
构件在多处接触而构成平面高副且各 接触点处的公法线彼此重合时，只有 一个高副起约束作用，如图中凸轮与 从动杆构成的两高副A 、B之一为虚约 束。
A
这时：
B
F=3×2－2×2－1×1=1
第二章 机构的组成和结构分析 机构的结构分析 第二章
虚约束之五
机械工程控制基础【共81张PPT】精选全文完整版
2、传递函数确定
（1）对实验测得的系统对数幅频曲线进行分段处理。即用斜率 为20dB/dec整数倍的直线段来近似测量到的曲线。
（2）当某处系统对数幅频特性渐近线的斜率发生变化时，此 即为某个环节的转折频率。①当斜率变化+20dB/dec时,可知处 有一个一阶微分环节Ts+1; ②若斜率变化+40dB/dec时，则处 有一个二阶微分环节 (s2/ 2n+2s/n+1) ③ 若斜率变化 20dB/dec时,则处有一个惯性环节1/(Ts+1);③若斜率变化40dB/dec时，则处有一个二阶振荡环节1/ (s2/ 2n+2s/n+1) 。
系统开环的对数幅频特性:
n
L() 20 lg A() 20 lg[ Ai ()]
n
20 lg Ai ()
i 1
i 1 n
Li ()
开环相频特i性1 :
n
() G( j) i ()
由此看出，系统的开环i对1 数幅频特性L(ω)等于各
个串联环节对数幅频特性之和；系ቤተ መጻሕፍቲ ባይዱ的开环相频特
性 等于各个环节相频特性之和。
即用斜率为 20dB/dec整数倍的直线段来近似测量到的曲线。
绘图制4-1系7 统纯开微环分2对环数节幅的频Bo特de性图曲线的一般步骤：
2
(2) 将各环节的对数幅频特性和相频特性曲线分别画于半对数
极坐标图在 时，在实轴上的投影为实频特性 ，在虚轴上的投影为虚频特性
对数相频特性横轴采用对数分度，纵轴为线性分度，单位为度。
曲线。
对数幅频特性的纵轴
为L(ω)=20lgA(ω)采用线 性分度，A(ω)每增加10 倍，L(ω)增加20dB；横坐 标采用对数分度，即横 轴上的ω取对数后为等 分点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
拉氏变换的定义
第 二 节 拉 氏 变 换
1
阶跃函数
单位阶 跃函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
阶跃函数
阶跃响应 函数实例
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
单位脉冲函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
初值定理
应用
计算 初值
终值定理
应用
计算 终值
卷积定理
第二章 机械工程控制论的数学基础
拉氏逆变换的定义
第 三 拉 氏 逆 变 换
拉氏逆变换的定义
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉 氏 逆 变 换 的 数 学 方 法
有理函数法
根据拉氏逆变换公式 求解。 拉氏变换表查出相应 的原函。 通过代数运算将一个复 杂的象函数化为数个简 单的部分分式之和。
本 章 小 结
数学基础
复数和复变函数
拉氏变换
拉氏逆变换
复数； 复数运算规则； 复变函数； 复变函数零点和极点。
拉氏变换定义； 典型环节的拉氏变换； 拉氏逆变换定义； 拉氏逆变换的工程应用 拉氏变换定理； 拉氏变换表； 拉氏变换的工程应用。
第二章 机械工程控制论的数学基础
本 章 小 结
拉氏变换是分将微分方程代数化的数学工具，通过拉氏变换将 1 复杂的微积分运算变换为简单的代数运算，是分析机电控制系 统的基本数学方法之一。
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
f (t ) L1[ F ( s)] (4 3j)e ( 1 j) t (4 3j)e ( 1 j) t 5e2 t 3e 4 t e t [4(e( jt ) e( jt ) ) 3j(e jt e jt )] 5e2 t 3e4 t e t (8 cos t 6 sin t ) 5e 2 t 3e 4 t
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
拉氏逆变换的数学方法
通过拉氏变换将常微分方程化 第一步 为象函数的代数方程；
第二步 解出象函数；
由拉氏逆变换求得常微分方程 第三步 的解。
第二章 机械工程控制论的数学基础
1
虚数单位
注意！ j 是正体
2
虚数
3
复数
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
4
一个复数为零
5
共轭复数 复数有多种表示形式
6
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
两个复数相加（或相减）
2
两个复数相乘
3
两个复数相除
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床 动力滑台 示意图
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床动 力滑台动力 学模型
质量-弹簧阻尼系统
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
积分定理
多重积分的拉氏变换
当所有初始值均为零时
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
查表法
部分分式法
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉氏逆变换的求解
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
5
正弦函数和余弦函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
6
幂函数
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
1
卷积定理
9
2 相似定理
终值定理 8
拉氏变换 主要运算定理
3 时域位移定理
初值定理 7
6 5
4
复域位移定理
2 3
复变函数的零、极点表示 复变函数的零点
4
复变函数的极点
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
第二章 机械工程控制论的数学基础
第二章 机械工程控制论的数学基础
复数和复变函数
拉氏变换
拉氏逆变换
拉氏变换在控制工程中的应用
第二章 机械工程控制论的数学基础
典型环节的Bode图
第 一 节 复 数 和 复 变 函 数
复数
1
复数和 复变函数 复变函数零 3 点和极点
2 复数运
算规则
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
解： （1）列写时域内方程
时域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
（2）推导复域内方程
复域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
（3）求时域内解
时域内解
第二章 机械工程控制论的数学基础
典型的时间函数的拉氏变换、拉氏变换的主要运算定理有助于 2 分析和研究其他复杂系统函数的拉氏变换，简化运算。
3 拉氏逆变换是拉氏变换的逆变换。
拉式变换是分析研究线性动态系统的有力数学工具。通过拉式 4 变换将时域的微分方程变换为复数域的代数方程进行求解，通 过拉氏逆变换获得系统的时域解。
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
相同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
f(t) 分段函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
拉氏变换的定义域
拉氏变换 定义域
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
象函数
4
原函数
第二章 机械工程控制论的数学基础
第 二 节 拉 氏 变 换
单位脉冲函数
单位脉冲 函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
单位斜坡函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
4
指数函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
s1 r11 r1 (1 2 ) s2 r2 2 r2
极坐标运 算形式
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
1
复变函数 复变函数 =
G(s) u jv
实部
+
G ( s)
j虚部
K ( s z1 )(s z2 ) s( s p1 )(s p2 )
注意！ 代数运 算形式
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
用矢量表示复数
s1 (r11 )
s2 (r2 2 )
2
两个复数相乘
s1 s2 (r11 )(r22 ) r1r2(1 2 )
注意！ 3 两个复数相除
积分定理
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
相似定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
时域位移定理
复域位移定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
第 二 节 拉 氏 变 换
1
阶跃函数
单位阶 跃函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
阶跃函数
阶跃响应 函数实例
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
单位脉冲函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
初值定理
应用
计算 初值
终值定理
应用
计算 终值
卷积定理
第二章 机械工程控制论的数学基础
拉氏逆变换的定义
第 三 拉 氏 逆 变 换
拉氏逆变换的定义
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉 氏 逆 变 换 的 数 学 方 法
有理函数法
根据拉氏逆变换公式 求解。 拉氏变换表查出相应 的原函。 通过代数运算将一个复 杂的象函数化为数个简 单的部分分式之和。
本 章 小 结
数学基础
复数和复变函数
拉氏变换
拉氏逆变换
复数； 复数运算规则； 复变函数； 复变函数零点和极点。
拉氏变换定义； 典型环节的拉氏变换； 拉氏逆变换定义； 拉氏逆变换的工程应用 拉氏变换定理； 拉氏变换表； 拉氏变换的工程应用。
第二章 机械工程控制论的数学基础
本 章 小 结
拉氏变换是分将微分方程代数化的数学工具，通过拉氏变换将 1 复杂的微积分运算变换为简单的代数运算，是分析机电控制系 统的基本数学方法之一。
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
f (t ) L1[ F ( s)] (4 3j)e ( 1 j) t (4 3j)e ( 1 j) t 5e2 t 3e 4 t e t [4(e( jt ) e( jt ) ) 3j(e jt e jt )] 5e2 t 3e4 t e t (8 cos t 6 sin t ) 5e 2 t 3e 4 t
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
拉氏逆变换的数学方法
通过拉氏变换将常微分方程化 第一步 为象函数的代数方程；
第二步 解出象函数；
由拉氏逆变换求得常微分方程 第三步 的解。
第二章 机械工程控制论的数学基础
1
虚数单位
注意！ j 是正体
2
虚数
3
复数
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
4
一个复数为零
5
共轭复数 复数有多种表示形式
6
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
两个复数相加（或相减）
2
两个复数相乘
3
两个复数相除
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床 动力滑台 示意图
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床动 力滑台动力 学模型
质量-弹簧阻尼系统
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
积分定理
多重积分的拉氏变换
当所有初始值均为零时
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
查表法
部分分式法
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉氏逆变换的求解
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
5
正弦函数和余弦函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
6
幂函数
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
1
卷积定理
9
2 相似定理
终值定理 8
拉氏变换 主要运算定理
3 时域位移定理
初值定理 7
6 5
4
复域位移定理
2 3
复变函数的零、极点表示 复变函数的零点
4
复变函数的极点
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
第二章 机械工程控制论的数学基础
第二章 机械工程控制论的数学基础
复数和复变函数
拉氏变换
拉氏逆变换
拉氏变换在控制工程中的应用
第二章 机械工程控制论的数学基础
典型环节的Bode图
第 一 节 复 数 和 复 变 函 数
复数
1
复数和 复变函数 复变函数零 3 点和极点
2 复数运
算规则
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
解： （1）列写时域内方程
时域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
（2）推导复域内方程
复域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
（3）求时域内解
时域内解
第二章 机械工程控制论的数学基础
典型的时间函数的拉氏变换、拉氏变换的主要运算定理有助于 2 分析和研究其他复杂系统函数的拉氏变换，简化运算。
3 拉氏逆变换是拉氏变换的逆变换。
拉式变换是分析研究线性动态系统的有力数学工具。通过拉式 4 变换将时域的微分方程变换为复数域的代数方程进行求解，通 过拉氏逆变换获得系统的时域解。
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
相同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
f(t) 分段函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
拉氏变换的定义域
拉氏变换 定义域
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
象函数
4
原函数
第二章 机械工程控制论的数学基础
第 二 节 拉 氏 变 换
单位脉冲函数
单位脉冲 函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
单位斜坡函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
4
指数函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
s1 r11 r1 (1 2 ) s2 r2 2 r2
极坐标运 算形式
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
1
复变函数 复变函数 =
G(s) u jv
实部
+
G ( s)
j虚部
K ( s z1 )(s z2 ) s( s p1 )(s p2 )
注意！ 代数运 算形式
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
用矢量表示复数
s1 (r11 )
s2 (r2 2 )
2
两个复数相乘
s1 s2 (r11 )(r22 ) r1r2(1 2 )
注意！ 3 两个复数相除
积分定理
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
相似定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
时域位移定理
复域位移定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换