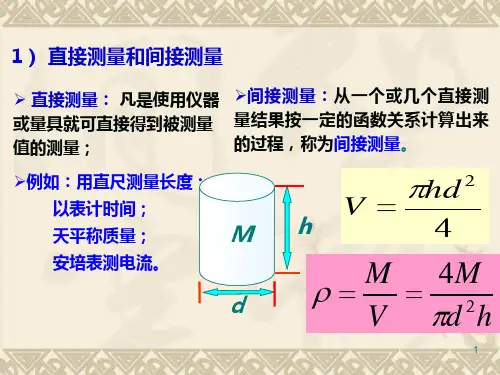
多次测得值的算术平均值常称为最佳估计值、最可信 赖值。
2.剩余误差
当进行有限次测量时,定义测得值与算术平均值之差为剩余
误差(残差):
_
vix ix
实际测量情况
(2.4.7)
比较:当测量次数n→∞时,测得值与实际值之差称为随机误 差:
i xi A
对(2.4.7)式两边求和:
对(2.4.7)式:
_
vix i 两x 边求和得:
P29式(2.4.19)
即:当n → ∞时,测量值x 落在 (EX± 1σ)范围内的概
率为68.3%。
或:在有限次的测定中,可以有68.3%的把握说, 在
(Ex±1σ)区间内包含真值。
或:在置信区间 (Ex±1σ)内,能以68.3%的概 率将最佳估值Ex包含在内。
同理当n → ∞时,随机误差落在(±2σ)范围内的概率
n11i n1vi2
(2.4.21)
4. 算术平均值的标准偏差(P31) 在等精度的测量中:进行 m组×n次的测量。 则每一组测量值都有一个算术平均值 , 就x _ 会组成平 均值列,即算术平均值也会有随机误差。
定义算术平均值的标准偏差为:
P32
x
n
同样定义算术平均值的极限误差为:
3
x
x
因此,测量结果可以表示:
能接近满刻度值(仪表上限,一般以指示值处于满度值的2/3 处为宜。 2.在同一量程内,测得值越小,示值相对误差越大。
由满度相对误差定义
m
x xm 10000
给出了仪表的精度等级 S 。
(2.1.8)
仪表精度等级定义为引用误差去掉“±”号和“ % ”号。
我国仪表精度等级依次划分为0.1、0.2、0.5、1.0、1.5、 2.0、等。(必须牢记!!!)