2014级光学技术基础复习
- 格式:docx
- 大小:312.64 KB
- 文档页数:20

光学复习题大学光学复习题大学光学是物理学中的一个重要分支,涉及到光的传播、反射、折射等现象。
对于学习光学的学生来说,复习题是巩固知识、检验理解的重要方式。
在这篇文章中,我们将为大家呈现一些光学复习题,帮助大家巩固光学知识。
1. 什么是光的折射?请解释折射定律。
光的折射是指光线从一种介质传播到另一种介质时的偏折现象。
折射定律是描述光线在两种介质交界面上折射的规律。
它可以用以下公式表示:n1sinθ1 = n2sinθ2其中,n1和n2分别表示两种介质的折射率,θ1和θ2分别表示入射角和折射角。
根据折射定律,我们可以计算出光线在不同介质中的传播方向和角度。
2. 什么是光的全反射?请解释全反射的条件。
光的全反射是指当光线从光密介质射向光疏介质时,入射角大于临界角时,光线完全被反射回光密介质中的现象。
全反射的条件是入射角大于临界角,临界角可以用以下公式计算:θc = arcsin(n2/n1)其中,n1和n2分别表示两种介质的折射率。
当入射角大于临界角时,光线无法从光疏介质中透射出来,发生全反射。
3. 请解释什么是薄透镜?薄透镜有哪些特点?薄透镜是指厚度远小于其曲率半径的透镜。
根据透镜的形状,薄透镜可以分为凸透镜和凹透镜。
薄透镜具有以下特点:- 平行光线经过薄透镜后会发生折射,形成会聚或发散的光线。
- 光线通过薄透镜时,会遵循透镜的成像规律,即光线会交叉或汇聚于一点,形成实像或虚像。
- 薄透镜的焦距可以通过以下公式计算:1/f = (n-1)(1/R1 - 1/R2),其中f表示焦距,n表示介质的折射率,R1和R2表示透镜的曲率半径。
4. 什么是干涉现象?请解释干涉的原理。
干涉是指两束或多束光线相遇时产生的明暗条纹现象。
干涉现象的原理基于光的波动性。
当两束光线相遇时,它们会相互干涉,产生干涉条纹。
干涉的原理可以用光的波动理论解释。
当两束光线相遇时,它们会形成叠加波,根据波的叠加原理,两束光线的干涉可以是相长干涉(增强)或相消干涉(减弱)。

2014级光学技术基础复习一、填空题1.光的直线传播定律指出光在同种均匀介质中沿直线传播。
2.全反射的条件是入射角等于或大于临界角,光从光光密介质射向光光疏介质产生全反射。
3.虚物点是发散光线的反向延长线的交点。
4.光学系统的物方焦点的共轭象点在像方的无穷远处,象方焦点的共轭点在物方的无穷远处。
5.某种透明物质对于空气的临界角为45°,该透明物质的折射率等于 1.41 。
6.在符号法则中,反射定律的数学式为。
7.通过物方主点的光线,必通过象方,其横向放大率为。
8.几何光学的三个基本定律是,和。
9.曲率半径为R的球面镜的焦距为,若将球面镜浸入折射率为n的液体内,该系统的焦距为。
10.在符号法则中(光线从左向右入射)规定:主光轴上的点的距离从量起,左负右正;轴外物点的距离上正下负;角度以为始边,顺时针旋转为正,反之为负,且取小于π/2的角度;在图上标明距离或角度时,必须用。
11.当物处于主光轴上无穷远处,入射光线平行于主光轴,得到的象点称为,薄透镜成象的高斯公式是。
12.主平面是理想光具组的一对共轭平面;节点是理想光具组的一对共轭点。
13.实象点是的光束的交点。
14.实物位于凹球面镜的焦点和曲率中心之间,象的位置在与之间。
二、计算题1.利用公式证明位于正薄透镜物方焦点前一倍焦距的物经透镜所成像为等高倒立实像,并作图验证之。
2置于空气中的玻璃球,折射率为n=1.5,半径为R。
(1)物在无穷远时经过玻璃球成像在何处?(2)物在玻璃球前2R处,经玻璃球成像在何处?大小如何?3一物体位于半径为R的凹面镜前何处可分别得到放大4倍的实像、放大4倍的虚像、缩小4倍的实像、缩小4倍的虚像,计算并作图验证解:(1)放大4倍的实像(2)放大四倍虚像(3)缩小四倍实像(4)缩小四倍虚像4.一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。

2014级光学技术基础复习一、填空题1.光的直线传播定律指出光在同种均匀介质中沿直线传播。
2.全反射的条件是入射角等于或大于临界角,光从光光密介质射向光光疏介质产生全反射。
3.虚物点是发散光线的反向延长线的交点。
4.光学系统的物方焦点的共轭象点在像方的无穷远处,象方焦点的共轭点在物方的无穷远处。
5.某种透明物质对于空气的临界角为45°,该透明物质的折射率等于 1.41 。
6.在符号法则中,反射定律的数学式为。
7.通过物方主点的光线,必通过象方,其横向放大率为。
8.几何光学的三个基本定律是,和。
9.曲率半径为R的球面镜的焦距为,若将球面镜浸入折射率为n的液体内,该系统的焦距为。
10.在符号法则中(光线从左向右入射)规定:主光轴上的点的距离从量起,左负右正;轴外物点的距离上正下负;角度以为始边,顺时针旋转为正,反之为负,且取小于π/2的角度;在图上标明距离或角度时,必须用。
11.当物处于主光轴上无穷远处,入射光线平行于主光轴,得到的象点称为,薄透镜成象的高斯公式是。
12.主平面是理想光具组的一对共轭平面;节点是理想光具组的一对共轭点。
13.实象点是的光束的交点。
14.实物位于凹球面镜的焦点和曲率中心之间,象的位置在与之间。
二、计算题1.利用公式证明位于正薄透镜物方焦点前一倍焦距的物经透镜所成像为等高倒立实像,并作图验证之。
2置于空气中的玻璃球,折射率为n=1.5,半径为R。
(1)物在无穷远时经过玻璃球成像在何处?(2)物在玻璃球前2R处,经玻璃球成像在何处?大小如何?3一物体位于半径为R的凹面镜前何处可分别得到放大4倍的实像、放大4倍的虚像、缩小4倍的实像、缩小4倍的虚像,计算并作图验证解:(1)放大4倍的实像(2)放大四倍虚像(3)缩小四倍实像(4)缩小四倍虚像4.一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
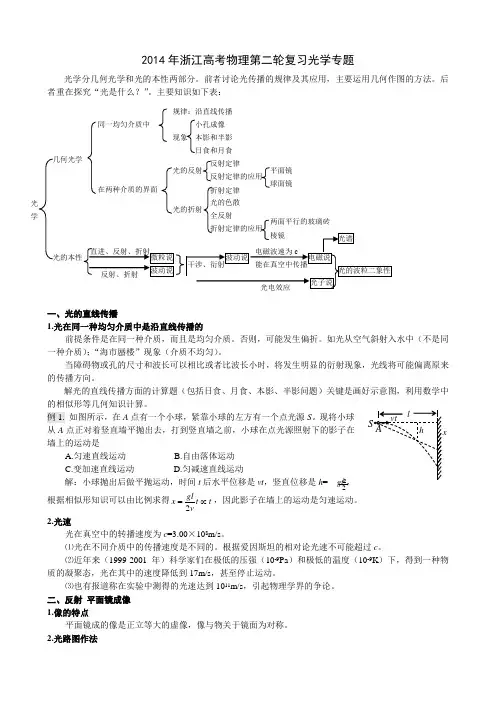
2014年浙江高考物理第二轮复习光学专题光学分几何光学和光的本性两部分。
前者讨论光传播的规律及其应用,主要运用几何作图的方法。
后者重在探究“光是什么?”。
主要知识如下表:一、光的直线传播1.光在同一种均匀介质中是沿直线传播的前提条件是在同一种介质,而且是均匀介质。
否则,可能发生偏折。
如光从空气斜射入水中(不是同一种介质);“海市蜃楼”现象(介质不均匀)。
当障碍物或孔的尺寸和波长可以相比或者比波长小时,将发生明显的衍射现象,光线将可能偏离原来的传播方向。
解光的直线传播方面的计算题(包括日食、月食、本影、半影问题)关键是画好示意图,利用数学中的相似形等几何知识计算。
例1. 如图所示,在A 点有一个小球,紧靠小球的左方有一个点光源S 。
现将小球从A 点正对着竖直墙平抛出去,打到竖直墙之前,小球在点光源照射下的影子在墙上的运动是A.匀速直线运动B.自由落体运动C.变加速直线运动D.匀减速直线运动解:小球抛出后做平抛运动,时间t 后水平位移是vt ,竖直位移是h = gt 2,根据相似形知识可以由比例求得t t vgl x ∝=2,因此影子在墙上的运动是匀速运动。
2.光速光在真空中的转播速度为c =3.00×108m/s 。
⑴光在不同介质中的传播速度是不同的。
根据爱因斯坦的相对论光速不可能超过c 。
⑵近年来(1999-2001年)科学家们在极低的压强(10-9Pa )和极低的温度(10-9K )下,得到一种物质的凝聚态,光在其中的速度降低到17m/s ,甚至停止运动。
⑶也有报道称在实验中测得的光速达到1011m/s ,引起物理学界的争论。
二、反射 平面镜成像1.像的特点平面镜成的像是正立等大的虚像,像与物关于镜面为对称。
2.光路图作法 规律:沿直线传播小孔成像 本影和半影 日食和月食 现象 同一均匀介质中光的本性几何光学 在两种介质的界面 光学 1 2根据平面镜成像的特点,在作光路图时,可以先画像,后补光路图。

2014级光学技术基础复习一、填空题1.光的直线传播定律指出光在同种均匀介质中沿直线传播。
2.全反射的条件是入射角等于或大于临界角,光从光光密介质射向光光疏介质产生全反射。
3.虚物点是发散光线的反向延长线的交点。
4.光学系统的物方焦点的共轭象点在像方的无穷远处,象方焦点的共轭点在物方的无穷远处。
5.某种透明物质对于空气的临界角为45°,该透明物质的折射率等于 1.41 。
6.在符号法则中,反射定律的数学式为。
7.通过物方主点的光线,必通过象方,其横向放大率为。
8.几何光学的三个基本定律是,和。
9.曲率半径为R的球面镜的焦距为,若将球面镜浸入折射率为n的液体内,该系统的焦距为。
10.在符号法则中(光线从左向右入射)规定:主光轴上的点的距离从量起,左负右正;轴外物点的距离上正下负;角度以为始边,顺时针旋转为正,反之为负,且取小于π/2的角度;在图上标明距离或角度时,必须用。
11.当物处于主光轴上无穷远处,入射光线平行于主光轴,得到的象点称为,薄透镜成象的高斯公式是。
12.主平面是理想光具组的一对共轭平面;节点是理想光具组的一对共轭点。
13.实象点是的光束的交点。
14.实物位于凹球面镜的焦点和曲率中心之间,象的位置在与之间。
二、计算题1.利用公式证明位于正薄透镜物方焦点前一倍焦距的物经透镜所成像为等高倒立实像,并作图验证之。
2置于空气中的玻璃球,折射率为n=1.5,半径为R。
(1)物在无穷远时经过玻璃球成像在何处?(2)物在玻璃球前2R处,经玻璃球成像在何处?大小如何?3一物体位于半径为R的凹面镜前何处可分别得到放大4倍的实像、放大4倍的虚像、缩小4倍的实像、缩小4倍的虚像,计算并作图验证解:(1)放大4倍的实像(2)放大四倍虚像(3)缩小四倍实像(4)缩小四倍虚像4.一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。


光学复习题集及答案光学是物理学中的一个重要分支,研究光的传播、折射、反射、干涉和衍射等现象。
光学作为一门基础学科,是许多科学和技术领域的基础。
为了帮助大家更好地复习光学知识,本文将提供一套光学复习题集及答案,希望能对大家的学习有所帮助。
一、选择题1. 光是一种怎样的物质?A. 波动物质B. 电磁波C. 粒子物质D. 固体物质答案:B. 电磁波2. 在以下哪种介质中光速最快?A. 真空B. 空气C. 水D. 玻璃答案:A. 真空3. 光的折射定律是由谁提出的?A. 牛顿B. 惠更斯C. 费马D. 斯内尔答案:C. 费马4. 光的干涉现象中,两束光发生干涉的条件是什么?A. 光程差不为零B. 光程差为整数倍波长C. 光程差为半整数倍波长D. 光程差为奇数倍波长答案:B. 光程差为整数倍波长5. 光的波动性最早是由谁提出的?A. 亚里士多德B. 盖洛乌C. 光栅D. 亨利答案:A. 亚里士多德二、判断题1. 光在真空中传播速度恒定。
答案:对2. 在光的折射定律中,光线从光密介质入射到光疏介质时,折射角大于入射角。
答案:错3. 光的波长越长,频率越高。
答案:错4. 紫光的频率比红光的频率高。
答案:对5. 光的干涉现象是光的波动性质的直接证据。
答案:对三、解答题1. 请解释光的干涉现象。
答案:光的干涉是指两束或多束光波相互叠加产生的明暗交替条纹的现象。
当两束光波的光程差为整数倍波长时,波峰与波峰相重合,或波谷与波谷相重合,此时出现明条纹。
而当两束光波的光程差为半整数倍波长时,波峰与波谷相重合,或波谷与波峰相重合,此时出现暗条纹。
这种干涉现象可以用来测量波长、厚度、折射率等物理量。
2. 请解释光的衍射现象。
答案:光的衍射是指光通过一个小孔或经过物体边缘后的传播现象。
当光通过一个小孔时,它会朝着各个方向弯曲,形成一个扩散的光斑。
而当光通过物体边缘时,它会绕过物体边缘并向后投射出一片阴影区,边缘附近会出现衍射光条纹。

光学这一章内容比较多,重要的是光的几种特性,包括:折射、干涉、衍射、偏振和光的全反射。
但是通过比较天津近几年的高考题咱们可以发现,天津的高考对这一章的要求还是比较低的,只是一个选择题,考察的也只是对基本知识的应用和理解。
所以咱们的复习也从这些方面展开。
以下为基本的知识网络:一 光的反射:1.光沿直线传播的条件是:光在同一种均匀介质中传播2.平面镜成像的特点是:正立、等大的虚像二 光的折射:折射定律:折射光线和入射光线以及法线在同一平面内,折射光线和入射光线分居法线两侧,入射角的正弦与折射角的正弦成正比。
(在光的折射中光路是可逆的)折射率:光从真空射入某介质时,入射角的正弦和折射角的正弦之比,称为折射率,用字母n 表示。
实验证明:vc n (c 表示光在真空中的速度,v 表示光在介质中的速度) 注意:(任何介质的折射路均>1。
到这里又引出两个概念来:光密介质和光疏介质 n 大的是光密介质,n 小的是光疏介质,两者是相对的。
当光从光疏介质进入光密介质时,折射角小于入射角。
当光从光密介质进入光疏介质时,折射角大于入射角。
)对折射率的理解:介质折射率的大小取决于介质本身及入射光的频率,不同介质的折射率不同,与入射角、折射角的大小无关。
当光从真空射入介质中时,入射角、折射角以及它们的正弦值是可以改变的,但是正弦值之比是一个常数。
不同的介质,入射角的正弦跟折射角的正弦之比也是一个常数,但不同的介质具有不同的常数,说明常数反映着介质的光学特性。
介质的折射率跟光的传播速度有关,由于光在真空中的传播速度大于光在其他任何介质中的传播速度,所以任何介质的折射率都大于光从真空射入任何介质。
测定玻璃的折射率:如图所示为两面平行的玻璃砖对光路的侧移,用插针法找出与入射光线AO 对应的出射光线B,确定出点,画出,量出入射角和折射角的度数。
根据公式:计算出玻璃的折射率。
光从一种介质当中进入另一种介质中,频率、波长、光速是否变化1.光从一种介质进入另一种介质中,由于其频率是由光源决定的,与介质无关,所以光的频率不发生变化,但光速。


光学工程基础考试试题
1. (10分)请简要描述光学工程的定义和应用领域。
2. (15分)请解释以下术语:
a) 反射率
b) 折射率
c) 散射
d) 光程差
e) 像差
3. (20分)光学薄膜是光学器件中的重要组成部分。
请简要说明光学薄膜的制备方法,并列举几种常见的光学薄膜材料及其应用。
4. (25分)请解释以下光学元件的工作原理和应用:
a) 凸透镜
b) 平面镜
c) 光栅
d) 偏振器
e) 相位调制器
5. (15分)在光学传输中,有时会遇到衍射现象。
请简述衍射的基本原理,并说明它在光学工程中的应用。
6. (15分)请解释光学干涉的基本原理,并提供一个实际应用的例子。
7. (约300字)请简要概述光学系统设计的基本步骤和方法,以及需要考虑的关键因素。
8. (约500字)请结合实际案例,描述光学工程在现代科技中的重要应用,并讨论其对社会进步和发展的影响。
考试结束。
(注意:本试卷共计3000字,每题总分均已标明。
请在规定时间内完成试题,准备好交卷。
祝你好运!)。

光学复习题及答案1. 光的干涉现象是如何产生的?答:光的干涉现象是由于两个或多个相干光波相遇时,由于光波的相位差导致光强的增强或减弱。
当两波的相位差为0或2π的整数倍时,光波相互加强,形成亮条纹;当相位差为π或奇数倍π时,光波相互抵消,形成暗条纹。
2. 描述光的衍射现象及其应用。
答:光的衍射现象是指光波遇到障碍物或通过狭缝时,光波会偏离直线传播路径,向障碍物的阴影区域或狭缝的两侧弯曲。
衍射现象的应用包括光栅光谱分析、光学成像系统的设计等。
3. 什么是偏振光?偏振光有哪些应用?答:偏振光是指光波的电场矢量在特定方向上振动的光。
偏振光的应用包括偏振太阳镜减少眩光、液晶显示技术以及光学显微镜中的偏振滤光片等。
4. 简述全反射现象及其条件。
答:全反射现象是指光从光密介质射向光疏介质时,当入射角大于临界角时,光波完全反射回光密介质中,不会发生折射。
全反射的条件是光必须从光密介质射向光疏介质,且入射角大于临界角。
5. 什么是色散现象?色散现象如何影响光学系统?答:色散现象是指不同波长的光在介质中传播速度不同,导致光的分散。
在光学系统中,色散现象会导致成像模糊、色差等问题,需要通过设计合适的光学系统来校正色差。
6. 光的波动性和粒子性是如何体现的?答:光的波动性体现在光的干涉、衍射和偏振等现象中,而粒子性则体现在光电效应和康普顿散射等现象中。
光的波动性和粒子性是光的波粒二象性的表现。
7. 描述光的多普勒效应及其应用。
答:光的多普勒效应是指当光源和观察者之间存在相对运动时,观察者接收到的光波频率会发生变化。
多普勒效应的应用包括雷达测速、天文学中测量恒星的相对速度等。
8. 什么是光的相干性?如何提高光的相干性?答:光的相干性是指光波之间的相位关系。
提高光的相干性可以通过使用激光光源、使用干涉滤光片等方法来实现。
9. 简述光的波粒二象性。
答:光的波粒二象性是指光既表现出波动性也表现出粒子性。
在某些实验中,光表现为波动,如干涉和衍射现象;而在其他实验中,光表现为粒子,如光电效应。
补充题1. 折射率为1.30的油膜覆盖在折射率为1.50的玻璃片上,用白光垂直照射油膜,观察到透射光中波长为500nm 的绿光加强,则油膜的最小厚度是:(A )83.3nm (B )250nm (C)192.3nm (D)96.2nm2. 用两块平玻璃片形成一个空气劈,用波长为600nm 和500nm 的两种单色光垂直入射,观察反射光形成的干涉条纹,从两玻璃接触的棱边处数起,两种光的第五个明纹所对应的空气膜厚度之差为( )3.人眼的瞳孔直径为3.0mm ,对视觉较为灵敏的光波长为550nm ,若在教室的黑板上写一等号,其两横线相距4.0mm ,试问教室的长度不超过( ),才能使坐在最后一排的学生能分别这两条横线。
4.一束自然光以布儒斯特角48.09º从某透明液体入射到玻璃表面上,玻璃的折射率为1.56,则该液体的折射率为( )5.用白光垂直照射到厚度为400nm 如图1所示的薄膜上,若薄膜的折射率为n 2=1.40,且n 1>n 2>n 3,问反射光中哪种波长的可见光得到加强?若薄膜厚度为350 nm ,且n 2<n 1,n 2<n 3,问反射光中哪几种波长的光得到加强,透射光中哪几种波长的光会消失?6.一双缝装置的一个缝被折射率为1.40的薄玻璃片所遮盖,另一个缝被折射率为1.70的薄玻璃片所遮盖,在玻璃片插入以后,屏上原来的中央极大所在点,现变为第五级明纹。
若入射波长为480nm ,设两玻璃片厚度均为d ,求d 。
7.如图2所示,利用空气劈尖测细丝直径,已知入射波长589.3nm ,L =0.02888m ,测n 3 图1图2得30条条纹的总宽度为0.004295m,求细丝直径d。
8.在牛顿环实验中,当透镜与玻璃间充满某种液体时,第10个亮环的直径由0.0140m变为0.0127m,试求这种液体的折射率。
9.已知单缝宽度为0.0001m,透镜焦距为0.50m,用入射波长分别为400nm和760nm的单色平行光分别垂直照射,求这两种光的第一级明纹离屏中心的距离,以及这两条明纹之间的距离。
光学复习提纲一、光的直线传播1.光在同一种均匀介质中是沿直线传播的2.光速光在真空中的转播速度为c =3.00×108m/s 。
光在不同介质中的传播速度是不同的。
根据爱因斯坦的相对论光速不可能超过c 。
二、反射 平面镜成像1.像的特点平面镜成的像是正立等大的虚像,像与物关于镜面为对称。
2.光路图作法根据平面镜成像的特点,在作光路图时,可以先画像,后补光路图。
三、折射与全反射1.折射定律折射定律的各种表达形式: (θ1为入、折射角中的较大者。
)021sin 1sin sin C v c n ='===λλθθ折射光路也是可逆的。
2.各种色光性质比较可见光中,红光的折射率n 最小,频率ν最小,在同种介质中(除真空外)传播速度v 最大,波长λ最大,从同种介质射向真空时发生全反射的临界角C 最大,以相同入射角在介质间发生折射时的偏折角最小(注意区分偏折角和折射角)。
以上各种色光的性质比较在定性分析时非常重要,一定要牢记。
4.光导纤维全反射的一个重要应用就是用于光导纤维(简称光纤)。
光纤有内、外两层材料,其中内层是光密介质,外层是光疏介质。
光在光纤中传播时,每次射到内、外两层材料的界面,都要求入射角大于临界角,从而发生全反射。
这样使从一个端面入射的光,经过多次全反射能够没有损失地全部从另一个端面射出。
应用---蜃景、光导纤维。
四、棱镜1.棱镜对光的偏折作用一般所说的棱镜都是用光密介质制作的。
入射光线经三棱镜两次折射后,射出方向与入射方向相比,向底边偏折。
(若棱镜的折射率比棱镜外介质小则结论相反。
)作图时尽量利用对称性(把棱镜中的光线画成与底边平行)。
由于各种色光的折射率不同,因此一束白光经三棱镜折射后发生色散现象(红光偏折最小,紫光偏折最大。
)4.全反射棱镜横截面是等腰直角三角形的棱镜叫全反射棱镜。
选择适当的入射点,可以使入射光线经过全反射棱镜的作用在射出后偏转90o (右图1)或180o (右图2)。
光学复习要点梳理与总结光学是物理学中的重要分支,研究光的传播、反射、折射、干涉、衍射等现象和规律。
它在生活中的应用广泛,涉及到光学仪器、光学信号传输、光纤通信、光学成像等领域。
为了更好地复习光学知识,以下是一些光学复习的要点梳理与总结。
一、光的传播与光的本质1. 光的传播方式:直线传播、反射和折射。
2. 光的本质:光既有波动性,也有微粒性。
二、几何光学1. 光线与光线的相交规律:入射角、反射角、折射角和光线相交于同一平面。
2. 光的反射定律:入射角等于反射角。
3. 光的折射定律:折射角由入射角和介质的折射率决定。
4. 光的全反射:当光从光密介质射向光疏介质,入射角超过临界角时发生全反射。
5. 光的干涉:两道相干光发生干涉时,会形成明暗条纹,干涉可以分为构造干涉和反射干涉。
6. 光的衍射:光通过物体边缘或孔隙时,会发生衍射现象,衍射的程度取决于波长和物体尺寸之比。
三、光学仪器1. 透镜:凸透镜和凹透镜,透镜的成像规律(薄透镜公式)。
2. 显微镜:组成结构、主要功能和成像原理。
3. 望远镜:组成结构、主要功能和成像原理。
4. 光栅:由许多平行狭缝构成,利用光的干涉和衍射现象进行光谱分析。
四、光与波动光学1. 光的叠加原理:光的干涉现象可以用叠加原理解释。
2. 双缝干涉:当光通过双缝时,会出现干涉条纹,干涉条纹与缝宽、波长和距离的关系。
3. 单缝衍射:当光通过单缝时,会出现衍射现象,衍射的规律与缝宽、波长和距离的关系。
4. 光的偏振:光可以是自然光(非偏振光)和偏振光,偏振光的振动方向与光束的传播方向垂直。
5. 波长与频率:光波的波长和频率之间的数学关系。
通过对光学的复习要点梳理与总结,我们可以进一步加深对光学知识的理解和掌握。
光学作为一门重要的学科,对我们的科学研究和生活应用都有着深远的影响。
因此,加强对光学知识的学习和掌握,将有助于我们更好地应用光学原理,推动科学技术的发展。
希望以上的复习要点能对你在光学方面的学习提供一些帮助和指导。
2014级光学技术基础复习一、填空题i .光的直线传播定律指出光在 同种均匀 _____________ 介质中沿直线传播。
2•全反射的条件是 入射角等于或 大于_________ ,光从光 光密 介质射向光 光疏 介质产生全反射。
3 .虚物点是 发散光线 ______________ 的___________ 的交点。
4.光学系统的物方焦点的共轭象点在 ___________________________ 像方的无穷远处 ,象方焦点的共轭点在 _____ 物方的无穷远处。
6 .在符号法则中,反射定律的数学式为 _______________________________8.几何光学的三个基本定律是 ________________ , _______________ 和9 .曲率半径为 R 的球面镜的焦距为 ___________________ ,若将球面镜浸入折射率为n 的液体内,该系统的焦距10 .在符号法则中(光线从左向右入射)规定:主光轴上的点的距离从 __________ 量起,左负右正;轴外物点的距离上正下负;角度以 ______________ 为始边,顺时针旋转为正,反之为负,且取小于 n /2的角度;在图上标明距离或角度时,必须用 _________________ 。
11.当物处于主光轴上无穷远处,入射光线平行于主光轴,得到的象点称为 12 .主平面是理想光具组的 ________ 一对共轭平面;节点是理想光具组的 ____________________ 一对共轭点。
13 .实象点是 _______________ 的 ______________ 光束的交点。
14 .实物位于凹球面镜的焦点和曲率中心之间,象的位置在 _______________ 与 ________ 之间。
二、计算题1.利用公式证明位于正薄透镜物方焦点前一倍焦距的物经透镜所成像为等高倒立实像,并作图验证之。
(1) 物在无穷远时经过玻璃球成像在何处?5•某种透明物质对于空气的临界角为45°,该透明物质的折射率等于 1.417 .通过物方主点的光线,必通过象方__________ ,其横向放大率为 _____________________________ ,薄透镜成象的高斯公式2置于空气中的玻璃球,折射率为n=1.5,半径为(2)物在玻璃球前2R处,经玻璃球成像在何处?大小如何?—7,51 1 2-- I F — = -—B一-得到;8.1 1 r1“5?'= 一24. 一束平行细光束入射到一半径r=30mm折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,倍的虚像,计算并作图验证解:(1放大4倍的实像同理,(2)放大四倍虚像(3)缩小四倍实像同理,得到:(4)缩小四倍虚像同理,得到:3 一物体位于半径为R的凹面镜前何处可分别得到放大4倍的实像、放大4倍的虚像、缩小4倍的实像、缩小4其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,n' n n'-nr 1 r设凸面为第一面,凹面为第二面。
(1)苴先考虑光束射入玻璃球第一面时的状态,使用高斯公由丑,.£1 =珥 I $ = 1.5 , = 30 s Hi = 1 , ?! =oc1J 1】h得到=1; = 90mm式:对于第二面,d = 6Qynm > 1.- d = 90- 60 = 30WJNJ得到:1、= 15wn?会聚点位于第二面后15mm处。
(2)将第一面镀膜,就相当于凸面镜119由一+ — = — > 1 =oc 得到厂=111 1 r人=-lOmm像位于第二面前10mm处。
(4)在经过第一面折射60-10= 50mw > 禺=1.5 ,禺=1 , r=30 ,比宀「,叫1) h r3 得到:厶=75«WJ(3)光线经过第一面折射:与物虑实相反,对于第二面,物虑,所以为实像•5. 人照镜子时,要想看到自己的全身,问镜子要多长?人离镜子的距离有没有关系?解;镜子的高度为1/2人身高,和前后距离无关。
6. 一等边三角形棱镜,若入射光线和出射光线对棱镜对称,出射光线对入射光线的偏角为40度,求该棱镜材料的折射率因为”入射光统和出射光线弔对嚴对称"所以棱輪中的光线必平行于底边作圉可得Sin50=nSin30 n=L5327. 有一正薄透镜对某一物成倒立的实像,像高为物高的一半,现将物向透镜移近100mm 成等高实像,求透镜的焦距。
解;AXj2目、=——=—1— x, = 1 008. 一个各向均匀发光的灯泡, 其光视效能为15lm/w ,发出的光通过一个距离 130毫米处口径为150毫米的聚光镜后,2斤A•3小s ? rtipJ乃丛L*解得:照明15米远处直径为2.5米的圆,假设忽略聚光镜的光能损失,如果要求照明面上的平均光照度为50勒克斯,问聚光镜的焦距应该为多少?灯泡的功率应该为多少?9•一个6v15w 的钨丝灯,已知光效为 14lm/w ,该灯与一聚光镜联用,灯丝中心对聚光镜所张的孔径角灯丝是各向均匀发光,求 1)灯泡总的光通量及进入聚光镜的能量;2)求平均发光强度1) 求总的光通量丸:j; = Mnn0 = P# = 14"5=21[)加. I P ■ 2) 求进入系统的能氢 ⑴伽11(丁)==°网"也u s sinU = 0.25眩-点周辭部空砌立体角为? R 护沪讪!卩进入系统的能壘占全1K 1.6% = ? ^ = 0 016 x 210 = 3 3 6?m3)发光强度暑 70 == 210/477 = 16 7(cd)10.如果要求照明器要照明10米远直径为2米的圆面积,要求被照射处的平均照度为50勒克斯,则照明范围内接受的总光通量为 多少流明?如果灯泡发出的投射到透镜上的光束的立体角是 变为0.02球面度,试求灯泡的发光强度和灯泡通过透镜后在照明区域的平均发光强度以及灯泡的功率分别是多少? (采用钨丝充气灯泡,其光视效能 K=15流明/瓦)11. 可视为双余弦辐射体的一平面螺旋状灯丝,大小为 0.4CM *0.5 CM ,若功率为200W,发光效率为15 LM/W,其光亮度为多少?沿灯丝平面法线方向的发光强度为多少,沿灯丝平面法线夹角为 60度方向的发光强度为多大?若光源与聚光镜联用,所构成的孔径角为30度,进入聚光镜的光通量有多少?12. 桌面OB 上方有一盏100W 钨丝充气灯泡P ,光源在各方向均匀发光,灯泡可在垂直桌面方向上下移动,问灯泡离桌面多高时,B 点(OB=1m )处的光照度最大,该光照度等于多少?13. 如图所示的照明系统,在 15m 远的地方照明直径为 2.5m 的圆形屏,要求达到屏上达到的平均照度为50lx ,聚光镜的焦距为150mm ,通光直径为150mm ,假定灯泡选用钨丝充气灯,其光视效能 K=15 lm/w ,求:灯泡的发光强度及灯泡通过聚光镜后在照明范围内的平均发光强度; 灯泡的功率和位置。
0.25,若设0.8球面度,而通过透镜后光束的立体角在均匀照明的情况下:①=EA = 50x^x(l ・25尸=246加 z ■、 1.25-0.075 ere 如_0) = ------------ = 0.0783150=—4.5。
u = -30°Q f= 4^ sin 2-^- = 4^ sin 2(2.25°) = 0.0195 sr Q = 4^sin 2- = 4^ sin 2(15°) = 0.845“15mtgu = tgu-= -0.0783-^-150=-0.578=292cd Q 0.845如果灯泡在各方向均匀发光,则灯泡所发出的总光通量为①=4^7 = 4^" x 292 = 367( 'Im假楚光视效自融=15加/W,则灯泡的功率为① 3670 O = —= = 245W eK 15h 75灯泡的位置/ = = ------ = -130 mm tgu 0.57814 •玻璃棒一端成半球形,其曲率半径为2cm ,将它水平浸入水中(折射率为1.33),沿轴线方向离球面顶点8cm处的水中有一物体,求象的位置及横向放大率,并作出光路图。
—=246 =L26xl04cr7 I —ST 0.0195 ,① 246n n n f~n1.5133 1.5^1.33雅:/ $ r*一H2' 5r= - 1 &也… _ns f _1,33x(-18) _-ns ~ L5x(-S)—n9—n•- r•t nr L5x 23-1If-n ~7- 1.5-133 _ 0J7L33x2 _ 2,66=-15.65C7TJL5-1.33 " (JJ715 .凸透镜的焦距为10cm,凹透镜的焦距为4cm,两透镜相距12cm,已知高为1cm的物体放在凸透镜左边20cm 处,物体先经凸透镜成象再由凹透镜成象,求象的位置和性质,并作出光路图。
16.凸透镜的焦距为10cm,在它右方3倍的焦距处有一平面反射镜。
已知物在凸透镜左方20cm处,求象的位置和性质。
17 .一薄透镜L i置于空气中,焦距为10厘米,实物AB正立在透镜左方15厘米处,长为1厘米。
(1)求物经L1后成象的位置、虚实、正倒和大小。
(2)今有两个透镜,一个为凸透镜,一为凹透镜,焦距均为12厘米,选用哪个透镜,把它放在L1右方什么距离处,才能使物经L1和第二透镜后获得为原物12倍的倒立的实象。
18.两个焦距分别为10cm和-5cm的薄透镜,相距10cm ,组成共轴系统,高为3mm的物体在第一透镜的左方20cm 处,试求物体最后的成象位置及其大小,并作出光路图。
19.物置于焦距为10cm的会聚透镜前40cm处,另一个焦距为20cm的会聚透镜位于第一透镜后30cm处,求象的位置、大小、虚实和正倒。
20.有一半径为10cm、折射率为1.5的玻璃半球,其平面镀铝,在球面前10cm处有一小物点,试计算和说明成像的位置和性质。
21.高1厘米的物体放在一薄凸透镜(焦距为10厘米)前20厘米处,在此透镜后10厘米处放一块曲率半径为30厘米的凸面反射镜,求物体经此系统最后所成的象的位置和性质。
22 .凸透镜L i 和凹透镜L 2共轴放置,相距10cm ,凸透镜的象方焦距为20cm ,凹透镜的物方焦距为 20cm ,物体A位于凸透镜前方 30cm 处。
试确定物体所成的象的位置和性质。
23 .凸透镜的焦距为10cm ,在它的右方12cm 处有一焦距为 4cm 的凹透镜,已知物在凸透镜左方20cm 处,求象的位置和性质。