商人过河问题matlab程序

数学建模实验一报告实验题目：研究商人过河问题一、实验目的：编写一个程序（可以是C,C++或Mathlab ）实现商人安全过河问题。

二、实验环境：Turbo c 2.0、Microsoft Visual C++ 6.0、Matlab 6.0以上 三、实验要求：要求该程序不仅能找出一组安全过河的可行方案，还可以得到所有的安全过河可行方案。

并且该程序具有一定的可扩展性，即不仅可以实现3个商人，3个随从的过河问题。

还应能实现 n 个商人，n 个随从的过河问题以及n 个不同对象且每个对象有m 个元素问题(说明：对于3个商人，3个随从问题分别对应于n=2,m=3)的过河问题。

从而给出课后习题5（n=4,m=1）的全部安全过河方案。

四、实验步骤：第一步：问题分析。

这是一个多步决策过程，涉及到每一次船上的人员以及要考虑此岸和彼岸上剩余的商人数和随从数，在安全的条件下（两岸的随从数不比商人多），经有限步使全体人员过河。

第二步：分析模型的构成。

记第k 次渡河前此岸的商人数为k x ，随从数为k y ，2,1=k ，n y x k k 2,1,=，（具有可扩展性），将）（k k y x ,定义为状态，状态集合成为允许状态集合（S ）。

S={2,1;3,2,1,0,3;3,2,1,0,0|,======y x y x y x y x ）（}记第k 次渡船的商人数为k u ，随从数为k v ，决策为),(k k v u ，安全渡河条件下，决策的集合为允许决策集合。

允许决策集合记作D ，所以D={2,1,0,,21|,=<+<v u v u v u ）（|1<u+v<2,u,v=0,1,2},因为k 为奇数时船从此岸驶向彼岸，k 为偶数时船由彼岸驶向此岸，所以状态k s 随决策k d 变化的规律是k k k k d s s )1(1-+=-，此式为状态转移律。

制定安全渡河方案归结为如下的多步决策模型：求决策)2,1(n k D d k =∈，使状态S s k ∈按照转移律，由初始状态)3,3(1=s 经有限n 步到达)0,0(1=+n s第三步：模型求解。

数学建模课程作业论文题目：对商人过河问题的研究指导教师：黄光辉小组成员：黄志宇（20156260）车辆工程04班牛凯春（20151927）电气工程05班文逸楚（20150382）工商管理02班一、问题重述3名商人带3名随从乘一条小船过河，小船每次只能承载至多两人。

随从们密约，在河的任一岸，一旦随从的人数比商人多，就杀人越货。

乘船渡河的方案由商人决定，商人们如何才能安全渡河呢？二、问题分析本题针对商人们能否安全过河问题，需要选择一种合理的过河方案。

对该问题可视为一个多步决策模型，通过对每一次过河的方案的筛选优化，最终得到商人们全部安全过到河对岸的最优决策方案。

对于每一次的过河过程都看成一个随机决策状态量，商人们能够安全到达彼岸或此岸我们可以看成目标决策允许的状态量，通过对允许的状态量的层层筛选，从而得到过河的目标。

三、模型假设1.过河途中不会出现不可抗力的自然因素。

2.当随从人数大于商人数时，随从们不会改变杀人的计划。

3．船的质量很好，在多次满载的情况下也能正常运作。

4.随从会听从商人的调度，所有人都到达河对岸。

四、符号说明第k次渡河前此岸的商人数第k次渡河前此岸的随从数过程的状态向量允许状态集合第k次渡船上的商人数第k次渡船上的随从数决策向量允许决策集合x y 3322110s 1s n +1d 1d 11五、模型建立本题为多步决策模型，每一次过河都是状态量的转移过程。

用二维向量表示过程的状态，其中分别表示对应时刻此岸的商人，仆人数以及船的行进方向，其中则允许状态集合:=又将二维向量定义为决策，则允许的决策合集为:因为k 为奇数时船从此岸驶向彼岸，k 为偶数时船从彼岸驶向此岸，所以状态随决策的变化规律是该式称为状态转移律。

求决策，使,并按照转移律，由经过有限步n 到达状态六、模型求解本模型使用MATLAB 软件编程，通过穷举法获得决策方案如下(完整matlab 程序详见附录):初始状态：可用图片表示为：X0=33状态为:S =3132303111220203010200决策为:D =0201020120112001020102七、模型推广该商人和随从过河模型可以完美解决此类商人过河的决策问题，并且该模型还可推广至解决m个商人和n个随从过河，以及小船的最大载重人数改变时的问题，只需适当地改变相关的语句即可轻松实现模型的转换。

《数学建模实验》课程考试试题----商人安全过河数学建模与求解一．问题提出：4名商人带4名随从乘一条小船过河，小船每次自能承载至多两人。

随从们密约, 在河的任一岸, 一旦随从的人数比商人多, 就杀人越货.乘船渡河的方案由商人决定，商人们如何才能安全渡河呢二．模型假设：商人和随从都会划船，天气很好，无大风大浪，且船的质量很好，可以保证很多次安全的运载商人和随从。

三．问题分析：商随过河问题可以视为一个多步决策过程，通过多次优化，最后获取一个全局最优的决策方案。

对于每一步，即船由此岸驶向彼岸或由彼岸驶向此岸，都要对船上的人员作出决策，在保证两岸的商人数不少于随从数的前提下，在有限步内使全部人员过河。

用状态变量表示某一岸的人员状况，决策变量表示船上的人员状况，可以找出状态随决策变化的规律，问题转化为在状态的允许变化范围内(即安全渡河条件)，确定每一步的决策，达到安全渡河的目标。

四．模型构成：k x ~第k 次渡河前此岸的商人数，k y ~第k 次渡河前此岸的随从数 k x , k y =0,1,2,3,4; k =1,2,… …k S =(k x , k y )~过程的状态,S ~ 允许状态集合，S={(x , y )| x =0, y =0,1,2,3,4; x =4 ,y =0,1,2,3,4; x =y =1,2,3} k u ~第k 次渡船上的商人数k v ~第k 次渡船上的随从数k d =(k u , k v )~决策，D={(u , v )| 21≤+≤v u ,k u , k v =0,1,2} ~允许决策集合 k =1,2,… …因为k 为奇数时船从此岸驶向彼岸，k 为偶数时船从彼岸驶向此岸，所以状态k S 随决策k d 的变化规律是1+k S =k S +k )1(-k d ~状态转移律求k d ∈D(k =1,2, …n), 使k S ∈S, 并按转移律由1S =(4,4)到达状态1+n S =(0,0)。

商人过河问题一、三名商人各带一名随从的情况1．问题（略）2．模型假设①当一边岸满足随从数大于商人数，但商人数为0时仍为一种安全状态；②小船至多可容纳2人，且渡河时由随从（或者商人）来划船。

3．分析与建模商人过河需要一步一步实现，比如第一步：两个仆人过河，第二步：一个仆人驾船回来，第三步：又是两个仆人过河，第四步：……其中每一步都使当前状态发生变化，而且是从一种安全状态变为另一种安全状态。

如果我们把每一种安全状态看成一个点，又如果存在某种过河方式使状态a变到状态b，则在点a和点b之间连一条边，这样我们把商人过河问题和图联系起来，有可能用图论方法来解决商人过河问题。

建模步骤：⑴首先要确定过河过程中的所有安全状态，我们用二元数组(,)x y 表示一个安全状态（不管此岸还是彼岸），其中x表示留在此岸的主人数，y表示留在此岸的随从数。

两岸各有十种安全状态：(0,0),(0,1),(0,2),(0,3),(2,2),(1,1),(3,0),(3,1),(3,2),(3,3)⑵在两岸的安全状态之间，如存在一种渡河方法能使一种状态变为另一种安全状态，则在这两种状态之间连一条边。

这样，得到如下一个二部图（图1），其中下方顶点表示此岸状态，上方顶点表示彼岸状态。

我们的目的是要找出一条从此岸(3,3)到彼岸(0,0)的最短路。

⑶观察发现此岸的状态(0,0)，(3,0)和彼岸的状态(0,3)，(3,3)都是孤立点，在求最短路的过程中不涉及这些点，把它们删去。

两岸的点用1,2, (16)新标号。

（3,3）（3,2）（3,1）（3,0）（1,1）（2,2）（0,3）（0,2）（0,3）（0,0）○②④⑥⑧⑩○○12○14○16①③⑤○⑦⑨○11○13○15○（3,3）（3,2）（3,1）（3,0）（1,1）（2,2）（0,3）（0,2）（0,3）（0,0）(图1)4．模型求解求最短路程的matlab程序如下：function route=sroute(G,opt)%求图的最短路的Dijkstra算法程序，规定起点为1，顶点连续编号%G是给定图的邻接矩阵或弧表矩阵，程序能够自动识别%当opt=0（或缺省）时求无向图的最短路，当opt=1时求有向图的最短路%d——标记最短距离%route是一个矩阵，第一行标记顶点，第二行标记1到该点的最短路，第三行标记最短路上该点的先驱顶点while 1 %此循环自动识别或由弧表矩阵生成邻接矩阵if G(1,1)==0A=G;breakelsee=Gn=max([e(:,1);e(:,2)]); %顶点数m=size(e,1); %边数M=sum(e(:,3)); %代表无穷大A=M*ones(n,n);for k=1:mA(e(k,1),e(k,2))=e(k,3);if opt==0A(e(k,2),e(k,1))=e(k,3); %形成无向图的邻接矩阵endendA=A-M*eye(n) %形成图的邻接矩阵endbreakendpb(1:length(A))=0;pb(1)=1;index1=1;index2=ones(1,length(A));d(1:length(A))=M;d(1)=0; %标记距离temp=1;while sum(pb)<length(A)tb=find(pb==0);d(tb)=min(d(tb),d(temp)+A(temp,tb)); %更新距离temp=find(d(tb)==min(d(tb))); %确定新最小距离点temp=tb(temp(1));pb(temp)=1;index1=[index1,temp];index=index1(find(d(index1)==d(temp)-A(temp,index1)));if length(index)>=2index=index(1);endindex2(temp)=index; %记录前驱顶点endroute=[1:n;d;index2];在matlab的命令窗口输入图（1）的弧表矩阵e:e=[1 2;1 4;1 10;3 4;3 6;3 10;5 6;5 8;7 14;7 16;9 8;9 12;11 12;11 14;13 14;13 16;15 16];e=[e,ones(17,1)]; %边权都设为1调用程序：route=sroute(e,0)运行结果：e =1 2 11 4 11 10 13 4 13 6 13 10 15 6 15 8 17 14 17 16 19 8 19 12 111 12 111 14 113 14 113 16 115 16 1route =1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 160 1 2 1 4 3 10 5 6 1 8 7 10 9 12 111 1 4 1 6 3 14 5 8 1 12 9 14 11 16 7这表示存在一条从1到16的长度为11的路：1 4 3 6 5 8 912 11 14 7 16，此路对应商人成功渡河的一个方案：（3,3）变为（3,1）变为（3,2）变为（3,0）变为（3,1）变为（1,1）变为（2,2）变为（0,2）变为（0,3）变为（0,1）变为（1,1）变为（0,0）即：两个仆人过河，一个仆人回来；有两个仆人过河，一个仆人回来；两个主人过河，一主一仆回来；有两个主人过河，一个仆人回来；两个仆人过河，一个仆人回来；最后两个仆人过河。

数学建模题目：商人安全过河问题学院：数理与信息工程学院专业：数学与应用数学组员：指导老师：评分：摘要本文通过MATLAB编程来解决商人安全过河问题。

运用编程来计算分析，动态规划思想的应用步骤。

最后利用计算机编程进行求解，获得过河问题的完整求解过程；有效地求解类似多步决策问题。

针对此问题，为了求解3个商人和3个随从的过河问题，用数学分析方法，建立多步决策数学模型，并且加以求解。

首先通过图解法求解3个商人和3个随从的过河问题，引进状态、允许状态集合、状态转移等，通过多步决策将初始状态到最终状态来解决问题。

总之，问题转化为多步决策模型通过计算机、图解法解决了问题过河需要经过11此来回。

关键词：多步决策；计算机求解；状态转移律；图解法；MATLAB程序1 问题重述三名商人各带一个随从过河，一只小船只能容纳两个人，随从们约定，只要在河的任何一岸，一旦随从人数多于商人人数就杀人越货，但是商人们知道了他们的约定，并且如何过河的大权掌握在商人们手中，商人们该采取怎样的策略才能安全过河呢？S个商人各带一个随从乘船过河，一只小船只能容纳K人，由他们自己划船。

商人们窃听到随从们密谋，在河的任意一岸上，只要随从的人数比商人多，就杀掉商人。

但是如何乘船渡河的决策权在商人手中，商人们如何安排渡河计划确保自身安全？2 模型假设1.假设记第k次过河前A岸的商人数为X K，随从数为Y K，k=1，2，⋯ X K,Y K=0,1,2,3，将二维向量S K=(X K,Y K)定义为状态．把满足安全渡河条件下的状态集合称为允许状态集合。

记作S。

则S={(X K,Y K)|(X K=0,Y K=0,1,2,3),(X K=3,Y K=0,1,2,3),(X K=Y K=1)(X K =Y K=2)}2.假设记第k次过河船上的商人数为U K，随从数为V K将二维向量D K=(U K ,V K)定义为决策。

由小船的容量可知允许决策集合（记作D)为D={(U K ,V K)|U K+V K=1,2}={(0,1);(0,2);(1,0);(1,1);(2,0)}3 模型的建立与求解3.1 问题一3.1.1 问题分解在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。

s=[3,3];m=[0,0];d=zeros(1,2);k=1;l=0; d=3*ones(1,2); while any(s~=0) k=k+1 %渡河 d1=[0,2;1,1;2,0]'; %每种渡河的方案 for i=d1 s1=s; m1=m; s1=s1-i‘; m1=m1+i'; if all(s1==0) l=l+1; d=[d;i']; s=s1; m=m1; else if all(s1>=0) & all(m1>=0) if (s1(1)==0 | s1(1)>=s1(2)) & (m1(1)==0 | m1(1)>=m1(2)) & any(i'~=d(end,:)) %back d2=[0 1;1 0;1 1]'; for j=d2 s2=s1; m2=m1; s2=s2+j‘; m2=m2-j'; if all(s2>=0) & all(m2>=0) if (s2(1)==0 | s2(1)>=s2(2)) & (m2(1)==0 | m2(1)>=m2(2)) l=l+1; d=[d;i']; d=[d;j']; m=m2; s=s2; l=l+1; break end; end; end break end; end; end; end;end d(2:end,:)
答案
商人过河问题
• 三名商人个带一个随从乘船渡河,一只小船 支能容纳二人,由他们自己划行,随从们密约, 在河的任一岸,一旦随从的人数比商人多,就 杀人越货.但是如何乘船渡河的大权掌握在 商人们手中,那么商人们应该怎样才能安全 渡河呢? • 对于这类智力问题可以通过逻辑思维判断 得出解决方案.也可以通过计算机枚举种种 可能,得到合理的解.（考虑过 表示出发岸边的人数； %m--表示河对岸的人数； %d--表示过河的每种决策 clear all s=[3,3];m=[0,0];

数学建模实验一报告实验题目：研究商人过河问题一、实验目的：编写一个程序（可以是C,C++或Mathlab ）实现商人安全过河问题。

二、实验环境：Turbo c 2.0、Microsoft Visual C++ 6.0、Matlab 6.0以上 三、实验要求：要求该程序不仅能找出一组安全过河的可行方案，还可以得到所有的安全过河可行方案。

并且该程序具有一定的可扩展性，即不仅可以实现3个商人，3个随从的过河问题。

还应能实现 n 个商人，n 个随从的过河问题以及n 个不同对象且每个对象有m 个元素问题(说明：对于3个商人，3个随从问题分别对应于n=2,m=3)的过河问题。

从而给出课后习题5（n=4,m=1）的全部安全过河方案。

四、实验步骤：第一步：问题分析。

这是一个多步决策过程，涉及到每一次船上的人员以及要考虑此岸和彼岸上剩余的商人数和随从数，在安全的条件下（两岸的随从数不比商人多），经有限步使全体人员过河。

第二步：分析模型的构成。

记第k 次渡河前此岸的商人数为k x ，随从数为k y ，2,1=k ，n y x k k 2,1,=，（具有可扩展性），将）（k k y x ,定义为状态，状态集合成为允许状态集合（S ）。

S={2,1;3,2,1,0,3;3,2,1,0,0|,======y x y x y x y x ）（}记第k 次渡船的商人数为k u ，随从数为k v ，决策为),(k k v u ，安全渡河条件下，决策的集合为允许决策集合。

允许决策集合记作D ，所以D={2,1,0,,21|,=<+<v u v u v u ）（|1<u+v<2,u,v=0,1,2},因为k 为奇数时船从此岸驶向彼岸，k 为偶数时船由彼岸驶向此岸，所以状态k s 随决策k d 变化的规律是k k k k d s s )1(1-+=-，此式为状态转移律。

制定安全渡河方案归结为如下的多步决策模型：求决策)2,1(n k D d k =∈，使状态S s k ∈按照转移律，由初始状态)3,3(1=s 经有限n 步到达)0,0(1=+n s第三步：模型求解。

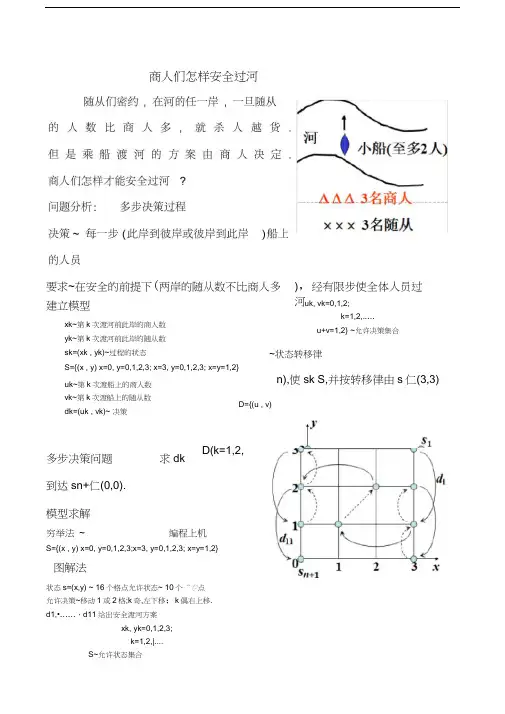
商人们怎样安全过河建立模型xk~第k次渡河前此岸的商人数yk~第k次渡河前此岸的随从数sk=(xk , yk)~过程的状态S={(x , y) x=0, y=0,1,2,3; x=3, y=0,1,2,3; x=y=1,2} uk~第k次渡船上的商人数vk~第k次渡船上的随从数dk=(uk , vk)~ 决策多步决策问题求dk到达sn+仁(0,0).模型求解穷举法~ 编程上机S={(x , y) x=0, y=0,1,2,3;x=3, y=0,1,2,3; x=y=1,2}图解法状态s=(x,y) ~ 16个格点允许状态~ 10个“专点允许决策~移动1或2格;k奇,左下移；k偶右上移.d1,•……，d11给出安全渡河方案xk, yk=0,1,2,3;k=1,2,|....S~允许状态集合uk, vk=0,1,2;k=1,2,..…u+v=1,2} ~允许决策集合~状态转移律n),使sk S,并按转移律由s仁(3,3)要求~在安全的前提下(两岸的随从数不比商人多)，经有限步使全体人员过河D={(u , v)D(k=1,2,评注和思考规格化方法 ,易于推广考虑 4 名商人各带一随从的情况 程序%%%%%%%%%%%%%%%% 开始 %%%%%%%%%%%%%%%%%%%%%% function jueche=guohe clear all clc%%%%%%%%%% 程序开始需要知道商人和仆人数； %%%%%%%%%%%%% shangren=input(' 输入商人数目 : '); puren=input(' 输入仆人数目 : ');rongliang=input(' 输入船的最大容量 : ');if puren>shangren shangren=input(' 输入商人数目 :'); puren=input(' 输入仆人数目 :'); rongliang=input(' 输入船的最大容量 :');end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 决 策 生成jc=1; %决策向量放在矩阵 fori=0:rongliangfor j=0:rongliangif (i+j<=rongliang)&(i+j>0)d(jc,1:3)=[i,j ,1];d(jc+1,1:3)=[-i,-j,-1];jc=jc+2;endendj=0; end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 状态数 组生成kx=1; % 状态向量放在 A 矩阵中，生成方法同矩阵生成；for i=shangren:-1:0for j=puren:-1:0if ((i>=j)&((shangren-i)>=(puren-j)))|((i==0)|(i==shangren))% (i>=j)&((shangren-i)>=(puren-j)))|((i==0)|(i==shangren)) 为可以存在的状态的约束条件A(kx,1:3)=[i,j,1];%生成状态数组集合 D 'A(kx+1,1:3)=[i,j,0];kx=kx+2;endend 中， jc 为插入新元素的行标初始为 1； % 满足条 D={(u,v)|1<=u+v<=rongliang,u,v=0,1,2} %生成一个决策向量立刻扩充为三维； % 同时生成他的负向量； 由于生成两个决策向量，则 jc。

数学建模题目：商人安全过河问题学院：数理与信息工程学院专业：数学与应用数学组员：指导老师：评分：摘要本文通过MATLAB编程来解决商人安全过河问题。

运用编程来计算分析，动态规划思想的应用步骤。

最后利用计算机编程进行求解，获得过河问题的完整求解过程；有效地求解类似多步决策问题。

针对此问题，为了求解3个商人和3个随从的过河问题，用数学分析方法，建立多步决策数学模型，并且加以求解。

首先通过图解法求解3个商人和3个随从的过河问题，引进状态、允许状态集合、状态转移等，通过多步决策将初始状态到最终状态来解决问题。

总之，问题转化为多步决策模型通过计算机、图解法解决了问题过河需要经过11此来回。

关键词：多步决策；计算机求解；状态转移律；图解法；MATLAB程序1 问题重述三名商人各带一个随从过河，一只小船只能容纳两个人，随从们约定，只要在河的任何一岸，一旦随从人数多于商人人数就杀人越货，但是商人们知道了他们的约定，并且如何过河的大权掌握在商人们手中，商人们该采取怎样的策略才能安全过河呢？S个商人各带一个随从乘船过河，一只小船只能容纳K人，由他们自己划船。

商人们窃听到随从们密谋，在河的任意一岸上，只要随从的人数比商人多，就杀掉商人。

但是如何乘船渡河的决策权在商人手中，商人们如何安排渡河计划确保自身安全？2 模型假设1.假设记第k次过河前A岸的商人数为X K，随从数为Y K，k=1，2，⋯ X K,Y K=0,1,2,3，将二维向量S K=(X K,Y K)定义为状态．把满足安全渡河条件下的状态集合称为允许状态集合。

记作S。

则S={(X K,Y K)|(X K=0,Y K=0,1,2,3),(X K=3,Y K=0,1,2,3),(X K=Y K=1)(X K =Y K=2)}2.假设记第k次过河船上的商人数为U K，随从数为V K将二维向量D K=(U K ,V K)定义为决策。

由小船的容量可知允许决策集合（记作D)为D={(U K ,V K)|U K+V K=1,2}={(0,1);(0,2);(1,0);(1,1);(2,0)}3 模型的建立与求解3.1 问题一3.1.1 问题分解在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。

商人过河问题摘要：为了求解3个商人和3个随从的过河问题，用数学分析方法，建立数学模型，并且加以求解，展示动态规划思想的应用步骤。

最后利用计算机编程进行求解，获得过河问题的完整求解过程；有效地求解类似多步决策问题的作用。

关键词：多步决策计算机求解状态转移律图解法 MATLAB程序一．问题提出S个商人各带一个随从乘船过河，一只小船只能容纳K人，由他们自己划船。

商人们窃听到随从们密谋，在河的任意一岸上，只要随从的人数比商人多，就杀掉商人。

但是如何乘船渡河的决策权在商人手中，商人们如何安排渡河计划确保自身安全？二．问题的关键解决的关键集中在商人和随从的数量上，以及小船的容量上，该问题就是考虑过河步骤的安排和数量上。

各个步骤对应的状态及决策的表示法也是关键。

三．问题的分析在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。

由于船上人数限制，这需要多步决策过程，必须考虑每一步船上的人员。

动态规划法正是求解多步决策的有效方法。

它要求把解的问题一层一层地分解成一级一级、规模逐步缩小的子问题。

直到可以直接求出其解的子问题为止。

分解成所有子问题按层次关系构成一棵子问题树．树根是原问题。

原问题的解依赖于子问题树中所有子问题的解。

四．模型假设记第k次过河前A岸的商人数为XK，随从数为YK k=1，2，⋯ XK ,YK=0，1，2，3，将二维向量SK=(XK，YK)定义为状态．把满足安全渡河条件下的状态集合称作为允许状态集合。

记作S。

则 S={(XK ,YK)|(XK =0,YK =0,1,2,3),(XK =3,YK =0,1,2,3),(XK =YK =1)(XK =YK =2)}记第k次过河船上的商人数为UK，随从数为VK将二维向量DK=(UK ,VK)定义为决策。

由小船的容量可知允许决策集合（记作D)为D={(UK ,VK)|UK +VK=l,2}={(O,1);(O,2);(1,O);(1,1);(2,O)}五．模型建立：动态规划法正是求解多步决策的有效方法。

return;
end;
function jueche=guohe
%%%%%%%%%%%%%%%%%%%%%%
程序开始需要知道商人和仆人数；
n=input(‘输入商人数目:’,’12’);
nn=input(‘输入仆人数目:’,’12’);
nnn=input(‘输入船的最大容量:’,’20’);
if nn>n
return 0;
pointer=pointer-> next;
}
return 1;
}
}
int judge(int a,int b,int c,int d,int n) /*判断这个状态是否可行，其中使用了history函数*/
{
if(history(a,b,n)==0) return 0;
if(a> =0&&b> =0&&a <=3&&b <=3&&c> =0&&d> =0&&c <=3&&d <=3&&a+c==3&&b+d==3)
c=A(i,:)+d(j,:) ;
x=find((A(:,1)==c(1))&(A(:,2)==c(2))&(A(:,3)==c(3))) ;
v(i,x)=1; %x为空不会改变v值
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% dijstra算法
{
int x;
int y;

Ａｕｔ ｒ’ ａｄｄｒ ｓ Ｘｉ ｗｅ Ｍ ｉ ｉ Ｉ ｕｓｒ Ｅｍｐｌｙ ｅ ’ ｈｏ Ｓ ｅｓ ｎ ｎ ｎｎｇ ｎｄ ｔｙ ｏ ｅ ｓ
【 — ２ ｏＯ ＝ ｓ ｃ
又 因为船头始终指 向 曰点 ， 以 ｔｎ＝ｘ ， 所 ａＯ 从而
Ｙ
、 ＋ ／ 即
产
ｌ 舞 （
ｆ ｘ Ｖ— ２ ｉＯ ＝ １ ｎ ｓ
关 键 词 显 式 公 式 隐 式公 式 四 阶预 报一 校 正 公 式
Ｆ ｒｓ ｈ Ｑｕｓ ｏ ａ ｅ ｇ ｅ ｔ Ｗ０ ｋ Ａ ｉＦ ｏｄ ｔｅ ｅｔ ｎ Ａｒｂ Ｌ ａ ｕ ｏ ｉ ｒ ｓ Ｓ ａ
Ｍ ａｌｂ Ｓ ｌｔ ｎ ／ ｈ ｎ Ｌ ｉ ｔａ ｏ ｕ ｏ ｉ ／Ｃ ｅ ｅ Ａｂ ｔ ａ ｔ Ｔ ｉ ｒ ｃｅ ｆｒ ｅ ｅ ｑ ｅ ｔ ｎ ｔ ｉ ｅ ｔ ｅｐ ｏ ｅ ｕ ｅ ｓｒ ｃ ｈ ｓａｔ ｌ ｄ ｄ ｔ ｕ ｓｉ ｇ ｖ ｈ ｒ ｃ ｄ ｒ ｉ ｏ ｈ ｏ ｏ ｗｈ ｃ ｎ ｅｒ ｓ ｌ ｔ ｅｆ ｕ ｈ ｏｄ ｒ ｏ ｅ ａ ｔ ｕ ｄ ｔ ｇ ｆｒ ｌ ｉｈ ａ ｄ ｔ ｅ ｕ ｔ ｈ ｏ ｒ － ｒ ｅ ｒ ｃ ｓ－ ｐ ａｉ ｍｕ ａ ｈ ｔ ｆ ｎ ｏ ｓ ｌｅ ．’ｉ ｍｅｈ ｄ ｉ ｔ ｅｅ ｐ ｉ ｉ ｆ ｒ ｌ ｎ ｈ ｍｐ ｉ ｉ ｆ ｒ ｏ ｖ ｄ １ ｌ ｔｏ ｈ ｘ ｌ ｔ ｏ ｍｕ ａ ａ ｄ ｔ ｅｉ ｌ ｔ ｏ － ｝ｓ ｓ ｃ ｃ ｍｕ ａ ｕ ｉｎ ｕ ｅｍｕ ｔ ｓ ｐ ， ｎ ｅ ｄ ｈ ｕ ｔ — ｒ ｅ ｒ ｇ ｎ ｌ ｎ ｏ ｓ ｌ — ｔ ｓ ａ ｄ ｎ ｅ ｓｔ ｅ ｆ ｒ ｏ ｄ ｒｄ ａ ｏ ｉ ｅ ｏ ｈ ｓ ｎ ａ ｄ Ｋｕｔ ｔ ｏ ｏ ｇｖ ｅ ｅ ａ ｋ ｎ ａｕ ． ｔ ｄ ｒ — ｔ ｍｅ ｈ ｄ ｔ ｉｅ ｔ ｍｂ ｒ ｉ ｇ ｖ ｌ ｅ ａ ａ ｈ Ｋｅ ｗｏ ｄ ｘ ｌ ｉ ｆ ｒ ｕ ａ ｍｐ ｉ ｉ ｆ ｒ ｕ ａ ｏ ｒｈ— ｒ ｅ ｙ ｒ ｓ ｅ ｐｉ ｔ ｏ ｃ ｍ ｌ；ｉ ｌ ｔ ｏ ｃ ｍ ｌ；ｆ ｕ ｔ ｏｄ ｒ ｆ ｒ ｃ ｓ－ ｐ ａ ｉ ｇｆ ｒ ｕ ａ ｏ ｅ ａ ｔ ｕ ｄ ｔ ｏ ｎ ｍ ｌ

商人过河functionjueche=guohe%程序开始需要知道商人和仆人数；n=input('输入商人数目:');nn=input('输入仆人数目:');nnn=input('输入船的最大容量:');ifnn>nn=input(''输入商人数目:');nn=input('输入仆人数目:');nnn=input('输入船的最大容量:');end%决策生成jc=1;%决策向量放在矩阵d中，jc为插入新元素的行标初始为1；for i=0:nnnfor j=0:nnnif(i+j<=nnn)&(i+j>0)%满足条D={(u,v)|1<=u+v<=nnn,u,v=0,1,2}d(jc,1:3)=[i,j，1]；%生成一个决策向量立刻扩充为三维；d(jc+1,1:3)=[-i,-j,-1];%同时生成他的负向量；jc=jc+2;%由于生成两个决策向量，则jc要向下移动两个；end endj=0;end%状态数组生成kx=1;%状态向量放在A矩阵中，生成方法同矩阵生成；for i=n:-1:0for j=nn:-1:0if((i>=j)&((n-i)>=(nn-j)))|((i==0)|(i==n))%(i>=j)&((n-i)>=(nn-j)))|((i==0)|(i==n))为可以存在状态的约束条件A(kx,1:3)=[i,j,1];%生成状态数组集合D`A(kx+1,1:3)=[i,j,0];kx=kx+2;endendj=nn;end; %将状态向量生成抽象矩阵k=(1/2)*size(A,1);CX=zeros(2*k,2*k);a=size(d,1);for i=1:2*kfor j=1:ac=A(i,:)+d(j,:);x=find((A(:,1)==c(1))&(A(:,2)==c(2))&(A(:,3)==c(3)));v(i,x)=1;%x为空不会改变v值endend%dijstra算法x=1;y=size(A,1);m=size(v,1);T=zeros(m,1);T=T.^-1;lmd=T;P=T;S=zeros(m,1);S(x)=1;P(x)=0;lmd(x)=0;k=x;while(1)a=find(S==0);aa=find(S==1);if size(aa,1)==mbreak;endfor j=1:size(a,1)pp=a(j,1);if v(k,pp)~=0if T(pp)>(P(k)+v(k,pp))T(pp)=(P(k)+v(k,pp));lmd(pp)=k;endendendmi=min(T(a));if mi==infbreak;elsed=find(T==mi);d=d(1);P(d)=mi;T(d)=inf;k=d;S(d)=1;endendif lmd(y)==infjueche='cannotreach'; return;endjueche(1)=y;g=2;h=y;while(1)if h==xbreak;endjueche(g)=lmd(h);g=g+1;h=lmd(h);endjueche=A(jueche,:); jueche(:,3)=[];。

商人过河m a t l a b程序以及解析The latest revision on November 22, 2020数学建模作业班级：数学131姓名：丁延辉学号：（二）商人过河Matlab代码三个商人三个随从z=zeros(30,3);%z为由(a,b,c)的列向量组成的3行30列数组，初始化为0矩阵，a,b,c代表此刻此岸的商人，仆人数量以及船的运行状态，c=1表示即将向彼岸运行m=zeros(1,20);%m为一维行向量，初始化为1矩阵，用于在后面的程序中判断第k次选择的乘船方案d=[0,1,1;0,2,1;1,0,1;1,1,1;2,0,1];%共有5种可以选择的乘船方案，最后面一列全为1，即用于在后面表示使得z(k,3)的取值保持随着k的奇偶性保持着0-1变换.z(1,:)=[3,3,1];%初始状态为[3,3,1]k=1;m(k)=1;%第一次默认的乘船方案为决策1——d(1)flag=1;%用于在后面判断是否成功找到方案answer=0;%用于在后面判断是否找到答案whilek>0%保持k>0ifm(k)>5flag=0;break;endp=0;z(k+1,:)=z(k,:)+(-1)^k*d(m(k),:);%每一次的运算规则都是z(k+1)=z(k)-(-1)^k*d(m(k),:),d(m(k),:)表示决策方案a=z(k+1,1);%将当前情况的矩阵数值复制给a商人,b仆人b=z(k+1,2);c=z(k+1,3);if(a==3&&(b==0||b==1||b==2||b==3))||(a==1&&b==1)||(a==2&&b= =2)||(a==0&&(b==0||b==1||b==2||b==3))%判断(a,b)是否符合限定情况forj=1:k%判断是否此岸a,b,c与之前有重复，如果是，结束此次循环，重新选择乘船方案ifa==z(j,1)&&b==z(j,2)&&c==z(j,3)ifm(k)~=5%决策方案只有5种，所以m(k)<=5，m(k)=m(k)+1;%因为有重复，所以换下一种决策方案elsewhile(m(k)==5)&&(k>1)k=k-1;%回溯，这一步骤已经把所有决策取尽，无可用解法，于是将后退一步，同时换下一种决策方案end%while循环的目的是防止前面几步的决策都是5，导致k=k-1,m(k)=m(k)+1后数组越界，一直找到前面不是m(k)=5的步骤m(k)=m(k)+1;endp=1;break;elsep=0;endendifp==1%程序在跳出内层for循环之后，因为要换成决策方案，所以同时跳出，直接进入下一次while循环，continue;endifa==0&&b==0%判断是否达到目标情况answer=1;fprintf('Successfullyfound!\n每一次的此岸人员分布：商人仆人\n')fori=1:100fprintf('第%2d次%d%d\n',i,z(i,1),z(i,2))ifz(i,1)==0&&z(i,2)==0break;endend%如果不是，进入下一步骤，计算z(k+2)ifm(k)~=5m(k)=m(k)+1;%这是正常的进入下一次，所以仍从d1乘船决策1开始elsewhile(m(k)==5)&&(k>1)k=k-1;end;m(k)=m(k)+1;endcontinue;elsek=k+1;%如果不是，进入下一步骤，计算z(k+2)m(k)=1;%这是正常的进入下一次，所以仍从d1乘船决策1开始continue;endelseifm(k)~=5m(k)=m(k)+1;%如果没有符合限定情况，结束该次循环，改变上一次的乘船方案elsewhile(m(k)==5)&&(k>1)k=k-1;endm(k)=m(k)+1;%回溯，这一步骤已经把所有决策取尽，无可用解法，于是将后退一步，同时换下一种决策方案continue;endendendifanswer==0&&flag==0fprintf('NoAnswer!\n')end。

《数学模型实验》实验报告姓名：王佳蕾学院：数学与信息科学学院地点：主楼402学号：20151001055专业：数学类时间：2017年4 月 16日一、实验名称：商人和仆人安全渡河问题的matlab实现二、实验目的：1.熟悉matlab基础知识，初步了解matlab程序设计；2.研究多步决策过程的程序设计方法；3.（允许）状态集合、（允许）决策集合以及状态转移公式的matlab表示；三、实验任务：只有一艘船，三个商人三个仆人过河，每一次船仅且能坐1-2个人，而且任何一边河岸上仆人比商人多的时候，仆人会杀人越货。

怎么在保证商人安全的情况下，六个人都到河对岸去，建模并matlab实现。

要求：代码运行流畅，结果正确，为关键语句加详细注释。

四、实验步骤：1.模型构成2.求决策3.设计程序4.得出结论（最佳解决方案）五、实验内容：（一）构造模型并求决策设第k次渡河前此岸的商人数为xk，随从数为yk，k=1,2,...，xk，yk=0,1,2,3.将二维向量sk=（xk，yk）定义为状态，安全渡河条件下的状态集合称为允许状态集合，记作S，S 对此岸和彼岸都是安全的。

S={(x,y)|x=0,y=0,1,2,3;x=3,y=0,1,2,3;x=y=1,2}设第k次渡船上的商人数为uk，随从数vk，将二维变量dk=（uk，vk）定义为决策，允许决策集合记为D,由小船的容量可知，D={(u,v)|1<=u+v<=2,u,v=0,1,2}k为奇数时，船从此岸驶向彼岸，k为偶数时，船从彼岸驶向此岸，状态sk随决策变量dk的变化规律为sk+1=sk+(-1)^k*dk（状态转移律）这样制定安全渡河方案归结为如下的多步决策模型：求决策dk∈D(k=1,2,...,n)，使状态sk∈S，按照转移律，由初始状态s1=（3,3）经有限步n到达状态sn+1=（0,0）。

（二）程序设计（三）运行结果六、结论体会：安全渡河问题可以看成一个多步决策过程。

商人带工人过河matlab程序function boat(m,k)%输入变量m表示商人或工人数，k表示小船的最大容量.%%本程序编程思路是用单元型变量B和C分别表示允许状态集合S和决策d.%将S中的每一个元素用所有决策d按照状态转移律迭代.%对于每一步中每一个元素的迭代结果,剔除掉不符合事实的情况.%当某一个迭代结果是[0,0]时,说明当商人或工人个数是m个,小船的最大容量是k时可以在有限的步骤下安全过河.%当所有迭代结果都被剔除时,说明当商人或工人个数是m个,小船的最大容量是k个时不可以在有限的步骤下安全过河.%%本程序的优点是可以计算出小船最大容量超过2时的情况.%%下面三个for语句是根据参数m算出所有允许状态集合S中的元素,用B表示.for i=1:m+1A=[m,i-1];B{i}=A;endfor i=m+2:2*mA=[i-(m+1),i-(m+1)];B{i}=A;endfor i=2*m+1:3*m+1A=[0,i-(2*m+1)];B{i}=A;end%下面的for语句是根据参数k算出所有决策d,用C表示. t=1;for u=0:1:kfor v=0:1:kif u+v>=1&u+v<=kC{t}=[u,v];t=t+1;endendendD{1,1}=[m,m];% D{1,1}表示初始状态.w=1;% w控制是否能够迭代成功.h=1;% h控制元素的个数.j=2;% j表示迭代的次数.x=0;% x是用来剔除掉不在允许状态集合中的元素.y=0;% y是防止重复剔除同一个元素.l=0;% l使用来标记元素是否被剔除.z(1)=0;z(2)=1;% z(j)表示上一步迭代后所剩下的所有元素.while w>0% p表示可以进行下一步迭代的所有元素.for p=z(j-1)+1:z(j)% q表示每一个元素要经过k*(k+3)/2种决策迭代.for q=1:k*(k+3)/2D{h+1,j}=D{p,j-1}+(-1)^(j-1).*C{q};h=h+1;l=1;%下面的for语句是核查迭代结果是否在允许状态集合B 中.for e=1:3*m+1if D{h,j}==B{e}x=1;break;endendif x==0h=h-1;y=1;l=0;end%下面的if语句是剔除掉本次迭代过程中出现的重复元素.if j>2&y==0for i=z(j)+1:h-1if D{h,j}==D{i,j};h=h-1;l=0;break;endendend%下面的if语句是剔除掉以前重复的元素.if j>2&y==0if j==3for i=z(1)+1:z(2)if D{h,j}==D{i,j-2} h=h-1;l=0;break;endendelsefor i=z(j-2)+1:z(j-1)if D{h,j}==D{i,j-2} h=h-1;l=0;break;endendendendif l==1for g=1:j-1D{h,g}=D{p,g};endendif l==1&D{h,j}==[0,0]w=-1;%w=-1表示商人和工人可以在有限的步骤下安全过河.break;endx=0;y=0;l=0;endif w==-1;%w=-1表示商人和工人可以在有限的步骤下安全过河.break;endendj=j+1;z(j)=h;if z(j)==z(j-1)w=-2;%w=-2表示商人和工人不可以在有限的步骤下安全过河.break;endendif w==-1disp('商人和工人可以在有限的步骤下安全过河') disp('步骤如下:')for g=1:j-1D{h,g}endendif w==-2disp('商人和工人不可以在有限的步骤下安全过河') end。

商人过河的MATLAB程序n=4;m=4;h=2; %初始状态及数据m0=0;n0=0;ticLS=0; % 允许的状态集合S与个数LSLD=0; %允许的决策集合D与个数LDfor i=0:nfor j=0:mif i>=j&n-i>=m-j|i==n|i==0LS=LS+1;S(LS,:)=[i j];endif i+j>0&i+j<=h&(i>=j|i==0)LD=LD+1;D(LD,:)=[i j];endendend%用搜寻法找出符合条件的渡河方案N=18;Q1=inf*ones(2*N,2*N);Q2=inf*ones(2*N,2*N);t=1;le=1;q=[m n];f0=0; %判断循环终止标记while f0~=1&t<="" p="">k=1;sa=[];sb=[];for i0=1:le %第n次允许的策略集逐次搜索s0=q(i0,:);breakendfor i=1:LD %由s0搜索D后得到允许的状态s1=s0+(-1)^t*D(i,:); if s1==[m0,n0]sa=[m0,n0];sb=D(i,:);f0=1;breakendfor j=2:LS-1 %搜索对比S后允许状态if s1==S(j,:)if k==1sa(k,:)=s1;sb(k,:)=D(i,:);k=k+1;breakendif k>1 %对重复状态删除处理f1=0;for ii=1:k-1if s1==sa(ii,:)f1=1;breakendendend %……if f1==0sa(k,:)=s1;sb(k,:)=D(i,:);breakendendend %…………………end %………………………………end %……………………………………………q=sa; le=size(q,1);Q1(1:le,t*2-1:t*2)=q;Q2(1:le,t*2-1:t*2)=sb;t=t+1;endif length(q)==6tr=t-1;saa1=sa;SA=zeros(tr,2);SB=zeros(tr,2);for k=tr:-1:2k1=k-1;f0=0;sbb=Q2(:,k*2-1:k*2);saa=Q1(:,k1*2-1:k1*2);for i=1:2*Nsaa2=saa1-(-1)^k*sbb(i,:);for j=1:2*Nif saa2==saa(j,:)saa1=saa2;sbb1=sbb(i,:);f0=1;breakendendif f0==1endendSA(k1,:)=saa1;SB(k,:)=sbb1;endSA(tr,:)=[m0 n0];SB(1,:)=[m,n]-SA(1,:); %………………………………………………………………………………………………￥￥disp '初始状态：'X0=[m,n]disp '状态为:'SAdisp '决策为:'SBtocendif length(q)~=6disp '没有可行的方法过河'enddisp '可以走的状态为：'；q。