三角函数的图像和性质(第一课时)

教学设计学校：沙雅县第二中学年级：高中电话：内容：高中数学必修四第一章1.4三角函数的图像性质第一课时三角函数的图像与性质（一）本节课教材是人教版必修四第四课（1.4）<<三角函数图像与性质>>，可将其划分为三小节来设计，即：<<正弦函数、余弦函数图像>>、<<正弦函数、余弦函数性质>>、<<正切函数的性质与图象>>。

一、教学内容分析本节课是学生学习了函数的定义、图象和性质，掌握了研究函数的一般思路，并对三角函数的基本知识比较熟悉的情况下，进一步利用函数图象来研究三角函数的有关性质，为学生以后利用数形结合的方式来解决有关三角函数方面的知识做铺垫,同时，可以对高中阶段系统研究指数函数、对数函数、导函数等做铺垫，进一步巩固和深化三角函数的概念和性质等知识，融会贯通前面所学的函数的基本性质，使学生得到较系统的掌握函数知识和研究函数的方法，掌握运用三角函数图像来解决有关问题。

二、教学目标分析1、知识与技能：（ 1）．能画出y=sin x, y=c os x的图像，了解三角函数的周期性；（2）．借助图像理解正弦函数、余弦函数在[0，2π]（如单调性、最大和最小值、图像与x轴交点及奇偶性等）；2、过程与方法：培养学生应用所学知识解决问题的能力，独立思考能力，规范解题的标准。

3、情感态度与价值观：培养学生全面的分析问题和认真的学习态度，渗透辩证唯物主义思想。

三、学情分析教学背景本课是高一年级必修四的一堂数学基础课程，本节课主要学习通过图像来研究三角函数的有关性质。

在通过简谐运动的现象，得到正弦或余弦函数图像。

在运用五点法作出它们的图像，让学生分小组讨论，总结和概括它们的性质，后期会用同样方法来研究正切图像和它的相关性质。

学生背景：高一学生已具备一定的教学知识和学习能力，所教的班是重点班,对于知识的归纳总结也有一定的能力，对于新问题，有主动思考问题、探索问题的信习和勇气，因此，本课遵循“以教师为主导，学生为主体”，“数学教学是数学活动的教学”等教学思想，把提问题作为教学出发点，指导尝试，总结反思。

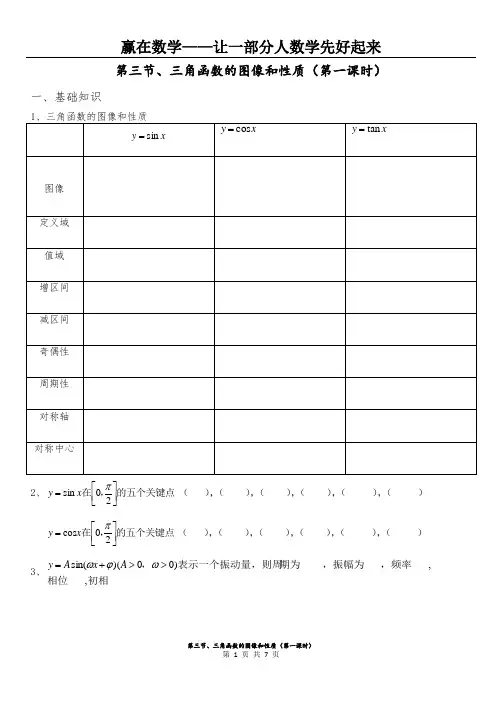
第三节、三角函数的图像和性质（第一课时）一、基础知识 1、三角函数的图像和性质 x y sin =x y cos = x y tan =图像定义域值域增区间减区间奇偶性周期性对称轴对称中心2、的五个关键点，在⎥⎦⎤⎢⎣⎡=20sin πx y （ ），（ ），（ ），（ ），（ ），（ ） 的五个关键点，在⎥⎦⎤⎢⎣⎡=20cos πx y （ ），（ ），（ ），（ ），（ ），（ ） 3、______,___,_______)00)(sin(初相相位，频率，振幅为期为表示一个振动量，则周，>>+=ωϕωA x A y1、三角函数图像及其之间的关系图像变换而来的样由的图像，并说明它是怎、做出例x y x y sin 1)62sin(21=++-=π练习：的周期性的图像，并研究、作出函数的图像、作出函数出该函数的周期的图像，并根据图像求、作出函数)(1sin 2)(3sin tan 12cos 112x f y x x f x xy x y =+=⋅=-=2、根据图像确定函数解析式k x A y ++=)sin(ϕω示，则函数表达式（）的部分函数图像如图所、函数例)2,0)(sin(1πϕωϕω<>+=x A yA 、)48sin(4ππ+-=x y B 、)48sin(4ππ-=x y C 、)48sin(4ππ--=x y D 、)48sin(4ππ+=x y练习： ____B )sin(1示，试写出函数表达式的部分函数图像如图所、函数++=ϕωx A y3、三角函数图像的应用[][]求这两个根的和的范围求实数实数根，上有且仅有两个不同的在区间的方程、关于例的范围点，则有且仅有两个不同的交的图像和直线，、函数例)2()1(2,00cos 3sin 2____2,0sin 2sin )(1a a x x x k k y x x x x f ππ=++=∈+=[]_____0,21cos N 0,21sin 4,0212sin 3=⋂⎭⎬⎫⎩⎨⎧≤≤≤=⎭⎬⎫⎩⎨⎧≤≤≥=∈≥N M M x x x ，则，、若集合例的集合且的、求例πθθθπθθθπ的实数解个数、求方程例的实数解的个数、求方程例x x x x cos 26cos 52==4、三角函数图像的周期)63sin(2)3)(4121sin()2(2cos 11π-=+==x y x y x y ）（、求下列函数周期例x x y x y x y x y x y 2cos 12cos 151)63cos(2)4()63cos(2)3()4121sin(4)2(sin 12++-=+-=-=+==）（）（、求下列函数周期例ππ[][]的解析式，，求当时，若当是周期函数证明：对称的图像关于上的偶函数，且是定义在、已知函数例的值为则时，当，的最小正周期为数，若既是偶函数又是周期函上的函数、定义在例的值求为周期的偶函数，且是以、例)(2,61)(2,2)2()()1(2)()(5_____)35(,sin )(2,0)()(4)617(,1)3(2)(32x f x x x f x x f x x f y R x f f x x f x x f x f R f f x f --∈+-=-∈===⎥⎦⎤⎢⎣⎡∈-=ππππππ5、三角函数的定义域x x y x x x y x y x x y tan log 2)4()82cos(1tan )1sin 2lg()3(1sin 1log )2(cos lg 36)1(12122++=+--+-=-=+-=π、求下列函数的定义域例6、三角函数的奇偶性)1sin lg(sin )4(cos sin 1cos sin 1sin cos 1cos sin 1)3)(sin(cos )2)(cos()1(12++=-+++⨯++-+==+=x y xx x x x x x x y x y x x y π性、判断下列函数的奇偶例练习：______0)sin()4(1cos cos 1)3(sin 1cos )2(cos sin )1(等于上的偶函数则）是（若函数ϕπϕϕR x y x x y xx y x x y ≤≤+=-+-=-==7、三角函数的单调性)4sin()4(1cos 2cos 2)3)(43cos(log )2)(21sin(3)1(1221πππ+-=--=+=+-=x y x x y x y x y 间、求下列函数的单调区例的取值范围单减，则在，函数、已知例ωπππωω),2()4sin()(02+=>x x f （） A 、⎥⎦⎤⎢⎣⎡4521， B 、⎥⎦⎤⎢⎣⎡4321， C 、⎥⎦⎤ ⎝⎛210， D 、(]20，的取值范围单增，求在，函数练习、已知ωππωω⎥⎦⎤⎢⎣⎡-=>4,3sin 2)(0x x f)83sin(cos )83sin(sin )4(160cos 194sin )3)(20)(cos(sin )sin(cos )2(47cos 101sin ,23cos )1(300πππ与与与，、比较函数各组的大小例<<-x x x练习：____2sin cos )2,0(1的大小关系为与，试比较，且，、已知πβαβαπβα+>∈ 2、C B A C B A ABC cos cos cos ______sin sin sin ++++中，则有在锐角三角形8、三角函数的对称性____2)20(cos 24____3)0(cos 3382cos 2sin 2)32sin(21围成的封闭图形面积为的图像与直线、函数例轴围成的图形面积为及的图像与直线、函数例的值对称，求的图像关于直线、如果函数例的对称中心、求函数例=≤≤=-=≤≤==+=-=y x x y y y x x y a x x a x y x y ππππ。

《三角函数三角函数的图象与性质课件pptx》2023-10-26•引言•三角函数的概念与性质•三角函数的图象表示目录•三角函数的应用•习题解答•总结与展望01引言三角函数是数学中的基础科目，对于高中生来说，掌握好三角函数的知识可以为后续的高等数学学习打下基础。

在本课程中，我们将从定义、图象、性质和应用等方面全面介绍三角函数的知识。

课程背景介绍课程目标熟悉三角函数的图象和变化趋势。

让学生掌握三角函数的定义、公式和基本性质。

培养学生的数学思维和逻辑推理能力。

能够灵活运用三角函数解决实际问题。

课程大纲•第一部分：三角函数的定义与公式•正弦函数、余弦函数和正切函数的定义与基本公式。

•角度与弧度的转换。

•第二部分：三角函数的图象与性质•正弦函数、余弦函数和正切函数的图象与性质。

•三角函数的周期性、最值和对称性。

•第三部分：三角函数的应用•利用三角函数解决实际问题，如物理、工程、计算机等领域的问题。

•三角函数在复数、极坐标系中的应用。

02三角函数的概念与性质1 2 3$y = \sin x$，表示单位圆上点的纵坐标。

正弦函数$y = \cos x$，表示单位圆上点的横坐标。

余弦函数$y = \tan x$，表示单位圆上点的纵坐标与横坐标的比值。

正切函数奇偶性正弦函数和正切函数为奇函数，余弦函数为偶函数。

值域正弦函数和余弦函数的值域为$\lbrack -1,1\rbrack$，正切函数的值域为全体实数。

周期性正弦函数、余弦函数和正切函数都具有周期性，最小正周期为$2\pi$。

定义域正弦函数和余弦函数的定义域为全体实数，正切函数的定义域为不等于$\frac{k\pi}{2} + \pi$的全体实数。

正弦函数的周期性$y = \sin x$的周期为$2\pi$，即$\sin(x + 2k\pi) = \sin x(k \in \mathbf{Z})$。

三角函数的周期性余弦函数的周期性$y = \cos x$的周期为$2\pi$，即$\cos(x + 2k\pi) = \cos x(k \in \mathbf{Z})$。

三角函数的图像和性质(第一课时说课案) 下面我将从四个方面说明本节课的教学设计。

一、教材分析二、教学方法分析三、教学流程四、教学说明一、教材分析1、地位与作用：本节课是在学生掌握了单位圆中的正弦线和诱导公式的基础上进行的，不仅是对前面所学知识应用的考察，也是后续学习正、余弦函数性质的基础。

对函数图像清晰而准确的掌握也为学生在解题实践中提供了有力的工具。

2、学情分析：（1）知识与技能：学生已掌握了一些初等基本函数的图像和性质，并了解一些函数图像的画法。

（2）心理与生理：高一上学期的学生已经对高中数学体系中函数问题的处理方法和过程有了初步认识，且具有了较强的分析、判断、理解能力和一定层次上的交流沟通能力。

3、教学目标（1）知识与技能目标：通过研究掌握正弦函数图像及其画法；掌握余弦函数图像；深刻理解五点作图法中五点（零点、最高点、最低点）的本质即：图像中走向趋势发生变化的点。

（2）过程与方法：通过主动思考，主动发现，亲历知识的形成过程，使对正弦函数单调、对称、“周而复始”等性质的认知更为深刻。

（3）情感态度与价值观：用联系的观点看待问题，善于类比联想，直观想象，对数形结合有进一步认识，激发学习数学的兴趣，养成良好的数学品质。

4、重、难点分析：（1）重点：用单位圆中的正弦线作正弦函数在]2,0[π的图象、“五点法”作图；（2）难点：如何由正弦函数在]2,0[π上的图象得到正弦函数在R上的图象；如何在正弦函数的图像上找出“五点”。

二、教学方法教学方法：演示法、示范教学法、启发式引导、互动式讨论、反馈式评价。

学习方法：观察发现、合作交流、归纳总结、反馈模仿。

教学手段：运用多媒体网络教学平台，构建学生自主探究的教学环境。

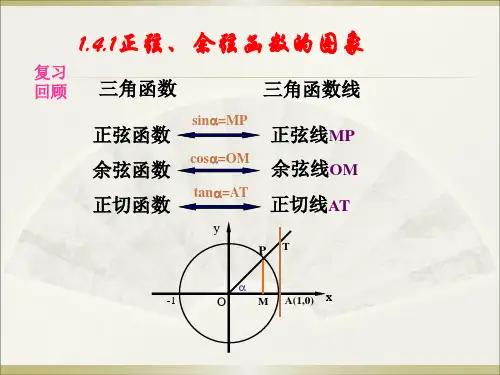
三、教学流程1、复习、引入：复习内容有：描点作函数图像的一般步骤；弧度定义；正、余弦函数定义；正弦线、余弦线；诱导公式。

设置的目的是让学生再次回顾弧度的定义（强调弧度与实数一一对应的关系）与正弦线（实质是函数值），为利用正弦线作出正弦函数的图像做准备。