三角函数的图像与性质

三角函数的图像与性质三角函数是数学中的重要概念，它们在几何、物理、工程等领域都有广泛的应用。

本文将探讨三角函数的图像与性质，并通过图像展示它们的特点。

一、正弦函数（sine function）正弦函数是最基本的三角函数之一，常用符号为sin(x)。

它的图像是一条连续的曲线，表现出周期性的波动。

正弦函数的性质如下：1. 周期性：正弦函数的周期为2π，即在每个2π的区间内，函数的值会重复。

2. 对称性：正弦函数是奇函数，即满足sin(-x)=-sin(x)。

这意味着它的图像关于原点对称。

3. 取值范围：正弦函数的值域在[-1, 1]之间，即函数的值不会超过这个范围。

二、余弦函数（cosine function）余弦函数是另一个常见的三角函数，常用符号为cos(x)。

它的图像也是一条连续的曲线，与正弦函数的图像非常相似。

余弦函数的性质如下：1. 周期性：余弦函数的周期也是2π，与正弦函数相同。

2. 对称性：余弦函数是偶函数，即满足cos(-x)=cos(x)。

这意味着它的图像关于y轴对称。

3. 取值范围：余弦函数的值域也在[-1, 1]之间，与正弦函数相同。

三、正切函数（tangent function）正切函数是三角函数中的另一个重要概念，常用符号为tan(x)。

正切函数的图像也是一条连续的曲线，但与正弦和余弦函数有所不同。

正切函数的性质如下：1. 周期性：正切函数的周期为π，即在每个π的区间内，函数的值会重复。

2. 奇点：正切函数在π/2和-π/2处有奇点，即函数在这些点上无定义。

3. 取值范围：正切函数的值域为整个实数轴，即它可以取到任意的实数值。

四、其他三角函数除了正弦、余弦和正切函数，还有许多衍生的三角函数，如余切函数、正割函数和余割函数等。

它们的图像和性质与前面介绍的三角函数类似，只是在计算和应用中有一些特殊的情况。

五、图像展示为了更好地理解三角函数的图像与性质，下面是一些图像展示：（插入正弦函数、余弦函数和正切函数的图像）从图中可以清楚地看出正弦函数和余弦函数的周期性和对称性，以及正切函数的特殊性。

三角函数的图像和性质三角函数是数学中的一类特殊函数，以其图像的周期性和性质的多样性而被广泛研究和应用。

本文将介绍三角函数的图像特点和基本性质。

一、正弦函数的图像和性质正弦函数是最基本的三角函数之一，用sin(x)表示。

其图像为周期性曲线，其周期为2π。

在一个周期内，正弦函数的值在[-1,1]之间变化。

图像在x轴上的零点是正弦函数的特殊点，记为x=kπ，其中k为整数。

正弦函数的图像在x=kπ时经过极大值或极小值。

正弦函数的性质：1. 周期性：sin(x+2π)=sin(x)，即正弦函数在过一周期后会重复。

2. 奇偶性：sin(-x)=-sin(x)，即正弦函数关于原点对称。

3. 对称性：sin(π-x)=sin(x)，即正弦函数关于y轴对称。

二、余弦函数的图像和性质余弦函数是另一个常见的三角函数，用cos(x)表示。

余弦函数的图像也是周期性曲线，其周期同样为2π。

在一个周期内，余弦函数的值同样在[-1,1]之间变化。

与正弦函数不同的是，余弦函数的图像在x=kπ时经过极大值或极小值。

余弦函数的性质：1. 周期性：cos(x+2π)=cos(x)，即余弦函数在过一周期后会重复。

2. 奇偶性：cos(-x)=cos(x)，即余弦函数关于y轴对称。

3. 对称性：cos(π-x)=-cos(x)，即余弦函数关于原点对称。

三、正切函数的图像和性质正切函数是三角函数中另一个常见的函数，用tan(x)表示。

正切函数的图像为周期性曲线，其周期为π。

正切函数的图像在x=kπ+π/2时会出现无穷大的间断点，即tan(x)在这些点是无界的。

正切函数的性质：1. 周期性：tan(x+π)=tan(x)，即正切函数在过一个周期后会重复。

2. 奇偶性：tan(-x)=-tan(x)，即正切函数关于原点对称。

四、其他三角函数除了正弦函数、余弦函数和正切函数，还有其他与它们密切相关的三角函数。

1. 反正弦函数：用arcsin(x)表示，表示一个角的正弦值等于x，返回值在[-π/2, π/2]之间。

三角函数图像与性质
三角函数是基本的初等函数之一，它以角度为自变量，以任意角度的终边与单位圆或其比值的交点坐标为因变量。

接下来看看常见三角函数的图像和性质。

三角函数的图像
三角函数的性质
1.正弦函数
在直角三角形中，任意一锐角∠A的对边与斜边的比叫做∠A 的正弦，记作sinA，即sinA=∠A的对边/斜边。

正弦值在[2kπ-π/2,2kπ+π/2](k∈Z)随角度增大(减小)而增大(减小)，在[2kπ+π/2,2kπ+3π/2](k∈Z)随角度增大(减小)而减小(增大)。

图像：波形曲线
值域：[-1,1]
定义域：R
2.余弦函数
在Rt△ABC(直角三角形)中，∠C=90°(如图所示)，∠A的余弦是它的邻边比三角形的斜边，即cosA=b/c，也可写为
cosa=AC/AB。

余弦函数：f(x)=cosx(x∈R)。

余弦值在[2kπ-π,2kπ](k∈Z)随角度增大(减小)而增大(减小)，在[2kπ,2kπ+π](k∈Z)随角度增大(减小)而减小(增大)。

图像：波形曲线
值域：[-1,1]
定义域：R
3.正切函数
在Rt△ABC(直角三角形)中，∠C=90°，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是
tanB=b/a，即tanB=AC/BC。

正切值在[kπ-π/2,kπ+π/2](k∈Z)随角度增大(减小)而增大(减小)。

图像：右图平面直角坐标系反映
定义域：{x|x≠(π/2)+kπ,k∈Z}
值域：实数集R。

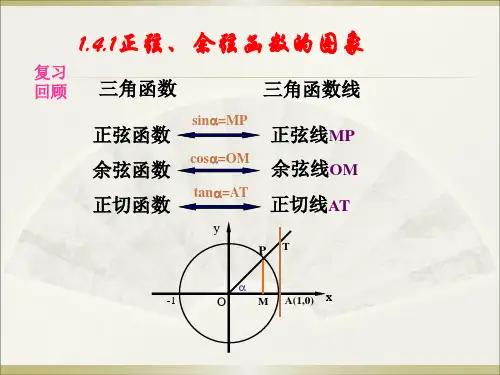
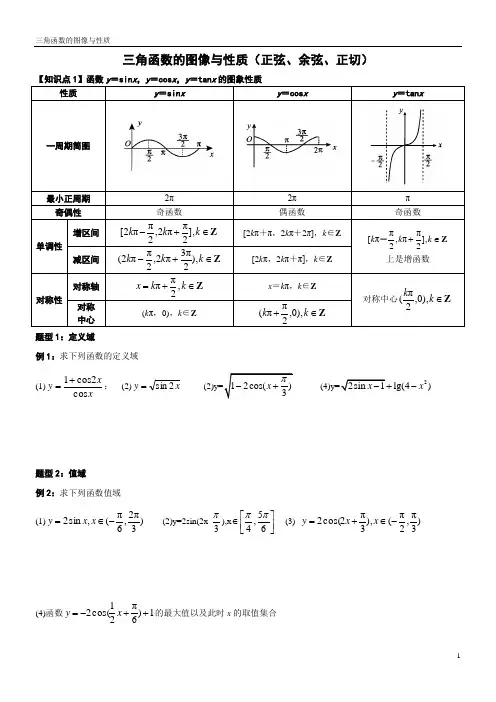
三角函数的图像与性质（正弦、余弦、正切）【知识点1】函数y ＝sin x ，y ＝cos x ，y ＝tan x 的图象性质题型1：定义域例1：求下列函数的定义域(1)xx y cos 2cos 1+=； (2)x y 2sin = 2lg(4)x -题型2：值域 例2：求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3：周期例3：求下列函数的周期： （1）f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) （4）y=sin x 例4： 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5：若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2，则ϖ=________.例6：使x y ωsin =（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为【 】A ．π25B ．π45C ．πD ．π23例7：设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立，则12x x -的最小值是A.4B.2C.1D.12题型4：奇偶性 例8：函数y ＝sin （x ＋2π）（x ∈［－2π，2π］）是【 】A.增函数B.减函数C.偶函数D.奇函数例9：判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10：已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5：单调性例11：函数y =21log sin(2x +4π)的单调递减区间是【 】 A.（k π－4π,k π］(k ∈Z ) B.（k π－8π,k π+8π］(k ∈Z ) C.（k π－83π,k π+8π］(k ∈ D.（k π+8π,k π+83π］(k ∈Z )例12：.求1cos()3412logx y π+=的单调区间例13：求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ；(3))23πsin(2x y -=例14：（1）求函数y=2sin(2x-3π)的单调递减区间。

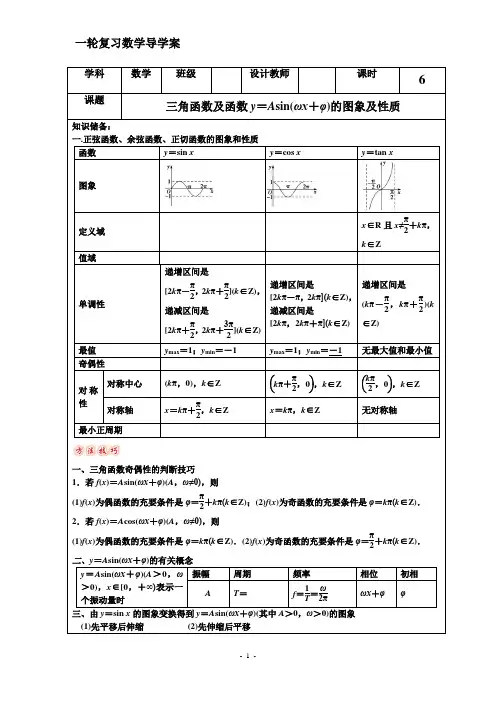
三角函数的图像与性质一.正弦函数和余弦函数的图象:y=sinx打 3口正弦函数y = sin x 和余弦函数y = cos x 图象的作图方法：五点法：先取横坐标分别为0,-,兀,3-,2兀的2 2五点，再用光滑的曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象。

二、正弦函数y = sin x (x G R )、 余弦函数 y = cos x (x G R )的性质：(1)定义域：都是R 。

(2)值域：1、都是［-1,1］，2、y = sin x ，当 x = 2 k -+-(k G Z )时，y 取最大值 1；当 x = 2 k -+ 3-( k G Z )时，y 取最小值一1； 2 2 3、y = cos x ，当 x = 2k - (k G Z )时，y 取最大值 1,当 x = 2k -+-(k G Z )时，y 取最小值一1。

例：(1)若函数y = a - b sin(3x + -)的最大值为3，最小值为-L 则a = , b =622——(答：a = —, b = 1或 b = —1 )；22.函数y=-2sinx+10取最小值时，自变量x 的集合是课堂练习：1、函数y = sin x - sin x 的值域是2.已知f (x )的定义域为[0, 1],求f (c os x )的定义域；(3)周期性：①y = sin x 、y = cos x 的最小正周期都是2兀；2兀②f (x ) = A sin (3x +。

和f (x ) = A cos (3x +中)的最小正周期都是T = ——。

13| 兀x例：(1)若 f (x ) = sin 一，则 f (1)+ f (2) + f (3) + .・・ + f (2003)=—(答：0)； ^3⑵.下列函数中，最小正周期为兀的是()(4)奇偶性与对称性：1、正弦函数y —sin x (x E R ) 7是奇函数，对称中心是(k 兀,0)(k E z ),对称轴是直线x — k K+-(k E Z )；2 2、余弦函数y — cos x (x E R )是偶函数，对称中心是(k K +-,0 ](k E Z ),对称轴是直线x — k R (k E Z ) I 2)(正(余)弦型函数的对称轴为过最高点或最低点且垂直于x 轴的直线，对称中心为图象与x 轴的交点)。