使用状态方程计算天然气焦耳-汤姆逊系数

第一章 热力学第一定律一、选择题1．下述说法中，哪一种正确（ ）(A)热容C 不是状态函数； (B)热容C 与途径无关；(C)恒压热容C p 不是状态函数；(D)恒容热容C V 不是状态函数。

2．对于内能是体系状态的单值函数概念，错误理解是（ ）(A) 体系处于一定的状态，具有一定的内能；(B) 对应于某一状态，内能只能有一数值不能有两个以上的数值；(C) 状态发生变化，内能也一定跟着变化；(D) 对应于一个内能值，可以有多个状态。

3．某高压容器中盛有可能的气体是O 2 ,Ar, CO 2, NH 3中的一种，在298K 时由5dm3绝热可逆膨胀到6dm3，温度降低21K ，则容器中的气体（ ）(A) O 2 (B) Ar (C) CO 2 (D) NH 34．戊烷的标准摩尔燃烧焓为-3520kJ·mol -1，CO 2(g)和H 2O(l)标准摩尔生成焓分别为-395 kJ·mol -1和-286 kJ·mol -1，则戊烷的标准摩尔生成焓为（ ）(A) 2839 kJ·mol -1 (B) -2839 kJ·mol -1 (C) 171 kJ·mol -1 (D) -171 kJ·mol -15．已知反应)()(21)(222g O H g O g H =+的标准摩尔反应焓为)(T H m r θ∆，下列说法中不正确的是（ ）。

(A).)(T H m r θ∆是H 2O(g)的标准摩尔生成焓 (B). )(T H m r θ∆是H 2O(g)的标准摩尔燃烧焓 (C). )(T H m r θ∆是负值 (D). )(T H m r θ∆与反应的θm r U ∆数值相等 6．在指定的条件下与物质数量无关的一组物理量是（ ）(A) T , P, n (B) U m , C p, C V(C) ΔH, ΔU, Δξ (D) V m , ΔH f,m (B), ΔH c,m (B)7．实际气体的节流膨胀过程中，下列那一组的描述是正确的（ ）(A) Q=0 ΔH=0 ΔP< 0 ΔT≠0 (B) Q=0 ΔH<0 ΔP> 0 ΔT>0(C) Q>0 ΔH=0 ΔP< 0 ΔT<0 (D) Q<0 ΔH=0 ΔP< 0 ΔT≠08．已知反应 H 2(g) + 1/2O 2(g) →H 2O(l)的热效应为ΔH ，下面说法中不正确的是（ ）(A) ΔH 是H 2O(l)的生成热 (B) ΔH 是H 2(g)的燃烧热(C) ΔH 与反应 的ΔU 的数量不等 (D) ΔH 与ΔH θ数值相等9．为判断某气体能否液化，需考察在该条件下的（ ）(A) μJ-T > 0 (B) μJ-T < 0 (C) μJ-T = 0 (D) 不必考虑μJ-T 的数值10．某气体的状态方程为PV=RT+bP(b>0)，1mol 该气体经等温等压压缩后其内能变化为（ ）(A) ΔU>0 (B) ΔU <0 (C) ΔU =0 (D) 该过程本身不能实现11．均相纯物质在相同温度下C V > C P的情况是（）(A) (∂P/∂T)V<0 (B) (∂V/∂T)P<0(C) (∂P/∂V)T<0 (D) 不可能出现C V>C P12．理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力，则其终态的温度，体积和体系的焓变必定是（）(A) T可逆> T不可逆, V可逆> V不可逆, ΔH可逆>ΔH不可逆(B) T可逆< T不可逆, V可逆< V不可逆, ΔH可逆<ΔH不可逆(C) T可逆< T不可逆, V可逆> V不可逆, ΔH可逆<ΔH不可逆(D) T可逆< T不可逆, V可逆< V不可逆, ΔH可逆>ΔH不可逆13．1mol、373K、1atm下的水经下列两个不同过程达到373K、1atm下的水汽：(1)等温可逆蒸发，(2)真空蒸发。

第一章 热力学第一定律一、选择题1．下述说法中,哪一种正确（ ）（A ）热容C 不是状态函数； (B ）热容C 与途径无关;(C ）恒压热容C p 不是状态函数；（D ）恒容热容C V 不是状态函数。

2．对于内能是体系状态的单值函数概念，错误理解是( ）(A) 体系处于一定的状态，具有一定的内能；（B ） 对应于某一状态，内能只能有一数值不能有两个以上的数值；（C ） 状态发生变化，内能也一定跟着变化;(D) 对应于一个内能值，可以有多个状态.3．某高压容器中盛有可能的气体是O 2 ,Ar ， CO 2， NH 3中的一种,在298K 时由5dm3绝热可逆膨胀到6dm3，温度降低21K ，则容器中的气体（ ）(A ） O 2 （B) Ar （C ） CO 2 （D ） NH 34．戊烷的标准摩尔燃烧焓为—3520kJ·mol -1，CO 2（g)和H 2O(l ）标准摩尔生成焓分别为—395 kJ·mol —1和-286 kJ·mol —1，则戊烷的标准摩尔生成焓为( ）（A ） 2839 kJ·mol —1 （B ） -2839 kJ·mol —1 （C) 171 kJ·mol -1 (D ） —171 kJ·mol —15．已知反应)()(21)(222g O H g O g H =+的标准摩尔反应焓为)(T H m r θ∆，下列说法中不正确的是（ ）.(A ）。

)(T H m r θ∆是H 2O （g ）的标准摩尔生成焓 （B)。

)(T H m r θ∆是H 2O （g)的标准摩尔燃烧焓 (C)。

)(T H m r θ∆是负值 （D ）. )(T H m r θ∆与反应的θm r U ∆数值相等 6．在指定的条件下与物质数量无关的一组物理量是（ ）（A ） T ， P ， n (B ） U m ， C p, C V(C) ΔH, ΔU ， Δξ (D) V m ， ΔH f,m （B ）， ΔH c,m (B ）7．实际气体的节流膨胀过程中，下列那一组的描述是正确的（ ）(A ） Q=0 ΔH=0 ΔP< 0 ΔT≠0 （B ） Q=0 ΔH<0 ΔP 〉 0 ΔT>0(C) Q 〉0 ΔH=0 ΔP 〈 0 ΔT 〈0 （D ） Q<0 ΔH=0 ΔP 〈 0 ΔT≠08．已知反应 H 2(g) + 1/2O 2（g ） →H 2O （l)的热效应为ΔH ，下面说法中不正确的是（ )(A ） ΔH 是H 2O （l)的生成热 （B ） ΔH 是H 2(g)的燃烧热(C) ΔH 与反应 的ΔU 的数量不等 (D ） ΔH 与ΔH θ数值相等9．为判断某气体能否液化，需考察在该条件下的( )（A) μJ —T > 0 （B ） μJ-T < 0 （C ） μJ-T = 0 (D) 不必考虑μJ —T 的数值10．某气体的状态方程为PV=RT+bP （b>0),1mol 该气体经等温等压压缩后其内能变化为（ ）(A) ΔU>0 (B) ΔU <0 (C）ΔU =0 (D）该过程本身不能实现11．均相纯物质在相同温度下C V 〉C P的情况是（）（A) （∂P/∂T)V<0 (B) (∂V/∂T)P〈0(C）（∂P/∂V)T〈0 (D）不可能出现C V〉C P12．理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力,则其终态的温度，体积和体系的焓变必定是（）（A）T可逆> T不可逆，V可逆〉V不可逆，ΔH可逆〉ΔH不可逆(B）T可逆< T不可逆, V可逆< V不可逆，ΔH可逆〈ΔH不可逆(C) T可逆〈T不可逆, V可逆> V不可逆, ΔH可逆<ΔH不可逆（D) T可逆〈T不可逆，V可逆< V不可逆, ΔH可逆〉ΔH不可逆13．1mol、373K、1atm下的水经下列两个不同过程达到373K、1atm下的水汽：(1）等温可逆蒸发，（2)真空蒸发。

整个计算过程的公式包括三部分：一. 天然气物性参数及管线压降与温降的计算 二. 天然气水合物的形成预测模型 三. 注醇量计算方法.天然气物性参数及管线压降与温降的计算 20 C 标准状态1y i M i24.055任意温度与压力下Y i M i式中厂混合气体的密度，P —任意温度、压力下i 组分的密度，kg/m 3; y i — i 组分的摩尔分数； M i —i组分的分子量， V i —i 组分摩尔容积， 天然气密度计算公式pMW gZRT天然气相对密度天然气相对密度△的定义为：在相同温度，压力下，天然气的密度与空气密 度之比。

天然气分子量标准状态下，Ikmol 天然气的质量定义为天然气的平均分子量,Y i M iM式中 M —气体的平均分子量，kg/kmol ; y i —气体第i 组分的摩尔分数；M —气体第i 组分的分子量，kg/kmol天然气密度混合气体密度指单位体积混合气体的质量。

0 °C 标准状态按下面公式计算:1 22.414y i M i简称分子量。

(1)kg/m 3；kg/kmol；⑹式中 △—气体相对密度；厂气体密度，kg/m 3；p —空气密度，kg/m 3,在 P o =1O1.325kPa, T o =273.15K 时，p =1.293kg/m 3;在 P o =1O1.325kPa T O =273.15K 时，p =1.293kg/m 3。

因为空气的分子量为28.96,固有28.96假设，混合气和空气的性质都可用理想气体状态方程描述，则可用下列关系 式表示天然气的相对密度天然气的虚拟临界参数任何气体在温度低于某一数值时都可以等温压缩成液体，但当高于该温度时, 无论压力增加到多大，都不能使气体液化。

可以使气体压缩成液态的这个极限温 度称为该气体的临界温度。

当温度等于临界温度时，使气体压缩成液体所需压力 称为临界压力，此时状态称为临界状态。

混合气体的虚拟临界温度、虚拟临界压 力和虚拟临界密度可按混合气体中各组分的摩尔分数以及临界温度、临界压力和 临界密度求得，按下式计算。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载第五版物理化学第三章习题答案地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功等于不可逆热机作出的功－W。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证：（反证法）设不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

整个计算过程的公式包括三部分：一．天然气物性参数及管线压降与温降的计算 二．天然气水合物的形成预测模型 三．注醇量计算方法一．天然气物性参数及管线压降与温降的计算 天然气分子量标准状态下，1kmol 天然气的质量定义为天然气的平均分子量，简称分子量。

∑=ii M y M(1) 式中 M —气体的平均分子量，kg/kmol ；y i —气体第i 组分的摩尔分数；M i —气体第i 组分的分子量，kg/kmol 。

天然气密度混合气体密度指单位体积混合气体的质量。

按下面公式计算： 0℃标准状态∑=i i M y 14.4221ρ (2) 20℃标准状态∑=i i M y 055241.ρ (3) 任意温度与压力下∑∑=ii ii V y M y ρ(4)式中 ρ—混合气体的密度，kg/m 3；ρi —任意温度、压力下i 组分的密度，kg/m 3； y i —i 组分的摩尔分数；M i —i 组分的分子量，kg/kmol ； V i —i 组分摩尔容积，m 3 /kmol 。

天然气密度计算公式gpMW ZRTρ= (5)天然气相对密度天然气相对密度Δ的定义为：在相同温度，压力下，天然气的密度与空气密度之比。

aρρ∆=(6) 式中 Δ—气体相对密度；ρ—气体密度，kg/m 3； ρa —空气密度，kg/m 3，在P 0=101.325kPa ，T 0=273.15K 时，ρa =1.293kg/m 3；在P 0=101.325kPa ，T 0=273.15K 时，ρa =1.293kg/m 3。

因为空气的分子量为28.96，固有28.96M∆=(7) 假设，混合气和空气的性质都可用理想气体状态方程描述，则可用下列关系式表示天然气的相对密度28.96gg ga a pMW MW MW RT pMW MW RT∆===(8) 式中 MW a —空气视相对分子质量；MW g —天然气视相对分子质量。

天然气的虚拟临界参数任何气体在温度低于某一数值时都可以等温压缩成液体，但当高于该温度时，无论压力增加到多大，都不能使气体液化。

海底天然气物理化学性质第一节海底天然气组成表示法一、海底天然气组成海底天然气是由多种可燃和不可燃的气体组成的混合气体。

以低分子饱和烃类气体为主，并含有少量非烃类气体。

在烃类气体中，甲烷（CH4）占绝大部分，乙烷（C2H6）、丙烷（C3H8）、丁烷（C4H10）和戊烷（C5H12）含量不多，庚烷以上（C5+）烷烃含量极少。

另外，所含的少量非烃类气体一般有氮气（N2）、二氧化碳（CO2）、氢气（H2）、硫化氢（H2S）和水汽（H2O）以及微量的惰性气体。

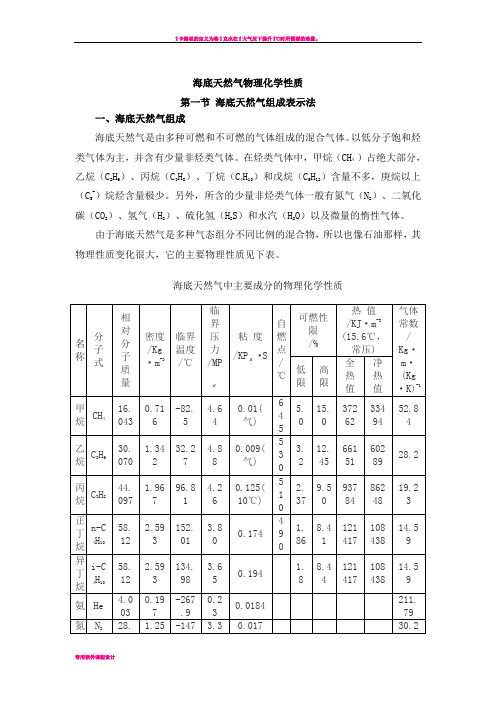
由于海底天然气是多种气态组分不同比例的混合物，所以也像石油那样，其物理性质变化很大，它的主要物理性质见下表。

海底天然气中主要成分的物理化学性质二、海底天然气容积分数和摩尔分数定义混合物中各组分的容积为V i ，总容积V ；摩尔分数y i ：i 组分的摩尔数n i 与混合物总摩尔数n 的比值。

∑=='ii i i V VV V y ； 1='∑i y ；∑==i i i i n n n n y ； 1=∑i y由分压定律，存在P i V= n i R M T ；P i V=n R M T 由分容定律，存在PV i = n i R M T ；PV=n R M Tpp n n y ii i ==； i i i i y n n V V y ===' 结论：对于理想气体混合物，任意组分的摩尔分数可以用该组分的分压与混合物总压的比值表示，且摩尔分数与容积分数相等。

三、海底天然气分子量标准状态下，1kmol 天然气的质量定义为天然气的平均分子量，简称分子量。

∑=i i M y M 四、海底天然气密度（1）平均密度混合气体密度指单位体积混合气体的质量。

按下面公式计算：0℃标准状态 ∑=i i M y 414.221ρ； 20℃标准状态 ∑=i i M y 055.241ρ 任意温度与压力下 i i i i V y M y ∑∑=/ρ （2）相对密度在标准状态下，气体的密度与干空气的密度之比称为相对密度。

第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源汲取的热及向低温热源放出的热。

解：卡诺热机的效率为依据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不行逆热机与卡诺机结合操作时，若令卡诺热机得到的功r W 等于不行逆热机作出的功－W 。

假设不行逆热机的热机效率大于卡诺热机效率，其结果必定是有热量从低温热源流向高温热源，而违背势热力学第二定律的克劳修斯说法。

证： （反证法） 设 r ir ηη>不行逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不行逆热机从高温热源汲取的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ的热干脆从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。

求下列三种状况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不行逆热机效率。

（3）不行逆热机效率。

解：设热机向低温热源放热，依据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7 已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与100℃的热源接触。

（2）系统先与55℃的热源接触至热平衡，再与100℃的热源接触。

天然气管道输送第一章天然气输送概述1、什么是天然气虚拟临界常数，在实际中有何应用？2、根据热力学稳定判据，推导RK、SRK和PR状态方程的2个参数a、b的表达式。

3、按照压缩系数方程RK、SRK、PR和BWRS，编程计算不同压力和温度下的压缩系数，并说明它们的大致使用范围。

4、什么是气体的对比态原理，在实际中有何应用？5、根据气体焓和熵的热力学关系，利用RK、SRK、PR状态方程分别推导实际气体焓和熵的计算公式。

6、根据表1-1和表1-2所提供的不同气田天然气组分，分别按照式1-95和1-102计算不同压力和温度下的气体焓和熵，并与按照图法得到的结果进行比较。

7、根据热力学关系，证明气体质量定压热容和质量定容热容满足式1-108。

8、根据气体热力学关系，证明气体焦耳-汤姆逊系数满足式1-119。

9、如何用RK、SRK、PR状态方程来计算气体的质量定压热容、质量定容热容和焦耳-汤姆逊系数？10、什么是燃气的燃烧值？在实际生产中为什么采用低热值而不是高热值？11、什么是燃气的爆炸极限？惰性气体含量对爆炸极限有何影响？12、定性说明温度对液体和气体粘度的不同影响。

13、根据粘度计算方法，编程计算天然气在不同压力和温度下的粘度。

14、什么是气体的导热系数？给出计算实际气体导热系数的步骤并编程。

15、什么是天然气的水露点和烃露点？说明确定水露点和烃露点的几种方法。

16、如何根据平成常数列线图计算天然气的烃露点？17、试说明气体流动连续方程1-159、运动方程1-161和能量方程1-163的物理意义和适用条件。

第二章输气管水力计算1、在什么情况下，输气管的流量计算公式中可以忽略速度变化对流量的影响？2、为什么管道沿线地形起伏、高差超过200m以上，要考虑地形对工艺参数Q或P 的影响？3、公式2-53~2-62适用于何种流态？若管内实际流动偏离该液态，应如何处理？4、为什么干线输气管道采用高压输气较为经济？5、对于已建成的一条输气管道，若要增大输气量，其扩建工程可以采用哪些措施？6、流量系数法能解决哪些复杂输气管道的设计计算？7、用公式2-112、2-115、2-120、2-124计算的流量是整个输气管道的通过能力，这一说法是否正确？试说明用上述任意一个公式计算沿线既有分气工况又有进气工况时的步骤，并编写计算机程序。

天然气的焦耳汤姆孙效应天然气的焦耳-汤姆孙效应天然气是一种极其重要的可再生能源，它的发展对于实现世界可持续发展具有重要意义。

然而，由于天然气分子具有很高的活性，在天然气储存、输送和使用过程中，它们很容易发生反应，从而形成焦耳。

这就是所谓的汤姆孙效应，是天然气反应性的一种表现形式。

汤姆孙效应是由英国化学家威廉·汤姆·孙在19世纪末发现的，他发现天然气在高温下会发生反应，形成焦耳，这种反应叫做汤姆孙效应。

汤姆孙效应是天然气储存、输送和使用过程中常见的问题，它可以造成严重的经济损失，也会影响到天然气的安全性。

汤姆孙效应的机制是由于天然气的活性，它们可以与温度和压力变化而变化，从而产生反应。

根据反应机理，汤姆孙效应包括化学催化反应和物理催化反应两种形式。

化学催化反应是指天然气中的气体分子，通过活性中间体的形成，形成反应物，从而形成焦耳。

物理催化反应是指在高温、高压和有机物的影响下，天然气中的气体分子受到外部刺激而发生反应，从而形成焦耳。

另外，汤姆孙效应还受到其他因素的影响，如催化剂、氧化剂和水的存在。

这些因素可以加速汤姆孙效应的发生，从而对天然气的安全性产生负面影响。

为了有效地控制汤姆孙效应，业界应采取一些有效的措施，如采用新型低活性分子来改善储存、输送和使用过程中的安全性，采用高效的氧化剂，减少水的含量，采用新型催化剂等。

当然，要有效地控制汤姆孙效应，还需要改善天然气的质量，主要是改善天然气的温度和压力，减少其中悬浮物的含量，提高天然气的纯度等，以避免汤姆孙效应的发生。

总之，汤姆孙效应是天然气反应性的一种表现形式，可能会对天然气的安全性产生负面影响，因此，需要采取有效的措施来控制汤姆孙效应，以确保天然气的安全性。

海底天然气物理化学性质第一节海底天然气组成表示法一、海底天然气组成海底天然气是由多种可燃和不可燃的气体组成的混合气体。

以低分子饱和烃类气体为主，并含有少量非烃类气体。

在烃类气体中，甲烷（CH4）占绝大部分，乙烷（C2H6）、丙烷（C3H8）、丁烷（C4H10）和戊烷（C5H12）含量不多，庚烷以上（C5+）烷烃含量极少。

另外，所含的少量非烃类气体一般有氮气（N2）、二氧化碳（CO2）、氢气（H2）、硫化氢（H2S）和水汽（H2O）以及微量的惰性气体。

由于海底天然气是多种气态组分不同比例的混合物，所以也像石油那样，其物理性质变化很大，它的主要物理性质见下表。

海底天然气中主要成分的物理化学性质二、海底天然气容积分数和摩尔分数定义混合物中各组分的容积为V i ，总容积V ；摩尔分数y i ：i 组分的摩尔数n i 与混合物总摩尔数n 的比值。

∑=='ii i i V VV V y ； 1='∑i y ；∑==i i i i n n n n y ； 1=∑i y由分压定律，存在P i V= n i R M T ；P i V=n R M T 由分容定律，存在PV i = n i R M T ；PV=n R M Tpp n n y ii i ==； i i i i y n n V V y ===' 结论：对于理想气体混合物，任意组分的摩尔分数可以用该组分的分压与混合物总压的比值表示，且摩尔分数与容积分数相等。

三、海底天然气分子量标准状态下，1kmol 天然气的质量定义为天然气的平均分子量，简称分子量。

∑=i i M y M四、海底天然气密度（1）平均密度混合气体密度指单位体积混合气体的质量。

按下面公式计算： 0℃标准状态 ∑=i i M y 414.221ρ； 20℃标准状态 ∑=i i M y 055.241ρ 任意温度与压力下 i i i i V y M y ∑∑=/ρ （2）相对密度在标准状态下，气体的密度与干空气的密度之比称为相对密度。

基于亥姆霍兹能量方程的天然气密度计算方法张平李洪烈李灿彭太罛梁烽(国家管网集团西气东输公司)摘要提出一种基于亥姆霍兹能量方程的天然气密度计算方法，通过实际数值计算证明该方法计算结果精度高,与色谱分析仪测量的结果相比误差不超过0.1%。

关键词天然气密度亥姆霍兹能量方程数值计算中图分类号TE642文献标识码A文章编号1000-3932(2021)01-0049-04随着天然气的贸易计量方式逐步由体积计量转换为能量计量，天然气的物性参数，尤其是密度、热值、组分计算的准确性对贸易计量争议的影响越来越明显［1，2］%目前天然气计量的方法是流量计算机通过获取天然气的工况流量、温度及压力等信息，结合预设的气质组分参数换算成标准状态下(20!,101.325kPa)的天然气体积,用于和用户的贸易交接［3'4］%供气方提供天然气日分输体积总累积量和当日的气质组分表作为交接凭据％流量计算机具备根据在线色谱分析仪提供的天然气高、低位发热量计算日分输天然气总能量的能力，这也将是推行天然气贸易能量计量的主要指标。

因此，需要一种精确、可靠的算法来根据已知组分的天然气测算密度、热值等物性参数的方法。

1研究方法1.1目前研究的普遍方法目前针对气体的物性参数计算，基于气体状态方程的算法主要有LKP状态方程、SRK状态方程和BWR状态方程％有学者在关联大量实验数据的基础上，对BWR方程的应用范围和精确度做了进一步提高，形成了修正的BWR状态方程(BWRS)，这被认为是当前烃类计算中的最佳模型%文献［5］提出可利用BWRS方程计算单组分烃类气体和多组分混合气体的密度和焦耳-汤姆逊系数，结果显示BWRS计算方法简单、精确度高％但该方法计算精度受比热容关系的影响明显，对于天然气，需要提供可靠的比热容关系式来进一步提高计算精度［5~9］。

BWRS方程的形式如下：p=pRT+网T-V*0-*"2+"3+"!'+f"7+¥(1+#P2)exp(-$P2)(1)其中，p为介质绝对压力，kPa；p为介质密度，kmol/m3；&为气体常数，kJ/(kmol-K);T为介质温度,K；相关参数A0"B0"C0"D0"E0"a，、b、c、.、％，、$必须通过大量的实验得到［8］%从式(1)可以看出，气体压力p是以密度p和温度T为自变量的二元函数％同样，基于密度p和温度T的热力学函数吉布斯能量方程(Gibbs En­ergy)和亥姆霍兹能量方程(Helmholtz Energy)也可用于气体的物性参数计算％但实际研究表明，吉布斯能量方程在介质从液态转换为气态过程中并不连续，较亥姆霍兹能量方程气液两相连续特性的局限性较大，因此笔者采用亥姆霍兹能量方程作为计算基础％1.2亥姆霍兹能量方程对于某种介质而言，亥姆霍兹能量-通常表示为理想状态下能量贡献-0和能量贡献修正值-r 的总和［10412］，即:a(T,p')=-(T,p')+-(T,p')(2)基金项目：国家管网集团西气东输公司科技项目(KJ202002)%作者简介:张平(1988-)，工程师，从事天然气集输与控制的研究，******************。

埋地天然气管道泄漏温度场模拟李鹤，封辉，池强(中国石油集团石油管工程技术研究院石油管材及装备材料服役行为与结构安全国家重点实验室，陕西西安710077)摘要:为了解埋地管道泄漏后附近温度场的分布情况，以便对管道发生小孔泄漏进行泄漏检测，本文对埋地输气管道泄漏前后建立了二维物理模型和数学模型并给出了相应的边界条件。

利用计算流体软件Fluent对环境温度、输送压力、泄漏口孔径与泄漏方向四种泄漏工况分别进行了管道泄漏后的数值模拟。

结果表明:环境温度、输送压力是决定管道泄漏后土壤温度场分布的决定性因素;泄漏口孔径也会对土壤温度分布造成影响，但影响效果小于环境温度和输送压力的影响;泄漏方向更大程度影响冷影响区的相对位置,而对冷影响区域的大小影响不大。

本文最终得到了不同工况下管道泄漏后周围土壤温度场的分布情况，对当前广泛应用的光纤传感器的现场应用有一定的指导意义’关键词:埋地输气管道;小孔泄漏;温度场分布#数值模拟中图分类号:TE973文献标识码：A文章编号：1008-021X(2021)05-0145-05The Simulation of Tempertur Fielf of Underground Natural Gas Pi-eline LeakageLi He,Feng Hui,CCi Qiang(CNPC Tubular Goods Research Institute,Sm—Key Labom———-Pe—ormanco andStructure S—ety of Petroleum Tubular Goods and Equiyment Materials,XiVn710077, China)Abstract：In order to understand the disGibu—on of temperature—elU in the vicinity of bu—ed pipelines—ter leakage and to detect the leakage of smal l holes in pipelines,a too-dicensional physical model and mathema—cal model we—established before and —ter the leakage of bu—ed gas pipdPes,and the corresponding bounda—conditions we—given.The numerical simulation of pipe—ne leakage under—umeaka/e conditions,namely,environmental temperature,ddive—pressure,aperture of leakage port and direction of leakage,was carried out by using the computa—onal—uid software Fluent.The—su—s show that ambOnt temperature and conveying pressure are the decisive factors—r the distribution of soil temperature field—ter pipeline leakage；the pore size of the makage port a—e—fects the soil—mperatu—distribution,but the edect is less than that of the ambOnt temperature and transport pressure；the direction of leakage has more influence on the relative position of the cold Hec—d area, but has lip—in—uenco on the size of the colU Hec—d area.In this paper,the distribution of the so——mperatu——elU a—und the pipe leakage under dPerent working conditions is obtained,which has a certain guiding significance—r the—elU application of —ber opt—sensors widely used at present.Key words:bu—ed gas pipeline；aperture leak；temperature—eld distribution；numerical simulation管道以成本低、能耗低、安全性高、运行稳定等优点成为天然气的主要输送工具，截止2017年末，我国气体管道总里程近八万千米⑴。

焦耳-汤姆逊系数计算方法研究
毛伟;张立德
【期刊名称】《特种油气藏》
【年(卷),期】2002(009)005
【摘要】对气井井筒温度预测时所必需的焦耳-汤姆逊系数的计算方法进行进一步研究,推出了焦耳-汤姆逊系数计算公式,指出了计算焦耳-汤姆逊系数的关键在于定压下压缩因子对温度的偏导数.以立方型状态方程通式为基础,该通式中的系数取不同值可变为VDW、RK、SRK、PR方程,推出了定压下压缩因子对温度的偏导数.最后预测了不同压力、温度下甲烷的焦耳-汤姆逊系数,通过和实测值的对比,分析了产生误差的原因,给出了计算焦耳-汤姆逊系数时选择状态方程的依据.
【总页数】3页(P44-46)
【作者】毛伟;张立德
【作者单位】大庆油田有限责任公司勘探开发研究院,黑龙江,大庆,163712;吉林油田分公司乾安采油厂,吉林,长春,131400
【正文语种】中文
【中图分类】TE329
【相关文献】
1.计算焦耳—汤姆逊系数的LKP方法 [J], 谢太浩
2.空气静压润滑焦耳-汤姆逊系数的计算方法 [J], 程阳;李东升;胡佳成
3.使用状态方程计算天然气焦耳-汤姆逊系数 [J], YUAN Weimin;WANG
Hui;CHEN Xueyan;WANG Le;LEI Jiangkai;ZHANG Xiaohui;CHEN Li
4.非广延热力学中的焦耳-汤姆逊系数 [J], 郑利宁
5.计算天然气焦耳-汤姆逊系数的BWRS方法 [J], 董正远;肖荣鸽
因版权原因，仅展示原文概要，查看原文内容请购买。

物理化学主要公式与使用条件第一章 气体的pVT 关系 主要公式与使用条件1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ，V ，T 与n 单位分别为Pa ，m 3，K 与mol 。

m /V V n =称为气体的摩尔体积，其单位为m 3 ·mol -1。

R =8.314510 J ·mol -1 ·K -1，称为摩尔气体常数。

此式适用于理想气体，近似地适用于低压的真实气体。

2. 气体混合物 （1） 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B*=V ϕ∑*AVy Am,A式中∑AA n 为混合气体总的物质的量。

A m,*V 表示在一定T ，p 下纯气体A 的摩尔体积。

∑*AA m,A V y 为在一定T ，p 下混合之前各纯组分体积的总和。

（2） 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量，∑=BB n n 为混合气体总的物质的量。

上述各式适用于任意的气体混合物。

〔3〕V V p p n n y ///B B B B *=== 式中p B 为气体B ，在混合的T ，V 条件下，单独存在时所产生的压力，称为B 的分压力。

*B V 为B 气体在混合气体的T ，p 下，单独存在时所占的体积。

3. 道尔顿定律p B = y B p ，∑=BB p p上式适用于任意气体。

对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。

5. X 德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa ·m 6 ·mol -2，b 的单位为m 3 ·mol -1，a 和b 皆为只与气体的种类有关的常数，称为X 德华常数。

干气密封的实际气体焦耳-汤姆逊效应分析邓成香;宋鹏云;马爱琳【摘要】干气密封系统中气体通过过滤器、阀门、孔板和密封端面等组件时会发生焦耳-汤姆逊（JT）效应，可能导致密封气温度降低，甚至出现液相凝析。

焦耳-汤姆逊效应一般通过焦耳-汤姆逊系数来反映。

针对干气密封常面临的氢气、氮气、空气和二氧化碳，利用VDW方程、RK方程、SRK方程和PR方程4个经典状态方程（EOS）分别计算了相应的焦耳-汤姆逊（JT）系数，并与文献实验数据进行了比较，选择最佳状态方程作出各气体的 JT系数曲线和焦耳-汤姆逊反转曲线（JTIC），并利用编程计算出空气和氮气通过干气密封端面时，由于JT效应引起的气体温降。

结果表明：实际气体的焦耳-汤姆逊效应，对干气密封的节流环节会产生重要影响。

常温条件下，氢气发生致热效应，而氮气、空气和二氧化碳气体发生致冷效应。

采用4种状态方程计算焦耳-汤姆逊系数时，RK方程的平均相对误差和最大相对误差最低且分别小于4%和10%。

干气密封气体的实际气体焦耳-汤姆逊效应能引起较大的温度变化，其中气体介质压力比介质温度对温差的影响更大。

压力较小时JT效应引起的温降可以忽略。

%In a system sealed by dry gas, the Joule-Thomson (JT) effect occurs when the gas flows through the components of filters, valves, orifices and end faces, which may cause the temperature drop of sealing gas, even the appearance of liquid condensation. Generally, the Joule-Thomson effect is represented byJoule-Thomson coefficient. As to the hydrogen, nitrogen, air and carbon dioxide, which are often encountered for the cases of sealing by dry gas, the corresponding Joule-Thomson (JT) coefficients were calculated by four classical equations of state (EOS) of VDW, RK, SRK and PR. Subsequently,those calculated coefficients are compared with the experimental data in the literatures. The JT coefficient curves and Joule-Thomson inversion curves (JTIC) were plotted using the optimal equation of state. As to air and nitrogen through the end faces of dry sealing gas, the gas temperature drops caused by JT effect were calculated by applying the computer program. It shows that the Joule-Thomson effect of real gas, which have important influence on the throttle of dry sealing gas. At room temperature, hydrogen showed exothermic effect, while nitrogen, air and carbon dioxide endothermic (cooling) effect. The corresponding Joule-Thomson (JT) coefficients were calculated by the four classical EOS, the average relative error and maximum relative error of RK equation were the minimum, less than 4% and 10%, respectively. The JT effect of real gas causes large temperature difference in the dry sealing gas, of which the gas pressure more&nbsp;influences on the temperature drop than the gas temperature does. When the pressure is small, the temperature drop by the JT effect can be negligible.【期刊名称】《化工学报》【年(卷),期】2016(067)009【总页数】10页(P3833-3842)【关键词】干气密封;实际气体;状态方程;焦耳-汤姆逊系数;反转曲线【作者】邓成香;宋鹏云;马爱琳【作者单位】昆明理工大学化学工程学院，云南昆明 650500;昆明理工大学化学工程学院，云南昆明 650500;昆明理工大学化学工程学院，云南昆明 650500【正文语种】中文【中图分类】TB42;TQ031.1引言实际气体流动过程，由于节流效应，气体发生绝热不可逆膨胀导致温度变化的现象称为焦耳-汤姆逊效应。