河北省2019届中考数学系统复习 第六单元 圆 滚动小专题(九)与圆有关的计算与证明课件
- 格式:ppt
- 大小:1.83 MB
- 文档页数:22
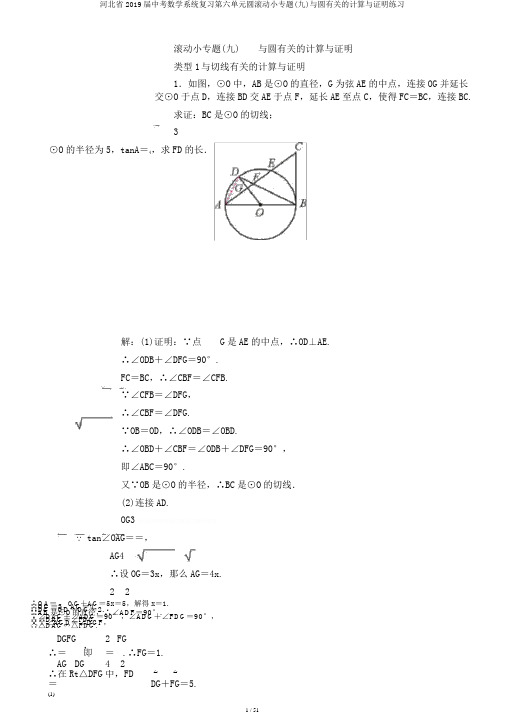
滚动小专题(九) 与圆有关的计算与证明类型1 与切线有关的计算与证明1.如图,⊙O 中,AB 是⊙O 的直径,G 为弦AE 的中点,连接OG 并延长交⊙O 于点D ,连接BD 交AE 于点F ,延长AE 至点C ,使得FC =BC ,连接BC.求证:BC 是⊙O 的切线;3⊙O 的半径为5,tanA =4,求FD 的长.解:(1)证明:∵点 G 是AE 的中点,∴OD⊥AE.∴∠ODB+∠DFG=90°.FC =BC ,∴∠CBF=∠CFB.∵∠CFB=∠DFG,∴∠CBF=∠DFG.∵OB=OD ,∴∠ODB=∠OBD.∴∠OBD+∠CBF=∠ODB+∠DFG=90°,即∠ABC=90°.又∵OB 是⊙O 的半径,∴BC 是⊙O 的切线.(2)连接AD.OG3∵ tan ∠OAG==,AG4∴设OG =3x ,那么AG =4x.2 2∴OA = OG +AG =5x =5,解得x =1. ∴OG =3,AG =4. ∴DG =OD -OG =2. ∵AB 是⊙O 的直径,∴∠ADF =90°. ∵∠DAG +∠ADG =90°,∠ADG +∠FDG =90°, ∴∠DAG =∠F DG. 又∵∠AGD =∠DGF , ∴△DAG ∽△FDG. DGFG 2 FG ∴= ,即 = .∴FG=1.AG DG 4 2 ∴在Rt △DFG 中,FD= 2 2 DG +FG =5.(1)(3)2.如图,四边形ABCD内接于⊙O,∠BAD=90°,过点C作CE⊥AD,垂足为E,且∠EDC=∠BDC.(4)求证:CE是⊙O的切线;假设DE+CE=4,AB=6,求BD的值.1(3)(4)(5)(6)(7)(8)(9)(10) 解:(1)证明:∵∠BAD =90°,(11) ∴∠BCD =90°.(12) ∵CE ⊥AD ,∴∠E =90°.(13) ∵∠EDC +∠DCE =90°,(14) ∠EDC =∠BDC ,(15) ∴∠BDC +∠DCE =90°.(16) ∵OD =OC ,∴∠ODC =∠OCD.(17) ∴∠OCD +∠DCE =90°,即 OC ⊥CE.(18) 又∵OC 是⊙O 的半径,∴CE 是⊙O 的切线.过点O 作OF ⊥AE ,垂足为F ,那么AF =DF ,∴OF =1AB =1×6=3.2 2 23 易证得四边形 OFEC 为矩形,∴CE =OF.4 ∵DE +CE =4,∴DE =1.5 2在Rt △DCE 中,CD =1+3=10.∵∠EDC =∠BDC ,∴Rt △BDC ∽Rt △CDE.BD CDBD10∴= ,即 10 =.CD DE 1∴BD =10.类型2 与弧长及面积有关的计算3.如图,在⊙O 中,半径 OA ⊥OB ,过 OA 的中点C 作FD ∥OB 交⊙O 于D ,F 两点,且 CD = 3,以O 为圆心,OC 为︵半径作CE ,交OB 于E 点.(1)求⊙O 的半径OA 的长;(2)计算阴影局部的面积.解:(1)连接OD.FD ∥OB ,OA ⊥OB ,∴OA ⊥FD.∵C 为OA 的中点,21 1∴OC=2OA=2OD.∴在Rt△OCD中,∠ODC=30°.∴OC=CD·tan30°=1.∴OD=2OC=2,即⊙O的半径OA的长为2.(2)S阴影=S扇形BOD+S△OCD-S扇形COE21230×π×290×π×1=360+2×1×3-360π312+2.4.如图,风车的支杆O E垂直于桌面MN,风车中心O到桌面的距离 OE为25cm,小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A,B,C,D在同一圆O上,⊙O的半径为10cm.风车在转动过程中,当∠AOE=45°时,求点A到桌面的距离(结果保存根号);(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路径长(结果保存π).备用图1备用图2解:(1)如图1,当点A运动到点A1的位置时,∠AOE=45°.作A1F⊥MN于点F,A1G⊥OE于点G,∴A1F=GE.在Rt△A1OG中,∵∠A1OG=45°,OA1=10,122.∴OG=OA·cos45°=10×2=5∵OE=25,∴GE=OE-OG=25-5 2.∴A1F=GE=25-52.答:点A到桌面的距离是(25-52).cm(2)如图2,点A在旋转过程中运动到点A2,A3的位置时,点A到桌面的距离等于20.cm作A2H⊥MN于点H,那么A2H=20.作A2D⊥OE于点D,∴DE=A2H.∵OE=25,∴OD=OE-DE=25-20=5.在Rt△A2OD中,∵OA2=10,OD1cos∠A2OD==.OA22∴∠A2OD=60°.由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.120×π×1020π∴点A所经过的路径长为180=3.答:点A所经过的路径长为203πcm.32π+4π=6π.图1 图25.如图,有一直径 MN =4的半圆形纸片,其圆心为点 P ,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至 位置Ⅴ,其中,位置Ⅰ中的 MN 平行于数轴,且半圆 P 与数轴相切于原点 O ;位置Ⅱ和位置Ⅳ中的 MN 垂直于数轴; 位置Ⅲ中的 MN 在数轴上;位置Ⅴ中的点 N 到数轴的距离为 3,且半圆 P 与数轴相切于点 A. 解答以下问题:位置Ⅰ中的MN 与数轴之间的距离为2;位置Ⅱ中的半圆P 与数轴的位置关系是相切; 求位置Ⅲ中的圆心P 在数轴上表示的数;纸片半圆P 从位置Ⅲ翻滚到位置Ⅳ时,求点N 所经过路径长及该纸片所扫过图形的面积; 求OA 的长.[(2)(3)(4) 中的结果保存 π]︵︵ 解:(2)位置Ⅰ中ON 的长与数轴上线段 ON 相等,︵ 90×π×2∵ON 的长为 =π,NP =2,180∴位置Ⅲ中的圆心 P 在数轴上表示的数为 π+2.90×π×4(3)点N 所经过路径长为 =2π,180 2 2S 半圆=180×π×2 90×π×4 =4π.360 =2π,S 扇形= 360∴半圆P 所扫过图形的面积为作NC 垂直数轴于点C ,作PH ⊥NC 于点H ,连接PA ,那么四边形PHCA 为矩形.在Rt △NPH 中,PN =2,NH =NC -HC =NC -PA =1.NH1∵ sin ∠NPH ==,∴∠NPH =30°.PN2∴∠MPA =60°.︵ 60×π×22∴MA 的长为 180 =π.32 5∴OA =π+4+3π=3π+4.4。


第25讲与圆有关的计算命点近8年的命形式考方向高考点型呈形式比丰富,、2021(T25(1)解),2021(T23(2)解、填空、解答三种型都有出,弧的扇形弧、面的算T25(3)解),2021(T25解),2021(T26考重于弧公式的考,算,解),2021(T19填),2021(T14)扇形面的考重在化程中形成的区域面,可用多种方法行化成求扇形面.重于有关正多形面的算,一般都有正多形与2021(T15)技巧性,需要我熟掌握正多形的各个量之的关系,并能把正多形行分割与拼接.命点1扇形弧、面的算1.(2021·河北T14·3分)如,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=23.S阴影=(D)A.πB.2π C.23 D.2 33π2.(2021·河北T19·3分)如,将8cm的首尾相接成半径2cm的扇形.S扇形=4cm2.命点2 正多形与S3.(2021·河北T15·3分)如,a的正六形内有两个三角形(数据如),阴影=(C)S空白A.3 B .4 C .5 D .6重点1 弧的算如,△ABC是正三角形,曲CDEFG⋯叫做“正三角形的开〞,曲的各局部弧.1(1)中已有4段弧,接着画出第5段弧GH;2πa10πa(2)△ABC的a,第1段弧的是3;第5段弧的是3;前5段弧的和(即曲CDEFGH的)是10πa;(3)似地有“正方形的开〞“正五形的开〞⋯,a的正方形的开的前5段弧的和是15πa;2(4)猜测:30πa①a的正n形的前5段弧的和是n;m〔m+1〕πa②a的正n形的前m段弧的和是n.【思路点】(1)以点B心,BG半径画弧即可;(2)利用弧公式算.但要先确定弧所的心角都是120度,半径却在不断地增大,第1段弧的半径是a,第2段弧的半径是2a,第3段弧的半径是3a,依此下去第5段弧的半径是5a,和就是把五段弧加起来;(3)先利用正方形的性求出正方形的外角度数,合每段弧所在的半径化律,利用弧公式算每段弧,最后求和;(4)可以利用前面的探究方法,合正n形的性解决.【式1】(2021·淄博)如,⊙O的直径AB=6.假设∠BAC=50°,劣弧AC的(D)8π3π4πA.2π B.3 C.4 D.3【式2】(2021·廊坊模)如,在 6的菱形ABCD中,分以各点心,以的一半半径,在菱形内作四条弧,中阴影局部的周是6π.(果保存π)方法指1.求弧,要先确定两个要素,一是弧所在的半径,二是弧所在扇形的心角,再代入弧公式算即可.2.同一正多形的开每局部弧所的心角不,半径后一段比相的前一段增加一个正多形的.2π×ma模型建立a的正n形的开第m段弧.n重点2 扇形面的有关算如1,直径AB 6的半,点A逆旋60°,此点B到达点B′,求中阴影局部的面.2图1 图2图3【变式1】 (2021·大庆)如图2,在Rt △ABC 中,∠ACB=90°,AC =BC =2,将Rt △ABC 绕点A逆时针旋转30°后得到Rt △ADE,点B 经过的路径为弧BD ,那么图中阴影局部的面积为23π.【变式2】 如图3,在Rt △ABC 中,∠ACB=90°,AC =1,∠ABC=30°,将Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE,点B 经过的路径为弧BD ,那么图中阴影局部的面积是1π.3【变式3】 如图4,在△ABC 中,AB =6,将△ABC 绕点B顺时针旋转60°后得到△DBE,点A 经过的路径为弧AD ,那么图中阴影局部的面积是π6.图4图5【变式4】如图5,在Rt △ABC 中,∠ACB=90°,BC =1,将Rt △ABC 绕点C 顺时针旋转60°,此时点B 恰π3好在DE 上,其中点A 经过的路径为弧AD ,那么图中阴影局部的面积是2-4 .(注:所有小题结果保存π)【思路点拨】阴影局部的面积可以看作以旋转点为圆心,旋转角为圆心角, AB 为半径的扇形面积;只有变式4阴影局部的面积是 S-S.扇形ACD△BC E【自主解答】解:∵AB=AB′=6,∠BAB′=60°,∴S=S+S-S=S60 2阴影 扇形B′A B 半圆O′ 半圆 扇形B′A B =360×π×6=6π.O方法指导 在圆中求阴影局部面积大致有以下方法:弓形或弓形的一局部可转化成扇形减去三角形的面积;新月形可以用扇形减去一个弓形的面积;可以利用等积变换求阴影局部的面积;可以利用轴对称、中心对称求阴影局部的面积;旋转形成阴影局部的面积,往往可以转化成求一个扇形的面积.重难点3 正多边形和圆(2021·河北模拟 )如图是由有两个公共顶点的正六边形与正方形组成的一个图形.假设阴影局部的周长为10,那么这个图形的外轮廓线的周长为()AA.18B.183C.22D.223【思路点拨】从图形上能看出,正方形的边长等于正六边形边长的2倍.提示:设正六边形的边长为a,那么正方形的边长为2a,由题意,得5a=10,解得a=2.那么外轮廓线的周长为3a2a×3=9a=18.【变式训练3】(2021·河北模拟 )如图,正六边形与正方形有重合的中心 O.假设∠BOC是正n边形的一个外角,那么n的值为(C)3A.8 B.10 C.12 D.16【变式训练4】(2021·石家庄二模)正六边形ABCDEF与正三角形△ACG按如下图位置摆放,在六边形AGCDEFS阴影中,S空白的值是(D)A.52B.51C.61D.71方法指导1.熟悉常见正多边形边长与对角线的数量关系.360°2.正n边形的中心角与每一个外角相等,都等于(n≥3).n3.研究面积相关问题时可采用割补与拼接等方法,研究周长可采用化曲为直等方法.注:正多边形与圆中,正多边形通常是指正方形,正五边形,正六边形,正八边形等常见的正多边形.1.(2021·盘锦)如图,一段公路的转弯处是一段圆弧︵︵(AB),那么AB的展直长度为(B).3πm .6πm C.9.12πmA Bπm D2.(2021·成都)如图,在?ABCD中,∠B=60°,⊙C的半径为3,那么图中阴影局部的面积是 (C)A.πB.2π C .3πD.6π3.(2021·德州)如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形,那么此扇形的面积为(A)π23222A.2mB.2πm C.πm D.2πm44.(2021·河北模拟)如图,分别把正六边形边AB,EF,CD向两个方向延长,相交于点M,N,Q,那么阴影局部与空白局部的面积比为(A)1121A.2B.3C.5D.45.(2021·河北模拟)如图,六边形ABCDEF和六边形MNPQGH都是正六边形.假设AB=10,那么MN的值可能是(D)53C.52D.53A.B.526.(2021·株洲)如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,那么∠BOM=48°.7.(2021·石家庄藁城区模拟)如图,M,N分别是正五边形ABCDE的边AB,AE的中点,四边形MNHG 是位于该正五边形内的正方形,那么∠BMH的度数是99°.8.(2021·盐城)如图,图1是由假设干个相同的图形(图2)组成的美丽图案的一局部,图2中图形的相关数据:半径OA=2cm,∠AOB=120°.那么图2的图形周长为8πcm(结果保存π).359.(2021·河南)如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到︵53△A′B′C′,其中点B的运动路径为BB′,那么图中阴影局部的面积为4π-2.10.(2021·邢台宁晋县模拟︵︵)如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,那么AP与QB的长度之和为()BA.2πB.4πC.5πD.π333︵︵1204提示:连接OP,OQ,易知△OPQ为等边三角形,lAP+lQB=180×π×2=3π.11.(2021·威海)如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,那么图中阴影局部的面积是(C)A.18+36π B.24+18π C .18+18πD.12+18π提示:作 FH⊥BC 交BC 延长线于点H ,连接AE ,S 阴影=S +S 半圆 -S -S=12×12+ 2×π×6-2×12×6- 2×65×65=18+18π.正方形ABCD △ABE △AEF1 2 1 112.(2021·河北模拟)如图,点 P 是⊙O 外一点,PA 切⊙O 于点A ,AB 是⊙O 的直径,连接 OP ,过点B 作BC∥OP交⊙O 于点C ,连接AC 交OP 于点D.(1)求证:PC 是⊙O 的切线;6(2)假设PD=16,AC=8,那么图中阴影局部的面积为25π-482;3cm cm2cm︵在(2)的条件下,假设点E是AB的中点,连接CE,求CE的长.解:(1)证明:连接OC,∵PA切⊙O于点A,∴∠PAO=90°.∵OP∥BC,∴∠AOP=∠OBC,∠COP=∠OCB.∵OC=OB,∴∠OBC=∠OCB.∴∠AOP=∠COP.OA=OC,在△PAO和△PCO中,∠AOP=∠COP,OP=OP,∴△PAO≌△PCO(SAS).∴∠PAO=∠PCO=90°.又∵OC是⊙O的半径,∴PC是⊙O的切线.连接AE,BE,过点B作BM⊥CE于点M,∴∠CMB=∠EMB=90°,∠AEB=90°.︵︵︵又∵点E是AB的中点,∴AE=BE.1∴∠ECB=∠ACE=2∠ACB=45°.又∵∠CMB=90°,∴∠CBM=45°.∴BM=CM.在Rt△BCM中,由勾股定理,得∴CM=BM=32cm.又∵∠ABE=∠ACE=45°,2 2 2 2 2CM+BM=BC,即CM+BM=36,∴在Rt△AEB中,BE=AB·cos∠ABE=5 2cm.在Rt△BEM中,由勾股定理,得EM=2222=42(cm),BE-BM=〔52〕-〔32〕∴CE=CM+EM=7 2cm,即CE的长为72cm.13.(2021·宜宾)刘徽是中国古代卓越的数学家之一,他在?九章算术?中提出了“割圆术〞,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1.假设用圆O的外切正六边形的面积来近似估计圆O的面积,7那么S=2 3.(结果保存根号)8。



滚动小专题(九) 圆中的简单计算与证明类型1 与垂径定理有关的计算与证明1.如图、在平面直角坐标系中、一段圆弧经过格点A 、B 、C 、其中点B 坐标为(4、3).(1)请写出该圆弧所在的圆的圆心D 的坐标(2、-1);(2)⊙D 的半径为(3)求ABC ︵的长(结果保留π).解:(1)如图、作线段AB 与BC 的垂直平分线、交点即为点D 、∴圆心D 的坐标为(2、-1).(2)连接AD 、则AD =AE 2+DE 2=2 5.(3)过点D 作DF ⊥AO 延长线于点F 、过点C 作CG ⊥FD 于点G.连接CD.在△ADF 和△DCG 中、DF =CG =2, ∠AFD =∠DGC =90°、AF =DG =4、∴△ADF ≌△DCG(SAS).∴∠ADF =∠DCG.∵∠DCG +∠CDG =90°、∴∠ADF +∠CDG =90°、即∠ADC =90°.∴lABC ︵=90180π×25=5π.2.如图、AB 是⊙O 的直径、弦CD ⊥AB 于点E 、且CD =16、点M 在⊙O 上、MD 经过圆心O 、连接MB.(1)若BE =8、求⊙O 的半径;(2)若∠DMB =∠D 、求线段OE 的长.解:(1)∵AB ⊥CD 、CD =16、∴CE =DE =8.设OB =x.又∵BE =4、∴x 2=(x -4)2+82、解得x =10.∴⊙O 的直径是20.(2)∵∠M =12∠BOD 、∠M =∠D 、 ∴∠D =12∠BOD. ∵AB ⊥CD 、∴∠D =30°.∴tanD =OE DE =33.∴OE =33DE =833.3.如图、射线PG 平分∠EPF 、O 为射线PG 上一点、以O 为圆心、10为半径作⊙O 、分别与∠EPF 两边相交于A 、B 和C 、D 、连接OA 、此时有OA ∥PE.(1)求证:AP =AO ;(2)若tan ∠OPB =12、求AB.解:(1)证明:∵PG 平分∠EPF 、∴∠DPO =∠BPO.∵OA ∥PE 、∴∠DPO =∠POA.∴∠BPO =∠POA.∴PA =OA.(2)过点O 作OH ⊥AB 于点H 、则AH =HB =12AB. ∵tan ∠OPB =OH PH =12、∴PH =2OH. 设OH =x 、则PH =2x.由(1)可知PA =OA =10、∴AH =PH -PA =2x -10.∵AH 2+OH 2=OA 2、∴(2x -10)2+x 2=102, 解得x 1=0(不合题意、舍去)、x 2=8.∴AH =6.∴AB =2AH =12.类型2 与切线相关的证明与计算4.(2016·资阳)如图、在⊙O 中、点C 是直径AB 延长线上一点、过点C 作⊙O 的切线、切点为D 、连接BD.(1)求证:∠A =∠BDC ;(2)若CM 平分∠ACD 、且分别交AD 、BD 于点M 、N 、当DM =1时、求MN 的长.解:(1)证明:连接OD.∵AB 为⊙O 的直径、∴∠ADB =90°、即∠A +∠ABD =90°.又∵CD 与⊙O 相切于点D 、∴∠CDB +∠ODB =90°.∵OD =OB 、∴∠ABD =∠ODB.∴∠A =∠BDC.(2)∵CM 平分∠ACD 、∴∠DCM =∠ACM.又∵∠A =∠BDC 、∴∠A +∠ACM =∠BDC +∠DCM 、即∠DMN =∠DNM.∴DN =DM =1.又∵∠ADB =90°、∴MN =DM 2+DN 2= 2.5.(2016·南充)如图、在Rt △ABC 中、∠ACB =90°、∠BAC 的平分线交BC 于点O 、OC =1、以点O 为圆心OC 为半径作半圆.(1)求证:AB 为⊙O 的切线;(2)如果tan ∠CAO =13、求cosB 的值.解:(1)证明:作OM ⊥AB 于点M.∵OA 平分∠CAB 、OC ⊥AC 、OM ⊥AB 、∴OC =OM.∴AB 是⊙O 的切线.(2)设BM =x 、OB =y 、则y 2-x 2=1.①由(1)知AC 、AM 均为⊙O 切线、∴AC =AM.∵tan ∠CAO =OC AC =13. ∴AC =AM =3.∵cosB =BM OB =BC AB、 ∴x y =y +1x +3、即x 2+3x =y 2+y.② 由①②可以得到y =3x -1.∴(3x -1)2-x 2=1、解得x =34、y =54. ∴cosB =x y =35.6.如图、AB 为⊙O 的直径、弦CD ⊥AB 、垂足为点P 、直线BF 与AD 的延长线交于点F 、且∠A FB =∠ABC.(1)求证:直线BF 是⊙O 的切线;(2)若CD =23、OP =1、求线段BF 的长.解:(1)证明:∵∠AFB =∠ABC 、∠ABC =∠ADC 、∴∠AFB =∠ADC.∴CD ∥BF.又∵CD ⊥AB 、∴AB ⊥BF.∴直线BF 是⊙O 的切线.(2)连接OD.∵CD ⊥AB 、∴PD =12CD = 3. ∵OP =1、∴OD =OP 2+PD 2=2.又∵CD ∥BF 、∴△APD ∽△ABF.∴AP AB =PD BF 、即34=3BF .∴BF =43 3.7.(2016·威海)如图、在△BCE 中、点A 是边BE 上一点、以AB 为直径的⊙O 与CE 相切于点D 、AD ∥OC 、点F 为OC 与⊙O 的交点、连接AF.(1)求证:CB 是⊙O 的切线;(2)若∠ECB =60°、AB =6、求图中阴影部分的面积.解:(1)证明:连接OD 、与AF 相交于点G.∵CE 与⊙O 相切于点D 、∴OD ⊥CE 、即∠CDO =90°.∵AD ∥OC 、∴∠ADO =∠DOC 、∠DA O =∠BOC.又∵OA =OD 、∴∠ADO =∠DAO.∴∠DOC =∠BOC.又OD =OB 、CO =CO 、∴△CD O ≌△CBO(SAS).∴∠CBO =∠CDO =90°.∴CB 是⊙O 的切线.(2)由(1)可知∠DCO =∠B CO 、∠DOC =∠BOC 、∵∠ECB =60°、∴∠DCO =12∠ECB =30°. ∴∠DOC =∠BOC =60°.∴∠AOD =60°.∵OA =OD 、∴△OAD 是等边三角形.∴AD =OD =OF.∵∠DOC =∠ADO 、∠FGO =∠AGD 、∴△ADG ≌△FOG(AAS).∴S △ADG =S △FOG .∵AB =6、∴⊙O 的半径为3.∴S 阴影=S 扇形ODF =60π×33360=32π.。
中考数学复习:与圆有关的几何题型及解题技巧初中的数学是不是让你抓破脑袋?有哪些好的数学学习方法呢?以下是小编给大家带来的2019年中考数学复习:与圆有关的几何题型及解题技巧,仅供考生参考,欢迎大家阅读!2019年中考数学解题基本技巧介绍1.观察与实验(1)观察法:有目的有计划的通过视觉直观的发现数学对象的规律、性质和解决问题的途径。
(2)实验法:实验法是有目的的、模拟的创设一些有利于观察的数学对象,通过观察研究将复杂的问题直观化、简单化。
它具有直观性强,特征清晰,同时可以试探解法、检验结论的重要优势。
2.比较与分类(1)比较法是确定事物共同点和不同点的思维方法。
在数学上两类数学对象必须有一定的关系才好比较。
我们常比较两类数学对象的相同点、相异点或者是同异综合比较。
(2)分类的方法分类是在比较的基础上,依据数学对象的性质的异同,把相同性质的对象归入一类,不同性质的对象归为不同类的思维方法。
如上图中一次函数的k在不等于零的情况下的分类是大于零和小于零体现了不重不漏的原则。
3.特殊与一般(1)特殊化的方法特殊化的方法是从给定的区域内缩小范围,甚至缩小到一个特殊的值、特殊的点、特殊的图形等情况,再去考虑问题的解答和合理性。
(2)一般化的方法4.联想与猜想(1)类比联想类比就是根据两个对象或两类事物间存在着的相同或不同属性,联想到另一事物也可能具有某种属性的思维方法。
通过类比联想可以发现新的知识;通过类比联想可以寻求到数学解题的方法和途径:(2)归纳猜想牛顿说过:没有大胆的猜想就没有伟大的发明。
猜想可以发现真理,发现论断;猜想可以预见证明的方法和思路。
初中数学主要是对命题的条件观察得出对结论的猜想,或对条件和结论的观察提出解决问题的方案与方法的猜想。
归纳是对同类事物中的所蕴含的同类性或相似性而得出的一般性结论的思维过程。
归纳有完全归纳和不完全归纳。
完全归纳得出的猜想是正确的,不完全归纳得出的猜想有可能正确也有可能错误,因此作为结论是需要证明的。