三角形的外接圆和内切圆(复习)

相似三角形的内切圆与外接圆在数学中，当两个三角形的对应角相等，并且对应边成比例时，我们称这两个三角形为相似三角形。

在相似三角形中，存在着一些特殊的圆，即内切圆和外接圆。

本文将讨论相似三角形与它们的内切圆和外接圆之间的关系。

一、相似三角形的内切圆内切圆是能够与三角形的三条边都相切的圆。

对于相似三角形而言，它们的内切圆有一个重要的性质：内切圆的半径与三角形的相似比例相等。

假设有两个相似三角形ABC和DEF，且它们的相似比例为k，则内切圆的半径R满足以下关系：R(ABC) / R(DEF) = k这个结论可以通过相似三角形的性质来证明。

因为相似三角形的对应角相等，所以它们的切点、顶点和圆心共线，从而可以得到三角形的内切圆。

二、相似三角形的外接圆外接圆是能够与三角形的三个顶点相切的圆。

对于相似三角形而言，它们的外接圆有一个重要的性质：外接圆的半径与三角形的相似比例的倒数相等。

仍假设有两个相似三角形ABC和DEF，且它们的相似比例为k，则外接圆的半径r满足以下关系：r(ABC) / r(DEF) = 1 / k这个结论可以通过相似三角形的性质来证明。

因为相似三角形的对应角相等，所以它们的顶点、圆心和切点共线，从而可以得到三角形的外接圆。

三、内切圆与外接圆的关系在相似三角形中，内切圆和外接圆之间存在着一定的关系。

如果两个三角形是相似的，它们的内切圆和外接圆的圆心可以看做是同一个点。

实际上，内切圆和外接圆的圆心都位于相似三角形的相似中心上。

相似中心是一个点，使得从它出发，分别向两个相似三角形的对应顶点连线的比等于相似比例。

通过这个性质，我们可以进一步得到内切圆和外接圆的半径之间的关系。

设R为内切圆的半径，r为外接圆的半径，则有：R / r = k其中，k为相似比例。

结论综上所述，相似三角形的内切圆与外接圆之间存在着一些关系。

内切圆的半径与相似比例相等，而外接圆的半径与相似比例的倒数相等。

此外，内切圆和外接圆的圆心可以看做是同一个点，即相似三角形的相似中心。

三角形内切圆和外接圆的半径公式三角形是几何学中的基本图形之一，而内切圆和外接圆是与三角形密切相关的重要概念。

本文将介绍三角形内切圆和外接圆的半径公式以及相关性质和应用。

一、三角形内切圆的半径公式内切圆是指与三角形的三条边都相切的圆。

假设三角形的三边长分别为a、b和c，内切圆的半径为r，则根据三角形的性质，可以得到内切圆半径的计算公式：r = √[(s-a)(s-b)(s-c)/s]其中，s表示三角形的半周长，即s = (a + b + c)/2。

这个公式的原理是利用海伦公式，将三角形的面积与半周长s关联起来。

根据海伦公式，三角形的面积S可以表示为：S = √[s(s-a)(s-b)(s-c)]而内切圆的半径r与三角形的面积S之间存在如下关系：S = rs将上述海伦公式和内切圆半径的关系代入，即可得到内切圆半径的计算公式。

二、三角形外接圆的半径公式外接圆是指能够将三角形的三个顶点都与圆上某一点相切的圆。

假设三角形的三个顶点坐标分别为A(x1, y1)，B(x2, y2)和C(x3, y3)，外接圆的圆心坐标为O(x, y)，半径为R。

根据圆的性质，可以得到外接圆半径的计算公式：R = a/(2sinA) = b/(2sinB) = c/(2sinC)其中，a、b和c分别为三角形的三边长，A、B和C为对应的内角。

这个公式的推导基于正弦定理。

根据正弦定理，三角形的边长与对应内角的正弦值之间存在如下关系：a/sinA = b/sinB = c/sinC将上述关系变形，即可得到外接圆半径的计算公式。

三、内切圆和外接圆的相关性质和应用1. 内切圆和外接圆的圆心和半径关系：内切圆的圆心与三角形的三条角平分线的交点重合，而外接圆的圆心与三角形的三个顶点的垂直平分线的交点重合。

内切圆的半径r 和外接圆的半径R满足如下关系：r = √[(s-a)(s-b)(s-c)/s]，R = a/(2sinA) = b/(2sinB) = c/(2sinC)。

三角形的内切圆和外接圆综合练习题三角形是几何学中的基本图形之一，而三角形的内切圆和外接圆是与三角形密切相关的重要概念。

本文将针对内切圆和外接圆，提供一些综合练习题，帮助读者更好地理解和掌握这些概念。

练习题一：内切圆的性质1. 证明：对于任意三角形ABC，其内切圆的圆心O与三角形的内心I和重心G共线。

2. 若三角形ABC的内切圆的半径为r，三角形的半周长为s，证明：AI+BI+CI=2s。

3. 若三角形ABC的内切圆的半径为r，三角形的面积为S，证明：S=r*s，其中s为三角形的半周长。

练习题二：内接圆与外接圆关系1. 如果一个三角形的内切圆和外接圆的半径分别为r和R，证明：r<=R/2。

2. 若一个三角形的内切圆和外接圆的半径分别为r和R，证明：r^2=2Rr，其中r和R分别为内切圆和外接圆的半径。

3. 若一个三角形的内切圆和外接圆的半径分别为r和R，证明：r(R+r)=s，其中s为三角形的半周长。

练习题三：内切圆和外接圆的半径关系1. 三角形ABC的内切圆半径为r，外接圆半径为R，外接圆的圆心为O。

若角A=60°，角B=90°，求R:r。

2. 已知三角形ABC的内切圆半径为r，三角形BCD的外接圆半径为R，求证：(R-r)^2=(a-b)(a-c)，其中a、b、c分别为三角形BCD的三边长。

这些练习题旨在帮助读者巩固对于三角形内切圆和外接圆的理解，掌握相关的性质和公式，并能够运用这些知识解决具体的问题。

通过练习，读者将能更加深入地理解三角形的性质与相关的几何概念。

总结：本文围绕三角形的内切圆和外接圆的知识点，给出了一些综合练习题。

这些练习题覆盖了内切圆和外接圆的性质、关系和半径之间的关系。

通过解答这些练习题，读者能够提高对于三角形相关概念的理解和应用能力，为进一步的几何学知识的学习打下坚实的基础。

继续努力学习和练习，相信读者能够在几何学领域取得更大的成就！。

三角形的外接圆与内切圆的关系三角形是几何学中最基本的图形之一，它由三条边和三个内角组成。

而在三角形中，外接圆和内切圆是两个与之密切相关的圆形。

外接圆，正如其名所示，是指可以完整地包围三角形的圆。

它的圆心位于三角形的外部，且圆心到三角形的每个顶点距离相等，这个距离叫做外接圆的半径。

那么，三角形的外接圆与内切圆之间存在着怎样的关系呢？内切圆是指可以刚好与三角形的三条边相切的圆形。

内切圆的圆心位于三角形的内部，且圆心到三角形的每条边的距离相等，这个距离叫做内切圆的半径。

根据三角形的性质，三角形的三条角平分线交于一个点，而这个点恰好是内切圆的圆心。

由此可见，三角形的内切圆与角平分线有紧密的关系。

除此之外，三角形的外接圆和内切圆还存在着一些相互关系。

首先，两个圆的圆心和三角形的顶点是共线的，也就是说它们在同一条直线上。

此外，三角形的任意一条边都是两个圆的切线，也可以说两个圆与三角形的每条边相切。

这一属性对于解决一些与圆有关的几何问题非常有用。

进一步地，我们还可以通过三角形的边长和角度来确定外接圆和内切圆的半径。

对于外接圆而言，其半径等于三角形的边长之积除以四倍三角形的面积。

而内切圆的半径则等于三角形的面积除以半周长（半周长等于三边之和的一半）。

利用外接圆和内切圆的性质，我们可以解决一些实际问题，比如计算三角形的面积、判断三角形的类型等。

在工程学、建筑学以及地理学等领域，对三角形的外接圆和内切圆的关系有着广泛的应用。

综上所述，三角形的外接圆与内切圆存在着紧密的关系。

两个圆的圆心和三角形的顶点共线，圆与三角形的顶点和边存在相切关系。

通过三角形的边长和角度，我们可以推导出外接圆和内切圆的半径。

这些性质不仅仅是几何学的基础知识，还在实际中有着重要的应用和意义。

1 / 24.2 与圆有关的位置关系考点5 三角形与圆1．(2019·衡阳)已知圆的半径是6，则圆内接正三角形的边长是 ．2．(2019·宿迁)直角三角形的两条直角边分别是5和12，则它的内切圆半径为 ．3．(2019·荆门)如图，△ABC 内心为I ，连接AI 并延长交△ABC 的外接圆于D ，则线段DI 与DB 的关系是( )A ．DI ＝DBB ．DI ＞DBC ．DI ＜DBD ．不确定4.(2019 山东省德州市)如图，点O 为线段BC 的中点，点A ，C ，D 到点O 的距离相等，若40ABC ∠=︒，则ADC ∠的度数是( )A ．130︒B ．140︒C ．150︒D ．160︒5．（2018•河北）如图，点I 为△ABC 的内心，AB=4，AC=3，BC=2，将∠ACB 平移使其顶点与I 重合，则图中阴影部分的周长为（ ）A ．4.5B ．4C ．3D ．26．如图，△ABC 是一张周长为17cm 的三角形的纸片，BC ＝5cm ，⊙O 是它的内切圆，小明准备用剪刀在⊙O 的右侧沿着与⊙O 相切的任意一条直线MN 剪下△AMN ，则剪下的三角形的周长为（ ）A ．12cmB ．7cmC ．6cmD ．随直线MN 的变化而变化7．(2019·常州)如图，半径为3的⊙O 与边长为8的等边三角形ABC 的两边AB ，BC 都相切，连接OC ，则tan ∠OCB ＝ ．2 / 28.（2018年山东省威海市）如图，在扇形CAB 中，CD ⊥AB ，垂足为D ，⊙E 是△ACD 的内切圆，连接AE ，BE ，则∠AEB 的度数为 ．9．(2019·鄂州)如图，在平面直角坐标系中，已知C(3，4)，以点C 为圆心的圆与y 轴相切．点A ，B 在x 轴上，且OA ＝OB.点P 为⊙C 上的动点，∠APB ＝90°，则AB 长度的最大值为 ．10. (2019 山东省淄博市)如图，在Rt ABC ∆中，90B ∠=︒，BAC ∠的平分线AD 交BC 于点D ，点E 在AC 上，以AE 为直径的O e 经过点D ．（1）求证：①BC 是O e 的切线；②2CD CE CA =g ；（2）若点F 是劣弧AD 的中点，且3CE =，试求阴影部分的面积．11．(2018·江西)如图，在△ABC 中，O 为AC 上一点，以点O 为圆心，OC 为半径作圆，与BC 相切于点C ，过点A 作AD ⊥BO 交BO 的延长线于点D ，且∠AOD ＝∠BAD.(1)求证：AB 为⊙O 的切线；(2)若BC ＝6，tan ∠ABC ＝43，求AD 的长．。

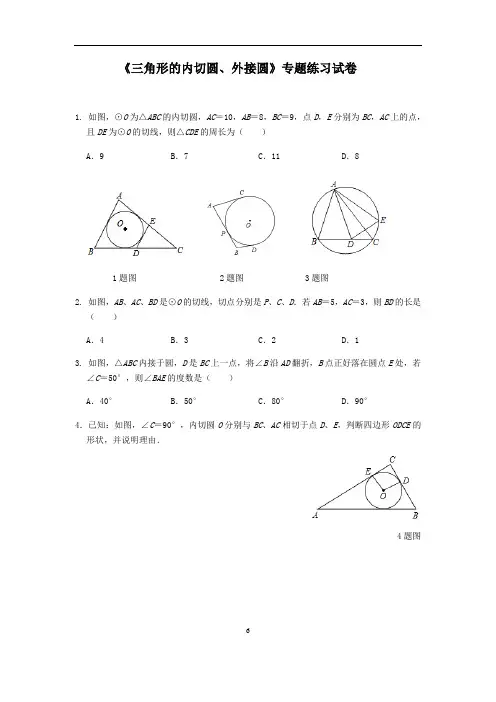
6《三角形的内切圆、外接圆》专题练习试卷1. 如图，⊙O 为△ABC 的内切圆，AC ＝10，AB ＝8，BC ＝9，点D ，E 分别为BC ，AC 上的点，且DE 为⊙O 的切线，则△CDE 的周长为（ ）A ．9B ．7C ．11D ．81题图 2题图 3题图2. 如图，AB 、AC 、BD 是⊙O 的切线，切点分别是P 、C 、D ．若AB ＝5，AC ＝3，则BD 的长是（ ）A ．4B ．3C ．2D ．13. 如图，△ABC 内接于圆，D 是BC 上一点，将∠B 沿AD 翻折，B 点正好落在圆点E 处，若∠C ＝50°，则∠BAE 的度数是（ ）A ．40°B ．50°C ．80°D ．90°4．已知：如图，∠C ＝90°，内切圆O 分别与BC 、AC 相切于点D 、E ，判断四边形ODCE 的形状，并说明理由．4题图65．如图，在△ABC 中，∠A ＝60°，∠C ＝70°，点O 是△ABC 的内心，BO 的延长线交AC 于点D ，求∠BDC 的度数．5题图弧长和扇形面积题型：1. 已知正六边形的边长为8，则较短的对角线长为 ．2. 如图，正六边形ABCDEF 内接于⊙O 其边长为2，则⊙O 的内接正三角形ACE 的边长为 ．2题图 5题图 3．一圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图所对应的扇形的圆心角是( )．A ．120° B．180° C．240° D．300°4．底面圆半径为3cm ，高为4cm 的圆锥侧面积是( )．A ．7.5π cm 2B ．12π cm 2C ．15πcm 2D ．24π cm 25．如图是两个半圆，点O 为大半圆的圆心， AB 是大半圆的弦关与小半圆相切，且AB =24．问：能求出阴影部分的面积吗？若能，求出此面积；若不能，试说明理由．6．如图，若⊙O的周长为20πcm，⊙A、⊙B的周长都是4πcm，⊙A在⊙O内沿⊙O滚动，⊙B在⊙O外沿⊙O滚动，⊙B转动6周回到原来的位置，而⊙A只需转动4周即可，你能说出其中的道理吗？6题图参考答案1. C. 解析：设AB，AC，BC和圆的切点分别是P，N，M，CM＝x，根据切线长定理，得CN＝CM＝x，BM＝BP＝9﹣x，AN＝AP＝10﹣x．则有9﹣x+10﹣x＝8，解得：x＝5.5．所以△CDE的周长＝CD+CE+QF+DQ＝2x＝11．故选：C．1题图2. C. 解析：∵AC、AP为⊙O的切线，∴AC＝AP＝3，∵BP、BD为⊙O的切线，∴BP＝BD，∴BD＝PB＝AB﹣AP＝5﹣3＝2．故选：C．63. C. 解析：连接BE，如图所示：，由折叠的性质可得：AB＝AE，∴AB AE∴∠ABE＝∠AEB＝∠C＝50°，∴∠BAE＝180°﹣50°﹣50°＝80°．故选：C．Array3题图4. 解：四边形ODCE为正方形，理由如下：∵内切圆O分别与BC、AC相切于点D、E，∴OE⊥AC，OD⊥BC．∵∠C＝90°，∴四边形ODCE为矩形．又∵OD＝OE，∴四边形ODCE为正方形．5. 解：∵∠A＝60°，∠C＝70°，∴∠ABC＝50°，∵点O为△ABC的内心，∴∠DBC＝∠ABC＝25°，∵∠ACB＝78°，∠DBC+∠C+∠BDC＝180°，∴∠BDC＝180°﹣78°﹣25°＝77°．66弧长和扇形面积题型：1. 8. 解析：如图，六边形ABCDEF 是正六边形，连接BF ，作AH ⊥BF 于点H ，1题图根据题意可知：BF 为较短对角线，∵六边形ABCDEF 是正六边形，∴AB ＝AF ＝8，∠BAF ＝120°，∵AH ⊥BF ，∴∠BAH=12∠BAF ＝60°， ∴∠ABH ＝30°，∴AH=12AB ＝4， 根据勾股定理，得4，∴BF ＝2BH ＝8． 故答案为：8．2. 2. 解析：连接OB 交AC 于H ．2题图在正六边形ABCDEF 中，∵AB ＝BC ，∠ABC ＝120°，6∴AB BC =，∴OB ⊥AC ，∴∠ABH ＝∠CBH ＝60°，AH ＝CH ，∴AH，∴AC ＝，故答案为．3. B. 解析：由得，∴．∴n ＝180°． 4. C. 解析：可求圆锥母线长是5cm ．∴圆锥的侧面积为：π×3×5=15π.5. 解：将小圆向右平移，使两圆变成同心圆，如图，连OB ，过O 作OC ⊥AB 于C 点，则AC=BC =12，∵AB 是大半圆的弦且与小半圆相切，∴OC 为小圆的半径，∴S 阴影部分=S 大半圆-S 小半圆=12π•OB 2-12π•OC 2=12π（OB 2-OC 2）=12πAC 2=72π． 故答案为72π．5题图6. 解：∵圆O 的周长为20πcm ，∴圆O 的半径=10cm ，∵圆A 圆B 周长都是4πcm ，∴圆A 圆B 周长半径都是2，∴圆A 在圆O 内沿圆O 滚动半径是10﹣2=8，圆B 在圆O 外沿圆O 滚动半径是10+2=12∴要回到原来的位置，圆B 转动的周数=12÷2=6，圆A 转动的周数=8÷2=4．22rl r ππ=2l r =22180n r r ππ=。

三角形的外心与内切圆关系性质解析三角形是几何学中最基本的图形之一，它具有丰富的性质与关系。

其中，外心与内切圆是三角形中重要的概念。

本文将对三角形的外心与内切圆的关系性质进行解析。

一、外心与内切圆的定义1. 外心：三角形的外接圆的圆心被称为外心，它是三条边的垂直平分线的交点。

外接圆的半径等于外心到三角形任意顶点的距离。

2. 内切圆：三角形内切圆的圆心被称为内心，它是三角形三条内切线的交点。

内切圆的半径等于内心到三条边的距离。

二、外心与内切圆的位置关系1. 外心与内心的连线垂直于三角形的一条边：外心与内心之间的连线垂直于三角形的一条边。

根据垂直平分线的性质可知，外心与该边的中点相重合。

2. 外心是三角形三条高的交点：三角形的高是指从三个顶点到对边的垂线段。

外心是三条高的交点，同时也是三条边上的垂直平分线的交点。

3. 内心是三角形内角的平分线的交点：三角形的内心是三个内角的平分线的交点。

内心到三条边的距离相等，等于内切圆的半径。

4. 内切圆切分三角形的面积：三角形被内切圆切分成三个小三角形，每个小三角形的面积等于半周长与边长之差的乘积。

三、外心与内切圆的关系性质1. 外心、内心和重心共线：重心是三角形三条中线的交点，它也是三角形内接圆三条角平分线的交点。

根据欧拉定理可知，外心、内心和重心三点共线，且内心与重心在外心与重心的连线上的一半距离。

2. 内切圆半径与外接圆半径的关系：内切圆半径r和外接圆半径R之间有如下关系：r = R / 2，即内切圆半径是外接圆半径的一半。

3. 外心到顶点的距离等于外接圆半径：外心到三角形任意顶点的距离等于外接圆的半径，即OA = OB = OC = R，其中O为外心，A、B、C为三角形的顶点。

4. 内心到顶点的距离等于内切圆半径：内心到三角形任意顶点的距离等于内切圆的半径，即IA = IB = IC = r，其中I为内心。

四、应用与拓展外心与内切圆的关系性质不仅在几何学中有重要应用，也在其他学科中有广泛的拓展。

三角形的外接圆和内切圆推导在数学中，三角形是一个非常基础且重要的几何形状。

而与三角形相关的一个重要概念是外接圆和内切圆。

本文将推导三角形的外接圆和内切圆的相关性质和推论。

外接圆是指一个圆恰好可以通过三角形的三个顶点，即三个顶点位于圆上的三角形。

下面我们来推导一下三角形的外接圆的性质。

设三角形的三个顶点分别为A、B、C，它们所对应的三条边分别为a、b、c。

我们可以通过下面的推导来得到外接圆的性质。

首先，设三角形的外接圆O半径为R。

根据圆的性质，O到三个顶点的距离都等于R。

设点D为BC边的中点，即D=(B+C)/2。

根据圆的性质，OD为OA的中垂线，因此OD垂直于BC，并且OD的长度等于R。

又根据勾股定理，可以得到OD^2 = BD^2 - BO^2。

由于BD = BC/2，因此BD = c/2。

又由于BO = R，所以BO^2 =R^2。

将这些值代入上述公式中，得到OD^2 = (c/2)^2 - R^2。

类似地，我们可以推导出OE^2 = (a/2)^2 - R^2（E为AC边的中点），OF^2 = (b/2)^2 - R^2（F为AB边的中点）。

根据上述推导结果，我们可以得到以下等式：OD^2 = OE^2 = OF^2 = R^2。

由此可知，三条垂直平分线的交点O就是三角形的外接圆圆心，并且外接圆的半径R可以通过OD、OE或OF求得。

接下来，我们来推导一下三角形的内切圆的性质。

内切圆是指一个圆恰好与三角形的三个边相切，即与三角形的内部正好有一个相切点。

下面我们来推导一下三角形的内切圆的性质。

设三角形的内切圆I半径为r。

根据圆的性质，I到三个边的距离都等于r。

设点M为BC边上与内切圆I相切的点。

根据圆的性质，IM是BI和CI的角平分线，因此IM垂直于BC，并且IM的长度等于r。

又根据勾股定理，可以得到IM^2 = BM^2 -BI^2。

由于BM = p - a（p为三角形的半周长），BI = r，所以BM^2 - BI^2 = (p - a)^2 - r^2。

三角形内接圆和外接圆的半径公式
三角形内切圆和外切圆半径计算公式：
1、三角形内切圆半径：r=2s/(a+b+c)。

式中s是三角形的面积，(a+b+c)是三角形的周长。

2、三角形外接圆的半径：R=abc/4s公式中a，b，c分别为三角形的三边，S为面积。

3、与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

三角形的内心是三角形三条角平分线的交点。

三角形一定有内切圆且内切圆圆心定在三角形内部。

4、与多边形各顶点都相交的圆叫做多边形的外接圆。

三角形有外接圆，其他的图形不一定有外接圆。

三角形的外接圆圆心是任意两边的垂直平分线的交点。

三角形外接圆圆心叫外心。

三角形的内切圆与外接圆的半径关系三角形是几何学中最基本的图形之一，而三角形的内切圆和外接圆在数学研究中也有重要的地位。

本文将探讨三角形的内切圆与外接圆的半径关系。

1. 三角形的内切圆内切圆是指一个圆与三角形的三条边都相切于一点的情况。

内切圆的圆心与三角形的三条边的交点共线，这个交点称为三角形的内心。

对于任意三角形，都存在一个内切圆。

我们来研究内切圆的半径与三角形的性质之间的关系。

设三角形的内切圆的半径为 r，三角形的三条边分别为 a、b、c，三角形的半周长为 s（s = (a + b + c)/2）。

根据三角形的面积公式，可以得到三角形的面积 S：S = √(s(s-a)(s-b)(s-c))另一方面，根据内切圆与三角形的接触性质，我们可以得到内切圆的半径与三角形的面积 S 之间的关系：S = rs将这两个等式结合起来，可以得到内切圆的半径与三角形边长之间的关系：r = √((s-a)(s-b)(s-c)/s)2. 三角形的外接圆外接圆是指一个圆完全包围三角形的情况，三角形的三个顶点都位于圆周上。

外接圆的圆心位于三角形的外心处，外接圆的半径称为三角形的外接圆半径。

我们同样研究外接圆的半径与三角形的性质之间的关系。

设三角形的外接圆的半径为 R。

根据外接圆的性质，我们可以得到外接圆半径与三角形边长之间的关系：R = (abc)/(4S)其中，a、b、c 分别为三角形的三条边的长度，S 表示三角形的面积。

3. 内切圆与外接圆半径关系我们已经得到了三角形的内切圆半径 r 和外接圆半径 R 分别与三角形的边长和面积之间的关系。

现在我们来探讨内切圆半径 r 与外接圆半径 R 之间的关系。

由于三角形的内切圆和外接圆的圆心均为三角形的某个特殊点，根据特殊点的位置关系，我们可以得到内切圆半径 r 与外接圆半径 R 之间的关系：2r = R也就是说，三角形的内切圆半径是外接圆半径的一半。

通过上述推导，我们得到了三角形的内切圆与外接圆的半径关系。

尺规作图：三角形的外接圆、内切圆
◆三角形的外接圆：过三角形三个顶点的圆，即圆心到三角形各个顶点的距离
相等
尺规作图步骤：
（1）找圆心：任取三角形的两条边（如取边BC 和AC ），找它们的垂直平分线的交点
①选一半径R>2
1BC ，分别以B 、C 为圆心画圆弧交于两点，过两个点的直
（1）找圆心：任取三角形的两个角（如取∠B 与∠C ），找它们角平分线的交点
①任取一半径长，过顶点B 画圆弧与∠B 的两边交于两点，任取一半径长大于这两个交点的距离的一半，分别以两个交点为圆心画等半径的圆弧，交于一点，过顶点B 和该交点作射线，这条射线就是∠B 的角平分线。

同样的原理画出∠C 的角平分线，与∠B 的角平分线交于点O ，点O 就是该三角形内切圆的圆心
（2）确定半径，画圆：找圆心O 在三角形任一边上的垂足，O 与垂足之间的距离即为内切圆的半径长
②过O作任意三角形的边（如BC）的垂线：以O为圆心，分别以OB、OC 为半径画圆弧，于BC边的下方有另一交点，过O与该交点作直线于BC交于点D，则OD为内切圆的半径
③以OD为半径，O为圆心画圆。

三角形的外接圆与内切圆半径三角形是几何学中最基本的图形之一，在研究三角形的性质时，外接圆和内切圆起着重要的作用。

本文将探讨三角形的外接圆与内切圆的半径，并说明它们之间的关系。

1. 外接圆的半径三角形的外接圆是经过三角形三个顶点的圆。

在任意三角形ABC 中，假设三边的长度分别为a、b、c，外接圆的半径可表示为R。

为了求解外接圆的半径，我们可以利用下列公式之一：1.1 传统公式传统公式是较为常用的求解外接圆半径的方法，公式如下：R = a*b*c / 4Δ其中，Δ表示三角形的面积。

这个公式可以通过计算三角形的面积后进行代入计算。

1.2 角度公式角度公式是另一种求解外接圆半径的方法，它以三角形的角度为基础。

公式如下：R = a / 2sinA = b / 2sinB = c / 2sinC其中，A、B、C分别为三角形的内角。

2. 内切圆的半径三角形的内切圆是与三角形三条边相切的圆，它的半径常用r表示。

同样，我们可以利用下列公式之一来求解内切圆的半径：2.1 传统公式传统公式是常用的求解内切圆半径的方法，公式如下：r = Δ / s其中，s为三角形的半周长，即s = (a + b + c) / 2。

2.2 边长公式边长公式是另一种求解内切圆半径的方法，根据三角形的边长来计算。

公式如下：r = √[(s-a)(s-b)(s-c) / s]3. 外接圆与内切圆的关系有趣的是，对于任意三角形，内切圆的圆心、外接圆的圆心和顶点三个点共线，且内切圆与外接圆的半径满足以下关系：r = R / 2其中，r为内切圆的半径，R为外接圆的半径。

这个关系式对任意三角形均成立，无论是锐角三角形、钝角三角形还是直角三角形。

这也是三角形性质中的一条重要定理。

综上所述，我们可以计算三角形的外接圆和内切圆的半径。

根据已知的三角形边长、角度或者面积，我们可以采用相应的公式来求解。

同时，我们还了解到内切圆与外接圆之间的关系，即内切圆的半径是外接圆半径的一半。

三角形内切圆外接圆的关系一、内切圆和外接圆的定义1.内切圆：一个圆能够同时和三角形的三边相切，这个圆就被称为三角形的内切圆。

内切圆的圆心称为内切圆圆心。

2.外接圆：一个圆能够同时和三角形的三个顶点相切，这个圆就被称为三角形的外接圆。

外接圆的圆心称为外接圆圆心。

二、内切圆和外接圆的关系1.内切圆和外接圆的圆心是同一点。

即内切圆圆心就是外接圆圆心，这个点称为三角形的垂心。

2.内切圆和外接圆的半径之间存在一定的关系。

设三角形的边长分别为a、b、c，内切圆半径为r，外接圆半径为R，则有：R = (a + b + c) / (4 * r)同时，根据三角形的面积公式，有：S = (1/2) * a * r = (1/2) * R * (a + b + c)将R的表达式代入上式，可以得到：(1/2) * a * r = (1/2) * ((a + b + c) / (4 * r)) * (a + b + c)化简后可得：r^2 = (a + b + c) / (4 * a)三、内切圆和外接圆的性质1.三角形的内切圆圆心、外接圆圆心和垂心是同一点。

2.三角形的内切圆和外接圆的半径之间存在固定的比例关系，即R = (a + b + c) / (4 * r)。

3.三角形的面积可以用内切圆半径和外接圆半径表示，即S = (1/2) * a * r = (1/2) * R * (a + b + c)。

4.内切圆和外接圆的圆心到三角形各顶点的距离相等。

四、内切圆和外接圆的应用1.在解决三角形相关的问题时，可以利用内切圆和外接圆的关系来简化计算。

2.内切圆和外接圆的性质在证明几何问题时非常有用，可以帮助我们找到证明的线索。

3.在实际应用中，如建筑工程、土地测量等领域，内切圆和外接圆的关系可以帮助我们快速计算三角形的面积和其他相关参数。

习题及方法：1.习题：设三角形ABC的内切圆半径为r，外接圆半径为R，且AB=6,BC=8, AC=10。

中考数学外接圆和内切圆知识点是什么要学好数学，要把握好以下⼏要点，对于数学的学习成绩的提⾼，⾃学能⼒的养成肯定有促进的。

下⾯是⼩编给⼤家带来的中考数学外接圆和内切圆知识点，欢迎⼤家阅读参考，我们⼀起来看看吧!中考数学：外接圆圆⼼坐标公式把三点的坐标相加，然后除以三，就是：((x1+x2+x3)/3,(y1+y2+y3)/3)则为外⼼的坐标(x1，就是第⼀个点的横坐标，y1就是第⼀个点的纵坐标，依此类推)。

外⼼坐标即那个外接圆的圆⼼了。

外接圆性质锐⾓三⾓形外⼼在三⾓形内部。

直⾓三⾓形外⼼在三⾓形斜边中点。

钝⾓三⾓形外⼼在三⾓形外。

有外⼼的图形，⼀定有外接圆(各边中垂线的交点，叫做外⼼)外接圆圆⼼到三⾓形各个顶点的线段长度相等过三⾓形的三个顶点的圆叫做三⾓形的外接圆，其圆⼼叫做三⾓形的外⼼。

在三⾓形中，三⾓形的外⼼不⼀定在三⾓形内部，可能在三⾓形外部(如钝⾓三⾓形)也可能在三⾓形边上(如直⾓三⾓形)。

过不在同⼀直线上的三点可作⼀个圆(且只有⼀个圆)。

中考数学：经过⼀点可以画⼏个圆经过⼀点可以画⽆数个圆，因为半径没有确定，所以可以画⽆数个⼤⼩不⼀的圆。

在⼀个平⾯内，围绕⼀个点并以⼀定长度为距离旋转⼀周所形成的封闭曲线叫做圆。

圆有⽆数条对称轴。

圆形圆形是⼀种圆锥曲线，由平⾏于圆锥底⾯的平⾯截圆锥得到。

圆形规定为360°，是古巴⽐伦⼈在观察地平线太阳升起的时候，⼤约每4分钟移动⼀个位置，⼀天24⼩时移动了360个位置，所以规定⼀个圆内⾓为360°。

这个°，代表太阳。

圆是⼀种⼏何图形。

根据定义，通常⽤圆规来画圆。

同圆内圆的直径、半径的长度永远相同，圆有⽆数条半径和⽆数条直径。

圆是轴对称、中⼼对称图形。

对称轴是直径所在的直线。

同时，圆⼜是“正⽆限多边形”，⽽“⽆限”只是⼀个概念。

圆可以看成由⽆数个⽆限⼩的点组成的正多边形，当多边形的边数越多时，其形状、周长、⾯积就都越接近于圆。

所以，世界上没有真正的圆，圆实际上只是⼀种概念性的图形。

三角形的内切圆与外接圆几何形中的圆与三角形关系在几何学中，三角形与圆之间存在着紧密的关系。

其中，三角形的内切圆和外接圆是研究三角形与圆关系的重要内容。

本文将从内切圆和外接圆的定义、性质和应用三个方面探讨圆与三角形之间的关系。

一、内切圆的定义、性质及应用1. 定义：三角形的内切圆是与三角形的三条边都相切于一点的圆。

2. 性质：（1）内切圆的圆心与三角形的角平分线交于一点，该点称为内切圆心。

（2）内切圆的半径等于三角形三边之和与周长的一半的比值。

（3）内切圆与三角形的接点构成三角形的内切圆切点三角形，内切圆切点三角形的面积是原三角形面积的四分之一。

3. 应用：（1）内切圆可以用于确定三角形的性质和计算其面积。

（2）内切圆与三角形的关系可用于解决一些实际问题，如建筑、机械等。

二、外接圆的定义、性质及应用1. 定义：三角形的外接圆是以三角形三个顶点为圆心的圆。

（1）外接圆的圆心是三角形三个顶点的垂直平分线的交点。

（2）外接圆的半径等于三角形三边的乘积与面积的比值的倒数。

（3）外接圆的直径等于三角形的周长。

3. 应用：（1）外接圆可以用于确定三角形的性质和计算其面积。

（2）外接圆与三角形的关系可用于解决一些实际问题，如导航算法、航海定位等。

三、圆与三角形的关系及应用举例1. 关系：（1）三角形的内切圆与外接圆都能够确定三角形的性质，如角平分线、垂直平分线等。

（2）内切圆、外接圆与三角形的顶点和边的关系可以用于计算三角形的面积、边长等。

2. 应用举例：（1）在建筑领域，利用三角形内切圆与外接圆的关系可以设计出更加稳固的结构，提高建筑物的稳定性。

（2）在机械制造中，通过三角形内切圆与外接圆的关系可以确定机械零部件的尺寸和装配方式，提高产品的精度和质量。

圆与三角形的关系是几何学中重要的研究内容之一。

通过研究三角形的内切圆和外接圆的定义、性质及应用，我们能够更深入地理解圆与三角形之间的紧密联系。

这种关系不仅在理论上有着重要意义，同时在实际应用中也具有广泛的应用价值。

三角形的内切圆和外接圆第29,30次课【知识要点】1．确定圆的条件是什么？2．过平面任意三点可以作圆吗？若能，如何作？3．锐角、直角、钝角三角形的外接圆圆心位置有什么规律吗？ 4．三角形的外接圆（1）过三角形三个顶点的圆，叫做三角形的外接圆，三条边中垂线的交点，叫做三角形的外心。

三角形的外心到各顶点的距离相等．（2）锐角三角形的外心在三角形内部，钝角三角形的外心在三角形的外部，直角三角形的外心在斜边中点，外接圆半径2c R =(c 为斜边长)．5．三角形的内切圆（1）到三角形三条边距离都相等的圆，叫三角形的内切圆，三角形中，三个内角平分线的交点，叫三角形的内心，三角形内心到三条边的距离相等，内心都在三角形的内部．（2）若三角形的面积为ABC S ∆，周长为a+b+c,则内切圆半径为:cb a S r ABC ++=∆2，当b a ,为直角三角形的直角边，c 为斜边时，内切圆半径cb a ab r ++=或2cb a r -+=.6．圆内接四边形的性质（1）圆内接四边形的对角互补；（2）圆内接四边形的任何一个外角等于它的对角．注意：①圆内接平行四边形为矩形；②圆内接梯形为等腰梯形． 6．两个结论：圆的外切四边形对边和相等；圆的外切等腰梯形的中位线等于腰长． 【典型例题】 例1．填空和选择（1）一个三角形的内心，外心都在三角形内，则这个三角形一定是( ) A 、直角三角形 B 、锐角三角形 C 、钝角三角形 D 、等腰三角形·I A BC（2）如右图，I是ABC∆的内心，则下列式子正确的是（）A、∠BIC=︒180-2∠A B、∠BIC=2∠A C、∠BIC=︒90+∠A/2 D、∠BIC=︒90-∠A/2（3）ABC∆∆的外心是ABC ∆外切于⊙O，E、F、G分别是⊙O与各边的切点，则EFG的。

（4）直角三角形的两条直角边分别为5和12，那么它的外接圆的半径为，内切圆半径为．（5）等边三角形内切圆半径，外接圆半径分别为Rr:= ．r,，则R（6）圆外切等腰梯形底角为︒60，腰长为10，则圆的半径长为．（7）等边三角形一边长为2，则其内切圆半径等于．（8）等边三角形的内切圆半径，外接圆半径的和高的比是．（9）ABC135，∆的内切圆⊙I与AB、BC、CA分别切于D、E、F点，且∠FID=∠EID=︒则ABC∆为．例4．已知ABC∆三边长为6，8，10，则它的内心，外心间的距离为【经典练习】【大展身手】一、选择题1．下列说法正确的是（）A．三点确定一个圆B．三角形有且只有一个外接圆C．四边形都有一个外接圆D．圆有且只有一个内接三角形2．下列命题中的假命题是（）A．三角形的外心到三角形各顶点的距离相等B．三角形的外心到三角形三边的距离相等C．三角形的外心一定在三角形一边的中垂线上D．三角形任意两边的中垂线的交点，是这个三角形的外心3．下列图形一定有外接圆的是（）A．三角形B．平行四边形C．梯形D．菱形4．下列说法正确的是（）A．过一点A的圆的圆心可以是平面上任意点B．过两点A、B的圆的圆心在一条直线上C．过三点A、B、C的圆的圆心有且只有一点D．过四点A、B、C、D的圆不存在5．在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，则它的外心与顶点C的距离为（）A．5cm B．6cm C．7cm D．8cm6．等边三角形的外接圆的半径等于边长的（ ）倍． A ．23B ．33C ．3D ．217．三角形的外心具有的性质是（ ） A ．到三边距离相等 B ．到三个顶点距离相等 C ．外心在三角形外D ．外心在三角形内8．对于三角形的外心，下列说法错误的是（ ） A ．它到三角形三个顶点的距离相等 B ．它与三角形三个顶点的连线平分三内角C ．它到任一顶点的距离等于这三角形的外接圆半径D ．以它为圆心，它到三角形一顶点的距离为半径作圆，必通过另外两个顶点9．在一个圆中任意引两条直径，顺次连接它们的四个端点组成一个四边形，则这个四边形一定是（ ） A ．菱形B ．等腰梯形C ．矩形D ．正方形10．如图所示，圆的内接四边形ABCD ，DA 、CB 延长线交于P ，AC 和BD 交于Q ，则图中相似三角形有（ ） A 、1对 B 、2对 C 、3对D 、4对11．∠DCE 是圆内接四边形ABCD 的一个外角，那么一定有（ ） A 、∠DCE+∠A=︒180 B 、∠DCE+∠B=︒180 C 、∠DCE=∠A `D 、∠DCE=∠B二、填空题：1．△ABC 的三边3，2，13，设其三条高的交点为H ，外心为O ，则OH= ．2．△ABC 的外心是它的两条中线交点，则△ABC 的形状为 ．7．如图所示，在ABC ∆的外接圆中，AB=AC ，D 为AB 的中点，若∠EAD=︒114 ，则∠BAD= ．A D CBPQ·ACBD OE例6 已知：如图，四边形ABCD 内接于⊙O ，点P 在AB 的延长线上，且PC ∥BD 。