二次函数与等腰三角形

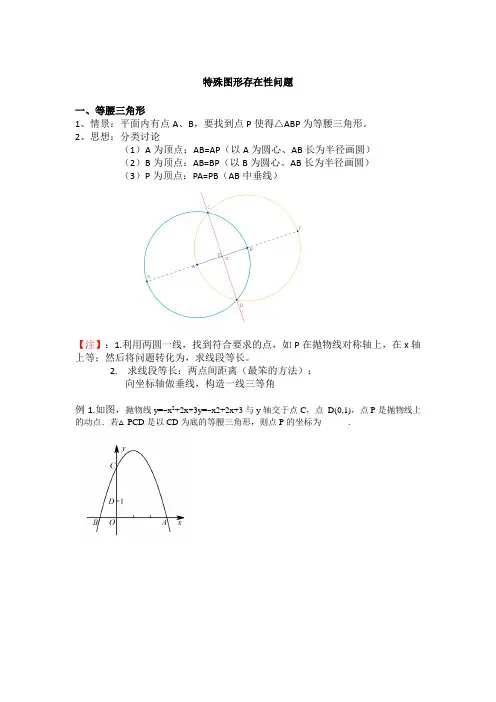
特殊图形存在性问题一、等腰三角形1、情景：平面内有点A、B，要找到点P使得△ABP为等腰三角形。

2、思想：分类讨论（1）A为顶点：AB=AP（以A为圆心、AB长为半径画圆）（2）B为顶点：AB=BP（以B为圆心、AB长为半径画圆）（3）P为顶点：PA=PB（AB中垂线）【注】：1.利用两圆一线，找到符合要求的点，如P在抛物线对称轴上，在x轴上等；然后将问题转化为，求线段等长。

2.求线段等长：两点间距离（最笨的方法）；向坐标轴做垂线，构造一线三等角例1.如图，抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C，点D(0,1)，点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为______．练习1.如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A,B 两点，A点在原点的左侧，B点的坐标为(3,0)，与y轴交于C(0,−3)点，点P是直线BC下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．练习2、已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．练习3.如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣x+1与y轴交于点D．（1）求抛物线的解析式；（2）证明：△DBO∽△EBC；（3）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．练习4.如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点，与y轴交于点C(0,−3)，其顶点为D．(1)求该抛物线的解析式，并用配方法把解析式化为y=a(x−h)2+k的形式；(2)动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM,BM，当t为何值时，△OMB为等腰三角形？练习5.如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n （m＜n）分别是方程x2﹣2x﹣3=0的两根．（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E 两点（点D在y轴右侧），连接OD、BD．①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标．25．（10分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过原点O，与x轴交于点A（5，0），第一象限的点C（m，4）在抛物线上，y轴上有一点B（0，10）．（Ⅰ）求抛物线的解析式及它的对称轴；（Ⅱ）点P（0，n）在线段OB上，点Q在线段BC上，若OP＝2BQ，且P A＝QA．求n 的值；（Ⅲ）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．19-红桥一模25．（10分）如图，抛物线y＝x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A，B，且B点的坐标为（2，0）．（1）求该抛物线的解析式．（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．(17河北一模)25(10分）如图，己知抛物线y=x2+bx+c图象经过点A（﹣1，0），B（0，﹣3），抛物线与x轴的另一个交点为C．（1）求这个抛物线的解析式：（2）若抛物线的对称轴上有一动点D，且△BCD为等腰三角形（CB≠CD），试求点D的坐标；二、直角三角形1.情景：平面内有点A、B，要找到点P使得△ABP为直角三角形2.思想：分类讨论（1）A为顶点：∠A（过A做垂线）（2）B为顶点：∠B（过B做垂线）（3）P为顶点：∠C（AB为直径的圆）【注】1.等腰直角三角形，只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A，B与x 轴交于点E，F且B，E两点的坐标分别为B(2，32)E(−1，0)(1)求二次函数的解析式；(2)在抛物线上是否存在点Q，使△QBF为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．练习1.如图，抛物线y=x2+bx+3顶点为P，且分别与x轴、y轴交于A、B两点，点A在点P的右侧，tan∠ABO=13(1)求抛物线的对称轴和PP的坐标．(2)在抛物线的对称轴上是否存在这样的点D，使△ABD为直角三角形？如果存在，求点D 的坐标；如果不存在，请说明理由．例2.如图，抛物线y=−x2+bx+c与x轴相交于AB两点，与y 轴相交与点C，且点B与点CC 的坐标分别为(3,0)，C(0,3)，点M是抛物线的顶点．(1)求二次函数的关系式(2)在MB上是否存在点P，过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由练习2.如图，在平面直角坐标系中，直线y=−13x+2交x轴点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E(−1,0)，并与直线相交于A、B两点．(1)求抛物线的解析式（关系式）；(2)过点A作AC⊥AB交x轴于点C，求点C的坐标；(3)除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．练习3.如图，抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．（1）求抛物线的解析式；（2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．（3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．（18东丽-一模）25.如图，在平面直角坐标系中，点A、B的坐标分别为（1，1）、（1，2），过点A、B分别作y轴的垂线，垂足为D、C，得到正方形ABCD，抛物线y=x2+bx+c经过A、C两点，点P为第一象限内抛物线上一点（不与点A重合），过点P分别作x轴y轴的垂线，垂足为E、F，设点P的横坐标为m，矩形PFOE与正方形ABCD重叠部分图形的周长为l．（1）直接写出抛物线所对应的函数表达式．（2）当矩形PFOE的面积被抛物线的对称轴平分时，求m的值．（3）当m＜2时，求L与m之间的函数关系式．（4）设线段BD与矩形PFOE的边交于点Q，当△FDQ为等腰直角三角形时，直接写出m的取值范围．三、平行四边形存在性问题类型一：1.情景：一直平面内三点A、B、C，求一点P使四边形ABCP为平行四边形2.思想：分类讨论（1）以AC为对角线：ABCP1（2）以AB为对角线：ACBP3（3）以BC为对角线：ACP2B【注】找到P点后，用平行四边形的判定定理，求等长线段，或利用等角度、平行线求坐标即可。

二次函数中等腰直角三角形 -回复
您好，关于二次函数中等腰直角三角形，我们可以通过以下步骤来解决：
1. 二次函数一般式：$y=ax^2+bx+c$。

2. 因为中位线长度为右腰，所以这个中位线对应的$x$可以用平移的方法求出：设中位线长度为$t$，则该中位线对应的$x$值为$-\frac{b}{2a}+t$。

3. 由直角三角形性质可知，斜边的平方等于直角腰的平方和，即$(\frac{t}{2})^2+(at^2+c)^2=(\frac{t}{2}+b)^2$。

4. 将第3步中的方程式化简后解出$t$，再带回第2步中的式子，求出该中位线对应的$x$值。

5. 根据对称性，可以得出第二条中位线的长度与第一条中位线相等，且对应的$x$值也相等。

6. 根据中位线长度与底边长度相等的定义，可以得出三角形的底边长度为$2\times(\frac{t}{2}+b)$。

7. 最终，我们就可以得出该等腰直角三角形的底边长、两条直角边长及其顶点的坐标。

希望以上解释能够解决您的问题，任何疑问，请随时追问。

等腰三角形直角三角形存在性问题典例1，如图,二次函数的图象与x轴交于点A、B两点,且A 点坐标为,与y轴交于点.(1)求出这个二次函数的解析式;(2)直接写出点B的坐标为(3)在x轴是否存在一点P,使是等腰三角形?假设存在,求出满足条件的P 点坐标;假设不存在,请说明理由;(4)在第一象限中的抛物线上是否存在一点Q,使得四边形ABQC的面积最大?假设存在,请求出Q点坐标及面积的最大值;假设不存在,请说明理由.答案详解解:(1)的图象经过,,,,所求解析式为:,答:这个二次函数的解析式是.(2)解:,故答案为:.(3)解:在中,,,,,①当时在x轴的负半轴),;②当时在x轴的正半轴),;③当时在x轴的正半轴),;④当时在x轴的正半轴),在中,设,那么解得:,;答:在x轴存在一点P,使是等腰三角形,满足条件的P点坐标是或或或.(4)解:如图,设Q点坐标为,因为点Q在上,即:Q点坐标为,连接OQ,,,,,Q点坐标为,答:在第一象限中的抛物线上存在一点Q,使得四边形ABQC的面积最大,Q点坐标是,面积的最大值是.解析:(1)因为的图象经过,,代入求出c、a的值,即可得到答案;(2)把代入求出x的值,即可得到答案;(3)在中根据勾股定理求出AC,根据等腰三角形的性质求出,①当时在x轴的负半轴),;②当时在x轴的正半轴),;③当时在x轴的正半轴),;④当时在x 轴的正半轴),,即可得出答案;(4)设Q点坐标为,因为点Q在上,得出Q点坐标为,连接OQ,根据,代入求出即可.此题主要考察对用待定系数法求二次函数的解析式,等腰三角形的判定,三角形的面积,二次函数图象上点的坐标特征,二次函数的最值等知识点的理解和掌握,综合运用这些性质进展计算是解此题的关键.题型较好,综合性强.练习：如图,抛物线与x轴交于点和点,与y 轴交于点C.(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使为等腰三角形?假设存在,请求出符合条件的点P的坐标;假设不存在,请说明理由.答案详解解:(1)由题知:解得:所求抛物线解析式为:;(2)抛物线解析式为:,其对称轴为,设P点坐标为,当时,,,①当时,,解得,点坐标为:;②当时,,解得,点坐标为:或;③当时,由勾股定理得:,解得,点坐标为:综上所述存在符合条件的点P,其坐标为或或或;解析:(1)抛物线过A、B两点,可将两点的坐标代入抛物线的解析式中,用待定系数法即可求出二次函数的解析式;(2)可根据(1)的函数解析式得出抛物线的对称轴,也就得出了M点的坐标,由于C是抛物线与y 轴的交点,因此C的坐标为,根据M、C的坐标可求出CM的距离.然后分三种情况进展讨论:①当时,P位于CM的垂直平分线上.求P点坐标关键是求P的纵坐标,过P作轴于Q,如果设,那么直角三角形CPQ中,OM的长,可根据M的坐标得出,,因此可根据勾股定理求出x的值,P点的横坐标与M的横坐标一样,纵坐标为x,由此可得出P的坐标.②当时,根据CM的长即可求出P的纵坐标,也就得出了P的坐标(要注意分上下两点).③当时,因为C的坐标为,那么直线必垂直平分PM,因此P的纵坐标是6,由此可得出P的坐标;此题主要考察了二次函数的综合知识,要注意的是(2)中,不确定等腰三角形哪条边是底边的情况下,要分类进展求解,不要漏解.典例2，练习：如图，在平面直角坐标系中，抛物线〔〕与轴相交于，两点，与轴相交于点，直线〔〕经过，两点，，，且。

二次函数顶点与x轴两交点为等腰直角三角形数学中的二次函数是一种常见的函数形式，它的一般形式可以表示为y = ax^2 + bx + c，其中a、b、c都是实数且a不为0。

而顶点形式则可以写成y = a(x - h)^2 + k，其中(h, k)为顶点的坐标。

令二次函数的顶点坐标为(h,k)。

根据等腰直角三角形的性质，顶点与x轴两交点的距离应该相等，即，x₁-h，=，x₂-h。

令其中一个交点为(x₁,0)，另一个交点为(x₂,0)。

接下来，我们来推导顶点与x轴两交点为等腰直角三角形的条件下，a、h、k和x₁、x₂之间的关系。

根据等腰直角三角形的性质，顶点与x轴两交点的距离应该相等，即，x₁-h，=，x₂-h。

我们可以有以下两种情况进行讨论：情况一：x₁>h（即x₁在顶点右侧）那么，x₁-h，=x₁-h。

同样地，我们有，x₂-h，=h-x₂。

由于顶点与x轴两交点的距离相等，我们有：x₁-h=h-x₂化简得：2h=x₁+x₂又因为顶点的x坐标为h，代入二次函数的顶点形式，我们有：h=-b/(2a)所以，当顶点与x轴两交点为等腰直角三角形时，h=-b/(2a)。

情况二：x₂>h（即x₂在顶点右侧）那么，x₁-h，=h-x₁。

同样地，我们有，x₂-h，=x₂-h。

由于顶点与x轴两交点的距离相等，我们有：h-x₁=x₂-h化简得：2h=x₁+x₂同理可得h=-b/(2a)。

所以，不论x₁>h还是x₂>h，当顶点与x轴两交点为等腰直角三角形时，h=-b/(2a)。

接下来，我们考虑顶点的纵坐标k。

由于顶点是二次函数的最值点，因此顶点的纵坐标k等于二次函数的值在该点的取值。

代入二次函数的顶点形式，我们有：k=a(h-h)^2+k化简得：k=k所以，顶点的纵坐标k可以是任意实数。

最后，我们来具体说明一个例子。

假设我们有一个二次函数y=-2(x-3)^2+5、根据前面的推导，我们可以得出顶点的坐标为(h,k)=(3,5)。

专题06 二次函数与等腰三角形有关问题（专项训练）1．（2022•榆阳区一模）如图，已知抛物线y＝mx2+4x+n与x轴交于A、B两点，与y轴交于点C．直线y＝x﹣3经过B，C两点．（1）求抛物线的函数表达式；（2）抛物线的顶点为M，在该抛物线的对称轴l上是否存在点P，使得以C，M，P为顶点的三角形是等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）y＝x﹣3中，令x＝0，则y＝﹣3，∴C（0，﹣3），令y＝0，则x＝3，∴B（3，0），将C（0，﹣3），B（3，0）代入y＝mx2+4x+n中，∴，解得，∴y＝﹣x2+4x﹣3；（2）存在点P，使得以C，M，P为顶点的三角形是等腰三角形，理由如下：∵y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴M（2，1），对称轴为直线x＝2，设P（2，t），∴MP＝|t﹣1|，MC＝2，CP＝，①当MP＝MC时，|t﹣1|＝2，∴t＝2+1或t＝﹣2+1，∴P（2，2+1）或（2，﹣2+1）；②当MP＝CP时，|t﹣1|＝，解得t＝﹣，∴P（2，﹣）；③当MC＝CP时，2＝，解得t＝1（舍）或t＝﹣7，∴P（2，7）；综上所述：P点坐标为（2，2+1）或（2，﹣2+1）或（2，﹣）或（2，7）．2．（2022•岚山区一模）已知抛物线y＝ax2+bx+8与x轴交于A（﹣3，0），B（8，0）两点，交y轴于点C，点P是抛物线上一个动点，且点P的横坐标为m．（1）求抛物线的解析式；（2）如图2，将直线BC沿y轴向下平移5个单位，交x轴于点M，交y轴于点N．过点P作x轴的垂线，交直线MN于点D，是否存在一点P，使△BMD是等腰三角形？若存在，请直接写出符合条件的m的值；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+8与x轴交于A（﹣3，0），B（8，0）两点，∴，解得，，∴抛物线的解析式为y＝﹣x2+x+8；（3）易证线BC的解析式为y＝﹣x+8，向下平移5个单位得到y＝﹣x+3，当y＝0时，x＝3，∴M（3，0），当x＝0时，y＝3，∴N（0，3），由题意得PD⊥MB，∵MB＝8﹣3＝5，D（m，﹣m+3），∴MD2＝（m﹣3）2+（﹣m+3）2，BD2＝（8﹣m）2+（﹣m+3）2，若△BMD是等腰三角形，可分三种情况：①当MB＝MD时，∴（m﹣3）2+（﹣m+3）2＝25，解得m1＝3+，m2＝3﹣，②当MB＝BD时，∴（8﹣m）2+（﹣m+3）2＝25，解得，m1＝3（舍去），m2＝8（舍去），③当MD+BD时，∴（8﹣m）2+（﹣m+3）2＝（m﹣3）2+（﹣m+3）2，解得，m＝5.5．综上所述，m的值为3+或3﹣或5.5时，△BMD是等腰三角形．3．（2022•兴宁区校级模拟）如图，抛物线y＝﹣x2+bx+c过点A、B，抛物线的对称轴交x 轴于点D，直线y＝﹣x+3与x轴交于点B，与y轴交于点C，且．（1）求抛物线的解析式；（2）在x轴上是否存在点P，使得△PDC为等腰三角形？若存在，请求出点P的坐标，若不存在，请说明理由．【解答】解：（1）对于直线y＝﹣x+3，令y＝0，即﹣x+3＝0，解得：x＝3，令x＝0，得y＝3，∴B（3，0），C（0，3），∵A为x轴负半轴上一点，且OA＝OB，∴A（﹣1，0）．将点A、B的坐标分别代入y＝﹣x2+bx+c中，得，解得，∴抛物线的解析式为y＝﹣x2+2x+3；（3）存在．如图2，∵点P在x轴上，∴设P（m，0）．∵C（0，3），D（1，0），∴由勾股定理，得：CD2＝OC2+OD2＝32+12＝10，PD2＝（m﹣1）2，CP2＝OP2+OC2＝m2+32＝m2+9，分为三种情况讨论：①当CD＝PD时，CD2＝PD2，即10＝（m﹣1）2，解得m1＝1+，m2＝1﹣，此时点P的坐标为（1+，0）或（1﹣，0）；②当CD＝CP时，CD2＝CP2，即10＝m2+9，解得m1＝﹣1，m2＝1（不符合题意，舍去），此时点P的坐标为（﹣1，0）；③当PC＝PD时，PC2＝PD2，即m2+9＝（m﹣1）2，解得m＝﹣4，此时点P的坐标为（﹣4，0）．综上所述，在x轴上存在点P，使得△PDC为等腰三角形，满足条件的点P的坐标为（1+，0）或（1﹣，0）或（﹣1，0）或（﹣4，0）．4．（2022•百色）已知抛物线经过A（﹣1，0）、B（0，3）、C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM，交BC于点F．（1）求抛物线的表达式；（2）求证：∠BOF＝∠BDF；（3）是否存在点M，使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME 的长．【解答】（1）解：设抛物线的表达式为y＝ax2+bx+c，把A（﹣1，0）、B（0，3）、C（3，0）代入得：，解得，∴抛物线的表达式为：y＝﹣x2+2x+3；（2）证明：∵正方形OBDC，∴∠OBC＝∠DBC，BD＝OB，∵BF＝BF，∴△BOF≌△BDF，∴∠BOF＝∠BDF；（3）解：∵抛物线交正方形OBDC的边BD于点E，∴令y＝3，则3＝﹣x2+2x+3，解得：x1＝0，x2＝2，∴E（2，3），①如图，当M在线段BD的延长线上时，∠BDF为锐角，∴∠FDM为钝角，∵△MDF为等腰三角形，∴DF＝DM，∴∠M＝∠DFM，∴∠BDF＝∠M+∠DFM＝2∠M，∵BM∥OC，∴∠M＝∠MOC，由（2）得∠BOF＝∠BDF，∴∠BDF+∠MOC＝3∠M＝90°，∴∠M＝30°，在Rt△BOM中，BM＝，∴ME＝BM﹣BE＝3﹣2；②如图，当M在线段BD上时，∠DMF为钝角，∵△MDF为等腰三角形，∴MF＝DM，∴∠BDF＝∠MFD，∴∠BMO＝∠BDF+∠MFD＝2∠BDF，由（2）得∠BOF＝∠BDF，∴∠BMO＝2∠BOM，∴∠BOM+∠BMO＝3∠BOM＝90°，∴∠BOM＝30°，在Rt△BOM中，BM＝，∴ME＝BE﹣BM＝2﹣，综上所述，ME的值为：3﹣2或2﹣．5．（2022•山西）综合与探究如图，二次函数y＝﹣x2+x+4的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．点P是第一象限内二次函数图象上的一个动点，设点P的横坐标为m．过点P作直线PD⊥x轴于点D，作直线BC交PD于点E．（1）求A，B，C三点的坐标，并直接写出直线BC的函数表达式；（2）当△CEP是以PE为底边的等腰三角形时，求点P的坐标；【解答】解：（1）在y＝﹣x2+x+4中，令x＝0得y＝4，令y＝0得x＝8或x＝﹣2，∴A（﹣2，0），B（8，0），C（0，4），设直线BC解析式为y＝kx+4，将B（8，0）代入得：8k+4＝0，解得k＝﹣，∴直线BC解析式为y＝﹣x+4；（2）过C作CG⊥PD于G，如图：设P（m，﹣m2+m+4），∴PD＝﹣m2+m+4，∵∠COD＝∠PDO＝∠CGD＝90°，∴四边形CODG是矩形，∴DG＝OC＝4，CG＝OD＝m，∴PG＝PD﹣DG＝﹣m2+m+4﹣4＝﹣m2+m，∵CP＝CE，CG⊥PD，∴GE＝PG＝﹣m2+m，∵∠GCE＝∠OBC，∠CGE＝90°＝∠BOC，∴△CGE∽△BOC，∴＝，即＝，解得m＝0（舍去）或m＝4，∴P（4，6）；6．（2021•攀枝花）如图，开口向上的抛物线与x轴交于A（x1，0）、B（x2，0）两点，与y轴交于点C，且AC⊥BC，其中x1，x2是方程x2+3x﹣4＝0的两个根．（1）求点C的坐标，并求出抛物线的表达式；（2）垂直于线段BC的直线l交x轴于点D，交线段BC于点E，连接CD，求△CDE的面积的最大值及此时点D的坐标；（3）在（2）的结论下，抛物线的对称轴上是否存在点P，使得△PDE是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）由x2+3x﹣4＝0得x1＝﹣4，x2＝1，∴A（﹣4，0），B（1，0），∴OA＝4，OB＝1，∵AC⊥BC，∴∠ACO＝90°﹣∠BCO＝∠OBC，∵∠AOC＝∠BOC＝90°，∴△AOC∽△COB，∴＝，即＝，∴OC＝2，∴C（0，﹣2），设抛物线解析式为y＝a（x+4）（x﹣1），将C（0，﹣2）代入得﹣2＝﹣4a，∴a＝，∴抛物线解析式为y＝（x+4）（x﹣1）＝x2+x﹣2；（2）如图：由A（﹣4，0），B（1，0），C（0，﹣2）得：AB＝5，BC＝，AC＝2，∵DE⊥BC，AC⊥BC，∴DE∥AC，∴△ABC∽△DBE，∴＝＝，设D（t，0），则BD＝1﹣t，∴＝＝，∴DE＝（1﹣t），BE＝（1﹣t），∴S△BDE＝DE•BE＝（1﹣t）2，而S△BDC＝BD•OC＝（1﹣t）×2＝1﹣t，∴S△CDE＝S△BDC﹣S△BDE＝1﹣t﹣（1﹣t）2＝﹣t2﹣t+＝﹣（t+）2+，∵﹣＜0，∴t＝﹣时，S△CDE最大为，此时D（﹣，0）；（3）存在，由y＝x2+x﹣2知抛物线对称轴为直线x＝﹣，而D（﹣，0），∴D在对称轴上，由（2）得DE＝×[1﹣（﹣）]＝，当DE＝DP时，如图：∴DP＝，∴P（﹣，）或（﹣，﹣），当DE＝PE时，过E作EH⊥x轴于H，如图：∵∠HDE＝∠EDB，∠DHE＝∠BED＝90°，∴△DHE∽△DEB，∴＝＝，即＝＝，∴HE＝1，DH＝2，∴E（，﹣1），∵E在DP的垂直平分线上，∴P（﹣，﹣2），当PD＝PE时，如图：设P（﹣，m），则m2＝（﹣﹣）2+（m+1）2，解得m＝﹣，∴P（﹣，﹣），综上所述，P的坐标为（﹣，）或（﹣，﹣）或（﹣，﹣2）或（﹣，﹣）．7．（2021•宿迁）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（4，0），与y轴交于点C．连接AC，BC，点P在抛物线上运动．（1）求抛物线的表达式；（2）如图②，若点P在第一象限，直线AP交BC于点F，过点P作x轴的垂线交BC 于点H，当△PFH为等腰三角形时，求线段PH的长．【解答】解：（1）∵A（﹣1，0），B（4，0）是抛物线y＝﹣x2+bx+c与x轴的两个交点，且二次项系数a＝，∴根据抛物线的两点式知，y＝．（2）设PH与x轴的交点为Q1，P（a，），则H（a，），PH＝，若FP＝FH，则∠FPH＝∠FHP＝∠BHQ1＝∠BCO，∴tan∠APQ1＝tan∠BCO＝2，∴AQ1＝2PQ1，即a+1＝2（），解得a＝3（﹣1舍去），此时PH＝．若PF＝PH，过点F作FM⊥y轴于点M，∴∠PFH＝∠PHF，∵∠CF A＝∠PFH，∠Q1HB＝∠PHF，∴∠CF A＝∠Q1HB，又∵∠ACF＝∠BQ1H＝90°，∴△ACF∽△BQ1H，∴CF＝AC＝，在Rt△CMF中，MF＝1，CM＝，F（1，），∴AF：，将上式和抛物线解析式联立并解得x＝（﹣1舍去），此时PH＝．若HF＝HP，过点C作CE∥AB交AP于点E（见上图），∵∠CAF+∠CF A＝90°，∠P AQ+∠HPF＝90°，∠CF A＝∠HFP＝∠HPF，∴∠CAF＝∠P AQ1，即AP平分∠CAB，∴CE＝CA＝，∴E（，2），∴AE：，联立抛物线解析式，解得x＝5﹣（﹣1舍去）．此时PH＝．∴当FP＝FH时，PH＝；当PF＝PH时，PH＝；当HF＝HP时，PH＝；8．（2020•济南）如图1，抛物线y＝﹣x2+bx+c过点A（﹣1，0），点B（3，0），与y轴交于点C．在x轴上有一动点E（m，0）（0＜m＜3），过点E作直线l⊥x轴，交抛物线于点M．（1）求抛物线的解析式及C点坐标；（2）当m＝1时，D是直线l上的点且在第一象限内，若△ACD是以∠DCA为底角的等腰三角形，求点D的坐标；【解答】解：（1）将点A、B的坐标代入抛物线表达式得，解得，故抛物线的表达式为y＝﹣x2+2x+3，当x＝0时，y＝3，故点C（0，3）；（2）当m＝1时，点E（1，0），设点D的坐标为（1，a），由点A、C、D的坐标得，AC＝＝，同理可得：AD＝，CD＝，①当CD＝AD时，即＝，解得a＝1；②当AC＝AD时，同理可得a＝（舍去负值）；故点D的坐标为（1，1）或（1，）；9．（2020•桂林）如图，已知抛物线y＝a（x+6）（x﹣2）过点C（0，2），交x轴于点A 和点B（点A在点B的左侧），抛物线的顶点为D，对称轴DE交x轴于点E，连接EC．（1）直接写出a的值，点A的坐标和抛物线对称轴的表达式；（2）若点M是抛物线对称轴DE上的点，当△MCE是等腰三角形时，求点M的坐标；【解答】解：（1）∵抛物线y＝a（x+6）（x﹣2）过点C（0，2），∴2＝a（0+6）（0﹣2），∴a＝﹣，∴抛物线的解析式为y＝﹣（x+6）（x﹣2）＝﹣（x+2）2+，∴抛物线的对称轴为直线x＝﹣2；针对于抛物线的解析式为y＝﹣（x+6）（x﹣2），令y＝0，则﹣（x+6）（x﹣2）＝0，∴x＝2或x＝﹣6，∴A（﹣6，0）；（2）如图1，由（1）知，抛物线的对称轴为x＝﹣2，∴E（﹣2，0），∵C（0，2），∴OC＝OE＝2，∴CE＝OC＝2，∠CED＝45°，∵△CME是等腰三角形，∴①当ME＝MC时，∴∠ECM＝∠CED＝45°，∴∠CME＝90°，∴M（﹣2，2），②当CE＝CM时，∴MM1＝CM＝2，∴EM1＝4，∴M1（﹣2，4），③当EM＝CE时，∴EM2＝EM3＝2，∴M2（﹣2，﹣2），M3（﹣2，2），即满足条件的点M的坐标为（﹣2，2）或（﹣2，4）或（﹣2，2）或（﹣2，﹣2）；10．（2020•枣庄）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q．（1）求抛物线的表达式；（2）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．【解答】解：（1）将点A、B的坐标代入抛物线表达式得，解得，故抛物线的表达式为：y＝﹣x2+x+4；（2）存在，理由：点A、C的坐标分别为（﹣3，0）、（0，4），则AC＝5，①当AC＝CQ时，过点Q作QE⊥y轴于点E，连接AQ，则CQ2＝CE2+EQ2，即m2+[4﹣（﹣m+4）]2＝25，解得：m＝±（舍去负值），故点Q（，）；②当AC＝AQ时，则AQ＝AC＝5，在Rt△AMQ中，由勾股定理得：[m﹣（﹣3）]2+（﹣m+4）2＝25，解得：m＝1或0（舍去0），故点Q（1，3）；③当CQ＝AQ时，则2m2＝[m﹣（﹣3）]2+（﹣m+4）2，解得：m＝（舍去）；综上，点Q的坐标为（1，3）或（，）．11．（2019•本溪）抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（5，0）两点，顶点为C，对称轴交x轴于点D，点P为抛物线对称轴CD上的一动点（点P不与C，D 重合）．过点C作直线PB的垂线交PB于点E，交x轴于点F．（1）求抛物线的解析式；（2）当△PCF为等腰三角形时，请直接写出点P的坐标．【解答】解：（1）函数的表达式为：y＝﹣（x+1）（x﹣5）＝﹣x2+x+；（32）由（2）确定的点F的坐标得：CP2＝（2﹣m）2，CF2＝（）2+4，PF2＝（）2+m2，①当CP＝CF时，即：（2﹣m）2＝（）2+4，解得：m＝0或（0舍去），②当CP＝PF时，同理可得：m＝，③当CF＝PF时，同理可得：m＝±2（舍去2），故点P（2，）或（2，﹣2）或（2，）或（2，）。

二次函数中的存在性问题(等腰三角形)[07福建龙岩]如图，抛物线254y ax ax =-+经过ABC △已知BC x ∥轴，点A 在x 轴上，点C 在y 轴上，且AC BC =． （1）求抛物线的对称轴；（2）写出A B C ，，三点的坐标并求抛物线的解析式；（3）探究：若点P 是抛物线对称轴上且在x 轴下方的动点， 是否存在PAB △是等腰三角形．若存在，求出所有符合条 件的点P 坐标；不存在，请说明理由． 解：（1）抛物线的对称轴5522a x a -=-= （2）(30)A -， (54)B ， (04)C ，把点A 坐标代入254y ax ax =-+中，解得16a =-215466y x x ∴=-++（3）存在符合条件的点P 共有3个．以下分三类情形探索．设抛物线对称轴与x 轴交于N ，与CB 交于M ．过点B 作BQ x ⊥轴于Q ，易得4BQ =，8AQ =， 5.5AN =，2BM = ① 以AB 为腰且顶角为角A 的PAB △有1个：1P AB △．222228480AB AQ BQ ∴=+=+= 在1Rt ANP △中，1PN ==== 152P ⎛∴ ⎝⎭ ② AB 为腰且顶角为角B 的PAB △有1个：2P AB △．在2Rt BMP △中，22MP ==== 252P ⎛∴ ⎝⎭③以AB 为底，顶角为角P 的PAB △有1个，即3P AB △．画AB 的垂直平分线交抛物线对称轴于3P ，此时平分线必过等腰ABC △的顶点C ．过点3P 作3P K 垂直y 轴，垂足为K ，显然3Rt Rt PCK BAQ △∽△．312P K BQ CK AQ ∴==． 3 2.5P K = 5CK ∴= 于是1OK = 3(2.51)P ∴-，[07广西河池]如图，已知抛物线224233y x x =-++的图象与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线的对称轴与x 轴交于点D ． 点M 从O 点出发，以每秒1的速度向B 运动，过M 作x 轴的垂线，交抛物线于点P ，交BC 于（1）求点B 和点C 的坐标；（2）设当点M 运动了x （秒）时，四边形OBPC 的面积为S ， 求S 与x 的函数关系式，并指出自变量x 的取值范围．（3）在线段BC 上是否存在点Q ，使得△DBQ 成为以BQ 等腰三角形？若存在，求出点Q 的坐标，若不存在，说明理由．（1）把x =0代入224233y x x =-++得点C 的坐标为C （0，2） 把y =0代入224233y x x =-++得点B 的坐标为B （3，0）（2）连结OP ，设点P 的坐标为P （x ，y ）OBPC S 四边形=OPC S △+OPB S △ =112322x y ⨯⨯+⨯⨯= 3223x ⎛+- ⎝∵ 点M 运动到B 点上停止，∴03x ≤≤∴23324S x ⎛⎫=--+ ⎪⎝⎭（03x ≤≤）（3）存在． BC=13 ① 若BQ = DQ∵ BQ = DQ ，BD = 2 ∴ BM = 1 ∴OM = 3-1 = 2 ∴2tan 3QM OC OBC BM OB ∠=== ∴QM =23 所以Q的坐标为Q （2，23） ． ② 若BQ =BD =2 ∵ △BQM ∽△BCO ，∴BQ BC =QM CO =BMBO∴=2QM∴ QM∵BQ BC =BM OB ∴ 3BM∴ BM ∴ OM = 3 ··················································· 11分 所以Q 的坐标为Q （313-，13） ··················································· 12分[07年云南省]已知：如图，抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点． （1）求抛物线的函数关系式；（2）若过点C 的直线y kx b =+与抛物线相交于点E （4，m ）， 请求出△CBE 的面积S 的值；（3）在抛物线上求一点0P 使得△ABP 0为等腰三角形并 写出0P 点的坐标；（4）除（3）中所求的0P 点外，在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形？若存在，请求出一共有几个满足条件的点P （要求简要说明理由，但不证明）；若不存在这样的点P ，请说明理由． 解：（1）∵抛物线经过点(1,0)A 、(5,0)B ∴(1)(5)y a x x =--． 又∵抛物线经过点(0,5)C ∴55a =，1a =．∴抛物线的解析式为2(1)(5)65y x x x x =--=-+．（2）∵E 点在抛物线上， ∴m = 42–4×6+5 = -3．∵直线y = kx +b 过点C （0， 5）、E （4， –3）， ∴5,4 3.b k b =⎧⎨+=-⎩解得k = -2，b = 5．设直线y =-2x +5与x 轴的交点为D ，当y =0时，-2x +5=0，解得x =52．∴D 点的坐标为（52，0）． ∴S =S △BDC + S △BDE =1515(5)5+(5)32222⨯-⨯⨯-⨯=10．（3）∵抛物线的顶点0(3,4)P -既在抛物线的对称轴上又在抛物线上，∴点0(3,4)P -为所求满足条件的点．（4）除0P 点外，在抛物线上还存在其它的点P 使得△ABP 为等腰三角形．理由如下：∵220024254AP BP ==+=>，∴分别以A 、B 为圆心半径长为4画圆，分别与抛物线 交于点B 、1P 、2P 、3P 、A 、4P 、5P 、6P ， 除去B 、A 两个点外，其余6个点为满足条件的点． （说明：只说出P 点个数但未简要说明理由的不给分）xyC B AE–1 1 O[07山东威海]如图①，在平面直角坐标系中，点A 的坐标为(12)，，点B 的坐标为(31)，，二次函数2y x =的图象记为抛物线1l ．（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的一个抛物线的函数表达式： （任写一个即可）．（2）平移抛物线1l ，使平移后的抛物线过A B ，两点，记为抛物线2l ，如图②，求抛物线2l 的函数表达式． （3）设抛物线2l 的顶点为C ，K 为y 轴上一点．若ABK ABC S S =△△，求点K 的坐标．（4）请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ，使ABP △为等腰三角形．若存在，请判断点P 共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由．解：（1）有多种答案，符合条件即可．例如21y x =+，2y x x =+，2(1)2y x =-+或223y x x =-+，2(1)y x =+，2(1y x =-．（2）设抛物线2l 的函数表达式为2y x bx c =++，点(12)A ，，(31)B ，在抛物线2l 上，12931b c b c ++=⎧∴⎨++=⎩，解得9211.2b c ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线2l 的函数表达式为291122y x x =-+． （3）229119722416y x x x ⎛⎫=-+=-+ ⎪⎝⎭，C ∴点的坐标为97416⎛⎫⎪⎝⎭，．过A B C ，，三点分别作x 轴的垂线，垂足分别为D E F ，，， 则2AD =，716CF =，1BE =，2DE =，54DF =，34FE =． ABC ADEB ADFC CFEB S S S S ∴=--△梯形梯形梯形117517315(21)22122164216416⎛⎫⎛⎫=+⨯-+⨯-+⨯= ⎪ ⎪⎝⎭⎝⎭．x图①x图②x图③x延长BA 交y 轴于点G ，设直线AB 的函数表达式为y mx n =+， 点(12)A ，，(31)B ，在直线AB 上，213.m n m n =+⎧∴⎨=+⎩，解得125.2m n ⎧=-⎪⎪⎨⎪=⎪⎩，∴直线AB 的函数表达式为1522y x =-+．G ∴点的坐标为502⎛⎫ ⎪⎝⎭，． 设K 点坐标为(0)h ，，分两种情况： 若K 点位于G 点的上方，则52KG h =-．连结AK BK ，． 151553122222ABK BKG AKG S S S h h h ⎛⎫⎛⎫=-=⨯⨯--⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭△△△． 1516ABK ABC S S ==△△，515216h ∴-=，解得5516h =．K ∴点的坐标为55016⎛⎫ ⎪⎝⎭，．若K 点位于G 点的下方，则52KG h =-．同理可得，2516h =．K ∴点的坐标为25016⎛⎫⎪⎝⎭，． （4）作图痕迹如图③所示． 由图③可知，点P 共有3个可能的位置．注：作出线段AB 的中垂线得1分，画出另外两段弧得1分．x[07山东泰安]如图，在OAB △中，90B ∠=，30BOA ∠=，4OA =，将OAB △绕点O 按逆时针方向旋转至OA B ''△，C 点的坐标为（0，4）． （1）求A '点的坐标； （2）求过C ，A '，A 三点的抛物线2y ax bx c =++的解析式；（3）在（2）中的抛物线上是否存在点P ，使以O A P ，，为顶点的三角形 是等腰直角三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由 解：（1）过点A '作A D '垂直于x 轴，垂足为D ,则四边形OB A D ''为矩形 在A DO '△中，A D OA ''=sin 4sin 6023A OD '∠=⨯=2OD A B AB''=== ∴点A '的坐标为(2 （2）(04)C ，在抛物线上，4c ∴= 24y ax bx∴=++(40)A ，，(2A '，在抛物线24y ax bx =++上 16440424a b a b ++=⎧⎪∴⎨++=⎪⎩，3a b ⎧=⎪⎨⎪=⎩ ∴所求解析式为23)42y x x =++． （3）①若以点O 为直角顶点，由于4OC OA ==，点C 在抛物线上，则点(04)C ，为满足条件的点． ②若以点A 为直角顶点，则使PAO △为等腰直角三角形的点P 的坐标应为(44)，或(44)-，，经计算知；此两点不在抛物线上．③若以点P 为直角顶点，则使PAO △为等腰直角三角形的点P 的坐标应为(22)，或(22)-，，经计算知；此两点也不在抛物线上．综上述在抛物线上只有一点(04)P ，使OAP △为等腰直角三角形[08广东梅州]如图11所示，在梯形ABCD 中，已知AB ∥CD ， AD ⊥DB ， AD =DC =CB ，AB =4．以AB 所在直线为x 轴，过D 且垂直于 AB 的直线为y 轴建立平面直角坐标系．（1）求∠DAB 的度数及A 、D 、C 三点的坐标；（2）求过A 、D 、C 三点的抛物线的解析式及其对称轴L ． （3）若P 是抛物线的对称轴L 上的点，那么使∆PDB 为等腰三角形的点P 有几个?（不必求点P 的坐标，只需说明理由）解： （1） DC ∥AB ，AD =DC =CB ， ∴ ∠CDB =∠CBD =∠DBA ， ∠DAB =∠CBA ， ∴∠DAB =2∠DBA ，∠DAB +∠DBA =90 ， ∴∠DAB =60 ， ∠DBA =30 ， AB =4， ∴DC =AD =2， R t ∆AOD ，OA =1，OD =3，.∴A （-1，0），D （0， 3），C （2， 3）．（2）根据抛物线和等腰梯形的对称性知，满足条件的抛物线必过点A （－1，0），B （3，0）， 故可设所求为 y =a （x +1）（ x -3） 将点D （0，3）的坐标代入上式得， a =33-． 所求抛物线的解析式为 y =).3)(1(33-+-x x ···································· 7分 其对称轴L 为直线x =1． ········································································· 8分 （3） ∆PDB 为等腰三角形，有以下三种情况：①因直线L 与DB 不平行，DB 的垂直平分线与L 仅有一个交点P 1，P 1D =P 1B ，∆P 1DB 为等腰三角形； ·········································································· 9分 ②因为以D 为圆心，DB 为半径的圆与直线L 有两个交点P 2、P 3，DB =DP 2，DB =DP 3， ∆P 2DB ， ∆P 3DB 为等腰三角形；③与②同理，L 上也有两个点P 4、P 5，使得 BD =BP 4，BD =BP 5． ··················· 10分 由于以上各点互不重合，所以在直线L 上，使∆PDB 为等腰三角形的点P 有5个．[08福建南平]如图，平面直角坐标系中有一矩形纸片OABC ，O 为原点，点A C ，分别在x 轴，y 轴上，点B 坐标为(2)m ，（其中0m >），在BC 边上选取适当的点E 和点F ，将OCE △沿OE 翻折，得到OGE △；再将ABF △沿AF 翻折，恰好使点B 与点G 重合，得到AGF △，且90OGA ∠=．（1）求m 的值；（2）求过点O G A ，，的抛物线的解析式和对称轴； （3）在抛物线的对称轴．．．上是否存在点P ，使得OPG △是 等腰三角形？若不存在，请说明理由；若存在，直接答出．．．． 所有满足条件的点P 的坐标（不要求写出求解过程）． （1）(2)B m ，，由题意可知2AG AB ==2OG OC ==OA m =90OGA ∠=，222OG AG OA ∴+= 222m ∴+=．又0m >，2m ∴=（2）过G 作直线GH x ⊥轴于H ，则1OH =，1HG =，故(11)G ，．又由（1）知(20)A ，， 设过O G A ，，三点的抛物线解析式为2y ax bx c =++ 抛物线过原点，0c ∴=．又抛物线过G A ，两点，1420a b a b +=⎧∴⎨+=⎩解得12a b =-⎧⎨=⎩∴所求抛物线为22y x x =-+ ∴它的对称轴为1x =．（3）答：存在,满足条件的点P 有(10)，，(11)-，，(112)，，(112)+，．[08湖南株洲]如图（1），在平面直角坐标系中，点A 的坐标为（1，-2），点B 的坐标为（3，-1），二次函数2y x =-的图象为1l .（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的抛物线的一个解析式（任写一个即可）.（2）平移抛物线1l ，使平移后的抛物线过A 、B 两点，记抛物线为2l ，如图（2），求抛物线2l 的函数解析式及顶点C 的坐标.（3）设P 为y 轴上一点，且ABC ABP S S ∆∆=，求点P 的坐标.（4）请在图（2）上用尺规作图的方式探究抛物线2l 上是否存在点Q ，使QAB ∆为等腰三角形. 若存在，请判断点Q 共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由.（1）222345y x x y x x =-+-=-+-或等 （满足条件即可） ……1分（2）设2l 的解析式为2y x bx c =-++，联立方程组21193b c b c-=-++⎧⎨-=-++⎩， 解得：911,22b c ==-，则2l 的解析式为291122y x x =-+-， ……3分点C 的坐标为（97,416-） ……4分（3）如答图23-1，过点A 、B 、C 三点分别作x 轴的垂线，垂足分别为D 、E 、F ，则2AD =，716CF =，1BE =，2DE =，54DF =，34FE =.得：1516ABC ABED BCFE CFD S S S S ∆=--=梯形梯形梯形A . ……5分延长BA 交y 轴于点G ，直线AB 的解析式为1522y x =-，则点G 的坐标为（0，52-），设点P 的坐y ox 图（1）yo x 图（2） l 1l 2标为（0，h ）①当点P 位于点G 的下方时，52PG h =--，连结AP 、BP ，则52ABP BPG APG S S S h ∆∆∆=-=--，又1516ABC ABP S S ∆∆==，得5516h =-，点P 的坐标为（0，5516-）. …… 6分②当点P 位于点G 的上方时，52PG h =+，同理2516h =-，点P 的坐标为（0，2516-）.综上所述所求点P 的坐标为（0，5516-）或（0，2516-） …… 7分(4) 作图痕迹如答图23-2所示.由图可知，满足条件的点有1Q 、2Q 、3Q 、4Q ，共4个可能的位置. …… 10分答图23-2EF 答图23-1[08浙江温州]如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）； （3）是否存在点P ，使PQR △为等腰三角形？若存在， 请求出所有满足要求的x 的值；若不存在，请说明理由． 解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=． 点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△，DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=．（2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x-∴=， 即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 10C ∴∠===，45QM QP ∴=，1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=．②当PQ RQ =时，312655x -+=，6x ∴=． ③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BA C CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形．A BCD ER P H QA BCD ER P H QM2 1 HA B CDE RPHQ二次函数中的存在性问题(直角三角形)[08辽宁十二市]如图16，在平面直角坐标系中，直线y =-x 轴交于点A ，与y 轴交于点C ，抛物线2(0)3y ax x c a =-+≠经过A B C ，，三点． （1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．x。

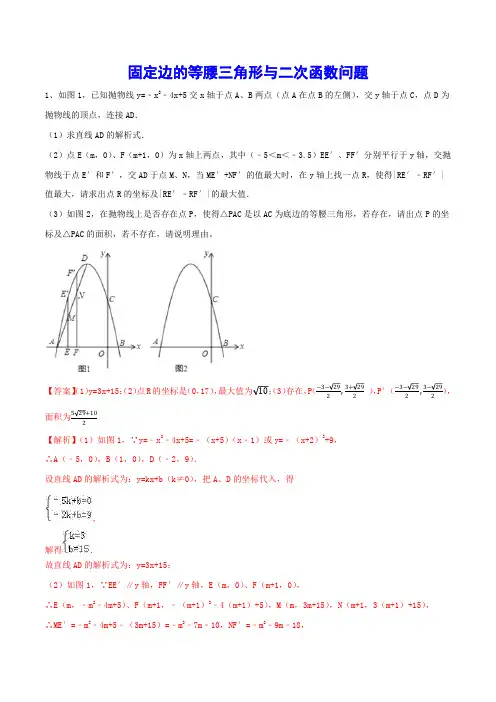
固定边的等腰三角形与二次函数问题1、如图1，已知抛物线y=﹣x2﹣4x+5交x轴于点A、B两点（点A在点B的左侧），交y轴于点C，点D为抛物线的顶点，连接AD．（1）求直线AD的解析式．（2）点E（m，0）、F（m+1，0）为x轴上两点，其中（﹣5＜m＜﹣3.5）EE′、FF′分别平行于y轴，交抛物线于点E′和F′，交AD于点M、N，当ME′+NF′的值最大时，在y轴上找一点R，使得|RE′﹣RF′|值最大，请求出点R的坐标及|RE′﹣RF′|的最大值．（3）如图2，在抛物线上是否存在点P，使得△PAC是以AC为底边的等腰三角形，若存在，请出点P的坐标及△PAC的面积，若不存在，请说明理由。

【答案】（1）y=3x+15；（2）点R的坐标是（0，17），最大值为 午；（3）存在，P），P′，【解析】（1）如图1，∵y=﹣x2﹣4x+5=﹣（x+5）（x﹣1）或y=﹣（x+2）2+9，∴A（﹣5，0），B（1，0），D（﹣2，9）．设直线AD的解析式为：y=kx+b（k≠0），把A、D的坐标代入，得，解得．故直线AD的解析式为：y=3x+15；（2）如图1，∵EE′∥y轴，FF′∥y轴，E（m，0）、F（m+1，0），∴E（m，﹣m2﹣4m+5）、F（m+1，﹣（m+1）2﹣4（m+1）+5），M（m，3m+15），N（m+1，3（m+1）+15），∴ME′=﹣m2﹣4m+5﹣（3m+15）=﹣m2﹣7m﹣10，NF′=﹣m2﹣9m﹣18，∴ME′+NF′=﹣m 2﹣7m﹣10﹣m 2﹣9m﹣18=2m 2﹣16m﹣28．∵﹣2＜0，∴m=﹣=﹣4，∴ME′+NF′有最大值，此时E′（﹣4，5），F′（﹣3，8），要使|RE′﹣RF′|值最大，则点E′、F′、R 三点在一条直线上，∴设直线E′F′：y=kx+b（k≠0），则，解得，∴直线E′F′：y=3x+17（k≠0）．当x=0时，y=17，则点R 的坐标是（0，17）．此时，|RE′﹣RF′|的最大值为=；（3）如图2，设点P（x，﹣x 2﹣4x+5）．当PA=PC 时，点P 在线段AC 的垂直平分线上，∵OC=OA，∴点O 在线段AC 的垂直平分线上，∴点P 在∠AOC 的角平分线上，∴﹣x=﹣x 2﹣4x+5，解得x 1=，x 2=，∴P（，），P′（，）．∴PH=OP﹣OH=，P′H=OP′+OH=，∴S △PAC =AC•PH=×5×=或S △PAC =AC•P′H=×5×=．2、已知一次函数4y x =+的图象与二次函数(2)y ax x =-的图象相交于(1,)A b -和B ，点P 是线段AB 上的动点（不与,A B 重合），过点P 作PC x ⊥轴，与二次函数(2)y ax x =-的图象交于点C ．（1）求,a b 的值；（2）求线段PC 长的最大值；（3）当PAC ∆为90ACP ︒∠=的等腰直角三角形时，求出此时点P 的坐标．【答案】（1）1，3；（2）最大值为254；（3）()3,7P 【解析】解：（1）∵(1,)A b -在直线4y x =+上，∴143b =-+=，∴(1,3)A -．又∵(1,3)A -在拋物线(2)y ax x =-上，∴3(12)a =-⋅--，解得1a =．（2）设(,4)P m m +，则()2,2C m m m -，∴()2(4)2PC m m m =+--234m m =-++232524m ⎛⎫=--+ ⎪⎝⎭，∴当32m =时，PC 有最大值，最大值为254．（3）如图，∵PAC ∆为90ACP ︒∠=的等腰三角形且PC x ⊥轴，∴连接AC ，AC y ⊥轴，∵()2(,4),2(1,3)P m m C m m m A +--，，，∴(1)1C A AC x x m m =-=--=+，()22(4)234P C PC y y m m m m m =-=+--=-++．∵AC PC =，∴2134m m m +=-++，化简，得2230m m --=，解得3m =，1m =-（不合题意，舍去）．当3m =时，47m +=，∴此时点P 的坐标为()3,7P ．3、如图，在平面直角坐标系中．直线y=﹣x+3与x 轴交于点B，与y 轴交于点C，抛物线y=ax 2+bx+c 经过B，C 两点，与x 轴负半轴交于点A，连结AC，A(-1,0)（1）求抛物线的解析式；（2）点P（m，n）是抛物线上在第一象限内的一点，求四边形OCPB 面积S 关于m 的函数表达式及S 的最大值；（3）若M 为抛物线的顶点，点Q 在直线BC 上，点N 在直线BM 上，Q，M，N 三点构成以MN 为底边的等腰直角三角形，求点N 的坐标．【答案】（1）y==﹣x2+2x+3；（2）S=﹣32（m﹣32）2+638，当m=32时，S有最大值是638；（3）点N的坐标为（2，2）或（﹣1，8）【解析】解：（1）∵直线y=﹣x+3与x轴交于点B，与y轴交于点C，∴当x=0时，y=3，∴C（0，3），∴OC=3，当y=0时，-x+3=0，x=3，∴B（3，0），设抛物线的解析式为：y=a（x+1）（x-3），把C（0，3）代入得：3=a（0+1）（0-3），a=-1，∴y=-（x+1）（x-3）=-x2+2x+3；（2）如图1，过P作PE⊥x轴于E，∵P（m，n），∴OE=m，BE=3-m，PE=n，S=S 梯形COEP +S △PEB =12OE（PE+OC）+12BE•PE，=12m（n+3）+12n（3-m），=32m+32n，∵n=-m 2+2m+3，∴S=32m+32（-m 2+2m+3）=-32m 2+92m+92=-32（m-32）2+638，当m=32时，S 有最大值是638；（3）y=-x 2+2x+3=-（x-1）2+4，∴M（1，4），设直线BM 的解析式为：y=kx+b，把B（3，0），M（1，4）代入得：304k b k b +⎧⎨+⎩＝＝，解得：26k b -⎧⎨⎩＝＝，∴直线BM 的解析式为：y=-2x+6，设N（a，-2a+6），Q（n，-n+3），分两种情况：①当N 在射线MB 上时，如图2，过Q 作EF∥y 轴，分别过M、N 作x 轴的平行线，交EF 于E、F，∵△EQN 是等腰直角三角形，∴MQ=QN，∠MQN=90°，∴∠EQM+∠FQN=90°，∵∠EQM+∠EMQ=90°，∴∠FQN=∠EMQ，∵∠QEM=∠QFN=90°，∴△EMQ≌△FQN，∴EM=FQ，EQ=FN，∴13(26)4(3)n n an a n--+--+⎧⎨--+-⎩＝＝，解得：212an⎧⎪⎨⎪⎩＝＝，当a=2时，y=-2a+6=-2×2+6=2，∴N（2，2），②当N在射线BM上时，如图3，同理作辅助线，得△ENQ≌△FQM，∴EN=FQ，EQ=FM，∴3426(3)1n a na n n-+-+-⎧⎨-+--+-+⎩＝＝，解得：12an-⎧⎨-⎩＝＝，∴N（-1，8），综上所述，点N的坐标为（2，2）或（-1，8）．4、抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．（1）求抛物线的解析式；（2）求出C、D 两点的坐标（3）在第四象限抛物线上有一点P，若△PCD 是以CD 为底边的等腰三角形，求出点P 的坐标．【答案】（1）y＝x 2，﹣2）.【思路引导】（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入y ＝ax 2+bx ﹣3可得抛物线解析式．（2）当x ＝0时可求C 点坐标，求出直线AB 解析式，当x ＝0可求D 点坐标．（3）由题意可知P 点纵坐标为﹣2，代入抛物线解析式可求P 点横坐标．【解析】解：（1）把A（﹣1，0）、B（2，﹣3）两点坐标代入y＝ax 2+bx﹣3可得304233a b a b --=⎧⎨+-=-⎩解得12a b =⎧⎨=-⎩∴y＝x 2﹣2x﹣3（2）把x＝0代入y＝x 2﹣2x﹣3中可得y＝﹣3∴C（0，﹣3）设y＝kx+b，把A（﹣1，0）、B（2，﹣3）两点坐标代入023k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩∴y＝﹣x﹣1∴D（0，﹣1）（3）由C（0，﹣3），D（0，﹣1）可知CD 的垂直平分线经过（0，﹣2）∴P 点纵坐标为﹣2，∴x 2﹣2x﹣3＝﹣2．，﹣2）【方法总结】本题是二次函数综合题，用待定系数法求二次函数的解析式，把x ＝0代入二次函数解析式和一次函数解析式可求图象与y 轴交点坐标，知道点P 纵坐标带入抛物线解析式可求点P 的横坐标．5、如图，在平面直角坐标系中，抛物线C 1：y ＝ax 2+bx ﹣1经过点A (﹣2，1)和点B (﹣1，﹣1)，抛物线C 2：y ＝2x 2+x +1，动直线x ＝t 与抛物线C 1交于点N ，与抛物线C 2交于点M ．（1）求抛物线C 1的表达式；（2）直接用含t 的代数式表达线段MN 的长；（3）当△AMN 是以MN 为直角边的等腰直角三角形时，求t 的值．【答案】（1）y ＝x 2+x ﹣1；（2）MN ＝t 2+2；（3）t ＝0或1【解析】解：（1）将点A 、B 的坐标代入抛物线表达式得：421111a b a b --=⎧⎨--=-⎩，解得：11a b =⎧⎨=⎩，故抛物线C 1的表达式为：y ＝x 2+x ﹣1；（2）点M 、N 的坐标分别为：（t ，2t 2+t +1）、（t ，t 2+t ﹣1），则MN ＝（2t 2+t +1）﹣（t 2+t ﹣1）＝t 2+2；（3）①当∠ANM ＝90°时，AN ＝MN ，AN ＝t ﹣（﹣2）＝t +2，MN ＝t 2+2，t ＝t 2+2，解得：t ＝0或1（舍去0），故t ＝1；②当∠AMN ＝90°时，AM ＝MN ，AM ＝t +2＝MN ＝t 2+2，解得：t ＝0或1（舍去1），故t ＝1；综上，t ＝0或1．6、如图1，抛物线y ＝ax 2＋bx ＋c （a 、b 、c 是常数，a ≠0）的对称轴为y 轴，且经过(0,0)和1(,)16a 两点，点P 在该抛物线上运动，以点P 为圆心的⊙P 总经过定点A (0,2)．（1）求a 、b 、c 的值；（2）求证：在点P 运动的过程中，⊙P 始终与x 轴相交；（3）设⊙P 与x 轴相交于M (x 1,0)、N (x 2,0)两点，当△AMN 为等腰三角形时，求圆心P 的纵坐标．图1思路点拨1．不算不知道，一算真奇妙，原来⊙P 在x 轴上截得的弦长MN ＝4是定值．2．等腰三角形AMN 存在三种情况，其中MA ＝MN 和NA ＝NM 两种情况时，点P 的纵坐标是相等的．满分解答（1）已知抛物线的顶点为(0,0)，所以y ＝ax 2．所以b ＝0，c ＝0．将1(,)16a 代入y ＝ax 2，得2116a =．解得14a =（舍去了负值）．（2）抛物线的解析式为214y x =，设点P 的坐标为21(,)4x x ．已知A (0,2)，所以222411(2)4416PA x x x =+-=+＞214x ．而圆心P 到x 轴的距离为214x ，所以半径PA ＞圆心P 到x 轴的距离．所以在点P 运动的过程中，⊙P 始终与x 轴相交．（3）如图2，设MN 的中点为H ，那么PH 垂直平分MN ．在Rt△PMH 中，2241416PM PA x ==+，22411()416PH x x ==，所以MH 2＝4．所以MH ＝2．因此MN ＝4，为定值．等腰△AMN 存在三种情况：①如图3，当AM ＝AN 时，点P 为原点O 重合，此时点P 的纵坐标为0．图2图3②如图4，当MA ＝MN 时，在Rt△AOM 中，OA ＝2，AM ＝4，所以OM此时x ＝OH 2．所以点P 的纵坐标为222112)1)444x =+=+=+．③如图5，当NA ＝NM 时，点P 的纵坐标为也为4+．图4图5考点伸展如果点P 在抛物线214y x =上运动，以点P 为圆心的⊙P 总经过定点B (0,1)，那么在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．这是因为：设点P 的坐标为21(,)4x x ．已知B (0,1)，所以2114PB x =+．而圆心P 到直线y ＝－1的距离也为2114x +，所以半径PB ＝圆心P 到直线y ＝－1的距离．所以在点P运动的过程中，⊙P始终与直线y＝－1相切．7、如图1，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，点D为边BC的中点，DE⊥BC交边AC于点E，点P 为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ＝90°．（1）求ED、EC的长；（2）若BP＝2，求CQ的长；（3）记线段PQ与线段DE的交点为F，若△PDF为等腰三角形，求BP的长．图1备用图思路点拨1．第（2）题BP＝2分两种情况．2．解第（2）题时，画准确的示意图有利于理解题意，观察线段之间的和差关系．3．第（3）题探求等腰三角形PDF时，根据相似三角形的传递性，转化为探求等腰三角形CDQ．满分解答（1）在Rt△ABC中，AB＝6，AC＝8，所以BC＝10．在Rt△CDE中，CD＝5，所以315tan544ED CD C=⋅∠=⨯=，254EC=．（2）如图2，过点D作DM⊥AB，DN⊥AC，垂足分别为M、N，那么DM、DN是△ABC的两条中位线，DM＝4，DN＝3．由∠PDQ＝90°，∠MDN＝90°，可得∠PDM＝∠QDN．因此△PDM∽△QDN．所以43PM DMQN DN==．所以34QN PM=，43PM QN=．图2图3图4①如图3，当BP ＝2，P 在BM 上时，PM ＝1．此时3344QN PM ==．所以319444CQ CN QN =+=+=．②如图4，当BP ＝2，P 在MB 的延长线上时，PM ＝5．此时31544QN PM ==．所以1531444CQ CN QN =+=+=．（3）如图5，如图2，在Rt△PDQ 中，3tan 4QD DN QPD PD DM ∠===．在Rt△ABC 中，3tan 4BA C CA ∠==．所以∠QPD ＝∠C ．由∠PDQ ＝90°，∠CDE ＝90°，可得∠PDF ＝∠CDQ ．因此△PDF ∽△CDQ ．当△PDF 是等腰三角形时，△CDQ 也是等腰三角形．①如图5，当CQ ＝CD ＝5时，QN ＝CQ －CN ＝5－4＝1（如图3所示）．此时4433PM QN ==．所以45333BP BM PM =-=-=．②如图6，当QC ＝QD 时，由cos CH C CQ =，可得5425258CQ =÷=．所以QN ＝CN －CQ ＝257488-=（如图2所示）．此时4736PM QN ==．所以725366BP BM PM =+=+=．③不存在DP ＝DF 的情况．这是因为∠DFP ≥∠DQP ＞∠DPQ （如图5，图6所示）．图5图6考点伸展如图6，当△CDQ 是等腰三角形时，根据等角的余角相等，可以得到△BDP 也是等腰三角形，PB ＝PD ．在△BDP 中可以直接求解256BP =．9、如图1，抛物线y ＝ax 2＋bx ＋c 经过A (－1,0)、B (3,0)、C (0,3)三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P 是直线l 上的一个动点，当△PAC 的周长最小时，求点P 的坐标；（3）在直线l 上是否存在点M ，使△MAC 为等腰三角形，若存在，直接写出所有符合条件的点M 的坐标；若不存在，请说明理由．图1思路点拨1．第（2）题是典型的“牛喝水”问题，点P 在线段BC 上时△PAC 的周长最小．2．第（3）题分三种情况列方程讨论等腰三角形的存在性．满分解答（1）因为抛物线与x 轴交于A (－1,0)、B (3,0)两点，设y ＝a (x ＋1)(x －3)，代入点C (0,3)，得－3a ＝3．解得a ＝－1．所以抛物线的函数关系式是y＝－(x ＋1)(x －3)＝－x 2＋2x ＋3．（2）如图2，抛物线的对称轴是直线x ＝1．当点P 落在线段BC 上时，PA ＋PC 最小，△PAC 的周长最小．设抛物线的对称轴与x 轴的交点为H ．由BH PH BO CO=，BO ＝CO ，得PH ＝BH ＝2．所以点P 的坐标为(1,2)．图2（3）点M 的坐标为(1,)、(1,)或(1,0)．考点伸展第（3）题的解题过程是这样的：设点M 的坐标为(1,m )．在△MAC中，AC2＝10，MC2＝1＋(m－3)2，MA2＝4＋m2．①如图3，当MA＝MC时，MA2＝MC2．解方程4＋m2＝1＋(m－3)2，得m＝1．此时点M的坐标为(1,1)．②如图4，当AM＝AC时，AM2＝AC2．解方程4＋m2＝10，得m=．此时点M)或(1,)．③如图5，当CM＝CA时，CM2＝CA2．解方程1＋(m－3)2＝10，得m＝0或6．当M(1,6)时，M、A、C三点共线，所以此时符合条件的点M的坐标为(1,0)．图3图4图59、如图1，点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°至OB的位置．（1）求点B的坐标；（2）求经过A 、O 、B 的抛物线的解析式；（3）在此抛物线的对称轴上，是否存在点P ，使得以点P 、O 、B 为顶点的三角形是等腰三角形？若存在，求点P 的坐标；若不存在，请说明理由．图1思路点拨1．用代数法探求等腰三角形分三步：先分类，按腰相等分三种情况；再根据两点间的距离公式列方程；然后解方程并检验．2．本题中等腰三角形的角度特殊，三种情况的点P 重合在一起．满分解答（1）如图2，过点B 作BC ⊥y 轴，垂足为C ．在Rt△OBC 中，∠BOC ＝30°，OB ＝4，所以BC ＝2，OC =所以点B 的坐标为(2,--．（2）因为抛物线与x 轴交于O 、A (4,0)，设抛物线的解析式为y ＝ax (x －4)，代入点B (2,--，2(6)a -=-⨯-．解得36a =-．所以抛物线的解析式为2(4)663y x x =--=-+．（3）抛物线的对称轴是直线x ＝2，设点P 的坐标为(2,y )．①当OP ＝OB ＝4时，OP 2＝16．所以4+y 2＝16．解得y =±当P 在(2,时，B 、O 、P 三点共线（如图2）．②当BP ＝BO ＝4时，BP 2＝16．所以224(16y ++=．解得12y y ==-③当PB ＝PO 时，PB 2＝PO 2．所以22224(2y y ++=+．解得y =-．综合①、②、③，点P 的坐标为(2,-，如图2所示．图2图3考点伸展如图3，在本题中，设抛物线的顶点为D ，那么△DOA 与△OAB 是两个相似的等腰三角形．由23323(4)(2)663y x x x =--=-+，得抛物线的顶点为23(2,3D ．因此23tan DOA ∠=DOA ＝30°，∠ODA ＝120°．10、如图1，已知一次函数y ＝－x ＋7与正比例函数43y x =的图象交于点A ，且与x 轴交于点B ．（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l //y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O —C —A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形？若存在，求t 的值；若不存在，请说明理由．图1思路点拨1．把图1复制若干个，在每一个图形中解决一个问题．2．求△APR 的面积等于8，按照点P 的位置分两种情况讨论．事实上，P 在CA 上运动时，高是定值4，最大面积为6，因此不存在面积为8的可能．3．讨论等腰三角形APQ ，按照点P 的位置分两种情况讨论，点P 的每一种位置又要讨论三种情况．满分解答（1）解方程组7,4,3y x y x =-+⎧⎪⎨=⎪⎩得3,4.x y =⎧⎨=⎩所以点A 的坐标是(3，4)．令70y x =-+=，得7x =．所以点B 的坐标是(7，0)．（2）①如图2，当P 在OC 上运动时，0≤t ＜4．由8APR ACP POR CORA S S S S =--=△△△梯形，得1113+7)44(4)(7)8222t t t t -⨯-⨯⨯--⨯-=（．整理，得28120t t -+=．解得t ＝2或t ＝6（舍去）．如图3，当P 在CA 上运动时，△APR 的最大面积为6．因此，当t ＝2时，以A、P、R 为顶点的三角形的面积为8．图2图3图4②我们先讨论P 在OC 上运动时的情形，0≤t ＜4．如图1，在△AOB 中，∠B ＝45°，∠AOB ＞45°，OB＝7，AB =OB ＞AB ．因此∠OAB ＞∠AOB ＞∠B ．如图4，点P 由O 向C 运动的过程中，OP ＝BR ＝RQ ，所以PQ //x 轴．因此∠AQP ＝45°保持不变，∠PAQ 越来越大，所以只存在∠APQ ＝∠AQP 的情况．此时点A 在PQ 的垂直平分线上，OR ＝2CA ＝6．所以BR ＝1，t ＝1．我们再来讨论P 在CA 上运动时的情形，4≤t ＜7．在△APQ 中，3cos 5A ∠=为定值，7AP t =-，5520333AQ OA OQ OA OR t =-=-=-．如图5，当AP＝AQ时，解方程520733t t-=-，得418t=．如图6，当QP＝QA时，点Q在PA的垂直平分线上，AP＝2(OR－OP)．解方程72[(7)(4)]t t t-=---，得5t=．如7，当PA＝PQ时，那么12cosAQAAP∠=．因此2cosAQ AP A=⋅∠．解方程52032(7)335t t-=-⨯，得22643t=．综上所述，t＝1或418或5或22643时，△APQ是等腰三角形．图5图6图7。

二次函数等腰直角三角形问题结论一、二次函数的基本概念1.大家都知道，二次函数就是形如(y=ax^2+bx+c)的函数，听起来有点复杂，但其实它和我们日常生活中的许多现象都有关系。

想象一下，高高的抛物线，它的两端慢慢向外延展，仿佛一对展开的翅膀，展现出一种优雅的弯曲感。

像极了小时候玩的小玩具——弹簧，拉伸到极限后，就会呈现出这种形状。

没错，这就是二次函数的图像，它的“抛物线”就是我们所熟知的数学形状。

二次函数有个特点，就是它的图像总是对称的，不管你怎么移动它，它总是像一面镜子，左边和右边永远一样，简直像是一对孪生兄弟。

2.二次函数的这种对称性不仅在数学中有应用，生活中也随处可见。

比如说，我们常常见到的运动抛物线——篮球投篮的轨迹，基本上就是一个典型的二次函数图像。

当我们投篮时，篮球是沿着抛物线的轨迹飞行的，如果你投得准确，篮筐正好处于这个轨迹的“最低点”，球就能进网。

是不是很神奇呢？这个低点，数学上称为“顶点”，它在二次函数的图像中有着特别的地位。

你可以把顶点想象成二次函数的“心脏”，一切的美丽都源自它的存在。

3.了解了二次函数的基本特点后，我们接下来要说说它与等腰直角三角形的关系了。

乍一听，这两者似乎毫无联系，对吧？但它们之间有着奇妙的“心灵感应”。

等腰直角三角形是什么？简单来说，它就是两个直角边长度相等的三角形，大家小时候做数学题的时候，肯定见过这种形状。

这个三角形的最神奇之处就在于，它的斜边总是比直角边长一倍，简直是个数学界的“小天才”。

二、二次函数与等腰直角三角形的关联1.现在让我们把目光投向这两个看似毫不相干的数学图形，试着找找它们之间的共通点。

二次函数的图像——就是抛物线，像不像等腰直角三角形的一个半面？把一个等腰直角三角形的两个直角边沿着某个方向延伸，你就会发现，它们的图像和二次函数有着某种“呼应”的关系。

可以说，二次函数的对称轴和等腰直角三角形的顶角处的“斜边”是一种心有灵犀的联系。

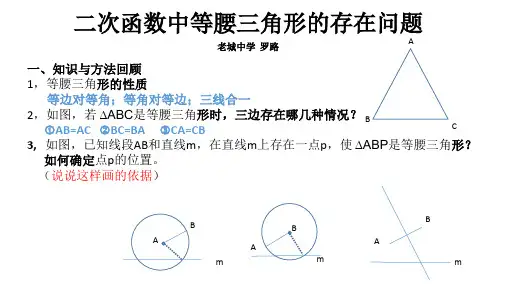
专题：二次函数中等腰三角形存在性问题类型一、等腰三角形存在性问题以(,)A A A x y 、(,)B B B x y 为三角形的边，在x 轴上找一点P 使得△PAB 为等腰三角形（二定一动）一.找法：画圆和作垂直平分线①以A 为圆心，线段AB 为半径画圆，与x 轴交点即为1P 、2P 点；（AB=AP ）②以B 为圆心，线段AB 为半径画圆，与x 轴交点即为3P 、4P 点；（AB=BP ）③作线段AB 的垂直平分线，与x 轴交点即为5P 点；（AP=BP ）二、算法：利用两点距离公式进行计算 公式：22()()A B A B AB x x y y =-+- ，设(,)p p P x y ，分三种情况：①AB=AP 时 2222()()()()A B A B A P A P x x y y x x y y -+-=-+-可得1P 、2P ，（特殊情况可能是一个点，例如2P 与B 重合）②AB=BP 时2222()()()()A B A B B P B P x x y y x x y y -+-=-+-可得3P 、4P ，（特殊情况可能是一个点，例如3P 与A 重合）③AP=BP 时2222()()()()A P A P B P B P x x y y x x y y -+-=-+-可得5P 、例题1、如图，已知二次函数2y x bx c =++的图像与x 轴交于点A 、B 两点，其中A 点坐标为（-3,0），与y 轴交于点C ，点D （-2，-3）在抛物线上.（1）求抛物线的表达式；（2）抛物线的对称轴上是否存在动点Q ，使得△BCQ 为等腰三角形？若存在，求出点Q 的坐标；若不存在，说明理由.1、（2021·云南九年级一模）如图所示，抛物线()240y ax bx a =++≠经过点()1,0A -，点()4,0B ，与y 轴交于点C ，连接AC ，BC ．点M 是线段OB 上不与点O 、B 重合的点，过点M 作DM x ⊥轴，交抛物线于点D ，交BC 于点E ．（1）求抛物线的表达式；（2）过点D 作DF BC ⊥，垂足为点F ．设M 点的坐标为(),0M m ，请用含m 的代数式表示线段DF 的长，并求出当m 为何值时DF 有最大值，最大值是多少？（3）试探究是否存在这样的点E ，使得以A ，C ，E 为顶点的三角形是等腰三角形．若存在，请求出此时点E 的坐标；若不存在，请说明理由．2、（八中2020级初三第三次月考）如图在平面直角坐标系中，已知抛物线2(0)y ax bx c a =++≠交x 轴于A （-4,0），B （1,0），交y 轴于C （0,3）（1）求此抛物线解析式；（2）如图1，点P 为直线AC 上方抛物线上一点，过点P 作PQ ⊥x 轴于点Q ，再过点Q 作QR//AC 交y 轴于点R ，求PQ+QR 的最大值及此时点P 的坐标；（3）如图2，点E 在抛物线上，横坐标为-3，连接AE ，将线段AE 沿直线AC 平移，得到线段''A E ，连接'CE ，当△''A E C 为等腰三角形时，只写写出点'A 的坐标。

基于分类讨论思想研究二次函数与等腰三角形结合问题的解决策略摘要：就当前来说，二次函数动点提问已经成为了每个学生学习过程中十分强烈的拦路虎，往往发生在选项题、填空题、回答问题中的最后一题上，也成了考试与数学考试区别不同层次学习者的主要方式。

对于有效处理中学数学二次函数与等腰三角形组合提问策略的研究方法非常多，本章将从分析讨论思路入手，以二次函数与等腰三角形组合的数学题为例，把看似复杂的动态提问层层分析，并逐步减轻了其复杂度，将其变成常见的数学题目，并最终帮助他们建立克服困难的勇气。

关键词：分类讨论；中学数学；二次函数引言：现代数学基础知识主要可分为二大类：一种是代数，其典型代表知识点是函数；另一类则是几何学，其中三角是在中学阶段掌握的基础图形之一。

函数问题与三角形的结合是常见的问题，主要考查学生对二次函数及三角形的基本性质是否熟练掌握，属于综合性较强的问题。

分类讨论思维，在数学领域是十分重要的数学思维方式，是中学数学中最基本的思维方式一种，更是历年考试的重心。

学会了掌握它就可以增强分析问题和解决问题的能力。

一、应用分类讨论思想的重要性及讨论原因1、分类讨论思想的重要性分析针对中国当前的教学改革形势，对中学的数学教学模式也将产生诸多的深远影响。

中学数学是对学生学习的主要学科，数学课程也是对学生思维能力训练的主要课题。

在初中学阶段也是对学生学习的黄金期，学生在这一阶段对新奇的事情更加好奇，在教育过程中，老师必须能全面的关注学生这一特点。

实际在数学专业教育过程中，学校应该可以采用多种多样的教学方式进行实际应用，以提高学生的读书自主积极性。

数学的理解与教学中，往往会出现分类探讨的问题，这对学生的更多思维能力的训练具有意义。

同时分类探讨也是数学解题中最主要的思维方式，对学生处理实际问题也具有促进意义。

而学生往往在解题过程中，并不知怎样分类探讨，于是这就要求老师可以通过与课本内容以及学生实际的学习状况相结合，进行创造情境并对方法的运用加以强调，从而激发和引导学生对分类探讨的解题思路进行更灵活多样的运用，使分类探讨的思维与实质都能进行更全面的展现[1]。

专题训练二等腰三角形、直角三角形的存在性问题专题攻略如果△ ABC是等腰三角形，那么存在①AB=AC,②BA=BC,③CA = CB三种情况.找法：两圆一线—一已知腰长分别作以端点为圆心腰长为半径的圆，已知底边作底边的垂直平分线.算法：几何法：分类、画图、计算.代数法：罗列三边长，分类列方程，解方程并检验.典型例题如图，已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y= - x2- 2x+3经过A、B两点，与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.问x轴上是否存在点P使得以P、B、C为顶点的三角形是等腰三角形？若有，写出所有符变式:问y轴正半轴上是否存在点P使得以P、B、C为顶点的三角形是以BC为腰的等腰三角形?专题攻略如果△ ABC是直角三角形，那么存在①AB±AC,②BA±BC,③CA±CB三种情况.找法：两线一圆—-已知直角边分别过端点作垂线，已知斜边作以斜边中点为圆心斜边为半径的直角三角形.算法：几何法：先分类；再画图，构造相似；列比例式求解代数法：罗列三边长，分类列方程，解方程并检验.解析法：分类画图；K 1• K2 =-1；求直线解析式、交点坐标典型例题如图，已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y= - x2- 2x+3经过A、B两点，与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.问抛物线上是否存在点P使得以P、B、C为顶点的三角形是直角三角形？若有，写出所有(1)问对称轴上是否存在点P使得以P、B、C为顶点的三角形是BC为斜边的直角三角形?1.如图，已知二次函数的图象经过点A (3, 3)、B (4, 0)和原点O. P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为D (m, 0),并与直线OA交于点C.(1)求出二次函数的解析式； (2)当点P在直线OA的上方时，用含m的代数式表示线段PC 的长，并求线段PC的最大值；(3)当m>0时，探索是否存在点P,使得APCO为等腰三角形，如果存在，请直接写出所有P 的坐标；如果不存在，请说明理由., 直线y = %'3x — 2於经过点C ,交y 轴于点G .(1)求顶点在直线y = <3x — 2自上且经过点C 、D 的抛物线的解析式；(2)将(1)中的抛物线沿直线y =於x - 2、：3平移，平移后的抛物线交y 轴于点F ,顶点 为点E (顶点在y 轴右侧).平移后是否存在这样的抛物线，使^EFG 为等腰三角形？若存 在，请求出此时抛物线的解析式；若不存在，请说明理由.2<3 2.如图，在平面直角坐标系xoy 中，矩形ABCD 的边AB 在x 轴上，且AB = 3, BC =1 113.已知抛物线y = —2 x 2 +4x—3与坐标轴交与A (1.5,0), B (4,0), C (0,3)三点。

2021新版挑战中考数学压轴题之学霸秘笈大揭秘专题3二次函数与等腰直角三角形问题二次函数与等腰直角三角形的相结合的综合问题，是中考数学压轴题中比较常见的一种，涉及到的知识点有：等腰直角三角形的性质、直角三角形的性质、斜边的中线、全等三角形与相似三角形、角平分线、方程与函数模型、函数的基本性质等。

等腰直角三角形与二次函数综合问题常见的有三种类型：两定一动探索直角三角形问题；一定两动探索等腰直角三角形问题；三动探索等腰直角三角形问题；常见的思路中，不管是哪种类型的等腰直角三角形三角形问题，分类讨论的依据都是三个角分别为直角，解决的思路是通过构造K型全等或相似图来列方程解决。

【例1】（2020•甘肃省兰州市中考第28题）如图，二次函数y=14x2+bx+c的图象过点A（4，﹣4），B（﹣2，m），交y轴于点C（0，﹣4）．直线BO与抛物线相交于另一点D，连接AB，AD，点E是线段AB上的一动点，过点E作EF∥BD交AD于点F．（1）求二次函数y=14x2+bx+c的表达式；（2）判断△ABD的形状，并说明理由；（3）在点E的运动过程中，直线BD上存在一点G，使得四边形AFGE为矩形，请判断此时AG与BD 的数量关系，并求出点E的坐标；（4）点H是抛物物的顶点，在（3）的条件下，点P是平面内使得∠EPF＝90°的点，在抛物线的对称轴上，是否存在点Q，使得△HPQ是以∠PQH为直角的等腰直角三角形，若存在，直接写出符合条件的所有点Q的坐标；若不存在，请说明理由．【例2】（2020•湖北省武汉市中考第24题）将抛物线C：y＝（x﹣2）2向下平移6个单位长度得到抛物线C1，再将抛物线C1向左平移2个单位长度得到抛物线C2．（1）直接写出抛物线C1，C2的解析式；（2）如图（1），点A在抛物线C1（对称轴l右侧）上，点B在对称轴l上，△OAB是以OB为斜边的等腰直角三角形，求点A的坐标；（3）如图（2），直线y＝kx（k≠0，k为常数）与抛物线C2交于E，F两点，M为线段EF的中点；直线y=−4k x与抛物线C2交于G，H两点，N为线段GH的中点．求证：直线MN经过一个定点．【例3】（2020•湖南省岳阳市中考第24题）如图1所示，在平面直角坐标系中，抛物线F1：y＝a（x−2 5）2+6415与x轴交于点A（−65，0）和点B，与y轴交于点C．（1）求抛物线F1的表达式；（2）如图2，将抛物线F1先向左平移1个单位，再向下平移3个单位，得到抛物线F2，若抛物线F1与抛物线F2相交于点D，连接BD，CD，BC．①求点D的坐标；②判断△BCD的形状，并说明理由；（3）在（2）的条件下，抛物线F2上是否存在点P，使得△BDP为等腰直角三角形，若存在，求出点P 的坐标；若不存在，请说明理由．【例4】（2020•江苏省盐城市中考第24题）若二次函数y＝ax2+bx+c的图象与x轴有两个交点M（x1，0），N（x2，0）（0＜x1＜x2），且经过点A（0，2）．过点A的直线l与x轴交于点C，与该函数的图象交于点B（异于点A）．满足△ACN是等腰直角三角形，记△AMN的面积为S1，△BMN的面积为S2，且S2=52S1．（1）抛物线的开口方向（填“上”或“下”）；（2）求直线l相应的函数表达式；（3）求该二次函数的表达式．【题组一】1．（2020•雁塔区校级模拟）如图，抛物线C1：y=−12x2+2x+2的顶点为A，且与y轴于点B，将抛物线C1沿y＝a对称后，得到抛物线C2与y轴交于点C．（1）求A、B两点坐标；（2）若抛物线C2上存在点D，使得△BCD为等腰直角三角形，求出此时抛物线C2的表达式．2．（2020•沙坪坝区校级一模）如图1，抛物线y=√24x2+2x﹣6√2交x轴于A、B两点（点A在点B的左侧），交y轴于C点，D点是该抛物线的顶点，连接AC、AD、CD．（1）求△ACD的面积；（2）如图1，点P是线段AD下方的抛物线上的一点，过P作PE∥y轴分别交AC于点E，交AD于点F，过P作PG⊥AD于点G，求EF+√52FG的最大值，以及此时P点的坐标；（3）如图2，在对称轴左侧抛物线上有一动点M，在y轴上有一动点N，是否存在以BN为直角边的等腰Rt△BMN？若存在，求出点M的横坐标，若不存在，请说明理由．3．（2020•陕西模拟）如图，抛物线C的顶点坐标为（2，8），与x轴相交于A，B两点（点A在点B的左侧），与y轴交于点D（0，6）．（1）求抛物线C的函数表达式以及点B的坐标；（2）平移抛物线C，使平移后的抛物线C′的顶点P落在线段BD上，过P作x轴的垂线，交抛物线C 于点Q，再过点Q作QE∥x轴交抛物线C于另一点E，连接PE，若△PQE是等腰直角三角形，请求出所有满足条件的抛物线C′的函数表达式．4．（2019秋•青龙县模拟）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于A，B两点，与y轴交于点C（0，3），且OB＝OC．直线y＝x+1与抛物线交于A、D两点，与y轴交于点E，点Q是抛物线的顶点，设直线AD上方的抛物线上的动点P的横坐标为m．（1）求该抛物线的解析式及顶点Q的坐标．（2）连接CQ，直接写出线段CQ与线段AE的数量关系和位置关系．（3）连接P A、PD，当m为何值时S△APD=12S△DAB？（4）在直线AD上是否存在一点H，使△PQH为等腰直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．【题组二】5．（2020•鹿邑县一模）已知：如图，直线y＝﹣x﹣3交坐标轴于A、C两点，抛物线y＝x2+bx+c过A、C 两点，（1）求抛物线的解析式；（2）若点P为抛物线位于第三象限上一动点，连接P A，PC，试问△P AC的面积是否存在最大值，若存在，请求出△APC面积的最大值，以及此时点P的坐标；若不存在，请说明理由；（3）点M为抛物线上一点，点N为抛物线对称轴上一点，若△NMC是以∠NMC为直角的等腰直角三角形，请直接写出点M的坐标．6．（2020•碑林区校级模拟）抛物线C1：y=−14x2−12x+2交x轴于A、B两点（点A在点B的右侧），与y轴交于点C．（1）求A，B两点的坐标．（2）M为平面内一点，将抛物线C1绕点M旋转180°后得到抛物线C2，C2经过点A且抛物线C2上有一点P，使△BCP是以∠B为直角的等腰直角三角形．是否存在这样的点M？若存在，求出点M的坐标，若不存在，说明理由．7．（2020•灌南县一模）如图，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（﹣1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．（1）求抛物线的解析式和直线BC的解析式；（2）当点P在线段OB上运动时，求线段MN的最大值；（3）当点P在线段OB上运动时，若△CMN是以MN为腰的等腰直角三角形时，求m的值；（4）当以C、O、M、N为顶点的四边形是平行四边形时，直接写出m的值．8．（2019•黄冈中考）如图①，在平面直角坐标系xOy中，已知A（﹣2，2），B（﹣2，0），C（0，2），D （2，0）四点，动点M以每秒√2个单位长度的速度沿B→C→D运动（M不与点B、点D重合），设运动时间为t（秒）．（1）求经过A、C、D三点的抛物线的解析式；（2）点P在（1）中的抛物线上，当M为BC的中点时，若△P AM≌△PBM，求点P的坐标；（3）当M在CD上运动时，如图②．过点M作MF⊥x轴，垂足为F，ME⊥AB，垂足为E．设矩形MEBF 与△BCD重叠部分的面积为S，求S与t的函数关系式，并求出S的最大值；（4）点Q为x轴上一点，直线AQ与直线BC交于点H，与y轴交于点K．是否存在点Q，使得△HOK 为等腰三角形？若存在，直接写出符合条件的所有Q点的坐标；若不存在，请说明理由．【题组三】9．（2019•西藏中考）已知：如图，抛物线y＝ax2+bx+3与坐标轴分别交于点A，B（﹣3，0），C（1，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线解析式；（2）当点P运动到什么位置时，△P AB的面积最大？（3）过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连接DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求点P的坐标；若不存在，说明理由．10．（2018•眉山中考）如图①，已知抛物线y＝ax2+bx+c的图象经过点A（0，3）、B（1，0），其对称轴为直线l：x＝2，过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m．（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；（3）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．11．（2018•德阳中考）如图，在等腰直角三角形ABC中，∠BAC＝90°，点A在x轴上，点B在y轴上，点C（3，1），二次函数y=13x2+bx−32的图象经过点C．（1）求二次函数的解析式，并把解析式化成y＝a（x﹣h）2+k的形式；（2）把△ABC沿x轴正方向平移，当点B落在抛物线上时，求△ABC扫过区域的面积；（3）在抛物线上是否存在异于点C的点P，使△ABP是以AB为直角边的等腰直角三角形？如果存在，请求出所有符合条件的点P的坐标；如果不存在，请说明理由．12．（2018•资阳中考）已知：如图，抛物线y＝ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△P AB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．【题组四】13．（2019•陕西模拟）在平面直角坐标系中，二次函数抛物线y＝ax2+bx+c过点A（﹣1，0）和C（0，3），对称轴为直线x＝1．（1）求二次函数的表达式和顶点M的坐标．（2）将抛物线在坐标平面内平移，使其过原点，若在平移后，第二象限的抛物线上存在点P，使△P AC 为等腰直角三角形，请求出抛物线平移后的表达式，并指出其中一种情况的平移方式．14．（2019•兰州中考）二次函数y＝ax2+bx+2的图象交x轴于点（﹣1，0），B（4，0）两点，交y轴于点C．动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）连接BD，当t=32时，求△DNB的面积；（3）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标；（4）当t=54时，在直线MN上存在一点Q，使得∠AQC+∠OAC＝90°，求点Q的坐标．15．（2020•项城市校级二模）二次函数y＝ax2+bx+2的图象交x轴于点A（﹣1，0），点B（4，0）两点，交y轴于点C．动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）连接BD，当t=32时，求△DNB的面积；（3）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．16．（2020•浙江自主招生）x、y是一个函数的两个变量，若当a≤x≤b时，有a≤y≤b（a＜b），则称此函数为a≤x≤b上的闭函数．如y＝﹣x+3，当x＝1时y＝2；当x＝2时y＝1，即当1≤x≤2时，1≤y≤2，所以y＝﹣x+3是1≤x≤2上的闭函数．（1）请说明y=30x是1≤x≤30上的闭函数；（2）已知二次函数y＝x2+4x+k是t≤x≤﹣2上的闭函数，求k和t的值；（3）在（2）的情况下，设A为抛物线顶点，B为直线x＝t上一点，C为抛物线与y轴的交点，若△ABC 为等腰直角三角形，请直接写出它的腰长为．【题组五】17．（2019秋•南召县模拟）在平面直角坐标系中，直线y=12x﹣2与x轴交于点B，与y轴交于点C，二次函数y=12x2+bx+c的图象经过B，C两点，且与x轴的负半轴交于点A．（1）直接写出：b的值为；c的值为；点A的坐标为；（2）点M是线段BC上的一动点，动点D在直线BC下方的二次函数图象上．设点D的横坐标为m．①如图1，过点D作DM⊥BC于点M，求线段DM关于m的函数关系式，并求线段DM的最大值；②若△CDM为等腰直角三角形，直接写出点M的坐标．18．（2020•濉溪县一模）在平面直角坐标系中，直线y=12x﹣2与x轴交于点B，与y轴交于点C，二次函数y=12x2+bx+c的图象经过B，C两点，且与x轴的负半轴交于点A．（1）求二次函数的解析式；（2）如图1，点M是线段BC上的一动点，动点D在直线BC下方的二次函数图象上．设点D的横坐标为m．①过点D作DM⊥BC于点M，求线段DM关于m的函数关系式，并求线段DM的最大值；②若△CDM为等腰直角三角形，直接写出点M的坐标．19．（2020•石屏县一模）在平面直角坐标系中，二次函数y＝ax2+bx+2的图象与x轴交于A（﹣3，0），B （1，0）两点，与y轴交于点C．（1）求这个二次函数的关系解析式；（2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P 的坐标；若不存在，说明理由；（3）在平面直角坐标系中，是否存在点Q，使△BCQ是以BC为腰的等腰直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；20．（2019•福建中考）已知抛物线y＝ax2+bx+c（b＜0）与x轴只有一个公共点．（1）若抛物线与x轴的公共点坐标为（2，0），求a、c满足的关系式；（2）设A为抛物线上的一定点，直线l：y＝kx+1﹣k与抛物线交于点B、C，直线BD垂直于直线y＝﹣1，垂足为点D．当k＝0时，直线l与抛物线的一个交点在y轴上，且△ABC为等腰直角三角形．①求点A的坐标和抛物线的解析式；②证明：对于每个给定的实数k，都有A、D、C三点共线．。