八年级分式和二次根式综合

填空题1. 有意义的条件是 。

【答案】x ≥4【分析】二次根号内的数必须大于等于零，所以x-4≥0，解得x ≥42. 当__________【答案】-2≤x ≤21【分析】x+2≥0，1-2x ≥0解得x ≥－2，x ≤213. 11m +有意义，则m 的取值范围是 。

【答案】m ≤0且m ≠﹣1【分析】﹣m ≥0解得m ≤0，因为分母不能为零，所以m ＋1≠0解得m ≠﹣14. 当__________x 是二次根式。

【答案】x 为任意实数【分析】﹙1－x ﹚2是恒大于等于0的，不论x 的取值，都恒大于等于0，所以x 为任意实数5. 在实数范围内分解因式：429__________,2__________x x -=-+=。

【答案】﹙x 2＋3﹚﹙x ＋3﹚﹙x －3﹚，﹙x －2﹚2【分析】运用两次平方差公式：x 4－9＝﹙x 2＋3﹚﹙x 2－3﹚＝﹙x 2＋3﹚﹙x ＋3﹚﹙x －3﹚，运用完全平方差公式：x 2－22x ＋2＝﹙x －2﹚26. 2x =，则x 的取值范围是 。

【答案】x ≥0【分析】二次根式开根号以后得到的数是正数，所以2x ≥0，解得x ≥07. 2x =-，则x 的取值范围是 。

【答案】x ≤2【分析】二次根式开根号以后得到的数是正数，所以2－x ≥0，解得x ≤28. )1x p 的结果是 。

【答案】1－x【分析】122+-x x ＝2)1(-x ，因为()21-x ≥0，x ＜1所以结果为1－x9. 当15x ≤p 5_____________x -=。

【答案】4【分析】因为x ≥1所以()21-x ＝1-x ，因为x ＜5所以x －5的绝对值为5－x ，x －1＋5－x ＝410. 把的根号外的因式移到根号内等于 。

【答案】﹣a -【分析】通过a a 1-有意义可以知道a ≤0，a a 1-≤0，所以a a 1-＝﹣⎪⎭⎫ ⎝⎛-⨯a a 12＝﹣a -11. =成立的条件是 。

二次根式的混合运算
本文介绍了二次根式的混合运算，其中重点剖析了有理化因式和分母有理化的方法，以及二次根式混合运算的注意事项。

在计算中，需要注意运算顺序和最简二次根式的表示。

文章提供了典型例题，通过运用相关知识点进行计算。

二次根式的混合运算包括加、减、乘、除和整式的加、减、乘。

在实数范围内，过去学过的运算律仍然适用。

分母有理化的一般方法是用分母的有理化因式同时乘以分子和分母。

二次根式混合运算顺序与实数运算类似，先乘方、再乘除，最后加减，整式与分式的运算法则在根式中仍然适用。

每一个根式可看作是一个“单项式”，多个不是同类二次根式之和可以看成一个多项式，因此多项式乘法法则及乘法公式在根式运算中，仍然适用，以简便计算。

在二次根式的综合运算中，除按运算顺序进行以外，还要注意分式性质的灵活运用。

有理化因式不是唯一的，它可以相差一个常数。

例如，3
的有理化因式可以是3,23,33……但在一般情况下，我们所找
的有理化因式应是最简单的。

一般常见的互为有理化的两个代
数式有如下几种情形：a和a，a+b和a-b，a-b和a+b，ma+nb
和ma-nb。

二次根式的除法一般是先写成分式的形式，然后通
过分母有理化来进行。

典型例题中，例1的计算包括四个部分，分别是(1)、(2)、(3)和(4)。

在计算中，需要注意运用a-b=(a+b)(a-b)、分母有理化、最简二次根式的表示和整式除法法则等知识点。

通过对例题的计算，可以更好地理解二次根式的混合运算。

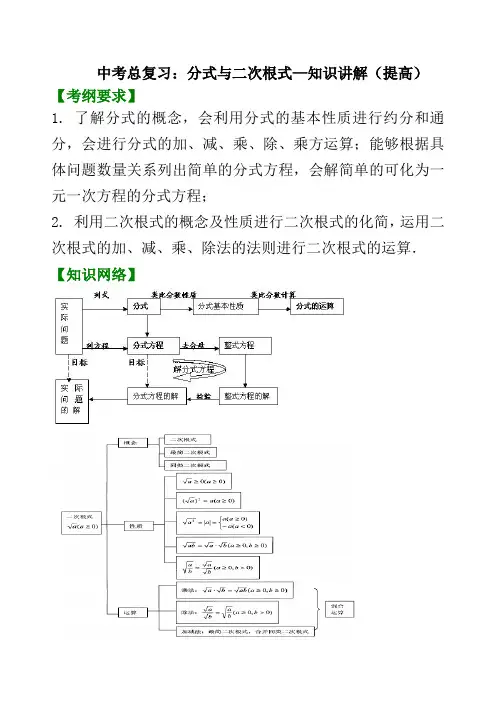
中考总复习：分式与二次根式—知识讲解（提高）【考纲要求】1. 了解分式的概念，会利用分式的基本性质进行约分和通分，会进行分式的加、减、乘、除、乘方运算；能够根据具体问题数量关系列出简单的分式方程，会解简单的可化为一元一次方程的分式方程；2. 利用二次根式的概念及性质进行二次根式的化简，运用二次根式的加、减、乘、除法的法则进行二次根式的运算．【知识网络】【考点梳理】考点一、分式的有关概念及性质1．分式设A、B表示两个整式．如果B中含有字母，式子就叫做分式．注意分母B的值不能为零，否则分式没有意义.2.分式的基本性质（M为不等于零的整式）.3．最简分式分子与分母没有公因式的分式叫做最简分式．如果分子分母有公因式，要进行约分化简.要点诠释：分式的概念需注意的问题：(1)分式是两个整式相除的商，其中分母是除式，分子是被除式，而分数线则可以理解为除号，还含有括号的作用；（2）分式中，A和B均为整式，A可含字母，也可不含字母，但B中必须含有字母且不为0；（3）判断一个代数式是否是分式，不要把原式约分变形，只根据它的原有形式进行判断．（4）分式有无意义的条件：在分式中，①当B≠0时，分式有意义；当分式有意义时，B ≠0．②当B=0时，分式无意义；当分式无意义时，B=0．③当B≠0且A = 0时，分式的值为零．考点二、分式的运算1．基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下:（1）加减运算错误！未找到引用源。

±错误！未找到引用源。

=错误！未找到引用源。

同分母的分式相加减，分母不变，把分子相加减.；异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法则进行计算.（2）乘法运算两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.（3）除法运算两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘.（4）乘方运算（分式乘方）分式的乘方，把分子分母分别乘方．2．零指数.3．负整数指数4．分式的混合运算顺序先算乘方，再算乘除，最后加减，有括号先算括号里面的．5．约分把一个分式的分子和分母的公因式约去，这种变形称为分式的约分．约分需明确的问题：(1)对于一个分式来说，约分就是要把分子与分母都除以同一个因式，使约分前后分式的值相等；(2)约分的关键是确定分式的分子和分母的公因式，其思考过程与分解因式中提取公因式时确定公因式的思考过程相似；在此，公因式是分子、分母系数的最大公约数和相同字母最低次幂的积．6．通分根据分式的基本性质，异分母的分式可以化为同分母的分式，这一过程称为分式的通分．通分注意事项：(1)通分的关键是确定最简公分母；最简公分母应为各分母系数的最小公倍数与所有因式的最高次幂的积．(2)不要把通分与去分母混淆，本是通分，却成了去分母，把分式中的分母丢掉．(3)确定最简公分母的方法：最简公分母的系数，取各分母系数的最小公倍数； 最简公分母的字母，取各分母所有字母因式的最高次幂的积.要点诠释：分式运算的常用技巧（1）顺序可加法：有些异分母式可加,最简公分母很复杂,如果采用先通分再可加的方法很繁琐.如果先把两个分式相加减,把所得结果与第三个分式可加减,顺序运算下去,极为简便.(2)整体通分法：当整式与分式相加减时,一般情况下,常常把分母为1的整式看做一个整体进行通分,依此方法计算,运算简便.(3)巧用裂项法：对于分子相同、分母是相邻两个连续整数的积的分式相加减，分式的项数是比较多的，无法进行通分，因此，常用分式111(1)1n n n n =-++进行裂项. (4)分组运算法: 当有三个以上的异分母分式相加减时,可考虑分组,原则是使各组运算后的结果能出现分子为常数,且值相同或为倍数关系,这样才能使运算简便.(5)化简分式法：有些分式的分子、分母都异常时如果先通分，运算量很大.应先把每一个分别化简，再相加减.（6）倒数法求值（取倒数法）.（7）活用分式变形求值.(8)设k求值法(参数法)(9)整体代换法.(10)消元代入法.考点三、分式方程及其应用1．分式方程的概念分母中含有未知数的方程叫做分式方程．2．分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程．3．分式方程的增根问题(1)增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根---增根；(2)验根：因为解分式方程可能出现增根，所以解分式方程必须验根．验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解．4．分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解．另外，还要注意从多角度思考、分析、解决问题，注意检验、解释结果的合理性．要点诠释：解分式方程注意事项：（1）去分母化成整式方程时不要与通分运算混淆；（2）解完分式方程必须进行检验，验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解．列分式方程解应用题的基本步骤：(1)审——仔细审题，找出等量关系；(2)设——合理设未知数；(3)列——根据等量关系列出方程；(4)解——解出方程；(5)验——检验增根；(6)答——答题．考点四、二次根式的主要性质1.0(0)≥≥；a a2.()2(0)a a a =≥； 3.2(0)||(0)a a a a a a ≥⎧==⎨-<⎩； 4. 积的算术平方根的性质：(00)ab a b a b =⋅≥≥，； 5. 商的算术平方根的性质：(00)a a a b b b =≥>，. 6.若0a b >≥，则a b >. 要点诠释： 与的异同点：（1）不同点：与表示的意义是不同的，表示一个正数a 的算术平方根的平方，而表示一个实数a 的平方的算术平方根；在中，而中a 可以是正实数，0，负实数．但与都是非负数，即，．因而它的运算的结果是有差别的，，而（2）相同点：当被开方数都是非负数，即时，=；时，无意义，而. 考点五、二次根式的运算1．二次根式的乘除运算(1)运算结果应满足以下两个要求：①应为最简二次根式或有理式；②分母中不含根号.(2)注意知道每一步运算的算理；(3)乘法公式的推广：123123123(0000)n n n a a a a a a a a a a a a ⋅⋅⋅⋅=⋅⋅⋅⋅≥≥≥≥，，，，2．二次根式的加减运算先化为最简二次根式，再类比整式加减运算，明确二次根式加减运算的实质；3．二次根式的混合运算(1)对二次根式的混合运算首先要明确运算的顺序，即先乘方、开方，再乘除，最后算加减，如有括号，应先算括号里面的；(2)二次根式的混合运算与整式、分式的混合运算有很多相似之处，整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.要点诠释：怎样快速准确地进行二次根式的混合运算.1.明确运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的；2.在二次根式的混合运算中，原来学过的运算律、运算法则及乘法公式仍然适用；3.在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能收到事半功倍的效果.(1)加法与乘法的混合运算，可分解为两个步骤完成，一是进行乘法运算，二是进行加法运算，使难点分散，易于理解和掌握.在运算过程中，对于各个根式不一定要先化简，可以先乘除，进行约分，达到化简的目的，但最后结果一定要化简. 例如82627⎛⎫+⨯ ⎪ ⎪⎝⎭，没有必要先对827进行化简，使计算繁琐，可以先根据乘法分配律进行乘法运算，884266262327273⎛⎫+⨯=⨯+⨯=+ ⎪ ⎪⎝⎭，通过约分达到化简目的； (2)多项式的乘法法则及乘法公式在二次根式的混合运算中同样适用. 如：()()()()223232321+-=-=，利用了平方差公式. 所以，在进行二次根式的混合运算时，借助乘法公式，会使运算简化.4．分母有理化把分母中的根号化去，分式的值不变，叫做分母有理化.两个含有二次根式的代数式相乘，若它们的积不含二次根式，则这两个代数式互为有理化因式.常用的二次根式的有理化因式：（1）a a 与互为有理化因式；（2）a b a b +-与互为有理化因式；一般地a c b a c b +-与互为有理化因式；（3）a b a b +-与互为有理化因式；一般地c a d b a d b +-与c互为有理化因式.【典型例题】 类型一、分式的意义1．若分式211x x -+的值为0，则x 的值等于 ．【答案】1；【解析】由分式的值为零的条件得2x ﹣1=0，x +1≠0，由2x ﹣1=0，得x =﹣1或x =1，由x +1≠0，得x ≠﹣1， ∴x =1， 故答案为1．【总结升华】若分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．举一反三： 【变式1】如果分式23273x x --的值为0，则x 的值应为 .【答案】由分式的值为零的条件得3x 2-27=0且x-3≠0，由3x 2-27=0，得3（x+3）（x-3）=0， ∴x=-3或x=3， 由x-3≠0，得x≠3． 综上，得x=-3，分式23273x x --的值为0．故答案为：-3．【分式与二次根式 ：例1】 【变式2】若分式mx x +-212不论x 取何实数总有意义，则m 的取值范围是 ．【答案】若分式mx x +-212不论x 取何实数总有意义，则分母22x x m -+≠0，设22y xx m =-+，当△＜0即可，440,1m m -＜＞.答案m ＞1.类型二、分式的性质2．已知,b c c a a b abc+++==求()()()abca b b c c a +++的值.【答案与解析】设b c c a a b k abc+++===,所以,,b c ak c a bk a b ck +=+=+= 所以,b c c a a b ak bk ck +++++=++ 所以2()(),()(2)0,a b c k a b c a b c k ++=++++-= 即2k =或()0,a b c ++= 当2k =,所求代数式33118abc abck k ===, 当0a b c ++=,所求代数式1=-. 即所求代数式等于18或1-.【总结升华】当已知条件以此等式出现时，可用设k 法求解. 举一反三：【变式】已知111111111,,,6915abbcac +=+=+=求abcab bc ac++的值. 【答案】因为 111111111,,,6915abbc a c+=+=+=各式可加得1111112,6915abc ⎛⎫++⨯=++ ⎪⎝⎭所以11131180a b c ++=，所以()1180.111()()31abc abc abc ab bc ac ab bc ac abc c a b÷===++++÷++类型三、分式的运算3．已知1,x y zy z z x x y++=+++且0x y z ++≠,求222x y z y z x z x y +++++的值.【答案与解析】 因为0x y z ++≠,所以原等式两边同时乘以x y z ++,得:()(().x x y z y x y z z x y z x y z y z z x x y++++++++=+++++） 即222()()(),x x y z y y z x z z x y x y z y z y z z x z x x y x y++++++++=++++++++ 所以222(),x y z x y z x y z y z z x x y +++++=+++++ 所以2220.x y z y z z x x y++=+++ 【总结升华】 条件分式的求值，如需把已知条件或所示条件分式变形，必须依据题目自身的特点，这样才能到事半功倍的效果，条件分式的求值问题体现了整体的数学思想和转化的数学思想.举一反三： 【变式1】已知,,,x y z a b c y z x z x y ===+++且abc o ≠,求111a b ca b c +++++的值. 【答案】由已知得1,y z a x+=所以111,y z x y z a x x ++++=+=即1a x y za x+++=,所以1a xa x y z=+++,同理,,11b y c z b x y z c x y z==++++++ 所以1111a b c x y z x y z a b c x y z x y z x y z x y z++++=++==+++++++++++. 【分式与二次根式：例2】【变式2】已知x ＋y=－4，xy=－12，求+++11x y 11++y x 的值．【答案】原式)1)(1()1()1(22+++++=y x x y =1121222++++++++y x xy x x y y 1)(2)(22)(2++++++-+=y x xy y x xy y x 将x ＋y ＝－4，xy ＝－12代入上式， ∴原式⋅-=+--+-⨯++-=153414122)4(224)4(2类型四、分式方程及应用4．a 何值时,关于x 的方程223242ax x x x +=--+会产生增根? 【答案与解析】方程两边都乘以(2)(2)x x +-,得2(2)3(2).x ax x ++=- 整理得(1)10a x -=-. 当a = 1 时,方程无解. 当1a ≠时,101x a =--. 如果方程有增根,那么(2)(2)0x x +-=,即2x =或2x =-.当2x =时,1021a -=-,所以4a =-; 当2x =-时,1021a -=--,所以a = 6 .所以当4a =-或a = 6原方程会产生增根.【总结升华】 因为所给方程的增根只能是2x =或2x =-，所以应先解所给的关于x 的分式方程，求出其根，然后求a 的值.5．甲．乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲．乙 共同整理20分钟后，乙需再单独整理20分钟才能完工． （1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？【答案与解析】（1）设乙单独整理x 分钟完工，根据题意得：120204020=++x解得x ＝80，经检验x ＝80是原分式方程的解． 答：乙单独整理80分钟完工． （2）设甲整理y 分钟完工，根据题意，得1408030≥+y 解得：y ≥25答：甲至少整理25分钟完工．【总结升华】分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．此题等量关系比较多，主要用到公式：工作总量＝工作效率×工作时间． （1）将总的工作量看作单位1，根据本工作分两段时间完成列出分式方程解之即可；（2）设甲整理y 分钟完工，根据整理时间不超过30分钟，列出一次不等式解之即可． 举一反三：【变式】小明乘出租车去体育场，有两条路线可供选择：路线一的全程是25千米，但交通比较拥堵，路线二的全程是30千米，平均车速比走路线一时的平均车速能提高80%，因此能比走路线一少用10分钟到达．若设走路线一时的平均速度为x 千米/小时，根据题意，得（ ） A ．00253010(18060xx -=+）B ．00253010(180xx-=+）C ．00302510(18060x x -=+） D ．00302510(180x x -=+）【答案】设走路线一时的平均速度为x 千米/小时，00253010(18060x x -=+）故选A ．类型五、二次根式的定义及性质6．要使式子aa 2+有意义，则a 的取值范围为 ．【答案】a≥－2且a≠0．【解析】根据题意得：a+2≥0且a≠0，解得：a≥－2且a≠0． 故答案为：a≥－2且a≠0．【总结升华】本题考查的考点为：分式有意义，分母不为0；二次根式的被开方数是非负数．可以求出x 的范围．类型六、二次根式的运算 【分式与二次根式 ：例3】7．（2015春•泗阳县期末）已知m是的小数部分．（1）求m2+2m+1的值；（2）求的值．【答案与解析】解：依题意得21m=-，则121=+m（1）原式=（m+1）2=2；（2）原式=|1m-|=|﹣1﹣（21+）|=2．m【总结升华】此题考查二次根式的化简求值，掌握完全平方公式和无理数的估算是解决问题的关键．举一反三：【变式】（2018•苏州模拟）计算：．【答案与解析】解：原式=﹣+2=4﹣+2=4+．。

数学知识点二次根式与分式的运算数学知识点：二次根式与分式的运算在数学中，二次根式与分式是常见的运算形式。

二次根式表示被开方数的平方根，而分式则表示数之间的比值。

正确地运用二次根式与分式的运算规则，能够更高效地解决问题。

本文将详细介绍二次根式与分式的运算方法和规则。

一、二次根式的运算二次根式是形如√a的表达式，其中a为非负实数。

在运算二次根式时，常见的操作有合并同类项、分解因式、有理化等。

1. 合并同类项合并同类项是将同一根号内的数合并，然后再进行开方。

例如：√9 + √4 = √(9+4) = √132. 分解因式分解因式是将根号内的数按照倍数的形式分解，以便于提取出根号外的因式。

例如：√12 = √(4×3) = √4 × √3 = 2√33. 有理化有理化是将二次根式中含有根号的分母进行处理，使其变为分母不含根号的形式。

例如：1/√2 = (1/√2) × (√2/√2) = √2/2二、分式的运算分式是形如a/b的表达式，其中a为分子，b为分母。

分式的运算包括四则运算、化简、通分、约分等。

1. 四则运算分式的四则运算与整数的四则运算类似，根据需要进行加、减、乘、除的操作。

例如：(1/2) + (1/3) = (3/6) + (2/6) = 5/62. 化简化简是将分式的分子与分母进行约分，使其达到最简形式。

例如：4/8 = (4÷4) / (8÷4) = 1/23. 通分通分是将分式的分母化为相同的公共分母，以便于进行加减运算。

例如：(1/2) + (1/3) = (3/6) + (2/6) = 5/64. 约分约分是将分数的分子与分母进行化简，使其达到最简形式。

例如：4/8 = (4÷4) / (8÷4) = 1/2三、综合运算在实际问题中，常常需要综合运用二次根式与分式的运算。

例如：例1：计算√(5+2√6) × √(5-2√6) 的值。

二次根式与分式的综合运用在数学学习中，二次根式与分式是两个重要的概念。

它们在解决实际问题时起到了至关重要的作用。

本文将探讨二次根式与分式的综合运用，揭示其在问题求解中的实际应用。

一、二次根式的综合运用二次根式是指形如√a的表达式，其中a是一个非负实数。

二次根式的运用非常广泛，无论是在几何学还是物理学中，都有其独特的应用。

1. 几何学中的二次根式在几何学中，二次根式被广泛运用于计算图形的周长、面积等属性。

以正方形为例，对于一个边长为a的正方形，其周长可以表示为4a，而面积可以表示为a²。

当我们需要计算边长或面积时，如果给定了周长或面积的数值，就需要通过解二次根式方程来求解。

例如，一块土地的周长为16米，我们需要计算其面积。

假设土地的边长为x，则方程可以表示为4x=16。

通过解方程4x=16，我们可以得到x=4，即土地的边长为4米。

进而，我们可以计算出土地的面积为16平方米。

2. 物理学中的二次根式在物理学领域，二次根式也有广泛的应用。

例如，在求解自由落体问题中，如果知道物体自由落体的时间t，可以通过二次根式来求解它的下落距离。

根据物理学的公式，自由落体的下落距离可以表示为s=1/2gt²，其中g是重力加速度。

如果给定时间t的数值，我们可以通过求解二次根式来计算下落的距离s。

例如，如果一个物体自由落体的时间为2秒，且重力加速度为10米/秒²，我们可以通过计算s=1/2×10×(2²)得出下落的距离为20米。

二、分式的综合运用分式是指形如a/b的表达式，其中a和b都是整数且b不等于零。

分式在数学中广泛应用于比例、概率等问题的解决。

1. 比例中的分式在比例问题中，分式被广泛运用于表示两个量之间的关系。

例如，在解决类似于“甲车每小时行驶100公里，乙车每小时行驶120公里，两车同时出发，多长时间后它们之间的距离将为200公里”的问题时，我们可以通过设置分式来解决。

二次根式1、算术平方根的定义：一般地，如果一个正数x的平方等于a，那么这个正数x叫做a的算术平方根。

2、解不等式（组）：尤其注意当不等式两边乘(除以)同一个负数，不等号方向改变。

如：-2x＞4，不等式两边同除以-2得x＜-2。

不等式组的解集是两个不等式解集的公共部分。

如｛3、分式有意义的条件：分母≠04、绝对值：｜a｜=a （a≥0）；｜a｜= - a （a＜0）一、二次根式的概念一般地，我们把形如 a （a≥0）的式子叫做二次根式，“”称为二次根号。

★正确理解二次根式的概念，要把握以下五点：（1）二次根式的概念是从形式上界定的，必须含有二次根号“”，“”的根指数为2，即“2”，我们一般省略根指数2，写作“”。

如25 可以写作 5 。

（2）二次根式中的被开方数既可以是一个数，也可以是一个含有字母的式子。

（3）式子 a 表示非负数a的算术平方根，因此a≥0， a ≥0。

其中a≥0是 a 有意义的前提条件。

（4）在具体问题中，如果已知二次根式 a ，就意味着给出了a≥0这一隐含条件。

（5）形如b a （a≥0）的式子也是二次根式，b与 a 是相乘的关系。

要注意当b是分数时不能写成带分数，例如832 可写成8 23，但不能写成 2232 。

练习：一、判断下列各式，哪些是二次根式？（1） 6 ；（2）-18 ；（3）x2+1 ；（4）3-8 ；（5）x2+2x+1 ；（6）3｜x｜；（7）1+2x （x＜-12）X≥-2X＜5的解集为-2≤x＜5。

二、当x 取什么实数时，下列各式有意义？（1）2-5x ；（2）4x 2+4x+1二、二次根式的性质：二次根式的性质符号语言文字语言应用与拓展注意a （a ≥0）的性质a ≥0 （a ≥0）一个非负数的算术平方根是非负数。

（1）二次根式的非负性（a ≥0，a ≥0）应用较多，如：a+1 +b-3 =0，则a+1=0，b-3=0，即a= -1，b=3；又如x-a +a-x ，则x 的取值范围是x-a ≥0，a-x ≥0，解得x=a 。

○热○点○考○点○解○读一、整式1．单项式与多项式单独的一个数或一个字母也是单项式．2．合并同类项合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母连同它的指数不变，例如：合并同类项3x 2y 和4x 2y 为3x 2y +4x 2y =（3+4）x 2y =7x 2y ．3．整式的运算（1）整式的加减运算实际就是合并同类项．（2）整式的乘法：()()a b m n am an bm bn ++=+++．（3）整式的除法：单项式除以单项式时，把系数、相同字母的幂分别相除，作为商的因式，对于只在被除式中含有的字母，则照抄下来；多项式除以单项式时，用多项式的每一项分别除以单项式，再把所得的商相加．（4）乘法公式①平方差公式：22()()a b a b a b +-=-．②完全平方公式：222()2a b a ab b ±=±+．4．幂的运算性质（1）同底数幂相乘法则：m n m n a a a +⋅=（,m n 为整数，0a ≠）（2）幂的乘方法则：()m n mn a a =（,m n 为整数，0a ≠）（3）积的乘方法则：()n n n ab a b =（n 为整数，0ab ≠）整式、分式、二次根式、因式分解常识必背语言叙述：两个数的平方和加上（或减去）这两个数的积的2倍，等于这两个数的和（或差）的平方．5．用十字相乘法分解因式利用十字相乘法分解因式，实质上是逆用（ax ＋b ）（cx ＋d ）乘法法则．它的一般规律是：（1）对于二次项系数为1的二次三项式，如果能把常数项q 分解成两个因数a ，b 的积，并且a ＋b 为一次项系数p ，那么它就可以运用公式（2）对于二次项系数不是1的二次三项式（a ，b ，c 都是整数且a ≠0）来说，如果存在四个整数，使，，且，那么．一个式子是分式需满足的三个条件：q px x ++2))(()(2b x a x ab x b a x ++=+++c bx ax ++22121,,,c c a a a a a =⋅21c c c =⋅21b c a c a =+1221c bx ax ++2))(()(2211211221221c x a c x a c c x c a c a x a a ++=+++=易错易混2．约分（1）分式约分时，要注意不注意符号导致的错误．（2）要注意约分不彻底导致的错误．（3）约分时需注意分式的分子、分母都是乘积形式时才能进行约分；分子、分母是多项式时，通常先将分子、分母分解因式，再约分．（4）约分的结果是整式或最简分式．（5）分式的约分是恒等变形，约分前后分式的值不变．3．分解因式要彻底．方法必知1．同类项（1）几个项是不是同类项，一看所含字母是否完全相同．二看相同字母的指数是否相同．“二同”缺一不可．（2）同类项与单项式的系数无关，与字母顺序无关，几个常数项也是同类项．（3）同类项不一定是两项，也可以是三项，四项……但至少为两项．2．合并同类项（1）合并同类项时，注意合并的只是系数，字母部分不变，不要漏掉．（2）合并同类项时，注意各项系数的符号，尤其系数为负数时，不要遗漏负号，同时不要丢项．（3）如果两个同类项的系数互为相反数，合并同类项的结果为0．3．整式的加减的最后结果的要求：（1）不能含有同类项，即要合并到不能再合并为止；（2）一般按照某一字母的降幂或升幂排列；（3）不能出现带分数，带分数必须要化为假分数．4．整式的化简求值（1）化简求值题一般先按整式的运算法则进行化简，然后再代入求值．（2）在求整式的值时，代入负数时应用括号括起来，作为底数的分数也应用括号括起来5．约分时需要注意的问题：（1）如果分子、分母中至少有一个是多顶式，就应先分解因式，然后找出分子、分母的公因式，再约分．（2）注意发现分式的分子和分母的一些隐含的公因式，如a﹣5与5﹣a表面虽不相同，但通过提取“﹣”可发现含有公因式（a﹣5）．（3）当分式的分子或分母的系数是负数时，可利用分式的基本性质，把负号提到分式的前面．通分时确定了分母乘什么，分子也必须随之乘什么，要防止只对分母变形而忽略了分子，导致变形前后分式的值发生变化而出错．6．分式的混合运算，关键是弄清运算顺序，与分数的加、减、乘、除及乘方的混合运算一样，先算乘方，再算乘除，最后算加减，有括号要先算括号里面的，在运算过程中要注意正确地运用运算法则，灵活地运用运算律，使运算尽量简便．7．因式分解（1）因式分解是针对多项式而言的，一个单项式本身就是数与字母的积，不需要再分解因式；（2）因式分解的结果是整式的积的形式，积中几个相同因式的积要写成幂的形式；（3）因式分解必须分解到每一个因式都不能再分解为止；（4）因式分解与整式乘法是方向相反的变形，二者不是互为逆运算．因式分解是一种恒等变形，而整式乘法是一种运算．8．提公因式法（1）多项式的公因式提取要彻底，当一个多项式提取公因式后，剩下的另一个因式中不能再有公因式．（2）提公因式后括号内的项数应与原多项式的项数一样．（3）若多项式首项系数为负数时，通常要提出负因数．9．十字相乘法这类式子在许多问题中经常出现，其特点是：（1）二次项系数是1；（2）常数项是两个数之积；（3）一次项系数是常数项的两个因数之和．◇以◇练◇带◇学1．（鞍山）下列运算正确的是( )A ．222(4)8ab a b =B ．22423a a a +=C ．642a a a ÷=D ．222()a b a b +=+2．（攀枝花）我们可以利用图形中的面积关系来解释很多代数恒等式．给出以下4组图形及相应的代数恒等式：其中，图形的面积关系能正确解释相应的代数恒等式的有( )A ．1个B ．2个C ．3个D ．4个3．（邵阳）下列计算正确的是( )A ．623a a a =B ．235()a a =C ．22()()a ba ba b a b +=+++D ．01()13-=4．（内蒙古）下列运算正确的是( )A+=B ．236()a a -=C ．11223a a a+=D ．21133b ab a b÷=5．（成都）若23320ab b --=，则代数式2222(1)ab b a ba a b---÷的值为 ．6．x 的取值范围是 ．7．（扬州）分解因式：24xy x -= ．8．（内蒙古）分解因式：34x x -= ．9．（盐城）先化简，再求值：2(3)(3)(3)a b a b a b +++-，其中2a =，1b =-．10．（滨州）先化简，再求值：22421()244a a a a a a a a -+-÷---+，其中a 满足211(6cos6004a a --⋅+︒=．1．（官渡区校级模拟）按一定规律排列的式子：a ，32a ，54a ，78a ，916a ，⋯，则第2024个式子为( )A ．202320252a B ．20244047(21)a -C ．202340472a D ．202440492a 2．（济南一模）下列运算正确的是( )A ．22a b ab+=B ．2222a b a b a b-=C ．238()a a =D ．84222a a a ÷=3．（金山区二模）单项式22a b -的系数和次数分别是( )A ．2-和2B ．2-和3C ．2和2D ．2和34．（龙岗区模拟）下列计算正确的是( )A ．236a a a ⋅=B ．2323a a a +=C ．2234(3)218ab ab a b -⋅=-D ．326(2)3ab ab b ÷-=-5．（中山市校级一模）下列各式从左到右的变形，因式分解正确的是( )A ．2()a a b a ab+=+B ．23()3a ab a a b +-=+-C ．22282(4)ab a a b -=-D ．228(2)(4)a a a a --=+-6．（钱塘区一模）下列因式分解正确的是( )A ．241(41)(41)a a a -=+-B ．225(5)(5)a a a -+=+-C ．22269(3)a ab b a b --=-D ．22816(8)a a a -+=-7．（新乡一模）化简2422a a a ---的结果是( )A ．2a +B ．2a -C ．12a +D ．12a -8．（东莞市校级模拟）分式23x x --的值为0时，x 的值是( )A ．0x =B ．2x =C ．3x =D ．2x =或3x =9．（碑林区校级一模）先化简，再求值：2[(2)(2)(2)](4)a b b a b a a --+-÷，其中12a =，2b =．10．（龙湖区校级一模）先化简，再求值：2344(111x x x x -+-÷++，其中3x =．1．按一定规律排列的单项式：3x ，54x -，79x ，916x -，⋯，第n 个单项式是( )A ．1221(1)n n n x ---B ．1221(1)n n n x ++-C ．1221(1)(1)n n n x ---+D ．1221(1)(1)n n n x ++-+2．下列运算正确的是( )A ．22(4)16x x -=-B ．325x y xy +=C ．432x x x ÷=D ．2224()xy x y =3．下列语句正确的是( )A ．5-不是单项式B ．a 可以表示负数C ．25a b -的系数是5，次数是2D ．221a ab ++是四次三项式4．下列因式分解正确的一项是( )A ．222()x y x y +=+B ．24(2)(2)x x x -=+-C ．2221(1)x x x --=-D ．242(2)xy x xy x +=+5．要使分式11x x -+有意义，则x 应满足的条件是( )A ．1x ≠-B ．1x ≠C ．1x <-D ．1x >-6．下列二次根式中，属于最简二次根式的是( )AB C D7．计算：0|1tan 60|(2024-︒+．8．先化简，再求值：2344(111x x x x -+-÷++，其中3x =．9．先化简，再求值：2(2)(4)a a a -++，其中a =．10．先化简，再求值：(2)(2)4()a b a b a a b -+--，其中2a =-，1b =．1．【答案】C【分析】根据积的乘方，合并同类项，同底数幂的除法法则，完全平方公式进行计算，逐一判断即可解答．【解答】解：A 、222(4)16ab a b =，故A 不符合题意；B 、22223a a a +=，故B 不符合题意；C 、642a a a ÷=，故C 符合题意；D 、222()2a b a ab b +=++，故D 不符合题意；故选：C ．2．【答案】D【分析】观察各个图形及相应的代数恒等式即可得到答案．【解答】解：图形的面积关系能正确解释相应的代数恒等式的有①②③④，故选：D ．3．【答案】D【分析】分别根据分式的加减法则、幂的乘方与积的乘方法则、零指数幂的运算法则对各选项进行逐一计算即可．【解答】解：A 、633a a a=，原计算错误，不符合题意；B 、236()a a =，原计算错误，不符合题意；C 、221()()a b a b a b a b+=+++，原计算错误，不符合题意；D 、01()13-=，正确，符合题意．故选：D ．4．【答案】D【分析】根据二次根式的加法、幂的乘法与积的乘方以及分式的运算的计算方法解题即可．【解答】解：A +=≠B ．2366()a a a -=-≠，故该选项不正确，不符合题意；C ．11123222223a a a a a a+=+=≠，故该选项不正确，不符合题意；21131.333b a D ab a ab b b ÷=⨯=，故该选项正确，符合题意；故选：D ．5．【答案】23．【分析】先根据分式的减法法则进行计算，再根据分式的除法法则把除法变成乘法，算乘法，最后代入求出答案即可．【解答】解：2222(1ab b a b a a b---÷2222(2)a ab b a b a a b--=⋅-222()a b a b a a b-=⋅-()b a b =-2ab b =-，23320ab b --= ，2332ab b ∴-=，223ab b ∴-=，∴原式23=．故答案为：23．6．【答案】3x >．【分析】根据记二次根式的被开方数是非负数、分母不为0列出不等式，解不等式得到答案．【解答】解：由题意得：30x ->，解得：3x >，故答案为：3x >．7．【分析】原式提取x ，再利用平方差公式分解即可．【解答】解：原式2(4)(2)(2)x y x y y =-=+-，故答案为：(2)(2)x y y +-8．【分析】应先提取公因式x ，再对余下的多项式利用平方差公式继续分解．【解答】解：34x x -，2(4)x x =-，(2)(2)x x x =+-．故答案为：(2)(2)x x x +-．9．【分析】依据题意，利用平方差公式和完全平方公式将原式进行化简，再将a ，b 的值代入计算即可求解．【解答】解：2(3)(3)(3)a b a b a b +++-2222699a ab b a b =+++-226a ab =+．当2a =，1b =-时，原式22262(1)=⨯+⨯⨯-812=-4=-．10．【答案】244a a -+，1．【分析】将括号里面通分运算，再利用分式的混合运算法则计算，结合负整数指数幂的性质、特殊角的三角函数值化简，整体代入得出答案．【解答】解：原式2421[(2)(2)a a a a a a a -+-=÷---224(2)(2)(1)[](2)(2)a a a a a a a a a a -+--=÷---22244(2)a a a a a a a ---+=÷-24(2)4a a a a a --=⋅-2(2)a =-244a a =-+， 211()6cos6004a a --⋅+︒=，2430a a ∴-+=，243a a ∴-=-，∴原式341=-+=．1．【答案】C【分析】由题目可得式子的一般性规律：第n 个式子为：1212n n a --⋅，当2024n =时，第2024个式子为：202340472a ⋅，即可得出答案．【解答】解：式子的系数为1，2，4，8，16， ，则第n 个式子的系数为：12n -；式子的指数为1，3，5，7，9， ，则第n 个式子的指数为：21n -，∴第n 个式子为：1212n n a --⋅，当2024n =时，第2024个式子为：202340472a ⋅，故选：C ．2．【答案】B【分析】根据合并同类项法则、幂的乘方法则、单项式除以单项式法则分别判断即可．【解答】解：A 、2a 与b 不是同类项，不能合并，故此选项不符合题意；B 、2222a b a b a b -=，故此选项符合题意；C 、236()a a =，故此选项不符合题意；D 、84422a a a ÷=，故此选项不符合题意；故选：B．3．【答案】B【分析】数字与字母的积叫做单项式，其中数字因数叫做单项式的系数，所有字母的指数之和叫做单项式的次数；由此计算即可．【解答】解：单项式22a b -的系数和次数分别是2-和3，故选：B ．4．【答案】D【分析】根据整式相关运算法则逐项判断即可．【解答】解：235a a a ⋅=，故A 错误，不符合题意；a 与22a 不能合并，故B 错误，不符合题意；2234(3)218ab ab a b -⋅=，故C 错误，不符合题意；326(2)3ab ab b ÷-=-，故D 正确，符合题意；故选：D ．5．【答案】D【分析】根据因式分解的定义逐个判断即可．【解答】解：A ．从左到右的变形属于整式乘法，不属于因式分解，故本选项不符合题意；B ．从左到右的变形不属于因式分解，故本选项不符合题意；C ．22282(4)2(2)(2)ab a a b a b b -=-=+-，分解不彻底，从左到右的变形不属于因式分解，故本选项不符合题意；D ．从左到右的变形属于因式分解，故本选项符合题意．故选：D ．6．【答案】B【分析】根据平方差公式和完全平方公式逐个判断即可．【解答】解：A ．241(21)(21)a a a -=+-，故本选项不符合题意；B ．225(5)(5)a a a -+=+-，故本选项符合题意；C ．22269(3)a ab b a b -+=-，故本选项不符合题意；D ．22816(4)a a a -+=-，故本选项不符合题意；故选：B ．7．【答案】A【分析】根据分式的加减法运算法则计算即可．【解答】解：2244(2)(2)22222a a a a a a a a a --+-===+----，故选：A ．8．【分析】分式的值为零时：分子等于零且分母不为零．据此求得x 的值．【解答】解：依题意得：20x -=，解得2x =．经检验当2x =时，分母30x -≠，符合题意．故选：B ．9．【答案】2a b -，1-．【分析】先利用平方差公式和完全平方公式进行计算，再根据多项式除以单项式的法则进行计算，最后把12a =，2b =代入计算即可．【解答】解：原式2222[44(4)](4)a ab b b a a =-+--÷2222(444)(4)a ab b b a a =-+-+÷2(84)(4)a ab a =-÷2a b =-，当12a =，2b =时，原式12212=⨯-=-．10．【答案】12x -，1．【分析】先算小括号里面的，然后算括号外面的，最后代入求值．【解答】解：原式213(2)()111x x x x x +-=-÷+++2211(2)x x x x -+=⋅+-12x =-，当3x =时，原式1132==-．1．【答案】B【分析】根据单项式的数字系数的符号，数字系数和指数的变化规律即可得出结果．【解答】解：在上述单项式中，可以发现：奇数项的数字系数的符号为正，偶数项的数字系数的符号为负，∴可得：第n 个单项式的数字系数的符号为：1(1)n --或1(1)n +-，单项式的数字系数为：1，4，9，16， ，∴第n 个单项式的数字系数为：2n ，单项式的指数为：3，5，7，9， ，∴第n 个单项式的指数为：21n +，∴第n 个单项式是1221(1)n n n x ++-，故选：B ．2．【答案】D【分析】根据整式的运算法则逐项分析判断即可．【解答】解：A 、22(4)816x x x -=-+，原计算错误，不符合题意；B 、3x 与2y 不是同类项，不能合并，故原计算错误，不符合题意；C 、43x x x ÷=，原计算错误不符合题意；D 、2224()xy x y =，正确，符合题意；故选：D ．3．【答案】B【分析】根据单项式的定义可判断A ，根据字母表示数的意义可判断B ，根据单项式系数和次数的定义可判断C ，根据多项式的项和次数的定义可判断D ，进而可得答案．【解答】解：A 、5-是单项式，故本选项错误，不符合题意；B 、a可以表示负数，故本选项正确，符合题意；C 、25a b -的系数是5-，次数是3，故本选项错误，不符合题意；D 、221a ab ++是二次三项式，故本选项错误，不符合题意；故选：B ．4．【答案】B【分析】根据因式分解的定义进行判断即可．【解答】解：A 、222()x y x y +≠+不符合因式分解的定义，故本选项不符合题意；B 、24(2)(2)x x x -=+-符合因式分解的定义，且因式分解正确，故本选项符合题意；C 、2221(1)x x x --≠-，不符合因式分解的定义，故本选项不符合题意；D 、242(2)xy x x y +=+，原因式分解错误，故本选项不符合题意；故选：B ．5．【分析】先根据分式有意义的条件列出关于x 的不等式，求出x 的取值范围即可．【解答】解：由题意，得10x +≠，解得1x ≠-，故选：A ．6．【分析】直接利用最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式．我们把满足上述两个条件的二次根式，叫做最简二次根式，进而得出答案．【解答】解：A =，不是最简二次根式，故此选项错误；B ，是最简二次根式，故此选项正确；C 2=，不是最简二次根式，故此选项错误；D =故选：B ．7．．【分析】根据二次根式的混合运算法则和零指数幂与特殊的三角函数值等知识点计算即可．【解答】解：原式11=---+11=-+=．8．【答案】12x -，1．【分析】先算小括号里面的，然后算括号外面的，最后代入求值．【解答】解：原式213(2)()111x x x x x +-=-÷+++2211(2)x x x x -+=⋅+-12x =-，当3x =时，原式1132==-．9．【答案】224a +，原式8=．【分析】先利用完全平方公式，单项式乘多项式的法则进行计算，然后把a 的值代入化简后的式子进行计算，即可解答．【解答】解：2(2)(4)a a a -++22444a a a a=-+++224a =+，当a =224224448=⨯+=⨯+=+=．10．【答案】24ab b -，原式9=-．【分析】先利用平方差公式，单项式乘多项式的法则进行计算，然后把a ，b 的值代入化简后的式子进行计算，即可解答．【解答】解：(2)(2)4()a b a b a a b -+--222444a b a ab=--+24ab b =-，当2a =-，1b =时，原式24(2)11819=⨯-⨯-=--=-．。

专题03 分式与二次根式综合过关检测（考试时间：90分钟，试卷满分：100分）一、单选题(每小题2分，共24分)A ．32x -=-B ．()3212x x --=-C ．()3212x x --=D ．632x x --=-8．《九章算术》中记录的一道题译为白话文是：把一封信件用慢马送到1000里外的城市，需要的时间比规定时间多2天；若用快马送，所需的时间比规定时间少3天，已知快马的速度是慢马的2倍．小明认为规定的时间为7天，小亮认为规定的时间为8天，关于两个人的观点，下列说法正确的是（ ） A ．小明的观点正确B ．小亮的观点正确C ．两人的观点都不正确D ．无法确定9．某农场开挖一条长480米的渠道，开工后每天比原计划多挖20米，结果提前4天完成任务，若设原计10．马站四季柚名扬天下，2023年第一季度某农户生产红心柚质量是白心柚的2倍，其中红心柚销售收入18000元，白心柚销售收入7800元，白心柚比红心柚价格每斤少3元.设白心柚价格x元/斤，则下列方程正11．某中学为使初三学生在中考体育测试中取得优异的成绩，在4月初安排全校体育教师对初三全体学生进行了一次模拟检测，在这一次检测中，甲组教师完成300个学生检测，乙组教师完成270个学生检测；已知甲组教师比乙组教师平均每分钟多检测4个学生，所用时间比乙组教师少用30分钟，求本次检测中甲、12．《四元玉鉴》是一部成就辉煌的数学名著，是宋元数学集大成者，也是我国古代水平最高的一部数学著作．该著作记载了“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽” ．大意是：现请人代买一批椽，这批椽的总售价为6210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设6210文购买椽的数量为x二、填空题（每小题3分，共36）三、解答题（每题9分，共27分）26．学校组织学生到距离为15千米的公园参加露营活动，一部分同学骑自行车先走，40分钟后，其余同学乘坐大巴前往，结果他们同时到达．如果大巴的平均速度是自行车平均速度的3倍，那么自行车的平均速度是多少？27．在国庆节期间，学校举行了诗歌朗诵等系列活动，嘉嘉和淇淇负责为班级参赛学生购置纪念品．他们发现，一个笔记本比一支钢笔贵3元，用225元购买的笔记本数量与用180元购买的钢笔数量相同．(1)笔记本和钢笔的单价各多少元？(2)若给参赛的30名学生每人发放一个笔记本或一支钢笔作为活动纪念品，要使购买纪念品的总费用不超过380元，最多可以购买多少个笔记本？++2018。

最新人教版八年级数学下册二次根式知识点归纳及题型总结二次根式知识点归纳和题型归类一、知识框图二、知识要点梳理知识点一、二次根式的主要性质：1.二次根式的定义：形如$\sqrt{a}$（$a\geq 0$）的式子叫做二次根式。

2.二次根式的双重非负性：$\sqrt{a}\geq 0$，即一个非负数的算术平方根是一个非负数。

3.二次根式的同底同指数相加减：$\sqrt{a}+\sqrt{b}=\sqrt{a+b}$，$\sqrt{a}-\sqrt{b}=\sqrt{a-b}$。

4.积的算术平方根的性质：$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}$。

5.商的算术平方根的性质：$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$（$b\neq 0$）。

6.若$a\geq 0$，则$\sqrt{a^2}=|a|$。

知识点二、二次根式的运算1.二次根式的乘除运算1) 运算结果应满足以下两个要求：①应为最简二次根式或有理式；②分母中不含根号。

2) 注意每一步运算的算理。

3) 乘法公式的推广：$(\sqrt{a}\pm\sqrt{b})^2=a+b\pm2\sqrt{ab}$。

2.二次根式的加减运算：先化简，再运算。

3.二次根式的混合运算1) 明确运算的顺序，即先乘方、开方，再乘除，最后算加减，有括号先算括号里。

2) 整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用。

例题：1.下列各式中一定是二次根式的是（）。

A。

$-3$；B。

$x$；C。

$x^2+1$；D。

$x-1$2.$x$取何值时，下列各式在实数范围内有意义。

1）$\sqrt{-15+x}$；（2）$\frac{1}{\sqrt{x+4}}$3）$\sqrt{x+4}+\sqrt{2x+1}$；（4）$\sqrt{x+1}-\sqrt{x}$5）$3-\sqrt{x+1}$；（6）$\frac{2x}{\sqrt{x+1}}$7）若$x(x-1)=\frac{1}{4}$，则$x$的取值范围是（）。

专题01 二次根式的有关概念和性质【思维导图】◎考点题型1 求二次根式的值例．（2022·浙江·九年级专题练习）当0x =时, ）A ．4B ．2CD ．0【答案】B 【解析】 【分析】把0x = 【详解】解：把0x =2= 故选：B ． 【点睛】本题考查了二次根式的定义和二次根式的性质,能灵活运用二次根式的性质进行计算是解题的关键．变式1．（2020·山东定陶·八年级期末）当 x ＝－3 时, ）A ．3B ．－3C ．±3D 【答案】A【分析】把x ＝－3代入二次根式进行化简即可求解. 【详解】解：当x ＝－3时3=. 故选A. 【点睛】本题考查了二次根式的计算,正确理解算术平方根的意义是关键. 变式2．（2020·北京·一模）如果31a ,那么代数式21(1)11aa a +÷--的值为（ ）A ．3BCD 2【答案】B 【解析】 【分析】先根据分式的混合运算法则化简原式,再把a 的值代入化简后的式子计算即可． 【详解】 解：原式=()()111a a a a a ÷--+=()()1111a a a a a a-+⨯=+-；当31a时,原式11+=故选：B ． 【点睛】本题考查了分式的化简求值,属于常考题型,熟练掌握分式的混合运算法则是解题关键．变式3．（2020·湖北鄂城· ）A B ．2 C ．22 D ．2±【答案】B 【解析】 【分析】根据乘方和开方的运算法则进行计算即可． 【详解】2=故答案为：B ．本题考查了开方和乘方的运算问题,掌握乘方和开方的运算法则是解题的关键．◎考点题型2 求二次根式中的参数例．（山东阳谷·,则正整数n的最小值是（）A．2B．4C．6D．8【答案】C【解析】【分析】,=则6n是完全平方数,满足条件的最小正整数n为6．【详解】解：24n=,∴,即6n是完全平方数；∴n的最小正整数值为6．故选：C．【点睛】本题主要考查了二次根式的定义,关键是根据乘除法则和二次根式有意义的条件,二次根式有意义的条件时被开方数是非负数进行解答变式1．（全国·,最小的正整数n是（）A．6B．3C．4D．2【答案】B【解析】【分析】根据题意,算数平方根是正整数,可得被开方数是能开方的正整数．【详解】是正整数,所以n 的最小正整数是3,故选：B．【点睛】本题主要考查了二次根式的定义,利用开方运算是解答本题的关键．变式2．（2020·四川三台·,则正整数n 的最小值是（ ） A ．2 B ．3C ．4D ．6【答案】B 【解析】 【分析】,然后再判断n 的最小正整数值． 【详解】=,,则也是整数； ∴n 的最小正整数值是3； 故选B ． 【点睛】变式3．（2020·江西南丰·20b -=,则2019()a b +的值是（ ）． A ．1 B ．－1C ．2019D ．－2019【答案】B 【解析】 【分析】利用非负数的性质列出方程组,求出方程组的解得到a 与b 的值,代入原式计算即可求出值． 【详解】20b -=,∴3020a b +=⎧⎨-=⎩, ∴32a b =-⎧⎨=⎩, ∴20192019()(32)1a b +=-+=-, 故选择：B. 【点睛】此题考查了非负数的性质及二元一次方程组,熟练掌握几个非负数的和为零,则每一个非负数都为零是解本题的关键．◎考点题型3 二次根式有意义的条件例．（2022·河北·在实数范围内有意义,则x 的值可能为（ ） A ．0 B ．﹣2 C ．﹣1 D ．1【答案】D 【解析】 【分析】,可列不等式组10,10x x 得到不等式组的解集,再逐一分析各选项即可. 【详解】解： , 1010x x ①②由①得：1,x ≥ 由②得：1,x ≠- 所以：1,x ≥故A,B,C 不符合题意,D 符合题意, 故选D 【点睛】本题考查的是分式有意义的条件,二次根式有意义的条件,掌握“分式与二次根式的综合形式的代数式有意义的条件”是解本题的关键.变式1．（2022·湖南岳阳·,则实数x 的取值范围是（ ） A ．1x ≥- B ．0x ≠C ．1≥xD ．0x >【答案】C 【解析】 【分析】根据二次根式的被开方数为非负数解答．解：由题意得10x -≥, 解得1≥x , 故选：C ． 【点睛】此题考查了二次根式的非负数,解题的关键是熟练掌握二次根式的双重非负性列式进行解答．变式2．（2022·福建惠安·有意义,则x 的取值范围为（ ） A ．1x ≥- B ．1x >- C ．1≥x D ．1x ≤【答案】A 【解析】 【分析】根据二次根式有意义的条件分析即可． 【详解】, ∴10x +≥ 解得1x ≥- 故选A 【点睛】本题考查了二次根式有意义的条件,理解被开方数为非负数是解题的关键．变式3中x 的取值范围是（ ） A ．x ＞2 B ．x ≥﹣2C ．x ≠2D ．x ≥﹣2且x ≠2【答案】D 【解析】 【分析】根据二次根式及分式有意义的条件可直接进行求解． 【详解】 解：由题意得：20x +≥且20x -≠,解得：2x ≥-且2x ≠； 故选D ．本题主要考查二次根式及分式有意义的条件,熟练掌握二次根式及分式有意义的条件是解题的关键．◎考点题型4 利用二次根式的性质化简例．（2022·贵州松桃·八年级期末）下列各式中正确的是（ ）A 2=-B 2=±C ．22= D ．(22=-【答案】C 【解析】 【分析】根据二次根式的性质即可依次判断． 【详解】A. 2,故错误；B. 2=,故错误；C.22=,正确；D. (22=,故错误；故选C ． 【点睛】此题主要考查二次根式的计算,解题的关键是熟知二次根式的性质．变式1．（2022·江苏·2x =-成立,则x 的取值范围是（ ） A ．2x ≤ B ．2x ≥C ．02x ≤≤D ．任意实数【答案】A 【解析】 【分析】根据实数的性质及去绝对值的方法即可求解． 【详解】22x x =-=-∴x -2≤0故选A ． 【点睛】此题主要考查实数的性质,解题的关键是熟知平方根的性质及去绝对值的方法． 变式2．（上海奉贤·七年级期末）下列计算错误的是（ ）A 2=-B 2C 2D ．2(2=【答案】A 【解析】 【分析】直接利用二次根式的性质以及二次根式的乘法运算法则化简,进而判断即可． 【详解】解：A 2,故此选项计算错误,符合题意；B 2=,故此选项计算正确,不合题意；C 2=,故此选项计算正确,不合题意；D ．2(2=,故此选项计算正确,不合题意； 故选：A ． 【点睛】此题考查了二次根式的性质及二次根式的乘法运算法则,熟记乘法法则是解题的关键．变式3．（2022·2的结果是（ ） A ．61x -- B ．1-C ．61x +D ．1【答案】D 【解析】 【分析】x 的取值范围,,利用二次根式的性质去根号,然后合并同类项即可． 【详解】0x ≥∴31=+x故原式化简为：3131x x +-=． 故选：D ． 【点睛】本题主要是考查了去二次根号以及二次根式的基本性质,熟练掌握二次根式的性质,求解该题的关键．◎考点题型5 复合二次根式的化简例．（浙江滨江·八年级期中）对式子,使根号外不含字母m ,正确的结果是（ ）A B ．C ．D 【答案】C 【解析】 【分析】直接利用二次根式的性质化简求出答案． 【详解】解：由题意可得：30m -≥,∴0m ≤∴=故选：C 【点睛】此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键．变式1．（河南原阳· ）AB C ．D ．【答案】D 【解析】 【分析】根据二次根式成立的条件确定x 的取值,从而利用二次根式的性质进行化简． 【详解】解：由题意可得：x ＜0∴(11x x x⋅=⋅-故选：D ． 【点睛】本题考查二次根式的化简,理解二次根式成立的条件及二次根式的性质正确化简计算是解题关键．变式2．（湖北鄂州·八年级期末）把(2-x) 2-x ）适当变形后移入根号内,得（ ）AB C ． D ．【答案】D 【解析】 【分析】由题意易得x>2,然后根据二次根式的性质可进行求解． 【详解】 解：由题意得： 102x >-,解得：x>2,∴(2x -= 故选D ． 【点睛】本题主要考查二次根式的性质,熟练掌握二次根式的性质是解题的关键．变式3．（2018·全国·2得（ ） A ．2 B ．﹣4x+4C ．xD ．5x ﹣2【答案】C 【解析】 【分析】根据二次函数的性质求解可得答案. 【详解】解:1-3x≥0,x≤13,∴2x-1≤1-3＜0,∴原式-(1-3x)=1-2x-1+3x=x, 故选C. 【点睛】主要考查了根据二次根式的意义及化简.:当a ＞0时=a;当a<0时,=-a.二次根式2=a,(a≥0).。