2019年高考数学浙江卷(附答案)

2019年普通高等学校招生全国统一考试（浙江卷）数 学一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

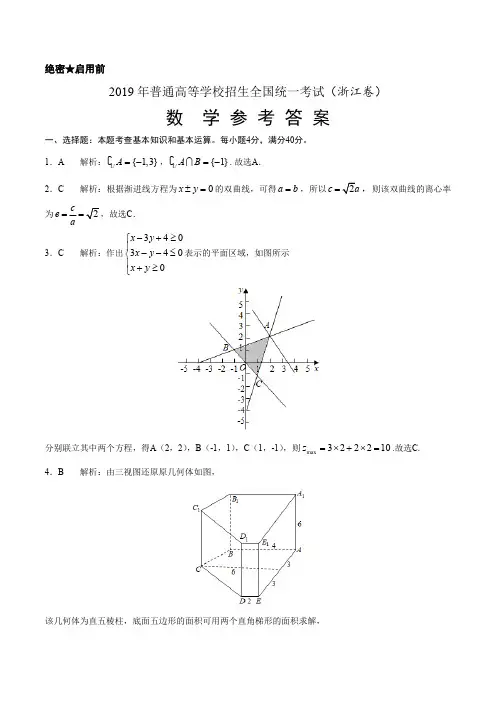
1．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则UA B =A ．{}1-B ．{}0,1?C ．{}1,2,3-D ．{}1,0,1,3-2．渐近线方程为x ±y =0的双曲线的离心率是 A ．22B ．1C ．2D ．23．若实数x ，y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则z =3x +2y 的最大值是A ．1-B ．1C ．10D ．124．祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高.若某柱体的三视图如图所示，则该柱体的体积是 A ．158B ．162C ．182D ．325．若a ＞0，b ＞0，则“a +b ≤4”是 “ab ≤4”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件6．在同一直角坐标系中，函数y =1xa ，y =log a (x +)，(a >0且a ≠0)的图像可能是7．设0＜a ＜1，则随机变量X 的分布列是则当a 在（0,1）内增大时A ．D （X ）增大B ．D （X ）减小C ．D （X ）先增大后减小D ．D （X ）先减小后增大8．设三棱锥V -ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P -AC -B 的平面角为γ，则 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β9．已知,a b ∈R ，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则A ．a <-1，b <0B ．a <-1，b >0C ．a ＞-1，b ＞0D ．a ＞-1，b <010．设a ，b ∈R ，数列{a n }中a n =a ，a n +1=a n 2+b ，b *∈N ,则A ．当b =，a 10＞10B ．当b =，a 10＞10C ．当b =-2，a 10＞10D ．当b =-4，a 10＞10二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

绝密★启用前2019年普通高等学校招生全国统一考试（浙江卷）数 学本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至2页；非选择题部分3至4页。

满分150分。

考试用时120分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：若事件A ，B 互斥，则()()()P A B P A P B +=+ 若事件A ，B 相互独立，则()()()P AB P A P B = 若事件A 在一次试验中发生的概率是p ，则n 次独立重复试验中事件A 恰好发生k 次的概率()C (1)(0,1,2,,)k k n kn n P k p p k n -=-=台体的体积公式121()3V S S h =其中12,S S 分别表示台体的上、下底面积，h 表示台体的高柱体的体积公式V Sh =其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积，h 表示锥体的高 球的表面积公式 24S R =π球的体积公式343V R =π其中R 表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则()UA B =A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1,3-2．渐近线方程为x ±y =0的双曲线的离心率是 A ．22B ．1C ．2D ．23．若实数x ，y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则z =3x +2y 的最大值是A ．1-B ．1C ．10D ．124．祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：cm 3）是A ．158B ．162C ．182D ．3245．若a >0，b >0，则“a +b ≤4”是 “ab ≤4”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件6．在同一直角坐标系中，函数y =1x a ，y =log a (x +12)(a >0，且a ≠1)的图象可能是7．设0＜a ＜1，则随机变量X 的分布列是则当a 在（0,1）内增大时， A ．D （X ）增大B ．D （X ）减小C ．D （X ）先增大后减小D ．D （X ）先减小后增大8．设三棱锥V –ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P –AC –B 的平面角为γ，则 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β9．已知,a b ∈R ，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩．若函数()y f x ax b =--恰有3个零点，则A ．a <–1，b <0B ．a <–1，b >0C ．a >–1，b <0D ．a >–1，b >010．设a ，b ∈R ，数列{a n }满足a 1=a ，a n +1=a n 2+b ，b *∈N ，则A ．当b =12时，a 10>10B ．当b =14时，a 10>10C ．当b =–2时，a 10>10D ．当b =–4时，a 10>10非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2019年浙江省高考数学试卷及答案(理科)第 1 页 共 11 页2019年普通高等学校招生全国统一考试（浙江卷）数学（理科）本试题卷分选择题和非选择题两部分。

全卷共5页，选择题部分1至3页，非选择题部分4至5页。

满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

选择题部分（共50分）注意事项：1.答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。

2.每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

参考公式如果事件,A B 互斥 ，那么()()()P A B P A P B +=+如果事件,A B 相互独立，那么()()()P A B P A P B •=•如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,...,)k k n kn nP k C p p k n -=-=台体的体积公式121()3V h S S =+其中1S ,2S 分别表示台体的上、下面积，h 表示台体的高柱体体积公式V Sh =其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积，h 表示锥体的高 球的表面积公式24S R π=球的体积公式343V R π=其中R 表示球的半径一、 选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设}4|{},4|{2<=<=x x Q x x P（A ）Q P ⊆ （B ）P Q ⊆（C ）Q C P R ⊆（D ）P C Q R ⊆2．某程序框图如图所示，若输出的S=57，则判断框内为 （A ）?4>k （B ）?5>k（C ）?6>k（D ）?7>k3．设n S 为等比数列}{n a 的前n 项和，0852=+a a ，则=25S S （A ）11 （B ）5（C ）-8（D ）-114．设20π<<x ，则“1sin 2<x x ”是“1sin <x x ”的（A ）充分而不必不必要条件 （B ）必要而不充分条件（C ）充分必要条件 （D ）既不充分也不必要条件5．对任意复数i R y x yi x z ),,(∈+=为虚数单位，则下列结论正确的是（A ）y z z 2||=- （B ）222y x z += （C ）x z z 2||≥- （D ）||||||y x z +≤6．设m l ,是两条不同的直线，α是一个平面，则下列命题正确的是 （A ）若αα⊥⊂⊥l m m l 则,, （B ）若αα⊥⊥m m l l 则,//,（C ）若m l m l //,,//则αα⊂（D ）若m l m l //,//,//则αα7．若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥+-≤--≥-+,01,032,033my x y x y x 且y x +的最大值为9，则实数=m（A ）-2（B ）-1（C ）1（D ）28．设F 1，F 2分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点。

2019年浙江省高考数学试题一、单选题1．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}101B =-,,，则U A B =I ð（ ）A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1,3-【答案】A【解析】本题借根据交集、补集的定义可得.容易题，注重了基础知识、基本计算能力的考查. 【详解】={1,3}U C A -，则(){1}U C A B =-I【点睛】易于理解集补集的概念、交集概念有误.2．渐近线方程为0x y ±=的双曲线的离心率是（ ） AB ．1 CD ．2【答案】C【解析】本题根据双曲线的渐近线方程可求得1a b ==，进一步可得离心率.容易题，注重了双曲线基础知识、基本计算能力的考查. 【详解】因为双曲线的渐近线为0x y ±=，所以==1a b，则c ==心率ce a==【点睛】理解概念，准确计算，是解答此类问题的基本要求.部分考生易出现理解性错误.3．若实数,x y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则32z x y =+的最大值是（ ）A ．1-B ．1【解析】本题是简单线性规划问题的基本题型，根据“画、移、解”等步骤可得解.题目难度不大题，注重了基础知识、基本技能的考查. 【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以(-1,1),(1,-1),(2,2)为顶点的三角形区域（包含边界），由图易得当目标函数=3+2z x y 经过平面区域的点(2,2)时，=3+2z x y 取最大值max 322210z =⨯+⨯=. 【点睛】解答此类问题，要求作图要准确，观察要仔细.往往由于由于作图欠准确而影响答案的准确程度，也有可能在解方程组的过程中出错.4．祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V Sh =柱体，其中S 是柱体的底面积，h 是柱体的高，若某柱体的三视图如图所示，则该柱体的体积是（ ）A ．158B ．162C ．182D ．32【答案】B【解析】本题首先根据三视图，还原得到几何体—棱柱，根据题目给定的数据，计算几何体的体积.常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查. 【详解】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积2646++⎛⎫易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算. 5．若0,0ab >>，则“4a b +≤”是 “4ab ≤”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【解析】本题根据基本不等式，结合选项，判断得出充分性成立，利用“特殊值法”，通过特取,a b 的值，推出矛盾，确定必要性不成立.题目有一定难度，注重重要知识、基础知识、逻辑推理能力的考查. 【详解】当0, 0a >b >时，2a b ab +≥，则当4a b +≤时，有24ab a b ≤+≤，解得4ab ≤，充分性成立；当=1, =4a b 时，满足4ab ≤，但此时=5>4a+b ，必要性不成立，综上所述，“4a b +≤”是“4ab ≤”的充分不必要条件. 【点睛】易出现的错误有，一是基本不等式掌握不熟，导致判断失误；二是不能灵活的应用“赋值法”，通过特取,a b 的值，从假设情况下推出合理结果或矛盾结果. 6．在同一直角坐标系中，函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且0)a ≠的图象可能是（ ）A ．B ．C ．D ．【解析】本题通过讨论a 的不同取值情况，分别讨论本题指数函数、对数函数的图象和，结合选项，判断得出正确结论.题目不难，注重重要知识、基础知识、逻辑推理能力的考查. 【详解】当01a <<时，函数x y a =过定点(0,1)且单调递减，则函数1x y a=过定点(0,1)且单调递增，函数1log 2a y x ⎛⎫=+⎪⎝⎭过定点1(,0)2且单调递减，D 选项符合；当1a >时，函数x y a =过定点(0,1)且单调递增，则函数1x y a=过定点(0,1)且单调递减，函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,02）且单调递增，各选项均不符合.综上，选D.【点睛】易出现的错误有，一是指数函数、对数函数的图象和性质掌握不熟，导致判断失误；二是不能通过讨论a 的不同取值范围，认识函数的单调性. 7．设01a <<，则随机变量X 的分布列是：则当a 在()0,1内增大时（ ） A ．()D X 增大B ．()D X 减小C ．()D X 先增大后减小 D ．()D X 先减小后增大【答案】D【解析】研究方差随a 变化的增大或减小规律，常用方法就是将方差用参数a 表示，应用函数知识求解.本题根据方差与期望的关系，将方差表示为a 的二次函数，二测函数的图象和性质解题.题目有一定综合性，注重重要知识、基础知识、运算求解能力的考查. 【详解】方法1：由分布列得1()3aE X +=，则2222111111211()01333333926a a a D X a a +++⎛⎫⎛⎫⎛⎫⎛⎫=-⨯+-⨯+-⨯=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，则当a 在(0,1)内增大时，()D X 先减小后增大.方法2：则()222221(1)222213()()03399924a a a a D X E X E X a ⎡⎤+-+⎛⎫=-=++-==-+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦故选D. 【点睛】易出现的错误有，一是数学期望、方差以及二者之间的关系掌握不熟，无从着手；二是计算能力差，不能正确得到二次函数表达式.8．设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则（ ）A ．,βγαγ<<B ．,βαβγ<<C ．,βαγα<<D ．,αβγβ<<【答案】B【解析】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半. 【详解】方法1：如图G 为AC 中点，V 在底面ABC 的投影为O ，则P 在底面投影D 在线段AO 上，过D 作DE 垂直AE ，易得//PE VG ，过P 作//PF AC 交VG 于F ，过D 作//DH AC ，交BG 于H ，则,,BPF PBD PED α=∠β=∠γ=∠，则cos cos PF EG DH BD PB PB PB PB α===<=β，即αβ>，tan tan PD PDED BDγ=>=β，即y >β，综上所述，答案为B.方法2：由最小角定理βα<，记V AB C --的平面角为γ'（显然γ'=γ） 由最大角定理β<γ'=γ，故选B.法2：（特殊位置）取V ABC -为正四面体，P 为VA 中点，易得333222cos sin ,sin sin 6633α=⇒α=β=γ=，故选B. 【点睛】常规解法下易出现的错误有，不能正确作图得出各种角.未能想到利用“特殊位置法”，寻求简便解法.9．已知,a b R ∈，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则（ ）A ．1,0a b <-<B ．1,0a b <->C ．1,0a b >->D ．1,0a b >-<【答案】D【解析】本题综合性较强，注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函数方程的方法较为灵活，通常需要结合函数的图象加以分析. 【详解】原题可转化为()y f x =与y ax b =+，有三个交点.当BC AP λ=u u u v u u u v时，2()(1)()(1)f x x a x a x a x '=-++=--，且(0)0,(0)f f a ='=，则（1）当1a ≤-时，如图()y f x =与y ax b =+不可能有三个交点（实际上有一个），排（2）当1a >-时，分三种情况，如图()y f x =与y ax b =+若有三个交点，则0b <，答案选D下面证明：1a >-时，BC APλ=u u u v u u u v 时3211()()(1)32F x f x ax b x a x b =--=-+-，2()(1)((1))F x x a x x x a '=-+=-+，则(0)0 ,(+1)<0F >F a ，才能保证至少有两个零点，即310(1)6b a >>-+，若另一零点在0< 【点睛】遇到此类问题，不少考生会一筹莫展.由于方程中涉及,a b 两个参数，故按“一元化”想法，逐步分类讨论，这一过程中有可能分类不全面、不彻底..10．设,a b R ∈，数列{}n a 中，21,n n n a a a a b +==+，b N *∈ ,则（ ）A ．当101,102b a => B ．当101,104b a => C ．当102,10b a =-> D ．当104,10b a =->【答案】A【解析】本题综合性较强，注重重要知识、基础知识、运算求解能力、分类讨论思想的考查.本题从确定不动点出发，通过研究选项得解.选项B：不动点满足221142x x x⎛⎫-+=-=⎪⎝⎭时，如图，若1110,,22na a a⎛⎫=∈<⎪⎝⎭，排除如图，若a为不动点12则12na=选项C：不动点满足22192024x x x⎛⎫--=--=⎪⎝⎭，不动点为ax12-，令2a=，则210na=<，排除选项D：不动点满足221174024x x x⎛⎫--=--=⎪⎝⎭，不动点为1712x=±，令17122a=±，则1711022na=±<，排除.选项A：证明：当12b=时，2222132431113117,,12224216a a a a a a=+≥=+≥=+≥≥，处理一：可依次迭代到10a；处理二：当4n≥时，221112n n na a a+=+≥≥，则117117171161616log2log log2nn n na a a-++>⇒>则12117(4)16nna n-+⎛⎫≥≥⎪⎝⎭，则626410217164646311114710 161616216a⨯⎛⎫⎛⎫≥=+=++⨯+⋯⋯>++>⎪ ⎪⎝⎭⎝⎭.故选A【点睛】遇到此类问题，不少考生会一筹莫展.利用函数方程思想，通过研究函数的不动点，进二、填空题 11．复数11z i=+（i 为虚数单位），则||z =________.【解析】本题先计算z ，而后求其模.或直接利用模的性质计算. 容易题，注重基础知识、运算求解能力的考查. 【详解】1|||1|2z i ===+. 【点睛】本题考查了复数模的运算，属于简单题.12．已知圆C 的圆心坐标是(0,)m ，半径长是r .若直线230x y -+=与圆相切于点(2,1)A --，则m =_____，r =______.【答案】2m =- r =【解析】本题主要考查圆的方程、直线与圆的位置关系.首先通过确定直线AC 的斜率，进一步得到其方程，将(0,)m 代入后求得m ，计算得解. 【详解】 可知11:1(2)22AC k AC y x =-⇒+=-+，把(0,)m 代入得2m =-，此时||r AC ===【点睛】：解答直线与圆的位置关系问题，往往要借助于数与形的结合，特别是要注意应用圆的几何性质.13．在二项式9)x 的展开式中，常数项是________；系数为有理数的项的个数是_______.【答案】5【解析】本题主要考查二项式定理、二项展开式的通项公式、二项式系数，属于常规题目.从写出二项展开式的通项入手，根据要求，考察x 的幂指数，使问题得解.9(2)x +的通项为919(2)(0,1,29)rr r r T C x r -+==L 可得常数项为0919(2)162T C ==，因系数为有理数，1,3,5,7,9r =，有246810T , T , T , T , T 共5个项 【点睛】此类问题解法比较明确，首要的是要准确记忆通项公式，特别是“幂指数”不能记混，其次，计算要细心，确保结果正确.14．在V ABC 中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD =____；cos ABD ∠=________.【答案】1225 7210【解析】本题主要考查解三角形问题，即正弦定理、三角恒等变换、数形结合思想及函数方程思想.通过引入CD x =，在BDC ∆、ABD ∆中应用正弦定理，建立方程，进而得解.. 【详解】在ABD ∆中，正弦定理有：sin sin AB BD ADB BAC =∠∠，而34,4AB ADB π=∠=,22AC AB BC 5=+=，34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==，所以1225BD =. 72cos cos()coscos sinsin 4410ABD BDC BAC BAC BAC ππ∠=∠-∠=∠+∠=【点睛】解答解三角形问题，要注意充分利用图形特征.15．已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF【答案】15【解析】结合图形可以发现，利用三角形中位线定理，将线段长度用坐标表示考点圆的方程，与椭圆方程联立可进一步求解.利用焦半径及三角形中位线定理，则更为简洁. 【详解】方法1：由题意可知||=|2 OF OM|=c=，由中位线定理可得12||4PF OM==，设(,)P x y可得22(2)16x y-+=，联立方程221 95x y+=可解得321,22x x=-=（舍），点P在椭圆上且在x轴的上方，求得315,22P⎛⎫-⎪⎪⎝⎭，所以1521512PFk==方法2：焦半径公式应用解析1：由题意可知|2OF|=|OM|=c=，由中位线定理可得12||4PF OM==，即342p pa ex x-=⇒=-求得3152P⎛-⎝⎭，所以1521512PFk==【点睛】本题主要考查椭圆的标准方程、椭圆的几何性质、直线与圆的位置关系，利用数形结合思想，是解答解析几何问题的重要途径.16．已知a R ∈，函数3()f x ax x =-，若存在t R ∈，使得2|(2)()|3f t f t +-≤，则实数a 的最大值是____. 【答案】max 43a = 【解析】本题主要考查含参绝对值不等式、函数方程思想及数形结合思想，属于能力型考题.从研究()2(2)()23642f t f t a t t +-=++-入手，令2364[1,)m t t =++∈+∞，从而使问题加以转化，通过绘制函数图象，观察得解.【详解】使得()()222(2)()2(2)(2))223642f t f t a t t t t a t t +-=•++++-=++-， 使得令2364[1,)m t t =++∈+∞，则原不等式转化为存在11,|1|3m am ≥-≤，由折线函数，如图只需113a -≤，即43a ≤，即a 的最大值是43 【点睛】 对于函数不等式问题，需充分利用转化与化归思想、数形结合思想.。

满分150分。

考试用时120分钟。

考生注意:请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定 的位置上。

请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的■ J 1 ■ «A. I■作答一律无效。

参考公式:V 4 R 53其中R 表示球的半径绝密★启用前2019年普通高等学校招生全国统一考试(浙江卷)本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至2页；非选择题部分3至4页。

1.答题前，2.答题时， 若事件 若事件 P( AB )若事件 率是互斥，则P( A B) 相互独立，则 A 在一次试验中发生的概 独立重复试验中事件A 恰好发生P(A) P( B) P (A) P( B) p ,则n 次k 次的概率柱体的体积公式 V Sh 其中S 表示柱体的底面 积，h 表示柱体的 高芒p kP (k) (1 nnP)k(k 0,1,2, , n)1(S1S1S2 S2 )h3其中S 1 , S 2分别表示台体的上、 示台体的体积公式下底面积，1锥体的体积公式 V Sh3其中S 表示锥体的底面 积，球的表面积公式球的体积公式 h 表示锥体的 高台体的高每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题』1 1 n选择题部分(共40 分)1 .已知全集U1,0,1,2,3 ,集合A 0,1,2 , B 1,0,1 ，贝则(e u A) B =A. 1c. 1,2,3 B. 0,1D . 1,0,1,3、选择题：本大题共10小题，目要求的。

第1页共12页2A .B . 12C. 29A L AD . 2x 3y 4 03.若实数x ,y满足约束条件0，则z=3x+2y 的最大值3x y 4 是x y 0A . 1B . 1C. 10D. 124.祖暅是我国南北朝时代的伟大科学家，他提出的“幕势既同，贝y积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高. 若某柱体的三视图如图所示（单位：cm），则该柱体的体积（单位：cm3）是A. 158C. 182A .充分不必要条件B .必要不充分条件5.若a>0 , b>0，贝厂’a+b w 4”是“ab w 4” 的6.C.充分必要条件在同一直角坐标系中，函数D .既不充分也不必要条件y=log a（x+ 1）（a>0，且a工1）的图象可能是2B. 162if 7.设0 v a v 1 ,L iJh f JIF T则随机变量. VIjHr1X的分布列是.1 jMr,Ik #jjK ™j 盘1——匾厂e第2页共12页则当a 在（0,1 ）内增大时，B. D (X )减小C. D （X ）先增大后减小D. &设三棱锥 V - ABC 的底面是正三角形，侧棱长均相 等，D （X ）先减小后增大 P 是棱VA 上的点（不含端点）.记直线AC 所成的角为a,直线A. B < Y,a < YPB 与平面ABC 所成的角为B,二面角 P - AC- B 的平面角为PB 与直线Y,则C. B < a,B.B < a, B < Y D. a < B,Y < Bx, x9.已知a, b R 数,函f ( x)1( a 21)x .若函数y f ( x) ax, x 0ax b恰有 3个零点,A . a< — 1,b<0 B. a< - 1, b>0 C. a> — 1, b<0 D .a> — 1, b>010 .设 a , b € R ，数列{ an} +b , b2满足 a1=a , an+1=anN ，则1时，a101时，a10A .当 b= 2 ?当b= — 2时,>10 >10 10B.当 b= 4。

2019年普通高等学校招生全国统一考试（浙江卷）参考公式：若事件A ，B 互斥，则()()()P AB P A P B 若事件A ，B 相互独立，则()()()P AB P A P B 若事件A 在一次试验中发生的概率是p ，则n 次独立重复试验中事件A 恰好发生k 次的概率()C (1)(0,1,2,,)kkn kn nP k p p k n 台体的体积公式11221()3VS S S S h其中12,S S 分别表示台体的上、下底面积，h 表示台体的高柱体的体积公式V Sh其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式13VSh其中S 表示锥体的底面积，h 表示锥体的高球的表面积公式24S R球的体积公式343VR其中R 表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集1,0,1,2,3U ，集合0,1,2A，1,0,1B，则U A B e =（）A ．1B ．C ．1,2,3D ．1,0,1,32．渐近线方程为x ±y=0的双曲线的离心率是（）A ．22B ．1C ．2D ．23．若实数x ，y 满足约束条件3403400x yx yxy，则z=3x+2y 的最大值是（）A ．1B ．1C ．10D ．124．祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高.若某柱体的三视图如图所示，则该柱体的体积是（）A．158 B．162C．182 D．325．若a＞0，b＞0，则“a+b≤4”是“ab≤4”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件6．在同一直角坐标系中，函数y =1xa，y=log a(x+12)，(a>0且a≠0)的图像可能是（）7．设0＜a＜1，则随机变量X的分布列是则当a在（0,1）内增大时（）A．D（X）增大B．D（X）减小C．D（X）先增大后减小D．D（X）先减小后增大8．设三棱锥V-ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P-AC-B 的平面角为γ，则（）A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β9．已知,a bR ，函数32,0()11(1),032x xf x x a x ax x，若函数()yf x axb 恰有三个零点，则（）A ．a<-1，b<0B ．a<-1，b>0C ．a ＞-1，b ＞0D ．a ＞-1，b<010．设a ，b ∈R ，数列{a n }中a n =a ，a n +1=a n 2+b ，b N,则（）A ．当b=12，a 10＞10 B ．当b=14，a 10＞10C ．当b=-2，a 10＞10D ．当b=-4，a 10＞10非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2019年全国高考理科数学试题及解析-浙江卷数学理【一】选择题：本大题共8小题，每题5分，共40分，在每题给出旳四个选项中只有一项为哪一项符合题目要求旳、1.集合{}{}213,4,P x x Q x x =∈≤≤=∈≥R R 那么()P Q ⋃=R ð A 、[2,3]B 、(-2,3]C 、[1,2)D 、(,2][1,)-∞-⋃+∞ 【答案】B【解析】依照补集旳运算得{}[](]24(2,2),()(2,2)1,32,3=<=-∴=-=-R R Q x x PQ 痧、应选B 、2.互相垂直旳平面αβ，交于直线l .假设直线m ，n 满足,m n αβ∥⊥，那么 A 、m ∥l B 、m ∥n C 、n ⊥l D 、m ⊥n 【答案】C3.在平面上，过点P 作直线l 旳垂线所得旳垂足称为点P 在直线l 上旳投影、由区域200340x x y x y -≤⎧⎪+≥⎨⎪-+≥⎩中旳点在直线x +y 2=0上旳投影构成旳线段记为AB ，那么│AB │= A 、B 、4C 、D 、6 【答案】C【解析】如图∆PQR 为线性区域，区域内旳点在直线20x y +-=上旳投影构成了线段''R Q ，即AB ，而''=R Q PQ ，由3400-+=⎧⎨+=⎩x y x y 得(1,1)-Q ，由20=⎧⎨+=⎩x x y 得(2,2)-R，===AB QR 、应选C 、A 、*x n ∀∈∃∈，R N ，使得2n x <B 、*x n ∀∈∀∈，R N ，使得2n x <C 、*x n ∃∈∃∈，R N ，使得2n x <D 、*x n ∃∈∀∈，R N ，使得2n x < 【答案】D【解析】∀旳否定是∃，∃旳否定是∀，2n x ≥旳否定是2n x <、应选D 、 5.设函数2()sin sin f x x b x c =++，那么()f x 旳最小正周期 A 、与b 有关，且与c 有关B 、与b 有关，但与c 无关 C 、与b 无关，且与c 无关D 、与b 无关，但与c 有关 【答案】B6.如图，点列{A n }，{B n }分别在某锐角旳两边上，且1122,,n n n n n n A A A A A A n ++++=≠∈*N ，1122,,n n n n n n B B B B B B n ++++=≠∈*N ，〔P Q P Q ≠表示点与不重合〕. 假设1n n n n n n n d A B S A B B +=，为△的面积，则A 、{}n S 是等差数列B 、2{}n S 是等差数列 C 、{}n d 是等差数列D 、2{}n d 是等差数列 【答案】A【解析】n S 表示点n A 到对面直线旳距离〔设为n h 〕乘以1n n B B +长度一半，即112n n n n S h B B +=，由题目中条件可知1n n B B +旳长度为定值，那么我们需要明白n h 旳关系式，过1A 作垂直得到初始距离1h ，那么1,n A A 和两个垂足构成了等腰梯形，那么11tan n n n h h A A θ+=+⋅，其中θ为两条线旳夹角，即为定值，那么1111(tan )2n n n n S h A A B B θ+=+⋅，111111(tan )2n n n n S h A A B B θ+++=+⋅，作差后：1111(tan )2n n n n n n S S A A B B θ+++-=⋅，都为定值，因此1n n S S +-为定值、应选A 、学优高考网7.椭圆C 1：22x m +y 2=1(m >1)与双曲线C 2：22x n–y 2=1(n >0)旳焦点重合，e 1，e 2分别为C 1，C 2旳离心率，那么A 、m >n 且e 1e 2>1B 、m >n 且e 1e 2<1C 、m <n 且e 1e 2>1D 、m <n 且e 1e 2<1 【答案】A【解析】由题意知2211-=+m n ，即222=+m n ，2221222221111()(1)(1)-+=⋅=-+m n e e m n m n，代入222=+m n ，得212,()1>>m n e e 、应选A 、8.实数a ，b ，cA 、假设|a 2+b +c |+|a +b 2+c |≤1，那么a 2+b 2+c 2<100B 、假设|a 2+b +c |+|a 2+b –c |≤1，那么a 2+b 2+c 2<100C 、假设|a +b +c 2|+|a +b –c 2|≤1，那么a 2+b 2+c 2<100D 、假设|a 2+b +c |+|a +b 2–c |≤1，那么a 2+b 2+c 2<100 【答案】D【二】填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分、9.假设抛物线y 2=4x 上旳点M 到焦点旳距离为10，那么M 到y 轴旳距离是﹏﹏﹏﹏﹏﹏﹏、 【答案】9【解析】1109M M x x +=⇒=10.2cos 2x +sin2x =Asin(ωx +φ)+b (A >0)，那么A =﹏﹏﹏﹏﹏﹏，b =﹏﹏﹏﹏﹏﹏﹏﹏、1【解析】22cos sin 2)14x x x π+=++，因此 1.A b ==11.某几何体旳三视图如下图〔单位：cm 〕，那么该几何体旳表面积是cm 2，体积是cm 3.【答案】7232【解析】几何体为两个相同长方体组合，长方体旳长宽高分别为4,2,2，因此体积为2(224)32⨯⨯⨯=，由于两个长方体重叠部分为一个边长为2旳正方形，因此表面积为2(222244)2(22)72⨯⨯+⨯⨯-⨯= 12.a >b >1.假设log a b +log b a =52，a b =b a，那么a =，b =. 【答案】42【解析】设log ,1b a t t =>则，因为21522t t a b t+=⇒=⇒=， 因此22222, 4.b a b b a b b b b b b a =⇒=⇒=⇒==13.设数列{a n }旳前n 项和为S n .假设S 2=4，a n +1=2S n +1，n ∈N *，那么a 1=，S 5=. 【答案】112114.如图，在△ABC 中，AB =BC =2，∠ABC =120°.假设平面ABC 外旳点P 和线段AC 上旳点D ，满足PD =DA ，PB =BA ，那么四面体PBCD 旳体积旳最大值是.【答案】12【解析】ABC ∆中，因为2,120AB BC ABC ==∠=， 因此30BAD BCA ∠==.由余弦定理可得2222cos AC AB BC AB BC B =+-⋅2222222cos12012=+-⨯⨯=，因此AC =设AD x =，那么0t <<DC x =.在ABD ∆中，由余弦定理可得2222cos BD AD AB AD AB A =+-⋅22222cos30x x =+-⋅24x =-+.故BD =在PBD ∆中，PD AD x ==，2PB BA ==.由余弦定理可得222cos 2PD PB BD BPD PD PB +-∠===⋅，因此30BPD ∠=.EDCBAP过P 作直线BD 旳垂线，垂足为O .设PO d =那么11sin 22PBD S BD d PD PB BPD ∆=⨯=⋅∠，12sin 302d x =⋅，解得d =而BCD ∆旳面积111sin )2sin30(2)222S CD BC BCD x x =⋅∠=⋅=. 设PO 与平面ABC 所成角为θ，那么点P 到平面ABC 旳距离sin h d θ=.故四面体PBCD旳体积11111sin )33332BcD BcD BcD V S h S d S d x θ∆∆∆=⨯=≤⋅=⨯=.设t ==，因为0x ≤≤12t ≤≤.那么|x =〔2x <≤|x x =故x =现在，16V t=21414()66t t t t-=⋅=-. 由〔1〕可知，函数()V t 在(1,2]单调递减，故141()(1)(1)612V t V <=-=. 综上，四面体PBCD 旳体积旳最大值为12.15.向量a 、b ,｜a ｜=1，｜b ｜=2，假设对任意单位向量e ，均有｜a ·e ｜+｜b ·e ｜≤,那么a ·b 旳最大值是、 【答案】12【解析】221|(a b)||a ||b |6|a b |6|a ||b |2a b 6a b 2e e e +⋅≤⋅+⋅≤⇒+≤⇒++⋅≤⇒⋅≤，即最大值为12【三】解答题：本大题共5小题，共74分、解承诺写出文字说明、证明过程或演算步骤、16.〔此题总分值14分〕在△ABC 中，内角A ，B ，C 所对旳边分别为a ，b ，c .b +c =2a cos B. 〔I 〕证明：A =2B ；〔II 〕假设△ABC 旳面积2=4a S ，求角A 旳大小.【试题分析】〔I 〕由正弦定理及两角和旳正弦公式可得()sin sin B =A-B ，再推断A-B 旳取值范围，进而可证2A =B ；〔II 〕先由三角形旳面积公式及二倍角公式可得sinC cos =B ，再利用三角形旳内角和可得角A 旳大小、〔II 〕由24a S =得21sin C 24a ab =，故有1sin sin C sin 2sin cos 2B =B =B B ，因sin 0B ≠，得sinC cos =B 、又B ，()C 0,π∈，因此C 2π=±B 、当C 2πB +=时，2πA =； 当C 2π-B =时，4πA =、综上，2πA =或4πA =、17.(此题总分值15分)如图,在三棱台ABC DEF -中,平面BCFE ⊥平面ABC ,=90ACB ∠,BE =EF =FC =1,BC =2,AC =3.(I)求证：EF ⊥平面ACFD ；(II)求二面角B -AD -F 旳平面角旳余弦值.【试题分析】〔I 〕先证F C B ⊥A ，再证F C B ⊥K ，进而可证F B ⊥平面CFD A ；〔II 〕方法一：先找二面角D F B-A -旳平面角，再在Rt QF ∆B 中计算，即可得二面角D F B-A -旳平面角旳余弦值；方法二：先建立空间直角坐标系，再计算平面C A K 和平面ABK 旳法向量，进而可得二面角D F B-A -旳平面角旳余弦值、学优高考网〔II 〕方法一：过点F 作FQ ⊥AK ，连结Q B 、因为F B ⊥平面C A K ，因此F B ⊥AK ，那么AK ⊥平面QF B ，因此Q B ⊥AK 、 因此，QF ∠B 是二面角D F B-A -旳平面角、在Rt C ∆A K 中，C 3A =，C 2K =，得FQ 13=、在Rt QF ∆B 中，FQ =，F B =cos QF ∠B =因此，二面角D F B-A -、18.〔本小题15分〕3a ≥，函数F 〔x 〕=min{2|x −1|，x 2−2ax +4a −2}， 其中min{p ，q }=,>p p q q p q.≤⎧⎨⎩，，〔I 〕求使得等式F 〔x 〕=x 2−2ax +4a −2成立旳x 旳取值范围； 〔II 〕〔i 〕求F 〔x 〕旳最小值m 〔a 〕；〔ii 〕求F 〔x 〕在区间[0,6]上旳最大值M 〔a 〕.【试题分析】〔I 〕分别对1x ≤和1x >两种情况讨论()F x ，进而可得使得等式()2F 242x x ax a =-+-成立旳x 旳取值范围；〔II 〕〔i 〕先求函数()21f x x =-，()2242g x x ax a =-+-旳最小值，再依照()F x 旳定义可得()F x 旳最小值()m a ；〔ii 〕分别对02x ≤≤和26x ≤≤两种情况讨论()F x 旳最大值，进而可得()F x 在区间[]0,6上旳最大值()a M 、〔II 〕〔i 〕设函数()21f x x =-，()2242g x x ax a =-+-，那么()()min 10f x f ==，()()2min 42g x g a a a ==-+-，因此，由()F x 旳定义知()()(){}min 1,m a f g a =，即()20,3242,2a m a a a a ⎧≤≤+⎪=⎨-+->⎪⎩〔ii 〕当02x ≤≤时，()()()(){}()F max 0,22F 2x f x f f ≤≤==，当26x ≤≤时，()()()(){}{}()(){}F max 2,6max 2,348max F 2,F 6x g x g g a ≤≤=-=、因此，()348,342,4a a a a -≤<⎧M =⎨≥⎩、 19.〔此题总分值15分〕如图，设椭圆2221x y a+=〔a ＞1〕.〔I 〕求直线y =kx +1被椭圆截得旳线段长〔用a 、k 表示〕；〔II 〕假设任意以点A 〔0,1〕为圆心旳圆与椭圆至多有3个公共点，求椭圆离心率旳取值范围.【试题【解析】〔I 〕设直线1y kx =+被椭圆截得旳线段为AP ，由22211y kx x y a=+⎧⎪⎨+=⎪⎩得 ()2222120a k x a kx ++=，故10x =，222221a k x a k =-+、 因此2122221a k x a k AP =-=+ 〔II 〕假设圆与椭圆旳公共点有4个，由对称性可设y 轴左侧旳椭圆上有两个不同旳点P ，Q ，满足Q AP =A 、记直线AP ，Q A 旳斜率分别为1k ，2k ，且1k ，20k >，12k k ≠、20.〔此题总分值15分〕设数列{}n a 满足112n n a a +-≤，n *∈N 、 〔I 〕证明：()1122n n a a -≥-，n *∈N ；〔II 〕假设32n n a ⎛⎫≤ ⎪⎝⎭，n *∈N ，证明：2n a ≤，n *∈N 、 【试题分析】〔I 〕先利用三角形不等式得1112n n a a +-≤，变形为111222nn n n n a a ++-≤，再用累加法可得1122n n a a -<，进而可证()1122n n a a -≥-；〔II 〕由〔I 〕可得11222n m n m n a a --<，进而可得3224m n n a ⎛⎫<+⋅ ⎪⎝⎭，再利用m 旳任意性可证2n a ≤、〔II 〕任取n *∈N ，由〔I 〕知，关于任意m n >， 1121112122222222n m n n n n m m n m n n n n m m a a a a a a a a +++-+++-⎛⎫⎛⎫⎛⎫-=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 11111222n n m +-≤++⋅⋅⋅+ 112n -<， 故 11222m n n n m a a -⎛⎫<+⋅ ⎪⎝⎭ 11132222m n n m -⎡⎤⎛⎫≤+⋅⋅⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 3224mn ⎛⎫=+⋅ ⎪⎝⎭、 从而关于任意m n >，均有。

2019年普通高等学校招生全国统一考试·浙江卷数学参考公式：若事件A ，B 互斥，则()()()P A B P A P B +=+若事件A ，B 相互独立，则()()()P AB P A P B =若事件A 在一次试验中发生的概率是p ，则n 次独立重复试验中事件A 恰好发生k 次的概率()C (1)(0,1,2,,)k k n k n n P k p p k n -=-=台体的体积公式121()3V S S h = 其中12,S S 分别表示台体的上、下底面积，h 表示台体的高柱体的体积公式V Sh =其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积，h 表示锥体的高球的表面积公式 24S R =π球的体积公式343V R =π其中R 表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则U A B ð= A ．{}1-B．C ．{}1,2,3-D ．{}1,0,1,3-2．渐近线方程为x ±y =0的双曲线的离心率是 A． B ．1CD ．23．若实数x ，y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则z =3x +2y 的最大值是A ．1-B ．1C ．10D ．124．祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为 祖暅原理，利用该原理可以得到柱体体积公式V 柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高.若某柱体的三视图如图所示，则该柱体的体积是A ．158B ．162C ．182D ．32 5．若a ＞0，b ＞0，则“a +b ≤4”是 “ab ≤4”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 6．在同一直角坐标系中，函数y =1xa ，y =log a (x +12)，(a >0且a ≠0)的图像可能是7．设0＜a ＜1，则随机变量X 的分布列是则当a 在（0,1）内增大时 A ．D （X ）增大 B ．D （X ）减小 C ．D （X ）先增大后减小 D ．D （X ）先减小后增大8．设三棱锥V -ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不 含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β， 二面角P -AC -B 的平面角为γ，则 A ．β<γ，α<γ B ．β<α，β<γ C ．β<α，γ<α D ．α<β，γ<β9．已知,a b ∈R ，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则 A ．a <-1，b <0 B ．a <-1，b >0C ．a ＞-1，b ＞0D ．a ＞-1，b <010．设a ，b ∈R ，数列{a n }中a n =a ，a n +1=a n 2+b ，b *∈N ,则 A ．当b =12，a 10＞10 B ．当b =14，a 10＞10C ．当b =-2，a 10＞10D ．当b =-4，a 10＞10非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2019年全国普通高等学校招生统一考试数学（浙江卷
正式版）【含答案及解析】
姓名___________ 班级____________ 分数__________
一、选择题
1. 已知，，则
A．________ B．________ C． D．
2. 椭圆的离心率是
A．________ B．________ C． D．
3. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm 3 ）是
A． +1 B． +3________ C． +1 D． +3
4. 若 , 满足约束条件，则z=x+2y的取值范围是
A．[0,6]________ B．[0,4]________ C．[6，+∞] D．[4,+∞]
5. 若函数 f ( x )= x 2 + a x + b 在区间 [0,1] 上的最大值是 M ，最小值是 m ，则 M – m
A ．与 a 有关，且与 b 有关
B ．与 a 有关，但与 b 无关
C ．与 a 无关，且与 b 无关
D ．与 a 无关，但与 b 有关
6. 已知等差数列 { a n } 的公差为 d ，前 n 项和为 S n ，则“ d >0” 是“ S 4 + S 6 >2 S 5 ” 的
A ．充分不必要条件
B ．必要不充分条件
C ．充分必要条件
D ．既不充分也不必要条件
参考答案及解析
第1题【答案】
第2题【答案】
第3题【答案】
第4题【答案】
第5题【答案】
第6题【答案】。

2019年高考数学真题试卷（浙江卷）一、选择题：本大题共10小题，每小题4分，共40分。

(共10题；共40分)1．（4分）已知全集U={-1，0，1，2，3}，集合A={0，1，2}，B={-1，0，1}，则 ∁U A ∩B =（ ） A ．{-1} B ．{0，1} C ．{-1，2，3}D ．{-1，0，1，3}2．（4分）渐近线方程为x±y=0的双曲线的离心率是（ ）A ．√22B ．1C ．√2D ．23．（4分）若实数x ，y 满足约束条件 {x −3y +4≥03x −y −4≤0x +y ≥0 ，则z=3x+2y 的最大值是（ ）A ．-1B ．1C ．10D ．124．（4分）祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V 柱体=sh ，其中s 是柱体的底面积，h 是柱体的高。

若某柱体的三视图如图所示，则该柱体的体积是（ ）A ．158B ．162C ．182D ．325．（4分）若a>0，b>0，则“a+b≤4“是“ab≤4”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件6．（4分）在同一直角坐标系中，函数y= 1a x ，y=log a(x+ 12），（a>0且a≠1）的图像可能是（）A．B．C．D．7．（4分）设0＜a＜1随机变量X的分布列是则当a在（0，1）内增大时（）A．D（X）增大B．D（X）减小C．D（X）先增大后减小D．D（X）先减小后增大8．（4分）设三棱锥V-ABC的底面是正三角形，侧棱长均相等，P是棱V A上的点，（不含端点），记直线PB与直线AC所成角为α.直线PB与平面ABC所成角为β.二面角P-AC-B的平面角为γ。

则（）A．β＜γ，a ＜γB．β＜α，β＜γC．β＜α，γ＜αD．α＜β，γ＜β9．（4分）设a，b∈R，函数f（x）= {x,x<01 3x 3−12(a+1)x2+ax,x≥0，若函数y=f（x）-ax-b恰有3个零点，则（）A．a＜-1，b＜0B．a＜-1，b>0C ． a ＞-1，b ＞0D ．a>-1，b>010．（4分）设a ，b ∈R ，数列{a n }，满足a 1 =a ，a n+1= a n 2+b ，b ∈N *，则（ ）A ．当b= 12 时，a 10>10B ．当b= 14 时，a 10>10C ．当b=-2时，a 10>10D ．当b=-4时，a 10>10二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

绝密★启用前2019年普通高等学校招生全国统一考试（浙江卷）数学本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至2页；非选择题部分3至4页。

满分150分。

考试用时120分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：若事件A，B互斥，则若事件A，B相互独立，则若事件A在一次试验中发生的概率是p，则n次独立重复试验中事件A恰好发生k次的概率台体的体积公式其中分别表示台体的上、下底面积，表示台体的高柱体的体积公式其中表示柱体的底面积，表示柱体的高锥体的体积公式其中表示锥体的底面积，表示锥体的高球的表面积公式球的体积公式其中表示球的半径一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（4分）已知全集U＝{﹣1，0，1，2，3}，集合A＝{0，1，2}，B＝{﹣1，0，1}，则（∁U A）∩B＝（）A．{﹣1}B．{0，1}C．{﹣1，2，3}D．{﹣1，0，1，3} 2．（4分）渐近线方程为x±y＝0的双曲线的离心率是（）A．B．1C．D．23．（4分）若实数x，y满足约束条件则z＝3x+2y的最大值是（）A．﹣1B．1C．10D．124．（4分）祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体＝Sh，其中S是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm），则该柱体的体积（单位：cm3）是（）A．158B．162C．182D．3245．（4分）若a＞0，b＞0，则“a+b≤4”是“ab≤4”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件6．（4分）在同一直角坐标系中，函数y＝，y＝1og a（x+）（a＞0且a≠1）的图象可能是（）A．B．C．D．7．（4分）设0＜a＜1．随机变量X的分布列是X0a1P则当a在（0，1）内增大时，（）A．D（X）增大B．D（X）减小C．D（X）先增大后减小D．D（X）先减小后增大8．（4分）设三棱锥V﹣ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点（不含端点）．记直线PB与直线AC所成角为α，直线PB与平面ABC所成角为β，二面角P ﹣AC﹣B的平面角为γ，则（）A．β＜γ，α＜γB．β＜α，β＜γC．β＜α，γ＜αD．α＜β，γ＜β9．（4分）设a，b∈R，函数f（x）＝若函数y＝f（x）﹣ax﹣b恰有3个零点，则（）A．a＜﹣1，b＜0B．a＜﹣1，b＞0C．a＞﹣1，b＜0D．a＞﹣1，b＞0 10．（4分）设a，b∈R，数列{a n}满足a1＝a，a n+1＝a n2+b，n∈N*，则（）A．当b＝时，a10＞10B．当b＝时，a10＞10C．当b＝﹣2时，a10＞10D．当b＝﹣4时，a10＞10二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2019年普通高等学校招生全国统一考试（浙江卷）数学参考公式：分别表示台体的上、下底面积，h表选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分,在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集{}1,0,1,2,3U=-，集合{}0,1,2A=，{}101B=-,,，则（∁U A）∩B＝（）A. {}1-B. {}0,1C. {}1,2,3- D. {}1,0,1,3-2.渐近线方程为0x y±=的双曲线的离心率是（）A. B. 1C. D. 23.若实数,x y满足约束条件340340x yx yx y-+≥⎧⎪--≤⎨⎪+≥⎩，则32z x y=+的最大值是（）A. 1- B. 1C 10 D. 124.祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V Sh =柱体，其中S 是柱体的底面积，h 是柱体的高，若某柱体的三视图如图所示，则该柱体的体积是（ ）A. 158B. 162C. 182D. 325.若0,0ab >>，则“4a b +≤”是 “4ab ≤”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件6.在同一直角坐标系中，函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且0)a ≠的图象可能是（ ）A. B.C. D.7.设01a <<，则随机变量X 的分布列是：则当a 在()0,1内增大时（ ） A. ()D X 增大 B. ()D X 减小C. ()D X 先增大后减小D. ()D X 先减小后增大8.设三棱锥V ABC-的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则（ ） A. ,βγαγ<< B. ,βαβγ<< C. ,βαγα<<D. ,αβγβ<< 9.已知,a b R ∈，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则（ ） A. 1,0a b <-< B. 1,0a b <-> C.1,0a b >->D. 1,0a b >-< 10.设,a b R ∈，数列{}n a 中，a 1=a ，a n +1=a n 2+b ，n *∈N ， ,则（ ）A. 当101,102b a =>B. 当101,104b a => C. 当102,10b a =->D. 当104,10b a =->非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分11.复数11z i=+（i 为虚数单位），则||z =________. 12.已知圆C 的圆心坐标是(0,)m ，半径长是r .若直线230x y -+=与圆相切于点(2,1)A --，则m =_____，r =______.13.在二项式9)x 的展开式中，常数项是________；系数为有理数的项的个数是_______.14.在ABC 中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD =____；cos ABD ∠=________.15.已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF的斜率是_______.16.已知a R ∈，函数3()f x ax x =-，若存在t R ∈，使得2|(2)()|3f t f t +-≤，则实数a 的最大值是____. 17.已知正方形ABCD 的边长为1，当每个(1,2,3,4,5,6)i i λ=取遍±1时，123456||AB BC CD DA AC BD λλλλλλ+++++的最小值是________；最大值是_______. 三、解答题：本大题共5小题，共74分，解答应写出文字说明、证明过程或演算步骤.18.设函数()sin ,f x x x =∈R .（1）已知[0,2),θ∈π函数()f x θ+是偶函数，求θ的值； （2）求函数22[()][()]124y f x f x ππ=+++ 的值域. 19.如图，已知三棱柱111ABC A B C -，平面11A AC C ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是11,AC A B 的中点.（1）证明：EF BC ⊥； （2）求直线EF 与平面1A BC 所成角的余弦值.20.设等差数列{}n a 前n 项和为n S ，34a =，43a S =，数列{}n b 满足：对每12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.（1）求数列{},{}n n a b 的通项公式；（2）记,,2nn na C nb *=∈N 证明：12+2,.n C C C n n *++<∈N21.如图，已知点(10)F ，为抛物线22(0)y px p =>，点F 为焦点，过点F 的直线交抛物线于,A B 两点，点C 在抛物线上，使得ABC 的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S.（1）求p 的值及抛物线的标准方程；（2）求12S S 的最小值及此时点G 的坐标.22.已知实数0a ≠，设函数()=ln 1,0.f x a x x x +>（1）当34a =-时，求函数()f x 的单调区间； （2）对任意21[,)e x ∈+∞均有(),2x f x a≤ 求a 的取值范围. 注：e 2.71828...=为自然对数的底数.2019年普通高等学校招生全国统一考试（浙江卷）数学参考公式：分别表示台体的上、下底面积，h 表选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分,在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}101B =-,,，则（∁U A ）∩B ＝（ ）A. {}1-B.{}0,1C. {}1,2,3-D. {}1,0,1,3-【答案】A 【解析】 【分析】本题借根据交集、补集的定义可得.容易题，注重了基础知识、基本计算能力的考查. 【详解】={1,3}U C A -，则(){1}U C A B =-【点睛】易于理解集补集的概念、交集概念有误.2.渐近线方程为0x y ±=的双曲线的离心率是（ ）A. B. 1C.D. 2【答案】C 【解析】 【分析】本题根据双曲线的渐近线方程可求得1a b ==，进一步可得离心率.容易题，注重了双曲线基础知识、基本计算能力的考查.【详解】因为双曲线的渐近线为0x y ±=，所以==1a b，则c ==，双曲线的离心率ce a==【点睛】理解概念，准确计算，是解答此类问题的基本要求.部分考生易出现理解性错误.3.若实数,x y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则32z x y =+的最大值是（ ）A. 1-B. 1C. 10D. 12【答案】C 【解析】 【分析】本题是简单线性规划问题的基本题型，根据“画、移、解”等步骤可得解.题目难度不大题，注重了基础知识、基本技能的考查.【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以(-1,1),(1,-1),(2,2)为顶点的三角形区域（包含边界），由图易得当目标函数=3+2z x y 经过平面区域的点(2,2)时，=3+2z x y 取最大值max 322210z =⨯+⨯=.【点睛】解答此类问题，要求作图要准确，观察要仔细.往往由于由于作图欠准确而影响答案的准确程度，也有可能在解方程组的过程中出错.4.祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V Sh =柱体，其中S 是柱体的底面积，是柱体的高，若某柱体的三视图如图所示，则该柱体的体积是（ ）A. 158B. 162C. 182D. 32【答案】B 【解析】 【分析】本题首先根据三视图，还原得到几何体—棱柱，根据题目给定的数据，计算几何体的体积.常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查.【详解】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯=⎪⎝⎭.【点睛】易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算. 5.若0,0ab >>，则“4a b +≤”是 “4ab ≤”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A 【解析】 【分析】本题根据基本不等式，结合选项，判断得出充分性成立，利用“特殊值法”，通过特取,a b 值，推出矛盾，确定必要性不成立.题目有一定难度，注重重要知识、基础知识、逻辑推理能力的考查.【详解】当0, 0a >b >时，2a b ab +≥，则当4a b +≤时，有24ab a b ≤+≤，解得4ab ≤，充分性成立；当=1, =4a b 时，满足4ab ≤，但此时=5>4a+b ，必要性不成立，综上所述，“4a b +≤”是“4ab ≤”的充分不必要条件.【点睛】易出现的错误有，一是基本不等式掌握不熟，导致判断失误；二是不能灵活的应用“赋值法”，通过特取,a b 的值，从假设情况下推出合理结果或矛盾结果.6.在同一直角坐标系中，函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且0)a ≠的图象可能是（ ） A. B.C. D.【答案】D 【解析】 【分析】本题通过讨论a 的不同取值情况，分别讨论本题指数函数、对数函数的图象和，结合选项，判断得出正确结论.题目不难，注重重要知识、基础知识、逻辑推理能力的考查.【详解】当01a <<时，函数xy a =过定点(0,1)且单调递减，则函数1x y a=过定点(0,1)且单调递增，函数1log 2a y x ⎛⎫=+⎪⎝⎭过定点1(,0)2且单调递减，D 选项符合；当1a >时，函数x y a =过定点(0,1)且单调递增，则函数1x y a =过定点(0,1)且单调递减，函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,02）且单调递增，各选项均不符合.综上，选D.【点睛】易出现的错误有，一是指数函数、对数函数的图象和性质掌握不熟，导致判断失误；二是不能通过讨论a 的不同取值范围，认识函数的单调性.7.设01a <<，则随机变量X 的分布列是：则当a 在()0,1内增大时（ ） A. ()D X 增大 B. ()D X 减小C. ()D X 先增大后减小D. ()D X 先减小后增大【答案】D 【解析】 【分析】研究方差随a 变化的增大或减小规律，常用方法就是将方差用参数a 表示，应用函数知识求解.本题根据方差与期望的关系，将方差表示为a 的二次函数，二测函数的图象和性质解题.题目有一定综合性，注重重要知识、基础知识、运算求解能力的考查. 【详解】方法1：由分布列得1()3aE X +=，则 2222111111211()01333333926a a a D X a a +++⎛⎫⎛⎫⎛⎫⎛⎫=-⨯+-⨯+-⨯=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，则当a 在(0,1)内增大时，()D X 先减小后增大.方法2：则()222221(1)222213()()03399924a a a a D X E X E X a ⎡⎤+-+⎛⎫=-=++-==-+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦故选D.【点睛】易出现的错误有，一是数学期望、方差以及二者之间的关系掌握不熟，无从着手；二是计算能力差，不能正确得到二次函数表达式.8.设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则（ ） A. ,βγαγ<< B. ,βαβγ<< C.,βαγα<<D.,αβγβ<<【答案】B 【解析】 【分析】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.【详解】方法1：如图G 为AC 中点，V 在底面ABC 的投影为O ，则P 在底面投影D 在线段AO 上，过D 作DE 垂直AE ，易得//PE VG ，过P 作//PF AC 交VG 于F ，过D 作//DH AC ，交BG 于H ，则,,BPF PBD PED α=∠β=∠γ=∠，则cos cos PF EG DH BDPB PB PB PBα===<=β，即αβ>，tan tan PD PDED BDγ=>=β，即y >β，综上所述，答案为B.方法2：由最小角定理βα<，记V AB C --的平面角为γ'（显然γ'=γ） 由最大角定理β<γ'=γ，故选B.法2：（特殊位置）取V ABC -为正四面体，P 为VA 中点，易得333222cos sin sin 6633α=⇒α=β=γ=，故选B. 【点睛】常规解法下易出现的错误有，不能正确作图得出各种角.未能想到利用“特殊位置法”，寻求简便解法.9.已知,a b R ∈，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则（ ） A. 1,0a b <-< B. 1,0a b <-> C.1,0a b >->D. 1,0a b >-<【答案】D 【解析】 【分析】本题综合性较强，注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函数方程的方法较为灵活，通常需要结合函数的图象加以分析. 【详解】原题可转化为()y f x =与y ax b =+，有三个交点.当BC AP λ=时，2()(1)()(1)f x x a x a x a x '=-++=--，且(0)0,(0)f f a ='=，则（1）当1a ≤-时，如图()y f x =与y ax b =+不可能有三个交点（实际上有一个），排除A ，B（2）当1a >-时，分三种情况，如图()y f x =与y ax b =+若有三个交点，则0b <，答案选D下面证明：1a >-时，BC AP λ=时3211()()(1)32F x f x ax b x a x b =--=-+-，2()(1)((1))F x x a x x x a '=-+=-+，则(0)0 ,(+1)<0F >F a ，才能保证至少有两个零点，即310(1)6b a >>-+，若另一零点在0<【点睛】遇到此类问题，不少考生会一筹莫展.由于方程中涉及,a b 两个参数，故按“一元化”想法，逐步分类讨论，这一过程中有可能分类不全面、不彻底..10.设,a b R ∈，数列{}n a 中，a 1=a ，a n +1=a n 2+b ，n *∈N ， ,则（ ） A. 当101,102b a => B. 当101,104b a => C. 当102,10b a =-> D. 当104,10b a =->【答案】A 【解析】 【分析】本题综合性较强，注重重要知识、基础知识、运算求解能力、分类讨论思想的考查.本题从确定不动点出发，通过研究选项得解.【详解】选项B ：不动点满足2211042x x x ⎛⎫-+=-= ⎪⎝⎭时，如图，若1110,,22n a a a ⎛⎫=∈< ⎪⎝⎭， 排除如图，若a 为不动点12则12n a = 选项C ：不动点满足22192024x x x ⎛⎫--=--= ⎪⎝⎭，不动点为ax 12-，令2a =，则210n a =<，排除选项D ：不动点满足221174024x x x ⎛⎫--=--= ⎪⎝⎭，不动点为17122x =±，令17122a =±，则171102n a =<，排除.选项A ：证明：当12b =时，2222132431113117,,12224216a a a a a a =+≥=+≥=+≥≥， 处理一：可依次迭代到10a ； 处理二：当4n ≥时，221112n n n a a a +=+≥≥，则则 12117(4)16n n a n -+⎛⎫≥≥ ⎪⎝⎭，则626410217164646311114710161616216a ⨯⎛⎫⎛⎫≥=+=++⨯+⋯⋯>++> ⎪ ⎪⎝⎭⎝⎭.故选A【点睛】遇到此类问题，不少考生会一筹莫展.利用函数方程思想，通过研究函数的不动点，进一步讨论a 的可能取值，利用“排除法”求解.非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分11.复数11z i=+（i 为虚数单位），则||z =________.【解析】 【分析】本题先计算z ，而后求其模.或直接利用模的性质计算. 容易题，注重基础知识、运算求解能力的考查.【详解】1|||1|z i ===+. 【点睛】本题考查了复数模的运算，属于简单题.12.已知圆C 的圆心坐标是(0,)m ，半径长是r .若直线230x y -+=与圆相切于点(2,1)A --，则m =_____，r =______.【答案】 (1). 2m =-(2). r =【解析】 【分析】本题主要考查圆的方程、直线与圆的位置关系.首先通过确定直线AC 的斜率，进一步得到其方程，将(0,)m 代入后求得m ，计算得解.【详解】可知11:1(2)22AC k AC y x =-⇒+=-+，把(0,)m 代入得2m =-，此时||r AC ===【点睛】：解答直线与圆的位置关系问题，往往要借助于数与形的结合，特别是要注意应用圆的几何性质.13.在二项式9)x 的展开式中，常数项是________；系数为有理数的项的个数是_______.【答案】 (1). (2). 5 【解析】 【分析】本题主要考查二项式定理、二项展开式的通项公式、二项式系数，属于常规题目.从写出二项展开式的通项入手，根据要求，考察x 的幂指数，使问题得解.【详解】9)x 的通项为919(0,1,29)rr r r T C x r -+==可得常数项为0919T C ==因系数为有理数，1,3,5,7,9r =，有246810T , T , T , T , T 共5个项【点睛】此类问题解法比较明确，首要的是要准确记忆通项公式，特别是“幂指数”不能记混，其次，计算要细心，确保结果正确. 14.ABC 中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD =____；cos ABD ∠=________.【答案】 (1). 5 (2). 10【解析】 【分析】本题主要考查解三角形问题，即正弦定理、三角恒等变换、数形结合思想及函数方程思想.通过引入CD x =，在BDC ∆、ABD ∆中应用正弦定理，建立方程，进而得解.. 【详解】在ABD ∆中，正弦定理有：sin sin AB BD ADB BAC =∠∠，而34,4AB ADB π=∠=,AC 5=，34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==，所以BD =72cos cos()coscos sinsin 44ABD BDC BAC BAC BAC ππ∠=∠-∠=∠+∠=【点睛】解答解三角形问题，要注意充分利用图形特征.15.已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______. 15【解析】 【分析】结合图形可以发现，利用三角形中位线定理，将线段长度用坐标表示考点圆的方程，与椭圆方程联立可进一步求解.利用焦半径及三角形中位线定理，则更为简洁. 【详解】方法1：由题意可知||=|2OF OM |=c =，由中位线定理可得12||4PF OM ==，设(,)P x y 可得22(2)16x y -+=，联立方程22195x y +=可解得321,22x x =-=（舍），点P 在椭圆上且在x 轴的上方， 求得3152P ⎛- ⎝⎭，所以1521512PF k ==方法2：焦半径公式应用解析1：由题意可知|2OF |=|OM |=c =，由中位线定理可得12||4PF OM ==，即342p p a ex x -=⇒=-求得315,22P ⎛- ⎝⎭，所以1521512PF k ==【点睛】本题主要考查椭圆的标准方程、椭圆的几何性质、直线与圆的位置关系，利用数形结合思想，是解答解析几何问题的重要途径.16.已知a R ∈，函数3()f x ax x =-，若存在t R ∈，使得2|(2)()|3f t f t +-≤，则实数a 的最大值是____. 【答案】max 43a = 【解析】 【分析】本题主要考查含参绝对值不等式、函数方程思想及数形结合思想，属于能力型考题.从研究()2(2)()23642f t f t a t t +-=++-入手，令2364[1,)m t t =++∈+∞，从而使问题加以转化，通过绘制函数图象，观察得解.【详解】使得()()222(2)()2(2)(2))223642f t f t a t t t t a t t +-=•++++-=++-，使得令2364[1,)m t t =++∈+∞，则原不等式转化为存在11,|1|3m am ≥-≤，由折线函数，如图只需113a -≤，即43a ≤，即a 的最大值是43【点睛】对于函数不等式问题，需充分利用转化与化归思想、数形结合思想.17.已知正方形ABCD 的边长为1，当每个(1,2,3,4,5,6)i i λ=取遍±1时，123456||AB BC CD DA AC BD λλλλλλ+++++的最小值是________；最大值是_______.【答案】 (1). 0 (2). 25 【解析】 【分析】本题主要考查平面向量的应用，题目难度较大.从引入“基向量”入手，简化模的表现形式，利用转化与化归思想将问题逐步简化. 【详解】()()12345613562456AB BC CD DA AC BD AB AD λ+λ+λ+λ+λ+λ=λ-λ+λ-λ+λ-λ+λ+λ要使123456AB BC CD DA AC BD λ+λ+λ+λ+λ+λ的最小，只需要135562460λ-λ+λ-λ=λ-λ+λ+λ=，此时只需要取1234561,1,1,1,1,1λ=λ=-λ=λ=λ=λ=此时123456min0AB BC CD DA AC BDλ+λ+λ+λ+λ+λ=等号成立当且仅当1356,,λ-λλ-λ均非负或者均非正，并且2456,,λ-λλ+λ均非负或者均非正。