圆的测试题

圆测试题及答案解析一、选择题1. 已知圆的半径为5，圆心到直线的距离为3，那么直线与圆的位置关系是什么？A. 直线与圆相离B. 直线与圆相切C. 直线与圆相交D. 直线在圆内答案：C解析：根据圆心到直线的距离小于圆的半径，可以判断直线与圆相交。

2. 圆的周长公式是什么？A. C = 2πrB. C = πr²C. C = 2rD. C = rπ答案：A解析：圆的周长公式是C = 2πr，其中C表示周长，r表示半径。

二、填空题1. 半径为7的圆的面积是 __________。

答案：153.94解析：圆的面积公式是A = πr²，将半径7代入公式得A = π ×7² ≈ 153.94。

2. 如果一个扇形的半径为10，圆心角为30°，那么它的弧长是__________。

答案：5π解析：弧长公式是L = θ × r，其中θ为圆心角（以弧度为单位），r为半径。

将圆心角30°转换为弧度是π/6，代入公式得L = π/6× 10 = 5π/3 ≈ 5。

三、简答题1. 描述圆的切线的性质。

答案：圆的切线在圆上某一点处与圆相切，且与过该点的半径垂直。

解析：圆的切线是一条直线，它恰好在一个点上与圆接触，并且这个接触点处的切线与从圆心到接触点的半径形成90°的角。

四、计算题1. 已知圆的半径为8，求圆的面积。

答案：圆的面积为200π。

解析：根据圆的面积公式A = πr²，将半径8代入公式得A = π × 8² = 64π ≈ 200π。

2. 已知圆的直径为20，求圆的周长。

答案：圆的周长为20π。

解析：圆的周长公式是C = πd，其中d为直径。

将直径20代入公式得C = π × 20 = 20π。

圆单元测试卷一、填空（第12题每格0.5分，其余每空1分，共35.5分）。

1．从圆心到圆上任意一点的线段叫( )。

通过（）并且（）都在（）的线段叫做直径。

圆的位置是由（）确定的，圆的大小决定于（）的长短。

2．在同一个圆里，所有的半径（），所有的（）也都相等，直径等于半径的（）。

3．圆周率表示同一圆内（）和（）的倍数关系，它用字母（）表示，保留两位小数后的近似值是（）。

4．在同一个圆内可以画（）条直径；如果用圆规画一个直径是10厘米的圆，圆规的两脚间的距离应该是（）厘米。

5．在长6厘米，宽4厘米的长方形内剪下一个最大的圆，这个圆的周长是（），面积是（），还剩下面积( )。

6．一个圆环，外圆半径是6分米，内圆半径4分米，圆环的面积是（）。

7．甲圆直径长8厘米，是乙圆直径的40%。

乙圆的周长是（）。

8．一个圆的半径是8厘米，这个圆面积的是（）平方厘米。

9．大圆的半径等于小圆直径，则大圆面积是小圆面积的（）倍，小圆周长是大圆周长的（）。

10．在一张长32厘米，宽16厘米的长方形内画半径是4厘米的圆，这样的圆最多能画（）个，这些圆的面积和是（）。

11．圆是（）图形，它有（）对称轴。

正方形有（）条对称轴，长方形有（）条对称轴，等边三角形有（）条对称轴。

12．填表：二、判断题。

（9分）1．圆的周长是它的直径的π倍。

（）2．半径为1厘米的圆的周长是3.14厘米。

（）3．一个圆的周长是12.56厘米，面积是12.56平方厘米。

（）4．圆的半径由6分米增加到9分米，圆的面积增加了45平方分米。

（）5．当长方形、正方形、圆的周长相等时，圆的面积最大。

（）6．水桶是圆形的。

（）7．半个圆的周长就是圆周长的一半。

（）8．所有的直径都相等。

（）9．π＝3.14．（）三、画一画。

(共7.5分)1．以O为圆心，画一个直径是 2．下面是正方形，在它的内4厘米的圆。

部画一个最大的圆。

·O3. 画出下列图形的所有对称轴。

(每条0.5分)四、计算下列各圆的周长。

圆测试题及答案
一、选择题
1. 下列哪个选项不是圆的基本性质？
A. 圆周上任意两点之间的线段称为弦。

B. 圆的直径是圆的最长弦。

C. 圆心到圆上任意一点的距离都相等。

D. 圆的面积与半径的平方成正比。

2. 圆的周长公式是什么？
A. C = πr
B. C = 2πr
C. C = 4πr
D. C = πr²
3. 已知圆的半径为3，求圆的周长。

A. 18π
B. 6π
C. 9π
D. 3π
二、填空题
4. 圆的面积公式为 \( A = \pi r^2 \)，其中 \( r \) 表示圆的________。

5. 如果圆的周长为12π，那么圆的半径是________。

三、计算题
6. 已知圆的半径为5厘米，求圆的周长和面积。

四、解答题
7. 如果一个圆的直径是14厘米，求圆的周长和面积，并用适当的单位表示结果。

答案：
一、选择题
1. D
2. B
3. A
二、填空题
4. 半径
5. 3
三、计算题
6. 圆的周长为 \( 2\pi \times 5 = 10\pi \) 厘米，圆的面积为\( \pi \times 5^2 = 25\pi \) 平方厘米。

四、解答题
7. 圆的周长为 \( 2\pi \times 7 = 14\pi \) 厘米，圆的面积为\( \pi \times (7)^2 = 49\pi \) 平方厘米。

初三数学圆测试题及答案初三数学圆测试题及答案一、填空题1、圆的位置由________决定，圆的大小决定于________的大小。

2、在平面上，到定点(0，0)和定直线x＝－2的距离相等的所有点构成图形是________；在球面上，到定点(－1，－1，－1)和定直线x ＋y＋z＝0的距离相等的所有点构成图形是________．3、圆可以看作是所有到定点(0，0)和定直线x＝＋t，y＝－t(t≥0)的距离相等的点的________．4、证明定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．5、木工椎木螺钉的螺纹是依据________制成的．6、计算公式＝________．7、等腰三角形两底角的平分线相等．；反之，等腰三角形两底角的平分线相等的三角形是．二、选择题8、雨花台区实验中学准备在体育场举办校运会，现将跑道内侧(跑道的内侧即是与终点线重合的短线)的直道部分改造为塑胶跑道，如果用半径为rcm的圆钢煨制(每个半径为rcm的圆钢可以将直道部分煨制30cm)，那么r为任意有理数时，所需的圆钢的总长度最少为( ) A. 60πcm B. 120πcm C. 75πcm D. 90πcm81、下列命题中正确的是( ) A. 平分弦的直径垂直于弦 B. 三角形的重心是其三条中线的交点 C. 能够完全重合的两个图形全等 D.一组对边平行且一组对角相等的四边形是平行四边形811、四边形ABCD内接于⊙O，则∠A，∠B，∠C，∠D这四个角之间的关系为( ) A. ∠A＋∠B＋∠C＋∠D＝360° B. ∠A＋∠B＋∠C＋∠D＝2π C. ∠A＋∠B＋∠C＋∠D＝π D. 无法确定三、解答题11、在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心，r为半径的圆与线段AB只有一个公共点，则半径r的取值范围是什么？111、小红在学习本节时，根据初步的几何知识知道半径相等的两个圆全等．她发现所有的圆形纸片都只有一条对称轴(即通过圆心的直线)，于是她大胆猜想：任何一个半径相等的圆都只有一条对称轴．你认为她的猜想正确吗？请说明理由．1111、等边三角形的半径为r，高为h，面积为S，根据已知条件填空：当等边三角形的半径为2时，高为________，面积为________；当等边三角形的半径为3时，高为________，面积为________；当等边三角形的半径为6时，高为________，面积为________．观察以上各题中半径、高和面积的数值关系，你发现了什么？。

人教版六年级上册数学第五单元《圆》测试卷一.选择题(共6题，共12分)1.在一张长8cm、宽6cm的长方形纸上画一个最大的圆，圆的半径是（）。

A.6cmB.3cmC.4c2.有大、小两个圆，大圆半径是5厘米，小圆半径是4厘米，小圆面积是大圆面积的（）。

A. B. C.3.画一个直径4厘米的圆，那么圆规两脚间的距离应该是（）厘米。

A.4厘米B.2厘米C.8厘米4.圆面积扩大16倍,则周长随着扩大（）。

A.16倍B.32倍C.4倍5.两个圆的周长不相等，是因为它们的（）。

A.圆心位置不同B.圆周率大小不等C.直径不相等6.在长15.6cm、宽7.5cm的长方形纸中，剪半径是1.5cm的圆，最多能剪（）个。

A.9B.10C.13二.判断题(共6题，共12分)1.面积相等的两个圆，它们的周长也一定相等。

（）2.用滚动法和绕绳法都可以测量硬币的周长。

（）3.任意一个圆的周长与它的直径的比值是3.14。

（）4.大圆和小圆的半径比是2:1，面积和周长的比都是2:1。

（）5.一个圆的半径的长短，决定了这个圆的大小。

（）6.两个半径不相等的圆，它们的周长与直径的比值也不相等。

（）三.填空题(共6题，共15分)1.圆的周长总是直径长度的（）倍多一些。

这个倍数是个固定的数，我们把它叫做（），用字母（）表示。

2.把一个圆平均分成若干（偶数）等份，剪开后可以拼成一个近似的（），这个长方形的长相当于圆的（），宽相当于圆的（）。

3.两个圆的半径比是1:4，这两个圆的周长比是（）:（）。

4.一个圆的半径是3厘米，这个圆的直径是（）厘米，周长是（）厘米。

5.一个周长是12.56厘米的圆，半径是（）厘米。

列式：（）。

6.三角形、四边形是直线图形，圆是（）图形；圆中心的一点叫做（），通过圆心，并且（）都在（）的线段叫做圆的直径；战国时期《墨经》一书中记载“圜（圆），一中同长也。

”表示圆心到圆上各点的距离都相等，即（）都相等。

四.计算题(共1题，共6分)1.求下面图形的周长。

六年级圆单元测试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 圆的周长公式是：A. C = πdB. C = πrC. C = 2πrD. C = 2d2. 半径为5厘米的圆的面积是：A. 25π cm²B. 50π cm²C. 78.5 cm²D. 314 cm²3. 下列哪个图形是圆？A. 正方形B. 长方形C. 三角形D. 所有点到圆心距离相等的图形4. 圆的直径是：A. 圆周上任意两点间的距离B. 圆心到圆周上任意一点的距离C. 通过圆心并且两端都在圆周上的线段D. 圆周上最长的线段5. 若一个圆的半径增加了2厘米，其周长将增加：A. 2厘米B. 4厘米C. 2π厘米D. 4π厘米二、判断题（每题1分，共5分）1. 圆的直径是半径的两倍。

（）2. 所有的直径都相等。

（）3. 圆的面积公式是A = πr²。

（）4. 圆的周长与半径成正比。

（）5. 圆的半径决定了圆的大小。

（）三、填空题（每题1分，共5分）1. 圆的面积公式是______。

2. 半径为r的圆的周长是______。

3. 若圆的周长是31.4厘米，则其半径是______厘米。

4. 圆的直径是半径的______倍。

5. 若圆的面积是28.26平方厘米，则其半径是______厘米。

四、简答题（每题2分，共10分）1. 解释什么是圆的半径。

2. 什么是圆的直径？3. 圆的周长与哪些因素有关？4. 如何计算圆的面积？5. 为什么说圆是最对称的图形？五、应用题（每题2分，共10分）1. 一个圆形花坛的直径是10米，计算花坛的周长和面积。

2. 若一个圆的周长是25.12厘米，求其半径。

3. 一个圆的面积是50.24平方厘米，求其半径和直径。

4. 如果一个圆的半径增加了3厘米，计算新圆的周长和面积。

5. 一个圆形池塘的半径是8米，计算池塘的面积。

六、分析题（每题5分，共10分）1. 小明家的圆形游泳池直径是12米，他想在游泳池周围铺设一圈鹅卵石，每米需要20颗鹅卵石。

一、填空：1、画圆时，圆规两脚之间的距离为4CM，那么这个圆的直径是（）CM，周长是（）CM ，面积是（）平方厘米。

2、圆的周长是它的直径的（）倍多一些，这个倍数是一个固定的数，我们把它叫（），常用字母（）表示。

它是一个（）小数，取两位小数是（）。

3、圆是（）图形，有（）条对称轴。

半圆有（）条对称轴。

4、把一个圆平均分成若干份，可以拼成一个近似于平行四边形的图形，分得越小，拼成的图形就越（）平行四边形。

平行四边形的底相当于圆周长的（），高相当于（），因为拼成的平行四边形的面积等于（），所以圆的面积就等于（），用字母表示是（）。

5、用一根长18.84DM的铁丝围成一个圆圈，所围成的圆圈的半径是（）DM，圆圈内的面积是（）平方分米。

6、在一个长8厘米、宽5厘米的长方形纸板上剪一个最大的圆，圆的面积是（）平方分米。

7、圆内两端都在圆上的线段有（）条，其中（）最长。

圆的直径和半径都有（）条。

8、圆心确定圆的（），（）确定圆的（）。

9、如果把一个圆的半径扩大到原来的2倍，则周长就会扩大到原来的（）倍，面积就会扩大到原来的（）倍。

10、有同一个圆心的圆叫（）圆，圆心位置不同而半径相等的圆叫（）圆。

二、判断：1、直径是半径的2倍，半径是直径的1/2。

2、两端都在圆上并且经过圆心的线段是直径。

3、圆的对称轴就是直径所在的直线。

4、圆的周长是直径的3.14倍。

5、两条半径就是一条直径。

6、半径为2厘米的圆，其面积和周长相等。

7、半圆的周长就是用圆的周长除以2。

8、把一个圆平均分成N个小扇形，当N的数值越来越大，每个小扇形就越来越接近三角形，其高越来越接近半径。

9、直径总比半径长。

10、用三根一样长的铁丝分别围成一个长方形、正方形和圆，圆的面积最大。

三、选择题。

把正确答案的序号填在（）里。

1、两个圆的面积不相等，是因为（）A、圆周率大小不同B、圆心的位置不同C、半径大小不同。

2、两个圆的周长相等，那么这两个圆的面积（）。

高中圆单元测试题及答案一、选择题（每题3分，共30分）1. 若圆的半径为3，则圆的面积为：A. 9πB. 18πC. 27πD. 36π2. 圆的周长公式为：A. C = 2πrB. C = πrC. C = 2πdD. C = πd3. 圆心角为60°的弧长为圆的周长的：A. 1/6B. 1/3C. 1/2D. 2/34. 圆的直径是半径的：A. 1倍B. 2倍C. 3倍D. 4倍5. 圆内接四边形的对角线：A. 相等B. 互补C. 垂直D. 平行6. 圆的切线垂直于：A. 圆心B. 圆的直径C. 圆的半径D. 圆的切点7. 圆的内切圆半径与外切圆半径之和等于：A. 内切圆半径B. 外切圆半径C. 两圆半径之和D. 两圆半径之差8. 圆的方程为(x-a)²+(y-b)²=r²，则圆心坐标为：A. (a, b)B. (b, a)C. (r, a)D. (a, r)9. 圆的切线与半径所成的角为：A. 90°B. 45°C. 30°D. 60°10. 圆的弦长公式为：A. L = 2r * sin(θ/2)B. L = 2r * cos(θ/2)C. L = 2r * tan(θ/2)D. L = 2r * cot(θ/2)二、填空题（每题2分，共20分）1. 半径为5的圆的面积为______。

2. 圆的周长为40π，则圆的半径为______。

3. 圆心角为90°的弧所对的弦长为圆的直径的______。

4. 圆的直径为10，则圆的周长为______。

5. 圆的内接三角形的内角和为______。

6. 圆的切线与半径所成的角的度数为______。

7. 圆的方程为(x-2)²+(y+3)²=25，则圆心坐标为______。

8. 圆的切线与半径所成的角的正弦值为______。

9. 圆的内切圆半径与外切圆半径之比为______。

圆测试题及答案一、填空题1、如图，AB是半圆O的直径，CB切⊙O于B，CD切⊙O于D，交BA的延长线于E，若EA=1，ED=2，则BC的长为．2、如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于点M．若OA=a，PM=√3a，那么△PMB的周长是．第1题图第2题图3、PA、PB切⊙O于A、B，∠APB=78°，点C是⊙O上异于A、B的任意一点，则∠ACB= ．4、如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的度数是度．5、如图，以△ABC的边AB为直径作⊙O交BC于D，过D作⊙O的切线交AC 于E，要使得DE⊥AC，则△ABC的边必须满足的条件是．6、如图，在Rt△ABC中，∠A=90°，⊙O分别与AB、AC相切于点E、F，圆心O在BC上，若AB=a，AC=b，则⊙O的半径等于第4题图第5题图第6题图二、选择题7、l1、l2表示直线，给出下列四个论断：①l1∥l2；②l1切⊙O于点A；③l2切⊙O 于点B；④AB是⊙O的直径．若以其中三个论断作为条件，余下的一个作为结论，可以构造出一些命题，在这些命题中，正确命题的个数为（）A、1B、2C、3D、48、如图，圆心O在边长为√2的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是（）A、2(√2-1)B、2(√2+1)C、2√2-1D、2√2+19、直角梯形ABCD中，AD∥BC，∠B=90°，AD+BC＜DC，若腰DC上有一点P，使AP⊥BP，则这样的点（）A、不存在B、只有一个C、只有两个D、有无数个10、如图，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，垂足是P，DH⊥BH，垂足是H，下列结论：①CH=CP；②AD=DB；③AP=BH；④DH为圆的切线．其中一定成立的是（）A、①②④B、①③④C、②③④D、①②③11、如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于C、D，交AB于E，AF为⊙O的直径，有下列结论：①∠ABP=∠AOP；②弧BC=弧DF；③OP∥BF；④AC平分∠PAB，其中结论正确的有（）A、1个B、2个C、3个D、4个第10题图第11题图第12题图12、如图，已知△ABC，过点A作外接圆的切线交BC延长线于点P，PC/PA=√2/2，点D在AC上，且AD/CD=1/2 ，延长PD交AB于点E，则AE/BE的值是（）三、解答题13、以等腰△ABC的一腰AB为直径的⊙O交BC于D，过D作DE⊥AC于E可得结论：DE是⊙O的切线．问：（1）若点O在AB上向点B移动，以O为圆心，OB长为半径的圆仍交BC于D，DE⊥AC的条件不变那么上述结论是否成立？请说明理由；（2）如果AB=AC=5cm，sinA=3/5 ，那么圆心O在AB的什么位置时，⊙O与AC 相切？14、已知Rt△ABC中，AC=5，BC=12，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）（1）当PQ∥AC，且Q为BC的中点时，求线段CP的长；（2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．15、如图1所示，在正方形ABCD中，AB=1，弧AC是以点B为圆心，AB长为半径的圆的一段弧，点E是边AD上的任意一点（点E与点A、D不重合），过E作AC所在圆的切线，交边DC于点F，G为切点．（1）当∠DEF=45°时，求证点G为线段EF的中点；（2）设AE=x，FC=y，求y关于x的函数解析式，并写出函数的定义域；（3）图2所示，将△DEF沿直线EF翻折后得△D1EF，当EF=5/6时，讨论△AD1D 与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．16、⊙O是△ABC的外接圆，已知∠ACB=45°，∠ABC=120°，⊙O的半径为1，（1）求弦AC、AB的长；（2）若P为CB的延长线上一点，试确定P点的位置，使PA与⊙O相切，并证明你的结论．17、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，∠POC=∠PCE．（1）求证：PC是⊙O的切线；（2）若OE：EA=1：2，PA=6，求⊙O的半径；（3）求sin∠PCA的值．18、（1）如图（a），已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F （不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连接AC、AD．求证：①∠BAD=∠CAG；②AC•AD=AE•AF；（2）在问题（1）中，当直线l向上平行移动，与⊙O相切时，其他条件不变．①请你在图（b）中画出变化后的图形，并对照图（a），标记字母；②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．19、如图，AB是⊙O的直径，点M是半径OA的中点，点P在线段AM上运动．点Q在上半圆上运动，且总保持PQ=PO，过点Q作⊙O的切线交BA的延长线于点C．（1）当∠QPA=90°时，判断△QCP是三角形；（2）当∠QPA=60°时，请你对△QCP的形状做出猜想，并给予证明；（3）由（1）、（2）得出的结论，进一步猜想，当点P在线段AM上运动到任何位置时，△QCP一定是三角形．20、如图，已知AB是半圆O的直径，AP为过点A的半圆的切线．在弧AB上任取一点C（点C与A、B不重合），过点C作半圆的切线CD交AP于点D；过点C作CE⊥AB，垂足为E．连接BD，交CE于点F．（1）当点C为弧AB的中点时（如图1），求证：CF=EF；（2）当点C不是弧AB的中点时（如图2），试判断CF与EF的相等关系是否保持不变，并证明你的结论．考点：切线的性质．21、如图△ABC中，∠C=90°，AC=6，BC=3，点D在AC边上，以D为圆心的⊙D与AB切于点E．（1）求证：△ADE∽△ABC；（2）设⊙D与BC交于点F，当CF=2时，求CD的长；（3）设CD=a，试给出一个a值使⊙D与BC没有公共点，并说明你给出的a值符合要求．22、如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D，求证AC2/BC2=AD/BD23、如图，⊙O′与x轴交于A、B两点，与y轴交于C、D两点，圆心O′的坐标为（1，-1），半径为√5．（1）求A，B，C，D四点的坐标；（2）求经过点D的切线解析式；（3）问过点A的切线与过点D的切线是否垂直？若垂直，请写出证明过程；若不垂直，试说明理由．第22题图第23题图24、当你进入博物馆的展览厅时，你知道站在何处观赏最理想？如图，设墙壁上的展品最高处点P距离地面a米，最低处点Q距离地面b米，观赏者的眼睛点E距离地面m米，当过P、Q、E三点的圆与过点E的水平线相切于点E时，视角∠PEQ最大，站在此处观赏最理想．（1）设点E到墙壁的距离为x米，求a、b、m、x的关系式；（2）当a=2.5，b=2，m=1.6，求：（ⅰ）点E和墙壁距离x；（ⅱ）最大视角∠PEQ的度数．（精确到1度）答案一、填空题（共6小题，每小题4分，满分24分）1、如图，AB是半圆O的直径，CB切⊙O于B，CD切⊙O于D，交BA的延长线于E，若EA=1，ED=2，则BC的长为．解：连接OD，由AB是半圆O的直径，得BC=DC，DE2=EA•EB，∵EA=1，ED=2，∴EB=4，∴AB=EB-EA=3，∴OD=OA=3/2 ，由CB切⊙O于B，CD切⊙O于D，知∠CBE=90°，∠ODE=90°，∴△CBE∽△ODE，解得EC=5，又∵CD和CB是⊙O的两条切线，∴CD=BC，则CD=EC-ED=5-2=3．2、如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于点M．若OA=a，PM=√3a，那么△PMB的周长是．解：连接OM；∵PM切⊙O于点M，∴∠OMP=90°，∵OA=OM=a，PM=√3a，∴tan∠MOP=MP：OM=√3，∴∠MOP=60°，∴OP=2a，∴PB=OP-OB=a；∵OM=OB，∴△OMB是等边三角形，MB=OB=a，∴△PMB的周长是（√3+2）a．3、PA、PB切⊙O于A、B，∠APB=78°，点C是⊙O上异于A、B的任意一点，则∠ACB= ．解：如图，连接OA，OB，∵PA、PB切⊙O于A、B，∴OA⊥PA，OB⊥PB，∴∠AOB=180°-∠BPA=180°-78°=102°，当C在优弧AB上，则∠ACB=1/2∠AOB=1/2 ×102°=51°；当C在劣弧AB上，即C′点，则∠AC′B=180°-51°=129°．4、如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的度数是度．解：∵EB、EC是⊙O的切线，∴EB=EC，又∵∠E=46°，∴∠ECB=∠EBC=67°，∴∠BCD=180°-（∠BCE+∠DCF）=180°-99°；∵四边形ADCB内接于⊙O，∴∠A+∠BCD=180°，∴∠A=99°．5、如图，以△ABC的边AB为直径作⊙O交BC于D，过D作⊙O的切线交AC 于E，要使得DE⊥AC，则△ABC的边必须满足的条件是．解：如图，连接OD，则OD⊥BC；∵DE⊥AC，∴OD∥AC，∴∠C=∠ODB；∵OD=OB，∴∠ODB=∠B，∴∠C=∠B，∴AC=AB．6、如图，在Rt△ABC中，∠A=90°，⊙O分别与AB、AC相切于点E、F，圆心O在BC上，若AB=a，AC=b，则⊙O的半径等于解：连接OA、OE、OF，∵AB、AC相切于点E、F，∴OE⊥AB，OF⊥AC，∵△OAC的面积= 1/2AC•OF=1/2 br，同理，△OAB的面积= 1/2AB•OE=1/2 ar，又∵△ABC的面积=△OAC的面积+△OAB的面积，∴ab= br+ ar，∴r=ab/(a+b) ．二、选择题（共8小题，每小题3分，满分24分）7、l1、l2表示直线，给出下列四个论断：①l1∥l2；②l1切⊙O于点A；③l2切⊙O 于点B；④AB是⊙O的直径．若以其中三个论断作为条件，余下的一个作为结论，可以构造出一些命题，在这些命题中，正确命题的个数为（）A、1B、2C、3D、4解：第一种情况：①②③⇒④∵l1切⊙O于点A，l2切⊙O于点B∴OA⊥l1，OB⊥l2又∵l1∥l2∴OA⊥l2∴OA、OB为在同一条上∴AB是⊙O的直径命题成立；第二种情况：①②④⇒③∵l1切⊙O于点A∴OA⊥l1，∵AB是⊙O的直径；l1∥l2∴AB⊥l2即l2切⊙O于点B命题成立；第三种情况：①③④⇒②同第二种情况；命题成立第四种情况：②③④⇒①．∵l1切⊙O于点A，l2切⊙O于点B∴OA⊥l1，OB⊥l2又∵AB是⊙O的直径∴l1∥l2命题成立．故答案为D8、如图，圆心O在边长为√2的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是（）A、2(√2-1)B、2(√2+1)C、2√2-1D、2√2+1解：连接OE、OF，如图，设圆的半径为r，∴四边形OEDF是正方形，∴OD= √2r，BD=2，∵OB=r，∴√2r+r=2，解得r=2 √2-2，故选A．9、直角梯形ABCD中，AD∥BC，∠B=90°，AD+BC＜DC，若腰DC上有一点P，使AP⊥BP，则这样的点（）A、不存在B、只有一个C、只有两个D、有无数个解：这样的点有2个．设AB中点是M，使AP⊥BP的点P在以M为圆心，以1/2AB长为半径的圆上；若CD与圆M相切时，则AD+BC=DC；若CD与圆M相离时，则AD+BC＞DC；已知AD+BC＜DC，则CD与圆M一定相交，有两个交点．故选C．10、如图，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，垂足是P，DH⊥BH，垂足是H，下列结论：①CH=CP；②AD=DB；③AP=BH；④DH为圆的切线．其中一定成立的是（）A、①②④B、①③④C、②③④D、①②③解：连接BD．由题意可证△PCD≌△HCD（HL），∴CH=CP；还可以证明△ADP≌△BDH（AAS），∴AD=DB；AP=BH．因圆的直径不确定，而无法证明DH为圆的切线．故选D．11、如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于C、D，交AB于E，AF为⊙O的直径，有下列结论：①∠ABP=∠AOP；②弧BC=弧DF；③OP∥BF；④AC平分∠PAB，其中结论正确的有（）A、1个B、2个C、3个D、4个12、如图，已知△ABC，过点A作外接圆的切线交BC延长线于点P，PC/PA=√2/2，点D在AC上，且AD/CD=1/2 ，延长PD交AB于点E，则AE/BE的值是（）解：如图，由∠PAC=∠B，则△PAC∽△PBA．故S△PAC/S△PBA =PC2/PA2 =1/2 ．又S△PAE/S△PBE=S△EAD/S△BED=AE/BE故S△PAD/S△PBD= AE/BE又S△PAD/S△PCD=AD/CD =S△BAD/S△BCD=1/2 ，则S△PAC/S△PBA=3S△PAD/(3/2S△PBD)=2×AE/BE．于是，2×AE/BE =1/2 ，AE/BE =1/4 ．三、解答题（共12小题，满分102分）15、如图，以等腰△ABC的一腰AB为直径的⊙O交BC于D，过D作DE⊥AC于E可得结论：DE是⊙O的切线．问：（1）若点O在AB上向点B移动，以O为圆心，OB长为半径的圆仍交BC于D，DE⊥AC的条件不变那么上述结论是否成立？请说明理由；（2）如果AB=AC=5cm，sinA=3/5 ，那么圆心O在AB的什么位置时，⊙O与AC相切？解：（1）连接OD；∵OD=OB，∴∠ABC=∠ODB，∵AB=AC，∴∠ABC=∠ACB，∴∠ACB=∠ODB，∴OD∥AC；又∵DE⊥AC，∴DE⊥OD即DE是⊙O的切线．（2）如图所示⊙O与AC相切与F，⊙O与AB相交于G．则OF⊥AC；在RT△AOF中，sinA=OF：AO=3：5；设OF=3X，AO=5X，则OB=OG=OF=3X，OG=2X，∴8x=AB=5，∴X=5/8 ，此时OB=3x=15/8 时，即当圆心O在AB上距B点为3x= 15/8时，⊙O与AC相切．14、已知Rt△ABC中，AC=5，BC=12，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）（1）如图，当PQ∥AC，且Q为BC的中点时，求线段CP的长；（2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．解：（1）在Rt△ABC中∠ACB=90°，AC=5，BC=12，∴AB=13；∵Q是BC的中点，∴CQ=QB；又∵PQ∥AC，∴AP=PB，即P是AB的中点，∴Rt△ABC中，CP= ．（2）解：当AC与PQ不平行时，只有∠CPQ为直角，△CPQ才可能是直角三角形．以CQ为直径作半圆D，①当半圆D与AB相切时，设切点为M，连接DM，则DM⊥AB，且AC=AM=5，∴MB=AB-AM=13-5=8；设CD=x，则DM=x，DB=12-x；在Rt△DMB中，DB2=DM2+MB2，即（12-x）2=x2+82，解之得x=10/3 ，∴CQ=2x=20/3 ；即当CQ= 20/3且点P运动到切点M位置时，△CPQ为直角三角形．②当20/3 ＜CQ＜12时，半圆D与直线AB有两个交点，当点P运动到这两个交点的位置时，△CPQ为直角三角形③当0＜CQ＜20/3 时，半圆D与直线AB相离，即点P在AB边上运动时，均在半圆D外，∠CPQ＜90°，此时△CPQ不可能为直角三角形．∴当20/3≤CQ＜12时，△CPQ可能为直角三角形．15、如图1所示，在正方形ABCD中，AB=1，弧AC是以点B为圆心，AB长为半径的圆的一段弧，点E是边AD上的任意一点（点E与点A、D不重合），过E作AC所在圆的切线，交边DC于点F，G为切点．（1）当∠DEF=45°时，求证点G为线段EF的中点；（2）设AE=x，FC=y，求y关于x的函数解析式，并写出函数的定义域；（3）图2所示，将△DEF沿直线EF翻折后得△D1EF，当EF=5/6时，讨论△AD1D 与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．证明：（1）∵∠DEF=45°，∴∠DFE=90°-∠DEF=45°．∴∠DFE=∠DEF．∴DE=DF．又∵AD=DC，∴AE=FC．∵AB是圆B的半径，AD⊥AB，∴AD切圆B于点A．同理：CD切圆B于点C．又∵EF切圆B于点G，∴AE=EG，FC=FG．∴EG=FG，即G为线段EF的中点．（2）根据（1）中的线段之间的关系，得EF=x+y，DE=1-x，DF=1-y，根据勾股定理，得：（x+y）2=（1-x）2+（1-y）2∴y=(1-x)/(1+x) （0＜y＜1）．（3）当EF= 5/6时，由（2）得EF=EG+FG=AE+FC，即x+ (1-x)/(1+x)= 5/6，解得x1=1/3 或x2= 1/2．①当AE=1/2 时，△AD1D∽△ED1F，证明：设直线EF交线段DD1于点H，由题意，得：△EDF≌△ED1F，EF⊥DD1且DH=D1H．∵AE=1/2 ，AD=1，∴AE=ED．∴EH∥AD1，∠AD1D=∠EHD=90°．又∵∠ED1F=∠EDF=90°，∴∠ED1F=∠AD1D．∴△ED1F∽△AD1D②当AE=1/3 时，△ED1F与△AD1D不相似．16、⊙O是△ABC的外接圆，已知∠ACB=45°，∠ABC=120°，⊙O的半径为1，（1）求弦AC、AB的长；（2）若P为CB的延长线上一点，试确定P点的位置，使PA与⊙O相切，并证明你的结论．17、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，∠POC=∠PCE．（1）求证：PC是⊙O的切线；（2）若OE：EA=1：2，PA=6，求⊙O的半径；（3）求sin∠PCA的值．解：（1）∵弦CD⊥AB于点E，∴∠CEP=90°．∵∠POC=∠PCE，∠P=∠P，∴△POC∽△PCE，∴∠PCO=∠CEP=90°．∴PC是⊙O的切线．18、（1）如图（a），已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F （不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连接AC、AD．求证：①∠BAD=∠CAG；②AC•AD=AE•AF；（2）在问题（1）中，当直线l向上平行移动，与⊙O相切时，其他条件不变．①请你在图（b）中画出变化后的图形，并对照图（a），标记字母；②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．解：（1）证明：①连接BD，∵AB是⊙O的直径，∴∠ADB=90°．∴∠AGC=∠ADB=90°．又∵ACDB是⊙O内接四边形，∴∠ACG=∠B．∴∠BAD=∠CAG．②连接CF，∵∠BAD=∠CAG，∠EAG=∠FAB，∴∠DAE=∠FAC．又∵∠ADC=∠F，∴△ADE∽△AFC．∴AD/AF=AE/AC ．∴AC•AD=AE•AF．（2）①如图；②两个结论都成立，证明如下：①连接BC，∵AB是直径，∴∠ACB=90°．∴∠ACB=∠AGC=90°．∵GC切⊙O于C，∴∠GCA=∠ABC．∴∠BAC=∠CAG（即∠BAD=∠CAG）．②连接CF，∵∠CAG=∠BAC，∠GCF=∠GAC，∴∠GCF=∠CAE，∠ACF=∠ACG-∠GFC，∠E=∠ACG-∠CAE．∴∠ACF=∠E．∴△ACF∽△AEC．∴AC/AE=AF/AC ．∴AC2=AE•AF（即AC•AD=AE•AF）．19、如图，AB是⊙O的直径，点M是半径OA的中点，点P在线段AM上运动．点Q在上半圆上运动，且总保持PQ=PO，过点Q作⊙O的切线交BA的延长线于点C．（1）当∠QPA=90°时，判断△QCP是三角形；（2）当∠QPA=60°时，请你对△QCP的形状做出猜想，并给予证明；（3）由（1）、（2）得出的结论，进一步猜想，当点P在线段AM上运动到任何位置时，△QCP一定是三角形．解：（1）等腰直角三角形；（2）当∠QPA=60°，△QCP是等边三角形．证明：连接OQ．CQ是⊙O的切线，∴∠OQC=90°．∵PQ=PO，∴∠PQO=∠QOP．∴∠QOP+∠QCO=90°，∠OQP+∠CQP=90°，∴∠QCO=∠CQP．∴PQ=PC．又∠QPA=60°，∴△QCP是等边三角形；（3）等腰三角形．20、如图，已知AB是半圆O的直径，AP为过点A的半圆的切线．在弧AB上任取一点C（点C与A、B不重合），过点C作半圆的切线CD交AP于点D；过点C 作CE⊥AB，垂足为E．连接BD，交CE于点F．（1）当点C为弧AB的中点时（如图1），求证：CF=EF；（2）当点C不是弧AB的中点时（如图2），试判断CF与EF的相等关系是否保持不变，并证明你的结论．考点：切线的性质．证明：（1）∵DA是切线，AB为直径，∴DA⊥AB．∵点C是弧AB的中点，且CE⊥AB，∴点E为半圆的圆心．又∵DC是切线，∴DC⊥EC．又∵CE⊥AB，∴四边形DAEC是矩形．∴CD∥AD，CD=AD．∴EF:AD =BE:AB=1/2 ．即EF=1/2AD=1/2EC．∴F为EC的中点，CF=EF．（2）CF=EF，证明：连接BC，并延长BC交AP于G点，连接AC，如图所示：∵AD、DC是半圆O的切线，∴DC=DA，∴∠DAC=∠DCA．∵AB是直径，∴∠ACB=90°，∴∠ACG=90°．∴∠DGC+∠DAC=∠DCA+∠DCG=90°．∴∠DGC=∠DCG．∴在△GDC中，GD=DC．∵DC=DA，∴GD=DA．∵AP是半圆O的切线，∴AP⊥AB，又CE⊥AB．∴CE∥AP．∴DG:CF=DB:FB=DA:FE．∵GD=AD，∴CF=EF．21、如图△ABC中，∠C=90°，AC=6，BC=3，点D在AC边上，以D为圆心的⊙D与AB切于点E．（1）求证：△ADE∽△ABC；（2）设⊙D与BC交于点F，当CF=2时，求CD的长；（3）设CD=a，试给出一个a值使⊙D与BC没有公共点，并说明你给出的a值符合要求．（1）证明：∵点E是切点∴∠AED=90°∵∠A=∠A，∠ACB=90°∴△ADE∽△ABC；22、如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D，求证AC2/BC2=AD/BD23、如图，⊙O′与x轴交于A、B两点，与y轴交于C、D两点，圆心O′的坐标为（1，-1），半径为√5．（1）求A，B，C，D四点的坐标；（2）求经过点D的切线解析式；（3）问过点A的切线与过点D的切线是否垂直？若垂直，请写出证明过程；若不垂直，试说明理由．24、当你进入博物馆的展览厅时，你知道站在何处观赏最理想？如图，设墙壁上的展品最高处点P距离地面a米，最低处点Q距离地面b米，观赏者的眼睛点E距离地面m米，当过P、Q、E三点的圆与过点E的水平线相切于点E时，视角∠PEQ最大，站在此处观赏最理想．（1）设点E到墙壁的距离为x米，求a、b、m、x的关系式；（2）当a=2.5，b=2，m=1.6，求：（ⅰ）点E和墙壁距离x；（ⅱ）最大视角∠PEQ的度数．（精确到1度）解：（1）由题意可知：据PR=a，QR=b，HR=m，HE=x，∴HQ=QR-HR=b-m，PH=PR-HR=a-m，∵HE是圆O的切线，∴HE2=HQ•HP，∴x2=（a-m）（b-m）．（2）①根据（1）中得出的x2=（a-m）（b-m），∴x2=（2.5-1.6）×（2-1.6）=0.36，∴x=0.6．②在直角三角形PHE中，EH=0.6，PH=0.9，∴tan∠PEH=PH/HE =3/2 ，因此∠PEH≈56.3°；在直角三角形HQE中，QH=0.4，EH=0.6，∴tan∠HEQ=QH/HE=2/3 ，因此∠HEQ≈33.7°；∴∠PEQ=∠PEH-∠HEQ=56.3-33.7=22.6°．。

2.5 米，在花坛一周铺了一条宽 0.5 米的碎石小路，小路的面积11． 两个圆的周长之比是 2：5，则它的面积之比是（A. 18.84 二、填空题13．如图，正方形 ABCD 的边 AB=1，弧 BD 和弧 AC 都是以 1 为半径的圆弧，则无阴影的两 部分的面积之差为 。

常考题》小学数学六年级上册第五单元《圆》测试卷（含答案解析）一、选择题 1． 圆是轴对称图形，它有（ ）条对称轴。

A. 一 B. 两 C. 无数 D. 四 2．把一个直径 10 厘米圆分成两个相等的半圆，两个半圆的周长的和是（ ） A. 31.4 B . 62.8 C . 41.4 D . 51.4 3．已知圆的周长是 18.84 厘米，它的直径是（ ） B. 12.56 厘米 A. 6 厘米 C. 12 厘米 4．在圆内剪去一个圆心角为 45 的扇形，余下部分的面积是剪去部分面积的（ ）倍． A. 9 5．两个圆的周长不相等，是因为它们的（ A. 圆心位置不同 B. 半径不相等 ）。

C. 圆周率不相等 6．大圆的半径是小圆的直径，则大圆面积是小圆面积的 A. 2 倍 B. 倍4 ）。

C. 12 D. 14 5cm，周长是（ A. 6.28cm 2 个半圆后，每个半圆的周长是 ） cm 。

C. 10π D. 10 π +10 ）。

B . 3.14cm C . 4.14cm D . 5.14cm A. 27.475 B . 9.42 C . 8.635 D .28.26 10．如果一个圆的半径由 A. 2 1 分米增加到 2 分米，它的周长增加了（ B . 6.28 C . 12.56 ）分米。

D . 18.84 A. 2： 5 B. ：5 2 C.： 425 D. 2：5 4 12．一个圆的半径是 6 厘米，它的周长是 ）厘米。

9．一个圆形花坛的半径是 是（ ）平方米。

）。

B. 37.68C. 113.0414． 如图所示的图形由 1 个大半圆弧和 6 个小半圆弧组成，已知最大半圆弧的直径是这个图形的周长为 _____ 。

圆精选测试题（一）一、填空题̂=CD̂=BD̂，M是AB上一动点，则CM+DM的最1.在⊙O中，AB是⊙O的直径，AB=8cm，AC小值为____________.2.如图，正三角形ABC的边长为2，D、E、F分别为BC、CA、AB的中点，以A、B、C三点为圆心，半径为1作圆，则圆中阴影部分的面积是____________.3.如图，在△ABC中，∠C=90°，∠A=25°，以点C为圆心，BC为半径的圆交AB于点D，̂的度数为．交AC于点E，则BD4.如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC=110°．连接AC，则∠A的度数是．5.如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为4，则阴影部分的面积等于___ ．6.如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙上一点，连接PD．已知PC=PD=BC．下列结论：（1）PD与⊙O相切;（2）四边形PCBD是菱形;（3）PO=AB;（4）∠PDB=120°.其中正确的是_____________.7.如图，半径为2，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为____________.二、解决问题1.如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．2.如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=BFD．（1）求证：FD是⊙O的切线；（2）若AB=10，AC=8，求DF的长．3.如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．（1）求AC、AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由．4.如图，AB是⊙O的直径，点C在0O上，连接BC，AC，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．（1)求证：DE是⊙O的切线；(2)若CEDE =23，求tan∠E和cos∠ABC的值.5.如图，AB，AC分别是半⊙O的直径和弦，OD⊥AC于点D，过点A作半⊙O的切线AP，AP 与OD的延长线交于点P,连接PC并延长与AB的延长线交于点F．（1）求证：PC是半⊙O的切线；（2）若∠CAB=30°，AB=10，求线段BF的长．6.如图，AB 是⊙O 的直径，延长AB 至P ，使BP=OB ，BD 垂直于弦BC ，垂足为点B ，点D 在PC 上．设∠PCB=α，∠POC=β．(1)下列结论：①BD ∥AC;②tan β2=BC AC ;③△PBD ∽△PAC.其中正确的有________________.(2)求证：tan α• tanβ=137.如图1，在⊙O 中，E 是弧AB 的中点，C 为⊙O 上的一动点（C 与E 在AB 异侧），连接EC 交AB 于点F ，r 是⊙O 的半径，EB=2r3，D 为AB 延长线上一点. (1)下列结论：①若DC=DF ，直线DC 是⊙O 的切线;②△EBF ∽△ECB;③EF•EC = 49r 2.其中正确的有____________________.(2)如图2，若F 是AB 的四等分点，求EF 和EC 的值.圆精选测试题（二）一、填空题1.如图，AB 是半圆的直径，点O 为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E ，交⊙O 于D ，连接BE ．设∠BEC=α，则sinα的值为____________.2.如图，水平放置的圆柱形排水管道的截面直径是1m ，其中水面的宽AB 为0.8m ，则排水管内水的深度为____________.3.如图，等腰直角△ABC 中， AB = AC = 8，以AB 为直径的半圆O 交斜边BC 于D ，阴影部分面积为____________. (结果保留π).4.如图，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为____________．5.图，圆内接正六边形的边长为4，以其各边为直径作半圆，则图中阴影部分的面积为____________.6.直线AB 与⊙O 相切于点A ，弦CD∥AB，E ，F 为圆上的两点，且∠CDE=∠ADF．若⊙O 的半径为52，CD=4，则弦EF 的长为____________. BA7.菱形ABCD 的边长为2，∠A=60°，以点B 为圆心的圆与AD ，DC 相切，与AB ，CB 的延长线分别相交于点E 、F ，则图中阴影部分的面积为____________.8.AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F.若∠ACF=65°，则∠E=____________.二、解决问题1.如图，⊙O 的半径为1，A ，P ，B ，C 是⊙O 上的四个点，∠APC=∠CPB=60°.（1）判断△ABC 的形状：______________；（2）试探究线段PA ，PB ，PC 之间的数量关系，并证明你的结论； （3）当点P 位于AB̂的什么位置时，四边形APBC 的面积最大？求出最大面积． B C P OA ACB O ABCHO D2.已知在△ABC 中，∠B=90o，以AB 上的一点O 为圆心，以OA 为半径的圆交AC 于点D ，交AB 于点E ．（1）求证：AC ·AD=AB ·AE ；（2）如果BD 是⊙O 的切线，D 是切点，E 是OB 的中点，当BC=2时，求AC 的长．3.如图,在△ABC 中,BA=BC,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，BC 的延长线与⊙O 的切线AF 交于点F.(1)求证：∠ABC=2∠CAF ；(2)若AC=2√10，CE:EB=1:4,求CE 的长. 4.如图，在△ABC 中，AB=AC ，以AC 为直径的⊙O 交AB 于点D ，交BC 于点E ．（1）求证：BE=CE ；（2）若BD=2，BE=3，求AC 的长．5.如图，点C 在以AB 为直径的⊙O 上，点D 是半圆AB 的中点，连接AC ，BC ，AD ，BD ，过点D 作DH ∥AB 交CB 的延长线于点H.（1）求证：直线DH 是⊙O 的切线；E DA O（2）若AB=10，BC=6，求AD ，BH 的长.6.如图，A 为⊙O 外一点，AB 切⊙O 于点B ，AO 交⊙O 于C ，CD ⊥OB 于E ，交⊙O 于点D ，连接OD ．若AB=12，AC=8．（1）求OD 的长；（2）求CD 的长．参考答案测试题（一）一、填空题1. 82. √3−π23. 50°4. 35°5. 16π36. ①②③④7. π2−1 二、解决问题1（1）提示：计算∠OCD=90°（2）2√3−2π32（1）提示：证明FD ∥AC（2）提示：相似，DF=203 3(1)AC=5√3,AD=5√2(2) 提示：计算∠OCP=90°4(1) 提示：证明△OCD ≌△OAD(2) tan ∠E=√24，cos ∠ABC =√335(1) 提示：证明△OCP ≌△OAP(2) BF=56(1) ①②③(2) tan α• tanβ=BD BC ∙BC AC =BD AC =13 7(1) ①②③(2) EF=2√3r 9,EC=2√3r 3测试题（二）一、填空题1. 3√313 提示：连接BC ，sin α=BC BE2. 0.8m3. 4π+244. 288°5. 24√3−4π6. 2√57. 3π+2√348. 50°二、解决问题1(1) 等边三角形.(2)PC=PA+PB 提示：在PC 上截取PD ，使PD ＝PA ，证明△PAB ≌△DAC.(3)中点，最大面积是√3.2(1) 提示：接连DE,证明△ADE ∽△ABC.(2) 30°3(1) 提示：接连BD,证明∠CBD=∠ABD ，∠ABD=∠CAF.(2) CE=2.提示：设CE=x,则BE=4x,AB=5x,勾股定理列方程可解. 4(1) 提示：三线合一.(2) AC=9.提示：连接DE ，△BDE ∽△BCA ．5(1)提示：平行法.（2）析：∠CAD=∠DBH ，∠ACD=∠BDH, △ACD ∽△BDH,AD BH =AC BD ,BH=254. 6(1) AC=5.提示：设半径是x,勾股定理.（2）析： CE∥AB ,△OEC∽△OBA，∠CAD=∠DBH ，∠ACD=∠BDH, △ACD ∽△BDH,CD=2013.。

人教版六年级上册数学第五单元《圆》测试卷一.选择题(共6题，共12分)1.画圆时首先要确定圆的位置，也就是要确定（）。

A.半径B.直径C.圆心2.用三根同样长的铁丝分别围成一个长方形、正方形、圆．这三个图形中面积最大的是（）。

A.长方形B.正方形C.圆3.大圆的半径6cm，小圆的半径3cm，大圆和小圆面积的比是（）。

A.2：1B.4：1C.1：24.直径是通过圆心并且两端都在圆上的（）。

A.直线B.射线C.线段5.把一个直径是2厘米的圆分成两个半圆后，每个半圆的周长是（）。

A.6.28厘米B.5.14厘米C.4.14厘米6.有两个大小不同的同心圆，大圆半径是3cm，小圆半径是2cm，则圆环的宽是（）cm。

A.5B.6C.1二.判断题(共6题，共12分)1.周长相等的两个圆，它们的面积也一定相等。

（）2.两个大小不同的圆，它们的圆周率不同。

（）3.在圆内，任意一条直径都是圆的对称轴。

（）4.圆周长是直径的3.14倍。

（）5.直径相等的两个圆，周长也相等。

（）6.圆的直径都相等。

（）三.填空题(共6题，共7分)1.用圆规画一个直径20厘米的圆，圆规两脚步间的距离是（）厘米。

2.在一个周长是16米的正方形纸片内，剪下一个最大的圆，这个圆的周长是（）米。

3.如图像∠AOB这样，顶点在（）的角叫做圆心角。

4.画一个直径为4厘米的圆，圆规两脚间的距离应该是（）。

5.把一块边长是10分米的正方形纸片，剪成一个最大的圆形，这个圆的周长是（）。

列式：（）。

6.汽车的车轮滚动一周，所行的路程是车轮的（）。

四.计算题(共1题，共6分)1.求下面图形的周长。

（单位：厘米）（1）（2）五.解答题(共6题，共36分)1.一只环形玉佩的外圆半径为2厘米，比内圆半径多1.5厘米，这只环形玉佩的面积是多少平方厘米？2.要在底面半径是14厘米的圆柱形水桶外面打上一个铁丝箍，接头部分是6厘米，需用铁丝多少厘米？3.一个圆形洞口，直径为1m，一个身高1.45m的小男孩不能直身钻进去，如果这个洞口的周长增加1.57m，小男孩能直身钻进去吗？（填能或不能）4.一个直径为8米的圆形花坛，要在花坛外围修一条1米宽的石头小路。

六年级数学圆测试题一、选择题（每题2分，共10分）1. 圆的周长公式是：A. C = 2πrB. C = πdC. C = πr²D. C = 2πd2. 圆的面积公式是：A. A = πr²B. A = 2πrC. A = πd²D. A = πr + d3. 半径为2厘米的圆的周长是：A. 12.56厘米B. 6.28厘米C. 4厘米D. 8厘米4. 半径为3厘米的圆的面积是：A. 28.26平方厘米B. 9π平方厘米C. 18π平方厘米D. 28π平方厘米5. 圆心角为60°的扇形，其面积占同圆面积的：A. 1/6B. 1/3C. 1/2D. 2/3二、填空题（每题2分，共10分）6. 半径为4厘米的圆的周长是______厘米。

7. 半径为5厘米的圆的面积是______平方厘米。

8. 一个圆的直径是10厘米，那么这个圆的半径是______厘米。

9. 圆的直径是半径的______倍。

10. 如果一个圆的周长是31.4厘米，那么这个圆的半径大约是______厘米。

三、计算题（每题5分，共15分）11. 计算半径为7厘米的圆的周长和面积。

周长：______厘米面积：______平方厘米12. 一个圆的周长是44厘米，求这个圆的半径。

半径：______厘米13. 一个圆的面积是78.5平方厘米，求这个圆的半径。

半径：______厘米四、应用题（每题10分，共20分）14. 一个圆形花坛的直径是20米，花坛周围有一条1米宽的小路。

求小路的面积。

15. 一个圆环，内圆半径是3厘米，外圆半径是5厘米。

求这个圆环的面积。

五、开放性问题（每题15分，共15分）16. 如果你有一个半径为10厘米的圆，要制作一个圆环，圆环的宽度是1厘米，求这个圆环的面积。

同时，如果这个圆环被均匀分成8个扇形，每个扇形的面积是多少？请注意，以上题目的答案需要根据圆的周长和面积公式进行计算。

圆的认识单元测试卷（一）一、填空（第12题每格0.5分，其余每空1分，共35.5分）。

1．从圆心到圆上任意一点的线段叫( )。

通过（）并且（）都在（）的线段叫做直径。

圆的位置是由（）确定的，圆的大小决定于（）的长短。

2．在同一个圆里，所有的半径（），所有的（）也都相等，直径等于半径的（）。

3．圆周率表示同一圆内（）和（）的倍数关系，它用字母（）表示，保留两位小数后的近似值是（）。

4．在同一个圆内可以画（）条直径；如果用圆规画一个直径是10厘米的圆，圆规的两脚间的距离应该是（）厘米。

5．在长6厘米，宽4厘米的长方形内剪下一个最大的圆，这个圆的周长是（），面积是（），还剩下面积( )。

6．一个圆环，外圆半径是6分米，内圆半径4分米，圆环的面积是（）。

7．甲圆直径长8厘米，是乙圆直径的40%。

乙圆的周长是（）。

8．一个圆的半径是8厘米，这个圆面积的是（）平方厘米。

9．大圆的半径等于小圆直径，则大圆面积是小圆面积的（）倍，小圆周长是大圆周长的（）。

10．在一张长32厘米，宽16厘米的长方形内画半径是4厘米的圆，这样的圆最多能画（）个，这些圆的面积和是（）。

11．圆是（）图形，它有（）对称轴。

正方形有（）条对称轴，长方形有（）条对称轴，等边三角形有（）条对称轴。

12．填表：1．圆的周长是它的直径的π倍。

（）2．半径为1厘米的圆的周长是3.14厘米。

（）3．一个圆的周长是12.56厘米，面积是12.56平方厘米。

（）4．圆的半径由6分米增加到9分米，圆的面积增加了45平方分米。

（）5．当长方形、正方形、圆的周长相等时，圆的面积最大。

（）6．水桶是圆形的。

（）7．半个圆的周长就是圆周长的一半。

（）8．所有的直径都相等。

（）9．π＝3.14．（）三、画一画。

(共7.5分)1．以O为圆心，画一个直径是4厘米的圆。

2.在正方形中画一个最大的圆。

3，画出所有对称轴。

·O四、计算下列各圆的周长。

（6分）1．直径是6厘米 2.半径是5分米五、计算下列各圆的面积。

《圆》的综合测试题学校:___________姓名：___________班级:___________考号：___________一、选择题（题型注释）1．用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为（ ）A ．2cmB ．1.5cmC ．cmD ．1cm2．已知⊙1O 的半径为5cm ,⊙2O 的半径为3cm ，两圆的圆心距为7cm ，则两圆的位置关系是( ),A 外离 ,B 外切 ,C 内切 ,D 相交3．如图是某公园的一角,∠AOB=90°，弧AB 的半径OA 长是6米，C 是OA 的中点，点D 在弧AB 上,CD∥OB,则图中休闲区（阴影部分)的面积是【 】A ．91032π⎛⎫- ⎪⎝⎭米2B ．932π⎛⎫- ⎪⎝⎭米2 C ．9632π⎛⎫- ⎪⎝⎭米2 D ．()693π-米24．如右图，圆心角∠AOB=100°，则∠ACB 的度数为（ ）OA BCA 、100°B 、50°C 、80°D 、45°5．如图，⊙O 是△ABC 的外接圆,已知∠ABO=30º，则∠ACB 的大小为( ）A ．30ºB ．45ºC ．50ºD ．60º6．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°,⊙O 的半径为3cm,则圆心O 到弦CD 的距离为( )A ．错误!cmB ．3 cmC ．3错误!cmD ．6cm7．圆心角为120°，弧长为12π的扇形半径为（ ）A ．6B ．9C ．18D ．368．⊙O 的直径AB ＝10cm ，弦CD ⊥AB ，垂足为P ．若OP ：OB ＝3：5，则CD 的长为（ )A ．6cmB ．4cmC ．8cmD ．91cm 9．如图,在△ABC 中，∠A ＝90º，AB ＝AC ＝2．以BC 的中点O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ，则图中阴影部分的面积是【 】A ．1－4πB ．4πC ．1－2πD ．2－2π 10．如图，PA 、PB 切⊙O 于A 、B 两点，CD 切⊙O 于点E ，交PA,PB 于C 、D ，若⊙O 的半径为r ，△PCD 的周长等于3r ，则tan ∠APB 的值是（ )A 51312．125 C 3135 D 2133二、填空题(题型注释)11．母线长为4,底面圆的半径为1的圆锥的侧面积为___________。

六年级圆的综合测试题一、选择题（每题3分，共30分）1. 圆的半径扩大3倍，它的周长就扩大（）倍。

A. 3B. 6C. 9D. 12解析：圆的周长公式为公式，当半径公式扩大3倍变为公式时，新的周长公式。

公式，所以周长扩大3倍，答案是A。

2. 一个圆的直径是10厘米，这个圆的面积是（）平方厘米。

A. 314B. 78.5C. 31.4D. 15.7解析：圆的面积公式为公式，已知直径公式厘米，那么半径公式厘米。

所以公式，公式取3.14时，公式平方厘米，答案是B。

3. 圆的周长总是它直径的（）倍。

B. 公式C. 3D. 6.28解析：根据圆的周长公式公式，所以圆的周长总是它直径的公式倍，答案是B。

4. 一个半圆的半径是公式，它的周长是（）。

A. 公式B. 公式C. 公式D. 公式解析：半圆的周长为圆周长的一半加上直径，圆的周长公式，圆周长的一半是公式，直径是公式，所以半圆的周长是公式，答案是C。

5. 在一个边长为公式厘米的正方形内画一个最大的圆，这个圆的面积是（）平方厘米。

A. 50.24B. 200.96C. 64解析：在正方形内画最大的圆，这个圆的直径等于正方形的边长公式厘米，所以半径公式厘米。

圆的面积公式，公式取3.14时，公式平方厘米，答案是A。

6. 把一个圆平均分成若干份，拼成一个近似的长方形，这个长方形的长相当于圆的（）。

A. 半径B. 直径C. 周长D. 周长的一半解析：把圆平均分成若干份拼成近似长方形时，长方形的长相当于圆周长的一半，宽相当于圆的半径，答案是D。

7. 一个圆的半径由公式厘米增加到公式厘米，圆的面积增加了（）平方厘米。

A. 15.7B. 12.56C. 28.26D. 18.84解析：原来圆的面积公式平方厘米，后来圆的面积公式平方厘米。

面积增加了公式，公式取3.14时，公式平方厘米，答案是A。

8. 车轮滚动一周，所行的路程是求车轮的（）。

A. 直径B. 周长C. 面积D. 半径解析：车轮滚动一周的路程就是车轮边缘一周的长度，也就是车轮的周长，答案是B。

一、选择题。

1．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（）A．1B．34C．13D．122．已知⊙O的周长为π6，若某直线l上有一点到圆心O的距离为3，则直线l与⊙O的位置关系是（）A．相交B．相切C．相离D．相切或相交3．已知两圆的半径分别为2和3，圆心距为5，则这两圆的位置关系是（）A．外离B．外切C．相交D．内切4．若一个圆锥的底面圆半径为2cm，母线长是6cm，则这个圆锥的侧面展开图的圆心角度数是（）A.40°B.80°C.120°D.150°5．两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视图是（）A．两个外离的圆B．两个外切的圆C．两个相交的圆D．两个内切的圆6．如图:⊙O是△ABC的内切圆,D、E、F是切点，若∠DEF=50º，则∠A等于（）A．40ºB．50ºC．80ºD．100º7．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（）．A．1 B．34C．12D．13(第1题)．OADBFCBA O8．如图，⊙O 中，弦AB 、CD 相交于点P ，若30A ∠=︒，70APD ∠=︒则等于（ ）A ．30° B．35° C．40° D ．50°9．已知⊙1O 的半径r 为3cm ，⊙2O 的半径R 为4cm ，两圆的圆心距1O 2O 为1cm ，则这两圆的位置关系是（ ）A ．相交B ．内含C ．内切D ．外切10．已知两圆的半径分别为2厘米和5厘米，圆心距为6厘米，则这两圆的位置关系是（ ）A ．相交B ．内切C ．外切D ．相离11．已知扇形的半径为2，圆心角为60°，则扇形的弧长为 （ ） A ．23 B.13π C.23π D.43π 12. 已知⊙O 1和⊙O 2的半径分别为5和3，O 1O 2＝8，则⊙O 1和⊙O 2的位置关系是（ ）A ．外离B ．外切C ．相交D ．内切 13．如图，EF 是圆O 的直径，5cm OE =，弦8cm MN =， 则E ，F 两点到直线MN 距离的和等于（ ） Ａ．12cm Ｂ．6cm Ｃ．8cm Ｄ．3cm14．如图，AB 是⊙O 的直径，AB =4，AC 是弦，AC =23，∠AOC 为（ ） A ．120° B ．1300 C ．140° D ．150°15．如图，A 是半径为22的⊙O 外一点，OA=4，AB 是⊙O 的切线，点B 是切点，弦BC ∥OA,则BC 的长为（ ） （A ）2（B ） 2 （C ）22 （D ）4 16．如图，PA 为O 的切线，A 为切点，PO 交⊙O 于点B ，43PA OA ==，，则sin AOP ∠的值为（ ）A ．34B ．35C ．45D ．43（第8题图）ＯＫ Ｍ Ｇ ＥＮ （第13题图）ACBOAP OBOl17．如图，⊙O的圆心O到直线l的距离为4cm，⊙O的半径为1cm，将直线l向右(垂直于l的方向)平移，使l与⊙O相切，则平移的距离为（）A、1cmB、3cmC、5cmD、3cm或5cm18. 如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为( )A．5米 B．53米 C．7米 D． 8米19．如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若∠AOB=120°，则大圆半径R与小圆半径r之间满足（）A、B、R=3r C、R=2r D、20．如图，A、B、C是⊙O上的点，AB = 2㎝，∠ACB=30°，那么⊙O的半径为（）A.32cm B. 3cm C. 2cm D. 4cm21．已知⊙Ｏ的半径ＯＡ＝６，扇形ＯＡＢ的面积等于１２π，则弧AB所对的圆周角的度数是（）Ａ．１２００Ｂ．９００Ｃ．６００Ｄ．３０22.半径为R的圆中，圆心角为︒n的扇形面积的计算公式是（）A、180RnSπ=扇形B、360RnSπ=扇形C、3602RnSπ=扇形D、1802RnSπ=扇形23．已知⊙O的半径为r，点P到点O的距离大于r，那么点P的位置（）A、一定在⊙O 的内部B、一定在⊙O 的外部C、一定在⊙O 的上D、不能确定24.如果圆锥的母线长为6cm，底面圆半径为3cm，则这个圆锥的侧面积为（）A. 9πcm2B. 18πcm2C. 27πcm2D. 36πcm225. 如图，在半径为5的⊙O中，如果弦AB的长为8，那么它的弦心距OC等于（）C OABD图31A. 2B. 3C. 4D. 626．已知圆锥的底面周长为58cm ，母线长为30cm ，求得圆锥的侧面积为（ ） A.870cm 2 B.908 cm 2 C.1125 cm 2 D.1740 cm 227．圆柱的高为6cm ，它的底面半径为4cm ，则这个圆柱的侧面积是（ ） A. 482πcmB. 242πcmC. 482cmD. 242cm28.如图8，小颖同学在手工制作中，把一个边长为12cm 的等边三角形纸片贴到一个圆形的纸片上，若三角形的三个顶点恰好都在这个圆上，则该圆的半径为( )A.3cmB.3cmC.4cmD.4cm29．在半径为1的⊙O 中，120º的圆心角所对的弧长是 （ ） A ．3π B ．23π C ．πD ．32π 30．已知⊙O 1和⊙O 2的半径分别为5和2，O 1O 2＝3，则⊙O 1和⊙O 2的位置关系是（ ）A 、外离B 、外切C 、相交D 、内切31．如图1，AB 是⊙O 的直径，C 是⊙O 上一点，若AC ︰BC ＝4︰3，AB ＝10cm ，OD ⊥BC 于点D ，则BD 的长为( ).A.cm 23B.3cmC.5cmD.6cm32．已知圆锥的母线长为5cm ，高线长是4cm ，则圆锥的底面积是( )cm 2A 、3πB 、9πC 、16πD 、25π33．若圆锥侧面积是底面积的2倍，则这个圆锥的侧面展开图的圆心角是 ( ) （A ）120˚ （B ）135˚ （C ）150˚ （D ）180˚34．已知⊙Ｏ的半径ＯＡ＝６，扇形ＯＡＢ的面积等于１２π，则弧AB 所对的圆周角的度数是（ ）Ａ．１２００ Ｂ．９００ Ｃ．６００ Ｄ．３００35．扇形的半径为３０ｃｍ，圆心角为１２００，用它做成一个圆锥的侧面，则圆锥底面半径为（ ）Ａ．１０ｃｍ Ｂ．２０ｃｍ Ｃ．１０πｃｍ Ｄ．２０πｃｍ36、如图2，AB 为⊙O 的直径，点C 在⊙O 上，∠B ＝50°， 则A 等于…（ ）A 、80°B 、60°C 、 50°D 、40°37．一个底面半径为5cm ，母线长为16cm 的圆锥，它的侧面展开图的面积是……（ ） A 、80πcm 2 B 、40πcm 2 C 、80cm 2 D 、40cm 238．已知圆A 和圆B 相切，两圆的圆心距为8cm ，圆A 的半径为3cm ，则圆B 的半径是（ ）．A ．5cmB ．11cmC ．3cmD ．5cm 或11cm 39．小红要过生日了，为了筹备生日聚会，准备自己动手用纸板制作圆锥形的生日礼帽。

六年级圆的周长测试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 圆的周长公式是（）。

A. C = πdB. C = 2πrC. C = πr²D. C = 2r2. 半径为5厘米的圆，其周长是（）厘米。

A. 15.7B. 31.4C. 78.5D. 62.83. 直径是半径的（）倍。

A. 1/2B. 1C. 2D. 34. 一个圆的周长是25.12厘米，那么这个圆的半径是（）厘米。

A. 4B. 8C. 16D. 325. 圆周率π的近似值是（）。

A. 3.1415B. 3.1416C. 3.142D. 3.14二、判断题（每题1分，共5分）1. 圆的周长与半径成正比。

（）2. 圆的周长是圆的边界。

（）3. 圆的周长公式是C = πd。

（）4. 半径越大，圆的周长越小。

（）5. 圆周率π是一个固定的值，不会改变。

（）三、填空题（每题1分，共5分）1. 圆的周长公式是C = 2π______。

2. 半径为10厘米的圆，其周长是______厘米。

3. 直径是半径的______倍。

4. 一个圆的周长是50.24厘米，那么这个圆的半径是______厘米。

5. 圆周率π的近似值是______。

四、简答题（每题2分，共10分）1. 解释什么是圆的周长。

2. 圆的周长与半径有什么关系？3. 圆周率π是什么？4. 如何计算圆的周长？5. 举例说明圆的周长在实际生活中的应用。

五、应用题（每题2分，共10分）1. 一个圆形花坛的直径是10米，求花坛的周长。

2. 一个车轮的半径是0.5米，求车轮转一圈的距离。

3. 一个圆的周长是18.84厘米，求这个圆的半径。

4. 一个圆形游泳池的周长是31.4米，求游泳池的半径。

5. 一个圆的周长是43.96厘米，求这个圆的直径。

六、分析题（每题5分，共10分）1. 小明在操场上跑步，跑道是一个圆形，跑道的周长是400米，小明跑了2圈，小明跑了多少米？2. 一个圆形的餐桌，直径是1.2米，求餐桌的周长，并说明这个周长在实际生活中的应用。

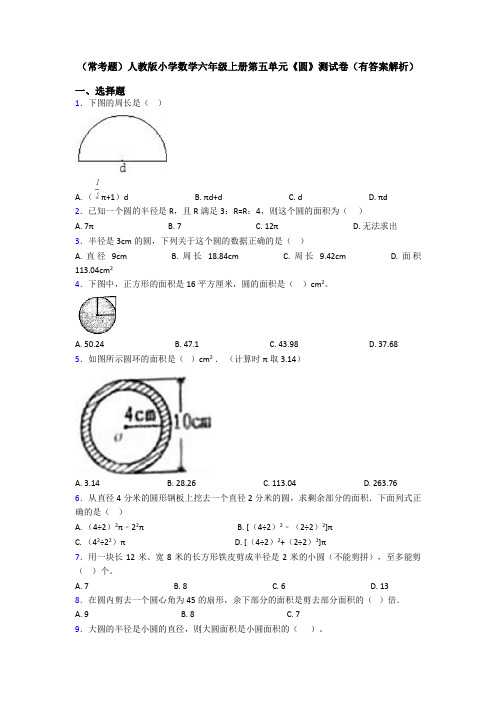
（常考题）人教版小学数学六年级上册第五单元《圆》测试卷（有答案解析）一、选择题1．下图的周长是（）A. （π+1）dB. πd+dC. dD. πd2．已知一个圆的半径是R，且R满足3：R=R：4，则这个圆的面积为（）A. 7πB. 7C. 12πD. 无法求出3．半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm24．下图中，正方形的面积是16平方厘米，圆的面积是（）cm2。

A. 50.24B. 47.1C. 43.98D. 37.68 5．如图所示圆环的面积是（）cm2．（计算时π取3.14）A. 3.14B. 28.26C. 113.04D. 263.76 6．从直径4分米的圆形钢板上挖去一个直径2分米的圆，求剩余部分的面积．下面列式正确的是（）A. （4÷2）2π﹣22πB. [（4÷2）2﹣（2÷2）2]πC. （42÷22）πD. [（4÷2）2+（2÷2）2]π7．用一块长12米、宽8米的长方形铁皮剪成半径是2米的小圆（不能剪拼），至多能剪（）个。

A. 7B. 8C. 6D. 138．在圆内剪去一个圆心角为45的扇形，余下部分的面积是剪去部分面积的（）倍．A. 9 B. 8 C. 79．大圆的半径是小圆的直径，则大圆面积是小圆面积的（）。

A. 2倍B. 4倍C. 12D. 14 10．东方公园有一个圆形的喷水池，经测量得出这个喷水池的周长是37 .68m。

这个喷水池占地（）m2。

A. 37.68B. 113.04C. 452.1611．下图是一个半径为5厘米的半圆，求它的周长的正确算式是（）。

A. 3.14×5+5×2B. （3.14×52） ÷2C. [3.14×（5×2）]÷2+5D. 3．14×5÷2+5 12．将圆的半径按3：1放大后，面积将扩大到原来的（）。