2006-2010年 立体几何高考题

立体几何分类汇编一、异面直线夹角（2007全国理I）如图，正四棱柱1111-ABCD A B C D 中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为A．51B．52C．53D．54（2008全国理II）已知正四棱锥S ABCD -的侧棱长与底面边长都相等，E 是SB 的中点，则AE SD ，所成的角的余弦值为（）A．13B．23D．23（2009全国理I）已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为111A B C 的中点，则异面直线AB 与1CC 所成的角的余弦值为D.34（2009全国理II）已知正四棱柱1111ABCD A B C D -中，12AA AB =，E 为1AA 中点，则异面直线BE 与1CD 所成的角的余弦值为A.10B.15C.10D.35（2012全国理I）三棱柱111ABC A B C -中，底面边长和侧棱长都相等，1160BAA CAA ∠=∠= ，则异面直线1AB 与1BC 所成角的余弦值为____________。

（2013全国理I）如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成角的大小是____________。

（2014全国理II）直三棱柱111ABC A B C -中，90BCA ∠= ，,M N 分别是1111,A B A C 的中点，1BC CA CC ==，则BM 与AN 所成的角的余弦值为（）A.110B.25C.D.二、线面夹角（2007全国理II）已知正三棱ABC A B C -111的侧棱长是底面边长相等，则AB 1与侧面ACC A 1所成角的正弦等于A.64B.104C.22D.32（2008全国理I）已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（）A．13B．23C．33D．23（2010全国理I）正方体1111ABCD A B C D -中,1BB 与平面1ACD 所成角的余弦值为（A）23（B）33（C）23（D）63（2016全国理I）平面α过正方体1111ABCD A B C D -的顶点A ，α 平面11CB D ，α 平面ABCD m =，α 平面11ABA B n =，则,m n 所成角的正弦值为A.32 B.22C.33D.13（2007全国理I）四棱锥S ABCD -中，底面ABCD 为平行四边形，侧面SBC ⊥底面ABCD 已知45ABC ∠= ,2,22,3AB BC SA SB ====（Ⅰ）证明：SA BC ⊥；（Ⅱ）求直线SD与平面SAB所成角的大小。

历年高考真题1、2003（理科）（本题满分12分）已知平行六面体ABCD —A 1B 1C 1D 1中，A 1A ⊥平面ABCD ，AB=4，AD=2.若B 1D ⊥BC ，直线B 1D 与平面ABCD 所成的角等于30°，求平行六面体ABCD —A 1B 1C 1D 1的体积.．[解]连结BD ，因为B 1B ⊥平面ABCD ，B 1D ⊥BC ，所以BC ⊥BD.在△BCD 中，BC=2，CD=4，所以BD=32.又因为直线B 1D 与平面ABCD 所成的角等于30°，所以 ∠B 1DB=30°，于是BB 1=31BD=2.故平行六面体ABCD —A 1B 1C 1D 1的体积为S ABCD ·BB 1=38. 2.2005（理科）(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.已知正三棱锥ABC P -的体积为372，侧面与底面所成的二面角的大小为 60. （1）证明：BC PA ⊥；（2）求底面中心O 到侧面的距离.[证明]（1）取BC 边的中点D ，连接AD 、PD ，则BC AD ⊥，BC PD ⊥，故⊥BC 平面APD . BCPA ⊥[解]（2）如图， 由（1）可知平面⊥PBC 平面APD ，则PDA ∠面所成二面角的平面角.过点O 作E PD OE ,⊥为垂足，则OE 就是点O 到侧面的距离. 设OE 为h ，由题意可知点O 在AD 上，∴ 60=∠PDO ，h OP 2=.h BC h OD 4,32=∴=,∴ 2234)4(43h h S ABC ==∆， ∵ 3233823431372h h h =⋅⋅=，∴ 3=h . 即底面中心O 到侧面的距离为3.3、2006（理科）（本题满分 14分）本题共有 2个小题，第 1小题满分 5分，第 2小题满分满分 9分。

在三棱柱 ABC —A1B1C1 中，∠ABC=90°，AB=BC=1。

高考数学真题立体几何习题1.(2010新课标)如图，已知四棱锥P－ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD中点．(1)证明：PE⊥BC；(2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值．2.(2011新课标) 如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明：PA⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

3.（2012新课标）如图，直三棱柱ABC-A1B1C1中，AC=BC=AA1，D是棱AA1的中点，DC1⊥BD。

（1）证明：DC1⊥BC；（2）求二面角A1-BD-C1的大小。

4.（2013新课标1卷）如图，三棱柱中，，，=60°.（Ⅰ）证明⊥;（Ⅱ）若平面⊥平面，，求直线与平面所成角的正弦值。

5.（2013新课标2卷）如图，直棱柱ABC-A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB=AB。

（Ⅰ）证明：BC1//平面A1CD1（Ⅱ）求二面角D-A1C-E的正弦值6.(2014新课标1卷)如图三棱锥中，侧面为菱形，. (Ⅰ) 证明：；（Ⅱ）若，，AB=Bc，求二面角的余弦值.7.（2014新课标2卷）如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.（Ⅰ）证明：PB∥平面AEC；（Ⅱ）设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积.8.（2010全国卷2）如图，直三棱柱中，，，为的中点，为上的一点，．（Ⅰ）证明：为异面直线与的公垂线；（Ⅱ）设异面直线与的夹角为45°，求二面角的大小．9.（2010湖南）如图5所示，在正方体ABCD—A1B1C1D1中，E是棱DD1的中点. （I）求直线BE和平面ABB1A1所成角的正弦值；（II）在棱C1D1上是否存在一点F，使B1F//平面A1BE？证明你的结论.10.（2010山东）如图，在五棱锥P—ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，ABC=45°，AB=，BC=2AE=4，三角形PAB是等腰三角形．（Ⅰ）求证：平面PCD⊥平面PAC；（Ⅱ）求直线PB与平面PCD所成角的大小；（Ⅲ）求四棱锥P—ACDE的体积．11.（2010江苏）如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。

石门中学2010—2011学年度第二学期高二理科数学三检专题复习（一）立体几何（2） 编辑：张展朋 校正：徐庆均 【感受高考】 2006年17、(本题14分)如图5所示，AF 、DE 分别是O 、1O 的直径，AD 与两圆所在的平面均垂直，8AD =.BC 是O 的直径，6AB AC ==,//OE AD .(I)求二面角B AD F --的大小；(II)求直线BD 与EF 所成的角.17、解：(Ⅰ)∵AD 与两圆所在的平面均垂直, ∴AD ⊥AB, AD ⊥AF,故∠BAD 是二面角B —AD —F 的平面角， 依题意可知，ABCD 是正方形，所以∠BAD ＝450. 即二面角B —AD —F 的大小为450；(Ⅱ)以O 为原点，BC 、AF 、OE 所在直线为坐标轴，建立空间直角坐标系（如图所示），则O （0，0，0），A （0，23-，0），B （23，0，0）,D （0，23-，8），E （0，0，8），F （0，23，0）所以，)8,23,0(),8,23,23(-=--=10828210064180||||,cos =⨯++=>=<FE BD 设异面直线BD与EF所成角为α，则1082|,cos |cos =><=α 直线BD 与EF 所成的角为1082arccos图5A FD19.（本小题满分14分）如图6所示，等腰△ABC 的底边AB =66,高CD =3，点E 是线段BD 上异于点B 、D 的动点.点F 在BC 边上，且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置，使PE ⊥AE .记BE x = V (x )表示四棱锥P-ACFE 的体积. （1）求V (x )的表达式；（2）当x 为何值时，V (x )取得最大值？（3）当V (x )取得最大值时，求异面直线AC 与PF 所成角的余弦值。

19.解: (1)11) (032V x x x =⋅<<即3V =-(0x <<;(2)22)V x x '==-,(0,6)x ∴∈时,0;V '>x ∴∈时,0;V '<6x ∴=时()V x 取得最大值.(3)以E 为空间坐标原点,直线EF 为x 轴,直线EB 为y 轴,直线EP 为z 轴建立空间直角坐标系,则(0,6(3,6A C AC --=;(0,0,6),(6,0,6)P F PF ∴=-,设异面直线AC 与PF 夹角是θ1cos 7θ∴==A20．（本小题满分14分）如图5所示，四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形，其中BD 是圆的直径，60ABD ∠=，45BDC ∠=，PD 垂直底面ABCD，PD =，E F ，分别是PB CD ，上的点，且PE DFEB FC =，过点E 作BC 的平行线交PC 于G ． （1）求BD 与平面ABP 所成角θ的正弦值； （2）证明：EFG △是直角三角形； （3）当12PE EB =时，求EFG △的面积．20．解：（1）在Rt BAD ∆中，60ABD ∠=，,AB R AD ∴==而PD 垂直底面ABCD ，PA ===PB ===,在PAB ∆中，222PA AB PB +=,即PAB ∆为以PAB ∠为直角的直角三角形。

解答题1. 如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，2,60AB BAD =∠=o .（Ⅰ）求证：BD ⊥平面;PAC（Ⅱ）若,PA AB =求PB 与AC 所成角的余弦值；（Ⅲ）当平面PBC 与平面PDC 垂直时，求PA 的长.2. 如图，四棱锥P -ABCD 中，P A ⊥底面ABCD ，四边形ABCD 中，AB ⊥AD ，AB +AD =4，CD =2，︒=∠45CDA ．（I ）求证：平面P AB ⊥平面P AD ；（II ）设AB =AP ．（i ）若直线PB 与平面PCD 所成的角为︒30，求线段AB 的长；（ii ）在线段AD 上是否存在一个点G ，使得点G 到点P ，B ，C ，D 的距离都相等？说明理由。

3. 如图5．在椎体P -ABCD 中，ABCD 是边长为1的棱形，且∠DAB =60︒，2PA PD ==,PB =2, E ,F 分别是BC ,PC 的中点．（1） 证明：AD ⊥平面DEF ;（2） 求二面角P -AD -B 的余弦值．4. 如图，已知正三棱柱111ABC A B C -的各棱长都是4，E 是BC 的中点，动点F 在侧棱1CC 上，且不与点C 重合．（Ⅰ）当CF =1时，求证：EF ⊥1A C ；（Ⅱ）设二面角C AF E --的大小为θ，求tan θ的最小值．A B DC FPE5. 如图，在圆锥PO中，已知PO=2，⊙O的直径2AB=,C是»AB的中点，D为AC 的中点．（Ⅰ）证明：平面POD⊥平面PAC;（Ⅱ）求二面角B PA C--的余弦值。

6. 如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=12 PD．（I）证明：平面PQC⊥平面DCQ；（II）求二面角Q—BP—C的余弦值．8. 如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB AD =，PD ⊥底面ABCD ．（I ）证明：PA BD ⊥；（II ）若PD =AD ，求二面角A -PB -C 的余弦值．9. 在如图所示的几何体中，四边形ABCD 为平行四边形，∠ ACB =90︒，ＥＡ⊥平面ＡＢＣＤ，EF ∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ.（Ⅰ）若Ｍ是线段ＡＤ的中点，求证：ＧＭ∥平面ＡＢＦＥ;（Ⅱ）若ＡＣ＝ＢＣ=２ＡＥ,求二面角Ａ－ＢＦ－Ｃ的大小．10. 如图，在ABC ∆中，60,90,ABC BAC AD ∠=∠=o o 是BC 上的高，沿AD 把ABC ∆折起，使90BCD ∠=o 。

2006年全国各地高考数学试题及解答分类汇编大全（13立体几何初步）一、选择题：1.(2006安徽文、理)表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为( )A．3B ．13πC ．23π D．3 1.解：此正八面体是每个面的边长均为a的正三角形，所以由284⨯=1a =，则此球A 。

2.（2006北京理）平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是（ ） （A ）一条直线 （B ）一个圆 （C ）一个椭圆 （D ）双曲线的一支2. 解：设l 与l '是其中的两条任意的直线，则这两条直线确定一个平面，且斜线AB 垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内，故动点C 都在这个平面与平面α的交线上，故选A3. (2006北京文)设A 、B 、C 、D 是空间四个不同的点，在下列命题中，不正确．．．的是（ ） （A ）若AC 与BD 共面，则AD 与BC 共面（B ）若AC 与BD 是异面直线，则AD 与BC 是异面直线 (C) 若AB =AC ，DB =DC ，则AD =BC (D) 若AB =AC ，DB =DC ，则AD ⊥BC 3. 解：A 显然正确；B 也正确，因为若AD 与BC 共面，则必有AC 与BD 共面与条件矛盾； C 不正确，如图所示：D 正确，用平面几何与立体几何的知识都可证明。

选C4.(2006福建文、理)已知正方体外接球的体积是π332，那么正方体的棱长等于( ) A.2 B.332 C.324 D.3344．解：正方体外接球的体积是323π，则外接球的半径R=2，正方体的对角线的长为4，棱长等于3，选D.5. (2006福建文、理)对于平面α和共面的直线m 、n ，下列命题中真命题是（ ）A.若m ⊥α，m ⊥n ，则n ∥αB.若m ∥α，n ∥α，则m ∥nC.若m ⊂α，n ∥α，则m ∥nD.若m 、n 与α所成的角相等，则n ∥m5．解：对于平面α和共面的直线m 、,n 真命题是“若,m n αα⊂∥,则m ∥n ”，选C.6. (2006广东)给出以下四个命题①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面; ③如果两条直线都平行于一个平面,那么这两条直线互相平行;④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直. 其中真命题的个数是（ ）A.4B.3C.2D.1 6. 解：①②④正确，故选B.A B CD7. (2006湖南理)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图1,则图中三角形(正四面体的截面)的面积是 ( )A.27．解：棱长为2的正四面体ABCD 的四个顶点都 在同一个球面上, 若过该球球心的一个截面如图为△ABF ，则图中AB=2，E 为AB 中点，则EF ⊥DC ，在△DCE 中，DE=EC=3，DC=2，∴EF=2，∴三角形ABF 的面积是2，选C.8. (2006湖南理)过平行六面体ABCD-A 1B 1C 1D 1任意两条棱的中点作直线,其中与平面DBB 1D 1平行的直线共有( ) A.4条 B.6条 C.8条 D.12条8．解：如图，过平行六面体1111D C B A ABCD -任意两条棱的中点作直线, 其中与平面11D DBB 平行的直线共有12条，选D.9．(2006湖南文)过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60°则该截面的面积是( )A ．π B. 2π C. 3π D. π329．解：过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60°，则截面圆的半径是21R=1，该截面的面积是π，选A.10、.(2006湖北文、理)关于直线m 、n 与平面α与β，有下列四个命题：（ ） ①若//,//m n αβ且//αβ，则//m n ； ②若,m n αβ⊥⊥且αβ⊥，则m n ⊥； ③若,//m n αβ⊥且//αβ，则m n ⊥；④若//,m n αβ⊥且αβ⊥，则//m n ； 其中真命题的序号是A ．①②B ．③④C ．①④D ．②③ 10. 解：用排除法可得选D11. (2006江苏)两相同的正四棱锥组成如图1所示的几何体，可放棱长为1的正方体内，使正四棱锥的底面ABCD 与正方体的某一个平面平行，且各顶点．．．均在正方体的面上，则这样的几何体体积的可能值有（ ） （A ）1个 （B ）2个（C ）3个 （D ）无穷多个11. 【思路点拨】本题主要考查空间想象能力，以及正四棱锥的体积【正确解答】由于两个正四棱锥相同，所以所求几何体的中心在正四棱锥底面正方形ABCD 中心，有对称性知正四棱锥的高为正方体棱长的一半，影响几何体体积的只能是正四棱锥底面正方形ABCD 的面积，问题转化为边长为1的正方形的内接正方形有多少种，所以选D.【解后反思】正方体是大家熟悉的几何体，它的一些内接或外接图形需要一定的空间想象能力，要学会将空间问题向平面问题转化。

2010年高考试题分类练习(理科：立体几何）（二）答案曾劲松 整理一．选择题1．B ．2．D ．3．D ．解析：直线B 1D 上取一点P ，连接P A 、PB 、PC 、PC 1、P A 1、PD 1，易知△P AB ≌△PCC 1≌△P A 1PD 1，于是这3个三角形的高相等，即P 到三条棱AB 、CC 1、A 1D 1所在直线的距离相等，所以有无穷多点满足条件，故选D .4．B ．解析：根据对称性可知，外接球的球心为上下两底连线的中点，在1R t AO O ∆中，1123232a AO O O =⨯==，2222()3212a O A R ==+=1272a,所以27744123a a S R πππ==⨯=球372a π. 5．B ．解析：过CD 作平面PCD ，使AB ⊥平面PCD ，交AB 与P ，设点P 到CD 的距离为h ，则有AB CD11222323V h h =⨯⨯⨯⨯=四面体,当直径通过AB 与CD 的中点时，max h ==m ax 3V =6．D ．解析：面EFQ 即为面11DCB A ，连结1AD ，由正方体的性质可得⊥1AD 面11DCB A ，过P 作PN ∥1AD ，交D A 1于N 点，则有⊥PN 面11DCB A ，即⊥PN 面EFQ ，又z PD PN 2245cos =︒=，222121211=⨯⨯=⨯=∆C B EF S EFQ ，由z z PN S V EFQ EFQ P 312223131=⨯=⨯=∆-.7．C ．解析：设底面边长为a ，则高212)22(222aa SAh -=-=，所以体积54221123131aa h a V -==，设642112a a y -=，则53348a a y -='，当y 取最值时，解得a =0或a =4时（a =0舍去），体积最大，此时22122=-=ah .二．填空题8．144． 9．4． 104．解析：过点A 作平面β的垂线，垂足为C ，在β内过C 作l 的垂线.垂足为D ．连结AD ，可知AD ⊥l ，故∠ADC 为二面角l αβ--的平面角，为60°．又由已知，∠ABD ＝30°．连结CB ，则∠ABC 为A B 与平面β所成的角．设AD ＝2，则ACCD ＝1，AB ＝sin 30A D ＝4，∴sin ∠ABC＝4A C A B=．11．321S S S <<．解析：由题意OC OB OA ,,，两两垂直，可将其放置在以O 为一顶点的长方体中，设三边OC OB OA ,,分别为c b a >>，从而易得22121cb a S +=，22221ca b S +=，22321bac S +=，()(222222214141ca b aS S -+=-)(222222241baccb a b-=+ )()2222241baccb -=+，又b a >，所以02221>-S S，即21S S >．同理，用平方后作差法可得32S S >．∴123S S S <<．三．解答题12.方法一：如图所示，建立空间直角坐标系，点A 为坐标原点，设1AB =,依题意得(0,2,0)D ,(1,2,1)F ,1(0,0,4)A ,31,,02E ⎛⎫⎪⎝⎭．（1）解：易得10,,12E F ⎛⎫= ⎪⎝⎭,1(0,2,4)A D =-．于是1113cos ,5EF A D EF A D EF A D==-．所以异面直线E F 与1A D 所成角的余弦值为35．（2）证明：已知(1,2,1)AF = ,131,,42EA ⎛⎫=-- ⎪⎝⎭ ,11,,02E D ⎛⎫=- ⎪⎝⎭ ．于是A F ·1E A =0，A F ·E D=0.α∙AB∙βCD∙因此，1AF EA ⊥,AF ED ⊥,又1EA ED E ⋂=，所以A F ⊥平面1A ED ．(3)解：设平面E F D 的法向量(,,)u x y z = ，则 ,即102102y z x y ⎧+=⎪⎪⎨⎪-+=⎪⎩．不妨令x =1,可得(1,21u →=-）．由（2）可知，A F →为平面1A ED 的一个法向量．于是2cos,==3||A F A F|A F|u u u →→→→→→∙，从而sin ,=3AF u →→．所以二面角1A -ED -F的正弦值为3．方法二：（1）解：设AB =1，可得AD =2,AA 1=4,CF =1.CE =12．连接B 1C ,BC 1，设B 1C 与BC 1交于点M ,易知A 1D ∥B 1C ，由1C E C F 1==C BC C 4,可知EF ∥BC 1.故BMC ∠是异面直线EF 与A 1D所成的角，易知BM =CM=11B C 2,所以2223cos 25BMC MBCBM C BM CM +-∠==,所以异面直线FE 与A 1D 所成角的余弦值为35（2）证明：连接AC ，设AC 与DE 交点N 因为12C D EC BCAB==，所以RtDCE ～RtCBA ， 从而CDE BCA ∠=∠， 又由于90CDE CED ∠+∠=︒, 所以90BCA CED ∠+∠=︒，故AC ⊥DE ,又因为CC 1⊥DE 且1CC AC C ⋂=，所以DE ⊥平面ACF ，从而AF ⊥DE . 连接BF ，同理可证B 1C ⊥平面ABF ,从而AF ⊥B 1C ,所以AF ⊥A 1D 因为1DE A D D ⋂=，所以AF ⊥平面A 1ED .(3)解：连接A 1N .FN ,由（2）可知DE ⊥平面ACF ,又NF ⊂平面ACF , A 1N ⊂平面ACF ，所∙以DE ⊥NF ,DE ⊥A 1N ,故1A N F ∠为二面角A 1-ED -F 的平面角.易知R t C N ER t C ∆∆ ，所以C N E C B CA C=，又AC =所以5C N =，在1305Rt N C F N F Rt A AN ∆==中，在中，在Rt △A 1AN中，15N A ==.连接A 1C 1,A 1F在111Rt A C F A F ∆==中，222111112cos 23A N FN A FRt A N F A N F A N FN +-∆∠==∙在中，．所以1sin 3A N F ∠=所以二面角A 1-DE -F正弦值为3.13．方法一：（Ⅰ）解：取EF 的中点H ，连结A H '， A E A F ''=及H 是EF 的中点，∴A H EF '⊥． 又因为平面A E F '⊥平面BEF ，及A H '⊂平面.A EF '所以A H '⊥平面BEF ． 如图建立空间直角坐标系.A xyz -则(2,2,(10,8,0),(4,0,0),(10,0,0).A C F D '故(2,2,(6,0,0)FN FD =-=．设(,,)n x y z = 为平面A F D '的一个法向量，所以22060x y x ⎧-++=⎪⎨=⎪⎩．取(0,z n ==-则．又平面BEF 的一个法向量(0,0,1)m =，故cos ,3||||n m n m n m ⋅<>==⋅．3（Ⅱ）解：设x FM =，£¬(4,0,0)FM x M x =+则．因为翻折后，C 与A 重合，所以CM =A M '．∙故222222(6)80(2)2x x -++=--++，得214x =．经检验，此时点N 在线段BG 上，所以21.4F M =方法二：（Ⅰ）解：取截段EF 的中点H ，AF 的中点G ，连结A G '，NH ，GH ． 因为A E A F ''=及H 是EF 的中点，所以A 'H //EF ． 又因为平面A 'EF ⊥平面BEF ，所以A 'H `⊥平面BEF ， 又AF ⊂平面BEF ，故A H AF '⊥，又因为G ，H 是AF ，EF 的中点，易知GH //AB ， 所以GH AF ⊥，于是AF ⊥面A 'GH ， 所以A GH '∠为二面角A '—DF —C 的平面角，在Rt A GH '∆中，2,A H G H A G ''===，所以cos 3A G H '∠=故二面角A '—DF —C 的余弦值为3．（Ⅱ）解：设FM x =，因为翻折后，G 与A '重合，所以CM A M '⊥， 而222228(6)CMDC DMx =+=+-，222222222(2)2A MA H M HA HM G G Hx '''=+=++-+++，得214x =经检验，此时点N 在线段BC 上，所以21.4F M =14．（Ⅰ）证明：在ABC ∆中，因为45ABC ∠=°，BC =4，AB =所以2222cos 458AC AB BC AB BC =+-⋅⋅=，因此AC =． 故222BCACAB =+，所以090B A C ∠=．又PA ⊥平面ABCDE ，AB //CD ，所以,C D P A C D A C ⊥⊥.又P A ，AC ⊂平面P AC ，且P A ∩AC =A ，所以CD ⊥平面P AC ，又CD ⊂平面PCD ， 所以平面PCD ⊥平面P AC ． （Ⅱ）解法一：因为A P B ∆是等腰三角形，所以PA AB ==4PB ==．又AB //CD ，所以点B 到平面PCD 的距离等于点A 到平面PCD 的距离． 由于CD ⊥平面P AC ，在Rt PAC ∆中，P A A C ==PC =4．故PC 边上的高为2，此即为点A 到平面PCD 的距离，所以B 到平面PCD 的距离为 2.h = 设直线PB 与平面PCD 所成的角为θ，则21sin 42h P Bθ===，又[,0]2πθ∈，所以.6πθ=解法二：由（Ⅰ）知AB ，AC ，AP 两两相互垂直，分别以AB ，AC ，AP 为x 轴，z 轴建立如图． 所示的空间直角坐标系，由于P A B ∆是等腰三角形，所以PA AB ==又AC =，因此(0,0,0),0,0),(0,0),(0,0,A B C P 因为AC //DE ，CD AC ⊥， 所以四边形ACDE 是直角梯形，因为02,45,//AE ABC AE BC =∠=．所以0135B A E ∠=，因此045C A E ∠=，故0sin 4522C D AE =⋅=⨯=，所以(0)D ．因此(0,(0,0)C P C D =-=． 设(,,)m x y z =是平面PCD 的一个法向量，则0,0m C P m C D ⋅=⋅=，解得0,x y z ==，取1,(0,1,1)y m ==得．又(0,BP =-，设θ表示向量B P与平面PCD 的法向量m 所成的角，则1cos 2||||m B P m B P θ⋅== ， 所以3πθ=，因此直线PB 与平面PCD 所成的角为.6π（Ⅲ）因为AC //ED ，CD AC ⊥，所以四边形ACDE 是直角梯形．因为02,45,//AE ABC AE BC =∠=， 所以0135B A E ∠=， 因此045C A E ∠=．故0sin 4522C D AE =⋅=⨯=， 0cos 4522ED AC AE =-⋅=⨯=所以 3.2A C D E S ==四边形 又PA ⊥平面ABCDE ，所以133P C D E V -=⨯⨯=15.解法一 ：（I ）⊥A A 1 平面ABC ，⊂BC 平面ABC ，BC A A ⊥∴1.AB 是圆O 的直径， AC BC ⊥∴.又A A A AC =1 ， ⊥∴BC 平面11ACC A ，而⊂BC 平面11BCC B ，所以平面11ACC A ⊥平面11BCC B ． （II ）（i ）设圆柱的底面半径为r ，则r AA AB 21==， 故三棱柱111_C B A ABC 的体积r AC V ⋅⋅=⋅⋅=BC AC 2r BC 211．又22224r AB BC AC==+ ， 22222r BC ACBC AC =+≤⋅∴．当且仅当r BC AC 2==时等号成立．从而，312r V ≤．而圆柱的体积3222r r r V ππ=⋅=，故ππ1223321=≤=rrVV p ，当且仅当r BC AC 2==，即AB OC ⊥时等号成立．所以，p 的最大值等于π1．（ii ）由（i ）可知p 取最大值时，AB OC ⊥.于是以O 为坐标原点，建立空间直角坐标系xyz O -（如图）. 则)0,0,(r C ，)0,,0(r B ，)2,,0(1r r B .⊥BC 平面11ACC A ，)0,,(r r BC -=∴→是平面11ACC A 的一个法向量.设平面OC B 1的法向量),,(z y x n =→.由⎪⎩⎪⎨⎧⊥⊥→→→→1OBn OCn ，得⎩⎨⎧=+=020rz ry rx ，解得⎩⎨⎧-==z y x 20.取1=z ，得平面OC B 1的一个法向量为)1,2,0(-=n .900≤<θ，解法二：（I ）同解法一（II ）（i ）设圆柱的底面半径为r ，则r AA AB 21==， 故三棱柱111_C B A ABC 的体积r AC V ⋅⋅=⋅⋅=BC AC 2r BC 211设)900(<<=∠ααBAC ，则ααcos 2cos r AB AC ==，αsin 2r BC =， 由于22222sin 2cos sin 4r r r BC AC ≤==⋅ααα，当且仅当12sin =α即45=α时等号成立，故312r V ≤．而圆柱的体积3222r r r V ππ=⋅=，故ππ1223321=≤=rrVV p ，当且仅当12sin =α即45=α时等号成立．所以，p 的最大值等于π1．（ii ）同解法一． 解法三：（I ）同解法一．（II ）（i ）设圆柱的底面半径r ，则r AA AB 21==，故圆柱的体积3222r r r V ππ=⋅=． 因为VV p 1=，所以当1V 取得最大值时，p 取得最大值．又因为点C 在圆周上运动，所以当AB OC ⊥时，ABC ∆的面积最大．进而，三棱柱111_C B A ABC 的体积最大，且其最大值为322221r r r r =⋅⋅⋅．故p 的最大值等于π1．（ii ）同解法一．。

人大行政管理考研复试真题心得分享作为考研复试的一部分，面试环节是很多考生备战过程中感到较为紧张的一环。

而作为人大行政管理的考研复试科目之一，面试的通过与否对考生未来的发展具有重要的影响。

在这里，我将分享一些关于人大行政管理考研复试真题的心得体会，希望对正在备考的考生们有所帮助。

首先，了解考研大纲是非常重要的。

考研大纲是考生备考的的重要依据，熟悉大纲不仅可以了解考试的内容和要求，还可以帮助考生明确备考的重点和方向，提高备考效率。

在备考过程中，我会仔细研读大纲，并将其划分为不同的模块，逐一进行学习和掌握。

同时，大纲中的每个考点都应该被掌握并独立进行总结，这样可以确保自己在复试中可以有足够的答题材料。

其次，考研笔记的整理与积累是备考过程中不可或缺的一环。

在复习的过程中，我会针对每个考点进行详细的笔记整理。

这不仅可以帮助我加深对知识点的理解和记忆，还可以方便我在复习过程中进行查阅。

考研笔记的整理应该注重概念的讲解、案例的引用以及自己对于知识的理解与补充，这样才能帮助我更好地回答问题和理解考研真题。

最后，复试真题的练习也是非常重要的。

通过做真题可以帮助我了解考试的形式和要求，熟悉考试的节奏和时间分配。

而且，真题可以帮助我发现自己的薄弱环节和需要加强的地方。

在进行真题练习时，我会模拟考试环境，合理安排时间，注重思路的清晰和表达的准确。

每做完一套真题，我会仔细分析自己的答题情况，找出不足之处，并进行针对性的复习和提高，以争取在实际考试中能够得心应手。

总结起来，人大行政管理考研复试是需要考生全方位准备的一个环节，综合素质和学科基础都是重要的考察要素。

在备考过程中，我们应该密切关注考研大纲，合理安排复习时间，积极整理和记忆相关知识点，同时进行适当的真题练习。

只有全面准备，才能在复试中取得好的成绩。

希望以上的分享能够对正在备考人大行政管理考研复试的考生们有所帮助。

祝愿大家能够顺利通过复试，实现自己的考研梦想！。

A浙江高考历年真题之立体几何大题（教师版）1、（2005年）如图，在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝12PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ． (Ⅰ)求证OD ∥平面PAB(Ⅱ) 求直线OD 与平面PBC 所成角的大小；解析： 方法一：(Ⅰ) ∵O 、D 分别为AC 、PC 中点，O D P A ∴ ∥PA PAB ⊂又平面，OD PAB ∴ 平面∥(Ⅱ)A B B C O A O C ⊥= ，，O A O B O C ∴== ，O P ABC ⊥ 又 平面，.PA PB PC ∴== E PE BC PO E ⊥取BC 中点，连结，则平面OF PE F DF OF PBC ⊥⊥作于，连结，则平面 ODF OD PBC ∴∠ 是与平面所成的角.sin 30O F R t O D F O D F O D∆∠==在中， arcsin30O D P B C ∴ 与平面所成的角为方法二：O P ABC O A O C AB BC ⊥== 平面，，，.O A O B O A O P O B O P ∴⊥⊥⊥ ，，()O O Pz O xyz -以为原点，射线为非负轴，建立空间直角坐标系如图，,0,0,,0,,0,0222AB a A B C⎫⎛⎫⎛⎫=-⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭设，则 ()0,0,.OP h P h =设，则()D PC 为的中点，Ⅰ1,0,,,0,422O D h PA ⎛⎫⎛∴=-=- ⎪ ⎪ ⎝⎭⎝ 又1 (2)O D PA O D PA O D PAB ∴=-∴∴平面∥∥()2,PA a = Ⅱ,h ∴=,,44O D ⎛⎫∴=-⎪⎪⎝⎭,PBC n ⎛=- ⎝ 可求得平面的法向量cos ,30OD nOD n OD n⋅∴〈〉==⋅OD PBC θ设与平面所成的角为，sin cos ,30O D n θ=〈〉=则arcsin30O D P B C ∴ 与平面所成的角为2、（2006年）如图，在四棱锥P-ABCD 中，底面为直角梯形,AD ∥BC,∠BAD=90° ,PA ⊥底面ABCD ，且PA ＝AD=AB=2BC,M 、N 分别为PC 、PB 的中点. (Ⅰ)求证：PB ⊥DM;(Ⅱ)求BD 与平面ADMN 所成的角。

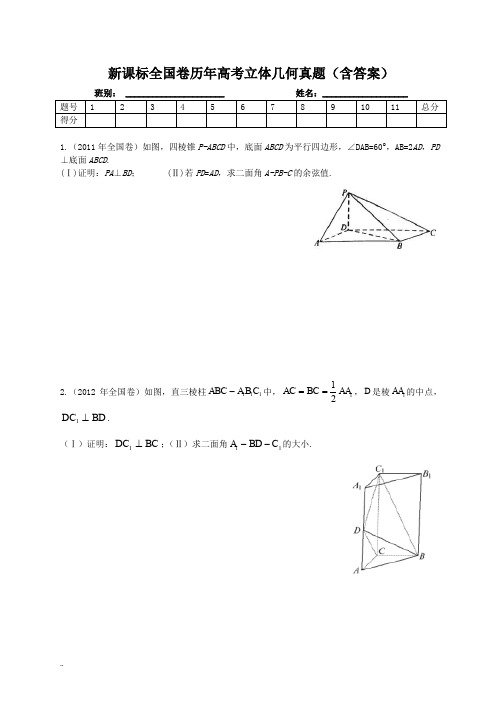
新课标全国卷历年高考立体几何真题（含答案）班别： ______________________ 姓名：___________________1.（2011年全国卷）如图，四棱锥P-ABCD 中，底面ABCD 为平行四边形，∠DAB=60°，AB=2AD ，PD ⊥底面ABCD .(Ⅰ)证明：PA ⊥BD ； (Ⅱ)若PD =AD ，求二面角A-PB-C 的余弦值.2.（2012年全国卷）如图，直三棱柱111ABC A B C -中，112AC BC AA ==，D 是棱1AA 的中点，BD DC ⊥1.（Ⅰ）证明：BC DC ⊥1；（Ⅱ）求二面角11C BD A --的大小.3.（2013年全国Ⅱ卷）如图，直棱柱ABC-A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1=AC=CB=2AB. （Ⅰ）证明：BC 1//平面A 1CD ， （Ⅱ）求二面角D-A 1C-E 的正弦值4.（2013年全国Ⅰ卷）如图，三棱柱111C B A ABC -中，CB CA =，1AA AB =， 601=∠BAA .（Ⅰ）证明C A AB 1⊥；（Ⅱ）若平面ABC ⊥平面AA 1B 1B ，AB=CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值.5.（2014年全国Ⅱ卷）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ；(Ⅱ)设二面角D-AE-C 为60°，AP=1，，求三棱锥E-ACD 的体积.6.（2014年全国Ⅰ卷）如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥. （Ⅰ） 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=BC ，求二面角111A A B C --的余弦值.7.（2015年全国Ⅱ卷）如图，长方体ABCD-A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说出画法和理由)；(Ⅱ)求直线AF 与平面α所成角的正弦值.8.（2015年全国Ⅰ卷）如图，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC.(Ⅰ)证明:平面AEC ⊥平面AFC ；(Ⅱ)求直线AE 与直线CF 所成角的余弦值.9.（2016年全国Ⅱ卷）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5,6AB AC ==，点,E F分别在,AD CD 上，54AE CF ==，EF 交BD 于点H ．将DEF ∆沿EF 折到'D EF ∆位置，OD '=（Ⅰ）证明：D H'⊥平面ABCD ； （Ⅱ）求二面角B D A C '--的正弦值．10.（2016年全国Ⅰ卷）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF =2FD ，90AFD ∠=，且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明：平面ABEF ⊥平面EFDC ；（II ）求二面角E -BC -A 的余弦值．11.（2016年全国3卷）如图，四棱锥P ABC -中，PA ⊥底面面ABCD ，AD ∥BC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN平面PAB ；（II ）求直线AN 与平面PMN 所成角的正弦值.自我总结：新课标全国卷历年高考例题几何真题（广西多用2卷）1.解：（Ⅰ）因为60,2DAB AB AD ∠=︒=,由余弦定理得BD = 从而BD 2+AD 2= AB 2，故BD⊥AD;又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴射线DB 为y 轴的正半轴，射线DP 为z 轴的正半轴，建立空间直角坐标系D-xyz ，则()1,0,0A,()0B,()C -,()0,0,1P.(1),(1,0,0)ABPB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n =（x,y,z ），则0⎧⋅=⎪⎨⋅=⎪⎩n AB n PB ,即00x z -+=-= 因此可取n =设平面PBC 的法向量为m ，则0⎧⋅=⎪⎨⋅=⎪⎩m PB m BC 可取m =（0，-1，，cos 7<>==-m,n 故二面角A-PB-C 的余弦值为 . 2.证明（Ⅰ）（1）在Rt DAC ∆中，AD AC =得：45ADC ︒∠=，同理：1114590A DC CDC ︒︒∠=⇒∠=，得：1,DC DC DC BD DC ⊥⊥⇒⊥又∵11,DC DC DC BD DC ⊥⊥⇒⊥平面1BCD DC BC ⇒⊥. （Ⅱ）（2）11,DC BC CC BC BC ⊥⊥⇒⊥平面11ACC A BC AC ⇒⊥取11A B 的中点O ，过点O 作OH BD ⊥于点H ，连接11,C O C H ，1111111AC B C C O A B =⇒⊥，C 1O ⊥A 1D 1C O ⇒⊥面1ABD 1OH BD C H BD ⊥⇒⊥ 得：点H 与点D 重合 ，即1C DO ∠是二面角11C BD A --的平面角 设AC a =，则1C O =111230C D C O C DO ︒==⇒∠= 即二面角11C BD A --的大小为30︒.3.（1）连接1AC ，交1A C 于点F ，连结1,DF BC ，则F 为1AC 的中点，因为D 为AB 的中点，所以DF//1BC ，又因为111FD ACD BC AC D ⊂⊄平面，平面，所以11//BC ACD 平面. (2)由AA 1AC CB AB ===，可设：AB ＝2a,则1,AA AC CB ===所以AC BC ⊥，又因为ABC-A 1B 1C 1为直三棱柱，所以以点C 为坐标原点，建立空间直角坐标系如图.则C （0,0,0）、)1,0A D ⎫⎪⎪⎝⎭、、,E ⎛⎫⎪ ⎪⎝⎭()122,0,2,,0CA a a CD a ⎛⎫== ⎪⎪⎝⎭，.CE ⎛⎫= ⎪ ⎪⎝⎭设平面1A CD 的法向量为(),,,n x y z =则0n CD ⋅=且10,n CA ⋅=可解得,y x z =-=令1,x =得平面1A CD 的一个法向量为()1,1,1n =--，同理可得平面1A CE 的一个法向量为()2,1,2m =-，则3cos ,n m <>=，所以6sin ,n m <>=所以二面角1D A C E -- 4.【解析】（Ⅰ）取AB 的中点O ，连结OC ，1OA ，B A 1.因为CB CA =，所以AB OC ⊥.由于1AA AB =， 601=∠BAA ，故B AA 1∆为等边三角形，所以AB OA ⊥1.因为O OA OC =1 ，所以⊥AB 面C OA 1.又⊂C A 1平面C OA 1，故C A AB 1⊥. （Ⅱ）由（Ⅰ）知，AB OC ⊥，AB OA ⊥1，又平面⊥ABC 平面11BB AA ，交线为AB ，所以⊥OC 平面11BB AA ，故OA ，OC ，1OA 两两互相垂直.以O 为坐标原点，的方向为x 轴的正方向，||为单位长度，建立如图所示的空间直角坐标系xyz O -，则有)0,0,1(A ，)0,3,0(1A ,)3,0,0(C ,)0,0,1(-B .则)3,0,1(=， )0,3,1(1-==AA BB ， )3,3,0(-=.设平面C C BB 11的法向量为),,(z y x =，则有⎪⎩⎪⎨⎧=⋅=⋅01BB ，即⎪⎩⎪⎨⎧=+-=+0303y x z x ，可取)1,1,3(-=.故510||||,cos 111-=⋅>=<C A n C A n C A n ，所以直线C A 1与平面C C BB 11所成角的正弦值为510.5.【解析】(1) 连接BD 交AC 于点为G,连接EG.在三角形PBD 中,中位线EG ∥PB, 且EG 在平面AEC 上，所以PB ∥平面AEC.(2)设CD=m,分别以AD,AB,AP 为x,y,z 轴建立坐标系,则A(0,0,0),D(,0,0),E 12⎫⎪⎪⎝⎭,C(,m,0).所以AD=(,0,0), AE=12⎫⎪⎪⎝⎭,AC=),0m .设平面ADE 的法向量为1n =(x 1,y 1,z 1),则1n AD ⋅=0, 1n AE ⋅=0,解得一个1n =(0,1,0).同理设平面ACE 的法向量为2n =(x 2,y 2,z 2),则2n AC ⋅=0, 2n AE ⋅=0,解得一个2n因为cos 3π=|cos<12,n n >|=1212n n n n⋅==12,解得m=32. 设F 为AD 的中点,则PA ∥EF,且PA=2EF =12,EF ⊥面ACD,即为三棱锥E-ACD 的高. 所以V E-ACD =·S △ACD ·EF=13×12×32×12.所以,三棱锥E-ACD .为坐标原点，方向，||为单位长度，的方向为y 轴的正方向，的方向为z 轴的正方向建立空间直角坐标系，∵∠，，（0，，0） =，，=，=设向量=，可取，）的一个法向量，），＞=A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),=(0,-6,8).=+080z .由∠ABC=120°,可得AG=GC=.由BE ⊥平面ABCD,AB=BC可知AE=EC.又AE ⊥EC,所以EG=,且EG ⊥AC.在Rt △EBG 中,可得BE=,故DF=.在Rt △FDG 中,可得FG=.在直角梯形BDFE 中,由BD=2,BE=,DF=,可得EF=.从而EG 2+FG 2=EF 2,所以EG ⊥FG.,又AC ∩FG=G,可得EG ⊥平面AFC.又因为EG ⊂平面AEC,所以平面AEC ⊥平面AFC. (2)如图,以G 为坐标原点,分别以,的方向为x 轴,y 轴正方向,||为单位长度,建立空间直角坐标系G-xyz.由(1)可得(,)A 00,(,E 10,(,F -10,()C 00， 所以(AE =1,(,CF =-1. 故cos ,||||AE CF AE CF AE CF ⋅<>==-3.所以直线AE 与直线CF所成角的余弦值为3 9.【解析】⑴∵ABEF 为正方形 ∴AF EF ⊥ ∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF ∴平面ABEF ⊥平面EFDC ⑵ 由⑴知60DFE CEF ∠=∠=︒∵AB EF ∥ AB ⊄平面EFDC EF ⊂平面EFDC ∴AB ∥平面ABCD AB ⊂平面ABCD ∵面ABCD 面EFDC CD = ∴AB CD ∥,∴CD EF ∥ ∴四边形EFDC 为等腰梯形以E 为原点，如图建标系，设FD a =()()000020E B a ，，，， ()02202a CA a a ⎛⎫ ⎪ ⎪⎝⎭，，， ()020EB a =，，，22a BC a ⎛⎫=- ⎪ ⎪⎝⎭，，()200AB a =-，，设面BEC 法向量为()m x y z =，，.00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩，即111120202a y a x ay z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩， ()301m =-，，设面ABC 法向量为()222n x y z =，， =00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即222220220a x ay ax ⎧-+=⎪⎨⎪=⎩，()034n=， 设二面角E BC A --的大小为θ.cos 3m nm n θ⋅===+⋅ ∴二面角E BC A --的余弦值为 10.【解析】⑴证明：∵54AE CF ==，∴AE CF AD CD=，∴EF AC ∥．∵四边形ABCD 为菱形，∴AC BD ⊥，∴EF BD ⊥，∴EF DH ⊥，∴EF D H '⊥．∵6AC =，∴3AO =；又5AB =，AO OB ⊥，∴4OB =， ∴1AE OH OD AO=⋅=，∴3DH D H '==，∴222'OD OH D H '=+， ∴'D H OH ⊥．又∵OH EF H =I ，∴'D H ⊥面ABCD ．⑵建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，，()430AB =uu u r ，，，()'133AD =-uuur ，，，()060AC =uuu r ，，，设面'ABD 法向量()1n x y z =，，u r ，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩，取345xy z=⎧⎪=-⎨⎪=⎩，∴()1345n =-u r ，，．同理可得面'AD C 的法向量()2301n =u u r ，，，∴1212cos n n n n θ⋅===u r u u r u r u u r∴sin θ=11.设),,(z y x =为平面PMN 的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM ， 即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=， 于是2558|||||,cos |==><AN n .。

空间几何体的结构及其三视图和直观图、 空间几何体的表面积与体积1.（2010·陕西高考理科·Ｔ7）若某空间几何体的三视图如图所示， 则该几何体的体积是（ ）(A) 13 (B) 23(C) 1 (D) 22.（2010·辽宁高考文科·Ｔ11）已知SABC 是球O 表面上的点，SA ⊥平面ABC ,AB ⊥BC ，SA =AB =1 BC =2,则球O 的表面积等于（ ） （A ）4π(B ）3π(C)2π(D) π3.（2010·辽宁高考理科·Ｔ12）有四根长都为2的直铁条，若再选两根长都为a 的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则a 的取值范围是（ ）(A)（0,62+） (B)（1,22） (C) (62-,62+） (D) （0,22） 4.（2010·安徽高考理科·Ｔ8）一个几何体的三视图如图， 该几何体的表面积为（ ） A 、280B 、292C 、360D 、3725.（2010·浙江高考文科·Ｔ8）若某几何体的三视图 （单位：cm ）如图所示，则此几何体的体积是（ ）（A ）3523cm 3 （B ）3203cm3（C ）2243cm 3 （D ）1603cm36.（2010·北京高考理科·Ｔ3）一个长方体 去掉一个小长方体，所得几何体的正（主）视 图与侧（左）视图分别如右图所示，则该几何 体的俯视图为（ ）7.（2010·北京高考理科·Ｔ8）如图，正方体ABCD-1111A B C D 的棱长为2，动点E 、F 在棱11A B 上，动点P ，Q 分别在棱AD ，CD 上，若EF=1，1A E=x ，DQ=y ，D Ｐ＝ｚ（ｘ，ｙ，ｚ大于零），则四面体PE ＦＱ的体积（ ）（Ａ）与ｘ，ｙ，ｚ都有关 （Ｂ）与ｘ有关，与ｙ，ｚ无关 （Ｃ）与ｙ有关，与ｘ，ｚ无关 （Ｄ）与ｚ有关，与ｘ，ｙ无关 8.（2010·北京高考文科·Ｔ8）如图，正方体1111ABCD-A B C D的棱长为2，动点E 、F 在棱11A B 上。

专题10 立体几何一．选择题10．1.【2005年普通高等学校招生全国统一考试湖北卷10】如图，在三棱柱ABC—A′B′C′中，点E 、F 、H 、 K 分别为AC′、CB′、A′B、B′C′的中点，G 为△ABC 的重心. 从K 、H 、G 、B′中取一点作为P ， 使得该棱柱恰有2条棱与平面PEF 平行，则P 为 （ ）A.K B ．H C ．G D ．B′【答案】C2. 【2006年普通高等学校招生全国统一考试湖北卷】关于直线与平面，有以下四个命题： ,m n ,αβ①若且，则；//,//m n αβ//αβ//m n ②若且，则；,m n αβ⊥⊥αβ⊥m n ⊥③若且，则；,//m n αβ⊥//αβm n ⊥④若且，则；//,m n αβ⊥αβ⊥//m n 其中真命题的序号是 ( )A ．①②B ．③④C ．①④D ．②③【答案】D.【解析】试题分析：用排除法可得选D.3.【2007年普通高等学校招生全国统一考试湖北卷4】平面外有两条直线和，如果和在平面αm n m nC 【答案】C∴∠EOA即为AC与PB所成的角或其补角AB于3.【2007年普通高等学校招生全国统一考试湖北卷18】如图，在三棱锥V-ABC中，VC⊥底面解法3：（Ⅰ）以点为原点，以所在的直线分别为轴、轴，建立如图所示的空间直角坐D DC DB 平x y 标4.【2008年普通高等学校招生全国统一考试湖北卷18】如图，在直三棱柱ABC-A1B1C1中，平面ABC⊥侧面A1ABB1.（Ⅰ）求证：AB⊥BC；（Ⅱ）若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ的大小关系，并予以证明.【解析】（Ⅰ）证明：如右图，过点A在平面A1ABB1内作AD⊥A1B于D，则由平面A1BC⊥侧面A1ABB1,且平面A1BC侧面A1ABB1=A1B,得AD⊥平面A1BC,又BC平面A1BC，所以AD⊥BC.因为三棱柱ABC—A1B1C1是直三棱柱，则AA1⊥底面ABC，所以AA1⊥BC.又AA1AD=A,从而BC⊥侧面A1ABB1，又AB侧面A1ABB1，故AB⊥BC.5.【2009年普通高等学校招生全国统一考试湖北卷面ABCD ，SD=2a ，点E 是SD 上的点，且2AD a =（Ⅰ）求证：对任意的，都有(0,2]λ∈（Ⅱ）设二面角C—AE—D 的大小为θ的值BE 在平面.2∴⊥根据三垂线定理，知：AC NP7.【2011年普通高等学校招生全国统一考试湖北卷18】如图，已知正三棱柱的各棱长是111ABC A B C -4，E 是BC 的中点，动点F 在侧棱上，且不与点C 重合1CC （Ⅰ）当CF=1时，求证：;1EF A C ⊥ （Ⅱ）设二面角C-AF-E 的大小为，求的最小值。

第九章直线、平面、简单几何体1.(2006年福建卷)已知正方体外接球的体积是323π,那么正方体的棱长等于..(.D)(A)(B)3(C)3(D)32.(2006年福建卷)对于平面α和共面的直线m 、,n 下列命题中真命题是....(C) (A)若,,m m n α⊥⊥则n α∥ (B)若m αα∥,n ∥,则m ∥n(C)若,m n αα⊂∥,则m ∥n (D)若m 、n 与α所成的角相等,则m ∥n3.(2006年安徽卷)表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为.A.3...............B.13π.....C.23π............D.3 解：此正八面体是每个面的边长均为a 的正三角形,所以由8=,1a =,故选A 。

4.(2006年安徽卷)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A 在平面α内,其余顶点在α的同侧,正方体上与顶点A 相邻的三个顶点到α的距离分别为1,2和4,P 是正方体的其余四个顶点中的一个,则P 到平面α的距离可能是：①3；.....②4；....③5；....④6；....⑤7以上结论正确的为______________。

(写出所有正确结论的编号．．) 解：如图,B 、D 、A 1到平面α的距离分别为1、2、4,则D 、A 1的中点到平面α的距离为3,所以D 1到平面α的距离为6；B 、A 1的中点到平面α的距离为52,所以B 1到平面α的距离为5；则D 、B 的中点到平面α的距离为32,所以C 到平面α的距离为3；C 、A 1的中点到平面α的距离为72,所以C 1到平面α的距离为7；而P 为C 、C 1、B 1、D 1中的一点,所以选①③④⑤。

5.(2006年广东卷)给出以下四个命题①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面; ③如果两条直线都平行于一个平面,那么这两条直线互相平行;④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直. 其中真命题的个数是A.4........B.3....C.2.........D.15、①②④正确,故选B.6.(2006年广东卷)若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为..........ABCDA 1B 1C 1D 1第16题图α6、ππ274233332==⇒=⇒=R S R d 7.(2006年陕西卷)已知平面α外不共线的三点,,A B B 到α的距离都相等,则正确的结论是.(D)(A)平面ABC 必不垂直于α (B)平面ABC 必平行于α (C)平面ABC 必与α相交(D)存在ABC ∆的一条中位线平行于α或在α内8.(2006年陕西卷)水平桌面α上放有4个半径均为2R 的球,且相邻的球都相切(球心的连线构成正方形)。

2010年高考数学试题分类汇编——立体几何一、选择题1、（2010浙江理数）（6）设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是 （A ）若l m ⊥，m α⊂，则l α⊥ （B ）若l α⊥，l m //，则m α⊥ （C ）若l α//，m α⊂，则l m // （D ）若l α//，m α//，则l m //解析：选B ，可对选项进行逐个检查。

本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理，也蕴含了对定理公理综合运用能力的考察，属中档题2、（2010全国卷2理数）（11）与正方体1111ABC D A B C D -的三条棱A B 、1C C 、11A D 所在直线的距离相等的点（A ）有且只有1个 （B ）有且只有2个 （C ）有且只有3个 （D ）有无数个 【答案】D【解析】直线上取一点，分别作垂直于于则分别作，垂足分别为M ，N ，Q ，连PM ，PN ，PQ ，由三垂线定理可得，PN ⊥PM ⊥；PQ ⊥AB ，由于正方体中各个表面、对等角全等，所以，∴PM=PN=PQ ，即P 到三条棱AB 、CC 1、A 1D 1.所在直线的距离相等所以有无穷多点满足条件，故选D.3、（2010全国卷2理数）（9）已知正四棱锥S A B C D -中，SA =，那么当该棱锥的体积最大时，它的高为（A ）1 （B （C ）2 （D ）3 【答案】C【命题意图】本试题主要考察椎体的体积，考察告辞函数的最值问题.【解析】设底面边长为a ，则高所以体积，设，则，当y 取最值时，，解得a=0或a=4时，体积最大，此时，故选C.4、（2010陕西文数） 8.若某空间几何体的三视图如图所示，则该几何体的体积是 [B]（A ）2 （B ）1（C ）23（D ）13解析：本题考查立体图形三视图及体积公式 如图，该立体图形为直三棱柱 所以其体积为122121=⨯⨯⨯5、（2010辽宁文数）（11）已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，A B B C ⊥，1SA A B ==，BC =O 的表面积等于（A ）4π （B ）3π （C ）2π （D ）π解析：选A.由已知，球O 的直径为22R SC ==，∴表面积为244.R ππ=7、（2010全国卷2文数）（11）与正方体ABCD —A 1B 1C 1D 1的三条棱AB 、CC 1、A 1D 1所在直线的距离相等的点（A ）有且只有1个 （B ）有且只有2个 （C ）有且只有3个 （D ）有无数个221【解析】D ：本题考查了空间想象能力∵到三条两垂直的直线距离相等的点在以三条直线为轴，以正方体边长为半径的圆柱面上，∴三个圆柱面有无数个交点，8、（2010全国卷2文数）（8）已知三棱锥S A B C -中，底面ABC 为边长等于2的等边三角形，S A 垂直于底面ABC ，S A =3，那么直线A B 与平面S B C 所成角的正弦值为（A ）4(B)4(C)4(D) 34【解析】D ：本题考查了立体几何的线与面、面与面位置关系及直线与平面所成角。

2010年高考试题分类练习(理科：立体几何）（一）答案曾劲松 整理一．选择题1．D ． 2．C ． 3. D .4．D ．5．D ．解析：记这两直线为1l ，2l ，异面直线的距离为k ，平面α为过1l 且平行于2l 的平面，设α上某个点P 满足条件．将2l 正投影到平面α上，其投影记为3l ，设P 到1l 及2l 的距离为t ，到3l 的距离为u ，则222u k t +=，即222t u k -=，这里k 为定值，t ，u 分别正是P 到α上两垂直直线1l ，2l 的距离，而1l 和3l 可看作α上的直角坐标系，由此可知，P 的轨迹就是双曲线.6．D ．解析：因为BB 1//DD 1，所以B 1B 与平面1ACD 所成角和DD 1与平面1ACD 所成角相等，连接BD ，设与AC 交于O ，在正方体中易知A C ⊥平面1O D D ，过D 作1D E O D ⊥于E ，则A C D E ⊥．又1D E AC O = ，则D E ⊥平面1A C D ，所以1D D O ∠即为所求角，易知1cos 3D D O ∠=7．A ．解析：根据条件，四根长为2的直铁条与两根长为a 的直铁条要组成三棱镜形的铁架，有以下两种情况：（1）地面是边长为2的正三角形，三条侧棱长为2，a ，a ，如图，此时a 可以取最大值，可知AD =，SD =<2+，即228a <+=，即有a (2)构成三棱锥的两条对角线长为a ，其他各边长为2，如图所示，此时a >0;综上分析可知a ∈（0+．二．填空题8．103． 9． 10．4． 11．3．三．解答题 12．解：（1）因为PD ⊥平面ABCD ，BC ⊂平面ABCD ，所以PD ⊥BC ．由∠BCD =90︒，得BC ⊥DC ， 又PD DC =D ，PD ⊂平面PCD ， DC ⊂平面PCD ，所以BC ⊥平面PCD ． 因为PC ⊂平面PCD ，故PC ⊥BC ． （2）连结AC .设点A 到平面PBC 的距离为h ．因为AB ∥DC ，∠BCD =90︒，所以∠ABC =90︒．从而由AB =2，BC =1，得A B C ∆的面积1ABC S ∆=． 由PD ⊥平面ABCD 及PD =1，得三棱锥P -ABC 的体积1133A B C V S P D ∆=⋅=．因为PD ⊥平面ABCD ，DC ⊂平面ABCD ，所以PD ⊥DC ． 又PD =DC =1，所以PC ==．由PC ⊥BC ，BC =1，得P B C ∆的面积2PBC S ∆=．由11213323PBC V S h h ∆===h ⋅⋅3131=，得h =，故点A 到平面PBC ．13． 解法一：（Ⅰ）在平面O A B 内作O N O A ⊥交A B 于N ，连接N C ． 又O A O C ⊥，OA ONC ∴⊥平面． NC ONC ⊂ 平面，O A N C ∴⊥．取Q 为A N 的中点，则NC PQ //．PQ OA ∴⊥在等腰AOB ∆中，120AOB ∠=，30OAB OBA ∴∠=∠=．在AON Rt ∆中，30O AN ∠=， 12O N A N A Q ∴==．在ONB ∆中， 1209030NOB NBO ∠=-==∠，DPCAA.N B O N A Q ∴== 3AB AQ∴=．（Ⅱ）连接 PO PN ,，由O C O A ⊥，O C O B ⊥知：OC OAB ⊥平面. 又O N O A B ⊂， O C O N ∴⊥．又由O N O A ⊥，ON AOC ⊥平面．∴O P 是N P 在平面A O C 内的射影．在等腰COA Rt ∆中，P 为A C 的中点，A C O P ∴⊥．于是可证A C N P ∴⊥． O P N ∴∠为二面角O A C B --的平面角．在等腰COA Rt ∆中，1O C O A ==，2O P ∴=．在AON Rt ∆中，tan 303O N O A ==，∴在PON Rt ∆中，6PN ==cos 56P O O PN P N∴∠===．解法二：取O 为坐标原点，分别以O A ，O C 所在的直线为x 轴，z 轴，建立空间直角坐标系O xyz - （如图所示）． 则1(1,0,0),(0,0,1),(,0)2A CB -P 为A C 中点，11(,0,)22P ∴．设 ((0,1)),AQ AB λλ=∈ 3(,0)22AB =- ． 33(1,0,0)(,0)(1,,0),2222O Q O A A Q λλλ∴=+=+-=-131(,,).2222P Q O QO P λ∴=-=--,P Q O A ⊥ ,0PQ O A ∴= 即13022λ-=，13λ=．所以存在点1(,0)26Q 使得 PQ OA ⊥ 且3AB AQ=．（Ⅱ）记平面ABC 的法向量为123(,,)n n n n =,则由n C A ⊥ ，n AB ⊥，且(1,0,1)C A =-，得132303022n n n -=⎧⎪⎨-+=⎪⎩，故可取n =（）． 又平面O AC 的法向量为 (0,1,0)e =．<∴e n ,cos cos ,n e ∴≥=，两面角O A C B --的平面角是锐角，记为θ，则cos 5θ=14.15．（1）证明： 连结C F ，因为 是半径为a 的半圆，A C 为直径，点E 为 的中点，所以E B A C ⊥．在RT BC E ∆中，EC ===．在B D F ∆中，BF D F ==，B D F ∆为等腰三角形，且点C 是底边B D 的中点，故CF BD ⊥．在C E F ∆中，222222)(2)6C E C F a a EF +=+== 2222)(2)6a a a EF +==，所以C E F ∆为R t ∆，且C F EC ⊥．因为C F BD ⊥，C F EC ⊥，且CE ∩BD =C ，所以C F ⊥平面BED ，而EB ⊂平面BED ，C F E B ∴⊥．因为E B A C ⊥，E B C F ⊥，且AC ∩CF =C ，所以EB ⊥平面B D F ， 而FD ⊂平面B D F ，EB FD ∴⊥． （2）设平面BED 与平面RQD 的交线为D G .由23F Q F E =，23F R F B =，知//QR EB .而EB ⊂平面BD E ，∴//QR 平面BD E ，而平面BD E I 平面RQD = D G ，∴////QR DG EB . 由（1）知，B E ⊥平面B D F ，∴D G ⊥平面B D F ， 而,DR DB ⊂平面B D F ，∴D G D R ⊥，DG DQ ⊥， ∴R D B ∠是平面BED 与平面RQD 所成二面角的平面角．在R t B C F ∆中，2C F a ===，sinFC RBD BF∠===cos RBD ∠==．在BD R ∆中，由23F R F B =知，133BR FB ==由余弦定理得，RD =3a ==由正弦定理得，sin sin B R R DR D BR B D=∠∠，即33sin R D B=∠，sin 29RD B ∠=．故平面BED 与平面RQD29解法二：如图，以B 为原点，BE为x 轴正方向，BD为y 轴正方向，过B 作平面BEC 的垂线，建立空间直角坐标系，由此得B （0,0,0），C （0，a ，0），D （0，2a ，0），E （a ，0，0）.FD=FB BC=CD,FC BD.FC=2a ∴⊥∴ ，. 22FQ =FE FR =FB ,33 ，12R 0,,33a a ⎛⎫∴ ⎪⎝⎭，22R Q =BE =,0,033a ⎛⎫⎪⎝⎭ .52R D =0,,33a a ⎛⎫∴- ⎪⎝⎭ .设平面RQD 的法向量为1(,,)n x y z =，则,1=(0,2,5)n ∴.∵平面BED 的法向量为2=(0,0,1)n，12cos ,29n n ∴<>=12sin ,29n n ∴<>= ∴平面BED 与平面RQD29。