中考数学专题复习小训练专题14几何初步知识三角形多边形
- 格式:doc
- 大小:968.50 KB
- 文档页数:3

专题14 几何初步知识、三角形、多边形1.2017·滨州有一个角为75°,则它的余角的度数为( )A.285° B.105° C.75° D.15°2.2017·宿迁如图Z14-1,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )图Z14-1A.80° B.85° C.95° D.100°3.2018·常德已知三角形的两边长分别是3和7,则此三角形第三边的长可能是( ) A.1 B.2 C.8 D.114.2017·长沙一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( ) A.锐角三角形 B.直角三角形C.钝角三角形 D.等腰直角三角形5.2018·大庆将正方体的表面沿某些棱剪开,得到如图Z14-2所示的平面图形,则原正方体中与“创”字所在的面相对的面上所标的汉字是( )图Z14-2A.庆 B.力 C.大 D.魅6.2018·菏泽如图Z14-3,直线a∥b,含45°角的三角尺的两个顶点分别落在直线a,b上,若∠1=30°,则∠2的度数是( )图Z14-3A.45° B.30° C.15° D.10°7.2017·绥化一个多边形的内角和等于900°,则这个多边形是________边形.8.2018·宿迁若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是________.9.2018·山西如图Z14-4①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=________度.图Z14-4。


中考数学几何图形专题复习知识点梳理1.过两点有且只有一条直线2.两点之间线段最短3.同角或等角的补角相等4.同角或等角的余角相等5.过一点有且只有一条直线和已知直线垂直6.直线外一点与直线上各点连接的所有线段中,垂线段最短7.平行公理经过直线外一点,有且只有一条直线与这条直线平行8.如果两条直线都和第三条直线平行,这两条直线也互相平行9.同位角相等,两直线平行10.内错角相等,两直线平行11.同旁内角互补,两直线平行12.两直线平行,同位角相等13.两直线平行,内错角相等14.两直线平行,同旁内角互补15.定理三角形两边的和大于第三边16.推论三角形两边的差小于第三边17.三角形内角和定理三角形三个内角的和等于180°18.推论1直角三角形的两个锐角互余19.推论2三角形的一个外角等于和它不相邻的两个内角的和20.推论3三角形的一个外角大于任何一个和它不相邻的内角21.全等三角形的对应边、对应角相等22.边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等23.角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等24.推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等25.边边边公理(SSS)有三边对应相等的两个三角形全等26.斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等27.定理1在角的平分线上的点到这个角的两边的距离相等28.定理2到一个角的两边的距离相同的点,在这个角的平分线上29.角的平分线是到角的两边距离相等的所有点的集合30.等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31.推论1等腰三角形顶角的平分线平分底边并且垂直于底边32.等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33.推论3等边三角形的各角都相等,并且每一个角都等于60°34.等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35.推论1三个角都相等的三角形是等边三角形36.推论2有一个角等于60°的等腰三角形是等边三角形37.在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38.直角三角形斜边上的中线等于斜边上的一半39.定理线段垂直平分线上的点和这条线段两个端点的距离相等40.逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42.定理1关于某条直线对称的两个图形是全等形43.定理2如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44.定理3两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45.逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46.勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a2+b2=c247.勾股定理的逆定理如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形48.定理四边形的内角和等于360°49.四边形的外角和等于360°50.多边形内角和定理n边形的内角的和等于(n-2)×180°51.推论任意多边的外角和等于360°52.平行四边形性质定理1平行四边形的对角相等53.平行四边形性质定理2平行四边形的对边相等54.推论夹在两条平行线间的平行线段相等55.平行四边形性质定理3平行四边形的对角线互相平分56.平行四边形判定定理1两组对角分别相等的四边形是平行四边形57.平行四边形判定定理2两组对边分别相等的四边形是平行四边形58.平行四边形判定定理3对角线互相平分的四边形是平行四边形59.平行四边形判定定理4一组对边平行相等的四边形是平行四边形60.矩形性质定理1矩形的四个角都是直角61.矩形性质定理2矩形的对角线相等62.矩形判定定理1有三个角是直角的四边形是矩形63.矩形判定定理2对角线相等的平行四边形是矩形64.菱形性质定理1菱形的四条边都相等65.菱形性质定理2菱形的对角线互相垂直,并且每一条对角线平分一组对角66.菱形面积=对角线乘积的一半,即S=(a×b)÷267.菱形判定定理1四边都相等的四边形是菱形68.菱形判定定理2对角线互相垂直的平行四边形是菱形69.正方形性质定理1正方形的四个角都是直角,四条边都相等70.正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71.定理1关于中心对称的两个图形是全等的72.定理2关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73.逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74.等腰梯形性质定理等腰梯形在同一底上的两个角相等75.等腰梯形的两条对角线相等76.等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77.对角线相等的梯形是等腰梯形78.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79.推论1经过梯形一腰的中点与底平行的直线,必平分另一腰80.推论2经过三角形一边的中点与另一边平行的直线,必平分第三边81.三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82.梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2S=L×h83.(1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84.(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85.(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87.推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88.定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89.平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90.定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91.相似三角形判定定理1两角对应相等,两三角形相似(ASA)92.直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93.判定定理2两边对应成比例且夹角相等,两三角形相似(SAS)94.判定定理3三边对应成比例,两三角形相似(SSS)95.定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96.性质定理1相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97.性质定理2相似三角形周长的比等于相似比98.性质定理3相似三角形面积的比等于相似比的平方99.任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100.任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101.圆是定点的距离等于定长的点的集合102.圆的内部可以看作是圆心的距离小于半径的点的集合103.圆的外部可以看作是圆心的距离大于半径的点的集合104.同圆或等圆的半径相等105.到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106.和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107.到已知角的两边距离相等的点的轨迹,是这个角的平分线108.到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109.定理不在同一直线上的三点确定一个圆。

中考数学复习《多边形》专项提升训练(附答案) 学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列说法中,正确的是( )A.直线有两个端点B.射线有两个端点C.有六边相等的多边形叫做正六边形D.有公共端点的两条射线组成的图形叫做角2.如图,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是( )A.7B.8C.9D.103.有下列说法:①由许多条线段连接而成的图形叫做多边形;②多边形的边数是不小于4的自然数;③从一个多边形(边数为n)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成(n-2)个三角形;其中正确的结论有( )A.1个B.2个C.3个D.4个4.一个多边形的外角中,钝角的个数不可能是( )A.1个B.2个C.3个D.4个5.若一个正多边形的一个外角是36°,则这个正多边形的边数是( )A.10B.9C.8D.66.如图,小华从A点出发,沿直线前进10米后左转24,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )A.140米B.150米C.160米D.240米7.如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2 的度数是( )A.15°B.25°C.30°D.45°8.如果仅用一种多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )A.正三角形B.正四边形C.正六边形D.正八边形9.用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第n个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )A.n2+4n+2B.6n+1C..n2+3n+3D.2n+410.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是( )A.222B.280C.286D.292二、填空题11.形状、大小完全相同的三角形________(填“能”或“不能”)铺满地面;形状、大小完全相同的四边形________(填“能”或“不能”)铺满地面.12.如果一个多边形的各个外角都是40°,那么这个多边形的内角和是.13.一个多边形有44条对角线,那么这个多边形内角和是__________.14.如图是由射线AB、BC、CD、DE、EA组成的图形,∠1+∠2+∠3+∠4+∠5=.15.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=_____度.16.两个完全相同的正五边形都有一边在直线上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB= .三、解答题17.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.18.若两个多边形的边数之比为1:2,两个多边形的内角和之和为1440°,求这两个多边形的边数.19.一个多边形的内角和比四边形的内角和多540°并且这个多边形的各个内角都相等,这个多边形的每个内角等于几度?20.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.21.如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.(1)若∠F=80,则∠ABC+∠BCD=;∠E=;(2)探索∠E与∠F有怎样的数量关系,并说明理由;(3)给四边形ABCD添加一个条件,使得∠E=∠F所添加的条件为.22.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.(1)观察直线AB与直线DE的位置关系,你能得出什么结论并说明理由;(2)试求∠AFE的度数.23.探索问题:(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请你用学过的知识予以证明;(2)如图②﹣1,则∠A+∠B+∠C+∠D+∠E=°;如图②﹣2,则∠A+∠B+∠C+∠D+∠E=°;如图②﹣3,则∠A+∠B+∠C+∠D+∠E=°;(3)如图③,下图是一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F =°.参考答案1.D2.B.3.A4.D5.A6.B.7.A8.D9.B10.D11.答案为:能,能.12.答案为:1260°.13.答案为:1 620°14.答案为:360°.15.答案为:360.16.答案为:108°.17.解:设这个多边形的边数是n依题意得(n﹣2)×180°=3×360°﹣180°,n﹣2=6﹣1,n=7. ∴这个多边形的边数是7.18.解:设这两个多边形的边数分别为n、2n,依题意得180(n﹣2)+180(2n﹣2)=1440540n﹣720=1440540n=2160n=4所以这两个多边形的边数分别为4和8所以这两个多边形的内角和分别为:180°×(4﹣2)=360°和180°×(8﹣2)=1080°19.解:设这个多边形的边数为n则有(n﹣2)•180°=360°+540°解得n=7.∵这个多边形的每个内角都相等∴它每一个内角的度数为900°÷7=20.解:连接AF.∵在△AOF和△COD中,∠AOF=∠COD∴∠C+∠D=∠OAF+∠AFD∴∠A+∠B+∠C+∠D+∠E+∠F=∠OAF+∠OFA+∠CFE+∠OAB+∠E+∠F=∠BAF+∠AFE+∠E+∠B=360°.21.解:(1)∵∠F=80∴∠FBC+∠BCF=180°﹣∠F=100°.∵∠ABC、∠BCD的角平分线交于点F∴∠ABC=2∠FBC,∠BCD=2∠BCF∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=200°;∵四边形ABCD的内角和为360°∴∠BAD+∠CDA=360°﹣(∠ABC+∠BCD)=160°.∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E∴∠DAE=12∠BAD,∠ADE=12∠CDA∴∠DAE+∠ADE=12∠BAD+12∠CDA=12(∠BAD+∠CDA)=80°∴∠E=180°﹣(∠DAE+∠ADE)=100°;(2)∠E+∠F=180°.理由如下:∵∠BAD+∠CDA+∠ABC+∠BCD=360°∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E∠ABC、∠BCD的角平分线交于点F∴∠DAE+∠ADE+∠FBC+∠BCF=180°∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°∴∠E+∠F=360°﹣(∠DAE+∠ADE+∠FBC+∠BCF)=180°;(3)AB∥CD.故答案为200°;100°;AB∥CD.22.解:(1)AB∥DE.理由如下:延长AF、DE相交于点G∵CD∥AF∴∠CDE+∠G=180°.∵∠CDE=∠BAF∴∠BAF+∠G=180°∴AB∥DE;(2)延长BC、ED相交于点H.∵AB⊥BC∴∠B=90°.∵AB∥DE∴∠H+∠B=180°∴∠H=90°.∵∠BCD=124°∴∠DCH=56°∴∠CDH=34°∴∠G=∠CDH=34°.∵∠DEF=80°∴∠EFG=80°﹣34°=46°∴∠AFE=180°﹣∠EFG=180°﹣46°=134°.23.解:(1)如图①,∠BOC=∠B+∠C+∠A.(2)如图②,∠A+∠B+∠C+∠D+∠E=180°.如图③根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D∵∠1+∠2+∠E=180°∴x=∠A+∠B+∠C+∠D+∠E=180°.如图④,延长EA交CD于点F,EA和BC交于点G根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B ∵∠GFC+∠FGC+∠C=180°∴x=∠A+∠B+∠C+∠D+∠E=180°.(3)如图⑤,∵∠BOD=70°∴∠A+∠C+∠E=70°∴∠B+∠D+∠F=70°∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.。

中考数学复习考点知识与题型专题讲解专题14 多边形【知识要点】多边形的相关知识:➢ 在平面中,由一些线段首尾顺次相接组成的图形叫做多边形,多边形中相邻两边组成的角叫做它的内角。
多边形的边与它邻边的延长线组成的角叫做外角。
➢ 连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
➢ 一个n 边形从一个顶点出发的对角线的条数为(n -3)条,其所有的对角线条数为2)3( n n凸多边形 :画出多边形的任何一条边所在的直线,如果多边形的其它边都在这条直线的同侧,那么这个多边形就是凸多边形。
正多边形 :各角相等,各边相等的多边形叫做正多边形。
(两个条件缺一不可,除了三角形以外,因为若三角形的三内角相等,则必有三边相等,反过来也成立)⏹ 多边形的内角和➢ n 边形的内角和定理:n 边形的内角和为(n −2)∙180°➢ n 边形的外角和定理:多边形的外角和等于360°,与多边形的形状和边数无关。
【考查题型】考查题型一多边形截角后的边数问题【解题思路】多边形减去一个角的方法可能有三种:经过两个相邻点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条.典例1.(2018·云南昭通市模拟)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是()A.16B.17C.18D.19【答案】A【详解】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n-1)边形.故当剪去一个角后,剩下的部分是一个18边形,则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.故选A.变式1-1.(2021·宁波市一模)把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是()A.六边形B.五边形C.四边形D.三角形【答案】A【解析】当剪去一个角后,剩下的部分是一个四边形,则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.故选A.考查题型二计算多边形的周长【解题思路】考查多边形的周长,解题在于掌握计算公式典例2.(2021·隆化县模拟)下列图形中,周长不是32 m的图形是( )A.B.C.D.【答案】B【提示】根据所给图形,分别计算出它们的周长,然后判断各选项即可.【详解】A. L=(6+10)×2=32,其周长为32.B. 该平行四边形的一边长为10,另一边长大于6,故其周长大于32.C. L=(6+10)×2=32,其周长为32.D. L=(6+10)×2=32,其周长为32.采用排除法即可选出B故选B.变式2-1.(2017·海南中考模拟)如图,□ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH ,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )A.12B.15C.16D.18【答案】B【解析】如图,分别作直线AB、BC、HG的延长线和反向延长线使它们交于点B、Q、P.∵六边形ABCDEF的六个角都是120°,∴六边形ABCDEF的每一个外角的度数都是60°.∴△APH、△BEF、△DHG、△CQG都是等边三角形.∴EF=BE=BF=1,DG=HG=HD=2.∴FC=5-1=4,AH=5-2= 3,CG=CD-DG=4−2=2.∴六边形的周长为1+3+3+2+2+4=15.故选B.考查题型三计算网格中的多边形面积【解题思路】利用分割法即可解决问题典例3.(2021·辽宁葫芦岛市模拟)如图是边长为1的正方形网格,A、B、C、D均为格点,则四边形的面积为()A .7B .10C .152D .8 【答案】A 【提示】利用分割法即可解决问题.【详解】解:S 四边形ABCD =3×4﹣12×2×1×2﹣12×1×3×2=12﹣5=7,故选:A . 变式3-1.(2021·山东烟台市模拟)如图,在边长为1的小正方形网格中,△ABC 的三个顶点均在格点上,若向正方形网格中投针,落在△ABC 内部的概率是()A .12B .14C .38D .516【答案】D【提示】用正方形的面积减去四个易求得三角形的面积,即可确定△ABC 面积,用△ABC 面积除以正方形的面积即可.【详解】解:正方形的面积=4×4=16,三角形ABC 的面积=11116434221222-⨯⨯-⨯⨯-⨯⨯=5, 所以落在△ABC 内部的概率是516, 故选D .变式3-2.(2021·江西九年级零模)如图,在边长为1的小正方形网格中,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形图中①,②,③,④四个格点多边形的面积分别记为1234,,,,S S S S 下列说法正确的是()A .12S SB .23S S =C .124S S S +=D .134S S S +=【答案】B【提示】根据题意判断格点多边形的面积,依次将1234S S S S 、、、计算出来,再找到等量关系.【详解】观察图形可得12342.5,3,3,6,S S S S ====∴23234,6S S S S S =+==,故选:B .考查题型四 计算多边形对角线条数【解题思路】熟记n 边形从一个顶点出发可引出(n-3)条对角线是解答此题的关键.典例4.(2017·山东济南市·中考真题)一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )A .12B .13C .14D .15【答案】C【解析】解:根据题意,得:(n ﹣2)•180=360°×2+180°,解得:n=7.则这个多边形的边数是7,七边形的对角线条数为7(73)2⨯-=14,故选C . 变式4-1.(2018·山东济南市·中考模拟)若凸n 边形的每个外角都是36°,则从一个顶点出发引的对角线条数是( )A .6B .7C .8D .9【答案】B【解析】360°÷36°=10,10−3=7.故从一个顶点出发引的对角线条数是7.故选:B.变式4-2.(2021·莆田市二模)从n边形的一个顶点出发可以连接8条对角线,则n ()A.8B.9C.10D.11【答案】D【提示】根据n边形从一个顶点出发可引出(n-3)条对角线,可得n-3=8,求出n的值即可.【详解】解:由题意得:n-3=8,解得n=11,故选:D.变式4-3.(2021·湖南长沙市模拟)已知一个正n边形的每个内角为120°,则这个多边形的对角线有()A.5条B.6条C.8条D.9条【答案】D【提示】多边形的每一个内角都等于120°,则每个外角是60°,而任何多边形的外角是360°,则求得多边形的边数;再根据多边形一个顶点出发的对角线=n﹣3,即可求得对角线的条数.【详解】解:∵多边形的每一个内角都等于120°,∴每个外角是60度,则多边形的边数为360°÷60°=6,则该多边形有6个顶点,则此多边形从一个顶点出发的对角线共有6﹣3=3条.∴这个多边形的对角线有12(6×3)=9条,故选:D.变式4-4.(2021·广东茂名市·中考模拟)若一个多边形从同一个顶点出发可以作5条对角线,则这个多边形的边数为()A.6B.7C.8D.9【答案】C【提示】可根据n边形从一个顶点引出的对角线有n-3条,即可求解.【详解】解:设这个多边形的边数为n,则n-3=5,解得n=8,故这个多边形的边数为8,故选:C.变式4-5.(2021·河北模拟)过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是()A.六边形B.七边形C.八边形D.九边形【答案】D【提示】根据n边形从一个顶点出发可引出(n-3)条对角线,可组成n-2个三角形,依此可得n的值.【详解】解:设这个多边形是n边形,由题意得,n-2=7,解得:n=9,即这个多边形是九边形,故选:D.考查题型五多边形内角和问题【解题思路】考查多边形的内角和公式,解题关键是牢记多边形的内角和公式.典例5.(2018·山东济宁市·中考真题)如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC、∠BCD,则∠P的度数是( )A.60°B.65°C.55°D.50°【答案】A【解析】根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC 与∠PCD 的角度和,进一步求得∠P 的度数.解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,∴∠BCD+∠CDE=540°﹣300°=240°,∵∠BCD 、∠CDE 的平分线在五边形内相交于点O ,∴∠PDC+∠PCD=(∠BCD+∠CDE )=120°,∴∠P=180°﹣120°=60°.故选A .变式5-1.(2021·甘肃庆阳市·中考真题)如图,足球图片正中的黑色正五边形的内角和是( ).A .180°B .360°C .540°D .720°【答案】C【提示】根据多边形内角和公式2180()n -⨯︒即可求出结果.【详解】解:黑色正五边形的内角和为:5218540(0)-⨯︒=︒,故选C .变式5-2.(2021·湖南湘西土家族苗族自治州·中考真题)已知一个多边形的内角和是1080°,则这个多边形是( )A .五边形B .六边形C .七边形D .八边形【答案】D【提示】根据多边形的内角和=(n ﹣2)•180°,列方程可求解.【详解】设所求多边形边数为n ,∴(n ﹣2)•180°=1080°,解得n =8.故选D.考查题型六正多边形内角和问题【解题思路】掌握并能运用多边形内角和公式是解题的关键典例6.(2021·湖南怀化市·中考真题)若一个多边形的内角和为1080°,则这个多边形的边数为()A.6B.7C.8D.9【答案】C【提示】设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),即可得方程180(n﹣2)=1080,解此方程即可求得答案:n=8.故选C.变式6-1.(2021·湖北宜昌市·中考真题)游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行.成功的招数不止一招,可助我们成功的一招是().A.每走完一段直路后沿向右偏72°方向行走B.每段直路要短C.每走完一段直路后沿向右偏108°方向行走D.每段直路要长【答案】A【提示】根据题意可知封闭的图形是正五边形,求出正五边形内角的度数即可解决问题.【详解】根据题意可知,从起点走五段相等直路之后回到起点的封闭图形是正五边形,∵正五边形的每个内角的度数为:(52)1801085-⨯︒=︒∴它的邻补角的度数为:180°-108°=72°,因此,每走完一段直路后沿向右偏72°方向行走,故选:A.变式6-2.(2021·河北中考真题)正六边形的一个内角是正n边形一个外角的4倍,则n=_________.【答案】12【提示】先根据外角和定理求出正六边形的外角为60°,进而得到其内角为120°,再求出正n边形的外角为30°,再根据外角和定理即可求解.【详解】解:由多边形的外角和定理可知,正六边形的外角为:360°÷6=60°,故正六边形的内角为180°-60°=120°,又正六边形的一个内角是正n边形一个外角的4倍,∴正n边形的外角为30°,∴正n边形的边数为:360°÷30°=12.故答案为:12.∠变式6-3.(2021·福建中考真题)如图所示的六边形花环是用六个全等的直角三角形拼成的,则ABC 等于_______度.【答案】30【提示】先证出内部的图形是正六边形,求出内部小正六边形的内角,即可得到∠ACB的度数,根据直角三角形的两个锐角互余即可求解.【详解】解:由题意六边形花环是用六个全等的直角三角形拼成,可得BD=AC,BC=AF,∴CD=CF,同理可证小六边形其他的边也相等,即里面的小六边形也是正六边形,∴∠1=()1621801206-⨯︒=︒, ∴∠2=180°-120°=60°,∴∠ABC=30°,故答案为:30.考查题型七 截角后的内角和问题【解题思路】剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个是解决本题的关键.典例7.(2021·五莲县一模)一个正方形被截掉一个角后,得到一个多边形,这个多边形的内角和是( )A .360°B .540°C .180°或360°D .540°或360°或180°【答案】D【提示】剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个,根据多边形的内角和定理即可求解.【详解】n 边形的内角和是(n ﹣2)•180°,边数增加1,则新的多边形的内角和是(4+1﹣2)×180°=540°,所得新的多边形的角不变,则新的多边形的内角和是(4﹣2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4﹣1﹣2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°,故选D .变式7-1.(2021·河北九年级其他模拟)一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是( )A .17B .16C .15D .16或15或17【答案】D【详解】多边形的内角和可以表示成()2180n -⋅︒ (3n ≥且n 是整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,根据()21802520,n -⋅︒=解得:n=16,则多边形的边数是15,16,17.故选D .变式7-2.(2021·贵州铜仁市·九年级零模)一个多边形切去一个角后得到的另一个多边形的内角和为900︒,那么原多边形的边数为()A .6或7或8B .6或7C .7或8D .7【答案】A【提示】首先求得内角和为900°的多边形的边数,即可确定原多边形的边数.【详解】解:设内角和为900°的多边形的边数是n ,则(n-2)•180°=900°,解得:n=7,如图,有如下几种切法,则原多边形的边数为6或7或8.故选:A .考查题型八 正多边形的外角问题【解题思路】解决问题的关键是掌握多边形的外角和等于360度.典例8.(2021·江苏无锡市·中考真题)正十边形的每一个外角的度数为()A.36︒B.30C.144︒D.150︒【答案】A【提示】利用多边形的外角性质计算即可求出值.【详解】解:360°÷10=36°,故选:A.变式8-1.(2021·江苏扬州市·中考真题)如图,小明从点A出发沿直线前进10米到达点B,向左转45︒后又沿直线前进10米到达点C,再向左转45︒后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为()A.100米B.80米C.60米D.40米【答案】B【提示】根据题意,小明走过的路程是正多边形,先用360°除以45°求出边数,然后再乘以10米即可.【详解】解:∵小明每次都是沿直线前进10米后再向左转45︒,∴他走过的图形是正多边形,边数n=360°÷45°=8,∴小明第一次回到出发点A时所走的路程=8×10=80米.故选:B.变式8-2.(2021·湖南娄底市·中考真题)正多边形的一个外角为60°,则这个多边形的边数为()A.5B.6C.7D.8【答案】B【提示】根据正多边形的外角和以及一个外角的度数,求得边数.【详解】解:正多边形的一个外角等于60°,且外角和为360°,则这个正多边形的边数是:360°÷60°=6,故选:B.考查题型九多边形外角和的实际应用【解题思路】典例9.(2021·湖北黄冈市·中考真题)如果一个多边形的每一个外角都是36°,那么这个多边形的边数是()A.7B.8C.9D.10【答案】D【提示】根据多边形的外角的性质,边数等于360°除以每一个外角的度数.【详解】∵一个多边形的每个外角都是36°,∴n=360°÷36°=10.故选D.变式9-1.(2021·山东德州市·中考真题)如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为()A.80米B.96米C.64米D.48米【答案】C【提示】根据多边形的外角和即可求出答案.【详解】解:根据题意可知,他需要转360÷45=8次才会回到原点,所以一共走了8×8=64米.故选:C考查题型十多边形内角和与外角和的综合应用【解题思路】熟悉多边形的内角和公式:n边形的内角和是(n-2)×180°;多边形的外角和是360度.典例10.(2021·西藏中考真题)一个多边形的内角和是外角和的4倍,则这个多边形的边数是()A.8B.9C.10D.11【答案】C【提示】利用多边形的内角和公式及外角和定理列方程即可解决问题.【详解】设这个多边形的边数是n,则有(n-2)×180°=360°×4,所有n=10.故选C.变式10-1.(2021·陆丰市模拟)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于()A.108°B.90°C.72°D.60°【答案】C【提示】首先设此多边形为n边形,根据题意得:180(n-2)=540,即可求得n=5,再由多边形的外角和等于360°,即可求得答案.【详解】解:设此多边形为n边形,根据题意得:180(n-2)=540,解得:n=5,∴这个正多边形的每一个外角等于:3605=72°.故选C.变式10-2.(2021·中江县模拟)已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是()A.8B.9C.10D.12【答案】A【解析】试题提示:设这个多边形的外角为x°,则内角为3x°,根据多边形的相邻的内角与外角互补可的方程x+3x=180,解可得外角的度数,再用外角和除以外角度数即可得到边数.解:设这个多边形的外角为x°,则内角为3x°,由题意得:x+3x=180,解得x=45,这个多边形的边数:360°÷45°=8,故选A.变式10-3.(2021·西宁市模拟)一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是()A.5B.6C.7D.8【答案】C【解析】解:设这个多边形的边数是n,根据题意得,(n-2)•180°=2×360°+180°, n=7.故选C.考查题型十一平面镶嵌【解题思路】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.典例11.下列多边形中,不能够单独铺满地面的是()A.正三角形B.正方形C.正五边形D.正六边形【答案】C【提示】由镶嵌的条件知,在一个顶点处各个内角和为360°.【详解】∵正三角形的内角=180°÷3=60°,360°÷60°=6,即6个正三角形可以铺满地面一个点,∴正三角形可以铺满地面;∵正方形的内角=360°÷4=90°,360°÷90°=4,即4个正方形可以铺满地面一个点,∴正方形可以铺满地面;∵正五边形的内角=180°-360°÷5=108°,360°÷108°≈3.3,∴正五边形不能铺满地面;∵正六边形的内角=180°-360°÷6=120°,360°÷120°=3,即3个正六边形可以铺满地面一个点,∴正六边形可以铺满地面.故选C.变式11-1小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可能...是()A.正三角形B.正方形C.正五边形D.正六边形【答案】C【提示】平面图形镶嵌的条件:判断一种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360,则说明能够进行平面镶嵌;反之则不能.【详解】解:因为用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,所以小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可以是正五边形.故选:C变式11-2.能够铺满地面的正多边形组合是()A.正六边形和正方形B.正五边形和正八边形C.正方形和正八边形D.正三角形和正十边形【答案】C【解析】A、正六边形的每个内角是120°,正方形的每个内角是90°,120m+90n=360°,显然n取任何正整数时,m不能得正整数,故不能铺满;B、正五边形每个内角是180°-360°÷5=108°,正八边形每个内角为135度,135m+108n=360°,显然n 取任何正整数时,m不能得正整数,故不能铺满;C、正方形的每个内角为90°,正八边形的每个内角为135°,两个正八边形和一个正方形刚好能铺满地面;D、正三角形每个内角为60度,正十边形每个内角为144度,60m+144n=360°,显然n取任何正整数时,m不能得正整数,故不能铺满.故选C.变式11-3下列边长相等的正多边形能完成镶嵌的是()A.2个正八边形和1个正三角形B.3个正方形和2个正三角形C.1个正五边形和1个正十边形D.2个正六边形和2个正三角形【答案】D【提示】只需要明确几个几何图形在一点进行平铺就是几个图形与这一点相邻的所有内角之和等于360°即可。

专题14 几何初步知识、三角形、多边形1.2018·郴州如图Z-14-1,直线a,b被直线c所截,下列条件中,不能判定a∥b 的是( )图Z-14-1A.∠2=∠4 B.∠1+∠4=180°C.∠5=∠4 D.∠1=∠32.2018·东营下列图形,根据AB∥CD能得到∠1=∠2的是( )图Z-14-23.2018·达州已知:如图Z-14-3,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )图Z-14-3A.30° B.35°C.40° D.45°4.2018·长沙下列长度的三条线段,能组成三角形的是( )A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cmC.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm5.2018·杭州若线段AM,AN分别是△ABC的BC边上的高和中线,则( )A.AM>AN B.AM≥ANC.AM<AN D.AM≤AN6.2018·潍坊把一副三角尺放在同一水平桌面上,摆放成如图Z-14-4所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )图Z-14-4A.45° B.60°C.75° D.82.5°7.2018·上海通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是________度.8.2018·泰州已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为________.9.2018·北京用一组a,b,c的值说明命题“若a<b,则ac<bc”是错误的,这组值可以是a=________,b=________,c=________.详解详析1.D 2.B 3.B 4.B 5.D 6.C7.540 8.5 9.答案不唯一,如1,2,-1。

中考重点多边形的认识与性质中考重点:多边形的认识与性质多边形是我们在数学学习中经常接触到的一个概念。
它是由多个线段组成的封闭图形,在中考中也是一个重要的考点。
本文将从多边形的基本认识和性质两个方面进行探讨,帮助大家更好地理解和应用多边形知识。
一、多边形的基本认识多边形是指由线段组成的封闭图形。
根据边的条数,我们可以将多边形分为三种情况:1. 三角形:边的条数为3的多边形。
三角形是最简单、最基本的多边形,根据三角形的边长和角度可以进一步分为等边三角形、等腰三角形和普通三角形等。
2. 四边形:边的条数为4的多边形。
四边形是中考中经常出现的一个考点,根据四边形的边长和角度可以进一步分为矩形、正方形、菱形、平行四边形等。
3. 多边形:边的条数大于4的多边形。
多边形的性质更加复杂,需要通过不同的定理和公式进行计算和推导。
二、多边形的性质多边形具有一些独特的性质,它们在中考中经常被考察。
1. 内角和定理:任意n边形的内角和等于180°×(n-2)。
这一定理是中考中经常使用的一个重要公式,通过它我们可以计算出任意n边形的内角和。
2. 对角线定理:任意n边形的对角线条数可以通过计算公式(n×(n-3))/2得到。
这一定理对于计算n边形的对角线非常有用。
3. 正多边形的性质:正多边形是指所有边相等、所有角相等的多边形。
它具有一些特殊的性质,如正n边形的内角等于180°×(n-2)/n,正n边形的外角等于360°/n等。
4. 面积计算:多边形的面积计算可以通过将其分解为不同的三角形进行计算。
根据不同的多边形类型和已知条件,我们可以使用不同的公式计算面积,如长方形的面积公式为长×宽,三角形的面积公式为底边×高/2等。
三、应用与拓展多边形的认识与性质在中考数学中有着广泛的应用。
除了基础知识的理解和记忆外,我们还需要能够灵活运用这些知识解决实际问题。
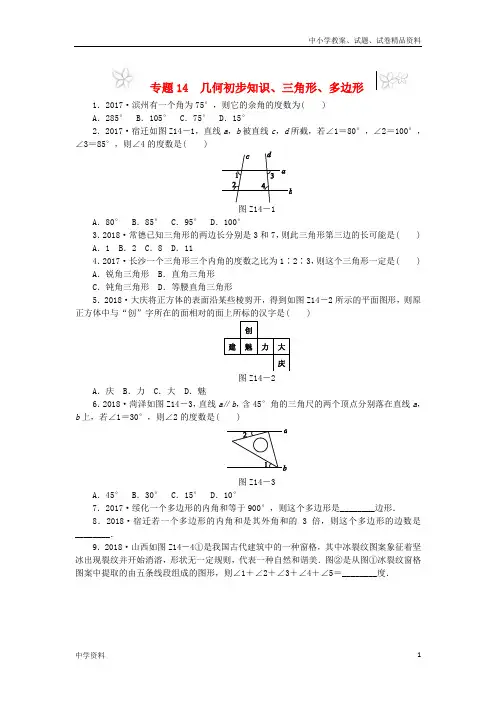
专题14 几何初步知识、三角形、多边形1.2017·滨州有一个角为75°,则它的余角的度数为( )A.285° B.105° C.75° D.15°2.2017·宿迁如图Z14-1,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )图Z14-1A.80° B.85° C.95° D.100°3.2018·常德已知三角形的两边长分别是3和7,则此三角形第三边的长可能是( ) A.1 B.2 C.8 D.114.2017·长沙一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( ) A.锐角三角形 B.直角三角形C.钝角三角形 D.等腰直角三角形5.2018·大庆将正方体的表面沿某些棱剪开,得到如图Z14-2所示的平面图形,则原正方体中与“创”字所在的面相对的面上所标的汉字是( )图Z14-2A.庆 B.力 C.大 D.魅6.2018·菏泽如图Z14-3,直线a∥b,含45°角的三角尺的两个顶点分别落在直线a,b上,若∠1=30°,则∠2的度数是( )图Z14-3A.45° B.30° C.15° D.10°7.2017·绥化一个多边形的内角和等于900°,则这个多边形是________边形.8.2018·宿迁若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是________.9.2018·山西如图Z14-4①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=________度.图Z14-4详解详析1.D 2.B 3.C 4.B 5.A 6.C7.七8.8 9.360。

初三数学中考复习三角形专项复习练习含解析1. 如图,图中以AB为边的三角形的个数共有( B )A.1个B.2个C.3个D.4个2. 如图所示,∠BAC的对边是( C )A.BD B.DC C.BC D.AD3. 若△ABC三条边分别为m,n,p,且|m-n|+(n-p)2=0,则那个三角形为( B )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形4. 如图,D为AC上一点,AD=DC,E为BC上一点,BE=EC,则下列说法不正确的是( D )A.DE是△BDC的中线B.BD是△ABC的中线C.D为AC中点,E为BC中点D.∠C的对边是DE5. 如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( A )A.40°B.45°C.80°D.85°6. 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E.则下列说法不正确的是( C )A.AC是△ABC的高B.DE是△BCD的高C.DE是△ABE的高D.AD是△ACD的高7. 若△ABC和△DEF全等,A和E,B和D分别是对应顶点,则下列结论错误的是( A )A.BC=EF B.∠B=∠D C.∠C=∠F D.AC=EF 8.如图,在△ABC与△DEF中,给出以下六个条件:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F.以其中三个条件作为已知,不能判定△ABC与△DEF全等的是( D )A.①②⑤B.①②③C.①④⑥D.②③④,第7题图),第8题图),第10题图)9.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( A ) A.80°B.100°C.60°D.45°10.已知三角形两边的长分别是3和8,则此三角形的周长取值范畴是( C )A.3<C<8 B.5<C<11 C.16<C<22 D.11<C<1 611.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC 的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S △BEF,且S△ABC=12,则S△ADF-S△BEF等于( B )A.1 B.2 C.3 D.412.假如一个三角形中任意两个内角的和大于第三个内角,那个三角形是__锐角__三角形.13. 如图,已知△ABC的面积是36 cm2,BD=4 cm,DC=8 cm,则阴影部分的面积是__12__cm2.14. 如图,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是__50°__.15.如图,点A在线段ED上,AC=CD,BC=CE,∠1=∠2,假如AB=7,AD=5,那么AE=__2__.16. 你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的过程中,两人上升的最大高度AA′,BB′的数量关系是___相等____.17. 等腰三角形的周长为20 cm,其中一边长为6 cm,则另两边长分别为_____6cm,8cm或7cm,7cm ____.18. 如图,在△ABC中,AD⊥BC,垂足为D,E为BD上的一点,E G∥AD,分别交AB和CA的延长线于点F,G,∠AFG=∠G.(1)试说明△ABD≌△ACD;(2)若∠B=40°,求∠G和∠FAG的大小.解:(1)由ASA可证△ABD≌△ACD(2)∠G=50°,∠FAG=80°19.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD,延长使DF=BD,过F点作AB的平行线段MF,连接MD并延长,在其延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你明白其中的道理吗?解:∵BD=DF,DE=DM,∠BDE=∠FDM,∴△BDE≌△FDM,故∠BEM=∠DMF,∴BE∥MF,又∵AB∥MF,依照过直线外一点有且只有一条直线与已知直线平行,∴A,C,E在一条直线上20.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图①所示放置,使得一直角边重合,连接BD,CE.(1)试说明:BD=CE;(2)延长BD交CE于点F,求∠BFC的度数;(3)若如图②放置,上面的结论还成立吗?请简单说明理由.解:(1)易得△ADB≌△AEC(SAS),∴BD=CE(2)∵△ADB≌△AEC,∴∠DBA=∠ECA,∴∠BFC=180°-∠AC E-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°(3)同样成立,BD=CE且∠BFC=90°.理由∵△ABC,△ADE是等腰直角三角形,∴AB=AC,AD=AE,且∠BAC=∠EAD,∴∠BAD=∠C AE,∴△ADB≌△AEC,∴BD=CE,∠ABF=∠ACF,∴∠BFC=∠BA C=90°。

初三数学几何知识点归纳一、三角形1. 三角形的基本概念- 三角形由不在同一直线上的三条线段首尾顺次相接所组成。
- 三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边。
例如,若三角形三边为a、b、c,则a + b>c,a - b<c。
2. 三角形的分类- 按角分类:- 锐角三角形:三个角都是锐角的三角形。
- 直角三角形:有一个角是直角的三角形,直角三角形中斜边最长,两直角边的平方和等于斜边的平方(勾股定理a^2+b^2=c^2,其中c为斜边,a、b为两直角边)。
- 钝角三角形:有一个角是钝角的三角形。
- 按边分类:- 不等边三角形:三边都不相等的三角形。
- 等腰三角形:有两边相等的三角形,相等的两边叫做腰,另一边叫做底边;两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等腰三角形两底角相等(等边对等角),等腰三角形三线合一(底边上的高、底边上的中线、顶角平分线互相重合)。
- 等边三角形:三边都相等的三角形,等边三角形三个角都是60^∘,等边三角形是特殊的等腰三角形。
3. 三角形的内角和与外角- 三角形内角和定理:三角形三个内角的和等于180^∘。
- 三角形的外角:三角形的一边与另一边的延长线组成的角。
三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个与它不相邻的内角。
二、四边形1. 平行四边形- 定义:两组对边分别平行的四边形叫做平行四边形。
- 性质:- 平行四边形的对边平行且相等。
- 平行四边形的对角相等,邻角互补。
- 平行四边形的对角线互相平分。
- 判定:- 两组对边分别平行的四边形是平行四边形。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
- 两组对角分别相等的四边形是平行四边形。
- 对角线互相平分的四边形是平行四边形。
2. 矩形- 定义:有一个角是直角的平行四边形叫做矩形。
- 性质:- 矩形具有平行四边形的所有性质。

中考数学专题复习小训练专题14几何初步知识三角形多边形凡读书......须要读得字字响亮,不可误一字,不可少一字,不可多一字,不可倒一字,不可牵强暗记,只是要多诵数遍,自然上口,久远不忘。
古人云,读书百遍,其义自见。
谓读得熟,则不待解说,自晓其义也。
余尝谓,读书有三到,谓心到,眼到,口到。
1.2022·滨州有一个角为75°,则它的余角的度数为()A.285°B.105°C.75°D.15°2.2022·宿迁如图Z14-1,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是()图Z14-1A.80°B.85°C.95°D.100°3.2022·常德已知三角形的两边长分别是3和7,则此三角形第三边的长可能是()A.1B.2C.8D.114.2022·长沙一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形5.2022·大庆将正方体的表面沿某些棱剪开,得到如图Z14-2所示的平面图形,则原正方体中与“创”字所在的面相对的面上所标的汉字是()图Z14-2A.庆B.力C.大D.魅6.2022·菏泽如图Z14-3,直线a∥b,含45°角的三角尺的两个顶点分别落在直线a,b上,若∠1=30°,则∠2的度数是()图Z14-3邴原少孤,数岁时,过书舍而泣。
师曰:童子何泣?原曰:孤者易伤,贫者易感。
夫书者,凡得学者,有亲也。
一则愿其不孤,二则羡其得学,中心伤感,故泣耳。
师恻然曰:欲书可耳原曰:无钱资。
师曰:童子苟有志吾徒相教不求资也。
1/2凡读书......须要读得字字响亮,不可误一字,不可少一字,不可多一字,不可倒一字,不可牵强暗记,只是要多诵数遍,自然上口,久远不忘。
初三多边形知识点归纳总结多边形是初中数学中的一个重要内容,它们在几何图形中起着重要的作用。
在初三阶段,我们需要掌握多边形的基本概念、性质和计算方法。
本文将对初三多边形的知识点进行归纳总结。
1. 多边形的定义多边形是由若干个线段首尾相连而形成的封闭图形,它的边数大于等于3。
2. 多边形的分类2.1 根据边数,多边形可以分为三角形、四边形、五边形等。
2.2 根据边的长短及角的大小,多边形可以分为等边形、等腰形、直角形等。
3. 三角形3.1 定义:三角形是由三条边和三个内角组成的多边形。
3.2 分类:- 根据边长关系:* 等边三角形:三边相等。
* 等腰三角形:两边相等。
* 普通三角形:三边都不相等。
- 根据角度关系:* 直角三角形:一个内角为直角(90°)。
* 钝角三角形:一个内角大于直角。
* 锐角三角形:三个内角都小于直角。
4. 四边形4.1 定义:四边形是由四条边和四个内角组成的多边形。
4.2 分类:- 矩形:四个内角都是直角。
- 正方形:四边相等且四个内角都是直角的矩形。
- 平行四边形:两组对边平行。
- 菱形:四边都相等。
- 梯形:至少有一对对边平行。
- 长方形:有四个直角的平行四边形。
5. 多边形的面积计算5.1 三角形的面积:面积 = 1/2 * 底边长 * 高。
5.2 矩形的面积:面积 = 长 * 宽。
5.3 正方形的面积:面积 = 边长 * 边长。
5.4 平行四边形的面积:面积 = 底边长 * 高。
5.5 梯形的面积:面积 = (上底 + 下底) * 高 / 2。
5.6 针对更复杂的多边形,在了解边长和角度信息后,可以利用分割成多个简单的形状计算各个部分面积,然后求和得到整个多边形的面积。
6. 多边形的周长计算6.1 多边形周长即为各边长的累加值。
7. 多边形的内角和7.1 对于n边形,即n个内角之和为(n-2)*180°。
8. 相似多边形8.1 定义:两个多边形的对应角相等,对应边成比例。
第14讲三角形和多边形1.了解等腰三角形、等边三角形、直角三角形的概念,会识别这三种图形;理解等腰三角形、等边三角形、直角三角形的性质和判定.2. 能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题.3. 会运用等腰三角形、等边三角形、直角三角形的知识解决有关问题.知识要点一、三角形的概念及其性质1.三角形的内角和外角(1)三角形的内角和等于180°.(2)三角形的任意一个外角等于和它不相邻的两个内角之和;三角形的一个外角大于任何一个和它不相邻的内角.2.三角形三边之间的关系三角形任意两边之和大于第三边,任意两边之差小于第三边.3.三角形内角与对边对应关系在同一个三角形内,大边对大角,大角对大边;在同一三角形中,等边对等角,等角对等边.4.三角形具有稳定性.5.三角形中的四条特殊的线段是:高线、角平分线、中线、中位线.要点诠释:(1)三角形的中位线:连结三角形两边中点的线段是三角形的中位线.(2)中位线定理:三角形的中位线平行于第三边且等于第三边的一半.二、特殊三角形考点1 等腰三角形1、有两条边相等的三角形叫做等腰三角形.性质:(1)具有三角形的一切性质;(2)两底角相等(等边对等角);(3)顶角的平分线,底边中线,底边上的高互相重合(三线合一);(4)等边三角形的各角都相等,且都等于60°.要点诠释:等边三角形中高线,中线,角平分线三线合一,共有三条.2、判定:(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);(2)三个角都相等的三角形是等边三角形;(3)有一个角为60°的等腰三角形是等边三角形.要点诠释:(1)腰、底、顶角、底角是等腰三角形特有的概念;(2)等边三角形是特殊的等腰三角形.考点二、直角三角形1、直角三角形:有一个角是直角的三角形叫做直角三角形.2、性质:(1)直角三角形中两锐角互余;(2)直角三角形中,30°锐角所对的直角边等于斜边的一半; (3)在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°;(4)勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方;(5)勾股定理逆定理:如果三角形的三边长a ,b ,c 满足a2+b2=c2,那么这个三角形是直角三角形;(6)直角三角形中,斜边上的中线等于斜边的一半.要点诠释:(1)直角三角形中,SRt △ABC=21ch=21ab ,其中a 、b 为两直角边,c 为斜边,h 为斜边上的高; (2)圆内接三角形,当一条边为直径时,该三角形是直角三角形.3.判定:(1)两内角互余的三角形是直角三角形;(2)一条边上的中线等于该边的一半,则这条边所对的角是直角,这个三角形是直角三角形;(3)如果三角形两边的平方和等于第三边的平方,则这个三角形是直角三角形,第三边为斜边.典型例题例1、如图点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,以OC为边作等边三角形OCD,连AC、AD.(1)当α=150°时,试判断△AOD的形状,并说明理由;(2)探究:当a为多少度时,△AOD是等腰三角形?例2、已知: 如图, 菱形ABCD中, E、F分别是CB、CD上的点,BE=DF.(1)求证:AE=AF. (2)若AE垂直平分BC,AF垂直平分CD,求证:△AEF为等边三角形.例3、如图,△ABC中,CF⊥AB,垂足为F,M为BC的中点,E为AC上一点,且ME=MF.(1)求证:BE⊥AC;(2)若∠A=50°,求∠FME的度数.例4、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE 于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.例5、如图①,△ABC 中.AB=AC ,P 为底边BC 上一点,PE ⊥AB ,PF ⊥AC ,CH ⊥AB ,垂足分别为E 、F 、H .易证PE+PF=CH .证明过程如下:如图①,连接AP .∵PE⊥AB,PF⊥AC,CH⊥AB,∴ABP S △=12AB•PE,ACP S △=12AC•PF,ABC S △=12AB•CH. 又∵ABP ACP ABC S S S +=△△△,∴12AB•PE+12AC•PF=12AB•CH.∵AB=AC,∴PE+PF=CH.(1)如图②,P 为BC 延长线上的点时,其它条件不变,PE 、PF 、CH 又有怎样的数量关系?请写出你的猜想,并加以证明:(2)填空:若∠A=30°,△ABC 的面积为49,点P 在直线BC 上,且P 到直线AC 的距离为PF ,当PF=3时,则AB 边上的高CH=______.点P 到AB 边的距离PE=________.例6、在△ABC中,AC=BC,,点D为AC的中点.(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连结CF,过点F作,交直线AB于点H.判断FH与FC的数量关系并加以证明.(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.1、把腰长为1的等腰直角三角形折叠两次后,得到的一个小三角形的周长是________.2、如图,△ABC为等边三角形,延长BC到D,延长BA到E,使AE=BD,连接CE、DE. 求证:CE=DE.3、以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,……,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积S n=________.4、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=CDBC; ②S⊿ABC+S⊿CDE≥S⊿ACE ; ③BM⊥DM;④BM=DM.正确结论的个数是()A.1个 B.2个 C.3个 D.4个课堂练习MECA1、有一段火车路线,含这段铁路的首尾两站在内共有5个车站(如图),图中共有几条线段?在这段线路上往返行车,需印制几种车票(每种车票要印出上车站与下车站)?2、如图,点A、B、C在直线l上,则图中共有______条线段.3、三角形三边长分别是6,2a﹣2,8,则a的取值范围是()A.1<a<2 B.<a<2 C.2<a<8 D.1<a<44、已知a,b,c为△ABC的三条边,化简得_________.5、下列命题:(1)等边三角形也是等腰三角形;(2)三角形的外角等于两个内角的和;(3)三角形中最大的内角不能小于60°;(4)锐角三角形中,任意两内角之和必大于90°,其中错误的个数是( )A.0 个B.1个C.2个D.3个课后练习1、一个多边形的内角和是900∘,这个多边形的边数是( )A. 10B. 9C. 8D. 72、如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角。
专题14 几何初步知识、三角形、
多边形
1.2017·滨州有一个角为75°,则它的余角的度数为( )
A.285° B.105° C.75° D.15°
2.2017·宿迁如图Z14-1,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
图Z14-1
A.80° B.85° C.95° D.100°
3.2018·常德已知三角形的两边长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
4.2017·长沙一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
5.2018·大庆将正方体的表面沿某些棱剪开,得到如图Z14-2所示的平面图形,则原正方体中与“创”字所在的面相对的面上所标的汉字是( )
图Z14-2
A.庆 B.力 C.大 D.魅
6.2018·菏泽如图Z14-3,直线a∥b,含45°角的三角尺的两个顶点分别落在直线a,b上,若∠1=30°,则∠2的度数是( )
图Z14-3
A.45° B.30° C.15° D.10°
7.2017·绥化一个多边形的内角和等于900°,则这个多边形是________边形.
8.2018·宿迁若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是________.
9.2018·山西如图Z14-4①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=________度.
图Z14-4。