下载文档原格式
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动，轴上装有4个轮子，如附图，主动轮2输入功率60kW ，从动轮1，3，4依次输出功率15kW ，15kW 和30kW 。
（1）作轴的扭矩图。
（2）将2，3轮的位置对调，扭矩图有何变化？ 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ，m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a)，最大扭矩为m kN M x ×=149.2max 。
(2) 2，3轮的位置对调后扭矩图见附图(b)，最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆，其两端受T =2kN·m 的外力偶矩作用而发生扭转，如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1，2，3点处的切应力和最大切应变，并在此三点处画出切应力的方向。
解答 1，2，3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
第三章练习题及参考解答3.1为研究中国各地区入境旅游状况，建立了各省市旅游外汇收入（Y，百万美元）、旅行社职工人数（X1，人）、国际旅游人数（X2，万人次）的模型，用某年31个省市的截面数据估计结果如下：Y = -151.0263 0.1179X1i1.5452X2it=（-3.066806）（6.652983）（3.378064）2 2R2=0.934331 R 0.92964 F=191.1894 n=311）从经济意义上考察估计模型的合理性。
2）在5%显著性水平上，分别检验参数M, ：2的显著性。
3）在5%显著性水平上，检验模型的整体显著性。
练习题3.1参考解答：（1）由模型估计结果可看出：从经济意义上说明，旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。
平均说来，旅行社职工人数增加1人，旅游外汇收入将增加0.1179百万美元；国际旅游人数增加1万人次，旅游外汇收入增加 1.5452百万美元。
这与经济理论及经验符合，是合理的。
矚慫润厲钐瘗睞枥庑赖。
（2）取。
=0.05，查表得t0.025（31 — 3） = 2.048因为3个参数t统计量的绝对值均大于t0.025（31 — 3） =2.048，说明经t检验3个参数均显著不为0,即旅行社职工人数和国际旅游人数分别对旅游外汇收入都有显著影响。
聞創沟燴鐺險爱氇谴净。
（3）取G =0.05，查表得F0.O5（2,28） =3.34，由于F =199.1894 a F0.05（2,28^ 3.34，说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响，线性回归方程显著成立。
残骛楼諍锩瀨濟溆塹籟。
3.2表3.6给出了有两个解释变量X2和.X3的回归模型方差分析的部分结果：n=14+1=15因为TSS=RSS+ESS 残差平方和RSS=TSS-ESS=66042-65965=77回归平方和的自由度为：k-仁3-仁2残差平方和RSS的自由度为：n-k=15-3=12（2）可决系数为：R2=65965 =0£98834TSS 660422 n -1 ' e215 -1 77修正的可决系数：R 1 "2=1 0.9986n —k送y, 15—3 66042（3）这说明两个解释变量X2和.X3联合起来对被解释变量有很显著的影响，但是还不能确定两个解释变量X2和.X3各自对Y 都有显著影响。
第3章单相正弦电路分析已知正弦电压（V）、（V），则u1与u2的相位差为，是否正确？为什么？分析讨论相位差问题时应当注意，只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的，能够确定超前、滞后的关系，而不同频率正弦量的相位差是随时间变化的，无法确定超前、滞后的关系，因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω，而u2的角频率为2ω，两者的频率不同，相位差随时间变化，无法确定超前、滞后的关系，因此不能进行相位的比较。
已知某正弦电流的有效值为10 A，频率为50 Hz，初相为45°。
（1）写出该电流的正弦函数表达式，并画出波形图；（2）求该正弦电流在s时的相位和瞬时值。
解（1）由题设已知正弦电流的有效值A，频率Hz，初相。
由频率f可得角频率ω为：（rad/s）所以，该电流的正弦函数表达式为：（A）波形图如图所示。
（2）s时的相位为：（rad）瞬时值为：（A）已知正弦电流（A）、（A），试求i1与i2的振幅、频率、初相、有效值和相位差，并画出其波形图。
解i1与i2的振幅分别为：（A）（A）频率分别为：（Hz）初相分别为：有效值分别为：（A）（A）i1与i2的相位差为：说明i1超前i2。
波形图如图所示。
图习题解答用图图习题解答用图设，，试计算、、AB、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型（极坐标型）等形式表示。
复数的加减运算就是将实部和虚部分别进行加减，因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加，复数的除法运算就是将模相除而辐角相减，因而采用指数型（极坐标型）比较方便。
解写出下列各正弦量所对应的相量，并画出其相量图。
（1）（mA）（2）（A）（3）（V）（4）（V）分析用相量来表示正弦量，就是用一个复数来反映正弦量的振幅（或有效值）和初相，即用相量的模来代表正弦量的振幅（或有效值），用相量的辐角来代表正弦量的初相。
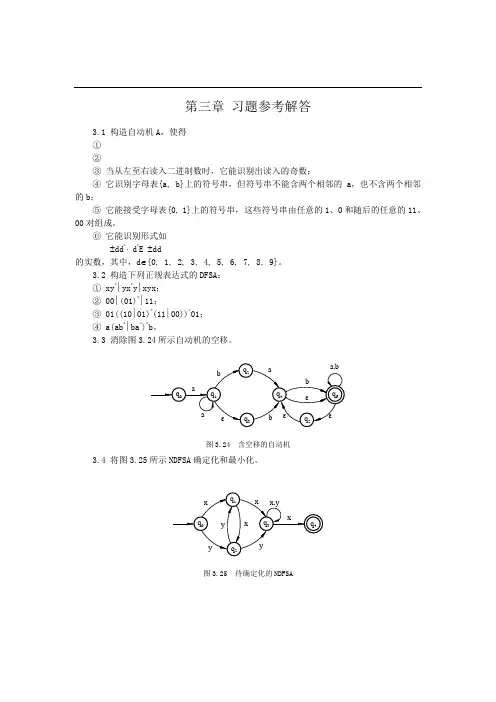
第三章习题参考解答3.1 构造自动机A，使得①②③当从左至右读入二进制数时，它能识别出读入的奇数；④它识别字母表{a, b}上的符号串，但符号串不能含两个相邻的a，也不含两个相邻的b；⑤它能接受字母表{0, 1}上的符号串，这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数，其中，d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA：① xy*∣yx*y∣xyx；② 00∣(01)*∣11；③ 01((10∣01)*(11∣00))*01；④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式，试证明① e∣e=e；② {{e}}={e}；③ {e}=ε∣e{e}；④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机，指明该自动机是不是确定的，并写出它相应的语言： G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中，f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA确定化。
3.8 设文法G[〈单词〉]：〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。
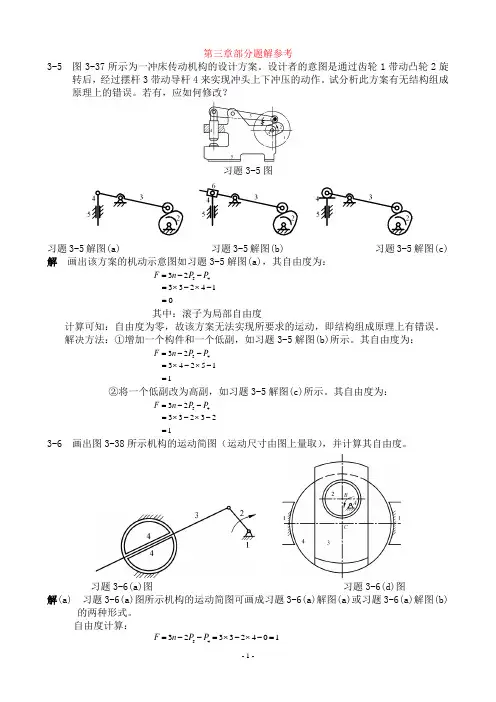
第三章部分题解参考3-5 图3-37所示为一冲床传动机构的设计方案。
设计者的意图是通过齿轮1带动凸轮2旋转后，经过摆杆3带动导杆4来实现冲头上下冲压的动作。
试分析此方案有无结构组成原理上的错误。
若有，应如何修改？习题3-5图习题3-5解图(a) 习题3-5解图(b) 习题3-5解图(c) 解 画出该方案的机动示意图如习题3-5解图(a)，其自由度为：14233 2345=-⨯-⨯=--=P P n F 其中：滚子为局部自由度计算可知：自由度为零，故该方案无法实现所要求的运动，即结构组成原理上有错误。
解决方法：①增加一个构件和一个低副，如习题3-5解图(b)所示。
其自由度为：115243 2345=-⨯-⨯=--=P P n F ②将一个低副改为高副，如习题3-5解图(c)所示。
其自由度为：123233 2345=-⨯-⨯=--=P P n F 3-6 画出图3-38所示机构的运动简图（运动尺寸由图上量取），并计算其自由度。
习题3-6(a)图 习题3-6(d)图解(a) 习题3-6(a)图所示机构的运动简图可画成习题3-6(a)解图(a)或习题3-6(a)解图(b)的两种形式。
自由度计算：1042332345=-⨯-⨯=--=P P n F习题3-6(a)解图(a)习题3-6(a)解图(b)解(d) 习题3-6(d)图所示机构的运动简图可画成习题3-6(d)解图(a)或习题3-6(d)解图(b)的两种形式。
自由度计算：1042332345=-⨯-⨯=--=P P n F习题3-6(d)解图(a) 习题3-6(d)解图(b)3-7 计算图3-39所示机构的自由度，并说明各机构应有的原动件数目。
解(a) 10102732345=-⨯-⨯=--=P P n FA 、B 、C 、D 为复合铰链原动件数目应为1说明：该机构为精确直线机构。
当满足BE =BC =CD =DE ，AB =AD ，AF =CF 条件时，E 点轨迹是精确直线，其轨迹垂直于机架连心线AF解(b) 1072532345=-⨯-⨯=--=P P n FB 为复合铰链，移动副E 、F 中有一个是虚约束 原动件数目应为1说明：该机构为飞剪机构，即在物体的运动过程中将其剪切。
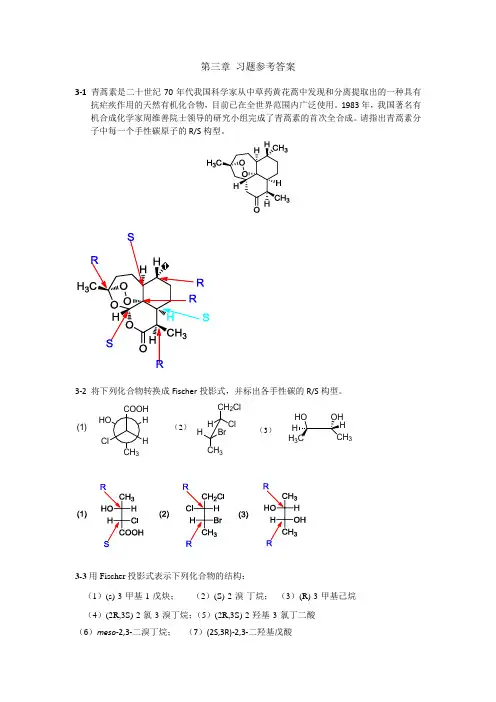
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物，目前已在全世界范围内广泛使用。
1983年，我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式，并标出各手性碳的R/S 构型。
（2）（3）3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构：（1）(s)-3-甲基-1-戊炔； （2）(S)-2-溴-丁烷； （3）(R)-3-甲基己烷 （4）(2R,3S)-2-氯-3-溴丁烷；（5）(2R,3S)-2-羟基-3-氯丁二酸 （6）meso -2,3-二溴丁烷； （7）(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时，习惯把含碳原子的基团放在竖键上，并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性？（1）、（3）、（5）、（7）、（9）无手性（2）、（4）、（6、）（8）、（10）有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫（一种植物害虫）分泌的性激素，其外消旋体目前已被人工合成，并商业化用于农田害虫的控制和诱杀。
最近，化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型（J. Org. Chem. 2013, 78, 6281−6284）。
通过全合成方法分别得到了A的2种立体异构体，发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性，而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似，说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
习题3.1 某三相同步发电机，三相绕组连接成星形时的线电压为10.5kV ，若将它连接成三角形，则线电压是多少？若连接成星形时，B 相绕组的首末端接反了，则3 个线电压的有效值 U AB 、U BC 、U CA 各是多少？解：三相绕组连接成星形时U L =3U P ，线电压为10.5kV ，则每相绕组的电压为6.06kV ，若连接成三角形U L =U P ，则线电压为6.06kV 。
若连接成星形时，B 相绕组的首末端接反了，则B 相相电压的相位与原来的相差1800， 根据相量计算可得U AB =6.06 kV 、U BC =6.06 kV 、U CA =10.5 kV 。
3.2 题3.2 图所示的三相对称电路，线电压U L =380V ，每相负载Z = 6+j8Ω，试求相电压、相电流和线电流，并画出电压和电流的相量图。
题3.2 图解：由题意：负载作星接U l =3U p 因U l =380V ，则U a =U b =U c = = 220 （V ）设U a = 220/0°（V ）因相电流即线电流，其大小为：.220/0°I A == 22/−53°(A) 6 + j 8.I B = 22/−173ο(A).I C = 22/67°(A) 此时的相量图略。
3.3 有一电源和负载都是星形连接的对称三相电路，已知电源相电压为220V ，负载每相阻抗Z = Ω10 ，试求负载的相电流和线电流。
3 380第3 章三相交流电路习题解答77解：负载的相电压等于电源的相电压：U p = 220（V）U P 220(A)I l = I p = = = 22Z 103.4 已知星形联接的对称三相负载，每相阻抗为40∠25°（Ω）；对称三相电源的线电压为380Ｖ。
求: 负载相电流，并绘出电压、电流的相量图。
解：ＵAB ＝380ＶＺ＝40∠25°Ω（１）三相对称电源接入三相对称负载令U A ＝２２０∠０°Ｖ则相线电流I A =U A ／Z＝５.５∠-２５°ＶI B ＝５.５∠－１４５°ＶI c ＝５.５∠９５°Ｖ(2) 矢量图如图所示。
