正方体长方体组合图形的表面积与体积·

长方体正方体的表面积公式
长方体和正方体的表面积公式分别如下：
长方体表面积公式：
设长方体的长、宽、高分别为a、b、c，则其表面积为：
S = 2ab + 2ac + 2bc
正方体表面积公式：
设正方体的边长为a，则其表面积为：
S = 6a²
其中，S表示表面积，a、b、c表示长方体的三条边长。

对于正方体，S表示表面积，a表示边长。

表面积是指几何体的所有表面积之和。

在这里，长方体和正方体的表面积公式均是由各个面积加和得出的。

对于长方体，有两个平面有相同的面积，所以需要计算两遍，而对于正方体，六个面的面积相等，因此只需要计算一遍，并将其乘以
6即可。

人教版小学数学五年级下册第三单元《长方体和正方体》教材分析1.通过观察、操作，学生能够认识长方体和正方体的特征以及它们的展开图。

2.学生能够理解体积（包括容积）的含义，并能够使用常用的度量单位（立方米、立方分米、立方厘米、升、毫升）建立1立方米、1立方分米、1立方厘米以及1升、1毫升的表象，并能够进行简单的换算。

3.学生能够掌握长方体、正方体的体积和表面积的计算方法，并能够解决一些简单的实际问题。

4.学生能够探索某些实物体积的测量方法。

长方体和正方体的认识本小节介绍了长方体和正方体的特征和形状，学生需要理解长方体各部分的名称，面、棱、顶点，并能够形成长方体和正方体的概念。

长方体一般是由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形，而正方体是由6个完全相同的正方形围成的立体图形，所有的棱长度相等。

长方体和正方体的体积和表面积计算本小节介绍了长方体和正方体的体积和表面积的计算方法，学生需要掌握体积计算公式的推导和体积单位间的进率及名数的换算。

同时，学生需要理解表面积的含义，并能够计算出长方体和正方体的表面积。

容积和容积单位本小节介绍了容积和容积单位的概念，学生需要理解容积的含义，并能够使用常用的容积单位（升、毫升）进行换算。

不规则物体的体积本小节介绍了如何测量不规则物体的体积，学生需要探索并掌握测量不规则物体体积的方法。

总体来说，本单元的教学目标是让学生通过观察、操作，认识长方体和正方体的特征以及它们的展开图，理解体积（包括容积）的含义，掌握长方体、正方体的体积和表面积的计算方法，并能够解决一些简单的实际问题。

同时，学生需要探索某些实物体积的测量方法。

同。

第二个价值是通过操作让学生深入理解长、宽、高的概念。

建议在活动中引导学生思考：为什么要把12条棱分成三组？为什么这三组棱分别叫长、宽、高？通过思考和操作，学生会逐渐理解长、宽、高的概念和它们之间的关系。

练五是应用题，要求学生根据长方体的特征计算面积、体积等。

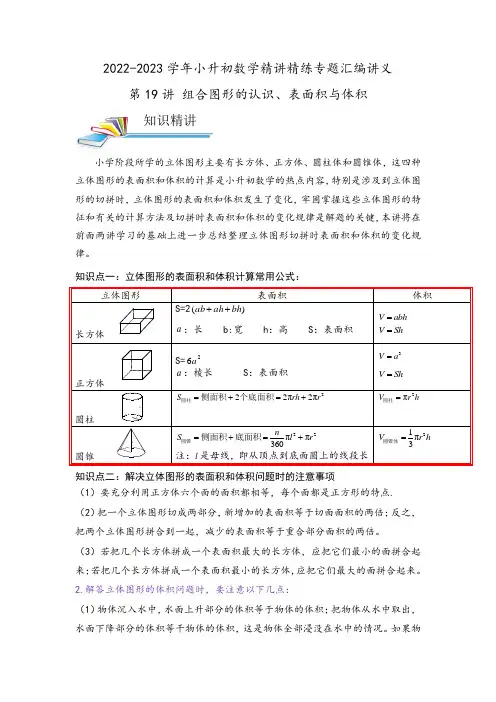
2022-2023学年小升初数学精讲精练专题汇编讲义第19讲 组合图形的认识、表面积与体积小学阶段所学的立体图形主要有长方体、正方体、圆柱体和圆锥体，这四种立体图形的表面积和体积的计算是小升初数学的热点内容，特别是涉及到立体图形的切拼时，立体图形的表面积和体积发生了变化，牢固掌握这些立体图形的特征和有关的计算方法及切拼时表面积和体积的变化规律是解题的关键，本讲将在前面两讲学习的基础上进一步总结整理立体图形切拼时表面积和体积的变化规律。

知识点一：立体图形的表面积和体积计算常用公式： 立体图形 表面积体积 长方体S=2)(bh ah ab ++a ：长 b:宽 h ：高 S ：表面积 V abh = V Sh = 正方体S=26a a ：棱长 S ：表面积 3V a = V Sh = 圆柱222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h =圆柱圆锥 22ππ360n S l r =+=+圆锥侧面积底面积 注：l 是母线，即从顶点到底面圆上的线段长 21π3V r h =圆锥体 知识点二：解决立体图形的表面积和体积问题时的注意事项（1）要充分利用正方体六个面的面积都相等，每个面都是正方形的特点.（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍；反之，把两个立体图形拼合到一起，减少的表面积等于重合部分面积的两倍。

（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来；若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。

2.解答立体图形的体积问题时，要注意以下几点：（1）物体沉入水中，水面上升部分的体积等于物体的体积；把物体从水中取出，水面下降部分的体积等干物体的体积，这是物体全部浸没在水中的情况。

如果物h r hr 知识精讲体不全部浸在水中，那么排开水的体积就等于浸在水中的那部分物体的体积. （2）把一种形状的物体变为另一种形状的物体后，形状变了，但它的体积保持不变.（3）求一些不规则物体体积时，可以通过变形的方法求体积。

表面积和体积（二）【知识点1】：长方体正方体的切割与拼接例1：一个长方体底面是一个边长为20厘米的正方形，高为40厘米，如果把它的高增加5厘米，它的表面积会增加多少平方厘米？练习1：有一个长方体，如果把高增加3cm后，就变成一个正方体，表面积就会增加96cm2。

求这个长方体的体积。

练习2：把一个长方体和一个正方体拼成一个新的长方体，这个新长方体的表面积比原来的长方体的表面积增加了80平方厘米，求正方体的表面积。

练习3：把一个长方体截去一个高为8厘米的长方形后，剩下的部分是一个正方体。

正方体的表面积比原来长方体的表面积减少320平方厘米。

求原来长方体的体积。

例2：把一根长80厘米，宽5厘米，高3厘米的长方体木料锯成长都是40厘米的两段，表面积比原来增加了多少平方厘米。

练习1:一个长方体正好可以切成5个同样大小的正方体，切成的５个正方体的表面积比原来长方体表面积多了２００平方厘米，求原来长方体的表面积？练习2：把一个正方体木块锯成3个大小一样的小长方体后，表面积增加了36平方厘米。

原来正方体的表面积是多少？练习3：用两个棱长是3厘米的正方体，拼成一个长方体，它的表面积比两个正方体的表面积少多少平方厘米，这个长方体的表面积是多少平方厘米。

例3：把棱长12厘米的正方体切割成棱长是3厘米的小正方体，可以切割成多少块？练习1：一个棱长为6厘米的正方体木块，如果把它锯成棱长为2厘米的小正方体，表面积增加了多少平方厘米？练习2：有一个棱长是1米的正方体木块，如果把它锯成相等的8个小正方体，表面积增加多少平方米？练习3：如下图，一个正方体被切成12个大大小小的长方体，这些长方体表面积的总和是350平方厘米，求原来正方体的表面积和体积。

例4：把一个长为10分米，宽为6分米，高为8分米的长方形，切割成相等的两个长方体，有几种切法，那种增加的表面积最多？哪种增加的表面积最少？练习1：把两个相同的长方体拼成一个大的长方体，已知小长方体的长是8cm，宽是6cm，高是3cm。

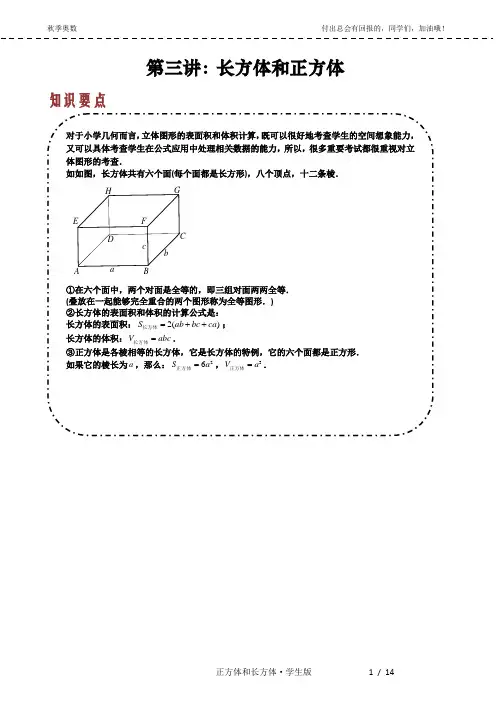
知识要点对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．如如图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．c b aHGFED CBA①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是： 长方体的表面积：2()S ab bc ca =++长方体； 长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形． 如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．第三讲：长方体和正方体（一）不规则立体图形1.右图中共有多少个面？多少条棱？后面前面右面左面下面上面2. 如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？立体图形的体积计算常用公式： 立体图形 示例 体积公式 相关要素长方体V abh = V Sh =三要素：a 、b 、h 二要素：S 、h正方体3V a = V Sh =一要素：a 二要素：S 、h不规则形体的体积常用方法： ①化虚为实法 ②切片转化法 ③先补后去法 ④实际操作法 ⑤画图建模法3.如右图，有一个边长是5的立方体，如果它的左上方截去一个边分别是5，3，2的长方体，那么它的表面积减少了多少?4.右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）5.如图，有一个边长为20厘米的大正方体，分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后，表面积变为2454平方厘米，那么挖掉的小立方体的边长是多少厘米？6.（《小学生数学报》邀请赛）从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？(写出符合要求的全部答案)7.从一个长8厘米、宽7厘米、高6厘米的长方体中截下一个最大的正方体(如下图)，剩下部分的表面积之和是平方厘米．866678.一个正方体木块，棱长是1米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少？9.右图是一个表面被涂上红色的棱长为10厘米的正方体木块，如果把它沿虚线切成8个正方体，这些小正方体中没有被涂上红色的所有表面的面积和是多少平方厘米？（二）重叠正方体10.边长分别是3、5、8的三个正方体拼在一起，在各种拼法中，表面积最小多少？11.如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？25块积木12.用6块右图所示(单位：cm)的长方体木块拼成一个大长方体，有许多种拼法，其中表面积最小的是多少平方厘米？最大是多少平方厘米？12313.如图，在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体，求这个立体图形的表面积．14.(2008年“希望杯”五年级第2试)如图，棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起，则所得到的多面体的表面积是_______平方厘米．15.边长为1厘米的正方体，如图这样层层重叠放置，那么当重叠到第5层时，这个立体图形的表面积是多少平方厘米？16.把19个棱长为1厘米的正方体重叠在一起，按右图中的方式拼成一个立体图形.，求这个立体图形的表面积．（三）三视图17.现有一个棱长为1厘米的正方体，一个长宽为1厘米高为2厘米的长方体，三个长宽为1厘米高为3厘米的长方体．下列图形是把这五个图形合并成某一立体图形时，从上面、前面、侧面所看到的图形．试利用下面三个图形把合并成的立体图形(如例)的样子画出来，并求出其表面积．例：侧前上18.如下图，用若干块单位正方体积木堆成一个立体，小明正确地画出了这个立体的正视图、俯视图和侧视图，问：所堆的立体的体积至少是多少？正视图俯视图侧视图19.(第十二届全国“华罗庚金杯”少年数学邀请赛)用一些棱长是1的小正方体码放成一个立体图形，从上向下看这个立体图形，如下图a，从正面看这个立体图形，如下图b，则这个立体图形的表面积最多是________．a b20. (2008年清华附中试题)选项中有4个立方体，其中是用左边图形折成的是( )．DCBA（四）体积求解21.(第四届《小数报》数学竞赛决赛)一根长方体木料，体积是0.078立方米．已知这根木料长1.3米．宽为3分米，高该是多少分米?孙健同学把高错算为3分米．这样，这根木料的体积要比0.078立方米多多少?22.(第六届“华杯赛”决赛口试)某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条(如图所示)在三个方向上的加固．所用尼龙编织条分别为365厘米，405厘米，485厘米．若每个尼龙加固时接头重叠都是5厘米．问这个长方体包装箱的体积是多少立方米?高宽长23.(第十届“迎春杯”)一个长方体的表面积是33.66平方分米，其中一个面的长是2.3分米，宽是2.1分米，它的体积是_____立方分米.24.(第十五届“迎春杯”决赛)把一根长2.4米的长方体木料锯成5段(如图)，表面积比原来增加了96平方厘米．这根木料原来的体积是_____立方厘米．2.4米25.(第五届《小数报》数学竞赛决赛)一个长方体的宽和高相等，并且都等于长的一半(如图)．将这个长方体切成12个小长方体，这些小长方体的表面之和为600平方分米．求这个大长方体的体积．26.有三个大小一样的正方体，将接触的面用胶粘接在一起成图示的形状，表面积比原来减少了16平方厘米.求所成形体的体积.27.把11块相同的长方体的砖拼成如图所示的大长方体，已知每块砖的体积是3288cm，则大长方体的表面积为多少？（五）水中投石28.有大、中、小三个正方形水池，它们的内边长分别是6米、3米、2米．把两堆碎石分别沉没在中、小水池的水里，两个水池的水面分别升高了6厘米和4厘米．如果将这两堆碎石都沉没在大水池的水里，大水池的水面升高了多少厘米？29.一个正方体容器，容器内部边长为24厘米，存有若干水，水深17.2厘米，现将一些碎铁块放入容器中，铁块沉入水底，水面上升2.5厘米，如果将这些铁块铸成一个和容器等高的实心圆柱，重新放入池中，则水面升高几厘米？30.（2009年迎春杯初赛六年级）如图，有一个棱长为10厘米的正方体铁块，现已在每两个对面的中央钻一个边长为4厘米的正方形孔（边平行于正方体的棱），且穿透．另有一长方体容器，从内部量，长、宽、高分别为15厘米、12厘米、9厘米，内部有水，水深3厘米．若将正方体铁块平放入长方体容器中，则铁块在水下部分的体积为立方厘米．（六）其他31.把一个长方体形状的木料分割成3小块，使这3小块的体积相等．已知这长方体的长为15厘米，宽为12厘米，高为9厘米．分割时要求只能锯两次，如图1就是一种分割线的图．除这种分割的方法外，还可有其他不同的分割方法，请把分割线分别画在图2的各图中．图1图232. (第三届“华杯赛”复赛)如图从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形，然后，沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米？139233. 小明用若干个大小相同的正方体木块堆成一个几何体，这个几何体从正面看如下图左,从上面看如下图右．那么这个几何体至少用了 块木块．一课一练1. 右图中共有多少个面？多少条棱？2. 在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下的立体图形的表面积是多少？3.如右图，一个正方体形状的木块，棱长l米，沿水平方向将它锯成3片，每片又锯成4长条，每条又锯成5小块，共得到大大小小的长方体60块．那么，这60块长方体表面积的和是多少平方米?4.(2008年走美六年级初赛)一个表面积为256cm的长方体如图切成27个小长方体，这27个小长方体表面积的和是2cm．5.用10块长5厘米，宽3厘米，高7厘米的长方体积木堆成一个长方体，这个长方体的表面积最小是多少?6.要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体，表面积最小是多少？7.用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米?8. (第六届“迎春杯”决赛)一个长方体的各条棱长的和是48厘米，并且它的长是宽的2倍，高与宽相等，那么这个长方体的体积是______ 立方厘米．9. (第七届“祖冲之杯”数学邀请赛)现有一张长40厘米、宽20厘米的长方形铁皮，请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计，容积越大越好)，你做出的铁皮盒容积是多少立方厘米?10.右图是由22个小正方体组成的立体图形，其中共有多少个大大小小的正方体？由两个小正方体组成的长方体有多少个？。

长方体与正方体的表面积与体积内容大纲1.知识梳理2.经典精讲3.综合练习4.拓展提高5.巩固练习知识梳理1、长方体和正方体的认识（1）、长方体的特征：有6个面，都是长方形，（有时相对的两个面是正方形），相对的面形状相同，面积（大小）相等；有12条棱，相对的棱长度相等；8个顶点。

（2）、正方体的特征：有6个面，都是正方形，6个面的面积相等；12条棱的长度相等；8个顶点。

说明：正方体是特殊的长方体（3）、长方体的棱长总和=（长+宽+高）×4 正方体的棱长总和= 棱长×122、长方体和正方体的表面积（1）、长方体的表面积计算公式：S=2(ab+ah+bh)，其中S为长方体的表面积，a为长，b 为宽，h为高。

（2）正方体的表面积计算公式：S=6×a×a=6a2，其中S为正方体的表面积，a为棱长。

3、长方体和正方体的体积或容积（1）体积：物体所占空间的大小，是物体的体积。

容积：容器所能容纳物体的体积，是容器的容积。

（2）长方体体积的计算公式：长方体体积=长×宽×高=底面积×高；用字母表示是：V=abh（3）正方体体积的计算公式：正方体体积=棱长×棱长×棱长；用字母表示是：V=3 a注意：长方体与正方体表面积与体积的变化关系把长方体或正方体截成若干个小长方体（或正方体）后，表面积增加了，体积不变。

长方体或正方体容器容积的计算方法，跟体积的计算方法相同。

但要从容器里面量长、宽、高。

所以，对于同一个物体，体积大于容积。

注意：长方体或正方体的长、宽、高同时扩大几倍，体积就会扩大倍数的立方倍。

如长、宽、高各扩大2倍，体积就会扩大到原来的8倍。

4、体积与容积单位换算常见的体积单位有：3cm ；3dm ；3m 等。

常见的容积单位有：L 、mL 等体积单位的换算有：3311000m dm =；3311000dm cm =；相邻体积单位间的进率是1000.容积单位的换算有：11000L mL =体积与容积间的单位换算：311000m L =；311dm L =；311000dm mL =；311cm mL =转换依据：（1）高级单位化为低级单位：乘以进率； （2）低级单位化为高级单位：除以进率。

《五年级下册长方体和正方体的表面积及体积》目录考点一正方体和长方体的棱长总和 (2)考点二组合图形的表面积 (3)考点三长方体和正方体的表面积（涂色、刷墙、铺装、有无盖问题） (5)考点四分段切割问题 (7)考点五高引起表面积和体积的变化 (8)考点六棱长扩大倍数引起棱长总和、表面积和体积的变化 (9)考点七等体问题一（熔铸、浇铸问题） (9)考点八等体问题二（倒沙、倒水/切成小正方体） (10)考点九水中浸物 (11)考点十挖最大的正方体 (11)考点十一去厚算容积问题 (12)考点一正方体和长方体的棱长总和【例题1】一个长方体长是10分米，宽是8分米，高是6分米，这个长方体的棱长总和是多少分米？【例题6】用一根长60厘米的铁丝围成一个长8CM，宽5CM的长方体框架，这个长方体框架的高是多少厘米？【例题7】把一根长84米的铁丝围成一个正方体框架，棱长是多少分米？【例题8】一个长方体相交于同一顶点的三条棱长度分别是10厘米，5分米，6厘米，这个长方体的棱长总和是多少分米？【例题2】如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？【例题3】如下图，有一个边长是5的立方体，如果它的左上方截去一个边分别是5，3，2的长方体，那么它的表面积减少了多少?【例题4】下图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具。

它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）【例题5】如图，在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体，求这个立体图形的表面积。

【例题6】如下图所示，由三个正方体木块粘合而成的模型，它们的棱长分别为1米、2米、4米，要在表面涂刷油漆，如果大正方体的下面不涂油漆，则模型涂刷油漆的面积是多少平方米？考点三长方体和正方体的表面积（涂色、刷墙、铺装、有无盖问题）【例题1】一个长方体的无盖铁皮水桶，长和宽都是3分米，深5分米。

组合图形的体积答案典题探究例1．棱长是1cm的小立方体组成如图所示的几何体，那么这个几何体的体积是10立方厘米，表面积是36平方厘米．考点：组合图形的体积；简单的立方体切拼问题．分析：可根据立方体的体积公式计算出一个立方体的体积再乘立方体的个数即是这个几何体的体积，几何体最下层有6个小立方体，中层有3个、最上层有1个，所以几何体中共有（6+3+1）个小立方体；几何体的表面积就是所有露出的面积的面积，可先计算出一个小立方体一个面的面积再乘露出的面积的个数即可，从几何体的下面观察有6个面，上面露出了6个面，左后面有6个面，右后面有6个面，前面露出了12个面，这个几何体共露出了（6+6+6+6+12）个小正方形的面，列式解答即可得到答案．解答：解：几何体中小立方体的个数为（1+3+6）个，几何体的体积为：1×1×1×（1+3+6）=1×10，=10（立方厘米）；几何体中共露出了（6+6+6+12）个小正方形的面，几何体的表面积为：1×1×（6+6+6+6+12）=1×36，=36（平方厘米）；故答案为：10，36．点评：解答此题的关键是先计算出一个小立方体的体积与一个小立方体一面的面积，然后再分别乘立方体的个数和几何体中的小立方体露出的面数即可．例2．计算体积．（单位：厘米）考点：组合图形的体积．专题：压轴题；立体图形的认识与计算．分析：由题意得：组合图形的体积=圆柱的体积+圆锥的体积，根据计算公式代数计算．解答：解：3.14×（4÷2）2×7+×（4÷2）2×3，=3.14×4×7+3.14×4，=87.92+12.56，=100.48（立方厘米）；答：这个图形的体积是100.48立方厘米．点评：此题主要考查组合图形的体积，要将所求图形分解成所学图形即可．例3．有一个深4分米的长方体容器，其内侧底面为边长3分米的正方形．当容器底面的一边紧贴桌面倾斜如图时，容器内的水刚好不溢出．容器内的水有22.5升．考点：组合图形的体积．分析：先根据长方体的体积公式求出容器的容积；无水的部分看作是底面是直角三角形的棱柱，再根据棱柱的体积公式求出无水的部分的体积；相减即可求得容器内的水的体积．解答：解：容器的容积：4×3×3=36（立方分米）；无水的部分看作是底面是直角三角形的棱柱，底面积是3×3÷2=4.5（平方分米），高是3分米．所以体积是4.5×3=13.5（立方分米）；所以容器内有水：36﹣13.5=22.5立方分米=22.5升．答：容器内的水有22.5升．故答案为：22.5．点评：考查了组合图形的体积，本题容器内的水的体积=容器的容积﹣无水的部分体积，难点是把无水的部分看作是底面是直角三角形的棱柱．例4．有一个棱长是10厘米的正方体木块，在它的上、左、前三个面中心分别穿一个3厘米见方的孔，直至对面．求穿孔后木块的体积．考点：组合图形的体积．分析：孔的体积中三个孔交汇处可以看成是一个棱长为3的正方体，只算一次就可以了，用一个孔的体积乘3后再减去2个交汇处的体积就是孔的总体积，穿孔后木块的体积是这个正方体的体积减去孔的体积．解答：解：3×3×10=90（立方厘米），穿三个孔时，体积应是：90×3﹣3×3×3×2=216（立方厘米）；所以穿孔后木块的体积是：10×10×10﹣216=784（立方厘米）答：穿孔后木块的体积是784立方厘米．点评：本题的关键是对三孔交汇处的求解，这一部分只能算一次．演练方阵A档（巩固专练）一．选择题（共5小题）1．如图，三个半径分别为l米、l．5米和2米的同轴圆柱，每个圆柱高0.5米，这三个圆柱组成一个立体图形，这个立体图形的表面积是（）平方米．A．42.39 B．39.25 C．36.11 D．25.12考点：组合图形的体积．分析：这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积，根据公式计算即可．解答：解：大圆柱的表面积：3.14×22×2+2×3.14×2×0.5，=25.12+6.28，=31.4（平方米），中圆柱侧面积：2×3.14×1.5×0.5=4.71（平方米），小圆柱侧面积：2×3.14×1×0.5=3.14（平方米），这个物体的表面积：31.4+4.71+3.14=39.25（平方米）；答：这个物体的表面积是39.25平方米．故选：B．点评：此题主要考查圆柱的侧面积、表面积公式及其计算．2．图形甲和图形乙所占空间的大小关系，是甲（）乙．A．＞B．＜C．﹦考点：组合图形的体积．专题：立体图形的认识与计算．分析：设每个小正方体的体积为“1”，表示出甲、乙的体积，然后比较即可，由此解答．解答：解：设每个小正方体的体积为“1”，则甲的体积是7，乙的体积也是7，所以，图形甲和图形乙所占空间的大小关系是：甲=乙．故选：C．点评：要理解物体所占空间的大小指的是物体的体积，设出每个小正方体的体积，表示出各个图形的体积，解决问题．3．把一个底面直径为a，高为a的圆柱恰好放入正方体盒子里，此时盒子剩余空间（）A．（1﹣）a3B．（1﹣）a3C．（1﹣）a3D．（1﹣）a3考点：组合图形的体积．专题：立体图形的认识与计算．分析：由题意可知，正方体盒子的棱长就是a，根据圆柱的体积公式：v=sh，正方体的体积公式：v=a3，把数据代入公式求出它们的体积差即可．解答：解：a3﹣π=×a==．答：此时盒子剩余空间是（1）a3．故选：B．点评：此题主要考查圆柱的体积公式、正方体的体积公式的灵活运用．4．两个棱长1分米的正方体并成一个长方体，并成的长方体的表面积（）原两个正方体的表面积之和．A．大于B．小于C．等于考点：组合图形的体积；长方体和正方体的表面积．分析：根据长方体、正方体的特征和长方体表面积的计算方法，两个棱长1分米的正方体并成一个长方体，由两个面重合在一起，因此长方体的表面积比原两个正方体的表面积之和少了两个正方形面的面积．解答：解：两个棱长1分米的正方体并成一个长方体，并成的长方体的表面积小于原两个正方体的表面积之和．故选：B．点评：此题主要考查长方体、正方体的特征和长方体的表面积计算方法．5．用两根完全相同的圆柱形木料分别制作成右图中的两个模型（图中涂色部分），甲与乙的体积相比（）A．甲大B．乙大C．相等考点：组合图形的体积．专题：立体图形的认识与计算．分析：根据圆锥的体积公式可得，底面积相同时，两个高为a的圆锥的体积之和，等于一个高为a的圆锥的体积；已知原来两个圆柱的体积相等，而空白处的图形的体积也相等，所以涂色部分的体积也相等，据此即可选择．解答：解：底面积相同时，两个高为a的圆锥的体积之和，等于一个高为a的圆锥的体积；已知原来两个圆柱的体积相等，而空白处的图形的体积也相等，所以涂色部分的体积也相等，故选：C．点评：此题主要考查圆锥的体积公式的灵活应用．二．填空题（共13小题）6．如图中，每个小长方体的体积都是1立方厘米，那么图形的体积是13立方厘米，表面积是48平方厘米．考点：组合图形的体积；规则立体图形的表面积．专题：立体图形的认识与计算．分析：（1）观察图形可知，这个立体图形一共有2层，下层10个小正方体，上层3个小正方体，一共有13个小正方体，则这个图形的体积就是13个小正方体的体积之和；（2）从上、下面看有10×2个面，从左右面看有5×2个面，从前后面看有9×2个面，据此即可求出这个立体图形的表面积．解答：解：体积是：1×13=13（立方厘米），体积是1立方厘米的正方体的棱长是1厘米，所有表面积是：（10×2+5×2+9×2）×1×1，=48（平方厘米），答：这个立体图形的体积是13立方厘米，表面积是48平方厘米．故答案为：13立方厘米；48平方厘米．点评：立体图形的体积等于组成的所有小正方体的体积之和，表面积就是六个面上的小正方体的面的面积之和，据此即可解决此类问题．7．如图，是一个直立于水平面上的几何体（它是圆柱的一部分，下底面为圆面，单位：cm）．则这个几何体的体积为62.8cm3．（计算结果保留π）考点：组合图形的体积．专题：立体图形的认识与计算．分析：由图形可知：上部分是一个半圆柱，下部分是一个高为4厘米，底面直径是4厘米的圆柱，根据圆柱的体积公式：v=sh，把数据代入公式解答即可．解答：解：3.14×（）2×（6﹣4）× 3.14×（）2×4，=3.14×4×2× 3.14×4×4，=12.56+50.24，=62.8（立方厘米）；答：它的体积是62.8立方厘米．故答案为：62.8．点评：解答求组合图形的体积，首先分析图形是由几部分组成，然后根据相应的体积公式解答即可．8．有一个草堆，上部是一个圆锥，下部是一个圆柱，圆锥高1.5m，底面半径2m，圆柱高3m，底面半径2m，这个草堆的体积是43.96m3．考点：组合图形的体积．专题：立体图形的认识与计算．分析：由题意知，上面是一个圆锥体，下面是一个圆柱体，根据圆锥的体积=×底面积×高，圆柱的体积=底面积×高，代入公式进行计算即可．解答：解：圆锥体积：×3.14×22×1.5，=×3.14×4×1.5，=6.28（立方米）；圆柱的体积：3.14×22×3，=3.14×4×3，=37.68（立方米）；6.28+37.68=43.96（立方米）；答：这个草堆的体积是43.96立方米；故答案为：43.96．点评：此题考查了圆柱与圆锥的体积公式的理解与应用．9．（•富源县）如图有5个棱长为20cm的正方体木箱堆放在墙角的形状，这些木箱的体积是40000cm3．考点：组合图形的体积．专题：立体图形的认识与计算．分析：由图形可知，这些木箱一共有5个，根据正方体的体积公式：v=a3，求一个木箱的体积再乘5即可．解答：解：20×20×20×5=8000×5，=40000（立方厘米），答：这些木箱的体积是40000立方厘米．故答案为：5个，40000．点评：此题主要考查正方体的体积计算方法及组合图形的体积计算．10．（•北京）一支未用过的圆柱形铅笔，长18厘米，体积是9立方厘米．使用一段时间后，变成了如图的样子．这时体积是多少立方厘米？考点：组合图形的体积．分析：先利用圆柱体的体积V=Sh求出这根铅笔的底面积，再分别利用圆柱和圆锥的体积公式，即可求出如图剩余部分的体积．解答：解：铅笔的底面积：9÷18=0.5（平方厘米）；0.5×6+0.5×3×，=3+0.5，=3.5（立方厘米）；答：这时体积是3.5立方厘米．点评：先利用圆柱的体积公式求出这根铅笔的底面积，是解答本题的关键．11．（•万州区）以直角梯形的上底为轴旋转一周，所得的立体图形的体积是108立方厘米．（π值取整数3）考点：组合图形的体积．专题：立体图形的认识与计算．分析：以直角梯形的上底为轴旋转一周，所得的立体图形整体是圆柱，上面是空心圆锥，圆锥的高是（11﹣5）厘米，根据圆柱的体积公式：v=sh，圆锥的体积公式：v=，把数据代入公式求出它们的体积差即可．解答：解：3×==132﹣24=108（立方厘米），答：所得的立体图形的体积是108立方厘米．故答案为：108．点评：此题主要考查圆柱、圆锥体积公式的灵活运用．12．如图，计算出它的体积为AD单位：厘米．A．л（2÷2）2×3×（1+）B．л×22×3×（1+）C．л（2÷2）2××（3+3）D．л×（2÷2）2×3××4．考点：组合图形的体积．分析：根据图可知，此图是由一个圆柱和圆锥组成的，且圆柱和圆锥是等底等高的，所以圆锥的体积等于圆柱体积的，把圆柱的体积求出来再加上圆柱体积的即可．解答：解：由图可知，圆柱和圆锥是等底等高的，所以圆锥的体积等于圆柱体积的，圆柱的底面直径为2厘米，高为3厘米，圆柱的体积：л（2÷2）2×3，（1）当把圆柱的体积看成单位“1”时，再加上圆锥的体积，也就是圆柱体积的，可以列式为：л（2÷2）2×3×（1+）；（2）当把圆锥的体积看成单位“1”时，圆柱的体积就是3个单位“1”，再加上圆锥的体积总共是4个单位“1”，所以也可以列式为：л×（2÷2）2×3××4；故选：A、D．点评：此题的关键是注意圆锥的体积等于和它等底等高的圆柱体积的，然后把圆柱的体积或者把圆锥的体积看成单位“1”来解决问题．13．以棱长10厘米的正方体的一个面，挖去一直径为4厘米的圆孔（挖去的圆孔为圆柱体），则挖去后这个物体的体积是874.4立方厘米．考点：组合图形的体积．专题：立体图形的认识与计算．分析：由题意得出等量关系式：挖去后这个物体的体积=正方体体积﹣圆柱体积，即：剩下的体积=a3﹣πr2h，代数计算即可．解答：解：103﹣3.14×（4÷2）2×10，=1000﹣125.6，=874.4（立方厘米）．答：挖去后这个物体的体积是874.4立方厘米．故答案为：874.4．点评：解决本题的关键是明确挖去后这个物体的体积=正方体体积﹣圆柱体积，代数计算即可．14．如图1，是三个直立于水平面上的形状完全相同的几何体（下底面为圆面．单位：cm）．将它们拼成如图2的新几何体，则该新几何体的体积为7.5πcm3．（计算结果保留π）考点：组合图形的体积．专题：综合题；综合填空题．分析：观察图形可知，拼组后的新几何体的体积就是图1中三个立体图形的体积之和，每个小立体图形的体积都是底面直径为2厘米，高为2厘米的圆柱的体积和底面直径为2厘米，高为3﹣2=1厘米的圆柱的一半的体积之和，由此利用圆柱的体积公式计算出1个小立体图形的体积，再乘以3就是新几何体的体积．解答：解：[π××2+π××（3﹣2）÷2]×3，=[π×1×2+π×1×1÷2]×3，=[2π+0.5π]×3，=2.5π×3，=7.5π（立方厘米），答：新几何体的体积是7.5π立方厘米．故答案为：7.5π．点评：此题考查了圆柱的体积公式的灵活应用以及组合图形的体积的计算方法．15．（•崇文区）一个长20厘米、宽10厘米、高20厘米的无盖长方体玻璃容器，里面盛有一些红色溶液．小明想知道溶液的深，他将一根底面边长5厘米，长1米的长方形木条垂直插入到容器底部，取出后量得木条被染红的部分长16厘米．原来容器内红色溶液深14厘米．考点：组合图形的体积；长方体和正方体的体积．分析：根据题干，将一根底面边长5厘米，长1米的长方形木条垂直插入到容器底部后，此时原玻璃容器内的液面上升了，那么上升的高度就是：底面边长为5厘米，高为16厘米的长方体木条排开液体的体积，除以原来玻璃容器的底面积所得到的高度；由此即可求得原来液面的高度．解答：解：放入木条后水面上升了：5×5×16÷（20×10），=400÷200，=2（厘米），所以原来液面的高度为：16﹣2=14（厘米），答：原来容器内红色溶液深14厘米．故答案为：14．点评：根据题干，得出木条排开液体的体积使液面上升的高度，是解决本题的关键．16．（•大安区）一根长方体木料，横截面是边长10厘米的正方形．从这根木料上截下6厘米长的一段，切削成一个最大的圆锥．圆锥的体积是157cm2，约占截下这段长方体木料体积的26.2%（百分号前面保留一位小数）．考点：组合图形的体积；长方体和正方体的体积．专题：压轴题．分析：（1）如图要求这个圆锥的体积，需要知道这个圆锥的底面半径和高，这里高显然就是这个长方体的高6厘米，圆锥的底面应是这个边长为10厘米的正方形底面内最大的圆，正方形内最大圆的直径等于这个正方形的边长，由此可得这个底面半径是10÷2=5厘米，由此即可利用圆锥的体积公式进行解答；（2）利用长方体的体积公式求得这段木料的体积，利用圆锥的体积÷这个长方体木料的体积即可解决问题．解答：解：（1）根据分析可得：10÷2=5（厘米），×3.14×52×6，=6.28×25，=157（立方厘米），（2）157÷（10×10×6），=157÷600，≈0.262，=26.2%，答：圆锥的体积是157平方厘米，约占截下这段长方体木料体积的26.2%．故答案为：157；26.2．点评：此题考查了圆锥和长方体的面积公式的灵活应用，这里根据正方形内最大圆的特点得出这个圆锥的底面半径是解决本题的关键．17．（•武汉模拟）已知某几何体的三视图如图所示，则该几何体的体积为3π（结果保留π）考点：组合图形的体积．专题：立体图形的认识与计算．分析：通过三视图判断几何体的特征，利用三视图的数据，求出几何体的体积即可．解答：解：由三视图可知几何体是圆柱底面半径为1高为6的圆柱，被截的一部分，如图所求几何体的体积为×12×6=3π．答：该几何体的体积为3π．故答案为：3π．点评：本题考查三视图与几何体的关系，正确判断几何体的特征是解题的关键，考查计算能力．18．祖冲之最早将圆周率精确地计算到小数点后面7位，请借助圆周率计算立体图形（如图）的侧面积为31.4平方厘米．考点：组合图形的体积．分析：先求出底面直径是2厘米，高是4厘米的圆柱的侧面积；再求出底面直径是2厘米，高是（6﹣4）厘米的圆柱的侧面积的一半；把两次求出的侧面积合起来即为组合图形的侧面积．解答：解：底面直径是2厘米，高是4厘米的圆柱的侧面积：3.14×2×4=25.12（平方厘米），底面直径是2厘米，高是（6﹣4）厘米的圆柱的侧面积的一半：3.14×2×（6﹣4）×=6.28（平方厘米），组合图形的侧面积：25.12+6.28=31.4（平方厘米）．答：立体图形的侧面积为31.4平方厘米．故答案为：祖冲之，31.4．点评：解决此题关键是先求出高是4厘米的圆柱的侧面积和高是2厘米的圆柱的侧面积的，两个侧面积之和即为组合图形的侧面积．B档（提升精练）一．解答题（共9小题）1．（•临川区）有一个粮仓，它们上面是圆锥体，下面是圆柱体，已知圆柱的底面周长是18.84米，高为4米，圆锥的高是1米，则这个粮仓的体积是多少立方米？考点：组合图形的体积．分析：粮仓的容积=圆柱部分的容积+圆锥部分的容积，先根据底面周长是18.84米求出这个粮仓的底面半径，再利用圆柱和圆锥的容积公式即可解答．解答：解：18.84÷3.14÷2=3（米），3.14×32×4+3.14×32×1×，=28.26×4+9.42，=113.04+9.42，=122.46（立方米），答：这个粮仓的体积是122.46立方米．点评：此题考查圆柱与圆锥的体积公式的应用．2．（•汉阳区）如图是丰裕粮仓示意图．如果每立方米稻谷重600千克，这个粮仓可储存稻谷多少千克？考点：组合图形的体积．专题：立体图形的认识与计算．分析：（1）先求这个粮囤的体积，根据圆锥与圆柱的体积公式，计算即可；（2）要求这个粮囤最多能装稻谷多少吨，用求得的粮囤的体积，乘单位体积的稻谷的重量即可．解答：解：（1）3.14×（4÷2）2×3+×3.14×（4÷2）2×（4.5﹣3），=37.68+6.28，=43.96（立方米）；（2）43.96×600=26376（千克）；答：这个粮仓可储存稻谷26376千克．点评：此题主要考查学生对圆锥与圆柱的体积公式的掌握与运用．3．（•龙泉驿区）请计算零件的表面积和体积（正方体棱长lOcm，圆柱的半径r=4cm，高h=6cm）．考点：组合图形的体积．专题：压轴题；立体图形的认识与计算．分析：观察图形可知，这个图形的表面积等于下面的正方体的表面积与上面的圆柱体的侧面积之和，体积等于正方体与圆柱体的体积之和，据此利用计算公式即可解答问题．解答：解：表面积是：10×10×6+3.14×4×2×6，=600+150.72，=750.72（平方厘米），体积是：10×10×10+3.14×42×6，=1000+301.44，=1301.44（立方厘米），答：这个图形的表面积是750.72平方厘米，体积是1301.44立方厘米．点评：此题考查正方体、圆柱体的表面积、体积公式的计算应用，熟记公式即可解答．4．（•上海）如图，（单位：dm）是一块零件的铜铸毛坯，每立方分米铜重8.9千克，这块零件铸铁毛坯的重量是多少吨？考点：组合图形的体积．分析：可以把这块毛坯分割成两个长方体进行计算，左边的长方体的长是8分米，宽是5分米，高是6分米；右边的长方体的长是8分米，宽是10﹣5=5分米，高是6﹣4=2分米；根据长方体的体积公式v=abh，求出两个长方体的体积和，再乘每立方分米铜的重量（9.8千克），把千克换算成用吨作单位；由此列式解答．解答：解：[8×5×6+8×（10﹣5）×（6﹣4）]×8.9，=[240+8×5×2]×8.9，=[240+80]×8.9，=320×8.9，=2848（千克）；2848千克=2.848吨．答：这块零件铸铁毛坯的重量是2.848吨．点评：此题是组合图形体积计算的实际应用，首先分析图形是由几部分组成，根据体积公式计算出它的体积，再根据每立方分米铜重8.9千克，求出它的重量，注意体积单位之间的换算．5．（•广州模拟）有一根长20厘米，半径为2厘米的圆钢，在它的两端各钻了一个深为4厘米，底面半径为2厘米的圆锥形小孔做成一个零件，如图这个零件的体积是多少立方厘米？考点：组合图形的体积；圆柱的侧面积、表面积和体积；圆锥的体积．分析：圆柱的体积减去2个圆锥的体积，就是零件的体积．解答：解：圆柱的体积：3.14×22×20=251.2（cm3）2个圆锥的体积：×3.14×22×4×2≈33.5（cm3）251.2﹣33.5=217.7（cm3）；答：零件的体积是217.7cm3．点评：把不规则的物体的体积，转化成规则物体的组合．6．（•陆良县模拟）每立方厘米的钢重7.8克，求下面一段钢管约重多少千克？（得数保留一位小数）（单位：厘米）考点：组合图形的体积．分析：此钢管的体积是底面直径为10厘米、高为80厘米的圆柱的体积与底面直径为8厘米、高为80厘米的圆柱的体积的差．利用圆柱的体积公式即可解决问题．解答：解：3.14×〔（10÷2）2﹣（8÷2）2〕×80，=3.14×〔52﹣42〕×80，=3.14×〔25﹣16〕×80，=3.14×9×80，=2260.8（立方厘米），2260.8×7.8=17634.24（克），17634.24克≈17.6千克，答：这根钢管约重17.6千克．点评：此题考查了圆柱的体积公式在实际问题中的灵活应用．7．（•黄冈模拟）计算图形的体积考点：组合图形的体积．专题：立体图形的认识与计算．分析：由图意可知：这个图形的体积=圆环的面积×这个图形的高度，将数据代入此关系式即可求解．解答：解：[3.14×（40÷2）2﹣3.14×（20÷2）2]×80=（3.14×400﹣3.14×100）×80=（1256﹣314）×80=942×80=75360（立方毫米）答：这个图形的体积是75360立方毫米．点评：解答此题的关键是明白：这个图形的体积=圆环的面积×这个图形的高度．8．（•海安县模拟）一次数学活动课上，同学们发现长方形的小旗旋转一周后，所扫过的空间是圆柱体形状，直角三角形的小旗，以任意一条直角边为轴旋转一周，所扫过的空间是圆锥体形状．小明受此启发，制作了这样一面小旗（如图），你能求到这面小旗以最长边为轴旋转一周，扫过的空间的大小吗？考点：组合图形的体积．专题：立体图形的认识与计算．分析：这面小旗旋转一周，扫过的空间是两个同底的圆锥，所以要求所扫过空间的大小就是求两个圆锥的体积之和．圆锥的底面半径是4cm，两个圆锥的底面积相等，高的和是12，根据圆锥的体积=底面积×高×，把数据代入公式解答即可．解答：解：3.14×42×12×=3.14×16×12×=50.24×12×=602.88×=200.96（立方厘米）答：扫过的空间是200.96立方厘米．点评：解答本题的关键是根据已知条件确定扫过的空间是两个同底的圆锥的体积的和．9．（•荔波县模拟）求下面图形的体积．考点：组合图形的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：（1）图形的体积是圆柱的体积加上和它等底等高的圆锥的体积，圆柱的体积=底面积×高，圆锥的体积=底面积×高×，把数据代入公式解答即可．（2）根据圆柱的体积=底面积×高，把数据代入公式解答即可．解答：（1）圆柱的底面积：3.14×（4÷2）2=12.56圆柱的体积：12.56×5=62.8圆锥的体积：12.56×3×=12.56组合图形的体积：62.8+12.56=75.36答：组合图形的体积是75.36．（2）3.14×52×10=3.14×25×10=78.5×10=785答：圆柱的体积是785．点评：本题考查的是圆柱的体积和圆锥的体积计算公式的应用．C档（跨越导练）一．填空题（共1小题）1．（•大安区）一根长方体木料，横截面是边长10厘米的正方形．从这根木料上截下6厘米长的一段，切削成一个最大的圆锥．圆锥的体积是157cm2，约占截下这段长方体木料体积的26.2%（百分号前面保留一位小数）．考点：组合图形的体积；长方体和正方体的体积．专题：压轴题．分析：（1）如图要求这个圆锥的体积，需要知道这个圆锥的底面半径和高，这里高显然就是这个长方体的高6厘米，圆锥的底面应是这个边长为10厘米的正方形底面内最大的圆，正方形内最大圆的直径等于这个正方形的边长，由此可得这个底面半径是10÷2=5厘米，由此即可利用圆锥的体积公式进行解答；（2）利用长方体的体积公式求得这段木料的体积，利用圆锥的体积÷这个长方体木料的体积即可解决问题．解答：解：（1）根据分析可得：10÷2=5（厘米），×3.14×52×6，=6.28×25，=157（立方厘米），（2）157÷（10×10×6），=157÷600，≈0.262，=26.2%，答：圆锥的体积是157平方厘米，约占截下这段长方体木料体积的26.2%．故答案为：157；26.2．点评：此题考查了圆锥和长方体的面积公式的灵活应用，这里根据正方形内最大圆的特点得出这个圆锥的底面半径是解决本题的关键．二．解答题（共3小题）2．（•广西）如图是蒙古族吉日格勒爷爷的家，它由一个圆柱和一个圆锥组成．吉日格勒爷爷的家所占的空间大约是多少立方米？考点：组合图形的体积．专题：压轴题；立体图形的认识与计算．分析：求吉日格勒爷爷的家所占的空间大约是多少立方米，根据体积的意义，物体所占空间的大小叫做物体的体积．利用圆锥的体积公式：v=πr2h，圆柱的体积公式：v=πr2h，求出圆锥的体积、圆柱的体积，然后合并起来即可．解答：解：3.14×（）2×3+×3.14×（）2×3，=3.14×（）2×（3+×3），=3.14×9×4，=3.14×36，≈113（立方米）；答：吉日格勒爷爷的家所占的空间大约是113立方米．点评：此题属于圆锥和圆柱体积计算的实际应用，求吉日格勒爷爷的家所占的空间根据圆锥和圆柱的体积公式解答．3．（•宜宾）下面两个图中，左边一个是梯形，绕它的6cm的边将这个梯形旋转一周得到如右边的立体图形，这个立体图形的体积是多少立方厘米？。

长方体和正方体的表面积和体积专项练习一、高减少或增加引起表面积的变化：例题：一个长方体高减少3厘米后，表面积减少了72平方厘米，剩下的刚好是一个正方体, 原来长方体的表面积是多少平方厘米？试一试：一个长方体，如果高增加2厘米，就成为一个正方体，这时表面积比原来增加了 64平方厘米，原来的长方体的表面积是多少平方厘米？二、拼接引起表面积的变化：例题：1.用两个长、宽、高分别是6分米、4分米、2分米的长方体拼成一个较大的长方体，这个长方体怎样拼表面积最大？怎样拼表面积最小？2.用6个棱长是1厘米的小正方体拼成一个较大的长方体，拼成的长方体的表面积比原来减少了多少平方厘米？试一试：10包长、宽、高分别为8厘米、5厘米、2厘米的中华牌香烟，若用包装纸将他们打包成一个长方体，不计接头处，至少需要多少平方厘米的包装纸？三、切割引起表面积的变化：例题：将一个长10厘米、宽6厘米、高5厘米的长方体切成两个完全相同的小长方体，这两个小长方体的表面积总和比原来增加了多少平方厘米？试一试：(1)有一个长方体，若用三种不同的方法切成两个完全一样的长方体，它们的表面积分别增加30平方厘米、20平方厘米、12平方厘米。

这个长方体的表面积是多少平方厘米？(2)如右图，一个正方体木块的表面积是36平方分米，把它沿虚线截成体积相等的8个小正方体木块，这时，表面积增加了多少平方厘米?四、挖去部分引起表面积的变化：例题：在一个长6厘米、宽4厘米、高3厘米的长方体上挖去一个棱长1厘米的小正方体, 剩余部分的表面积可能是多少平方厘米？试一试：用橡皮泥做一个棱长为4厘米的正方体。

(1)如右图，在顶面中心位置从上到下打一个边长为1厘米的正方形通孔，打孔后的橡皮泥块的表面积为多少平方厘米？(2)在第(1)题打孔后，再在正面中心位置处，从前到后打一个边长1 厘米的正方形通孔(如右图所示)，那么打孔后的橡皮泥内外的表面积总和是多少平方厘米？(3)在棱长为3厘米的正方体木块的每个面的中心上打一个直穿木块的洞, 洞口呈边长为1厘米的正方形(如图)。

第八讲长方体、正方体表面积、体积一、课程引入长方体、正方体的知识是小学数学“空间与图形”领域的重要内容。

前面我们已经学习了长方体以及正方体，知道长方体或正方体六个面面积的总和叫做长方体或正方体的表面积，会利用公式计算长方体正方体的表面积以及体积。

对于由几个长方体或正方体组合而成的几何形体，或者是一个长方体或正方体组合而面的几何形体，它们的表面积、体积又如何求呢？二、基本理论理论点1如果正方体的棱长用a表示，则正方体的表面积=6a²，体积a³；如果长方体的长用a表示、宽用b表示、高用h表示，那么长方体的表面积=（ab+ah+bh）×2，体积=abh。

理论点2对于由几个长方体或正方体组合而成的几何形体，或者是一个长方体或正方体组合而面的几何形体，这些图形的特点都是可以从六个方向去看，特别是求表面积时，就是上下、左右和前后六个方向（有时只考虑上、左、前三个方向）的平面图形的面积的总和。

三、例题精析【例题1】【题干】在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体（下图），求这个立体图形的表面积。

【答案】214平方分米【解析】解：上下方向：5×5×2=50（平方分米）侧面：5×5×4=100（平方分米）4×4×4=64（平方分米）这个立体图形的表面积为：50＋100＋64=214（平方分米）答;这个立体图形的表面积为214平方分米。

【例题2】【题干】一个正方体形状的木块，棱长为1米，沿着水平方向将它锯成3片，每片又按任意尺寸锯成4条，每条又按任意尺寸锯成5小块，共得到大大小小的长方体60块，如下图.问这60块长方体表面积的和是多少平方米？【答案】24平方米【解析】解：每锯一刀，就会得到两个1平方米的表面，1×2=2（平方米）。

一共锯了2＋3＋4=9（刀），得到：2×9=18（平方米）的表面。

《正方体、长方体的表面积》知识清单一、正方体的表面积1、正方体的特征正方体是一种由六个完全相同的正方形面围成的立体图形。

它的十二条棱长度都相等，八个顶点也完全相同。

2、正方体表面积的定义正方体的表面积就是指正方体六个面的总面积。

3、计算公式正方体的表面积＝棱长×棱长×6假设一个正方体的棱长为 a ，那么它一个面的面积就是 a×a ＝ a²，六个面的面积总和就是 6×a²。

例如，如果正方体的棱长是 5 厘米，那么它的表面积就是 5×5×6 ＝150（平方厘米）4、实际应用在日常生活中，我们经常会遇到需要计算正方体表面积的情况。

比如，要给一个正方体的盒子包装纸，就需要知道盒子的表面积，从而确定需要多少包装纸。

又比如，制作一个正方体的水箱，为了确定所需材料的面积，也需要计算水箱的表面积。

二、长方体的表面积1、长方体的特征长方体是由六个面组成的，相对的两个面完全相同。

它有十二条棱，分别为 4 条长、4 条宽和 4 条高。

2、长方体表面积的定义长方体六个面的总面积就是长方体的表面积。

3、计算公式长方体的表面积＝（长×宽＋长×高＋宽×高）×2设长方体的长、宽、高分别为 a、b、c ，那么它前面和后面的面积都是a×c ，上面和下面的面积都是a×b ，左面和右面的面积都是b×c 。

所以表面积就是 2×（a×b ＋ a×c ＋ b×c）例如，一个长方体的长是 6 厘米，宽是 4 厘米，高是 3 厘米，它的表面积就是（6×4 ＋ 6×3 ＋ 4×3）×2 ＝ 108（平方厘米）4、实际应用在建筑、装修等领域，经常需要计算长方体的表面积。

比如，要给一间长方体形状的房间贴壁纸，就需要计算房间四周和天花板的表面积，从而确定需要购买多少壁纸。