人教版高中数学课件二次函数根的分布

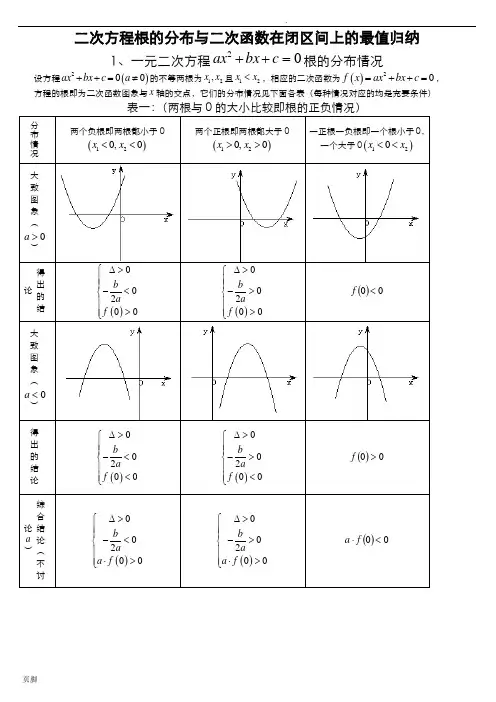
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）分布情况两个负根即两根都小于0 ()120,0x x << 两个正根即两根都大于0 ()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（>a ）得出的结论 ()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a ）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ，一个大于k 即21x k x <<大致图象（0>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（0<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a ） ()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种） 一根在()n m ,内，另一根在()q p ,内，q p n m <<<大致图象（>a ）得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象（0<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()0f m f n f p f q <⎧⎪⎨<⎪⎩综合结论（不讨论a ） ——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f ()n m ,12，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩； （2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <g 不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

二次函数根的分布二次函数是二次多项式的函数，其一般形式为y=ax^2+bx+c（其中a≠0）。

首先，我们需要了解二次函数的图像特点。

对于二次函数y=ax^2+bx+c，a决定了二次函数的开口方向和开口大小，a>0时开口向上，a<0时开口向下；b决定了二次函数的对称轴位置，对称轴的方程为x=-b/2a；c决定了二次函数与y轴的交点。

其次，我们来探讨二次函数的根的分布。

二次函数的根即方程的解，即使二次方程的解的个数以及位置。

对于一元二次方程ax^2+bx+c=0，我们可以利用判别式来判断解的情况：判别式Δ=b^2-4ac。

1.当Δ>0时，方程有两个不相等的实根。

实根的个数与开口方向无关，只与判别式Δ有关。

-当Δ>0时，方程有两个不相等的实根。

-当Δ=0时，方程有一个实根，这个实根称为方程的重根。

-当Δ<0时，方程无实根，但可以有两个共轭虚根。

值得注意的是，只有在a≠0时，方程为一元二次方程，才能求解二次函数的根。

接下来，我们来分析二次函数根的分布。

1.当Δ>0时，方程有两个不相等的实根。

此时，二次函数与x轴交于两个不同的点，也就是有两个实根。

这两个实根的位置由二次函数的对称轴决定，对称轴的方程为x=-b/2a。

假设根的位置为x1和x2，那么有以下三种情况：-当x1和x2均小于对称轴的x坐标时，二次函数开口向上，根的位置为x1>x2-当x1和x2均大于对称轴的x坐标时，二次函数开口向下，根的位置为x1<x2-当x1小于对称轴的x坐标，x2大于对称轴的x坐标时，一个根位于对称轴的左侧，一个根位于对称轴的右侧。

2.当Δ=0时，方程有一个实根，这个实根称为方程的重根。

此时，二次函数与x轴有且仅有一个交点，也就是有一个实根。

这个实根的位置正好位于二次函数的对称轴上，对称轴的方程为x=-b/2a。

3. 当Δ<0时，方程无实根，但可以有两个共轭虚根。

此时，二次函数与x轴没有交点，也就是无实根。

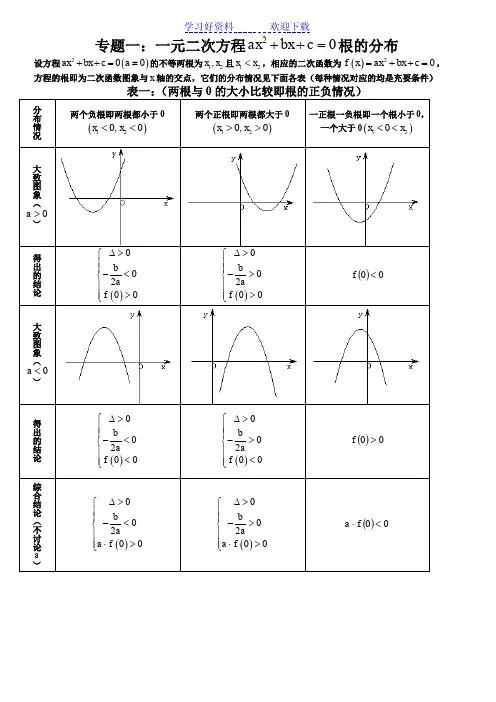
专题一：一元二次方程02=++c bx ax 根的分布设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）k k k根在区间上的分布还有一种情况：两根分别在区间外，即在区间两侧，（图形分别如下）需满足12的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩； （2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

如方程()2220m x m x -++=在区间()1,3上有一根，因为()10f =，所以()()()22212m x m x x m x -++=--，另一根为2m ，由213m<<得223m <<即为所求； 2︒ 方程有且只有一根，且这个根在区间()n m ,内，即0∆=，此时由0∆=可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数。

如方程24260x m x m -++=有且一根在区间()3,0-内，求m 的取值范围。

分析：①由()()300f f -<即()()141530m m ++<得出15314m -<<-；②由0∆=即()2164260m m -+=得出1m =-或32m =，当1m =-时，根()23,0x =-∈-，即1m =-满足题意；当32m =时，根()33,0x =∉-，故32m =不满足题意；综上分析，得出15314m -<<-或1m =-典例分析：例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根，求实数m 的取值范围。

二次函数根的分布本文介绍了一元二次方程根的分布情况以及与二次函数在闭区间上的最值归纳。

设方程 $ax^2+bx+c$ 的不等两根为$x_1,x_2$，且 $x_1<x_2$，相应的二次函数为$f(x)=ax^2+bx+c$，方程的根即为二次函数图象与 $x$ 轴的交点。

根的分布情况可归纳为三种情况，每种情况对应的均是充要条件。

第一种情况是两个负根即两根都小于 $0$，或两个正根即两根都大于 $0$，或一个正根一负根即一个根小于 $0$，一个大于 $0$。

此时，当 $a>0$ 时，$f(x)$ 最小值为$\frac{\Delta}{4a}$，当 $a<0$ 时，$f(x)$ 最大值为$\frac{\Delta}{4a}$。

第二种情况是两根与 $k$ 的大小比较，即两根都小于 $k$，或两根都大于$k$，或一个根小于$k$，一个大于$k$。

此时，当 $a>0$ 时，$f(k)$ 最小值为 $a(k-x_1)(k-x_2)$，当 $a<0$ 时，$f(k)$ 最大值为 $a(k-x_1)(k-x_2)$。

第三种情况是根在区间上的分布，包括两根都在$(m,n)$ 内，一根在 $(m,n)$ 内，另一根在 $(p,q)$，或两根有且仅有一根在 $(m,n)$ 内。

此时，当 $a>0$ 时，$f(x)$ 最小值为 $f\left(\frac{x_1+x_2}{2}\right)$，当 $a<0$ 时，$f(x)$ 最大值为 $f\left(\frac{x_1+x_2}{2}\right)$。

经过观察得出，文章中存在大量格式错误和重复内容，需要进行整理和删减。

同时，需要对每段话进行简单的改写，以提高可读性。

根据图像，可以得出以下结论：1.当mf(n)且f(n)>b，则有f(m)*f(n)<2a；若有f(m)<f(n)且f(n)<b，则有f(m)*f(n)<2a；若有f(m)<f(n)<b，则有f(m)*f(n)<f(p)*f(q)。

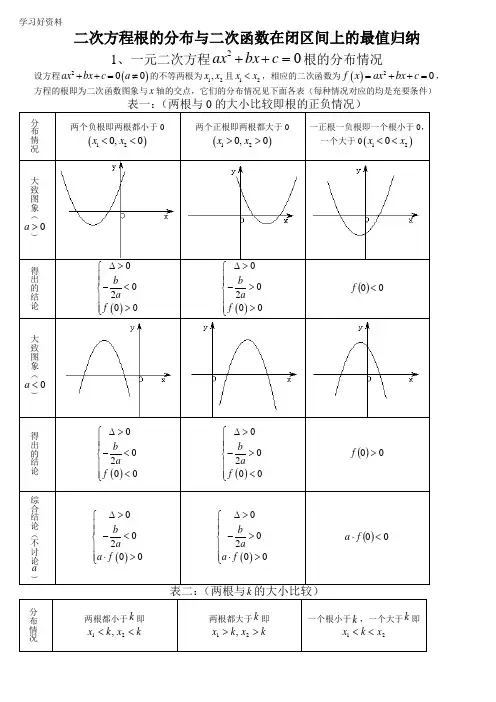
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f a分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种） 一根在()n m ,内，另一根在()q p ,内，q p n m <<<大致图象（>a ）kkk得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象（<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩综合结论（不讨论a）——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况：两根分别在区间()外，即在区间两侧12，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明： （1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

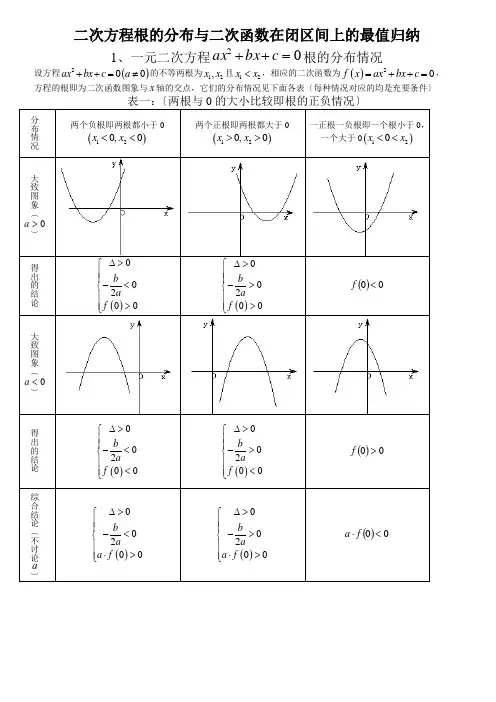
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表〔每种情况对应的均是充要条件〕表一：〔两根与0的大小比较即根的正负情况〕分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象〔>a 〕得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象〔<a 〕得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论〔不讨论a〕()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ，一个大于k 即21x k x <<大致图象〔>a 〕得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象〔<a 〕得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论〔不讨论a〕()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()nm,内两根有且仅有一根在()nm,内〔图象有两种情况，只画了一种〕一根在()nm,内，另一根在()qp,内，qpnm<<<大致图象〔0 > a〕得出的结论()()2f mf nbm na∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩大致图象〔0 < a〕得出的结论()()2f mf nbm na∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩综合结论〔不讨论a 〕——————()()0<⋅nfmf()()()()⎪⎩⎪⎨⎧<<qfpfnfmf根在区间上的分布还有一种情况：两根分别在区间()外，即在区间两侧12，〔图形分别如下〕需满足的条件是〔1〕0a >时，()()00f m f n <⎧⎪⎨<⎪⎩； 〔2〕0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：〔1〕两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 假设()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

第7课 二次方程根的分布
一、考纲要求：
能利用二次函数的图象研究一元二次方程的实根分布。

二、知识结构：
设方程的两不等实根为，且
，相应的二次函数为，方程的根即为二次函数图象与轴的交点，它们的分布情况见下表
根
的
分
布
图
象
充
要
条
件
根的分布在有且只有一个根
图
象
充
要
条
件
或
三、典型例题：
1、《学案P13 例1》设有一元二次方程
.试问：
（1）为何值时，方程有一正根，一负根；
（2）为何值时，方程有一根大于1、另一根小于1；
（3）为何值时，方程有两正根；
（4）为何值时，方程有两负根。

2、《学案P14 例2》若关于的方程的一个根在内，另一个根在内，求的范围。

练习：
1．《学案P14 变式1》若关于的方程
有两个都大于1的实数根，求实数的取值范围。

2．《学案P14 变式2》若关于的方程的两根均在区间内，求实数的范围。

3．若关于的方程在区间内有且只有一个根，求实数的范围。

4.《学案P14变式3》已知函数
并且是方程的两根，则的大小关系是（ ）
A. B.
C. D.
四、归纳反思：《学案》P14
五、课后作业：《课时作业》P215 1-8小题。

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f a分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种） 一根在()n m ,内，另一根在()q p ,内，q p n m <<<大致图象（>a ）kkk得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象（<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩综合结论（不讨论a）——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况：两根分别在区间()外，即在区间两侧12，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明： （1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。