当前位置：文档之家 › (完整word版)一维势垒问题总结

(完整word版)一维势垒问题总结

  • 格式：doc
  • 大小：1.07 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

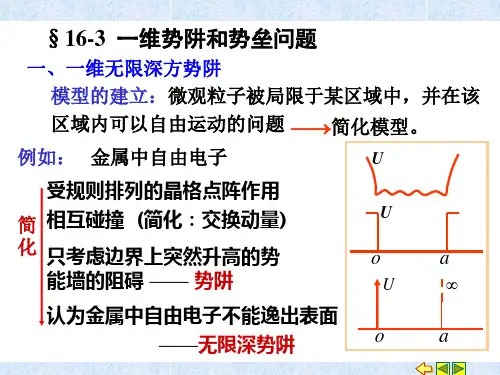
16-3 一维势阱和势垒问题

16-3 一维势阱和势垒问题

]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波： 由 x > a 处无反射波： B 3 = 0 令 A1 = 1（以入射波强度为标准） 以入射波强度为标准） 由波函数的 标准条件得 O 可解得
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立：微观粒子被局限于某区域中， 模型的建立：微观粒子被局限于某区域中，并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如： 例如： 金属中自由电子 受规则排列的晶格点阵作用 简化：交换动量) 简 相互碰撞 (简化：交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习： 练习
已知： 已知：
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞

163一维势阱和势垒问题

163一维势阱和势垒问题
mn
0,
mn mn
克罗内克符号
二、势垒穿透和隧道效应
有限高的方形势垒
数学形式：
U
(
x)
0,
U 0 ,
图形形式：
x 0(P区),x a(S区) 0 x a(Q区)
U
考虑粒子的动能 E小于势垒高
U0
度 U0的情况。（ E < U0 ）
E
PQ S
o ax
U (x) 0, x 0和x a
1
(0 x a)
(x 0及x a)
2
势阱内 0 < x < a
d 2 1
dx2
2E
2
1
0
势阱外 x ≤ 0 ;x ≥a
2 0
理由:因为势壁无限高,所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d 2
d x2
2E
2
0
E是粒子的总能量，E > 0，令 k
定态薛定谔方程变为
d 2
一维无限深方势阱的图形表达形式 ：
∞∞
U(x)
粒子只能在宽为 a 的两个无限 高势壁间运动，这种势称为一 维无限深方势阱。
0
ax
因为系统的势能与时间无关，因此这是一个定 态问题，可以用定态薛定谔方程进行求解。
2
2
2
U
(r)
(r )
E
(r )
————定态薛定谔方程
①列出各区域的定态薛定谔方程
若在样品与针尖之间
加一微小电压Ub电子 就会穿过电极间的势
垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。 若控制隧道电流不变，则探针在垂直于样品 方向上的高度变化就能反映样品表面的起伏。

第十八章4一维势阱势垒

第十八章4一维势阱势垒

求解定态薛定谔方程 2 2 h dψ − = Eψ (0 < x < a) 2
d2ψ(x) 2 + k ψ(x) = 0 2 dx ψ(x) = Asinkx + Bcoskx
由于阱壁无限高， 由于阱壁无限高，所以 ψ(0) = 0 阱壁无限高
ψ(a) = 0
Asin(0) + Bcos(0) = 0 Asin(a) + Bcos(a) = 0
Φn ( x) = a sin a
2
a
a
x, n = 1,2,3,⋅ ⋅ ⋅
En =
π 2h2
2ma
2
n , n = 1,2,3,⋅ ⋅ ⋅
10
则
Ψ( x) = C f ( x)
1 2 πx 2 2πx sin − sin = 2 a a a a 1 1 = Φ1 ( x) − Φ2 ( x) 2 2
时、空异号 为右行波
15
求出解的形式画于图中。 求出解的形式画于图中。 定义粒子穿过势垒的贯穿系数： 定义粒子穿过势垒的贯穿系数
隧道效应
I
II
III
势垒的宽度约50nm 以上时， 以上时， 当 时，势垒的宽度约 贯穿系数会小六个数量级以上。 贯穿系数会小六个数量级以上。隧道效应在 实际上已经没有意义了。量子概念过渡到经典了。 实际上已经没有意义了。量子概念过渡到经典了。
En = (
πh
2
2 2
2m a
)n , n = 1, 2, 3⋅ ⋅ ⋅
2
4
En = (
πh
2
2 2
2m a
)n , n = 1, 2, 3⋅ ⋅ ⋅
2

21.7 一维势阱 势垒 隧道效应

21.7 一维势阱 势垒 隧道效应

STM的发明者 宾尼、罗雷尔和电 子显微镜的发明者 卢斯卡分享了1986 年诺贝尔物理奖。
宾尼
罗雷尔
U0
电子云重叠 U0 U0 E
样 品
d
针 尖
扫描隧道显微镜（STM）装置示意图
用STM得到的神经细胞象
液体中观察原子图象
在电解液中得到的硫酸根离子吸附在铜 单晶表面的STM图象。
“扫描隧道绘画 ” 一氧化碳“分子人”
8 n1 x n2 y n3 z ( x, y, z ) sin sin sin l1l2 l3 l1 l2 l3
三维势阱中粒子的能量：
n12 2 2 n2 2 2 2 n32 2 2 E 2 2 2 2ml1 2ml2 2ml3
处在超晶格的一维量子线和两维量子阱中的电子 就属于一维和两维势阱中的粒子，而处在金属内的电 子可看作三维势阱中的粒子。
i En t
)e
i En t

( px En t )
C 2e
( px En t )
n ( x, t ) 是由两个沿相反方向传播的平面波叠加而
③粒子在阱中的分布 经典力学的结果：均匀分布 P ( x ) 1/ a a a P ( x)dx P ( x) dx P ( x)a 1
(4) 解方程、定常数 在 0<x<a 区域，定态薛定谔方程为
令
d x 2mE 2 x 0 2 dx 2mE 2 k 2 d 2 x 2 k x 0 2 dx
2
比较谐振动方程 特解为
d2x 2 x0 2 dt
( x ) C sin(kx )
2 2 2

16-3一维势阱和势垒问题解读

16-3一维势阱和势垒问题解读
n4
x a
a x
第k激发态(n=k+1)有k个节点。
（2）一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰：量子 经典均匀分布 0
a a n 1，x 处，几率最大 0 3 2 b n ，峰数 ，当n 时，
4
U0
II
III
o
a
x
而在微观粒子的情形，却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
（2）E<U0 从解薛定谔方程的结果来看，在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零，同时，在 x>a区域也存在波函数，所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数，由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑，粒子不可能透过阱壁，因而按照波 函数的统计诠释，要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况，即
(0) 0, (a) 0
————边界条件
(0) 0
这说明：并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件，只有当能量取上式 给出的那些分立的值 En（体系的能量本征值）时， 相应的波函数才是物理上有意义的，即本问题中体系 的能量是量子化的，亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a

【大学物理】§3-2薛定谔方程 一维势阱和势垒问题

【大学物理】§3-2薛定谔方程 一维势阱和势垒问题
§2-3 薛定谔方程
一、一维无限深方势阱
对于一维无限深方势阱有
一维势阱和势垒问题
∞
∞
U(x)
U
(
x)
0
(0 x a) ( 0 x, x a)
势阱内U(x) = 0，哈密顿算符为
H
2
2
d2 d x2
定态薛定谔方程为
0
a
令
2E
k
薛定谔方程的解为
d 2
d x2
2E
2
0
(x) Asin(kx )
由此解得最大值得位置为
x (2N 1) a 2n
例如
n 1, N 0
最大值位置
x 1a 2
n 2, N 0,1, 最大值位置 x 1 a , 3 a Nhomakorabea44
n 3, N 0,1, 2, 最大值位置 x 1 a , 3 a , 5 a.
6 66
可见，概率密度最大值的数目和量子数n相等。
10
2m dx2
2. 波函数
(
x)
2 sin( n x), 0 x a
aa
0,
x 0或x a
3. 能量
En
n
2
22
2ma 2
n 1,2,3
4. 概率密度
(x) 2 2 sin 2 ( n π x)
a
a
4
讨论
n (x)
2 sin n x
a a
(0 x a)
1.n=0给出的波函数
1
根据 (0，)可以0确定 = 0或m，m =1,2,3,。于是上式改写为
根据 (a) 0，得
(x) Asin kx
ka = n， n = 1,2,3, ···

52_6半无限深势阱_一维势垒

52_6半无限深势阱_一维势垒

ϕ1 ( x) = Ae + r e
ikx
1
−ikx
,
x≥a
x≤0
0≤ x≤a
ϕ2 ( x) = Cek x + De−k x ,
1
ϕ 1 (0) = ϕ 2 (0)
ϕ3 ( x) = te ,
ikx
ϕ 2 (a ) = ϕ 3 (a )
dϕ 1 ( x ) dϕ 2 ( x ) |x=0 = |x=0 dx dx
例如，电子可逸出金属表面， 例如，电子可逸出金属表面， 在金属表面形成一层电子气。 在金属表面形成一层电子气。 7
怎样理解粒子通过势垒区? 怎样理解粒子通过势垒区 经典物理：粒子不能进入E 的区域(动能 经典物理：粒子不能进入 < U的区域 动能< 0)。 的区域 动能< 。 量子物理：粒子有波动性，遵从不确定关系， 量子物理：粒子有波动性，遵从不确定关系， 粒子穿过势垒区和能量守恒并不矛盾。 粒子穿过势垒区和能量守恒并不矛盾。 只要势垒区宽度∆ 不是无限大， 只要势垒区宽度∆ x = a 不是无限大， 粒子能量就有不确定量∆ 粒子能量就有不确定量∆E
U ( x)
U0
方程的解必处处为零,根据 方程的解必处处为零 根据 波函数的标准化条件， 波函数的标准化条件，在边界上
ϕ ( x) = 0
x≤0
E2 E1
o
a
x
2、在0<x<a 区域粒子势能为零，定态薛定谔方程 、 区域粒子势能为零，
− ℏ 2 d 2ϕ ( x ) = Eϕ ( x ) 2 2m dx 0< x<a
ℏ 2 d 2ϕ 3 ( x ) − = E ϕ 3 ( x ), 2 2 m dx

一维势垒问题总结

一维势垒问题总结

一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数，对以上的透射系数的总结，推出了对于任意势垒中透射系数， 并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中，遇到的问题和 值得注意的地方。

在求方势垒波 函数中，首先要知道这是一个什 么样问题，满足什么样的方程， 方程可以写成什么样的形式，在 求解方程中，波函数的形式应该怎样需要怎样的分段，分段的过程中，特别要强调的边界条件问题。

并且验证了概率流密度。

在量子力学中，粒子在势垒附近发生的现象是不一样的，能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射，而能量小于0u 的粒子也会有部分穿过势垒，这在经典力学中是不会发生的。

下面讨论的是一维散射（即在非束缚态下问题，在无穷远处波函数不趋于零）。

重点讨论的是粒子通过势垒的透射和反射，重点在于求出波函数，这就必须求解薛定谔方程，由于)(x U 是与时间无关的，此处是定态薛定谔方程。

定态薛定谔方程通式：ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域：⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h （1） ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注： 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时，通解xq xq eC e C y ---+=21，当0>q 时，通解xq ixq ie C e C y -+=21方程（1）的解可以表示为：⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ （2）定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-，可以看到式子（2）的三式，第一项是左向右传播的平面波，第二项是由右向左传播的平面波，即入射波和反射波。

一一一维维维势势势垒垒垒贯贯贯穿穿穿

一一一维维维势势势垒垒垒贯贯贯穿穿穿
2 ˆ (x) = − � ψ (x)�� = Eψ (x) Hψ 2m
(2.88)
(2.89)
在x < 0, x > a的区域, 就是 ψ (x) + k = 0, 在0 ≤ x ≤ a, ψ (x) − β = 0,
�� 2 �� 2
k=
�
2mE �2
(2.90)
β=
�
2m(V0 − E ) . �2
.
(2.106)
2.4. 一维势垒贯穿
37
在以上计算的基础上, 我们来讨论些物理问题. 首先我们看到S 不等于零! 这意味着我们可以在势垒的右边找到粒子! 这一完 全不同于经典力学的结论称为隧 道 效 应 (tunneling effect). 下面作更详细的分析. 在势垒左边, x < 0区域, 我们可以计算几率流密度j . j= 1 ˆψ − ψ p ˆψ ∗ ), (ψ ∗ p 2m (2.107)
2 sinh2 βa V0 4E (V0 −E )
CHAPTER 2. 一维问题
= =
A + B, (A − B )β.
(2.95)
= =
Байду номын сангаас
Seika , ikSeika
(2.96)
= =
β + ik + R(β − ik ) β − ik + R(β + ik ). (2.97)
= =
eika−βa S (β + ik ) eika+βa S (β − ik ).
2 sin2 αa V0 4E (E −V0 )
(2.111) . (2.112)
我们应该可以观察到所谓的共振透射。当αa = nπ , n = 1, 2, 3, · · · , |S |2 = 1. 如果粒子遇到一个势井，V0 < 0, 会怎样？(2.112)仍然适用。唯一要注意的 是：当E → 0, T → 0.

一维势垒问题总结

一维势垒问题总结

一维势垒问题总结
一维势垒问题是指在一维空间中存在一个势能障碍的物理问题。

该问题涉及到粒子的运动和势能的影响，有着广泛的应用。

一维势垒问题的主要特点是势能障碍的存在。

这个势能障碍可以是有限高度的，也可以是无限高度的。

有限高度的势能障碍表示粒子可以跨越势垒，而无限高度的势能障碍表示粒子无法穿越势垒。

在求解一维势垒问题时，需要考虑的主要因素包括粒子的动能和势能。

根据量子力学的原理，粒子在势垒两侧会存在反射和透射两种情况。

对于势能障碍的高度低于粒子的能量，粒子可以自由穿越势垒，这称为透射现象。

透射的概率可以通过隧道效应来描述，隧道效应可以用量子力学中的波函数来解释。

对于势能障碍的高度高于粒子的能量，粒子会发生反射现象。

在经典力学中，反射的概率可以通过粒子的入射能量和势垒高度之间的关系来计算。

对于无限高度的势能障碍，粒子无法穿越势垒，只能发生反射现象。

这种情况下，粒子的能量必须超过势能障碍的高度才能透过。

一维势垒问题在物理学和化学领域都有广泛的应用。

例如，它可以用于解释原子核中的核反应、电子在导体中的传输等。

总之，一维势垒问题是涉及势能障碍的物理问题，涉及粒子的运动和势能的影响。

求解该问题需要考虑粒子的动能和势能，以及透射和反射两种现象。

一维势垒问题在科学研究中具有重要的应用价值。

16-3 一维势阱和势垒问题

16-3 一维势阱和势垒问题

ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为：
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高 所以粒子不能穿透势壁 理由 因为势壁无限高,所以粒子不能穿透势壁 故势 因为势壁无限高 所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量，E > 0，令 是粒子的总能量， 是粒子的总能量 ， 定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为： 谔方程简化为： d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式 ：
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式 ： ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动， 限高势壁间运动，这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关， 因为系统的势能与时间无关，因此这是一个定 态问题，可以用定态薛定谔方程进行求解。 态问题，可以用定态薛定谔方程进行求解。

一维问题的相关解释

一维问题的相关解释

Asin( n
a
x)
有 n 1 个节点，在
说明粒子在这些节点上出 现的概率为零。对于经典粒子 来说，它在0 x a 内任何 一点都有可能出现。
思考：若 n ，会出现什么情况？
9
二、一维无限深方势阱中的能量本征态(6)
4、束缚态
对一维无限深方势阱：
n
(
x)
2 sin(nx), 0 x a;
eipi r / 的成分，因此，| ( pi ) |2 应该代表粒子具
有动量 pi 的概率。
态叠加原理：量子态可按任意一组正交、归一、完备态分解
15
三、态叠加原理(3)
量子力学基本假设之四
4、将体系的状态波函数 用算符 Fˆ 的本征函数 n
展开，其中：Fˆn nn, Fˆ
cnn cd
E
1 2
mv2
h1gm
hgm
V0
绝对不可能越过势垒，换 句话说：越过势垒的概率 为零！
0
a
E V0
V
(
x)
V0 0,
, 0 x a; x 0, x a.
求解能量本征方程：
[
2
2
V
(r)]
(r )
E
(r )
2m
17
三、方势垒的反射与透射(2)
V0
方程
[
2
2
V (r )] (r )
E (r )
a
|
0
n
(
x)
|2
dx
1
n (x)
Asin( n
a
x)
(0 x a)
| A | 2 / a
归一化波函数为：
n

一维势阱和势垒问题

一维势阱和势垒问题
§16-3 一维势阱和势垒问题
1.一维无限深势阱
一维无限深方势阱是金属中自由电子的简化模型
粒子在势阱内受力为零，势能为零。在阱内自由运 动。在阱外势能为无穷大，在阱壁上受极大的斥力, 不能到阱外。
一维无限深方势阱的数学表达形式 ：
0 (0 x a) U (x) (x 0及x a )
无数峰：量子 经典均匀0分布4 2
a
n4
x
0
ax
n时
量子经典
|n | 2 n很大
En
0
a
一维无限深势阱
En n
n(x)
En ( x)

h2 8ma 2
n2
n (x)
2 sin n x
aa
n(x)

2 sin2( n
aa
x)
0
ax
例1: 证明无限深方势阱中，不同能级的粒子波函数 具有正交性：
0 x a;
0,
x 0, x a.
讨论：
① 粒子的能量
En

2k 2
2

22n2
2 a2
,
n 1,2,3,
粒子的最低能量状态称为基态，则一维无限深方势 阱的基态能量为：
E1
22 2a2
0
————零点能
与零点能相对应的，应存在零点运动。这与经典粒
子的运动是相矛盾的。零点能是微观粒子波动性的表 现，因为“静止的波”是没有意义的。
② 图形
一维无限深方势阱中粒子的能级、波函数和几率密度
（2 sin nx , 0 x a;
a a
0,
x 0, x a. 0
除端点外，

154一维势阱与势垒

154一维势阱与势垒
当a=10-10m时
E 37.7 n2eV
E (2n 1)37.7eV
在这种情况下，相邻能级间的距离是非常大 的，这时电子能量的量子化就明显的表现出来。
29
当n>>1 时 ,能级的相对间隔近似为
En En
2n
h2 8ma2
n2
h2 8ma2
2 n
可见能级的相对间隔 En 随着n的增加成反比地减小。
U
在P区和S区薛定谔方程的形式为
U0
其中
d2 (x)
dx2
k
2
(x)
0
k 2 2E
2
E PQ S
o ax
在Q区粒子应满足下面的方程式
d2 (x)
dx2
2
(x)
0
式中
2
2
2
(U 0
E)
34
用分离变量法求解，得
1 A1eikx B1eikx 2 A2ex B2ex
3 A3eikx
(P区) (Q区) (S区)
nx
A sin( )
x)
2
dx
a 1，得
A 2/a
归一化波函数为
n(x)
2 sin nx , aa
n 1,2,3,
一维无限深方势阱中粒子的能级、波函数和几率密度
n4 E4
n3
E3
n2
E2
E1
x0
n 1
xa
o
(a) n (x) 稳定的驻波能级
(b)
n (x) 2
ax
27
例题 1 设想一电子在无限深势阱，如果势阱宽度分别 为1.0×10-2m和10-10m 。试讨论这两中情况下相邻能 级的能量差。

§第三章 一维问题 §31 一维定态的一些特例 1, 一维方势阱问题

§第三章 一维问题 §31 一维定态的一些特例 1, 一维方势阱问题

§第三章 一维问题§3.1 一维定态的一些特例1, 一维方势阱问题，Landau 与Pauli 的矛盾《无限深方势阱》这是本章第一个例题，也是最简单的对一类物理问题的数学近似模型。

但有关它的动量波函数及其衍生问题却引起过争论，甚至导致严重误解：“量子力学的数学是错的”。

研究一维 Schrodinger 方程，其中位势为(3.1a) 于是定义在整个x 轴上的 Schrodinger 方程现在分为三个区域：第I 区a x -≤，第II 区a x <，第III 区a x ≥。

由于I 区和III 区中()+∞=x V （无穷位势问题见讨论i,），为使 Schrodinger 方程成立，这两个区域中的波函数()x ψ必须为零 —— 即有边界条件()0=x ψ()a x ≥。

说明微观粒子即便具有波动性，也难以渗透进非常高的势垒区里。

于是坐标波函数求解只须对第II 区进行，(3.1b)有时，这里的边界条件被简单地写作()()ψx =0x =a 1。

但由于对阱外情况未作规定，这种提法是含混的。

参见下面有关讨论。

显然，在第II 区x <a 内方程通解为1 这种用法见泡利《物理学讲义》第五卷，详见下面讨论v 的脚注。

()()122ψx =Asin kx +α2mE k =⎧⎪⎨⎛⎫⎪ ⎪⎝⎭⎩这里出现两个待定系数A 、α和一个待定参数k （它的数值将决定阱中粒子的能量）。

为了确定它们，利用两个边界条件()ψ±a =0（加上总几率归一条件，一共也是三个），即()()sin ka +α=0sin -ka +α=0⎧⎪⎨⎪⎩ 由此得n α=ka =π2，n =1,2,3, 。

最后，阱中粒子的能级和波函数分别为(3.2a)(3.2b)这虽然是一个最简单的例子，鉴于存在不少观点分歧，需要作一些讨论说明：i, 无限深方阱的势函数是对实际物理情况作出的近似的数学模写。

因为第一，介质中势能不可能真是无限大；第二，势函数也不可能是严格的阶跃。

一维方势垒

一维方势垒

(k k )s hk3 a A 2 A, (k1 k ) s hk3a 2ik1k3chk3a
2 1 2 2 3 2 3
2ik1k3e C 2 A, 2 2 (k1 k3 ) s hk3a 2ik1k3chk3a
ik1a
2.6 一维方势垒
反射系数和透射系数为：
2 2 (k12 k3 ) s h 2 k3 a R 2 , 2 2 2 2 2 (k1 k3 ) s h k3 a 4k1 k3 2 4k12 k3 T 2 2 2 2 (k1 k3 ) s h 2 k3 a 4k12 k3
2 2 2 1 2 2 2 2 2 2
A
2
透射系数为：
2 C JT 4k12 k2 T 2 2 2 2 2 2 2 J ( k k ) sin k a 4 k A 般情况下，透射系数 T 1 ， 反射系数R 0 ，而这之和为1。这表明，在量 子力学中，即是粒子的能量大于势垒高度，仍 有部分被反射回来。这正是微观粒子具有波动 性的体现。
由第二式可见，一般情况下透射系数 T 1 ， 当 k2 a n 的特定情况下，其透射系数T 1 ， 这种情形下的透射现象叫做 共振透射
2.6 一维方势垒
二、E U 0 的情形
k2 为虚数。但若令k2 ik3 ，则 此时， 2m 2 k3 2 (U 0 E )
系数关系变为
Be
ik2 a ik2 a ik1a Be Ce ik2 a ik1a k2 B e Ck1e
k2 Be
ik2 a
2.6 一维方势垒
可得出 A, C 与 A 关系
2i (k12 k22 )sin k2 a A A, 2 ik2 a 2 ik2 a (k1 k2 ) e (k1 k2 ) e 4k1k2e C A, 2 ik2 a 2 ik2 a (k1 k2 ) e (k1 k2 ) e

52_6半无限深势阱_一维势垒解读

52_6半无限深势阱_一维势垒解读
d 1 ( x ) d 2 ( x ) / 1 ( x ) | x a / 2 ( x ) |xa dx dx
2m 2 (U 0 E )
2
cos(ka) k sin(ka)
cos2 ( ka) 2 U 0 2 1 2 sin ( ka) k E
空气隙
样品
STM工作示意图
16
d变~ 10nm
i 变几十倍，非常灵敏。
竖直分辨本领可达约百分之几 nm； 横向分辨本领与探针、样品材料及绝缘物有关， 在真空中可达0.2nm 技术关键： 1. 消震：多级弹簧，底部铜盘涡流阻尼。 2. 探针尖加工：电化学腐蚀，强电场去污， 针尖只有1~2个原子！ 3. 驱动和到位：利用压电效应的逆效应 —— 电致伸缩，一步一步扫描。 扫描一步0.04nm， 扫描12 ，用0.7s
2 d 2 3 ( x ) E 3 ( x ), 2 2m dx
xa
9
2mE 令： k 2
2
2m(U 0 E ) k 2
2 1
三个区间的薛定谔方程化为
U
d 1 ( x) 2 k 1 ( x ) 0, 2 dx
2
x0
U0
d 2 3 ( x ) 2 k 3 ( x ) 0, 2 dx

2
2mE k 2
2
sin ( ka ) 1或
2
ka
h2 E U0 2 2 8ma 32ma
2 2
( x) Be
x
,
xa
结果说明粒子会出现在x＝a的表层附近
6
§6 一维方势垒 势垒贯穿（隧道效应） U
U ( x ) 0, x 0, x a

第三章 一维势场090909

第三章 一维势场090909

m even m odd
| A | cos
2
得：
|A|
2
1 a

A
1 a
（取实数）
第三章
[小结]
一维问题
由无穷深方势阱问题的求解可以看 出，解S—方程的一般步骤如下：
l l
一、列出各势域上的S—方程； 二、求解S—方程； 未知数和能量本征值；
l四、由归一化条件定出最后一个待定系数（归一化系
（4）由归一化条件定系数 A


|
m
| dx
2

a a
| |
I
| dx
2

a a
|
II m
| dx
2

a
|
III
| dx
2

II m
a
| dx
2 2
2
a a a a
| A | sin
2
m 2a m 2a
xdx 1 xdx 1
2n 1 2a
x
类似 I 中关于 n = m 的讨论可知：
( n 0,1, 2, )
综合 I 、II
Em m
2
结果，最后得：
2
第三章

2 2
一维问题
8a
I

m


III
0 m 2a x
( r , t ) ( r , t )
称波函数具有正宇称（或偶宇称）； 称波函数具有负宇称（或奇宇称）；
( r , t ) ( r , t )
（3）如果在空间反射下，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数，对以上的透射系数的总结，推出了对于任意势垒中透射系数， 并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中，遇到的问题和 值得注意的地方。

在求方势垒波 函数中，首先要知道这是一个什 么样问题，满足什么样的方程， 方程可以写成什么样的形式，在 求解方程中，波函数的形式应该怎样需要怎样的分段，分段的过程中，特别要强调的边界条件问题。

并且验证了概率流密度。

在量子力学中，粒子在势垒附近发生的现象是不一样的，能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射，而能量小于0u 的粒子也会有部分穿过势垒，这在经典力学中是不会发生的。

下面讨论的是一维散射（即在非束缚态下问题，在无穷远处波函数不趋于零）。

重点讨论的是粒子通过势垒的透射和反射，重点在于求出波函数，这就必须求解薛定谔方程，由于)(x U 是与时间无关的，此处是定态薛定谔方程。

定态薛定谔方程通式：ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域：⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h （1） ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注： 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时，通解xq xq eC e C y ---+=21，当0>q 时，通解xq ixq ie C e C y -+=21方程（1）的解可以表示为：⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ （2）定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-，可以看到式子（2）的三式，第一项是左向右传播的平面波，第二项是由右向左传播的平面波，即入射波和反射波。

在a x >区域内，只有入射波，无反射波，故0=d 。

利用波函数及其一阶导数在a x x ==,0连续的边界条件，可得如下:这里的hh )(2,2021u E m k mEk -==；由 ()()()()⎪⎩⎪⎨⎧======02010201x x x x dx x d dx x d x x ψψψψ 得 ⎩⎨⎧-=-+=+ck b k r k a k cb r a 2211 （3）由 ()()()()⎪⎩⎪⎨⎧======a x ax ax a x dx x d dx x d x x 3232ψψψψ ⎪⎩⎪⎨⎧=-=+--aik a ik a ik aik a ik a ik e tk eck e bk te ce be 122122122 （4） 可以写成： ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-c b k k k k r a 1212111111 （5） a ik a ik aik a ik aik te k k c b e e e e 12222211⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--- （6） 由式（5）和式（6）得：aik a ik a ik a ik a ik te e k k k k e k k k k e k k k k ek k k k r a 1222221122112211221121111111141⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛-- （7） 化解得： aik te a k k k k k i a k k k k k i a k r a 122112221122sin )(2sin )(2cos ⎪⎪⎪⎪⎪⎭⎫⎝⎛-+-=⎪⎪⎭⎫ ⎝⎛ 注：概率流密度的定义()ψψψψ∇-∇=**2mi J h； 此处入射波x ik ae 1，透射波x ik te 1，反射波x ik re 1-，分别代入概率流密度()()][21111**dxe a d e a dx e a d ae m i J x ik x ik xik x ik a ---=h ; 化简得：2a mi J a h =，同理2t m i J t h =，2r m i J r h =；注：透射概率流密度与入射概率流密度之比称为透射系数，即a x >区域粒子在单位时间内流过垂直与x 方向的单位面积的数目，与入射粒子在0<x 单位时间内流过垂直与x 方向的单位面积的数目之比。

从得出反射系数22ar J JR a r ==。

ak k kk k a k a k k k k k R 2222112222222112sin )(41cos sin )(41++-=化简的 ()()21222222122222214sinsink k a k k kak k kR +--=(8)同理透射系数T ， ()21222222122214sin4k k a k k kk k T +-=（9）由上式R 和T 之和等于1，证实了入射粒子一部分透射到x>a 区域，另一部分被势垒反射。

（以后要重点关注共振点） 这里常在文献中涉及到是，当...2,1,0,2==n n ak π反射为零，透射系数为1，产生的共振，此时只有透射波没有反射波，这个理解为第一个界面反射的波和第二个界面反射的波相消干涉。

即两个反射波之间有π相位差。

（这里也可以研究概率密2ψ度验证以上的结论） 讨论0u E <的情形，⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dxd m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h 解： ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<<+=<+=----a x te x a x be ae x x re e x x mEix E u m x E u m x mE i x mE i ,)(0,)(0,)(23)(2)(2222100ψψψ 其中)(2,2021E u m k mE k -==；边界条件：⎩⎨⎧-=-+=+bk a k r ik i k ba r 22111 ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---000*112222122t e ik e b a e k e k e e a ik a ik a k a k a k a k ()ak ch k ka k sh k kk k T 2222212222221222144+-=51015200.20.40.60.81.00.5 1.0 1.5 2.0 2.5 3.00.010.020.030.040.050.060.07无论是E>u0,还是E<u0,在同一个图中表示：⎪⎪⎩⎪⎪⎨⎧<->-=)(,))((2)(,))((2i i i i i x u E E x u m i x u E x u E m k h h我的验证过程是用的传递矩阵所求出的透射系数与书上推导出来的做的图是一致的，这里试图找到隧穿共振的点和图，πn a u E m =-2)(2 ，我在编程的过程中验证了一个非常有用简便的方法⎪⎪⎩⎪⎪⎨⎧<->-=)(,))((2)(,))((2i i i i i x u E E x u m i x u E x u E m k h h，这个等式在Mathematica 中可以统一写成h))((2i i x u E m k -=，这是正确的，以后完全不用再分段。

为保证完全正确，下面再进E>u0,a=0.8nm,u0=3eV E<u0,a=0.8nm,u0=3eV51015200.20.40.60.81.0a=0.8nm,u0=3eV一步验证。

双势垒模型设真空中质量为m ，能量为E 的粒子从左方入射，如上图所示的一维两个方势垒中，势垒的势能函数为⎪⎪⎩⎪⎪⎨⎧><<<<<=2211,0,20,10,0)(a x a x a u a x u x x u同样满足常数势垒求薛定谔方程， 当E>u1，u2时；⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧<<=+->=-<<=+-<=-2133232222442221221222211222),()()(2),()(20),()()(20),()(2ax a x E x u x dx d m ax x E x dx d m a x x E x u x dx d m x x E x dx d m ψψψψψψψψψψ解⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧>=<<+=<<+=<+=-------22321)(22)(2231)(21)(212221,)(,)(0,)(0,)(2211a x tex a x a e b e a x a x e b e a x x re ex xmEi x u E m i x u E m i x u E m i x u E m i x mE i x mE iψψψψ令)(2,)(2,222110u E m k u E m k mEk -=-==，可求得：⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-11110011111b a k k r k k⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----222211111212121211111111b a e k e k e e b a e k e k e e a ik a ik a ik a ik a ik a ik a ik a ik ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----222211111212121211111122b a e k e k e e b a e k e k e e a ik a ik a ik a ik a ik a ik a ik a ik ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---00010202222222202222t ek e b a e k e k e e a ik a ik a ik a ik a ik a ik⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛---------00011111202022222222121212121111111101222211111100t e k e e k e k e e e k e k e e e k e k e e k k k k r a ik a ik a ik a ik a ik a ik a ik a ik a ik a ik a ik a ik a ik a ik即有此通式 ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛++-++---++++11111111*21i i L ik i L ik i L ik L ik L ik L ik i L ik L ik i i i b a e k e k e e e e k e e k b a i i ii ii ii i i ii i i ii ⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛+--+=⎪⎪⎭⎫ ⎝⎛++-++++-++-+++++11)(1)(1)(1)(11111)1()1()1()1(*21i i L k k i i i L k k i i i L k k i i i Lk k i ii i i b a e k k e k k e k k e k k b a i i i ii i i i i ii i 注：上式作为通式很重要，一定要牢牢记住，可以为以后的计算省好多时间。