当前位置：文档之家 › 第一章 轴对称图形 复习课

第一章 轴对称图形 复习课

  • 格式：doc
  • 大小：106.23 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

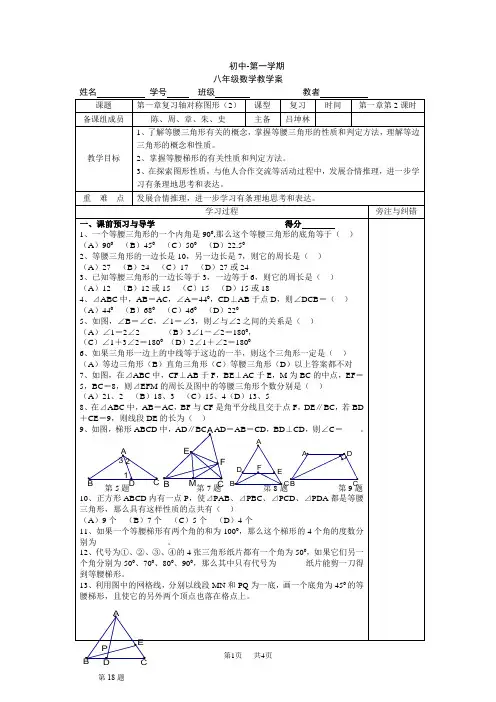
初中数学 第一章轴对称图形复习教学案(苏科版八年级上)

初中数学 第一章轴对称图形复习教学案(苏科版八年级上)

初中-第一学期 八年级数学教学案姓名 学号 班级 教者课题 第一章复习轴对称图形（2）课型 复习 时间 第一章第2课时备课组成员陈、周、章、朱、史 主备吕坤林教学目标1、了解等腰三角形有关的概念，掌握等腰三角形的性质和判定方法，理解等边三角形的概念和性质。

2、掌握等腰梯形的有关性质和判定方法。

3、在探索图形性质，与他人合作交流等活动过程中，发展合情推理，进一步学习有条理地思考和表达。

重 难 点 发展合情推理，进一步学习有条理地思考和表达。

学习过程 旁注与纠错一、课前预习与导学 得分 1、一个等腰三角形的一个内角是900,那么这个等腰三角形的底角等于（ ） （A ）900 （B ）450 （C ）500 （D ）22.502、等腰三角形的一边长是10，另一边长是7，则它的周长是（ ）（A ）27 （B ）24 （C ）17 （D ）27或243、已知等腰三角形的一边长等于3，一边等于6，则它的周长是（ ）（A ）12 （B ）12或15 （C ）15 （D ）15或18 4、⊿ABC 中，AB ＝AC ，∠A ＝440，CD ⊥AB 于点D ，则∠DCB ＝（ ） （A ）440 （B ）680 （C ）460 （D ）2205、如图，∠B ＝∠C ，∠1＝∠3，则∠与∠2之间的关系是（ ）（A ）∠1＝2∠2 （B ）3∠1－∠2＝1800，（C ）∠1＋3∠2＝1800（D ）2∠1＋∠2＝18006、如果三角形一边上的中线等于这边的一半，则这个三角形一定是（ ） （A ）等边三角形（B ）直角三角形（C ）等腰三角形（D ）以上答案都不对7、如图，在⊿ABC 中，CF ⊥AB 于F ，BE ⊥AC 于E ，M 为BC 的中点，EF ＝5，BC ＝8，则⊿EFM 的周长及图中的等腰三角形个数分别是（ ） （A ）21、2 （B ）18、3 （C ）15、4（D ）13、58、在⊿ABC 中，AB ＝AC ，BF 与CF 是角平分线且交于点F ，DE ∥BC ，若BD ＋CE ＝9，则线段DE 的长为（ ） 9、如图，梯形ABCD 中，AD ∥BC ，AD ＝AB ＝CD ，BD ⊥CD ，则∠C ＝____。

第一章轴对称图形复习PPT课件

第一章轴对称图形复习PPT课件

2021/7/23
11
判别等边三角形有哪些方法?
●3个角相等的三角形是等边三角形.
◆有两个角等于600的三角形是等边 三角形.
★有一个角等于600的等腰三角形是 等边三角形.
直角三角形斜边上的中线等于斜边的一半.
2021/7/23
12
⑴等腰三角形的一个内角为70o,那 么另外两内角为_________度
如果把一个图形沿着一条直线折叠直线两旁的部分能够互相重合那么这个图形叫做轴对称图形这条直线叫做对称一轴对称和轴对称图形1概念正方形矩形等边三角形菱形等腰梯形对称轴条数常见图形对称轴的位置长和宽的中垂线两条邻边的中垂线和对角线所在的直线三条边的中垂线对角线直径所在的直线一条底的中垂线所在的直线等腰三角形画出对称轴底边的中垂线是不是轴对称图形线段垂直平分线上的点到线段两端的距离相等
2021/7/23
5
1 .下列图案是几种名车的标志，在这 几个图案中是轴对称图形的共有（ ）
A.1个
2021/7/23
B.2个
C. 3个
D.4个
6
拓展与操作
1.如图，画出△ABC关于直线MN的对称图形.
如右图，四边形ABCD与四边形EFGH关于直
线MN的对称,ACBD交于P,怎样找出点P关于
直线MN的对称点Q?
A
D
F
2021/7/23
B
C
E
27
例7.如图,在梯形ABCD中，AD∥BC，E是 DC的中点，EF⊥AB于点F．
求证：S梯形ABCD=AB×EF．
AD
F
H
E
猜想：EF与HG 的关系
B
CG
平移底,梯形转化成:三角形.
2021/7/23

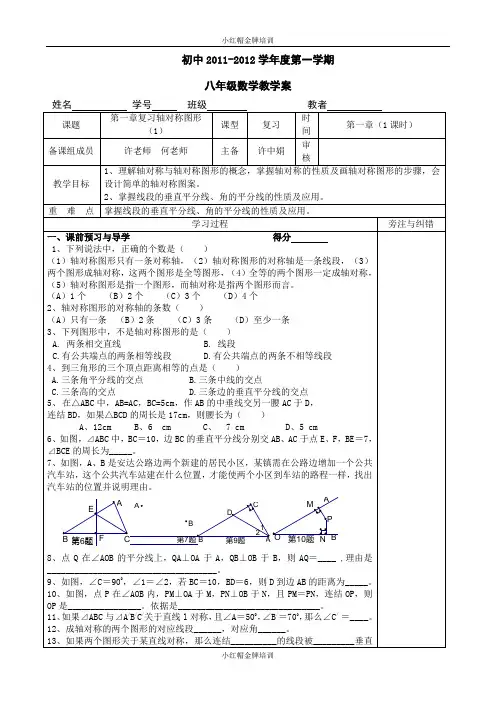
第一章轴对称图形复习教学案(1)(苏科版八年级上)

第一章轴对称图形复习教学案(1)(苏科版八年级上)
（A）1个 （B）2个 （C）3个 （D）4个
2、轴对称图形的对称轴的条数（ ）
（A）只有一条 （B）2条 （C）3条 （D）至少一条
3、下列图形中，不是轴对称图形的是（ ）
A.两条相交直线B.线段
C.有公共端点的两条相等线段D.有公共端点的两条不相等线段
4、到三角形的三个顶点距离相等的点是（ ）
A.三条角平分线的交点B.三条中线的交点
1）当MN满足什么条件时，将长方形ABED以MN为折痕翻折，翻折后能使C点恰好和A点重合；
2）梯形ABMN的面积与梯形CDNM的面积相等吗？为什么？
24、已知直线 及其两侧两点A、B，如图.
（1）在直线 上求一点P，使PA=PB；
（2）在直线 上求一点Q，使 平分∠AQB.
第23题
25、在矩形ABCD中，将△ABC绕AC对折至△AEC位置，CE与AD交于点F，如图.试说明EF=DF.
18、如图，己知AB=AC，DE垂直平分AB交AC、AB于D、E两点，若AB=12cm，BC=10cm,∠A=49º，求△BCE的周长和∠EBC的度数.
19、“西气东输”是造福子孙后代的创世工程，现有两条高速公路l1、l2和两个城镇A、B（如图），准备建一个燃气控制中心站P，使中心站到两条公路距离相等，并且到两个城镇等距离，请你画出中心站的位置。（保留画图痕迹，不写画法）
7、如图，A、B是安达公路边两个新建的居民小区，某镇需在公路边增加一个公共汽车站，这个公共汽车站建在什么位置，才能使两个小区到车站的路程一样，找出汽车站的位置并说明理由。
8、点Q在∠AOB的平分线上，QA⊥OA于A，QB⊥OB于B，则AQ＝____ ,理由是_____________________________________。

轴对称全章复习PPT课件

轴对称全章复习PPT课件
例、如图,在△ABC中,已知AB=AC,∠BAC=90°, D是BC上一点,△DEA等腰直角三角形，∠DAE=90°. 求证：（1）△ABD≌△ACE （2）EC⊥BC
A E
BD
C
第25页/共26页
谢谢您的观看！
第26页/共26页
轴对称的性质
轴
对
轴对称图形
中垂线的性质与判定
称 图
等腰三角形的性质
形
等腰三角形
等腰三角形的判定
等边三角形
含30°角的直角三角形的性质 应
用
第2页/共26页
一、轴对称相关定义和性质。
如果一个图形沿一条直线折叠，直线两旁
的部分能够互相重合，这个图形就叫做轴对称
定 图形，这条直线就是它的对称轴。
义
如果一个图形沿一条直线折叠，如果它能
1、如图（1），在△ABC中，∠BAC=110°，AB、BC 的垂直平分线分别交BC于点D、E，那么∠DAE= 40°.
若BC=15cm， 那么△ADE的周长是15cm .
A
A
B
DE C
图（1）
BD
EC
图（2）
2、如图（2），在△ABC中，AB=AC，∠A=120°， AB的垂直平分线交BC于点D，那么BD∶CD= 1∶2 .
第6页/共26页
四、等腰三角形的性质及判定。
有两边相等的三角形是等腰三角形.
判 定 如果一个三角形中有两个角相等,那
么这两个角所对的边也相等（简写 成“等角对等边”）.
第7页/共26页
五、等边三角形的性质及判定。
⑴等边三角形的三边都相等。
⑵等边三角形的三个内角都相等,并且
性
每一个角都等于60°。

第一章轴对称图形-复习课课件1

第一章轴对称图形-复习课课件1
(2)图②由5张全等的正方形组成，只移动其中 一张纸片，你能使它变成轴对称图形吗？
辨析与思考：
(1)如果一个图形沿着某条直线对折，两侧的图形能够完
全重合，这个图形就是轴对称图形
（）
(2)全等图形不一定是轴对称图形。 （ ）
(3)线段的对称轴是它的垂直平分线
Байду номын сангаас
（）
(4)等边三角形有３条对称轴。
（）
(5)一个角的角平分线就是这个角的对称轴 （ ）
(2)小丽用如图①的直角三角形铁皮，烙一块与铁皮形状、 大小相同的饼。如果烙好一面后就把饼翻身，那么这块 并不能正好落在“锅”中。如图②，小丽将饼切了一刀， 然后将两小块都翻身，结果饼就能正好落在“锅”中了， 这是为什么？
(3)如果用来烙饼的既不是等腰三角形也不是直角三角形 (如图③)，那么烙好一面后，怎样将烙饼翻身，才能使 烙饼仍能正好落在锅中？
20世纪著名数学家赫尔 曼·外 尔所说的，“对称是一 种思想，人们毕生追求，并创造 次序、美丽和完善……”
知识点复习：
轴对称 一个图形沿着某一条直线折叠,
如果它能够与另一个图形______,那么就
说这两个图形成轴对称.这条直线就是
______.两个图形中的对应点叫做
.
轴对称图形 一个图形沿着某条直线对折,
CF⊥BD于F，交DE于G，DF= 1 BC，试
说明∠FCB= 1∠B
2
2
D
F
A
G
B
E
C
本节课小结：
本节课我们复习了哪些知识点？ 你对本节课所复习的知识又有了哪些新的
认识？
设计轴对称图案
图案的对称不但要求图形对称外，有 时颜色也“对称”。

八年级数学上轴对称及轴对称图形(复习课)课件

八年级数学上轴对称及轴对称图形(复习课)课件

A D
C
E
B
4、如图，在△ABC中, ∠ACB=900,AB 的中垂线交BC于E,垂足为 D,∠CAE:∠EAB=3:2,则∠B=___ ． A
D C B
E
5、如图，△ABC中，AB的垂直平分线 分别交AB、BC于点D、E，AC的垂直 平分线分别交AC、BC于点F、G，若 BC=20，则△AEG的周长为多少？
五、巩固习题：
• 1、在等腰△ABC中，若∠A=80°，则
∠B=_______. • 2、在等腰△ABC中，若周长为8cm，且 AB=3cm，则BC=_________.
• 3、如图，在△ABC中，边AB
的垂直平分线分别交AB、BC 于点D、E，且AE平分 ∠BAC=80°若∠B=30 ° ， 则∠C=_______.
△ABC的一个顶点的一条直线，把 △ABC分成两个小三角形，如果这 两个小三角形也是等腰三角形，问 △ABC顶角的度数是多少？
自主探究
享受学习
第1章：轴对称及轴对称图形
（复习课）
竹条实验中学
一、知识结构
轴对称及轴对称图形
————————————————————
线 段
角
等 腰 三 角 形
等 边 三 角 形
二、知识点回顾： 1、轴对称：如果把一个图形沿着某 一条直线折叠后，能够与另一个图形 重合，那么这两个图形关于这条直线 成轴对称。 2、轴对称图形：把一个图形沿一条直线
讲练平台 例1：如图，如果△ACD的周长为17cm， △ABC的周长为25cm，DE垂直平分线 B E 段BC，根据这些条件，你可以求出哪 条线段的长?
D
A
C
思路点拨：
（1）△ACD的周长＝AD ＋CD＋AC＝17； （2）△ABC的周长＝AB＋AC＋BC＝25； （3）由DE是BC的垂直平分线得：BD＝CD；所以AD＋CD＝ AD＋BD＝AB。

八上 第一章 轴对称图形 复习课

八上 第一章 轴对称图形 复习课

（A）1个
（B）2个
（C）3个
（D）4个
2. 右图是从镜中看到的一串数字，这串数字 应为 .
（第 8 题）
苏州市吴中区木渎实验中学
3.如图，在△ABC中，∠B＝90°，∠A＝36°， AC的垂直平分线MN与AB交于点D，则∠BCD的 度数是____________.
A N D M B C
苏州市吴中区木渎实验中学
苏州市吴中区木渎实验中学
三、【典型例题】 例1、 已知△ABC中，AB=AC=10，DE垂直平分AB，交 AC于E，已知BEC的周长是16. 求ABC的周长.
.
苏州市吴中区木渎实验中学
例2、如图，已知D、E两点在线段BC上，AB＝AC， AD＝AE，试说明BD=CE的理由?
A
B
苏州市吴中区木渎形ABCD中，AD∥BC，对角线AC、BD 相交于点O． 试说明：AO＝DO．
苏州市吴中区木渎实验中学
再见
苏州市吴中区木渎实验中学
请各位专家批评指正！
苏州市吴中区木渎实验中学
苏州市吴中区木渎实验中学
4．已知AB垂直平分CD，AC=6cm,BD=4cm，则四边形 ADBC的周长是 .
5．如图，以正方形ABCD的一边CD为边向形外作等 边三角形CDE，则∠AEB= .
苏州市吴中区木渎实验中学
6. 等腰三角形ABC中，（1）若∠A=80°，则∠B= °； （2）若周长为8cm，AB=3cm，则BC= cm 7.等腰梯形的腰长为2，上、下底之和为10且有一底角 为60°，则它的两底长分别为____________．
苏州市吴中区木渎实验中学
6.等腰三角形的性质：等腰三角形的 等腰三角形的 、 互相重合. 7．直角三角形斜边上的中线 .

轴对称及轴对称图形(复习课)

轴对称及轴对称图形(复习课)
A 10 D 8 -x 10 6 F 8 -x 4 E x C
8 B
⒊如图,在梯形ABCD中，AD∥BC， 如图,在梯形ABCD中 AD∥BC， ABCD DC的中点 EF⊥AB于点 的中点， 于点F E是DC的中点，EF⊥AB于点F． 求证：S梯形ABCD=AB×EF． 求证： =AB×EF．
A F E D
B
C
G
平移底,梯形转化成:三角形. 平移底,梯形转化成:三角形.
5．在梯形ABCD中，AB∥DC，AD＝ 在梯形ABCD中 AB∥DC，AD＝ ABCD BC，AB=1，DC=5，AC⊥BD，BE⊥CD， BC，AB=1，DC=5，AC⊥BD，BE⊥CD， 则梯形的面积= 则梯形的面积= ．
A B
D
E
C
F
6．如图,梯形ABCD中，AD∥BC，E、F 如图,梯形ABCD中 AD∥BC， ABCD 分别是AD BC的中点,∠B+∠C=90° AD、 的中点,∠B+∠C=90 分别是AD、BC的中点,∠B+∠C=90°， 请说明EF= （BC-AD）． 请说明EF= 1 BC-AD）．
D C B
E
5、如图，△ABC中，AB的垂直平分线 如图， ABC中 分别交AB BC于点 AB、 于点D AC的垂直 分别交AB、BC于点D、E，AC的垂直 平分线分别交AC BC于点 AC、 于点F 平分线分别交AC、BC于点F、G，若 BC=20， AEG的周长为多少 的周长为多少？ BC=20，则△AEG的周长为多少？
A
F
N E
B M
C
10、已知△ABC是等腰三角形，过 10、已知 ABC是等腰三角形，过
△ABC的一个顶点的一条直线，把 ABC的一个顶点的一条直线，把 △ABC分成两个小三角形，如果这 ABC分成两个小三角形，如果这 两个小三角形也是等腰三角形，问 △ABC顶角的度数是多少？ ABC顶角的度数是多少？

八年级数学上册 第一章轴对称图形复习课课件 苏科版

八年级数学上册 第一章轴对称图形复习课课件 苏科版
O B
【知识梳理】 3．角的对称轴是 ， (1)角平分线上的点到____________的距离相等； (2)角的内部到__________距离相等的点，在___ ________________;
【热身练习】
4、（1）若等腰三角形的一个角为50°，则其 50 °，80°或65°，65． ° 它两个角的度数为 ________________ （2）在△ABC中，∠A＝80°，当∠B＝ 80°或20°或50° 时，△ABC是等 ________________ 腰三角形。
【热身练习】
5、等边△ABC中，点F在△ABC内，点D、E 分别在边BC、AC上，且BD=CE, 则 60 ∠AFE=______ °
【知识梳理】
5.等边三角形有___条对称轴，对称轴是____________ 等边三角形的性质： （1）具有___________的所有性质; （2）等边三角形的三条边都____，三个角都等于___; 等边三角形的判定： ⑴ 都相等的三角形是等边三角形； ⑵ 都相等的三角形是等边三角形； ⑶有一个角是 的等腰三角形是等边三角形.
6、如图，梯形ABCD中，AD‖BC,若∠A=120°, 60 °∠D=______ 120 ° ∠C=60°,则∠B=_____ 等腰 梯形 梯形ABCD是_______
A
.
D C
B
【知识梳理】
6.等腰梯形的对称轴是__________________;
等腰梯形的性质：
（1）等腰梯形_________________相等；
（2）等腰梯形_________________相等；
等腰梯形的判定： ______________________是等腰梯形；
二、【大展拳脚】 1、ቤተ መጻሕፍቲ ባይዱ图是4×4正方形网络，其中已有3个小方 格涂成了黑色。现在要从其余13个白色小方 格中选出一个也涂成黑色，使黑色部分成为 3 个. 轴对称图形，这样的白色小方格有_____

第一章复习课(第一课时)

第一章复习课(第一课时)

1.在下面四个图案中，如果不考虑图中的文字和字母， 那么不是轴对称图形的是（ ）
2.在下列四个图案中，既是轴对称图形，又是中心 对称图形的是( )
3.在平面直角坐标系中，请按下列要求分别作出变换 后的图形（图中每个小正方形的边长为个单位）： （1）向右平移个单位；（2）关于轴对称； （3）绕点顺时针方向旋转．
第一章 轴对称图形
——— 轴对称及轴对称图形的意义以及折叠问题
上峰中学：程志关
1．轴对称： 2．轴对称图形： 3．轴对称的性质： 4．简单的轴对称图形： 线段：有两条对称轴：线段所在直线和线段中垂线． 角：有一条对称轴：该角的平分线所在的直线． 等腰(非等边）三角形：有一条对称轴，底边中垂线． 等边三角形：有三条对称轴：每条边的中垂线． 等腰梯形：过两底中点的直线 5.图形对称轴的条数： 正n边形有n条对称轴 圆有无数条对称轴。
考点讲解： 考点讲解：
常见的折叠问题有两种类型： 常见的折叠问题有两种类型：一种是将一 个图形沿着某一条直线折叠到另一个位置， 个图形沿着某一条直线折叠到另一个位置，这 时候，这条直线两旁的图形全等； 时候，这条直线两旁的图形全等；另一种是将 一个图形沿着某一条直线折叠，使两个点重合， 一个图形沿着某一条直线折叠，使两个点重合， 此时， 此时，这折痕所在的直线是这两点连线的垂直 平分线。 平分线。
1．已知：点A、B分别在直线l的同侧，在直线l上 找一点P，使PA+PB最短。
D C A B l

A B A P B
变形1：正方形ABCD中，点E是AB边上的一点，在对角 线AC上找一点P，使PA+PB最短。 变形2：已知点A（1，6）、点B（6，4），在x轴和y轴上 各找一点C、D，使四边形ACDB的周长最短。

第一章轴对称图形基础知识复习讲义

第一章轴对称图形基础知识复习讲义

第一章轴对称图形基础知识复习讲义【知识点1】轴对称与轴对称图形概念：轴对称与轴对称图形的区别和联系：轴对称图形的对称轴：〖基础回顾〗1、判断下图是否为轴对称图形，如果是请画出对称轴。

【知识点2】轴对称的性质：；。

轴对称图形的画法：成轴对称的两个图形的任何部分也成〖基础回顾〗1、所示，画出△ABC关于直线MN的轴对称图形.2、两个三角形关于某条直线对称，∠1＝110,∠2＝46°,则x＝ .3、从地面小水洼观察到一辆小汽车的车牌号为如图，它的实际号是什么。

【知识点3】利用轴对称的性质，设计轴对称图案〖基础回顾〗由小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为一个轴对称图形。

方法1 方法2 方法3【知识点 4】 线段的轴对称性 ：线段是 ，对称轴是 。

结论1： 。

结论2： 。

线段垂直平分线的作法：〖基础回顾〗1、 △ABC 中，DE 垂直平分AC ，与AC 交于E ，与BC 交于D ， ∠C=150, ∠BAD=600，则△ABC 是__________三角形.2、 AB=AC=4cm ，∠A=40°，点A 和点B 关于直线l 对称，AC 与 L 相交于点D ，则∠C=_________，△BDC 的周长是________.【知识点 5】 角轴对称性：角是 图形, 对称轴是 。

角平分线上点的性质：判断点在角平分线上： 〖基础回顾〗1、 如图，在△ABC ，∠C=900，AD 平分∠BAC.，若CD=6， 则点D 到AB 的距离是 。

2、 P 是∠AOB 的平分线上的一个点，PC ⊥AO 于C ，PD ⊥OB 于D ， 写出图中一组相等的线段________【知识点 6】 线段、角轴对称性的应用lABPCDO〖基础回顾〗1、 现有三个村庄甲、乙、丙，现要新建一个水泵站P ，使它到三个村庄 的距离相等，应建在何处？（画出点P 的位置）2、 直线MN 表示一条小河的河边，一牧民在点A 处放马，现在要到河边去饮水，然后回到帐篷点B 处（A 、B 在小河同旁）。

第一章轴对称图形(复习课)079PPT课件

第一章轴对称图形(复习课)079PPT课件
①在BC上取一点D,使BD<CD,连结AD; ②作线段AF,使AF与AB关于AD所在的直线对称; ③作线段AE,使E在BC上,且AF与AC关于AE所在的
直线对称; ④连结DF,EF. (2)通过观察和测量,猜想△DEF是什么三角形.
等腰三角形、梯形的 轴对称性
回顾与复习
等腰三角形的性质： A
= （
P
且PC＝PD
O
∴点P在∠AOB的平分线上．
DB
简单应用
1. 指出下列图案是否是轴对称图形， 如果是请指出有几条对称轴
（5）
（6）
简单应用
2. 下列说法正确的是( B )
⑴ 全等的两个图形一定对称.
⑵ 成轴对称的两个图形一定全等. √
⑶ 若两个图形关于某直线对称,则它们 的对应点一定位于对称轴的两侧.
线段的垂直平分线 上的点到线段两端 的距离相等．
A
·P
a
B
练：《补充》/17（1）
动脑筋
12 如图,要在河边
修建一个水泵站, 向张庄、李庄送水. 修
在河边什么地方,可使使用的水管B最短？
A
∟
· ·P
a
把问题转化成第10题的形式画图。
练：《补充》/17（2） 课本38页/9
练一练
《课本》37-38页 复习巩固/1.2.3.4.5，9
4
形，首先应确定 对称轴，然后找
·D2
C·
出对称点。且点D 必须在格点上
·A ·B
综上所述：
·D 3
·D1
方格纸中符合要求的点D有4个。
8.分别画出（1）（2）（3）中,已知△ABC 关于直线l 的对称△A′B′C′
l
A
∟

轴对称复习课课件

轴对称复习课课件
1 如何判断一个形状是否具有轴对称性？
通过观察图形是否可以折叠或旋转成与自身完全重合的形状来判断是否具有轴对称性。
知识点三：轴对称在几何变换中的应用
在平对称来确定平移后的位置。
轴对称可以帮助确定旋转后的位 置。
通过轴对称可以实现等比例的缩 放。
轴对称在几何变换中的应用十分广泛，能够帮助我们更好地理解和操作图形。
如何应用轴对称完成各 种几何变换？
通过利用轴对称的性质和特 点，我们可以更轻松地完成 平移、旋转和缩放等几何变 换。
轴对称是什么，以及它 的性质和应用？
轴对称是一种图形的对称性 质，具有相等性、对称性、 可叠加性和保角性等特点， 并在日常生活和几何变换中 得到广泛应用。
轴对称复习课ppt课件
本课件将带您复习轴对称的重要概念和性质，并探讨其在几何变换和日常生 活中的应用。
知识点一：轴对称的定义及性质
什么是轴对称？
轴对称是指一个图形可以通过一条直线作为轴进 行对称，两侧完全相同。
轴对称的性质有哪些？
轴对称的图形具有对称性、相等性、可叠加性和 保角性等特点。
知识点二：轴对称的判断
知识点四：轴对称的作图方法
如何通过轴对称画出对称图形？
通过找到图形的轴对称中心，结合对称性质来作图。
知识点五：轴对称的应用
轴对称在日常生活中的应用举例
1. 建筑物的对称设计 2. 对称的艺术品和装饰品 3. 自然界中的轴对称形状
总结
轴对称是何时使用的几 何工具？
轴对称是一种用于描述和操 作图形的重要几何工具。

第一章轴对称和轴对称图形复习课

第一章轴对称和轴对称图形复习课

第一章轴对称和轴对称图形复习课（1）八年级数学组学习目标：能总体把握轴对称和轴对称图形的概念、性质；能理解掌握几个常见的轴对称图形的性质和判定并会灵活解题。

学习重难点：轴对称的性质和几个简单的轴对称图形的性质，是这部分的重点知识，应引起足够的重视。

学习过程：（一）知识概况本章着重学习轴对称的概念，性质，轴对称的作图，应用，以及轴对称图形和几个常见的轴对称图形的性质和判定。

1、概念如果把一个图形沿着某一条直线（）后，能够与另一个图形重合，那么这两个图形关于这条直线（），这条直线叫做（），两个图形中的对应点叫做（）。

如果把一个图形沿着一条直线（），直线两旁的部分能够互相重合，那么这个图形叫做（），这条直线叫做（）。

2、轴对称的性质：（1）（2）（二）几个常见的轴对称图形的性质1、线段线段是轴对称图形，它有两条对称轴，它的对称轴是，和。

线段垂直平分线上的点到线段两端的距离相等的点2、角：角是轴对称图形，它的对称轴是。

角平分线上的点；到角的两边的距离相等的点。

3、等腰三角形等边三角形4、等腰梯形从对称的角度理解等腰三角形和等腰梯形的性质和识别方法。

5、正多边形6、圆（三）小练笔1、下列图形中：①平行四边形；②有一个角是30°的直角三角形；③长方形；④等腰三角形. 其中是轴对称图形有（）个A．1个B．2个C．3个D．4个2、如图，下列图案是我国几家银行的标志，其中是轴对称图形的有（）A、1个B、2个C、3个D、4个3、下列命题中：①两个全等三角形合在一起是一个轴对称图形；②等腰三角形的对称轴是底边上的中线；③等边三角形一边上的高就是这边的垂直平分线；④一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形. 正确的说法有（）个A．1个B．2个C．3个D．4个（四）例题点拨例1：如图，如果△ACD的周长为17cm，△ABC的周长为25cm，根据这些条件，你能求出ＢＣ的长吗?例2：如图，AD是△ABC的中线，∠ADC＝60°，把△ADC沿直线AD折过来，C落在C′的位置，（1）在图中找出点C′，连结BC′；（2）如果BC＝4，求BC′的长。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章轴对称图形复习课
学习目标：
1、回顾和整理本章所学知识，用自己喜欢的方式进行总结的归纳，构建本章知识结构框架，使
所学知识系统化；
2、进一步巩固轴对称性质和简单的轴对称图形——线段、角、等腰三角形、等边三角形、等
腰梯形的性质，并能运用这些性质解决问题；
学习重点:轴对称图形的性质，以及运用于解题
学习难点:有条理地表达，熟练地运用已知结论解决问题
学习过程:
一、【知识梳理】
1. ，那么称这个图形是轴对称图形.
2．线段的对称轴是，线段的垂直平分线有什么性质？
3．角的对称轴是，角平分线有什么性质？
4.等腰三角形的判定：有相等的三角形是等腰三角形；有相等的三角形是等腰三角形
5.等边三角形的判定：都相等的三角形是等边三角形；都相等的三角形是等边三角形；有一个角是的等腰三角形是等边三角形.
6.等腰三角形的性质：等腰三角形的相等；等腰三角形的、、互相重合.
7．直角三角形斜边上的中线 .
8.等腰梯形的性质：（1）边：；（2）角：；
（3）对角线：.
9.等腰梯形的判定： .
二、【热身练习】
1．下列图形中，轴对称图形有（）．
（A ）1个 （B ）2个 （C ）3个 （D ）4个
2. 右图是从镜中看到的一串数字，这串数字应为 .
3.如右图，在△ABC 中，∠B ＝90°，∠A ＝36°，AC 的垂直平分线MN 与AB 交于点D ，则∠BCD 的度数是____________. 4．已知AB 垂直平分CD ，AC=6cm,BD=4cm ，则四边形ADBC 的周长是 .
5．如图，以正方形ABCD 的一边CD 为边向形外作等边三角形CDE ，则∠AEB= .
6. 等腰三角形ABC 中，（1）若∠A=80°，则∠B= °；
（2）若周长为8cm ，AB=3cm ，则BC= cm
7.等腰梯形的腰长为2，上、下底之和为10且有一底角为60°，则它的两底长分别为____________．
三、【典型例题】
例1、已知∆ABC 中，AB=AC=10，DE 垂直平分AB ，交AC 于E ，已知∆BEC 的周长是16.求∆ABC 的周长.
例2、如图，已知D 、E 两点在线段BC 上，AB ＝AC ，AD ＝AE ，试说明BD=CE 的理由?
B C D N M A
A B C
E
D
例3、如图，等腰梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ．
试说明：AO ＝DO ．
测试题
1.下列图形不是轴对称图形的是 （ ）
A 、有两个外角相等的三角形.
B 、有一个内角为45°的直角三角形.
C 、有一个内角为60°的等腰三角形.
D 、有一个内角为40°的直角三角形.
2．下列命题中，正确的是 ( )
A ．等腰三角形底边上的中线就是底边的垂直平分线
B ．等腰三角形的对称轴是底边上的高
C ．一条线段可看作是以它的垂直平分线为轴的轴对称图形
D ．等腰三角形的对称轴就是顶角平分线
3．下列说法正确的是 ( )
A ．等腰梯形的对角线互相平分
B ．有两个角相等的梯形是等腰梯形
C ．对角线相等的四边形是等腰梯形
D ．等腰梯形的对角线相等
4.如果等腰三角形两边长是6㎝和3㎝，那么它的周长是 （
） A 、9㎝ B 、12㎝ C 、12㎝或15㎝ D 、15㎝
5.等腰三角形是 对称图形，它至少有 条对称轴.
6.若等腰三角形的一个角为50°，则其他两个角的度数为________________．
7.等腰梯形的腰长为12cm ，上底长为15cm ，上底与腰的夹角为120°，则下底长
为 cm ．
8.如图，在梯形ABCD 中，AD ∥BC ，AB ＝CD ，∠A ＝120°，对角线BD 平分
∠ABC ，则∠BDC 的度数是 ；又若AD ＝5，则BC ＝ ．
O
C
D
A B D E A
9.如图，△ABC 中，AB =AC ，∠A =36°，AB 的中垂线DE 交AC 于D ，交AB 于E ，下述结论：
（1）BD 平分∠ABC ；（2）AD =BD =BC ；（3）△BDC 的周长等于AB +BC ；（4）D 是AC 中点.其中正确的命题序号是 .
10.在△ABC 中，∠C =90°，DE 垂直平分斜边AB ，分别交AB ，BC 于D ，E .若∠CAE = ∠B +30°，求∠AEB .
11如图，已知：△ABC 中，BD 、CE 分别是AC 、AB 边上的高，G 、F 分别是BC 、DE 的中点.试探索FG 与DE 的关系.
12.如图，AD 平分∠BAC ，
EF 垂直平分AD 交BC 的延长线于F ，连结AF.求证：∠B=∠CAF.
F E D C B
A E
B D
C A G F E
D C B
A · ·。