当前位置：文档之家 › 最新电磁感应-麦克斯韦电磁场理论ppt课件

最新电磁感应-麦克斯韦电磁场理论ppt课件

  • 格式：ppt
  • 大小：3.52 MB
  • 文档页数：71

下载文档原格式

  / 71

合集下载

麦克斯韦电磁理论电磁学.ppt

麦克斯韦电磁理论电磁学.ppt

电位移通量和位移电流
引入电位移通量：通过任一曲面S的电位移通
量。
D D • d S
由此，麦克斯韦S 定义了位移电流ID和电流密度 jD（电位移矢量的时间变化率）：
ID
d D dt
S
D •dS t
S
jD • d S
传导电流和位移电流合起来称为全电流。
I
S
j0
•
dS
S
D t
•
dS
S
(
j0
电磁波和光波是性质相同的波，因此v 麦1/ 克0斯0 韦 预言光就是电磁波。
§10.3.2定态波动方程
讨论在介质中的情况：一般介质的介电常数和磁导率 都是随电磁波的频率而变的，这种现象称为介质的色 散。
对于一般的电磁场，无法推导出电场和磁场的波动方 程，但在很多实际情况下，电磁场的激发源往往以大 致确定的频率作简谐振动，因而辐射的电磁波也以相 同频率作简谐振动，这种以一定频率作简谐振动的波， 称为定态电磁波或单色波。
代入自由空间的麦克斯韦方程组，并消去共同因子，
可得：
E j H
H j E
• E 0
• H 0
由此可得一定频率下电磁波的基本方程：
2 E k2 E 0
又称为Helmholtz方程，式中 k
总结起来，对在介质中传播的频率一定的单色 电磁波，麦克斯韦方程组可化为：
一般情况下，平面电磁波的表达式为：
E(x,t) E0e j(k•rt) 式中，k是沿电磁波传播方向的一个常矢量，
称为波矢，大小为：
k 2 /
电磁波的电场波动是横波：
由
• E E0 • e j(k•rt) jk • E 0
可得 k • E 0

麦克斯韦电磁场理论简介课件

麦克斯韦电磁场理论简介课件

全电流连续
I
ID
R
全电流连续不中断的，构成闭合回路
•麦克斯韦电磁场理论简介
全电流安培环路定理
H dl L
I传导 ID
位移电流
ID
dD
dt
d dt
D dS
S
D
dS
S t
讨论：
1. 传导电流：电荷定向运动
2. 若传导电流为零
H
位移电流：变化的电场
dl
D
dS
L
S t
产生磁场
变化电场
感生电场与变化磁场间的关系
L EV dl
B dS S t
感生电场
变化磁场
电磁波的产生 •麦克斯韦电磁场理论简介
三、位移电流的性质
1.位移电流 ID 的方向和 H
服从右螺旋关系
I dD
dt
H
2.位移电流与传导电流不同之处
位移电流
传导电流
实质 焦耳热
变化的电场 无
电荷定向运动 存在
主要存在于 真空、介质中
导体
•麦克斯韦电磁场理论简介
例 设平行板电容器极板为圆板，半径为R ，两极板间距为d,
用缓变电流IC ,对电容器充电，
求 P 点处的磁感应强度。
IC
解 极板间位移电流
ID IC
+ ++
P.
++
r
---
++
--
++
--
+-
D
由全电流安培环路定理
H L
dl
I全
I全
πr 2
ID R2
非稳恒电流

电磁感应-麦克斯韦电磁场理论

电磁感应-麦克斯韦电磁场理论

dB dt
导体
• 涡电流的机械效应(磁阻尼摆) • 涡电流的热效应
电磁灶
第24页 共48页
§13.4 自感和互感
13.4.1 自感 • 自感现象
因回路中电流变化,引起穿 过回路包围面积的全磁通变 化,从而在回路自身中产生感 生电动势的现象叫自感现象. • 自感系数
B I, 又 Ψ B Ψ I
1 12
2 21
• 互感系数
I1 I2
21 N221 M21I1
M12 M21 M 单位: 亨利(H)
M 称为互感系数简称互感.
12 N112 M12I2
第29页 共48页
• 互感电动势
根据法拉第电磁感应定律:
21
dΨ 21 dt
(M
dI1 dt
I1
dM dt
)
若M 保持不变
12
B
E内
E感 半 径 Oa Oc 0
o
E外
Oac Oa ac Oc ac
Rh
通过 Oac 的磁通量:
a
E内 b
c
Φm
B dS
S
B(SOab
S扇)
B(3
3 π R2) 12
dΦm 3 3 π R2 dB a () , c ( )
dt
12
dt
第22页 共48页
例题9. 某空间区域存在垂直向里且随时间变化的非均匀磁
场B=kxcost. 其中有一弯成角的金属框COD,OD与x轴重
合, 一导体棒沿x方向以速度v匀速运动. 设t =0时x =0, 求框
内的感应电动势. 解: 设某时刻导体棒位于l 处
y B
C
任取 dS ydx x tan dx

电磁感应与麦克斯韦方程组PPT课件

电磁感应与麦克斯韦方程组PPT课件

E
L
间变化 。感生电场具 有柱对称分布。
E
E 当r < R 时
当r>R 时0Βιβλιοθήκη Rr涡电流
涡电流是电荷在涡电场的作用下形成的 I 应用:用于金属熔炼,电磁灶,真空技术等 涡电流的危害与防止:变压器铁损.
电磁阻尼的应用
I
vF
实物演示 电磁跳环
I
I' I'
I
回顾与小结：两条思路
感生电场的性质:
(1)感生电场也同电场一样对 电荷有作用力 F qE
(2)感生L电E感场生源 d于l 变化S的Bt磁场dS
(3)对照静电场的环路定律: L E静电 dl 0
左旋!
E
B t
可见感生电场是不同于静电场的另一种电场.
(4)感生电场是非保守力场,是涡旋场,通常称为有旋电场. 感生电场的场线是无头无尾的闭合曲线。有旋,无源!
适用于一切产生感应电动 势的回路.
适用于切割磁力线的导体
回路中感应电动势方向的判断：
d 0 与回路绕行方向相反
dt
L
d 0 与回路绕行方向相同
dt
一段导体中动生电动势方向的判断：
等——能量守恒.
c
aB I
vl
b
(4)在产生动生电动势时是否出现了洛仑兹力作功的 问题?
洛伦兹力作功为零实质上表示了能量的转化和守恒。 它起了能量转换者的作用，一方面接受外力的功，同 时驱动电荷运动作功。
电移子动在的导 两线 个中 运参 动与.速随度导为线的运u动 和v 在导 线内
F e(u v ) B
d
ldx
2 x
N Il ln d a
2
d
L

《电磁场理论》课件

《电磁场理论》课件
《电磁场理论》PPT课件
探索电磁场的奇妙世界。从电磁场的基本概念出发，深入了解麦克斯韦方程 组的原理，并探究电场和磁场的相互作用。
电磁场的基本概念
1 电磁场的定义
介绍电磁场的基本概念和特性，包括电场和磁场的形成和作用。
2 电磁场的方程
了解麦克斯韦方程组，掌握其含义并探索其丰富的物理意义。
3 场强和场线
电场和磁场的相互作用
洛伦兹力
探讨洛伦兹力的作用机制和应用，以及电磁场与带电粒子之间的相互作用。
电磁感应
解释电磁感应的原理和应用，研究磁场变化对电流和电动势的影响。
电磁波的产生和传播
电磁波的产生
深入了解电磁波的产生机制，探究电场和磁场的交 替在空间中的传播特性，包括传播速度、 衰减和反射等现象。
深入了解电磁感应在电动机、变压器等
电磁波的应用
2
设备中的应用原理和工作机制。
探索电磁波在通信、遥感和医学等领域
的广泛应用和前沿技术。
3
磁共振成像
介绍磁共振成像技术的原理和应用，探 究其在医学和科研领域的重要性。
总结和展望
总结电磁场理论的核心概念和主要内容，并展望未来电磁场理论的发展方向和前景。
解释电磁场强度的概念和场线的作用，以及如何分析和表示电磁场的分布情况。
麦克斯韦方程组的介绍
1
高斯定律
详细阐述高斯定律的原理和应用，探讨电场和磁场的产生和分布规律。
2
法拉第定律
深入理解法拉第定律，包括电磁感应的原理、电动势的产生和磁场变化的影响。
3
安培定律
解释安培定律的含义和应用，了解电流和磁场的相互作用及其影响。
电磁场的能量和动量
1 能量守恒定律
探究电磁场能量的来源和 转化，以及能量守恒定律 在电磁场中的应用。

麦克斯韦电磁理论和电磁波ppt

麦克斯韦电磁理论和电磁波ppt

-
+ + + + + +
D
dq d ( S ) d dD I S S dt dt dt dt
第八章 — 麦克斯韦电磁理论和电磁波
dD+σ -σ - dt + - + - + + - + + D S S
3
§1 麦克斯韦电磁理论
2、麦克斯韦位移电流假说 变化的电场可以等效成一种电流，叫做位移电流。位移 电流密度等于电位移矢量对时间的变化率。即：
第八章 — 麦克斯韦电磁理论和电磁波
5
§1 麦克斯韦电磁理论
二、麦克斯韦方程组
1、积分形式
E E静电 E感生 D D静电 D感生
通量 D静电 dS 0dV S V D感生 dS 0
S
B B稳恒 B位移 H H传导 H位移
《电磁学》 多媒体教学课件
西安电子科技大学理学院
第八章 麦克斯韦电磁理论和电磁波
§1 麦克斯韦电磁理论 §2 电磁波 §3 电磁场的能流密度
第八章 — 麦克斯韦电磁理论和电磁波
2
§1 麦克斯韦电磁理论
一、位移电流
1、问题分析
H dl ?
l
在非恒定电流产生的磁场中，磁 场强度的环流与如何选取以闭合 回路为边界的曲面有关。选取不 同的曲面，环流有不同的值。 讨论：
在确定的边界条件下联合解上述方程，原则上可解 决电磁场的一般问题。 2. 爱因斯坦相对论的重要实验基础
第八章 — 麦克斯韦电磁理论和电磁波
13
§2 电磁波
3. 预言电磁波的存在 由微分方程出发 在各向同性介质中 且在 J 0 0

第7电磁感应与Maxwell方程组PPT课件

第7电磁感应与Maxwell方程组PPT课件
在导线旁共面一矩形线圈，求任一瞬间线圈中的
感应电动势。
[解]： B 0 I 2 r
顺时针为矩形线圈的绕
d
b
行正方向，
ds＝ldr
I
dΦ B cos 00 ds 0 I l dr 2 r
r dr 9
Φ dБайду номын сангаас= db 0 I ldr
d 2 r
d
b
0I0l sin t ln d b I
2
应用 热效应、电磁阻尼效应.
24
25
二、感生电场与静电场的区别：
The Deferences Between Induced Electric Field and Electrostatic Field
感生电场
静电场
1.涡旋场，电力线是闭 合的；
1.无旋场，电力线不 闭合；
2. E感 dl 0
eB
而
d( mv ) dt
eE感
e
2 R
ddt（ d R2B） －(2)
式中 B 为电子圆形轨道区域内的平均磁感应强度。
36
对（1）求导得：
dB dt
1 eR
ddt（mv）－－（3）
比较（2）、（3）两式，得 dB 1 dB
dt 2 dt
B 1B 2
－－B必须满足一定条件
37
§7.4 自感 (self-induction) 一、自感现象 (self-induction phenomenon) 当回路中电流随时间变化时，通过回路自身
4）统一积分变量，确定积分上、下限，求出ε；
5）根据积分的正负或由 v B 的方向确定ε
的正方向。 15
[例7-2]一长直载流导线，通有电流I，其旁共面

《麦克斯韦电磁理论》课件

《麦克斯韦电磁理论》课件

电磁波的概念
阐述电磁波的定义、特征和基本性质，包括振幅、波长、频率等。
电磁波的传播特性
探究电磁波在真空和介质中的传播特性，并解释折射、反射和干涉现象。
电磁波的波长和频率
波长 频率
解释波长及其在电磁波中的重要性。 深入了解频率的概念和对电磁波特性的影响。
电磁波的能量和辐射强度
能量
探讨电磁波的能量传递方式和能量密度。
《麦克斯韦电磁理论》 PPT课件
探索麦克斯韦电磁理论的奇妙世界，从电磁场基本概念到量子化，让我们一 同揭开电磁波的神秘面纱。
麦克斯韦电磁理论简介
介绍麦克斯韦电磁理论的发展背景、基本原理，并解释其在现代科学中的重要性。
电磁场基本概念
电场
讲解电场的定义、性质和电荷在电场中的相互作用。
磁场
探讨磁场的本质、磁感应线和磁场对带电粒子的影响。
探索电磁场在材料中的散射和吸收现象，解释光的颜色和材料的特性。

电磁场的量子化
1 普朗克常数
介绍普朗克常数和其在量子化电磁场中的作用。
2 光子理论
讲解光子理论和电磁辐射的量子性质。
电磁波的量子理论
探究电磁波的量子理论，如波粒二象性和希尔伯特空间描述。
电磁场与受力粒子运动方程
研究电磁场对带电粒子运动的影响，并推导粒子在电磁场中的运动方程。
电磁场偏振
探讨电磁场偏振的概念和特点，以及偏振光的产生和检测。
电磁场的相干性
解释电磁场的相干性和相干时间，以及相干光的特性。
电磁场的干涉和衍射
揭示电磁场的干涉与衍射现象，在博弈中解开波粒二象性之谜。
电磁场的散射和吸收
电磁感应
介绍电磁感应的原理和法拉第电磁感应定律。
麦克斯韦方程组

《麦克斯韦电磁理论》课件

《麦克斯韦电磁理论》课件

电流的磁效应
安培环路定律
描述了电流在其周围空间产生的磁场的闭合回路定律，即电 流在其周围空间产生的磁感应线总是形成一个闭合回路，且 回路上的磁感应线数与穿过回路的电流数相等。
互感现象
当两个线圈中有一个线圈中的电流发生变化时，另一个线圈 中产生感应电动势的现象，互感现象是电磁感应的一种表现 形式。
电磁感应定律
《麦克斯韦电磁理论》ppt课 件
CONTENTS
• 麦克斯韦生平简介 • 电磁理论的发展历程 • 麦克斯韦电磁理论的主要内容 • 麦克斯韦电磁理论的实验验证 • 麦克斯韦电磁理论的意义和影
响
01
麦克斯韦生平简介
麦克斯韦的成长经历
童年时期
展现出对科学的浓厚兴趣 ，经常进行简单实验。
学生时期
进入爱丁堡大学学习，后 转入剑桥大学，受到数学 家巴洛的影响，开始深入
对未来科技发展的启示
深入探索电磁波的应用
随着科技的发展，可以进一步探索麦克斯韦电磁波在信息传输、 能源利用等领域的应用。
创新实验验证手段
未来可以通过更先进的实验手段验证麦克斯韦的理论预言，推动物 理学实验技术的发展。
启发新理论
麦克斯韦的电磁理论仍有许多未解之谜，可以启发未来的新理论探 索和创新。
谢谢您的聆听
电磁波的预言
总结词
麦克斯韦预言了电磁波的存在，并给 出了电磁波在真空中传播的速度等于 光速的结论。
详细描述
这一预言是基于麦克斯韦方程组的推 导，揭示了光的本质是电磁波，为后 来光学的进一步发展奠定了基础。
光的电磁理论
总结词
光的电磁理论是麦克斯韦提出的一种理论，将光解释为电磁波的一种表现形式 。
详细描述
该理论认为光是由电磁场中的振荡波产生的，解释了光的反射、折射、干涉和 衍射等现象，成为现代光学的基础。

电磁感应课件ppt

电磁感应课件ppt
右手定则在直流电中的应用
用于判断电流方向与磁场方向的关系。
右手定则在交流电中的应用
用于判断电流方向与磁场方向的关系，但需注意交流电的矢量性。
楞次定律与右手定则的实例
楞次定律的实例
当一个条形磁铁插入线圈时，线 圈中会产生抵抗磁通变化的感应 电流，从而阻碍磁铁的插入。
右手定则的实例
当直流电通过一个线圈时，用右 手握住线圈，拇指指向电流方向 ，四指指向即为磁场方向。
法拉第电磁感应定律
说明电磁感应现象，磁场可由 电场感应产生，而电场也可由
磁场感应产生。
麦克斯韦方程组的实例
静电场的电势分布
通过电势分布来描述静电场的性质和规律 。
恒定电流的磁场
描述恒定电流产生的磁场分布和性质，如 磁感线的形状和方向。
电磁感应现象
如发电机的工作原理，磁场感应电场，电 场感应磁场等。
• 安培环路定律：$ • abla \times \overset{\longrightarrow}{E} = -\frac{\partial \overset{\longrightarrow}{B}}{\partial t}$ • 法拉第电磁感应定律：$ • abla \times \overset{\longrightarrow}{B} = \mu_{0}\overset{\longrightarrow}{J} + \frac{\partial
VS
详细描述
将一根导线置于磁场中，并通以交变电流 ，根据右手定则，用右手握住导线，让大 拇指指向电流方向，四指的弯曲方向就是 磁场方向。在实验中，可以通过观察电流 表指针的偏转方向来验证右手定则。
谢谢您的聆听
THANKS
楞次定律的表述
感应电流的方向总是要使感应电动势反抗 引起感应电流的原磁场的磁通变化。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

S LE E 感 感 d dl S 0S B tdS 无源、非保守(涡旋)场
E感
(4) 对场中电荷的作用力: F感qE感
第18页 共48页
• 感生电动势的计算
(1) 定义求解:
i LE感dl
若导体不闭合, 则 i LE感dl
该方法只能用于E感为已知或可求解的情况.
(2) 法拉第电磁感应定律求解:
电磁感应-麦克斯韦电磁场 理论
13.1 电磁感应现象及其基本规律
13.1.1 电磁感应现象 楞次定律 • 实验演示
当条形磁铁插入或拔出线 圈回路时, 在线圈回路中会 产生电流; 而当磁铁与线圈 保持相对静止时, 回路中不 存在电流.
第2页 共48页
结论:当穿过闭合回 路的磁通量发生变化时, 不管这种变化是由什么 原因的,回路中有电流产 生. 这一现象称为电磁 感应现象.
一导体棒沿x方向以速度v匀速运动. 设t=0时x=0, 求框内的 感应电动势.
解: dSydxxtad n x
ΦSB dS0lkxcostxtandx
1k3ltancost
3
i d d t 1 3 k 3 tlan sit n k2 d d lt ltac n o t s
lvt i1 3kv 3 t2ta(n tsi n t 3co t)s
根据磁通量变化的不同原因,把感应电动势分为两种情况.
动生电动势: 在稳恒磁场中运动着的导体内产生的感应 电动势.
感生电动势: 导体不动, 因磁场的变化产生的感应电动势.
动生电动势
感生电动势
恒定磁场中运动的导体
B B r
导体不动B , 磁B 场r发,t生变化
磁通量发生变化的原因
d dt
第9页 共48页
电磁感应现象中产生的电流称为感应电流,相应的电 动势称为感应电动势.
电磁感应现象的本质由感应电动势反映。
第3页 共48页
例题1. 导线ab弯成如图形状, 半径R=0.10m, B=0.50T, n =360转/分. 电路总电阻为1000. 求: 感应电动势和感应电 流以及最大感应电动势和最大感应电流.
第16页 共48页
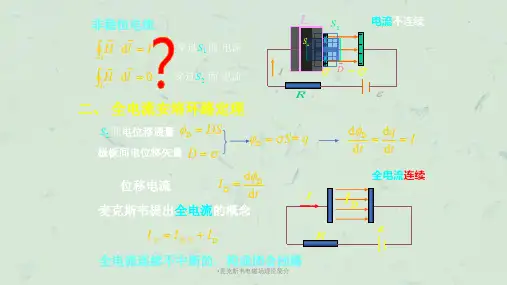
13.3 感生电动势 蜗旋电场
13.3.1 蜗旋电场的产生和性质
由法拉第电磁感应定律：
i d d t d d tSB d S S td S
问题: 是不是洛仑兹力?
导线不运动 vf 0q ,v B 0结论: 不是洛仑兹力.
只可能是一种新型的电场力.变化的磁场在周围空间将 激发电场. —— 非静电力
非静电: EkvB
电动势: b iL E kd l a(v B )d l
1. 动生电动势存在于运动导体上; 不动的导体不产生电动 势, 是提供电流运行的通路.
2. 没有回路的导体, 在磁场中运动, 有动生电动势但没有感 应(动生)电流.
3. 导线切割磁感线时才产生动生电动势.
第11页 共48页
0LlBdl
1BL2
2
动生电动势方向: aO
解2: S πL21L2 BS
2π 2
i
d1B2Ld1B2L
dt 2 dt 2
动生电动势方向: aO
第14页 共48页
例题5. 在亥姆霍兹线圈中间轴上放一半径为0.1m的小线 圈, 在小线圈所包围的面积内磁场近似均匀. 设在亥姆霍 兹线圈中通以交变磁场5.010-3(sin100t). 求小线圈中的 感应电动势.
解: 2πn12π0rad-1/s
60
Φ B S B cS o Bπs r2 cost
2
i
dΦBπr2si nt
dt 2
im12Bπr22.96V
Ii
i Bπr2sint
R 2R
Bπr2
Iim 2R 2.96mA
第7页 共48页
例题2. 一长直导线通以电流 iI0sint, 旁边有一个共面
• 动生电动势的计算
两种方法:
1. 公式求解:
i ab(v B )dl
2. 法拉第电磁感应定律求解:
i
d
dt
若回路不闭合, 需增加辅助线使其闭合.
计算时只计大小, 方向由楞次定律决定.
第12页 共48页
例题3. 一矩形导体线框, 宽为l, 与运动导体棒构成闭合回 路. 如果导体棒以速度v作匀速直线运动, 求回路内的感应
电解动 1: 势.i ab(v B )dl
l
0 vBdl vBl
电动势方向 AB
解2:
i
d
dt
Blx
i
d
dtΒιβλιοθήκη Bldx dti vBl 电动势方向 AB
第13页 共48页
例题4. 长为L的铜棒,在均匀磁场B中以角速度在与磁场方
向垂直的平面上作匀速转动.求棒的两端之间的感应电动势.
解1: i 0L(vB)dl0LvBdl
13.2.1 动生电动势
导线运动时,内部 自由电子受到向下洛
伦兹力: F m e (v B )
导体内部上、下端
正、负电荷的积聚,
形成静电场.自由电
子受到向上的静电
力.
FeeE
平衡时,电子不再因导体运动而移动, 导体两端相应具有一定的电势差,数值
上就等于动生电动势.
第10页 共48页
13.2.2 动生电 动势的表 达式 非静电力: F m e (v B )
i
d d
dt
dtSBdS
若导体不闭合, 需作辅助线.
第19页 共48页
例题7. 已知半径为R的长直螺线管中的电流随时间变化, 若
解: B5.01 0 3si3n1 t 4
I
I
Φπr2B
0.12π51 3 0si3n1 t 4
B
i
dΦ0.05co3s1t4 dt
第15页 共48页
例 题 6. 在 垂 直 于 纸 面 内 非 均 匀 的 随 时 间 变 化 的 磁 场
B=kxcost 中, 有一弯成角的金属框COD, OD与x轴重合,
的矩形线圈abcd. 求: 线圈中的感应电动势.
解: ΦSB dS rrl12π0ixl2dx
0I0l2si ntlnrl1
2π
r
i
d
dt
20π I0l2cotslnr rl1
当 0tπ时c， ots0,
2
i0 为 逆 时 针 转
当 πtπ时c， ots0,
2
i 0 为顺时针
第8页 共48页
13.2 动生电动势
1861年麦克斯韦假设:感生电流的产生就是这一电场作
用于导体中的自由电荷的结果. —— 感生电场(涡旋电场)
感生电动势： i LE感dl
第17页 共48页
•
感生电场
LE 感 dlS B tdS
电磁场的基本方程之一
(1) 变化的磁场能够激发电场.
B
“-”的含义:负右手螺旋
t
(2) 感生电场的性质: