第十章稳恒磁场
- 格式:doc
- 大小:9.49 MB
- 文档页数:15

大学物理第十章 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第十章稳恒磁场知识点5:电流的磁效应、磁场1、【】发现电流的磁效应的是:A:法拉第 B:安培 C:库仑 D:奥斯特2、【】提出分子电流假说的是:A:法拉第 B:安培 C:麦克斯韦 D:奥斯特3、【】下列说法错误的是:A:磁场和电场一样对其中的电荷都有力的作用;B:磁场只对其中的运动电荷有磁力的作用;C:运动的电荷激发磁场;D:磁场线永远是闭合的。
4、【】下列对象在磁场中不会受到磁场的作用的是:A:运动电荷 B:静止电荷 C:载流导体 D:小磁针5、【】关于静电场和磁场的异同,下列表述错误的是:A:静电场是有源场,而磁场是无源场;B:静电场是无旋场,而磁场是涡旋场;C:静电力是一种纵向力,而磁场力是一种横向力;D:静电场和磁场对其中的任何电荷都有力的作用。
知识点6:磁感应强度概念1、均匀圆电流I的半径为R,其圆心处的磁感应强度大小B=_________。
2、一条无限长载流导线折成如图示形状,导线上通有电流则P点的磁感强度B =______________.(μ0 = 4π×10-7 N·A-2)3、一长直载流导线,沿空间直角坐标Oy 轴放置,电流沿y 正向.在原点O 处取一电流元l Id ,则该电流元在(a ,0,0)(a 为正值),点处的磁感强度的大小为___ ___ _,方向为_____________.4、真空中稳恒电流I 流过两个半径分别为R 1,R 2的同心半圆形导线,两半圆导线间由沿直径的直导线连接,电流沿直导线流入. (1) 如果两个半圆共面 (图1) ,圆心O 点的磁感强度0B的大小为__________________,方向为___________;(2) 如果两个半圆面正交 (图2) ,则圆心O 点的磁感强度0B 的大小为______________,0B的方向与y 轴的夹角为_______________。



班级学号 第十次 稳恒磁场 得分 姓名 基本内容和主要公式1. 电流强度和电流密度电流强度:单位时间内通过导体截面的电荷量 (电流强度是标量,可正可负) 电流密度:电流密度是矢量,其方向决定于该点的场强E的方向(正电荷流动的方向),其大小等于通过该点并垂直于电流的单位截面的电流强度d QI d t = , dI j e dS=, ⎰⎰⋅=SS d j I2. 电流的连续性方程和恒定电流条件电流的连续性方程:流出闭合曲面的电流等于单位时间闭合曲面内电量增量的负值(其实质是电荷守恒定律) dt dq S d j -=⋅⎰⎰ , ( tj ∂∂-=⋅∇ρ )恒定电流条件: 0=⋅⎰⎰S d j, ( 0=⋅∇j)3. 欧姆定律和焦耳定律及其微分形式U I R=, j E σ=, 2Q A I Rt == , 2p E σ=4. 电动势的定义:单位正电荷沿闭合电路运行一周非静电力所作的功⎰+-⋅==l d K qAε, K dlε=⎰5. 磁感应强度:是描述磁场的物理量,是矢量,其大小为0sin F B q v θ=,式中F 是运动电荷0q 所受洛伦兹力,其方向由 0F q v B =⨯决定磁感应线:为了形象地表示磁场在空间的分布,引入一族曲线,曲线的切向表示磁场的方向,密度是磁感应强度的大小磁通量:sB dS φ=⎰⎰(可形象地看成是穿过曲面磁感应线的条数)6.毕奥一萨伐尔定律:034Idl r dB r μπ⨯=34LIdl rB rμπ⨯=⎰7.磁场的高斯定理和安培环路定理磁场的高斯定理:0SB dS =⎰⎰、 ( 0B ∇=) (表明磁场是无源场) 安培环路定理: 0i LiB dl I μ=∑⎰、 LSB dl j dS =⎰⎰⎰、(0B j μ∇⨯=)(安培环路定理表明磁场是有旋场)8.安培定律: dF Idl B =⨯、LF Idl B =⨯⎰磁场对载流线圈的作用: M m B =⨯ (m 是载流线圈的磁矩 m IS =)9.洛伦兹力:运动电荷所受磁场的作用力称为洛伦兹力 f qv B =⨯带电粒子在匀强磁场中的运动:运动电荷在匀强磁场中作螺旋运动,运动半径为m v R qB⊥=周期为 2m T qBπ=、螺距为 2m v h v T qBπ==霍尔效应 : 12H IB V V K h-= 式中H K 称为霍尔系数,可正可负,为正时表明正电荷导电,为负时表明负电荷导电 1H K nq=10.磁化强度 磁场强度 磁化电流 磁介质中的安培环路定理m M τ∑=∆ 、 L LM dl I =∑⎰ ,内 、 n i M e =⨯ , 0BH M μ=-、 m M H χ= 、 00m r B H H μχμμμ== (1+)H= 0i LiH dl I =∑⎰、 LSH dl j dS =⎰⎰⎰练习题一.选择题1.如图所示电路,已知电流流向,则A 、B 两点电热关系为 [ C ] A . A U 一定大于BUB . A U 一定小于B UC .不确定,要由ε,I ,R ,r 等值决定D . A U 等于BU2.把截面相同的直铜丝和钨丝串联接在一直流电路中,铜、钨的电流密度和电场强度的大小分别为j 1、j 2和E 1、E 2,则有: [ A ]A . 21j j =,21E E <B . 21j j =,21E E =C . 21j j =,21E E >D . 21j j >,21E E > E . 21j j <,21E E < 3.一电流元位于直角坐标系原点,电流沿z 轴正向,空间一点),,(z y x P 的磁感应强度沿x 轴的分量是 [ B ]A .02224()yIdlx y z μπ-++ B .0322224()yIdlx y z μπ-++C .0322224()xIdlx y z μπ-++ D . 04.四条相互平行的载流长直导线电流强度均为I ,分布在边长为a 2的正方形四个顶点上,电流方向如图-1所示,则中心O 点处的磁感应强度大小为 [ D ]A . 02IB aμπ=B.0IB aπ=C .0=BD .aI B πμ0=5.电流强度为I 的无限长载流导线弯成如图-2所示形状,其中四分之三圆周的圆心在O 点,半径为R 。





第十章 稳恒电流的磁场基 本 要 求一、理解磁感应强度、磁通量、磁矩等概念。
二、掌握反映稳恒电流磁场特性的两个基本定律,即高斯定理和安培环路定理。
三、掌握运用毕奥—萨伐尔定律和安培环路定理求载流导体周围磁场的基本方法。
四、掌握洛仑兹公式和安培定律,并能运用它们计算运动电荷和载流导线在磁场中所受的力以及载流线圈在磁场中所受的磁力矩。
五、掌握载流导线和载流线圈在磁场中运动时,磁力做功的计算方法。
内 容 提 要一、磁感应强度B磁感应强度可以用磁场力的三个公式(运动电荷所受的磁场力公式、电流所受的磁场力公式、载流线圈所受的磁力矩公式)定义。
例如从安培力的角度,B 定义为单位电流元在该处所受的最大安培力。
()IdldF B max安=二、磁力线 磁通量磁力线的特征 1. 闭合曲线;2. 与电流相互套连;3. 方向与电流的方向服从右手螺旋定则。
磁通量的定义式S B d d Φm ⋅=⎰⋅=Sm d ΦS B三、磁场的基本规律 1、毕−萨定律24r πId d r l B ⨯=真空磁导率 m /A T 10470⋅⨯=-πμ 磁介质的相对磁导率 r μ磁介质的绝对磁导率(简称磁导率) r μμμ0= 2、叠加原理∑=ii B B , ⎰=B B d利用毕−萨定律和叠加原理,原则上可以求任意电流的磁场分布。
3、B 的高斯定理 (磁通连续方程)⎰=⋅Sd 0S B4、安培环路定理真空中∑⎰=⋅内Id Lμl B有磁介质时∑⎰=⋅I d Ll HH B μ=四、几种典型电流的磁感应强度一段载流直导线 ()210c o s c o s 4φφ-=r πIμB 无限长载流直导线 rπIμB 20=无限长均匀载流薄圆筒 rπIμB B 2,00==外内 无限长载流密绕直螺线管,细螺绕环 0,0==外内B nI μB 圆电流圈的圆心和轴线上 ()23220轴线022/x R πISμB R I μB +==,中心五、磁力公式1、运动电荷所受的磁场力(洛仑兹力) B v f ⨯=q 洛2、电流所受的磁场力(安培力)电流元所受的磁场力 B l F ⨯=Id d 电流L 所受的磁场力 ⎰⨯=LId B l F3、载流线圈的磁矩和载流线圈受受的磁力矩载流线圈的磁矩 S p I m = 载流线圈受的磁力矩 B p M ⨯=m解题方法与例题分析一、运用毕−萨定律和叠加原理,求磁感应强度B解题思路:先将载流导线分割成电流元,任一电流元在空间某点产生的磁感应强度用B d 表示,根据场的叠加原理求得整个导线的磁感应强度⎰=B B d 。

第九章稳恒磁场静止电荷在周围只产生电场——静电场,而同一电荷在运动时周围既产生电场又产生磁场。
由于运动和静止是相对的,所以关于电场和磁场的这种现象说明电场和磁场有相对性联系。
磁场的性质用磁感应强度这一物理量来描述,磁感应强度通常随时间而改变,若磁感应强度不随时间而改变,则称为稳恒磁场。
本章将研究稳恒电流产生的磁场,导出磁场中的高斯定理和安培环路定理,从而得到稳恒磁场的场方程,并阐明稳恒磁场的基本规律。
最后,研究磁场对电流和带电粒子的作用以及磁场及磁介质的相互作用及影响。
一、教学目标1、熟练掌握毕奥- 萨伐尔定律2、掌握安培环路定律3、掌握磁场叠加原理4、理解洛仑兹力和安培力的公式,了解磁矩的概念二、教学重点安培环路定律的应用三、教学难点毕奥- 萨伐尔定律的应用四、教学方法讲授法、公式法、图象法、类比法五、教学过程§ 9.1 磁场磁感应强度一、基本磁现象磁现象:1、天然磁体周围有磁场;2、通电导线周围有磁场;3、电子束周围有磁场。
(这三条表现为磁场使小磁针发生偏转)4、 通电线能使小磁针偏转;5、 磁体的磁场能给通电线以力的作用;6、 通电导线之间有力的作用;7、 磁体的磁场能给通电线圈以力矩作用; 8通电线圈之间有力的作用;9、天然磁体能使电子束偏转。
(后面这几条表现为相互吸引、排斥、偏 转等)1820年,奥斯特发现了电流的磁效应。
安培指出:天然磁性的产生 也是由于磁体内部有电流流动,每个磁性分子内部,都自然地包含一环 形电流,称为分子电流,每个分子电流相当于一个极小的磁体,称为分 子磁距。
电荷的运动是一切磁现象的根源,一方面,运动的电荷在其周 围激发磁场;另一方面,运动电荷在空间除了受到电场力的作用外,还 受到磁场力的作用。
二、磁感应强度1、 磁场1) 磁力的传递者是磁场 2) 磁场对外的重要表现磁场对进入场中的运动电荷或载流导体有磁力的作用载流导体在磁场中移动时,磁场的作用力对载流导体作功,表明磁场 具有能量 磁场与电场一样、是客观存在的特殊形态的物质。
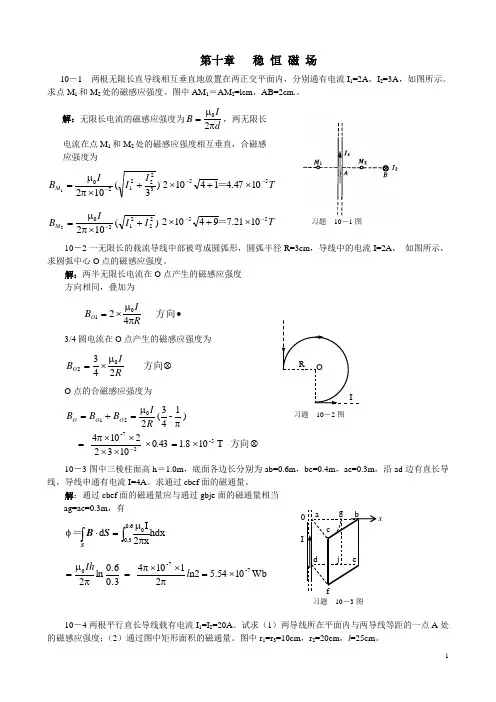
第十章 稳 恒 磁 场10-1 两根无限长直导线相互垂直地放置在两正交平面内,分别通有电流I 1=2A ,I 2=3A ,如图所示。
求点M 1和M 2处的磁感应强度。
图中AM 1=AM 2=lcm ,AB=2cm.。
解:无限长电流的磁感应强度为dIB πμ=20,两无限长 电流在点M 1和M 2处的磁感应强度相互垂直,合磁感 应强度为)3(10232221201I I I B M +⨯πμ=-T 551047.414102--⨯+⨯= )(1022221202I I I B M +⨯πμ=-T 551021.794102--⨯+⨯= 10-2一无限长的载流导线中部被弯成圆弧形,圆弧半径R=3cm ,导线中的电流I=2A , 如图所示,求圆弧中心O 点的磁感应强度。
解:两半无限长电流在O 点产生的磁感应强度 方向相同,叠加为•πμ⨯=方向 4201RIB O 3/4圆电流在O 点产生的磁感应强度为⊗μ⨯=方向 24302RI B O O 点的合磁感应强度为⊗⨯=⨯⨯⨯⨯⨯π=πμ=+=-方向 T 101.80.43 10322104 ) 1- 43( 25-27-021R I B B B O O O 10-3图中三棱柱面高h =1.0m ,底面各边长分别为ab=0.6m ,bc=0.4m ,ac=0.3m ,沿ad 边有直长导线,导线申通有电流I=4A 。
求通过cbef 面的磁通量。
解:通过cbef 面的磁通量应与通过gbje 面的磁通量相当 ag=ac=0.3m ,有 hdx x 2I d 6.03.00⎰⎰πμ=⋅φSS B =0.30.6ln20πμ=Ih Wb 1054.5n2 21104 7--7⨯=π⨯⨯π=l10-4两根平行直长导线载有电流I 1=I 2=20A 。
试求(1)两导线所在平面内与两导线等距的一点A 处的磁感应强度;(2)通过图中矩形面积的磁通量。
图中r 1=r 3=10cm ,r 2=20cm ,l =25cm 。
第十章 稳恒磁场10-8 如图所示,无限长载流导线附近,球面S向导线靠近,穿过S的磁通量Φ将不变,面上各点磁感应强度的大小将增大。
(均填“增大”或“减小”或“不变”)10-9 如图,载有电流I 的无限长直导线的一侧有一等腰直角三角形的回路MNO,回路和长直导线共面,回路的MN边与导线平行,相距为a ,而且MN和MO的长度也等于a ,求通过此回路的磁通量。
解:取如图所示的面积元(阴影部分),通过此面积元的磁通量为dr r a rIS d B d )2(20-=⋅=Φπμ所以,通过三角形面积的磁通量为)12ln 2(2)2(2020-=-=Φ=Φ⎰⎰πμπμIadr r a r I d aa10-15 图示为一张某粒子在均匀磁场B 中运动轨迹的照片,中间阴影区为铅板,粒子通过铅板后速度变小,从图中可以看出左半部轨迹较右半部弯曲得厉害些,则该粒子(B)(A)不带电。
()带正电。
(C)带负电。
(D)不能判断。
解:从图中可以看出粒子由右向左运动。
设粒子带正电,判断后发现其运动轨迹与图形符合,所以带正电。
10-17 图为某载流体(通电导体或半导体)的横截面,电流的方向垂直于纸面向。
若在铅直向上方向加一磁场,发现在载流体左右两侧堆积如图所示的电荷,则该载流体中运动的电荷是(B)。
(A)正电荷 (B)负电荷 (C)正、负电荷都可能10-19 如图,载流I的无限长直导线附近有导线PQ,载流1I ,如用下面的方法计算PQ受力:Ba I f 1=,b b a I dx x I B ba b+=⋅=⎰+ln 2200πμπμ,所以bb a a II f +=ln 210πμ 则是错误的,正确的解法是_______________________。
解:把PQ 看作许多电流元组成,任找一段电流元x d I1,则它所受的磁场力为dx I xIdxB I df 1012πμ==所以,PQ 受力为bba II dx I x I f ba b+==⎰+ln 221010πμπμ 10-1 如图,P点磁感应强度的大小等于________,方向为____________。
授课章节第10章稳恒磁场教学目的掌握运用毕奥-萨伐尔定律计算磁感应强度的方法.理解磁场的高斯定理.掌握安培环路定理及求解磁场分布的方法.熟练使用安培定律计算载流导线或载流回路所受的磁力和磁力矩.掌握洛仑兹力公式,并能用此求解运动问题.了解顺磁质、抗磁质和铁磁质的特点及磁化机理.掌握有磁介质时的安培环路定理,并能用其求解磁场分布.教学重点、难点毕奥-萨伐尔定律;安培环路定理;洛仑兹力;顺磁质、抗磁质的磁化机理;教学内容备注§10.1磁场磁感应强度一、基本磁现象磁体有不可分割两个磁极,N极和S极;1820年丹麦物理学家奥斯特发现电流的磁效应。
磁场和电场一样具有能量、动量和质量,是一种特殊的物质,叫场物质。
二、磁感应强度磁场对外的重要表现是:(1)磁场对进入场中的运动电荷或载流导体有磁力的作用;(2)载流导体在磁场中移动时,磁场的作用力将对载流导体作功,表明磁场具有能量。
1.磁矩设线圈的面积为ΔS,线圈中电流为I,则线圈的磁矩定义为mP=IΔS n磁矩mP是矢量,电流I 的方向与n的方向成右手螺旋系.线圈的磁矩是表征线圈本身特性的物理量。
2.试验线圈在磁场中受到的磁力矩:当线圈转到一定位置时、线圈受到的磁力矩为零,这个位置叫平衡位置; 线圈从平衡位置转过90°时线圈受到的磁力矩最大;m P M ∝max在磁场中的一定点、比值m P M m ax 不变;在磁场中的不同点比值mP M m ax不同。
3.磁感应强度矢量B大小为 B=mP M m ax; B 的单位 特斯拉, (T).三、磁通量 磁场中的高斯定理 1.磁力线 磁场中作一系列曲线,曲线上每一点的切线方向为磁场B方向,垂直于该点B 矢量的单位面积的磁力线条数,为该点B矢量的量值.(1)磁力线都是环绕电流的闭合曲线,磁场是涡旋场.(2)任何两条磁力线在空间不相交.(3)磁力线的环绕方向与电流方向用右手定则.2.磁通量穿过磁场中某一曲面的磁力线总数,称为穿过该曲面的磁通量,用符号m Φ表示.m d Φ=S d B⋅ 而通过曲面S 的磁通量为m Φ=⎰⋅SS d B磁通量的单位: 韦伯(Wb ),1Wb =12m T ⋅。
第九章 稳恒磁场9-1 如图所示,无限长载流导线附近,球面S向导线靠近,穿过S的磁通量Φ将不变,面上各点磁感应强度的大小将增大。
(均填“增大”或“减小”或“不变”)9-2 如图,载有电流I 的无限长直导线的一侧有一等腰直角三角形的回路MNO,回路和长直导线共面,回路的MN边与导线平行,相距为a ,而且MN和MO的长度也等于a ,求通过此回路的磁通量。
解:取如图所示的面积元(阴影部分),通过此面积元的磁通量为dr r a rIS d B d )2(20-=⋅=Φπμ所以,通过三角形面积的磁通量为)12ln 2(2)2(2020-=-=Φ=Φ⎰⎰πμπμIadr r a r I d aa9-3 图示为一张某粒子在均匀磁场B 中运动轨迹的照片,中间阴影区为铅板,粒子通过铅板后速度变小,从图中可以看出左半部轨迹较右半部弯曲得厉害些,则该粒子(B)(A)不带电。
()带正电。
(C)带负电。
(D)不能判断。
解:从图中可以看出粒子由右向左运动。
设粒子带正电,判断后发现其运动轨迹与图形符合,所以带正电。
9-4 如图,质量m 、电量e -的电子以速度v 水平射入均匀磁场B中,当它在水平方向运动l 距离后,有人计算其横向偏移y 如下(不计重力):evB f =,加速度m evB a =,时间vlt =,所以 )2/(2122mv eBl at y ==其错误在于电子做匀速圆周运动,不是抛物线运动。
正确答案是___。
解:正确解法如下:设电子作圆周运动的半径为R ,则eBmvR =。
由图可以得出 22l R R y --=-=eBmv 22)(l eBmv - 9-5 图为某载流体(通电导体或半导体)的横截面,电流的方向垂直于纸面向。
若在铅直向上方向加一磁场,发现在载流体左右两侧堆积如图所示的电荷,则该载流体中运动的电荷是(B)。
(A)正电荷 (B)负电荷 (C)正、负电荷都可能9-6 如图,载流I的无限长直导线附近有导线PQ,载流1I ,如用下面的方法计算PQ受力:Ba I f 1=,b b a I dx x I B ba b+=⋅=⎰+ln 2200πμπμ,所以bb a a II f +=ln 210πμ 则是错误的,正确的解法是_______________________。
解:把PQ 看作许多电流元组成,任找一段电流元x d I1,则它所受的磁场力为dx I xIdxB I df 1012πμ== 所以,PQ 受力为bba II dx I x I f ba b+==⎰+ln 221010πμπμ 9-7 在两条相互垂直的异面直导线AB和CD中,分别通以电流1I 、2I ,方向如图所示。
设AB为无限长。
CD对AB的张角为090;两直线间相距为0r 。
AB固定,O点是CD的中点。
求:(1)OC段电流所受的磁力;(2)DO段电流所受的磁力;(3)CD电流将如何运动? 解:(1)如图所示,在OC上任找一段电流元l d I2,则它所受的磁场力为θπμθsin 2sin 2102dl I rI dlB I dF == 因为θcos 0r r =,且θtg r l 0=,所以θθ20cos d r dl =。
代入上式得θθπμθθθθπμd tg I I d r I rI dF 2sin cos cos 2210202010=⋅⋅⋅=所以OC段电流所受的磁力⎰==dF F 2ln 4221040210πμθθπμπI I d tg II =⎰⊙(2)DO 段受力与CO 段大小相等、方向相反。
(3)CD 绕O 点转动。
9-8 载有电流1I 的长直导线旁有一底边长为d 。
载有电流2I 的等腰三角形回路。
三角形顶点C距直导线为a 。
底边DE与直导线平行,相距为b ,且回路与直导线共面。
求回路所受的磁力。
解:先求CD 边受力。
在CD 边上任找一电流元l d I2,则其所受磁场力为θπμπμcos 222102102drr I I dl I r I dlB I dF ===由于各F d方向一致,所以CD 边所受力为abI I r dr I I dF F baln cos 2cos 2210210θπμθπμ===⎰⎰方向垂直于CD 边指向左上方。
CE 边受力大小与CD 边相同,方向指向左下方。
DE 边受力bdI I Bd I F DE πμ22102== 指向右边。
在竖直方向上CD 与CE 的分力大小相等方向相反,所以回路所受的合力bd I I a bI I F F F DE CD πμθθπμθ2sin ln cos 22sin 2210210-=-==-=b d I I a b I I πμθπμ2ln tan 210210bdI I a b a b d I I πμπμ2ln )(2210210-- 水平向左。
9-9 如图所示,有一无限长直线电流1I ,另有一半径为R的圆形电流)(212I I I >>,其直径AB 与此直线重合,彼此绝缘。
试求在图示位置:⑴半圆弧ACB 所受的作用力(不计半圆弧ADB 对ACB 的作用);⑵整个圆形电流所受的作用力。
解:由对称分析得,不论是半圆环ACB 还是整个圆环,所受合力均向右。
(1)在半圆弧ACB 上找一电流元l d I2,它所受磁场力θθπμθπμd R RI I Rd I r I dlB I dF sin 222102102===θπμθd I I dF dF x 2sin 210== 半圆弧ACB 所受的作用力为→===⎰⎰2100210212I I d I I dF F x μθπμπ(2)整个圆形电流所受的作用力为→==='⎰⎰210202102I I d I I dF F x μθπμπ9-10 如图,在水平面内,三边质量都为m 、边长都为a 的正方形线框可绕水平轴O O '转动,线框处在与轴垂直的水平方向的均匀磁场中。
在线框中通以电流I ,若线框处于水平位置时恰好平衡,则磁感应强度的大小等于)/(2Ia mg ,方向水平向左。
解:线框所受重力力矩与磁力矩平衡:a BIa amg mga ⋅=⨯⨯+22 Iamg B 2=B的方向水平向左。
9-11 一塑料圆盘,半径为R ,电量q 均匀分布于表面,圆盘绕通过盘心垂直于盘面的轴转动,角速度为ω,用以下方法计算圆盘磁矩:通过圆盘的电流强度πω2qi =,圆盘的面积2R S π=,所以磁矩 q R R q iS P i 22212ωππω===但这是错误的,因为题目给出的是均匀带电圆盘,而解法中却是按均匀带电圆环来计算磁矩。
正确的解法是____________。
如果将此圆盘放在均匀磁场B中,B的方向与盘面的夹角为ϕ,如图所示,则磁场作用于圆盘的力矩大小为4/cos 2ϕωqB R 。
解:正确解法如下:如图所示,把均匀带电圆盘看作由许多均匀带电同心圆环组成,任取一半径为r 、宽度为dr 的圆环,由于转动它等校的电流为rdr R q rdr R q ds dI ωππππωσπω22222===则它的磁矩为dr r Rq rdr R q r sdI dP m 3222ωωππ===总磁矩为=m P ⎰=Rq R dr r Rq 023241ωω 若把它放入均匀磁场中,圆环电流所受的磁力矩为ϕωϕcos )90sin(320dr r B Rq B dP dM m =-= 总的磁力矩大小为ϕωϕωcos 41cos 2032qB R dr r B Rq dM M R ===⎰⎰9-12 如图,在均匀磁场B 中,半径为R 、圆心角θ的扇形硬导线OAB 线圈,载流I ,线圈平面与B垂直,则圆弧AB 所受到的安培力的大小为2/sin 2θIBR ,方向为垂直于AB且沿径向向外;该线圈的磁矩大小为2/2θIR ,方向为垂直纸面向里;该线圈所受磁力矩大小为0。
解:圆弧AB 所受到的安培力B I B l d I B l Id F d F B AB AB AAB⨯=⨯=⨯==⎰⎰⎰)(其大小为=AB F 2sin2θIBR方向垂直于AB 且沿径向向外。
该线圈的磁矩大小为θ221IR IS P m == 方向垂直纸面向里。
线圈所受磁力矩0=⨯=B P M M。
9-13 如图所示,半径为R 的半圆环导线中通以电流为I ,并置于均匀磁场B中。
试求导线所受安培力对O O '轴的力矩。
解:方法一:如图所示,任找一电流元l Id,其所受的安培力为θθθd IRB IdlB dF cos )90sin(0=-= ⊗它对O O '轴的力矩为θθθθθd IBR d IBR R rdF dM 22cos cos cos =⋅== ↓所以,半圆环导线所受的总的磁力矩为2022021cos IBR d B IR dM M πθθππ==⎰⎰= ↓方法二:连接直径CD ,使之构成一封闭电流。
由于CD 中电流与外磁场平行,所以,它不受磁场力作用,因此闭合电流所受的磁力矩等于半圆环导线所受的磁力矩。
根据磁力矩公式B P M m ⨯=,有IB R B P M m 202190sin π== ↓9-14 如图,电流元11l d I 和22l d I 在同一平面内,相距为r ,夹角为1θ、2θ,则22l d I所受的安培力大小为________,方向为_______;11l d I所受的安培力大小为______,方向为______;这两个力大小不相等、方向也不相反,是否说明牛顿第三定律不成立,为什么? 解:22l d I所受安培力为21110221222sin 4r dl I dl I B dl I dF θπμ== →同理,11l d I所受安培力为22220112111sin 4r dl I dl I B dl I dF θπμ== ↑因为22l d I 所受安培力是11l d I 产生的磁场(而不是11l d I )施加的,而11l d I所受安培力是22l d I 产生的磁场施加的, 所以1F d 与2F d不是作用力与反作用力的关系,21F d F d -≠不违背牛顿第三定律。
9-15 如图,P点磁感应强度的大小等于________,方向为____________。
解:MA 、DN 段电流在P 点激发的磁感应强度为0,即021==B BAB 、BC 、CD 段电流在P 点激发的磁感应强度分别为a I a I B πμππμ82)0sin 4(sin 4003=+=⊗ aI a I B πμπππμ42)4sin 4(sin 4004=+=⊗ πμππμa I a I B 82)0sin 4(sin 4005=+=⊗ 故P 点的总磁感应强度为πμa IB B B B B B 22054321=++++= ⊗ 9-16 载流为I 的无限长直导线,在P点处弯成半径R 的圆周,如图,若缝隙极窄,则圆心O 处磁感应强度B的大小为________,方向为________。