复数和向量的关系

复数与向量：复数运算和向量分析复数与向量是数学中重要而常用的概念，它们在代数和几何中都有广泛的应用。

本文将介绍复数的基本运算以及向量的分析性质，并深入探讨它们之间的联系和应用。

一、复数运算1.1 复数的定义和表示方法复数是由实数部分和虚数部分构成的数，可以用a+bi的形式表示，其中a是实数部分，b是虚数部分，i是虚数单位，满足i^2=-1。

复数可以表示为有序对(a, b)，其中a和b均为实数。

1.2 复数的基本运算复数的基本运算包括加法、减法、乘法和除法。

1.2.1 加法和减法两个复数相加时，实部与实部相加，虚部与虚部相加，即(a+bi) + (c+di) = (a+c)+(b+d)i。

减法同理，即(a+bi) - (c+di) = (a-c)+(b-d)i。

1.2.2 乘法两个复数相乘时，根据乘法分配律展开，并利用虚数单位i的平方性质，即(a+bi)(c+di) = (ac-bd)+(ad+bc)i。

1.2.3 除法两个复数相除时，将分子和分母都乘以共轭复数的同一个形式。

即(a+bi)/(c+di) = [(a+bi)(c-di)] / [(c+di)(c-di)]。

1.3 欧拉公式欧拉公式是复数运算中的重要公式，表达了自然对数底e的指数函数与三角函数的关系。

欧拉公式为e^(ix) = cos(x) + isin(x)，其中e为自然对数底，i为虚数单位，x为实数。

二、向量分析2.1 向量的定义和表示方法向量是有大小和方向的量，可以用箭头表示，也可以用坐标表示。

在二维空间中，一个向量可以表示为(x, y)，其中x和y分别表示向量在x轴和y轴上的分量。

在三维空间中，一个向量可以表示为(x, y, z)，其中x、y和z分别表示向量在x轴、y轴和z轴上的分量。

2.2 向量的基本运算向量的基本运算包括加法、减法、数乘和点乘。

2.2.1 加法和减法两个向量相加时，将它们的对应分量相加，即(x1, y1) + (x2, y2) =(x1+x2, y1+y2)。

复数的考点知识点归纳总结复数的考点知识点归纳总结复数是基础数学中的重要概念，广泛应用于数学、物理、工程等领域。

掌握复数的概念、性质和运算规则对于建立数学思维、解决实际问题具有重要意义。

本文将从复数的基本概念、运算法则和实际应用等方面进行归纳总结。

一、复数的基本概念1. 复数的定义：复数是由实部和虚部组成的数，形式为a+bi，其中a为实数部分，bi为虚数部分，i为虚数单位，满足i²=-1。

2. 复数的实部和虚部：复数a+bi中，a为实部，bi为虚部。

3. 复数的共轭复数：设复数z=a+bi，其共轭复数记为z*，则z*的实部与z相同，虚部的符号相反。

4. 复数的模：复数z=a+bi的模定义为|z|=√(a²+b²)。

5. 复数的辐角：复数z=a+bi的辐角定义为复数与正实轴正半轴的夹角，记作arg(z)。

6. 三角形式：复数z=a+bi可以写成三角形式r(cosθ+isinθ)，其中r为模，θ为辐角。

二、复数的运算法则1. 复数的加法和减法：复数的加法和减法运算与实数类似，实部与实部相加减，虚部与虚部相加减。

2. 复数的乘法：复数的乘法运算使用分配律和虚数单位的性质，即(a+bi)(c+di)=(ac-bd)+(ad+bc)i。

3. 复数的除法：复数的除法运算需要将分子分母同时乘以共轭复数，即(a+bi)/(c+di)=[(a+bi)(c-di)]/[(c+di)(c-di)]。

4. 复数的乘方和开方：复数的乘方和开方运算需要使用三角函数的性质和欧拉公式，即z^n=r^n[cos(nθ)+isin(nθ)]，√z=±√r[cos(θ/2)+isin(θ/2)]。

三、复数的性质和应用1. 复数的性质：复数具有加法和乘法的封闭性、交换律、结合律、分配律等性质。

2. 复数平面：复数可以用平面上的点来表示，实部为横坐标，虚部为纵坐标，构成复数平面。

3. 复数与向量：复数可以看作是向量的延伸，复数的运算有时可以用向量的加法和旋转来理解。

复数与向量的运算复数与向量是数学中的重要概念，在不同的数学领域和物理学中都有广泛的应用。

本文将探讨复数和向量的基本概念以及它们之间的数学运算。

第一部分：复数的定义和运算复数由实部和虚部组成，可以用二维数学对象来表示。

复数具有以下的形式：z = a + bi (其中a和b为实数，i为虚数单位)。

在复数中，实部和虚部可以分别进行加法和减法运算。

假设有两个复数z1 = a1 + b1i和z2 = a2 + b2i，则它们的和为z1 + z2 = (a1 + a2) + (b1 + b2)i，差为z1 - z2 = (a1 - a2) + (b1 - b2)i。

第二部分：复数的乘法和除法复数的乘法涉及到实部和虚部的乘法计算。

假设有两个复数z1 = a1 + b1i和z2 = a2 + b2i，则它们的乘积可以通过以下方式计算：z1 * z2 = (a1a2 - b1b2) + (a1b2 + a2b1)i。

复数的除法可以通过乘以共轭复数并除以模的平方来实现：z1 / z2 = (a1a2 + b1b2) / (a2^2 + b2^2) + (a2b1 -a1b2)i / (a2^2 + b2^2)。

第三部分：向量的定义和运算向量是一个具有大小和方向的量，通常用箭头表示。

向量可以在空间中表示为一组有序实数或复数。

向量的运算包括加法、减法、数量乘法和点积运算。

向量的加法可以通过将对应分量相加来实现。

假设有两个向量v1 = (x1, y1, z1)和v2 = (x2, y2, z2)，它们的和为v1 + v2 =(x1 + x2, y1 + y2, z1 + z2)。

向量的减法可以通过将对应分量相减来实现，即v1 - v2 = (x1 - x2, y1 - y2, z1 - z2)。

第四部分：向量的数量乘法和点积运算向量的数量乘法即将一个向量的每个分量与一个实数相乘。

如果有一个向量v = (x, y, z)和一个实数k，则v * k = (kx, ky, kz)。

复数的向量表示引言在数学中，复数是由实数和虚数组成的，可以用向量来表示。

复数在多个领域中有着广泛的应用，如电路分析、信号处理和量子力学等。

本文将介绍如何使用向量来表示复数，并讨论一些常见的运算和性质。

复数的定义复数是由实数部分和虚数部分组成的数。

一般形式为a + bi，其中a是实数部分，b是虚数部分，i是虚数单位。

虚数单位i定义为i² = -1。

复数表示了实数和虚数在数轴上的相互关系。

复数向量的表示复数可以用向量来表示。

在复平面上，横轴代表实数部分，纵轴代表虚数部分。

将一个复数视为一个向量，实数部分作为向量在横轴上的投影，虚数部分作为向量在纵轴上的投影。

通过在复平面上绘制向量，我们可以更直观地理解复数的性质和运算。

向量运算向量的加法复数的加法可以通过向量的加法来实现。

将两个复数的实数部分和虚数部分分别相加即可得到结果复数的实数部分和虚数部分。

例如，对于复数a + bi和c + di，它们的和计算如下：(a + bi) + (c + di) = (a + c) + (b + d)i向量的乘法复数的乘法也可以通过向量的乘法来实现。

将两个复数的实数部分和虚数部分相乘并进行适当的运算即可得到结果复数的实数部分和虚数部分。

例如，对于复数a + bi和c + di，它们的乘积计算如下：(a + bi) * (c + di) = (ac - bd) + (ad + bc)i向量的长度在复平面上，向量的长度称为模。

复数的模表示了复数到原点的距离，即复数的大小。

对于复数a + bi，它的模计算如下：|a + bi| = sqrt(a^2 + b^2)其中，sqrt表示开方运算。

向量的共轭对于复数a + bi，它的共轭复数记为a - bi。

共轭复数的实数部分与原复数相同，虚数部分取符号相反。

向量的除法复数的除法需要使用到共轭复数。

将除数与被除数乘以除数的共轭复数，然后进行适当的运算即可得到结果复数的实数部分和虚数部分。

重视复平面上复数与向量的联系作用平面向量与复数是高中数学的重要内容,联系紧密,联系是在复平面进行的;随着知识的发展,相互对应相互促进是联系的主要体现;复数中的概念、运算等在向量中可以作出几何解释；向量的运算,可以对应有关的复数运算.复数与向量的这种联系,只要我们需要,可以将它们组合起来,在计算推理中发挥它们的联系作用,将是一件高效快乐的事情.一 复数商与内积的联系复数运算,向量运算之间的许多联系,在现有课本里是可以学习到的,下面我们来看复数商与内积的联系.例1 复数z 1=a 1+b 1i, z 2=a 2+b 2i,它们的三角式分别为z 1=|z 1|cos θ1+isin θ1, z 2=|z 2|cos θ2+isin θ2,对应的向量分别是1oz =a 1,b 1、2oz =a 2,b 2.然后复数作商: 代数式作商:21z z =2221122121||)()(z i b a b a b b a a -++；-------------1 三角式作商：21z z =||||21z z cos θ1-θ2+isin θ1-θ2,------2 比较12式,可得||||21z z cos θ1-θ2=222121||z bb a a +, ……3 ||||21z z sin θ1-θ2=222112||z ba b a -………4 则从中可得下列变式：(1) 复数对应向量间的夹角余弦公式:cos θ1-θ2||||212121oz oz ⋅ , 我們总可以适当选择θ1、θ2的主值范围,使得|θ1-θ2|∈),0[π,所以1oz 与2oz 的夹角就是|θ1-θ2|. 2 向量内积:1oz ·2oz =a 1a 2+b 1b 2=|1oz |·|oz 2|cos θ1-θ2.若对4取绝对值得到:|1oz ×2oz |=|a 1b2-a 2b 1|=|1|oz |·2|oz |sin θ1-θ2|,这是空间xoy 平面上向量)0,,(),0,,(2121b b b a a a ==叉积的绝对值,是以线段oz 1、oz 2为邻边的平行四边形的面积公式.复数商运算式中,隐含着向量间的夹角公式,向量的内积,平行四边形面积的公式.若复数代数式i y x z i y x z 222111,-=+=的三角式分别是)sin (cos 1111θθi r z +=,=2z )],sin()[cos(222θθ-+-i r 然后,将它们的代数式,三角式分别相乘,比较结果,同样可以得到上面的三个式子.数学中的这种相互包容联系,真是体现了数学中的统一和谐之美.二 复数向向量表示上的转化联系利用复数与向量的联系,复数可以向向量表示上的转化,使有些复数的问题转化为向量问题或构造向量图像去处理,借向量之力去解决复数问题.例2 已知复数z 1、z 2的模为1,z 1+z 2i 2321+=,求复数21、z z . 解：根据题意,设复数21、z z 对应的向量为21oz 、oz ,以这两个向量为邻边,边长为1,构作一个平行四边形,并建如图1的直角坐标系.记z z z =+21,对应向量oz .∵oz 对应的复数是i 2321+∴1||=oz ,∠zoz 1=6001||1=oz ∴∆oz 1z 是正三角形,∆ ozz 2≅z oz 1∆ 2ozz ∆∴是正三角形. ∴11=z ,i z 23212+-=,或1,232121=+-=z i z . 本题在解题的思路上借助了复数向向量转化的作用.复数向向量转化是较常用的思想方法.此题纯粹用代数方法去做,计算量是较大的.例3复平面内,已知动点A,B 所对应的复数的辐角为定值,分别θ、-θ,)20(πθ∠∠,O 为原点,ΔAOB 的面积是定值S,求ΔAOB 的重心M 所对应的复数模的最小值.图2.解：根据题设,设向量OM 、OB 、OA对应复数、z 、z z 21且 ||||||||||||2211z OM 、r z OB 、r z OA =====,则有θ2sin 2121r r s =, θ2sin 221sr r = ∵)(31OB OA OM += 图2∴ )()(91||91||22OB OA OB OA OB OA OM +⋅+=+==)2|||(|9122OB OA OB OA ⋅++=)2cos 2(91212221θr r r r ++ ≥θθθ221cos 22sin 292)2cos 1(92⨯⨯=+sr r =θcot 94s ∴ |z|=|θcot 32|s OM ≥,即重心M 所对应的复数模的最小值θcot 32s 1z =θ2sin 2s )sin (cos 2sin 2),sin (cos 2θθθθθi s z i -=+时,取最小值.该题用向量方法可较简捷获解.复数向向量表示上的转化的特点是:能将复数条件化为特殊的向量图形, 或构造一个向量运算,然后,顺利进行推理运算,求得结果.三 向量向复数表示上的转化联系利用复数与平面向量的联系,由向量向复数表示上的转化,使向量问题转化为复数问题或构造复数的结论去处理,借复数之力去解决向量问题,并使人觉得返朴归真之感.例4已知三个不共线的向量,,,c b a 且,0=++c b a 证明:c b a ,,可构成一个三角形. 证明:不妨设c b a ,,对应复数的三角式分别为:),sin (cos 111θθi r +)sin (cos 222θθi r +,),sin (cos 333θθi r +且321r r r ≤≤.o c b a =++o i r i r i r =+++++∴)sin (cos )sin (cos )sin (cos 333222111θθθθθθ )1......(0cos cos cos 332211=++∴θθθr r r 332211sin sin sin θθθr r r ++=0 (2)由1,2解得)cos(22121222123θθ-++=r r r r rc b a ,, 不共线,)(21Z k k ∈≠-∴πθθ1)cos(121∠-∠-∴θθ2122212321222122r r r r r r r r r ++∠∠-+∴12312r r r r r +∠∠-∴c b a ,,∴可构成一个三角形.从证明过程知道,其逆也成立的,故此命题可写成充要条件的形式.该题纯粹用向量概念去证明是比较简单的,但学生听了后,并觉得没有复数解明白.向量向复数表示上的转化的特点是:转化为复数问题后能构造出复数的某些结论或某些代数公式,从而通过它们去实现目标完成.四 复数与向量并用联系用多种形式表示一个命题的方法,在数学中是常用的手段,而且是常用常新,也是知识、思想、方法融会贯通的重要途径.如有些命题既可以用复数表示、也可以用向量表示,对于这类命题的处理自然要选择合适的形式来表示,或者是两者并用,实现相互左证,这样可以使问题明了简单.例5已知线段AB 的中点C,以AC 和CB 为对角线作平行四边形AECD 和BFCG,又作平行四边形CFHD 和CGKE,求证H 、C 、K 三点在一条直线上,且CK=CH,如图3.证明:以C 为原点,AB 为X 轴建立直角直角坐标系.设向量CD 、CF 、CB对应复数321,z ，z z 那么,向量CE 、CG CA 、对应复数分别为31211z z 、z 、z z ----；又CD CF CH +=、CE CG CK +=分别对应复数32z z +、)()(3121z z z z --+-∵1)()(312132-=--+-+z z z z z z ,图3 ∴1-=CKCH ,∴CK 、CH 平行,但又有公共点C,故H 、C 、K 三点共线,且CK=CH. 例6已知k P k=1,2,……,n 是单位圆上的n 个等分点,P 是该圆上任意一点,求证22221||......||||n pp pp pp +++为一定值.如图4.证明:以单位圆的圆心O 为直角坐标的原点,OPn为X 轴,建立坐标系,则∠nkop p k n π2=当k=n 时,假定此角为2π, ∵ 点i nkn k z p k k ππ2sin 2cos +=对应的复数三角式为,对应向量是k op ,则其长为1,向量和01111==∑∑∑===nk k nk kn k kz zop 对应于复数和,即01=∑=nk k op .∴ 22221||......||||n pp pp pp +++=22221||......||||n pp pp pp +++=)()(.....)()()()2211op op op op op op op op op op op op n n -⋅-++-⋅-+-⋅-=)......(2||||......||||21222221n n op op op op op n op op op ++⋅-++++ =2n-2o op ⋅=2n,为定值.在这两个问题解决的过程中,我们既用了复数,又用到了向量及它们之间的等价结论.复数与向量并用的特点是:并用表示后,相互之间有左证作用或有等价结论,而且在各自的范围内有顺利进行计算推理的可能.在平面图中,证明点共线,直线平行,直线垂直,判断三角形的形状等时,经常用复数与向量之间来转换、或并用来表示命题的,从而实现共同之目的.复数与平面向量之间的联系是很多的,既有数形联系,又有等价结论联系.用好这些联系的意义是很大的.在教学中能揭示这些联系,可以活跃思维,培养兴趣,提高学习的积极性,提高学习的效率. 要牢固掌握这些联系,关键在平时要理清复数与向量的对应联系,并把它们装在心中,拿在手中,落实在应用中,千万别将它们分离.例4已知),.....,2,1(n k p k =是单位圆上的n 个等分点按逆时针排列,o 是原点,求证：o opnk k=∑=1证明:以单位圆的圆心O 为直角坐标的原点,OP n 为X 轴,建立直角坐标系,则∠nkop p k n π2=当k=n 时,假定此角为2π. ∵ 点i nkn k z p k k ππ2sin 2cos+=对应的复数三角式为,对应向量是k op ,则其长为1,向量和01111==∑∑∑===nk knk k nk k z z op 对应于, ∴01=∑=nk kop.这种等分圆周的有关向量求和问题,通过复数之后,可以转化为复数数列求和来完成.。

中学数学认识复数与向量的运算法则数学是一门令人惊叹的学科，它涵盖了各种各样的概念和运算法则。

在中学数学中，复数与向量是两个重要的主题。

本文将介绍复数与向量的运算法则，并讨论它们在实际问题中的应用。

一、复数的运算法则复数是由实数和虚数组成的数，其中虚数是指具有形式为bi的数，其中b是实数而i是虚数单位。

复数可以表达为a+bi的形式，其中a是实部，bi是虚部。

下面是复数的运算法则：1. 复数的加法：对于两个复数a+bi和c+di，它们的和等于(a+c)+(b+d)i。

2. 复数的减法：对于两个复数a+bi和c+di，它们的差等于(a-c)+(b-d)i。

3. 复数的乘法：对于两个复数a+bi和c+di，它们的乘积等于(ac-bd)+(ad+bc)i。

4. 复数的除法：对于两个复数a+bi和c+di，它们的商等于[(ac+bd)/(c^2+d^2)]+[(bc-ad)/(c^2+d^2)]i。

5. 复数的共轭：一个复数a+bi的共轭等于a-bi。

这些运算法则为我们解决复数相关的问题提供了便利。

复数在电路分析、信号处理等领域有着广泛的应用。

二、向量的运算法则向量是有大小和方向的量，它可以用有序数对(x, y)来表示。

向量的运算法则如下：1. 向量的加法：对于两个向量A(x1, y1)和B(x2, y2)，它们的和等于A+B=(x1+x2, y1+y2)。

2. 向量的减法：对于两个向量A(x1, y1)和B(x2, y2)，它们的差等于A-B=(x1-x2, y1-y2)。

3. 向量的数乘：对于一个向量A(x, y)和一个实数k，它们的数乘等于kA=(kx, ky)。

4. 向量的数量积：对于两个向量A(x1, y1)和B(x2, y2)，它们的数量积等于A·B=x1x2+y1y2。

5. 向量的夹角：对于两个非零向量A和B，它们的夹角θ的余弦等于cosθ=(A·B)/(|A||B|)，其中|A|和|B|分别表示向量A和B的模。

重视复平面上复数与向量得联系作用平面向量与复数就是高中数学得重要内容,联系紧密，联系就是在复平面进行得。

随着知识得发展,相互对应相互促进就是联系得主要体现。

复数中得概念、运算等在向量中可以作出几何解释;向量得运算，可以对应有关得复数运算、复数与向量得这种联系,只要我们需要,可以将它们组合起来，在计算推理中发挥它们得联系作用,将就是一件高效快乐得事情、一复数商与内积得联系复数运算,向量运算之间得许多联系,在现有课本里就是可以学习到得，下面我们来瞧复数商与内积得联系、例 1 复数z=a+bｉ，ｚ=a＋bi，它们得三角式分别为z=|z｜(cｏｓθ+isinθ), z=|ｚ|(cosθ+ｉsinθ)，对应得向量分别就是＝(ａ,ｂ)、＝(a，b)、然后复数作商:代数式作商:=;-－-－---－-－--－(１)三角式作商:=[cｏｓ(θ－θ）+ｉｓin(θ-θ)],-－－-－-(2)比较(1)（2）式,可得 [cos（θ－θ)]=, (3)［sｉn(θ-θ）]= (4)则从中可得下列变式：(1)复数对应向量间得夹角余弦公式:ｃos(θ-θ)= ，（我們总可以适当选择θ、θ得主值范围,使得|θ-θ|∈，所以与得夹角就就是|θ－θ|)、(2) 向量内积:·=ａa+ｂb=||·｜｜ｃos(θ-θ)、若对(４）取绝对值得到:|×|=｜ab-ab｜=||·|sin(θ-θ)｜，这就是空间平面上向量叉积得绝对值,就是以线段oz、ｏz为邻边得平行四边形得面积公式、复数商运算式中,隐含着向量间得夹角公式,向量得内积,平行四边形面积得公式、若复数代数式得三角式分别就是,然后，将它们得代数式,三角式分别相乘,比较结果,同样可以得到上面得三个式子、数学中得这种相互包容联系,真就是体现了数学中得统一与谐之美、二复数向向量表示上得转化联系利用复数与向量得联系,复数可以向向量表示上得转化，使有些复数得问题转化为向量问题或构造向量图像去处理,借向量之力去解决复数问题、例2 已知复数z、z得模为１,z+ｚ，求复数、解：根据题意，设复数对应得向量为,以这两个向量为邻边，边长为1,构作一个平行四边形,并建如图１得直角坐标系、记,对应向量、∵对应得复数就是x∴，∠ｚoz=60,ﻩ本题在解题得思路上借助了复数向向量转化得作用、复数向向量转化就是较常用得思想方法、此题纯粹用代数方法去做,计算量就是较大得、例３复平面内,已知动点Ａ,B所对应得复数得辐角为定值,分别θ、-θ,,O为原点,ΔAＯB得面积就是定值S,求ΔAOＢ得重心M所对应得复数模得最小值、图2、解:根据题设,设向量对应复数且|,则有,∵ 图2∴＝=≥=∴ ｜z|=|,即重心M 所对应得复数模得最小值(=时,取最小值)、该题用向量方法可较简捷获解、复数向向量表示上得转化得特点就是:能将复数条件化为特殊得向量图形, 或构造一个向量运算，然后,顺利进行推理运算,求得结果、三 向量向复数表示上得转化联系利用复数与平面向量得联系,由向量向复数表示上得转化,使向量问题转化为复数问题或构造复数得结论去处理,借复数之力去解决向量问题,并使人觉得返朴归真之感、例4已知三个不共线得向量且证明:可构成一个三角形、证明:不妨设对应复数得三角式分别为：,且、o i r i r i r =+++++∴)sin (cos )sin (cos )sin (cos 333222111θθθθθθ＝0 (2)由(１）,（2)解得不共线,可构成一个三角形、从证明过程知道,其逆也成立得,故此命题可写成充要条件得形式、该题纯粹用向量概念去证明就是比较简单得,但学生听了后,并觉得没有复数解明白、 向量向复数表示上得转化得特点就是:转化为复数问题后能构造出复数得某些结论或某些代数公式,从而通过它们去实现目标完成、四 复数与向量并用联系用多种形式表示一个命题得方法,在数学中就是常用得手段，而且就是常用常新,也就是知识、思想、方法融会贯通得重要途径、如有些命题既可以用复数表示、也可以用向量表示，对于这类命题得处理自然要选择合适得形式来表示,或者就是两者并用,实现相互左证,这样可以使问题明了简单、例5已知线段ＡＢ得中点Ｃ,以ＡC 与C Ｂ为对角线作平行四边形A ＥＣＤ与BFCG ，又作平行四边形CF ＨＤ与CGK Ｅ,求证H 、C 、Ｋ三点在一条直线上,且CK ＝C Ｈ,如图３、证明：以C 为原点,A Ｂ为X 轴建立直角直角坐标系、设向量对应复数那么,向量对应复数分别为;又、分别对应复数、∵ ,图3 ∴ ,∴平行,但又有公共点C,故Ｈ、C 、K 三点共线,且CK=CH 、例6已知(k=１，2,……,ｎ）就是单位圆上得n 个等分点,就是该圆上任意一点，求证 为一定值、如图４、证明:以单位圆得圆心Ｏ为直角坐标得原点，ＯP 为Ｘ轴,建立坐标系，则∠ (当k=n 时,假定此角为2)，∵ 点，对应向量就是，则其长为1,向量与，即、∴ = =()()(.....)()()()2211op op op op op op op op op op op op n n -⋅-++-⋅-+-⋅- =)......(2||||......||||21222221n n op op n op op op ++⋅-++++=２n-２=2n,为定值、在这两个问题解决得过程中，我们既用了复数,又用到了向量及它们之间得等价结论、复数与向量并用得特点就是:并用表示后,相互之间有左证作用或有等价结论,而且在各自得范围内有顺利进行计算推理得可能、在平面图中，证明点共线,直线平行，直线垂直,判断三角形得形状等时,经常用复数与向量之间来转换、或并用来表示命题得,从而实现共同之目得、复数与平面向量之间得联系就是很多得,既有数形联系,又有等价结论联系、用好这些联系得意义就是很大得、在教学中能揭示这些联系,可以活跃思维,培养兴趣,提高学习得积极性,提高学习得效率、 要牢固掌握这些联系,关键在平时要理清复数与向量得对应联系，并把它们装在心中,拿在手中,落实在应用中,千万别将它们分离、例４已知就是单位圆上得ｎ个等分点(按逆时针排列),o 就是原点,求证:证明:以单位圆得圆心Ｏ为直角坐标得原点,OP 为X 轴,建立直角坐标系，则∠ (当k=n 时,假定此角为2)、∵ 点,对应向量就是,则其长为1,向量与,∴ 、这种等分圆周得有关向量求与问题,通过复数之后,可以转化为复数数列求与来完成、。

数学中的复数与向量复数与向量作为数学中的两个重要概念，被广泛运用于各个领域，尤其在数学分析、力学和电磁学等学科中具有重要地位。

本文将从定义、基本运算及应用角度探讨复数与向量的关系和特性。

一、复数的定义与运算复数是由实数与虚数构成的数，通常用a+bi的形式表示，其中a为实部，bi为虚部。

实部与虚部可以是任意实数。

复数的运算包括加法、减法、乘法和除法。

复数的加法与减法遵循实数的运算规律，即实部相加（减），虚部相加（减）。

例如：(2+3i)+(4+2i)=6+5i复数的乘法按照分配律进行运算，通过展开得到结果。

例如：(2+3i)*(4+2i)=8+12i+6i-6=2+18i复数的除法涉及到分母的共轭复数，通过将分子与分母同乘以共轭复数的结果进行简化。

例如：(2+3i)/(4+2i)=(2+3i)*(4-2i)/(4^2-(2i)^2)=...二、向量的定义与运算向量是数学中用于表示大小与方向的量，常用箭头表示，例如A B⃗。

向量有长度、方向和初始点，可以通过在坐标系中标定起点和终点来表示。

向量的加法与减法遵循平行四边形法则，即将向量首尾相接形成的平行四边形的对角线即为向量和的结果。

例如：A B⃗+B C⃗=A C⃗向量的乘法有数量积和矢量积两种运算方式。

数量积（内积）：两个向量之间的数量积等于两个向量的模长乘积与夹角的余弦值的乘积。

例如：A B⃗·B C⃗=|A B⃗|·|B C⃗|·cosθ矢量积（外积）：两个向量之间的矢量积等于两个向量的模长乘积与夹角的正弦值的乘积，结果是一个新的向量。

例如：A B⃗×B C⃗=|A B⃗|·|B C⃗|·sinθ·n⃗三、复数与向量的联系与应用复数与向量之间存在着密切的联系，复数可以看作是二维平面上的向量，实部为x轴的分量，虚部为y轴的分量。

在复平面中，复数与点的坐标完全对应，实部和虚部分别表示点的横坐标和纵坐标。

复数与向量的复数与向量的关系及应用复数与向量都是数学中的重要概念，它们在各个学科领域中都有广泛的应用。

本文将探讨复数与向量之间的关系以及它们在实际问题中的具体应用。

一、复数与向量的定义及表示方法1. 复数的定义与表示方法复数是由实部和虚部组成的数，可以用a+bi的形式表示，其中a为实部，b为虚部，i为虚数单位。

实部和虚部都是实数。

例如，3+4i就是一个复数，其中实部为3，虚部为4。

2. 向量的定义与表示方法向量是由大小和方向组成的量，可以用有序数对表示。

我们通常用加粗的小写字母或带箭头的小写字母表示向量，例如v或→v。

向量可以在平面内或空间中表示，可以用点的坐标表示，也可以用向量的模和方向表示。

二、复数与向量的关系1. 复数与有序数对的关系复数的实部和虚部分别对应有序数对的横坐标和纵坐标，可以将复数看作是平面上的点。

实部和虚部的关系确定了复数在平面上的位置。

2. 复数与向量的关系复数也可以看作是一个向量，实部和虚部可分别看作向量在x轴和y轴上的分量。

因此，复数的模和方向可以表示一个向量的大小和方向。

三、复数与向量的应用1. 复数在电路分析中的应用复数在电路分析中有广泛的应用，特别是在交流电路中。

复数的实部和虚部分别表示电流和电压的实部和虚部，可以通过相量法对电路进行计算和分析。

2. 向量在几何学中的应用向量在几何学中经常用于表示线段、线、面等几何对象，计算和描述它们的特性。

例如，在计算线段的长度、线的方程或面的法向量时，都需要用到向量的相关知识。

3. 复数与向量在物理学中的应用复数和向量在物理学中也有广泛的应用。

例如，在力学中，向量经常用于表示力、速度和加速度等物理量；在电磁学中，复数用于描述电场和磁场的相位差和振幅。

四、复数与向量的扩展应用1. 复数与向量在信号处理中的应用复数和向量在信号处理中有重要的应用，例如在频域分析中，信号可以用复数表示，通过复频域处理可以对信号进行滤波、变换等操作。

2. 复数与向量在机器学习中的应用复数和向量在机器学习领域中也有应用，例如在图像处理中，可以将图像看作是复数矩阵或向量，可以使用复数的性质进行图像的处理和分析。

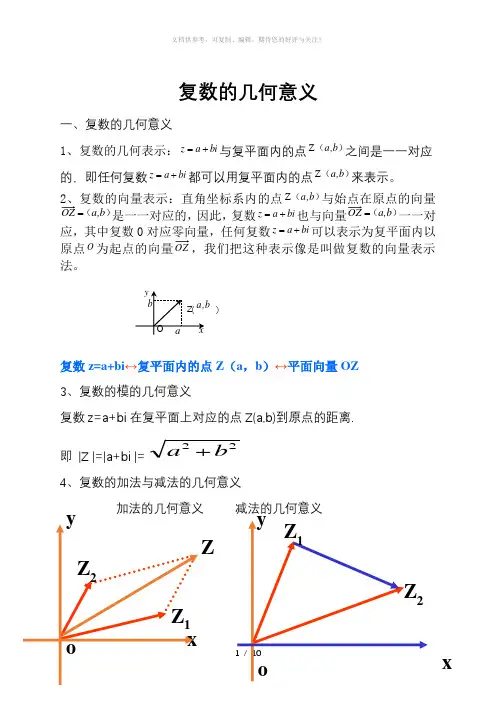
复数的几何意义一、复数的几何意义1、复数的几何表示：bi a z +=与复平面内的点）（b ,a Z 之间是一一对应的，即任何复数bi a z +=都可以用复平面内的点）（b ,a Z 来表示。

2、复数的向量表示：直角坐标系内的点）（b ,a Z 与始点在原点的向量）（b ,a OZ =是一一对应的，因此，复数bi a z +=也与向量）（b ,a OZ =一一对应，其中复数0对应零向量，任何复数bi a z +=可以表示为复平面内以原点O 为起点的向量OZ ，我们把这种表示像是叫做复数的向量表示法。

复数z=a+bi ↔复平面内的点Z （a ，b ）↔平面向量OZ 3、复数的模的几何意义复数z=a+bi 在复平面上对应的点Z(a,b)到原点的距离. 即 |Z |=|a+bi |=22b a +4、复数的加法与减法的几何意义加法的几何意义 减法的几何意义)ZZ 2Z1yz 1z 2≠0时， z 1+z 2对应的向量是以OZ 1、OZ 2、为邻边的平行四边形OZ 1ZZ 2的对角线OZ ， z 2-z 1对应的向量是Z 1Z 2 5、 复数乘法与除法的几何意义z 1=r 1（cos θ1+i sin θ1） z 2=r 2（cos θ2+i sin θ2）①乘法：z=z 1· z 2=r 1·r 2 [cos(θ1+θ2)+i sin(θ1+θ2)]如图：其对应的向量分别为oz oz oz 12→→→显然积对应的辐角是θ1+θ2 < 1 > 若θ2 > 0 则由oz 1→逆时针旋转θ2角模变为oz 1→的r 2倍所得向量便是积z 1·z 2=z 的向量oz →。

< 2 >若θ2< 0 则由向量oz 1→顺时针旋转θ2角模变为r 1·r 2所得向量便是积z 1·z 2=z 的向量oz →。

为此，若已知复数z 1的辐角为α，z 2的辐角为β求α+β时便可求出z 1·z 2=z a z 对应的辐角就是α+β这样便可将求“角”的问题转化为求“复数的积”的运算。

复数与向量复数（Complex numbers）和向量（Vectors）都是数学中非常重要的概念，它们在很多领域中都有广泛的应用，如物理学、工程学、计算机科学等。

尽管它们有相似之处，但它们仍然是不同的概念。

复数：复数是由实部和虚部组成的数。

实部是普通实数，而虚部是实数的倍数，通常用字母i （或j）表示。

虚数单位i的定义是i² = -1。

一个复数可以表示为 a + bi 的形式，其中a和b 是实数。

当虚部为零时，复数就变成实数。

复数的加法、减法和乘法运算可以通过相应的基本规则进行。

复数的几何表示通常使用复平面（complex plane），其中实部表示水平轴，虚部表示垂直轴。

复数z = a + bi 在复平面上的对应点(a, b)。

向量：向量是具有大小（长度，模）和方向的几何对象。

在数学中，向量通常用带箭头的线段表示。

向量可以表示为一对有序实数(x, y)，其中x和y是实数。

这两个实数分别表示向量在水平和垂直方向上的分量。

向量的加法和减法可以通过相应的几何规则进行。

向量的乘法包括点积（标量积）和叉积（向量积）。

点积返回一个标量，表示两个向量的大小和方向之间的相关性。

叉积返回一个垂直于两个向量所在平面的新向量，它的大小等于两个向量的大小与夹角正弦值的乘积。

总结：复数和向量都具有大小和方向的特性，但它们的应用和性质不同。

复数主要用于表示和解决涉及平方根的实数解为负数的问题，以及解析函数和信号处理等领域。

向量主要用于表示线性空间中的对象，以及在物理学、工程学、计算机科学等领域描述具有大小和方向的量。

平面向量的复数表示复数是数学中的一个重要概念，它既可以表示实数，也可以表示虚数。

而在平面向量的表示中，复数的使用也有着独特的意义和作用。

本文将介绍平面向量的复数表示方法，并探讨其应用。

一、复数与平面向量的关系复数是由实部和虚部构成的数，常用形式为a+bi，其中a为实部，b为虚部，i为虚数单位。

我们可以将复数看作是一个有序对(a,b)，与平面上的一个向量非常类似。

这种类比关系为我们理解复数与平面向量之间的联系奠定了基础。

二、向量的复数表示与几何意义1. 向量与复数的对应关系假设平面上有一个向量AB，其坐标分别为(x1,y1)，可以表示为复数z1=x1+iy1。

同样地，向量BA可以表示为z2=x2+iy2。

则向量AB与复数z1之间存在一一对应的关系。

2. 向量的模与幅角向量的模是指向量的长度，可以通过勾股定理来计算得到。

而复数的模定义为它与原点之间的距离，可以用公式|z|=√(a^2+b^2)来表示。

因此，向量的模与复数的模是等价的。

向量的幅角是指向量与x轴的夹角，可以用反三角函数来计算得到。

同样地，复数的幅角可以用反三角函数来计算得到。

向量AB的幅角即为与复数z1的幅角相对应。

三、平面向量的加减和数量积的复数表示1. 向量的加法与复数的加法向量的加法是指将两个向量的对应分量相加得到一个新的向量。

同样地，复数的加法是指将两个复数的实部与虚部分别相加得到一个新的复数。

假设有两个向量AB和AC，其复数表示分别为z1和z2。

则向量AB+AC的复数表示为z1+z2。

2. 向量的减法与复数的减法向量的减法是指将两个向量的对应分量相减得到一个新的向量。

同样地，复数的减法是指将两个复数的实部与虚部分别相减得到一个新的复数。

假设有两个向量AB和AC，其复数表示分别为z1和z2。

则向量AB-AC的复数表示为z1-z2。

3. 向量的数量积与复数的乘法向量的数量积是指将两个向量的对应分量相乘再相加得到一个实数。

同样地，复数的乘法是指将两个复数的实部与虚部分别相乘再相加得到一个新的复数。

复数的向量表示在数学和物理学中，复数是由实部和虚部组成的数，可以表示为a + bi的形式，其中a是实部，b是虚部，而i是虚数单位。

在向量表示中，复数可以被视为一个二维向量，由实部和虚部组成。

复数向量的表示可以提供更加简洁和方便的计算方式，尤其在涉及到向量运算和旋转操作的时候。

1. 复数向量的定义复数可以表示为一个向量(a, b)，其中a是实部，b是虚部。

这个向量可以用来表示复数的位置和方向。

2. 复数向量的运算对复数向量进行加法和乘法操作时，可以将其视为二维向量的运算。

具体地，复数向量的加法和乘法运算如下：加法：对于两个复数向量(a1, b1)和(a2, b2)，它们的加法运算为(a1 + a2, b1 + b2)。

乘法：对于两个复数向量(a1, b1)和(a2, b2)，它们的乘法运算为(a1 * a2 - b1 * b2, a1 * b2 + a2 * b1)。

3. 复数向量的表示和坐标系复数向量可以使用笛卡尔坐标系或极坐标系来表示。

在笛卡尔坐标系中，复数向量可以被视为一个有序对(a, b)，其中a是复数的实部，b是虚部。

而在极坐标系中，复数向量可以通过模长和幅角来表示。

笛卡尔坐标系：复数向量(a, b)可以被视为从坐标原点开始的有向线段，其中a表示线段的水平长度，b表示线段的垂直长度，且a和b的单位相同。

极坐标系：复数向量可以使用模长（也叫向量的长度）r和幅角（也叫向量的方向）θ来表示，即(r, θ)。

模长r表示复数向量与原点的距离，幅角θ表示向量与水平轴之间的夹角。

4. 复数向量的旋转由于复数向量可以表示为一个有向线段，因此可以通过旋转操作来改变复数向量的方向。

假设有一个复数向量(a, b)，我们希望将它顺时针旋转θ角度。

那么，我们可以通过以下公式计算旋转后的复数向量(a', b')：a' = a * cos(θ) - b * sin(θ)b' = a * sin(θ) + b * cos(θ)同样，如果我们希望将复数向量(a, b)逆时针旋转θ角度，那么可以使用以下公式计算旋转后的复数向量(a', b')：a' = a * cos(θ) + b * sin(θ)b' = -a * sin(θ) + b * cos(θ)5. 总结复数的向量表示为(a, b)，其中a是实部，b是虚部。

高中数学复数与向量的运算复数与向量是高中数学中重要的概念与工具，在数学的各个领域都有广泛的应用。

本文将介绍复数与向量的基本概念和运算，以及它们在数学中的应用。

一、复数的基本概念与运算1.1 复数的定义复数由实部和虚部构成，通常表示为z=a+bi。

其中，a称为实部，b 称为虚部，i为虚数单位，i满足i²=-1。

1.2 复数的运算复数的四则运算与实数类似，只需注意虚部之间的运算即可。

设z1=a1+b1i，z2=a2+b2i，其中a1、b1、a2、b2为实数，则复数的运算如下：- 加法：z1+z2=(a1+a2)+(b1+b2)i- 减法：z1-z2=(a1-a2)+(b1-b2)i- 乘法：z1*z2=(a1*a2-b1*b2)+(a1*b2+a2*b1)i- 除法：z1/z2=(a1*a2+b1*b2)/(a2²+b2²)+((a2*b1-a1*b2)/(a2²+b2²))i1.3 共轭复数若z=a+bi是一个复数，则它的共轭复数记作z*=a-bi。

共轭复数是复数的实部不变，虚部取相反数的结果。

1.4 复数的模与参数对于复数z=a+bi，它的模记作|z|=√(a²+b²)，参数记作θ=tan⁻¹(b/a)。

模表示复数的绝对值大小，参数表示复数所在的极坐标角度。

二、向量的基本概念与运算2.1 向量的定义向量是有方向和大小的量，通常用箭头表示。

在空间中，向量可以表示为一个有序数组(a₁, a₂, a₃)，其中a₁、a₂、a₃为实数。

2.2 向量的表示与坐标在平面直角坐标系中，向量可以表示为一个有向线段，起点为原点，终点为箭头所指向的位置。

向量也可以通过坐标表示，例如向量AB可以表示为向量→AB=(x₂-x₁, y₂-y₁)。

2.3 向量的加法与减法向量的加法和减法操作可以通过将向量首尾相接的方法进行。

设向量→A=(x₁, y₁)，→B=(x₂, y₂)，则向量的加法和减法如下：- 加法：→A+→B=(x₁+x₂, y₁+y₂)- 减法：→A-→B=(x₁-x₂, y₁-y₂)2.4 向量的数量积与向量积向量的数量积又称为点积，表示为→A·→B=|→A||→B|cosθ，其中θ为→A和→B之间的夹角。

数字的复数与向量在数学领域中，我们经常会遇到数字的复数和向量的概念。

虽然它们有不同的定义和用途，但在某些情况下，我们可以将它们联系起来。

本文将介绍数字的复数与向量之间的关系，并进一步探讨它们在数学和实际应用中的重要性。

一、数字的复数数字的复数是由实部和虚部组成的数，通常表示为a+bi的形式，其中a和b是实数，i是虚数单位，满足i^2 = -1。

实部a表示复数在实数轴上的位置，而虚部bi则表示复数在虚数轴上的位置。

复数在数学中有广泛的应用，特别是在代数和分析中。

它们可以用于解决方程、表示波动和振荡现象等。

复数还具有求模、共轭和幂等等运算属性，使得我们能够更方便地进行计算和推导。

在实际应用中，复数也扮演着重要的角色。

例如，复数的幅度和相位可以描述电路中的交流信号，从而帮助我们分析电路的行为。

此外，复数还可以用于描述波函数、频域分析等领域。

二、向量向量是具有大小和方向的量，通常用箭头或粗体字母表示。

向量可以在二维或三维空间中进行表达，也可以用更高维度的向量表示。

向量的重要性在于它可以用于表示物理量的方向和大小。

例如，位移、速度和加速度等都可以用向量进行描述。

向量还可以进行加法、减法和数量乘法等运算，以及与矩阵和标量的运算。

在几何学和物理学中，向量被广泛应用于描述物体的运动和力的作用。

通过向量运算，我们可以计算物体的位移、速度、加速度等，从而更好地理解物体的运动规律和行为。

三、数字的复数与向量的联系虽然数字的复数和向量本身是不同的概念，但在某些情况下，我们可以将它们联系起来。

例如，在二维平面中，可以将复数a+bi表示为向量(a, b)。

这种联系的好处是我们可以利用向量的性质来研究复数的性质。

例如，我们可以将复数的加法和乘法表示为向量的加法和数量乘法，从而更直观地理解和计算复数的运算。

此外，复数和向量都具有模的概念。

复数的模表示复数到原点的距离，而向量的模表示向量的大小。

我们可以使用向量的模来计算复数的模，从而更方便地求解复数的性质和运算。

复数的平面表示与乘法公式复数在数学中扮演着重要的角色，它们不仅可以通过平面上的向量来表示，并且拥有一套完整的乘法规则。

本文将详细介绍复数的平面表示以及乘法公式的应用。

一、复数的平面表示复数可以用平面上的向量表示，其中向量的模表示复数的绝对值，向量的方向表示复数的辐角。

具体而言，我们假设复数z的实部为x，虚部为y，则可以表示为z=x+yi，其中i为虚数单位，i²=-1。

在平面直角坐标系中，我们可以将复数z对应的向量OZ的起点放在原点O(0,0)，并将Z的终点坐标设为(z1, z2)，其中z1表示实部x方向上的长度，z2表示虚部y方向上的长度。

这样，向量OZ就完整地表示了复数z。

二、复数的乘法公式复数的乘法公式是复数的重要性质之一，它可以帮助我们计算两个复数的乘积。

假设有两个复数z₁=x₁+y₁i和z₂=x₂+y₂i，我们需要计算它们的乘积z=z₁z₂。

利用复数的定义，我们可以将z₁和z₂展开成实部和虚部的形式，即z₁=x₁+yi和z₂=x₂+y₂i。

根据乘法运算的性质，我们可以按照以下步骤来计算复数的乘积：1. 计算实部的乘积：z₁z₂的实部为(x₁+yi)(x₂+y₂i)的实部，即Re(z)=x₁x₂-y₁y₂。

2. 计算虚部的乘积：z₁z₂的虚部为(x₁+yi)(x₂+y₂i)的虚部，即Im(z)=x₁y₂+x₂y₁。

3. 结合实部和虚部的结果：将步骤1和步骤2得到的结果合并，即可得到复数z的具体表达形式。

三、复数乘法的几何解释复数的乘法公式不仅可以通过代数方法计算，还可以通过几何方法进行解释。

对于给定的复数z₁和z₂，将它们所对应的向量终点分别设为A和B，则复数乘法的几何解释如下：1. 复数的模的乘积：|z₁z₂|=|z₁||z₂|，即复数乘法的模等于乘积的模的乘积。

2. 复数的辐角的和：arg(z₁z₂)=arg(z₁)+arg(z₂)，即复数乘法的辐角等于乘积的辐角之和。

通过这些几何解释，我们可以更好地理解复数乘法的性质以及其在平面上的作用。