2014年秋季学期新版新人教版七年级数学上册2.2整式的加减教案设计
- 格式:doc
- 大小:74.00 KB
- 文档页数:5

合并同类项教学设计教材分析:1、教材所处的地位及作用:本节课选自新人教版数学七年级上册§2.2节,是学生进入初中阶段后,在学习了用字母表示数,单项式、多项式以及有理数运算的基础上,对同类项进行合并、探索、研究的一个课题。
合并同类项是本章的一个重点,其法则的应用是整式加减的基础,也是以后学习解方程、解不等式的基础。
另一方面,这节课与前面所学的知识有千丝万缕的联系:合并同类项的法则是建立实际生活中分类问题的基础之上;在合并同类项过程中,要不断运用数的运算法则。
可以说合并同类项是有理数加减运算的延伸与拓广。
因此,这节课是一节承上启下的课。
2、学情分析: 七年级学生刚刚跨入少年期,理性思维的发展还很有限,他们在身体发育、知识经验、心理品质方面,依然保留着小学生的天真活泼、对新生事物很感兴趣、求知欲望强、具有强烈的好奇心与求知欲,形象直观思维已比较成熟,但抽象思维能力还比较薄弱。
于是我根据学生和中小学教材衔接的特点设计了这节课。
二、教学目标:1.知识目标:(1)理解同类项的概念;(2)掌握合并同类项的方法;(3)通过生活实际中的分类方法探究合并同类项的法则,从中体会类比的数学思想.2.能力目标:(1)在具体的情景中,通过观察、比较、交流等活动认识同类项,了解数学分类的思想;并且能在多项式中准确判断出同类项。
(2)在具体情景中,通过探究、交流、反思等活动获得合并同类项的法则,体验探求规律的思想方法;并熟练运用法则进行合并同类项的运算,体验化繁为简的数学思想。
3.过程与方法:组织学生参与学习、讨论,在合作探究活动中获取知识。
4.情感态度与价值观:激发学生的求知欲,培养独立思考和合作交流的能力,让他们享受成功的喜悦。
三、教学重点、难点:根据学生的认知水平、认知能力以及教材的特点,确定以下重、难点:重点:同类项的概念及合并同类项的法则.难点:正确判断同类项,准确合并同类项.四、教学方法与教学策略:(1)教法分析:基于本节课内容的特点和七年级学生的心理特征,我在教学中选择互助式学习模式,与学生建立平等融洽的关系,营造自主探索与合作交流的氛围,共同在实验、演示、操作、观察、练习和展示等活动中运用多媒体来提高教学效率,验证结论,激发学生学习的兴趣和积极思考。

人教版数学七年级上册2.2《整式的加减(2)》教学设计一. 教材分析人教版数学七年级上册2.2《整式的加减(2)》主要包括了整式的加减运算,这一节内容是学生在学习了整式的加减(1)之后进一步加深对整式加减运算的理解和掌握。
教材通过例题和练习题,使学生能够熟练运用加减运算的规则,解决实际问题。
本节内容在初中数学中占有重要地位,为后续的代数学习和解决实际问题打下基础。
二. 学情分析学生在学习本节内容前,已经学习了整式的加减(1),对整式的加减运算有了初步的了解。
但部分学生可能对整式加减运算的规则理解不透彻,运算过程中容易出错。
因此,在教学过程中,需要关注学生的学习情况,针对性地进行讲解和辅导,帮助学生巩固知识,提高运算能力。
三. 教学目标1.理解整式加减的运算规则,能够熟练进行整式的加减运算。
2.能够运用整式加减运算解决实际问题。
3.培养学生的逻辑思维能力和团队合作能力。
四. 教学重难点1.教学重点:整式加减的运算规则和运用。
2.教学难点:整式加减运算在实际问题中的应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究整式加减的运算规则。
2.利用多媒体课件,直观展示整式加减的过程,帮助学生理解。
3.通过小组合作讨论,培养学生的团队合作能力。
4.注重练习,巩固所学知识,提高学生的运算能力。
六. 教学准备1.多媒体课件2.教学卡片七. 教学过程1.导入(5分钟)利用多媒体课件,展示一些实际问题,引导学生运用已学的整式加减知识解决。
让学生体会到整式加减在实际问题中的重要性。
2.呈现(10分钟)通过例题,讲解整式加减的运算规则。
引导学生观察、分析、总结运算规则。
在此过程中,注意关注学生的学习情况,及时进行讲解和辅导。
3.操练(10分钟)让学生分组进行练习,互相批改,教师巡回指导。
针对学生出现的问题,进行针对性讲解,帮助学生巩固知识。
4.巩固(10分钟)出示一些巩固练习题,让学生独立完成。
教师选取部分学生的作业进行讲解,分析其解题思路,帮助其他学生提高。



2.2 整式的加减第1课时 整式的加减(一)教学目标1.理解同类项的概念. 2.掌握合并同类项的法则.3.能够运用合并同类项的法则进行计算. 教学重点运用合并同类项的法则进行运算. 教学难点理解合并同类项法则. 教学设计 (设计者: )教学过程设计一、创设情境 明确目标 1.(1)5个人+8个人= (2)5 cm +8 cm = (3)5个人+8 cm =2.观察下列各单项式,把你认为相同类型的式子归为一类. 8x 2y ,-mn 2,5a ,-x 2y ,7mn 2,38,9a ,-xy 232,59,2xy 2.归类理由:________________________________________________________________________二、自主学习 指向目标自学教材第62至64页,完成下列问题:1.同类项是指所含__字母__相同,并且相同的__字母__的__指数__也相同的项. 2.下列各组式子中,为同类项的是( B )A .3x 2y 与-3xy 2B .3xy 与-2yxC .2x 与2x 2D .5xy 与5yz 3.若5x 2m y n与3x 4y2n -1是同类项,则m -n =__1__.4.把多项式中的__同类项__合并成一项,叫做合并同类项.5.合并同类项后,所得项的系数是合并前各同类项的__系数的和__,且字母连同它的__指数__不变.三、合作探究 达成目标 探究点一 同类项的概念活动一:找出下列各式中是同类项的归为一类: 8x 2y ,-mn 2,5a ,-x 2y ,7n 2m ,38,9a ,-xy 232,59,2xy 2.【展示点评】先观察两项中所含字母是否相同,再判定相同字母的指数是否相等,然后得出结论,注意所有的常数项都是同类项.【小组讨论】同类项需要满足什么条件?与系数有关吗?【反思小结】同类项应满足下列两个条件:(1)所含的字母相同;(2)相同字母的指数也分别相同.判断是否是同类项与字母的排列顺序无关,与系数无关;另外所有的常数项都是同类项.【针对训练】见“学生用书”. 探究点二 合并同类项活动二:合并下列各式的同类项: (1)xy 2-15xy 2;(2)-3x 2y +2x 2y +3xy 2-2xy 2; (3)4a 2+3b 2+2ab -4a 2-4b 2.【展示点评】先找出同类项,然后利用分配律对系数相加减,完成合并同类项. 【小组讨论】合并同类项的一般步骤是什么?同类项加减是计算的是哪一部分?合并同类项的依据是什么?【反思小结】合并同类项的一般步骤是:首先找出题目中的同类项,用加法的交换律和结合律把它们结合起来,然后运用合并同类项法则进行计算.合并同类项的依据是乘法的分配律.注意:(1)合并的前提是有同类项,不是同类项不能合并;(2)移项时要带着符号一起移动;(3)只是系数相加,字母及字母的指数不变.【针对训练】见“学生用书”. 四、总结梳理 内化目标 1.概念:同类项. 2.法则:合并同类项. 3.注意的问题.同类项―→合并同类项―→实际运用 五、达标检测 反思目标1.若3a 2b n与4a m b 4是同类项,则m =__2__,n =__4__.2.在7x 2-4x +1-x 2-2+6x 中,7x 2与__-x 2__是同类项,6x 与__-4x __是同类项,-2与__1__是同类项.3.34a 5b 2m 与-23a n b 6可以合并成一项,那么m +n =__8__. 4.下列各组中,不是同类项的是( A )A .2b 与3ab 2B .2x 2y 与-2x 2y C .5与13 D .-2x m 与-3x m5.合并同类项:(1)-3x 2y +5xy 2-6xy 2+4-7x 2y -9; (2)a 3-a 2b +ab 2+a 2b -ab 2+b 3. 解:(1)-xy 2-10x 2y -5 (2)a 3+b 3六、布置作业 巩固目标 课后作业 见“学生用书”.第2课时 整式的加减(二)教学目标1.会利用合并同类项的法则进行化简、求值. 2.能用整式的加减解决简单的实际问题. 教学重点多项式的化简、求值. 教学难点运用多项式的加减解决实际问题. 教学设计 (设计者: )教学过程设计一、创设情境 明确目标为了搞好班会活动,李明和X 强去购买一些水笔和软面抄作为奖品.他们首先购买了15本软面抄和20支水笔,经过预算,发现这么多奖品不够用,然后他们又去购买了6本软面抄和5支水笔.问:①他们两次共买了多少本软面抄和多少支水笔?②若设软面抄的单价为每本x 元,水笔的单价为每支y 元,则这次活动他们支出的总金额是多少元?二、自主学习 指向目标自学教材第64至65页,完成下列问题:1.求多项式的值,首先要__化简__,再代入__计算__.2.在求值代入时,省略的乘号要__写出__,负数遇乘方,乘除法时要添加__括号__. 3.如果两个同类项的系数是互为相反数,那么合并的结果为__0__. 三、合作探究 达成目标 探究点一 多项式的化简与求值活动一:(1)求多项式2x 2-5x +x 2+4x -3x 2-2的值,其中x =12;(2)求多项式3a +abc -13c 2-3a +13c 2的值,其中a =-16,b =2,c =-3.【展示点评】求多项式的值时,常先合并同类项,化简后再代入求值,这样比较简单. 【小组讨论】请你把字母的值直接代入原式求值.与例2的运算过程比较,哪种方法更简便?求多项式的值的一般步骤是什么?【反思小结】计算一个代数式的值有时需要先将代数式合并同类项,进行化简再把字母的取值代入进行计算比较简便.【针对训练】见“学生用书”. 探究点二 整式加减的实际应用活动二:(1)水库中水位第一天连续下降了a h ,每小时平均下降2 cm ;第二天连续上升了a h ,每小时平均上升0.5 cm ,这两某某位总的变化情况如何?(2)某商店原有5袋大米,每袋大米为x kg.上午卖出3袋,下午又购进同样包装的大米4袋.进货后这个商店有大米多少千克?【展示点评】运用正、负数的意义,列出整式,化简研判. 【小组讨论】说说相反意义的量如何表示出来.【反思小结】与整式的加减有关的实际问题,若出现上升、涨了、多了等词语,则用“+”,若出现了下降、跌了、少了、卖出等词语,则用“-”.【针对训练】见“学生用书”. 四、总结梳理 内化目标 1.整式的化简、求值. 2整式的求值的步骤. 五、达标检测 反思目标1.单项式2x 2,-5x 2y ,-x 2y 的和是__2x 2-6x 2y __. 2.多项式-3x 2y -10x 3+6x 3y +3x 2y -6x 3y +7x 3-2的值( B ) A .与x 、y 都有关 B .只与x 有关 C .只与y 有关 D .与x 、y 都无关3.当x =-1,y =12时,式子x 2+xy -3xy 的值是__2__.4.已知2x 6y 2与-13x 3m y n 是同类项,则多项式9m 2-5mn -17的值为( A )A .-1B .-2C .-3D .-45.求2x 2-3xy +y 2-2xy -2x 2+5xy -2y +1的值,其中x =-20132012,y =-1.解:4六、布置作业巩固目标课后作业见“学生用书”.第3课时整式的加减(三)教学目标1.能运用运算律探究去括号法则,掌握去括号法则.2.熟练地运用去括号法则化简整式.教学重点运用去括号法则化简整式.教学难点理解括号前面是负因数的去括号法则.教学设计(设计者:)教学过程设计一、创设情境明确目标现在我们来看本章引言中的问题(3):在格尔木到某某路段,如果列车通过冻土地段要t h,那么它通过非冻土地段的时间为(t-0.5) h,于是,冻土地段的路程为100t km,非冻土地段的路程为120(t-0.5) km,因此,这段铁路全长为100t+120(t-0.5) km①冻土地段与非冻土地段相差100t-120(t-0.5) km②上面的式子①、②都带有括号,它们应如何化简?二、自主学习指向目标自学教材第65至67页,完成下列问题:1.①120(t-0.5)=120t-120×0.5;②-120(t-,其理论依据是__乘法分配律__.2.比较1中的①与②等号左、右两边的异同,得出规律是:括号前面的因数是正数,去括号后__括号里各项的符号都不变__,括号前面的因数是负数,去括号后__括号里各项的符号都改变__.3.(1)+(x-2y+3)=__x-2y+3__;(2)-(x-2y+3)=__-x+2y-3__;(3)+(x-3)=__x-3__;(4)-(x-3)=__-x+3__.4.(1)括号前面是“+”号,去掉括号和它前面的“+”,括号里面各项都__不改变符号__;(2)括号前面是“-”号,去掉括号和它前面的“-”,括号里面各项都__改变符号__.三、合作探究达成目标探究点一应用去括号法则计算活动一:化简下列各式:(1)8a+2b+(5a-b);(2)(5a-3b)-3(a2-2b).【展示点评】第(1)题括号前是“+”号,去掉括号,括号里的各项不变号,第(2)题括号前有系数,要将这个数乘以括号内的每一项.【小组讨论】去括号时应注意什么?去括号的依据是什么?【反思小结】(1)去括号时,括号内的每一项都要参与,做到要变,括号内的每一项都变号;要不变,括号内的每一项都不改变号.去括号的依据是乘法的分配律.【针对训练】见“学生用书”.探究点二去括号法则的实际应用活动二:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是a km/h.(1)2 h后两船相距多远?(2)2 h后甲船比乙船多航行多少千米?【展示点评】船顺水航行的速度=船在静水中的速度+水速,船逆水航行速度=船在静水中行驶速度-水速.因此,甲船速度为(a +50) km/h ,乙船速度为(50-a) km/h ,2 h 后,甲船行程为2(a +50) km ,乙船行程为2(50-a) km.【小组讨论】想想风中飞行,是否同水中航行问题具有类似的道理.【反思小结】风中飞行同样具有顺风和逆风飞行的问题.顺风飞行速度=飞行物在无风中的飞行速度+风速;逆风飞行速度=飞行物在无风中的飞行速度-风速.【针对训练】见“学生用书”. 四、总结梳理 内化目标 1.法则:去括号. 2.依据:去括号.3.数的运算律和运算性质在整式的加减运算中仍然成立.去括号法则⎩⎪⎨⎪⎧括号外是正因数括号外是负因数―→实际运用五、达标检测 反思目标1.x +(y -z)=__x +y -z __,x -(y -z)=__x -y +z __. 2.2a -(a +b)=__a -b __,2a +(-a +b)=__a +b __. 3有理数-a +b -c 的相反数是__a -b +c __.4.如果长方形的周长为4m ,一边长为m -n ,则另一边长为__m +n __. 5.下列各式与x 3-5x 2-4x +9相等的是( C ) A .(x 3-5x 2)-(-4x +9) B .x 3-5x 2-(4x +9) C .-(-x 3+5x 2)-(4x -9) D .x 3+9-(5x 2-4x) 6.化简下列各式(1)-5(m 3-3)-2(3m 3-6); (2)2(x -3y)+3(2x -4y); (3)(2xy -y)-(-y +xy);(4)(6a 2-2b 2)-(-a 2+2ab +b 2)-(a 2-4ab +3b 2).解:(1)-11m3+27(2)8x-18y(3)xy(4)6a2-6b2+2ab六、布置作业巩固目标课后作业见“学生用书”.第4课时整式的加减(四)教学目标1.掌握整式的加减的运算法则,会进行整式的加减运算.2.能运用整式的加减运算解决一些简单的问题.教学重点进行整式的加减运算.教学难点运用整式的加减解决实际问题.教学设计(设计者:)教学过程设计一、创设情境明确目标某学生合唱团出场时第一排站了n名,从第二排起每一排都比前一排多一人,一共站了四排,则该合唱团一共有多少名学生参加?①学生写出答案:________________________________________________________________________②以上答案能进一步化简吗?如何化简?我们进行了哪些运算?二、自主学习指向目标自学教材第67至69页,完成下列问题:1.计算:(1)(2x-3y)+(5x+4y);(2)(8a-7b)-(4a-5b).解:(1)7x+y;(2)4a-2b.2.整式加减的实质是__合并同类项__. 三、合作探究 达成目标 探究点一 整式的加减活动一:求12x -2(x -13y 2)+(-32x +13y 2)的值,其中x =-2,y =23.【展示点评】先去括号,然后合并同类项,最后代入数值计算. 【小组讨论】进行整式的加减求值运算的一般步骤有哪些?【反思小结】去括号和合并同类项是整式加减的基础,整式加减的一般步骤可概括为:(1)如果有括号,先去括号;(2)如果有同类项,再合并同类项.【针对训练】见“学生用书”. 探究点二 整式加减的实际应用活动二:做大小两个长方体纸盒,尺寸如下(单位:cm)(1)做这两个纸盒共用料多少平方厘米? (2)做大纸盒比做小纸盒多用料多少平方厘米?【展示点评】先计算小纸盒的表面积,再计算大纸盒的表面积,然后将它们相加解第(1)问,相减解第(2)问.【小组讨论】解整式加减的实际应用题的一般步骤有哪些?【反思小结】通常是先根据实际情况,列出代数式,然后运用整式的加减原理化简计算. 【针对训练】见“学生用书”. 四、总结梳理 内化目标 1.法则:整式的加减. 2.步骤:整式的加减. 3.整式的加减的运用.word11 / 11 ⎭⎪⎬⎪⎫合并同类项去括号―→整式的加减―→实际应用 五、达标检测 反思目标1.-3(a +b)+(2a -b)=__-a -4b __.2.已知A =5a 2+2ab +6,B =7ab +8a 2-7,则A -B =__-3a 2-5ab +13__.3.一个多项式与多项式-a 3+6a -9的和是2a 3-3a 2+6a +5,则这个多项式为( B )A .a 3-3a 2+6a -4B .3a 3-3a 2+14C .a 3-3a 2-4D .-3a 3+3a 2-144.已知多项式A =x 2+2y 2,B =-4x 2+3y 2,且A +B +C =0,则C 为( B )A .-3x 2+5y 2B .3x 2-5y 2C .-3x 2-5y 2D .3x 2+5y 25.计算(1)(3xy -2x 2-3y 2)+(x 2-5xy +3y 2);(2)5(3a 2b -ab 2)-(ab 2+3a 2b);(3)3(x 2-5xy)-4(x 2+2xy -y 2)-(y 2-3xy).解:(1)-2xy -x 2(2)12a 2b -6ab 2(3)-x 2-20xy +3y 2六、布置作业 巩固目标课后作业 见“学生用书”.。
人教版七年级数学上册2.2《整式的加减》教学设计一. 教材分析人教版七年级数学上册2.2《整式的加减》是学生在掌握了整式的概念和运算法则的基础上进行学习的内容。
本节内容主要介绍了整式的加减法运算,包括同类项的定义、合并同类项的法则等。
通过本节内容的学习,学生能够熟练掌握整式的加减法运算,并能够解决实际问题。
二. 学情分析学生在进入七年级之前,已经学习了整数和分数的加减法运算,具备了一定的数学基础。
但是,对于整式的加减法运算,学生可能还存在着一些困惑,例如对同类项的理解和合并同类项的方法等。
因此,在教学过程中,需要注重对学生基础知识的巩固和拓展,通过实例讲解和练习,帮助学生理解和掌握整式的加减法运算。
三. 教学目标1.知识与技能:学生能够理解同类项的定义,掌握合并同类项的法则,能够进行整式的加减法运算。
2.过程与方法:通过实例讲解和练习,培养学生的数学思维能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣和热情,培养学生的团队合作意识和自主学习能力。
四. 教学重难点1.教学重点:同类项的定义,合并同类项的法则,整式的加减法运算。
2.教学难点:同类项的判断,合并同类项的技巧,解决实际问题。
五. 教学方法1.情境教学法:通过实例讲解和生活实际问题,引发学生的兴趣和思考,引导学生主动参与学习。
2.合作学习法:学生进行小组讨论和合作交流,培养学生的团队合作意识和沟通能力。
3.实践操作法:通过练习和操作,让学生动手动脑,巩固所学知识,提高解决问题的能力。
六. 教学准备1.教学PPT:制作精美的PPT,展示教学内容和实例。
2.练习题:准备适量的练习题,用于学生的操练和巩固。
3.教学工具:准备黑板、粉笔、投影仪等教学工具。
七. 教学过程1.导入(5分钟)利用PPT展示一些实际问题,如购物时找零、制作蛋糕等,引导学生思考如何运用整式的加减法来解决问题。
激发学生的兴趣和思考,为后续学习做好铺垫。
2.呈现(10分钟)通过PPT呈现同类项的定义和合并同类项的法则,结合实例进行讲解。
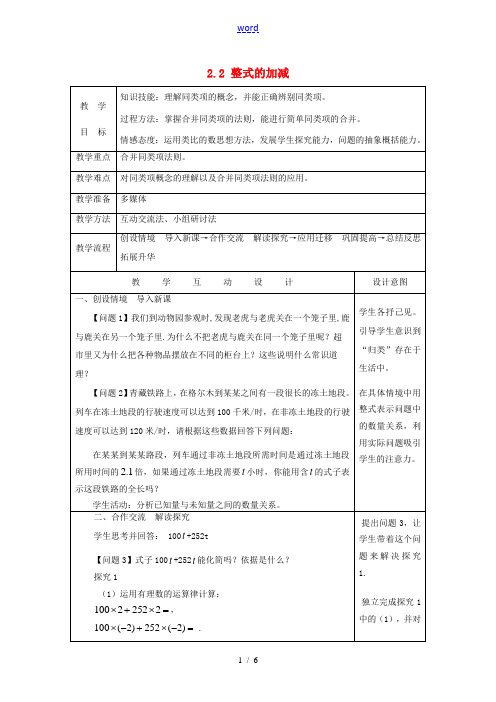
2.2 整式的加减教 学 目 标知识技能:理解同类项的概念,并能正确辨别同类项。
过程方法:掌握合并同类项的法则,能进行简单同类项的合并。
情感态度:运用类比的数思想方法,发展学生探究能力,问题的抽象概括能力。
教学重点 合并同类项法则。
教学难点 对同类项概念的理解以及合并同类项法则的应用。
教学准备 多媒体教学方法 互动交流法、小组研讨法 教学流程创设情境 导入新课→合作交流 解读探究→应用迁移 巩固提高→总结反思 拓展升华教 学 互 动 设 计设计意图 一、创设情境 导入新课【问题1】我们到动物园参观时,发现老虎与老虎关在一个笼子里,鹿与鹿关在另一个笼子里.为什么不把老虎与鹿关在同一个笼子里呢?超市里又为什么把各种物品摆放在不同的柜台上?这些说明什么常识道理?【问题2】青藏铁路上,在格尔木到拉萨之间有一段很长的冻土地段。
列车在冻土地段的行驶速度可以达到100千米/时,在非冻土地段的行驶速度可以达到120米/时,请根据这些数据回答下列问题:在西宁到拉萨路段,列车通过非冻土地段所需时间是通过冻土地段所用时间的1.2倍,如果通过冻土地段需要t 小时,你能用含t 的式子表示这段铁路的全长吗?学生活动:分析已知量与未知量之间的数量关系。
学生各抒己见。
引导学生意识到“归类”存在于生活中。
在具体情境中用整式表示问题中的数量关系,利用实际问题吸引学生的注意力。
二、合作交流 解读探究学生思考并回答: 100t +252t【问题3】式子100t +252t 能化简吗?依据是什么? 探究1(1)运用有理数的运算律计算: =⨯+⨯22522100 ,=-⨯+-⨯)2(252)2(100 .(2)根据(1)中的方法完成下面的运算,并说明其中的道理. =+t t 252100 . 探究2(1)=-t t 252100( )t (2)=+2223x x ( )2x (3)=-2243ab ab ( )学生活动:在独立完成的基础上,小组合作交流。
提出问题3,让学生带着这个问题来解决探究1.独立完成探究1中的(1),并对(2)进行分组讨论.通过对探究1和探究2的探讨,引出同类项的概念。
教师提问,想一想:1.上面三个多项式有哪些单项式组成? 2.每个多项式中的单项式有什么共同特点?你能运算吗? 观察多项式中各项的特点,得出同类项的概念以及合并同类项的概念. 同类项:所含字母相同,并且相同的字母的指数也相同的项. 合并同类项:把多项式中的同类项合并成一项. 1、玩一玩:找同类项朋友 方法:1、现在,黑板上有16张写有单项式的卡片; 2、同学们把认为是同类项的卡片用数字序号 找出来; 3、请其他同学做裁判,看看他们有没有找错朋友。
31,21,9,161,5,52,,4,1,2,5%,2,10,,222222322abc ab ab x y y x x y x yx ab ba c abc x -----π, 学生活动:合作交流,找出答案,明确过程。
教师活动:教师巡回指导,待学生完成后,叫学生回答,确认。
【问题4】 试一试:试着把多项式合并同类项:28372422--+++x x x x(1) 这个多项式中含有哪些项?(2) 各项的系数是多少?(3) 那些项可以合并成一项?为什么?类比有理数的运算,探究得出合并同类项的法则.法则:所得项的系数是合并前各同类项系数的和,字母部分不变. 注意:(1) 合并的前提是同类项。
(2) 合并指的是系数相加,字母和字母的指数保持不变。
(3) 合并同类项的根据是加法交换律、结合律以及分配律。
师生活动:教师引导下,师生合作得出结论,共同归纳总结。
3.练一练:下列计算对不对?若不对,请改正。
22)5(33)4(437)3(523)2(532)1(22422=-=-=-=+=+ba ab m n m n m n x x xy y x x x x师生活动:教师出示问题,学生合作交流,叫个别同学回答。
学生接受同类项的定义不是很难,但是做到判断无误却很困难,需要通过练习,反复强调同类项判断标准,使学生通过甄别、比较,逐步提高准确度和熟练程度.提出问题4,让学生通过对问题的解决,得出合并同类项概念以及合并同类项的法则。
三、应用迁移 巩固提高【例1】合并下列各式的同类项: (1)2251xy xy -; 再次强调同类项的概念,能够熟练的判别同类项(当字母不止一2.练一练 判断下列各组中的两项是否是同类项: (1) -5ab 3与3a 3b ( ) (2)3xy 与3x( ) (3) -5m 2n 3与2n 3m 2( ) (4)53与35 ( ) (5) x 3与53 ( )(2)22222323xy x y y x y x -++-; (3)222244234b a ab b a --++. 解(1)2254)511(xy xy =-= (2) 2222)23()23(xyy x xy y x +-=-++-=(3) abb abb a abb b a a 22)43()44(2)43()44(2222222+-=+-+-+-+-=【例2 】 (1) 求多项式2x 2-5x+x 2+4x-3x 2-2的值,其中12x =; (2) 求多项式22113333a abc c a c +--+的值,其中16a =-,b=2,c=-3的值。
解:(1)2522121 22)45()312(234522222-=--=--=-+-+-+=--++-时,原式=当x x x x x x x x x(2)13-261-3,2,61)3131()33(313313222)=()时,原式=(当⨯⨯-==-==+-++-=+--+c b a abcc abc a c a c abc a 【例3 】(1) 水库中水位第一天连续下降了a 小时,每小时平均下降2cm ;第二天连续上升了a 小时,每小时平均上升0.5m ,这两天水位总的变化情况如何?(2) 某商店原有5袋大米,每袋大米为x 千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?解:(1)把下降的水位变化量记为负,上升的水位变化量记为正,第一天水位的变化量是-2acm ,第二天水位的变化量是0.5acm.两天水位的总变化量(单位:cm )是 -2a+0.5a=(-2+0.5)a=-1.5a这两天水位总的变化情况为下降了1.5acm(2)把进货的数量记为正,售出的数量记为负。
进货后这个商店共有大米(单位:kg ) 5x-3x+4x=(5-3+4)x=6x个时,与字母的顺序无关,如(2)中的22xy -和x y 23通过例题,进一步使学生明确合并同类项的步骤、方法。
学生先独立完成,教师巡视,教师引导学生对以下两种做法进行比较:直接代入求值,先化简再求值,看哪种方法更简童。
教师引导学生回忆第一章中用正负数代表具有相反意义的量,然后由学生独立完成。
本次活动教师应重点关注:(1) 学生对同类项的辨别;(2) 学生应用合并同类项法则的准确性和熟练性;(3) 学生能否用正负数表示题目中具有相反学生活动:在独立完成的基础上,小组合作交流,讨论解题过程以及结果的合理性。
先完成(1)后教师讲评,学生再做。
教师活动:讲评(1)后,教师巡回指导,师生共同总结。
合并同类项一般步骤:1.找:找出多项中的同类项;2.移:将同类项移动位置,集中在一起;3.并:将系数相加,字母部分不变.注意:(1)只有同类项才能合并,移动项时应连同符号.(2)多项式中含有两种以上的同类项时,为防止漏项或混淆,可先在各项的下边用不同的记号标出各种同类项,然后进行合并.(3)合并后的结果通常按某个字母降幂或升幂排列。
方法:(1)系数:系数相加;(2)字母:字母和字母的指数不变。
【随堂练习】1.下列各组是同类项的是()A 2x3与3x2B 12ax与8bxC x4与a4D π与-32.合并同类项正确的是()A、4a+b=5abB、6xy2-6y2x=0C、6x2-4x2=2D、3x2+2x3=5x53.5x2y和42y m x n是同类项,则m=____, n=_____。
4. -4x2-6x+6-2x2+8x-45.若5xy2+axy2=-2xy2,则a=___; 意义的量;(4) 学生应用所学知识解决实际问题的能力。
四、板书设计1.同类项的定义:所含字母相同,并且相同字母的指数也相同的项叫做同类项。
所有的常数项也是同类项2.①判断同类项的依据:(1)所含字母相同;(2)相同字母的指数相同;②同类项与系数无关;③同类项与它们所含字母的顺序无关3.合并同类项的法则:把同类项的系数相加,作为结果的系数,字母及字母的指数不变。
五、总结反思拓展升华通过本节课的学习,你有哪些收获与感悟?1.同类项的定义。
2.同类项的判定方法。
3.合并同类项的法则。
六、作业设计P69 1 、 p70 5教学反思:。