Note 01 - 压电振子的振动模式 山东大学
- 格式:pps
- 大小:509.00 KB
- 文档页数:100

压电振子的振动模态压电振子是一种通过压电效应使机械振子发生振动的器件。
压电效应是一种物质在被施加压力或受到电场作用时,会产生电荷分离或电势变化的现象。
这种效应可以应用于振动系统中,使系统产生稳定的振荡。
由于压电振子是通过外部施加的电场来产生振动的,因此其振动模态受到电场频率的控制。
一般而言,压电振子的振动模态可以分为基频和谐波频率。
基频是指当压电振子处于自由状态下,不受外界干扰时,振动的最低频率。
在基频模态下,压电振子的振动呈现简谐振动的特征。
在正弦电场的作用下,振子在电场作用力的驱动下进行振动。
基频的振动模态可以通过拉普拉斯方程求解得到。
谐波频率是指压电振子在基频外的次低频率。
当外加电场与振子的固有频率相近时,谐波模态会发生共振。
共振时,振子的振幅会显著增加,使得振动效果更加明显。
由于谐波模态是由于电场频率与振子固有频率之间的匹配关系,因此谐波频率可以通过频率响应函数进行计算。
除了基频和谐波频率外,压电振子还可能存在其他振动模态,如多振模态和混态。
多振模态是指振子在外部驱动下,具有多个频率成分的振动。
混态是指振子同时存在多个振动模态,并且振幅可以分别控制。
压电振子的振动模态对于实际应用具有重要意义。
在传感器和执行器中,振动模态的选择可以根据所需的传感器频率或执行器频率来定制。
此外,通过调整外加电场的频率或幅值,可以有效地控制压电振子的振动模态。
这为实现高精度、低能耗的系统设计提供了可能性。
在实际应用中,压电振子的振动模态的计算和优化是一个复杂的问题。
需要考虑到振子的材料特性、几何形状、电场频率等多个因素的综合影响。
通过数值模拟和实验测试相结合的方法,可以得到较为准确的振动模态结果,为压电振子的设计与优化提供理论依据。
综上所述,压电振子的振动模态是基频和谐波频率等模态的叠加效应。
通过调整电场频率和幅值,可以实现不同频率和振幅的振动模态,为实际应用提供了灵活性和可调性。
压电振子的振动模态研究对于制造高性能的传感器和执行器具有重要意义。


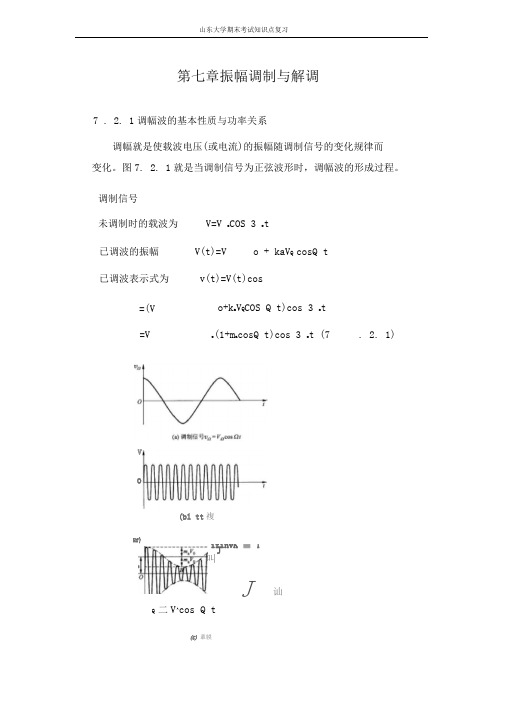
第七章振幅调制与解调7 . 2. 1调幅波的基本性质与功率关系调幅就是使载波电压(或电流)的振幅随调制信号的变化规律而变化。
图7. 2. 1就是当调制信号为正弦波形时,调幅波的形成过程。
Q 二V^cos Q t(C)輩膜未调制时的载波为V=V o COS 3 o t已调波的振幅V(t)=V o + kaV Q cosQ t已调波表示式为v(t)=V(t)cos=(V o+k a V Q COS Q t)cos 3 o t=V o(1+m a cosQ t)cos 3 o t (7 . 2. 1) 调制信号V(bl tt複0-r^cwOHf}i"ifinvK ■ TJ叫J讪』iir rlLU\ taw圏>宜1 ««液的聃Kt由式(7 . 2. 2)可见,由正弦波调制的调幅波包含三个频率:载幅波将包含上边带与下边带。
的功率为:.2. 2平方律调幅设图7 . 2 . 3的非线性器件特T 性为二二a o +aw i +a z v i? (7 . 2 . 6) _i=v (载波)+V Q (调制信号)=V o cos 3 o t+V Q cosQ t (7. 2 . 7)其中产生调幅作用的是a 2V i 2项,故称为平方律调幅。
滤波后,输出电 压为1'( fl = rt| IgCOS ⑴詁也」'」;I 芒 3(, +/J)' f+cos ( % -p) f]=8*r+2njF 打打朝Hi /Tlfoib=«i %( J + 曽4爲3只 I A J COS Wgf由上式显然可知;2«,调幅度叫土 畀d.波3 0;上边频(3 o + Q )和下边频(3 0- 所示。
Q ),其频谱如图7 . 2 . 2£ «若调制信号为非正弦波,包含许多频率,则调J :-上边擬__一—对于式(7 . 2. 2),将它加到负载电阻R 上, 则载波与两个边频裁波功率 下边频功率 上边频功率P 1悩P_I I 1…巴T 沪|丁)不吋 叫Ff 】1 5丁云y 凡(7.2. 3)(7.2.5)式中,输入电压为m 7,2.1养线性阴幅方幅圏(化2」)(7.2.9)7. 2. 5是斩波调幅器的方框图,它的调鞭虧路由式(7 . 2. 9)可以得出如下结论:1)调幅度m a 的大小由调制信号电压振幅 S 及调制器的特性曲线 所决定,亦即由a 、32所决定。

TrekStor压电振子特性与支撑方式分析压电振子的振动模式压电振子[X50-52}是压电驱动器的核心部件,起着将电能转换为机械能的作用。
某一几何尺寸的振子在特定条件(按所需方向极化、激励和设置电极等)下,其用以完成机械能和电能相互转换的振动方式多种多样,通常把这种振动方式称为振动模态。
此外,各种振动模态之间还存在着相互影响或藕合作用。
因此在设计压电振子时,除了选择合适的压电陶瓷材料外,还要选择合适的振子及其振动模态。
通常将压电陶瓷激发的振动分成以下四类,如上图所示。
(a)垂直于电场方向的伸缩振动(长度方向),用LE模表示;(b)平行于电场方向的伸缩振动(厚度方向),用TE模表示;(c)垂直于电场平面内的剪切振动(表面),用FS模表示;(d)平行于电场平面内的剪切振动(厚度),用TS模表示。
当这些振动模式作用到压电振子上时,将能产生弯曲振动、伸缩振动和扭转振动。
压电驱动器为了形成所需运动形式,通常使用这四种振动形式中的两种或一种,使两个以上方向的振动加以组合以达到目的。
按照所加电场与弹性波传播方向之间的关系,压电振动又可分为纵向效应和横向效应两大类。
当弹性波的传播方向平行于电场方向时称为纵向效应;当弹性波的传播方向垂直于电场方向时称为横向效应。
骨传导所采用的复合压电振子的振动模态为LE伸缩振动。
压电振子的谐振特性将施加到压电振子上电信号的频率从低频慢J漫地升到高频时,可以发现,通过压电振子的电流随电信号频率的变化而变化[[53-54]。
当电信号频率为某一频率时,电流出现极大值;当电信号频率变化到另一频率时,电流出现极小值。
压电振子的电流随频率而变化这一事实,也表明压电振子的等效阻抗Z随频率也发生变化,如图2.6所示。
图中,IZI代表阻抗的绝对值。
当电信号频率等于几时,压电振子的电流最大而阻抗最小;当电信号频率等于fn 时,压电振子电流最小而阻抗最大。
因此,通常称fm为最小阻抗频率或最大导纳频率(导纳=1}阻抗);,fn称为最大阻抗频率或最小导纳频率。

压电振动传感器原理
压电振动传感器是一种广泛用于测量机械振动和声压级的传感器,它的工作原理基于压电效应。
压电效应是指某些材料在受到外部压力或应变时会产生电荷或电势的变化,反之亦然。
以下是压电振动传感器的工作原理:
1. 压电材料:压电振动传感器的核心部分是一个压电材料,常用的压电材料包括石英晶体、陶瓷和聚偏氟乙烯(PVDF)等。
这些材料具有压电性质,即当它们受到机械应力或振动时,会在其表面产生电荷。
2. 传感器结构:压电振动传感器通常包括一个薄片状的压电材料,其一侧连接到机械振动源或声压源。
当机械振动或声压作用于传感器表面时,压电材料会变形或振动。
3. 电极:压电材料的两侧通常附有电极,用于收集产生的电荷或电势变化。
当材料发生振动或受到应力时,电荷分布会发生变化,从而在电极之间产生电压信号。
4. 信号处理:传感器的电压信号会通过电缆传输到信号处理器或数据采集系统。
这些系统可以测量、记录和分析传感器输出,以获得有关振动或声压的信息。
山大仪器分析知识点12以下是为大家整理的山大仪器分析知识点12的相关范文,本文关键词为山大,仪器,分析,知识点,,您可以从右上方搜索框检索更多相关文章,如果您觉得有用,请继续关注我们并推荐给您的好友,您可以在教育文库中查看更多范文。
山东大学期末考试知识点复习第十二章分子发光分析法1.分子荧光和磷光的产生过程荧光发射:多为由第一激发单重态的最低振动能级回到基态的各振动能级间的跃迁所产生的辐射(s1→s0跃迁)。
荧光的发射时间约为lo-7一10-9s。
磷光发射:电子由第一激发三重态的最低振动能级到基态各振动能级的跃迁(T1→s0跃迁)产生磷光。
三重激发态比单重激发态的能量还要低一些,故产生磷光的波长要比产生荧光的波长长。
由于s0一T1的跃迁属于禁阻跃迁,电子直接进入三重激发态的概率很小,发生T1→s0的跃迁也较难进行,另外,磷光的产生包括了多个过程:s0→激发→振动弛豫→内转移→系间跨越→振动弛豫→T1→s0,所以磷光的发光速度与荧光相比很慢,约10-4一100s。
光照停止后,各种过程仍在进行,且T1→s0的跃迁慢,故磷光发射还可持续一定时间。
2.非辐射能量传递过程振动弛豫:同一电子能级内以热能量交换形式由高振动能级至低相邻振动能级间的跃迁称为振动弛豫。
发生振动弛豫的时间约为10-12s。
内转换:相同多重态电子能级中,等能级间的无辐射能级交换称为内转换。
如通过振动弛豫和内转换,激发电子可由s2可转移到s1;T2转移到T1。
发生内转换的时间约为10-12s。
外转换:激发态分子与溶剂或其他分子之间产生相互碰撞而失去能量回到基态的非辐射跃迁称为外转换。
外转换可使荧光或磷光减弱或发生“猝灭”。
系间跨越:指不同多重态,在有重叠的转动能级间的非辐射跃迁,如由s1到T1的跃迁。
系间跨越改变了电子自旋状态,属禁阻跃迁,可通过自旋一轨道耦合进行。
3.荧光光谱发射光谱:固定激发波长,以发射波长为横坐标,发射光的强度为纵坐标的山东大学期末考试知识点复习谱图即为发射光谱图;激发光谱:固定发射波长,以激发波长为横坐标、激发光强为纵坐标的谱图即为激发光谱;荧光光谱的基本特征:荧光光谱显示的某些普遍特征为荧光物质的识别提供了基本原则。
压电式振动传感器原理振动传感器是一种能够检测物体振动的设备,它可以将物体的振动转换为电信号输出。
其中,压电式振动传感器是一种较为常见的振动传感器,它采用压电效应将物体的振动转换为电信号。
本文将介绍压电式振动传感器的原理、特点以及应用。
一、压电效应压电效应是指某些晶体在受到外力作用下会产生电荷,这种现象被称为压电效应。
具体地说,当物体受到压力或拉力作用时,其中的电荷分布会发生改变,从而产生电势差。
这种效应可以应用于传感器、声音设备等领域。
二、压电式振动传感器原理压电式振动传感器是利用压电效应来检测物体振动的一种传感器。
该传感器通常由压电陶瓷片、阻抗转换电路和信号处理电路组成。
当物体振动时,压电陶瓷片受到外力作用,会产生电荷分布的变化,从而在陶瓷片上产生电荷。
这些电荷通过阻抗转换电路传输到信号处理电路中,最终转换为电信号输出。
压电式振动传感器的输出信号通常是交流信号,其频率与物体振动的频率相同,振幅与物体振动的振幅成正比。
因此,可以通过测量输出信号的振幅和频率来确定物体的振动状态。
三、压电式振动传感器的特点1. 灵敏度高:压电式振动传感器可以快速响应物体的振动,具有高灵敏度。
2. 高精度:该传感器的输出信号可以精确地反映物体的振动状态,具有高精度。
3. 宽频带:压电式振动传感器的频响范围较广,可以检测多种振动频率。
4. 耐用性强:该传感器具有较好的耐用性,可以在恶劣环境下长期工作。
5. 安装方便:压电式振动传感器的安装方式较为简单,可以直接粘贴在被测物体表面。
四、压电式振动传感器的应用压电式振动传感器广泛应用于机械、汽车、航空等领域,用于检测设备的振动状态、故障诊断等。
具体应用包括以下几个方面:1. 振动监测:压电式振动传感器可以用于监测机械、电机、发动机等设备的振动状态,及时发现故障。
2. 振动分析:通过对压电式振动传感器输出信号的分析,可以了解设备的振动频率、振幅等信息,进一步分析设备的运行状态。
压电振子的振动模式vibration modes薄长条纵向伸缩振动薄圆片、棒、薄圆环、薄球壳、面切变、弯曲振动,厚度振动,能陷振动模,机电类比和线性机电网络,前几章我们根据晶体的对称性,分析讨论了不同对称性的压电晶体所具有的独立的介电常数、弹性常数、压电常数,以及这些量与电学量—电位移、电场强度等之间的关系,与机械量—应力、应变之间的关系(胡克定律),与电学量和机械量之间的关系(压电方程组)等等,但是未涉及到如何确定这些常数的数值。
在实验上通常是通过测定压电元件的谐振频率和反谐振频率的方法来确定这些常数的,这就要求对晶体的这些常数同晶片的谐振频率和反谐振频率之间的关系进行理论分析。
这种实验的和理论的分析工作,是研究压电晶体的一个重要方面。
确定材料参数另一方面,压电元件常用于振荡器、滤波器、换能器、光调幅器以及延迟线等等。
这些器件都是压电效应来激发压电体的机械振动。
因此,只有通过对压电元件的振动模式的讨论,才能较深入地了解压电元件的工作原理和工作性质。
元器件的设计虽然压电晶体(包括已极化的压电陶瓷)是各向异性体,但是压电元件都是根据工作需要,选择有利的方向切割下来的晶片,这些晶片大多数薄长片、圆片、方片等较简单的形状,它的基本振动模式(如伸缩振动、切变振动等)大体上与各向同性的弹性介质相同,都是在有限介质中以驻波的形式传播,只有在非常简单的情况下,才可能得到波动方程的准确解。
对于稍复杂的情况,只有近似解。
在本章中,不可能对各种振动方式都进行详细讨论,只是对其中最简单最常用的振动模式作较系统而全面的分析讨论,希望通过对特殊性的讨论了解普遍性。
薄长片压电振子的长度伸缩振动薄长片压电振子的长度伸缩振动,又称纵向振动,是压电元件中常采用的一种振动方式,也是最简单的振动方式。
在这一节中除了讨论压电振子的纵向振动特性外,还要讨论压电振子的等效电路以及压电材料的介电常数、弹性常数和压电常数的测量等内容。
薄长片压电振子的压电方程组设d310的压电晶体的zx切割晶片,长度l沿x方向,宽度lw 沿y方向,厚度lt沿z方向,并且有l>>lw 和lt,电极面与z轴垂直,如图6-3所示。
因为l>>lw 和lt,长度方向是主要因素,所以只考虑应力分量X1的作用,其它应力分量X2、X3、X4、X5、X6可以忽略不计。
图5-1 薄长片压电振子因为电极面垂直于z轴,所以只要考虑电场分量E3的作用,其它电场分量E1、E2可以忽略不计。
又因为测量时(或工作时)只是薄片的中心被夹住,片的两端为自由端,即薄片的边界条件为机械自由,在边界上的应力分量X 1|边界=0。
还有电极面是等位面。
在此情况下,可以选X 1、E 3为自变量,用第一类压电方程组,即:111131********EXx s X d E D d X E ε⎫=+⎪⎬=+⎪⎭根据牛顿第二运动定律得到薄长片的运动方程为:212u X t xρ∂∂=∂∂为了得到薄长片压电振子的波动方程,就需要根据压电方程组中应力与应变的关系式,13131133111111111E E E E x d u d X E E s s s x s ∂=-=-∂代入波动方程得:223132211111E Eu u d E t s x s xρ∂∂∂=-∂∂∂111131********EXx s X d E D d X E ε⎫=+⎪⎬=+⎪⎭212u X t xρ∂∂=∂∂因为压电振子的电极面是等位面,电场分量E 3在晶片中是均匀分布的,即有∂E/∂x=0。
将这些关系代入上式式即得薄长片压电振子的波动方程为:22222E 1122xu c x u s 1t u ∂∂=∂∂ρ=∂∂xE s d x u s 1t u 3E 113122E 1122∂∂-∂∂=∂∂ρ111Ec sρ=声速若压电振子是在交变电场E 3=E 0e j ωt 的激发下,通过压电效应产生纵向振动,则上式的通解为:()[cos()sin()]j tu x t A kx B kx eω=+,式中波矢k=ω/c ;A 、B 为待定系数,由边界条件确定。
满足边界条件的解因为压电振子的两端为自由端,它的机械自由边界条件为:x=0时,有X1|x=0=0;x=l时,有X1|x=l=0;X1=?, u(x)而应力的表达式可以写为:13131133********310111111[sin()cos()]E E E E j t j tE E x d u d X E E s s s x s d kA kx B kx ke E e s s ωω∂=-=-=∂=-+-()[cos()sin()]j tu x t A kx B kx eω=+,代入边界条件得:x=0时,X 1=0:310111110=-j t j tE E d Bke E es s ωω310111110[sin()cos()]=-+-j t j tE E d A kl B kl ke E es s ωωx=l 时, X 1=0:311011111[sin()cos()]j t j tE E d X kA kx B kx ke E es s ωω=-+-31d B E k=稍加整理即得:⎪⎪⎭⎪⎪⎬⎫-⋅==)kl sin(1)kl cos(k E d A k E d B 031031310111110[sin()cos()]=-+-j t j tE E d A kl B kl ke E es s ωω310[sin()cos()]A kl B kl k d E -+=3101sin()cos()A kl B kl d E k=-31d B E k=把A 、B 代回到波动方程的解中,得到满足边界条件的解为:310310313cos()1[cos()sin()]sin()cos(())cos()sin()cos(())cos()sin()j t j t d E kl u kx kx e k kl d E k l x kx e k kl d E k l x kx k kl ωω-=-=--=⋅=--=⋅为了对上式所表示的波形有较具体的了解,在图5-2中,绘出了t=0及t=π/ω=1/2周期时的波形。
从图5-2中可以看出上式代表纵驻波方程式,即在薄长片压电振子中传播的是纵驻波。
()313cos(())cos()sin()d E k l x kx u x t k kl --=⋅,图5-2 薄长片压电振子的纵向振动310cos()cos(())sin()--=⋅d E kx k l x u k kl t=0时:t=π/ω时:310cos(())cos()sin()--=⋅d E k l x kx u k kl)kl sin()kl cos(1k E d 031-⋅-)kl sin()kl cos(1k E d 031-⋅)kl sin()kl cos(1k E d 031-⋅)kl sin()kl cos(1k E d 031-⋅-x 0l/2lt=0u 0t=π/ωu薄长片压电振子中的应力、应变以及电位移与(x 、t )的关系为:1313sin(())sin()(,)sin()u k l x kx x x t d E x kl ∂-+==∂式中E 3=E 0e j ωt()313cos(())cos()sin()d E k l x kx u x t k kl --=⋅,313111sin(())sin()(,)1sin()E d E k l x kx X x t s kl ⎡⎤-+=-⎢⎥⎣⎦331133331333311(,)sin(())sin()[1]sin()XXE D x t d X E d E k l x kx E s kl εε=+=-+=-+13131133111111111E E E E x d u d X E E s s s x s ∂=-=-∂应力自由式中:313333311sin(())sin()(,)sin()xE d E k l x kx D x t E s kl ε-+=⋅+233333111/xX E d sεε=-或:313333311sin(())sin()(,)[1]sin()XE d E k l x kx D x t E s kl ε-+=-+传统电介质材料(知识回顾)介电常数ε,长l 、宽l w 、厚l t0w tl lC l εε=01t Cw l Z j C j l lωωεε==电容:容抗:0w C tV VI j l lZ l ωεε==电流:电流随频率单调增加,有位相差通过薄长片压电振子的电流因为通过压电振子电极面上的电流I 3等于电极面上的电荷Q 3随时间的变化率,即:dtdQ I 33=而电极面上的电荷Q 3与电位移D 3的关系为()330wll Q D x t dxdy=⎰⎰,(5-15)2313333300112313333110231333311231333311sin(())sin()sin()cos(())cos()sin()22cos()sin()tan()2wll xE lxw w Exw w Ex w w Ed E k l x kx Q E dxdy s kl d E l k l x kx l l E ks kl d E l kl l l E ks kl kl d E l l l E ks εεεε⎡⎤-+=+=⎢⎥⎣⎦⎡⎤--=⋅+=⎢⎥⎣⎦-=⋅+==⋅+⎰⎰2kl 313333311sin(())sin()(,)sin()xE d E k l x kx D x t E s kl ε-+=⋅+最后得到通过压电振子电极面的电流为:233313333113003tan()2,2[]x w w Ej t j tkl dQ dE l l d dE I l l kl dt dt s dt dE d E e j E e j E dt dtωωεωω⋅==⋅+===所以有:231333311tan()22x w Ekl d I j l l E kl s ωε⎡⎤⎢⎥=⋅+⎢⎥⎢⎥⎣⎦ω薄长片压电振子的等效导纳若通过薄长片压电振子的电流为I 3,两电极之间电压为V 3,则压电振子等效阻抗Z 为,33V I Z =压电振子的等效导纳G 为:33V /I Z /1G ==33/Z V I =或者两电极面之间的电压V 3为:3t l 033E l dz E V t==⎰压电振子的等效导纳为:2313311tan()22x w E t kl l l d G j kl l s ωε⎡⎤⎢⎥⋅=+⎢⎥⎢⎥⎣⎦231333311tan()22x w E kl d I j l l E kl s ωε⎡⎤⎢⎥=⋅+⎢⎥⎢⎥⎣⎦牛顿定律压电方程波动方程边界条件质点位移电位移电流,导纳材料参数,等效电路结果分析以上就是如何通过压电方程和波动方程求得压电振子的等效导纳方法。