中国人口发展趋势的预测模型-07年全国大学生数学建模竞赛全国二等奖论文
- 格式:doc
- 大小:336.00 KB
- 文档页数:12


承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):河南师范大学参赛队员(打印并签名) :1. 郑转2. 闫东旭3. 黄伟指导教师或指导教师组负责人(打印并签名):指导教师组日期: 2007年 9月 24 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):中国人口增长预测摘要:本文全面分析了中国人口短期、中期和长期的增长趋势以及它在老龄化进程加速、出生人口性别比持续升高、乡村人口城镇化等因素下的发展状况。
依据题目提供的大量可靠的原始数据,分析建立了以数据为基础的神经网络模型,并运用拟合、统计等相关知识,找出了人口增长趋势随当前时代发展变化的普遍规律。
此外,本文有效的分析了各个模型中的优点与不足之处,增加了明确的扩展方案。
由于信息真实可靠,数据丰富,且抽样统计人口随机,所以模型的合理性和准确性都比较好。
其间分析、处理数据的许多方法和技巧,对其他类似人口预测问题的分析,也有一定的借鉴意义。
模型一:微分方程模型,为了更加明确的研究中国人口在当前发展特点下的增长趋势,建立了适于一般情况的自然增长模型,结合抽样数据对中国人口作初步预测,并预测出我国人口2015年将达到13.771亿人,2075年达到18.58亿人,该数据说明微分方程模型只适于作短期预测。

2007全国数学建模中国人口增长预测摘要:针对题目所提要求,我们建立了两个中国人口预测模型,分别用于对中国人口的发展趋势做短期和中长期的预测。
为了对中国人口发展做短期的预测,考虑到题目所给的数据资料的不全面,我们由马尔萨斯的人口指数增长模型得到启发,针对中国人口发展的特点,把出生率和死亡率函数这两大对人口增长起主要作用的因素作为建模的关键参数,在附件中没有给出中国近年总人口数的情况下,建立了短期内预测中国人口增长的微分方程模型。
在该模型中,为了得到出生率和死亡率函数这两个重要参数,我们通过分析题目所给数据,提取出有效信息,计算归纳出2001年到2005年的出生率和死亡率,并在此基础上引入灰色模型,用于对出生率和死亡率进行预测,得出了出生率和死亡率关于时间的函数。
较准确的估计出了人口增长的关键参数,使得建立的人口增长短期预测模型不仅符合中国人口的发展特点,而且简单易用,能在未知总人口数的情况下预测人口的相对发展变化,这一优点使得可以方便且准确的用于预测中国人口短期内的发展趋势。
为了对中国人口发展做中长期的预测,考虑到短期模型在预测人口中长期发展中的局限性以及影响人口发展的众多因素的不确定性和它们之间关系的复杂性,我们利用灰色动态模型的特点,从《中国统计年鉴》中查到了中国近年的人口总数(见附表一),把人口数做为灰色量,对原始各年人口序列进行分段建模,对各分段模型进行定性分析比较,根据各阶段宏观指标的相关确定一组适当的权数,进行预测模型的最优组合,以确定最优预测模型,从而建立了中长期预测中国人口增长的灰色动态系统人口模型,对中国人口进行了中长期的预测。
在对中国总人口进行短期和中长期的总体预测后,我们从附件中提取出城、镇、乡三地人口、男女出生性别比、妇女生育率、老龄人口比率等相关数据,对中国未来城、镇、乡三地人口比例、男女出生性别比、妇女生育率、老龄人口比率等影响人口发展的主要因素做趋势预测,从而达到了对中国人口全方位的预测。

中国人口增长预测摘要本文从中国人口的实际情况和人口增长的特点出发,根据题目和中国统计年鉴中的相关数据,建立了两个关于中国人口增长的数学模型,并对中国人口做出了分析和预测。
模型一:利用中国统计年鉴中2000—2005 年人口的数据,运用灰色理论的基本原理建立GM(1,1) 模型。
该模型利用离散数据列进行生态处理,建立动态的微分方程,对我国近5年、10年、20年的总人口分别进行了预测。
又根据中国人口城乡分布不同且总趋势也不同的特点,把全国人口分为城市人口、城镇人口、乡村人口三部分分别进行灰色预测。
结果表明,该模型较好的反映并预测中国人口短中期和长期的变化情况。
模型二:按人口年龄结构特征,将人口分为幼年(0—14岁)男女、中年(15—49岁)男女、老年(50岁以上)男女。
各年龄段的人口变化是由出生率、死亡率和转化为其他年龄段的转化人数决定的。
根据各年龄段人口数量变化特点,对各年龄段转化人数引入转化因子,改进马尔萨斯模型,附带出生率、死亡率、生育率、出生性别比率等约束条件,建立了新的具有年龄结构的人口增长模型。
结合我国人口的特点,运用已知数据和利用微分方程的数值解,预测出男性和女性幼年、中年、老年的人口数量。
可反映中国不同年龄结构的人口分布情况。
关键词:灰色预测;小误差频率;微分方程组;人口模型;转移因子一.问题重述中国是一个人口大国,人口问题始终是制约我国发展的关键因素之一。
因此人口预测的科学性、准确性是至关重要的。
英国人口学家马尔萨斯的人口指数增长模型和荷兰生物学家的Logistic模型都是经典的人口预测模型。
但是,影响中国人口的因素较多,人口结构较复杂,这些模型对人口预测很粗略,甚至是不准确的。
因此,我们要根据我国具体的人口结构现状(如老龄化进程加速)、人口的分布现状(如乡村人口城镇化)、人口比率现状(如出生人口性别比持续升高)等特点,来较准确、较具体地对中国人口进行预测,建立人口增长的数学模型,由此对中国人口中短期和长期增长趋势做出预测。

中国人口政策问题模型【摘要】:中国是世界上的人口大国,近三十年来,我国的人口政策在控制人口数量方面取得了非凡的成绩,使得人口发展逐步走向有计划、可控制的平稳增长时期。
但随着经济的发展和人口老龄化等现象的出现,如何调整人口政策使之与社会发展相适应,是我们亟待研究思考的问题。
本文根据我国近三十年的人口数据对其人口现状,人口老龄化程度等方面进行分析,并给出我国调整人口生育政策的时机、具体方案以及根据模型给出我国人口增长状况的预测结果。
【关键词】:人口现状、老龄化、预测结果、人口政策一、问题的重述近三十年来,我国的人口政策在控制人口数量方面取得了非凡的成绩,但随着经济的发展和人口老龄化等现象的出现,使得我国调整人口生育政策成为可能。
(1)利用有关数据,给出我国人口现状的统计结果;(2)试建立模型,给出我国调整人口生育政策的时机、具体方案并预测结果。
(相关数据在下文的附录中给出)二、模型的假设(1)在模型中预期的时间内,人口不会因发生大的自然灾害、突发事故或战争等而受到大的影响;(2)在我国视为没有人口的迁入和迁出;(3)人口增长只与人口基数、生育、死亡和老龄化有关;(4)一段时期内我国人口的死亡率不发生大的波动,不同年龄段人口的分布也不随时间发生变化;三、问题的分析问题一:根据附表1中给出的相关数据关数据,将近30年人口数量用MATLAB 软件画出图形,给出我国人口现状的统计结果。
问题二:根据历年出生率和死亡率,利用MATLAB程序对数据进行拟合,分别得到出生率和死亡率的计算公式。
但结合出生率和死亡率的数据画出具体图形分析发现,数据分段呈现出一定的规律性,于是对数据进行分段拟合,并最终确定出人口的自然增长率,得到人口数的计算公式。
此公式能够较好反应中国近期及预测未来近15年内的人口数量。
根据公式得出相应图(图),发现人口数呈现的相关规律。
另外为了更好的分析人口的具体情况,我们根据附表2中的数据拟合并计算出人口老龄化的计算公式,根据直观图得出中国老龄化指数在未来15年内一直呈上升趋势,基于以上数据及分析,从而确定出我国调整人口生育政策的时机、具体方案以及给出相应的预测结果。
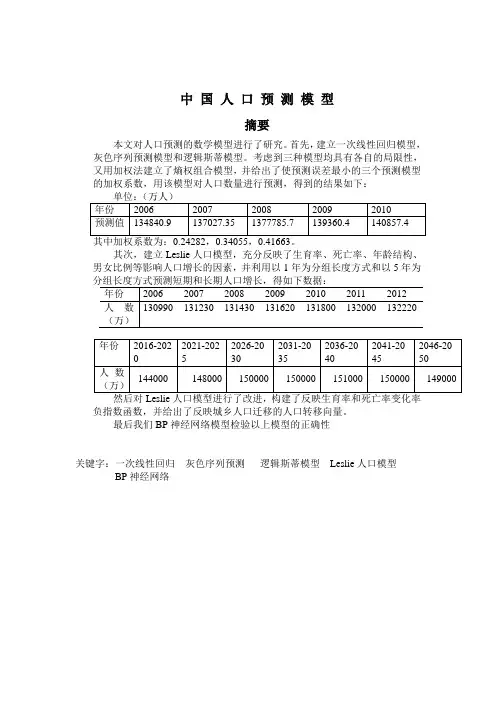
中国人口预测模型摘要本文对人口预测的数学模型进行了研究。
首先,建立一次线性回归模型,灰色序列预测模型和逻辑斯蒂模型。
考虑到三种模型均具有各自的局限性,又用加权法建立了熵权组合模型,并给出了使预测误差最小的三个预测模型的加权系数,用该模型对人口数量进行预测,得到的结果如下:其次,建立Leslie人口模型,充分反映了生育率、死亡率、年龄结构、男女比例等影响人口增长的因素,并利用以1年为分组长度方式和以5年为负指数函数,并给出了反映城乡人口迁移的人口转移向量。
最后我们BP神经网络模型检验以上模型的正确性关键字:一次线性回归灰色序列预测逻辑斯蒂模型Leslie人口模型BP神经网络一、问题重述1. 背景人口增长预测是随着社会经济发展而提出来的。
在过去的几千年里,由于人类社会生产力水平低,生产发展缓慢,人口变动和增长也不明显,生产自给自足或进行简单的以货易货,因而对未来人口发展变化的研究并不重要,根本不用进行人口增长预测。
而当今社会,经济发展迅速,生产力达到空前水平,这时的生产不仅为了满足个人需求,还要面向社会的需求,所以必须了解供求关系的未来趋势。
而人口增长预测是对未来进行预测的各环节中的一个重要方面。
准确地预测未来人口的发展趋势,制定合理的人口规划和人口布局方案具有重大的理论意义和实用意义。
2. 问题人口增长预测有短期、中期、长期预测之分,而各个国家和地区要根据实际情况进行短期、中期、长期的人口预测。
例如,中国人口预期寿命约为70岁左右,因此,长期人口预测最好预测到70年以后,中期40—50年,短期可以是5年、10年或20年。
根据2007年初发布的《国家人口发展战略研究报告》(附录一)及《中国人口年鉴》收集的数据(附录二),再结合中国的国情特点,如老龄化进程加速,人口性别比升高,乡村人口城镇化等因素,建立合理的关于中国人口增长的数学模型,并利用此模型对中国人口增长的中短期和长期趋势做出预测,同时指出此模型的合理性和局限性。

论文题目:中国人口增长趋势预测与分析摘要本文主要针对中国人口增长趋势和城、镇、乡人口结构进行短期和中长期的预测与分析。
同时对人口出生率人口增长的迟滞效应、人口老龄化等因素作出了合理预测。
方面一预测短期内人口的增长趋势,本文首先运用经典的Logistic模型描述人口的增长规律,它所描述的“慢速变化--急速上升--再慢速变化”的变化过程是符合人口的增长模式,由此预测出我国人口将于2020年达到15.6亿。
通过检验,Logistic模型的误差相对较大,精确度较低,因此本文用多项式拟合的方法进行预测。
在多项式拟合中我们分别进行了不同次函数的拟合,通过比较分析发现二次拟合为最优模型,能得到很好的线性拟合,于是本文进行二次函数拟合。
通过模型求解,本文预测出未来的10年内我国人口总量将持续上涨,并且到2015年总人口将达到13.76亿,2022年人口数将逼近14亿。
另一方面,由于人口素质的提高以及国家相关政策的执行,人口出生率将逐年下降。
方面二预测中长期中国人口增长趋势,此时Logistic模型和函数拟合就不再适用。
本文建立离散模型来表现人口数量的变化规律,选取2005年的相关数据用Leslie矩阵原理,分别计算城、镇、乡各年龄段的女性人口,再根据男女比例得到男性人口数,依次递推得到了以后各年的各年龄组的人口数。
同时对人口年龄结构和人口老龄化等现象进行预测,并且考虑到出生人口的“小高峰”想象,对人口出生的迟滞效应进行了分析。
通过模型求解,预测出中国人口总数中长期情况下将先增加后减少,在2020年左右将超过18亿,达到峰值。
育龄妇女的人口总数将逐渐下降,但由于人口增长迟滞效应,2015年左右我国将会出现人口出生的又一次小高峰。
同时我国人口老龄化现象将逐步严重,到2035年我国老龄人口所占比例将达到35%,给社会带来沉重负担。
关键词:Logistic模型;多项式拟合;Leslie模型;迟滞效应;人口结构分析中国人口增长趋势预测与分析摘要本文主要针对中国人口增长趋势和城、镇、乡人口结构进行短期和中长期的预测与分析。

中国人口增长预测要交论文中国人口增长预测摘要我国是一个人口大国,而人口问题也始终是制约我国发展的关键因素之一。
本文对中国人口增长的变化趋势做出预测。
模型一:指数增长模型。
我们忽略人口的年龄结构及出生率、死亡率等因素的影响,只考虑人口总数的增长率。
采用微积分这一数学工具,将人口总数可微函数,并利用1990—2008的总人口数据,用拟合的方法求解得到1990—2008总人口实际值与预测值对照表。
拟合效果较好。
最后采用该模型对2009—2050年的总人口进行了预测得到表3。
模型二—阻滞增长模型(Logistic模型)。
因为周围环境对人口的增长起着阻滞作用,而利用模型一并不能准确的预测出人口的变化趋势,所以我们采用了Logistic模型。
首先阻滞作用体现在对人口增长率r的影响上,设固有增长率为人口数目的线性函数,利用微分方程可以得到人口增长速度dx/dt随着x增加的变化图,用拟合的方法求解得到1990年—2008年间实际值与预测值的对照表。
拟合效果很好。
最后我们采用该一、问题重述1.1问题背景中国是一个人口大国,人口问题也始终是制约我国发展的关键因素之一。
而近年来中国的人口发展出现了一些新的特点,例如,老龄化、性别比失衡,城镇化,这些都影响着中国人口的增长。
1.2涉及材料背景2007年初发布的《国家人口发展战略研究报告》做出了进一步的分析。
关于中国人口问题已有多方面的研究,并积累了大量数据资料。
而附录2就是从《中国人口统计年鉴》上收集到的部分数据。
1.3问题提出从中国的实际情况和人口增长的特点出发,参考附录中的相关数据(也可以搜索相关文献和补充新的数据),建立中国人口增长的数学模型,并由此对中国人口增长的中短期和长期趋势做出预测;而且特别要指出你们模型中的优点与不足之处。
二、问题分析2.1 人口预测概述人口预测是社会未来预测的一种,它的任务是寻找客观存在的人口规律,运用现代科学技术方法,预测人口发展过程的变化趋势,协助政府决策机构提出与人口的发展更加适应的政策。
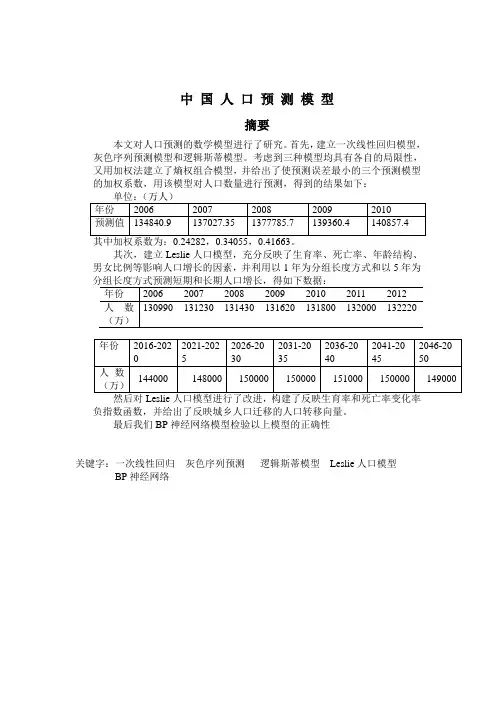
中国人口预测模型摘要本文对人口预测的数学模型进行了研究。
首先,建立一次线性回归模型,灰色序列预测模型和逻辑斯蒂模型。
考虑到三种模型均具有各自的局限性,又用加权法建立了熵权组合模型,并给出了使预测误差最小的三个预测模型的加权系数,用该模型对人口数量进行预测,得到的结果如下:其次,建立Leslie人口模型,充分反映了生育率、死亡率、年龄结构、男女比例等影响人口增长的因素,并利用以1年为分组长度方式和以5年为负指数函数,并给出了反映城乡人口迁移的人口转移向量。
最后我们BP神经网络模型检验以上模型的正确性关键字:一次线性回归灰色序列预测逻辑斯蒂模型Leslie人口模型BP神经网络一、问题重述1. 背景人口增长预测是随着社会经济发展而提出来的。
在过去的几千年里,由于人类社会生产力水平低,生产发展缓慢,人口变动和增长也不明显,生产自给自足或进行简单的以货易货,因而对未来人口发展变化的研究并不重要,根本不用进行人口增长预测。
而当今社会,经济发展迅速,生产力达到空前水平,这时的生产不仅为了满足个人需求,还要面向社会的需求,所以必须了解供求关系的未来趋势。
而人口增长预测是对未来进行预测的各环节中的一个重要方面。
准确地预测未来人口的发展趋势,制定合理的人口规划和人口布局方案具有重大的理论意义和实用意义。
2. 问题人口增长预测有短期、中期、长期预测之分,而各个国家和地区要根据实际情况进行短期、中期、长期的人口预测。
例如,中国人口预期寿命约为70岁左右,因此,长期人口预测最好预测到70年以后,中期40—50年,短期可以是5年、10年或20年。
根据2007年初发布的《国家人口发展战略研究报告》(附录一)及《中国人口年鉴》收集的数据(附录二),再结合中国的国情特点,如老龄化进程加速,人口性别比升高,乡村人口城镇化等因素,建立合理的关于中国人口增长的数学模型,并利用此模型对中国人口增长的中短期和长期趋势做出预测,同时指出此模型的合理性和局限性。

中国人口预测模型摘要:人口数量的变化,关系到一个国家的未来。
认识人口数量的变化规律,建立人口模型,能够较准确的预报,是有效控制人口增长的前提。
本文对人口预测的数学模型进行了研究。
首先,建立人口指数模型、Logistic模型及灰度预测模型。
对我国2005年以后45年的人口增长进行了预测,根据1982年人口基本数据运用模型对1982年~2005年进行了预测,并用实际数据对预测结果进行了检验。
我们将预测区间分为2006~2030年、2030~2050年两个区间,以量化未来我国短中期与长期的人口变化。
关键词:人口数量的变化人口指数模型 Logistic模型灰度预测模型MATLAB Excel目录第一部分问题重述 (3)第二部分问题分析 (3)第三部分模型的假设 (3)第四部分定义与符号说明 (3)第五部分模型的建立与求解 (3)5.1模型一 (3)5.2模型二 (8)5.3模型三 (12)第六部分对模型的评价 (14)第七部分参考文献 (15)第八部分附表 (15)一、问题重述人口问题始终是制约我国发展的关键因素之一。
本题要求根据已知数据,运用数学建模的思想对我国人口做出分析和预测。
具体问题如下:从中国的实际情况和人口增长的特点,例如我国老龄化进程加快、出生人口性别比持续升高、乡村人口城镇化等,利用参考附录中所提供的数据,建立中国人口增长的数学模型,由此对中国人口增长的中短期和长期趋势做出预测,并指出模型的优缺点。
二、 模型假设1、假设题目所给的数据真实可靠;2、假设不考虑我国人口大规模的朝国外迁移,也不考虑外国人大量涌入我国;3、假设不考虑战争、自然灾害、疾病对人口数目和性别比的影响;4、假设在本世纪中叶前,我国计划生育政策稳定。
5、假设中短期内生育率和死亡率保持相对稳定6、假设相同年龄段人口性别比基本稳定。
7、假设人口生育率不受传统观念和个人主观因素的影响。
三、符号说明符号说明:由于符号较多,在以后的模型中具体给出四、问题分析人口发展过程的定量预测,需要预测出未来的人口发展趋势,人口出生、死亡和自然增长率的变化以及在未来的人口构成等各项人口指数全部测算出来。

人口预测数学建模论文Revised on November 25, 2020中国人口政策问题模型【摘要】:中国是世界上的人口大国,近三十年来,我国的人口政策在控制人口数量方面取得了非凡的成绩,使得人口发展逐步走向有计划、可控制的平稳增长时期。
但随着经济的发展和人口老龄化等现象的出现,如何调整人口政策使之与社会发展相适应,是我们亟待研究思考的问题。
本文根据我国近三十年的人口数据对其人口现状,人口老龄化程度等方面进行分析,并给出我国调整人口生育政策的时机、具体方案以及根据模型给出我国人口增长状况的预测结果。
【关键词】:人口现状、老龄化、预测结果、人口政策一、问题的重述近三十年来,我国的人口政策在控制人口数量方面取得了非凡的成绩,但随着经济的发展和人口老龄化等现象的出现,使得我国调整人口生育政策成为可能。
(1)利用有关数据,给出我国人口现状的统计结果;(2)试建立模型,给出我国调整人口生育政策的时机、具体方案并预测结果。
(相关数据在下文的附录中给出)二、模型的假设(1)在模型中预期的时间内,人口不会因发生大的自然灾害、突发事故或战争等而受到大的影响;(2)在我国视为没有人口的迁入和迁出;(3)人口增长只与人口基数、生育、死亡和老龄化有关;(4)一段时期内我国人口的死亡率不发生大的波动,不同年龄段人口的分布也不随时间发生变化;三、问题的分析问题一:根据附表1中给出的相关数据关数据,将近30年人口数量用MATLAB软件画出图形,给出我国人口现状的统计结果。
问题二:根据历年出生率和死亡率,利用MATLAB程序对数据进行拟合,分别得到出生率和死亡率的计算公式。
但结合出生率和死亡率的数据画出具体图形分析发现,数据分段呈现出一定的规律性,于是对数据进行分段拟合,并最终确定出人口的自然增长率,得到人口数的计算公式。
此公式能够较好反应中国近期及预测未来近15年内的人口数量。
根据公式得出相应图(图),发现人口数呈现的相关规律。
全国大学生数学建模比赛论文人口预测模型 WEIHUA system office room 【WEIHUA 16H-WEIHUA WEIHUA8Q8-中国人口预测模型摘要:人口数量的变化,关系到一个国家的未来。
认识人口数量的变化规律,建立人口模型,能够较准确的预报,是有效控制人口增长的前提。
本文对人口预测的数学模型进行了研究。
首先,建立人口指数模型、Logistic模型及灰度预测模型。
对我国2005年以后45年的人口增长进行了预测,根据1982年人口基本数据运用模型对1982年~2005年进行了预测,并用实际数据对预测结果进行了检验。
我们将预测区间分为2006~2030年、2030~2050年两个区间,以量化未来我国短中期与长期的人口变化。
关键词:人口数量的变化人口指数模型 Logistic模型灰度预测模型MATLAB Excel目录第一部分问题重述 (3)第二部分问题分析 (3)第三部分模型的假设 (3)第四部分定义与符号说明 (3)第五部分模型的建立与求解 (3)模型一 (3)模型二 (8)模型三 (12)第六部分对模型的评价 (14)第七部分参考文献 (15)第八部分附表 (15)一、问题重述人口问题始终是制约我国发展的关键因素之一。
本题要求根据已知数据,运用数学建模的思想对我国人口做出分析和预测。
具体问题如下:从中国的实际情况和人口增长的特点,例如我国老龄化进程加快、出生人口性别比持续升高、乡村人口城镇化等,利用参考附录中所提供的数据,建立中国人口增长的数学模型,由此对中国人口增长的中短期和长期趋势做出预测,并指出模型的优缺点。
二、 模型假设1、假设题目所给的数据真实可靠;2、假设不考虑我国人口大规模的朝国外迁移,也不考虑外国人大量涌入我国;3、假设不考虑战争、自然灾害、疾病对人口数目和性别比的影响;4、假设在本世纪中叶前,我国计划生育政策稳定。
5、假设中短期内生育率和死亡率保持相对稳定6、假设相同年龄段人口性别比基本稳定。
中国人口发展趋势的预测模型摘要本文从宏观和微观两方面讨论了中国人口发展问题:建立时间序列分析法中的ARMA 模型, 对中国人口总数进行宏观预测;建立了微分方程的模型, 对中国人口的年龄结构以及男女性别比等几个方面进行微观预测。
对人口总数进行宏观预测时,根据处理后的数据的自相关函数和偏相关函数的拖尾性,估计出ARMA的参数p、q,并对估计的参数进行验证和调节,最终确定参数,建立出ARMA(p ,q)模型。
用此模型预测出2020年和2050年的人口分别为138135.3万人和143352.6万人,而且到2050年人口呈现缓慢下降趋势。
对人口组成结构进行微观预测时,引用Shape-Lotka-Mckendrick模型。
根据中国人口发展的特点,并加入影响因素改进原始模型,分别建立了带移民因素和两性具有不同出生率、死亡率的微分方程模型,并讨论得出带移民因素的模型对我国人口结构预测比Shape-Lotka-Mckendrick模型更合理。
在求解的过程中,本文将连续的微分方程离散化,用多项式拟合得到预测数据,求出方程的数值解,得到2006-2010年人口按年龄的结构分布(男女比例分布、生育率、死亡率、迁移率),并进一步预测出未来人口老龄化指数,其中2020年和2050年的老龄化指数分别为0.511和0.566。
关键字:时间序列微分方程模型连续函数的离散化多项式拟合摘要 (1)一问题的重述与分析 (3)1.1 问题重述 (3)1.2 问题的分析 (3)二模型的基本假设和符号说明 (3)2.1 模型假设 (3)2.2 符号说明 (3)三模型的建立及求解 (4)3.1 模型一 (4)3.2 模型二 (7)3.2.1 只考虑出生率和死亡率的Shape-Lotka-Mckendrick模型]4[ (7)3.2.2 考虑竞争死亡率的模型 (7)3.2.3 考虑两性具有不同出生率和死亡率的人口模型 (8)3.3模型的求解 (8)3.4 对结果的分析 (11)四模型的评价 (11)五参考文献 (12)六附录................................................. 错误!未定义书签。
第七届平顶山学院数学建模竞赛暨全国大学生数学建模竞赛选拔赛题目A题剪切线摘要首先我们对未来人口做了简单的预测,用到的是阻滞增长模型(Logistic模型),从网上搜集数据,分别以1954年、1963年、1980年作为初始年份,以2005年为终止年份。
运用MATLAB软件求出不同的参数x m、r。
来预测2010年的人口数,通过比较分析。
我们选取以1963年为初始年份的参数。
预测我国人口将在2033年达到145.5908千万。
然后又对老龄化问题进行了分析,预测出我国老龄化比例将在2032年20%,对于老龄化问题的加剧,我们提出一些相应措施。
总结出我国有必要对计划生育政策调整,针对深圳市的人口结构,搜集数据分析得到,用excel作图分析,在未来几年内深圳市计划生育调整,对人口结构起到微乎其微的作用,对几十年以后的预测发现,政策调整缓解了老龄化加剧,但随之而来的是劳动力减少,劳动力人口由由调整前的69%降到64%,影响经济发展。
计划生育调整的影响通过调整前后的数据对比,得到相应结论,计划生育调整不单要开放“单独二孩”,社会福利政策也许完善。
关键词:Logistic模型、老龄化、计划生育政策调整、单独二孩问题重述:人口的数量和结构是影响经济社会发展的重要因素。
从20世纪70年代后期以来,我国鼓励晚婚晚育,提倡一对夫妻生育一个孩子。
该政策实施30多年来,有效地控制了我国人口的过快增长,对经济发展和人民生活的改善做出了积极的贡献。
但另一方面,其负面影响也开始显现。
如小学招生人数、高校报名人数逐年下降,劳动人口绝对数量开始步入下降通道,这对经济社会健康、可持续发展将产生一系列影响,引起了中央和社会各界的重视。
党的十八届三中全会提出了开放单独二孩,今年以来许多省、市、自治区相继出台了具体的政策。
政策出台前后各方面人士对开放“单独二孩”的效应有过大量的研究和评论。
请收集一些典型的研究评论报告,根据每十年一次的全国人口普查数据,建立模型,对报告的假设和某些结论发表自己的独立见解,并针对深圳市或其他某区域,讨论计划生育新政策对未来人口数量。
中国人口发展趋势的预测模型摘要本文从宏观和微观两方面讨论了中国人口发展问题:建立时间序列分析法中的ARMA 模型, 对中国人口总数进行宏观预测;建立了微分方程的模型, 对中国人口的年龄结构以及男女性别比等几个方面进行微观预测。
对人口总数进行宏观预测时,根据处理后的数据的自相关函数和偏相关函数的拖尾性,估计出ARMA的参数p、q,并对估计的参数进行验证和调节,最终确定参数,建立出ARMA(p ,q)模型。
用此模型预测出2020年和2050年的人口分别为138135.3万人和143352.6万人,而且到2050年人口呈现缓慢下降趋势。
对人口组成结构进行微观预测时,引用Shape-Lotka-Mckendrick模型。
根据中国人口发展的特点,并加入影响因素改进原始模型,分别建立了带移民因素和两性具有不同出生率、死亡率的微分方程模型,并讨论得出带移民因素的模型对我国人口结构预测比Shape-Lotka-Mckendrick模型更合理。
在求解的过程中,本文将连续的微分方程离散化,用多项式拟合得到预测数据,求出方程的数值解,得到2006-2010年人口按年龄的结构分布(男女比例分布、生育率、死亡率、迁移率),并进一步预测出未来人口老龄化指数,其中2020年和2050年的老龄化指数分别为0.511和0.566。
关键字:时间序列微分方程模型连续函数的离散化多项式拟合摘要 (1)一问题的重述与分析 (3)1.1 问题重述 (3)1.2 问题的分析 (3)二模型的基本假设和符号说明 (3)2.1 模型假设 (3)2.2 符号说明 (3)三模型的建立及求解 (4)3.1 模型一 (4)3.2 模型二 (7)3.2.1 只考虑出生率和死亡率的Shape-Lotka-Mckendrick模型]4[ (7)3.2.2 考虑竞争死亡率的模型 (7)3.2.3 考虑两性具有不同出生率和死亡率的人口模型 (8)3.3模型的求解 (8)3.4 对结果的分析 (11)四模型的评价 (11)五参考文献 (12)六附录................................................. 错误!未定义书签。
一 问题的重述与分析1.1 问题重述合理的预测人口的发展趋势是一个非常重要的课题。
中国是一个人口大国,人口问题始终是制约我国发展的关键因素之一。
近年来中国的人口发展出现了一些新的特点,例如老龄化进程加速,出生人口性别比持续升高,以及乡村人口城镇化等因素,这些都影响着中国人口的增长。
根据实际情况和以上的特点,建立中国人口增长的数学模型,并由此对中国人口增长的中短期和长期趋势做出预测。
1.2 问题的分析要预测人口发展的总趋势,首先要预测的是人口总数。
在当代中国社会,环境稳定,如果没有大规模传染病和战争等的影响,每年的死亡率应该相对稳定,出生率也一直在国家政策的控制中,所以人口总数的预测可以看成一个平稳序列的预测,这样我们考虑用时间序列来进行预测。
仅仅预测出人口的总数还是远远不够的,我们还需要细致的对年龄结构、男女性别比、各年龄段的死亡率和城镇化等问题进行研究。
在微观上求出人口按年龄的结构分布就需要用到微分方程,我们可以考虑在微分方程中加入不同的约束项,得到考虑各种不同因素的微分方程。
对于人口的预测,在短期内可以细致的求出人口按年龄的分布,如果做长期预测,这样的微分方程求出的解将会不精确。
我们在拟合时发现2003年的三组生育率数据有误,由它算出的出生婴儿数为2003年实际0岁人口的1/10。
我们拿2003年的三组生育率数据分别与2002,2004年数据比较发现相对应数据大约相差10倍,故我们将2003年生育率的数据都乘以10进行修正。
二 模型的基本假设和符号说明2.1 模型假设1) 附录2中每年的人口数据均看成是当年年末的人口数据。
2) 假定在预测的年份不发生意外重大事故,如:大规模传染病,战争,自然灾害等。
3) 假设女性的生育年龄区间为[15,49]。
4) 假设90岁以上的人都按90岁计算。
5) 假设市、镇、乡中每个妇女一生生育的胎数分别为1、2、3。
2.2 符号说明r : 表示年龄。
t : 表示时间。
123,,i i i : 分别表示城、镇、乡三个系统。
(,,)p r t i : 表示i 系统t 时刻年龄为r 的人口分布密度函数;1(,,)p r t i 表示i 系统t 时刻年龄为r 的男性人口分布密度函数;2(,,)p r t i 表示i 系统t 时刻年龄为r 的女性人口分布密度函数。
(,,)r t i μ: 表示i 系统t 时刻年龄为r 的人口自然死亡率; 1(,,)r t i μ表示i 系统t 时刻年龄为r 的男性人口自然死亡率;2 (,,)r t i μ表示i 系统t 时刻年龄为r 的女性人口自然死亡率。
()N t : 表示t 时刻人口总数;(,)N t i 表示i 系统t 时刻的人口总数;1(,)N t i 表示i 系统t 时刻的男性人口总数;2(,)N t i i 系统t 时刻的女性人口总数;12 (,)(,)(,)N t i N t i N t i =+。
m r : 表示人口所能活到的最高年龄,我们把90岁以上的人口都按90岁计算,所以m r =90(,,)q r t i : 表示i 系统t 时刻年龄为r 的人口由于我国人口总数太多, 环境资源, 生存空间, 就业条件等引起竞争的限制因素引起的竞争死亡率。
(,,)r t i ψ: 表示i 系统t 时刻年龄为r 的人口总和死亡率,(,,)(,,)(,,)r t i r t i q r t i ψμ=+。
(,,)r t i ϕ: 表示i 系统t 时刻年龄为r 的妇女的生育率。
(,,)f r t i : 表示i 系统t 时刻年龄为r 的人口的迁移比率。
(,,)f r t i >0,表示迁入;(,,)f r t i <0,表示迁出。
(,)b t i : 表示i 系统t 时刻的人口出生率;1(,)b t i 表示i 系统t 时刻的男婴出生率; 2(,)b t i : 表示i 系统t 时刻的女婴出生率。
i λ: 表示i 系统的新生男婴在婴儿总数中的比例,i =1,2,3。
'i λ=1-i λ表示i 系统的新生女婴在婴儿总数中的比例。
P(t,i) 表示i 系统t 时刻1-99岁的人口密度分布矩阵。
β(t,i) 表示i 系统t 时刻的社会条件下,一个妇女(一生)平均生育胎数。
F(t,i) i 系统t 时刻1-99岁人口迁移矩阵。
[a, A]: 为妇女的生育年龄区间。
a=15,A=49。
)(t ω: t 年人口老龄化指数。
A(t): t 年人口平均年龄。
S(t): t 年人口平均寿命。
三 模型的建立及求解3.1 模型一对人口总数的预测我们首先想到用ARMA 模型,ARMA 方法是一种精确度较高的短期时间序列]1[,他将预测对象随时间变化形成的序列看作是一个随机序列。
ARMA 法的基本思想是:一串随时间变化而又相互关联的数字序列,可以用相应的模型加以近似描述。
我们把这个问题中人口数量的预测转化成一个平稳时间序列的预报,通过查阅资料]2[可以得到以往20年的人口数量。
将原始数据实现平稳化处理,可以作为观测到的时间序列12,k Z Z Z ,这样就可以用ARMA 模型进行预测,根据ARMA(p ,q)中参数p ,q 的拖尾性和截尾性,利用统计软件工具进行分析和预测,能够得到人口的走势。
对模型进行检验和参数调试,发现最优模型为ARMA(1,9)。
对时间序列的t X (t=1,2,…,N) 首先要进行相关性分析。
相关性分析的任务是计算序列{}t X 的样本自相关函数和样本偏相关函数,并由他们的截尾性和拖尾性来进行参数p,q 的初选。
参数p, q 并不能直接确定,而是需要先假定一组值,一般是从(1, 1)开始建立模型,然后逐步增大p, q 的值,求出一系列模型,并根据loss function 、AIC 等准则,找出一个最优模型。
对序列通过了平稳性检验并建立了相应ARMA 模型之后,为考核所建模型的优劣,一般还需对ARMA 模型残量12,N a a a 进行检验,判断其是否为白噪声,也就是说,如果经检验确实是白噪声序列,则可认为模型是合理的,否则,就应当进一步改进模型。
从1990年到2050年的人口预测图(左)和相关的预测参数表(右)如下: 横坐标表示各年份,如00表示2000年。
纵坐标表示人数,单位万人。
图表 2 2006年到2050年的人口预测图图表 3 残差(loss function)分析图下面用统计学软件[3]Eview进行统计检验和显著性分析,得出结果:图表 4 统计检验和显著性分析Dependent Variable: SER01Method: Least SquaresDate: 09/23/07 Time: 12:33Sample(adjusted): 1990 2005Included observations: 16 after adjusting endpointsConvergence achieved after 100 iterationsBackcast: 1980 1989Variable Coefficient Std. Error t-Statistic Prob.C 144813.8 453.2095 319.5295 0.0000AR(1) 0.950608 0.000943 1007.691 0.0000R-squared 0.999992 Mean dependent var 123510.7Adjusted R-squared 0.999990 S.D. dependent var 5256.911S.E. of regression 16.25633 Akaike info criterion 8.582203Sum squared resid 3435.488 Schwarz criterion 8.727063Log likelihood -65.65762 F-statistic 784284.9Durbin-Watson stat 1.278105 Prob(F-statistic) 0.000000Inverted AR Roots .95Inverted MA Roots .99 .80 -.58i .80+.58i .31-.94i.31+.94i -.31 -.94i -.31+.94i -.80 -.58i-.80+.58i -.99上表对结果进行了统计分析,其决定系数R2为0.999992,P值小于0.0001,剩余方差为0.000943,所有的指标都表明模型与数据拟合的很好。