小波变换与地震信号特征分析
- 格式:pdf
- 大小:215.81 KB
- 文档页数:7



利用小波包变换对地震信号进行时频分析时小波基函数的选取作者:曾宪伟,赵卫明,师海阔,李自芮来源:《地震研究》2010年第04期摘要:通过比较几种不同的小波基函数的幅频特性,并利用不同的小波基函数对模拟地震记录进行时频分析,以期找到可以更为准确地描述地震信号时频特性的小波基函数。
结果表明:利用dmey小波基函数可以更为准确地描述模拟地震信号的时频变化特征,因此,利用小波包变换对地震信号进行时频分析时选取dmey小波基函数较为合适。
关键词:小波基函数;时频分析;小波包;地震信号中图分类号:P315.63 文献标识码:A 文章编号:1000-0666(2010)04-0323-0 引言小波分析方法是一种窗口面积固定但其形状可以改变,即时间窗和频率窗都可以改变的时频局域化分析方法(飞思科技产品研发中心,2005)。
换句话说,小波变换具有弹性的时频窗,即在低频时小波变换的时间分辨率较低,而频率分辨率较高;在高频时小波变换的时间分辨率较高,而频率分辨率较低,因而小波变换可以保证时域分辨率和频域分辨率在各自需要的范围都达到很高的精度。
另外,由于小波变换可以采用频域紧支的小波基,因此很大程度上可以避免出现频率之间交叉泄漏的现象(曹晖等,2004)。
小波分析中所用的小波函数具有多样性,可以选择非正交小波、正交小波、双正交小波,甚至线性相关的小波(崔岩飞,李晋平,2003),且应用不同的小波基函数解决同一个问题会得到不同的结果,所以在小波分析方法处理信号的实际应用中(刘希强等,1998,2000;林大超等,2002;裴韬等,2004;陈顺云等,2006;曾宪伟等,2008),小波基函数选取是否合适,将对信号处理结果的分析和理解产生直接影响,所以对小波基函数的选取是处理和分析信号前必须要做的一项工作。
在不同的应用领域,小波基的选取标准不同,即使在同一应用领域,小波基的选取也没有统一的标准。
本文通过比较几种常见小波基函数的幅频特性,并利用不同的小波基函数对模拟地震记录进行时频分析,以期给出可以准确地描述地震信号时频特性的小波基函数。

基于小波变换的信号处理在地震预警中的应用一、前言近年来,地震频繁发生,给人们的生命财产造成严重威胁。
因此,地震预警系统成为了解决这个问题的重要手段之一。
然而,地震信号具有高噪声、复杂非线性等特性,如何处理这些信号成了地震预警系统的难点。
本文将介绍基于小波变换的信号处理在地震预警中的应用。
二、小波变换的基本概念小波变换是一种基于多分辨率的信号分析方法,它具有时频分析的优点。
它将信号分为尺度(scale)和位置(position)两个方面,采用不同的小波基将信号从时域(time domain)变换到小波域(wavelet domain)。
小波变换的基本公式如下:其中,x(t)和y(a,b)分别表示在时域和小波域中的信号,ψ(u)是小波基。
三、小波变换在地震预警中的应用1.小波变换在地震信号中的作用地震信号由于其高噪声、复杂非线性等特性,传统的傅里叶变换等处理方法难以处理这些信号。
而小波变换则可以有效地对地震信号进行处理,具体表现在以下几个方面:(1)时频分析小波变换可以将信号从时域转换到小波域,这使得我们可以同时观察到信号在时间和频率上的变化情况。
这对于地震信号的分析具有重要意义,可以更加准确地捕捉地震信号的时空特性。
(2)信号去噪地震信号中的噪声往往是比较大的,这会对地震预警系统的准确性产生较大的影响。
小波变换具有去噪的作用,可以将地震信号中的噪声滤除,发挥更好的作用。
(3)特征提取地震预警系统需要提取一些特征来判断地震的发生与否。
小波变换可以提取信号的一些重要特征,如能量、频率、相位等,这对于地震预警系统的准确性具有较大的帮助。
2.小波变换在地震预警系统中的应用在地震预警系统中,小波变换可以用于地震信号的预处理、特征提取、模式识别等方面。
具体来说,可以采取以下几个步骤:(1)对地震信号进行小波分解,得到不同尺度的小波系数。
(2)去除小波系数中的噪声,提高信噪比。
(3)利用小波系数中的特征进行模式识别,以判断地震的发生与否、其发生位置及强度等参数。

小波分析及其在地震工程中的应用摘要小波分析方法是一种较为先进的科学理论,已经在数学、工程、军事以及机械等领域中得到普遍运用,且获得一定的效果。
然而在地震工程中小波分析的使用还不是很成熟。
本文将对小波分析进行简单概述,介绍其涵义,并对地震工程中小波分析的具体应用进行分析。
关键词地震工程;小波分析;应用0引言近年来,在科学技术解出现了一种理论与手段,在科学界引起了较大的振动,即小波数学理论,随着科学技术的不断进步,人们对该理论的认识越来成熟。
学者认为小波理论是数学、工程以及物理等方面的综合。
目前。
在众多学科中小波理论得到广泛的使用,例如在土木工程中,小波分析能够进行信号奇异性的检查、对信号进行消噪处理,并且对含噪的信号内的有用信息进行有效识别等作用。
然而在地震工程中的使用还不够成熟,因此应该加强对小理论在地震工程中的运用。
1小波分析概述小波指的就是小的波形,而其中的“小”就是其具备衰减性,“波”则代表其具备波动性,它振幅正负向之间的一种震荡方式。
和Fourier变换相比较,小波变换主要是在空间或时间上局部频率的分析与研究,其利用伸缩平移运算对信号逐渐实行多尺度上的细化处理,从而实现高频处与低频处时间上的细化,可以自动满足时频信号分析的需要,进而能够将其集中在信号的任何一个部分上,有效处理好Fourier变换上的难题。
小波分析已经成为科学方法上的一个重要突破。
小波分析的明确涵义为:ψ(t)表示平方可积函数,也就是ψ(t)∈L2(R),如果ψ(t)能够达到允许的条件:那么ψ(t)就代表的是一个小波母函数或者是一个小波函数。
在母函数ψ(t)相同的情况下,通过平移与伸缩之后能够获得函数组,即ψa,b(t),被叫做一族小波。
就某种意义而言,小波交换是利用一族小波函数来代表函数或者是信号。
2 地震工程中小波分析的应用在地震工程中,小波分析的运用才刚刚起步,还不够成熟。
而目前在地震工程中已经运用到小波分析的主要有地震波的去噪与滤波等方面。
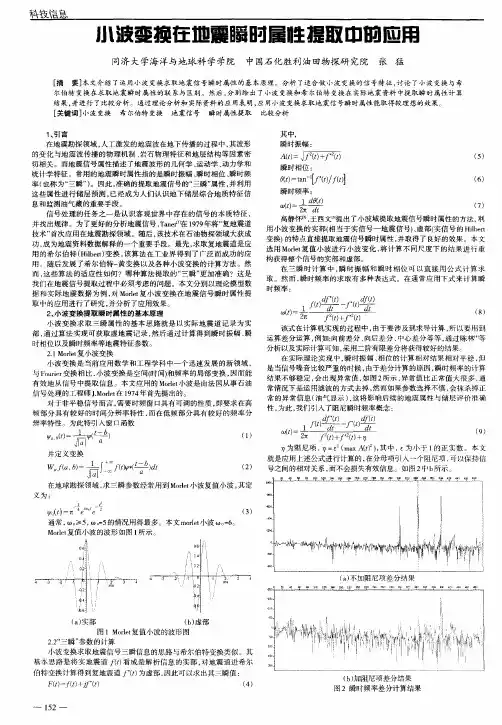

地震数据的频谱分析与波形滤波研究地震是自然界中最具破坏性的自然灾害之一,对人类的生命和财产造成了巨大的影响。
为了更好地了解地震的特性和预测未来可能发生的地震,研究地震数据的频谱分析和波形滤波显得尤为重要。
频谱分析是一种将时域信号转换为频域信号的方法,可以通过分析不同频率成分的大小和相位信息来研究信号的特性。
在地震数据中,频谱分析可以帮助我们了解地震波的频率分布情况、地震波的传播路径以及地震源的特征等信息。
常用的频谱分析方法包括傅里叶变换、小波变换和时频分析等。
傅里叶变换是一种将时域信号转换为频域信号的方法,可以将一个信号分解成不同频率的正弦波成分。
在地震数据中,傅里叶变换可以帮助我们分析地震波的频率分布情况,从而了解地震波在不同频率下的传播特性。
此外,傅里叶变换还可以用于滤波处理,去除地震数据中的噪声干扰。
小波变换是一种将时域信号转换为时频域信号的方法,可以将一个信号分解成不同尺度和不同频率的小波成分。
在地震数据中,小波变换可以帮助我们分析地震波的时频特性,从而了解地震波在不同时间和不同频率下的传播特性。
此外,小波变换还可以用于去除地震数据中的噪声干扰和提取地震信号中的有用信息。
时频分析是一种将时域信号转换为时频域信号的方法,可以同时分析信号在时间和频率上的特性。
在地震数据中,时频分析可以帮助我们了解地震波在不同时间和不同频率下的传播特性和地震源的特征等信息。
常用的时频分析方法包括短时傅里叶变换、小波包变换和Wigner-Ville分布等。
除了频谱分析,波形滤波也是研究地震数据的重要方法之一。
波形滤波是一种将地震数据中的噪声干扰去除或者弱化的方法,可以提高地震数据的质量和可靠性。
常用的波形滤波方法包括低通滤波、高通滤波、带通滤波和带阻滤波等。
低通滤波是一种将高频成分去除或者弱化的方法,可以去除地震数据中高频噪声干扰,保留低频信号成分。
高通滤波是一种将低频成分去除或者弱化的方法,可以去除地震数据中低频噪声干扰,保留高频信号成分。

小波变换在地震信号处理中的应用案例小波变换是一种在地震信号处理中广泛应用的数学工具。
它的独特性质使得它在地震学领域中具有重要的应用价值。
本文将从理论和实际应用两个方面探讨小波变换在地震信号处理中的应用案例。
一、小波变换的基本原理小波变换是一种时频分析方法,它能够将信号分解为不同频率和不同时间尺度上的成分。
与传统的傅里叶分析方法相比,小波变换具有更好的时域和频域分辨率。
其基本原理是通过将信号与一组称为小波基函数的函数进行卷积,得到信号在不同尺度上的频谱信息。
二、小波变换在地震信号处理中的应用案例1. 地震波形分析地震波形是地震信号的一种重要表现形式,通过对地震波形进行小波变换,可以获得地震信号在不同频率和不同时间尺度上的特征。
这对于地震学家来说是非常有价值的,因为地震波形中蕴含着地震事件的许多重要信息,如震源深度、震级等。
小波变换可以帮助地震学家更准确地解读地震波形,从而提高地震预测和监测的能力。
2. 地震信号去噪地震信号通常伴随着大量的噪声,这给地震信号的处理和分析带来了很大的困难。
小波变换具有良好的局部化特性,可以将信号分解为不同尺度上的成分,从而实现对噪声的有效去除。
通过选择合适的小波基函数和阈值处理方法,可以将地震信号中的噪声部分去除,提取出地震信号的有效信息。
3. 地震信号的频谱分析地震信号的频谱分析是地震学中的重要研究内容之一。
小波变换能够提供地震信号在不同频率上的频谱信息,从而帮助地震学家了解地震事件的频率特征。
通过对地震信号进行小波变换,可以得到地震信号的频谱图,进而分析地震信号的频率分布和能量分布等特征。
4. 地震信号的时频分析地震信号的时频分析是研究地震信号时域和频域特征的重要手段。
小波变换具有良好的时域和频域分辨率,可以提供地震信号在不同时间尺度和不同频率上的时频信息。
通过对地震信号进行小波变换,可以研究地震信号的时域演化和频域特征,进一步了解地震事件的动态过程。
三、小波变换在地震信号处理中的局限性尽管小波变换在地震信号处理中具有广泛的应用价值,但它也存在一些局限性。

小波变换在地震信号处理中的应用地震是自然界中一种常见而又危险的现象,对人类社会和经济造成了巨大的影响。
为了更好地理解和预测地震,地震信号处理成为了一个重要的研究领域。
而小波变换作为一种有效的信号处理工具,正逐渐被应用于地震信号的分析和处理中。
小波变换是一种时频分析方法,它可以将信号分解成不同频率的成分,并且能够提供信号在不同时间尺度上的细节信息。
在地震信号处理中,小波变换可以帮助我们识别和分析地震信号中的不同频率成分,从而更好地理解地震的特征和演化规律。
首先,小波变换可以用于地震信号的去噪处理。
地震信号中往往包含大量的噪声,这些噪声会干扰我们对地震信号的分析和判断。
通过应用小波变换,我们可以将地震信号分解成不同频率的子信号,然后根据子信号的能量分布情况,选择合适的阈值进行去噪。
这样可以有效地减少噪声对地震信号的影响,提高地震信号的质量和可靠性。
其次,小波变换还可以用于地震信号的特征提取。
地震信号中包含了丰富的地震波形信息,通过提取地震信号的特征参数,可以帮助我们判断地震的类型、规模和发生位置等重要信息。
小波变换可以将地震信号分解成不同频率的子信号,然后通过计算子信号的能量、频率和相位等特征参数,来描述地震信号的特征。
这些特征参数可以用于地震信号的分类和识别,为地震预测和灾害评估提供重要依据。
此外,小波变换还可以用于地震信号的时频分析。
地震信号的频率和振幅往往随着时间的变化而变化,通过应用小波变换,我们可以将地震信号分解成不同时间尺度的子信号,从而可以观察到地震信号在不同时间尺度上的频率和振幅变化情况。
这种时频分析方法可以帮助我们更好地理解地震信号的演化过程,揭示地震活动的规律和机制。
然而,小波变换在地震信号处理中也存在一些挑战和限制。
首先,小波变换的计算复杂度较高,对计算资源的要求较大。
在处理大规模地震数据时,计算时间和存储空间可能会成为问题。
其次,小波变换的参数选择对结果影响较大,需要经验和专业知识的指导。


地震监测数据的可视化与分析方法研究地震是一种破坏性极大的自然灾害,对人类社会造成了严重的影响。
为了能够更好地了解地震的发生规律和预测地震的可能性,科学家们使用各种监测设备来收集地震数据。
然而,单纯的数据收集并不能直观地揭示地震的模式和趋势,因此,可视化与分析地震监测数据成为了一种重要的研究方法。
一、地震监测数据的可视化方法地震监测数据的可视化方法主要包括地震波形图、时空图和三维可视化图等。
1. 地震波形图地震波形图是将地震信号以波形的形式进行展示,通过波形的振幅、频率和时间等信息可以获得地震的特征。
波形图可以直观地显示出地震的震级和震源位置,对于研究地震的强度和发生机理非常有价值。
2. 时空图时空图是通过将地震监测数据在时间和空间上进行绘制,以揭示地震的变化规律。
时空图可以将地震的分布情况、发生频率和震级等信息直观地展示出来,帮助人们更好地理解地震的演化过程。
3. 三维可视化图三维可视化图可以将地震监测数据以三维模型的形式呈现,使得人们可以在更直观的环境中观察和分析地震的特征。
通过三维可视化图,可以更全面地了解地震的结构和变化情况,进一步探究地震的成因和演化。
二、地震监测数据的分析方法地震监测数据的分析方法主要包括频谱分析、小波变换和时频分析等。
1. 频谱分析频谱分析可以将地震信号转换为频域信号,通过检测不同频率的成分来分析地震信号的特征。
频谱分析可以获得地震信号的主要频率成分,从而揭示地震的震级和震源特征。
2. 小波变换小波变换是一种能够在时域和频域上同时展现地震信号信息的分析方法。
通过小波变换,可以将地震信号分解为不同尺度和频率的成分,从而更全面地了解地震信号的特征。
3. 时频分析时频分析是将地震信号在时域和频域上同时进行分析的一种方法。
通过时频分析,可以获得地震信号的时间变化和频率变化情况,从而更准确地研究地震的发生机制和演化过程。
三、地震监测数据可视化与分析方法的应用地震监测数据的可视化与分析方法可以应用于地震预测、灾害评估和地震工程设计等领域。
摘要同步压缩小波变换(Synchrosqueezing Wavelet Transform,SSWT)是在小波变换(Wavelet Transform,CWT)基础上发展而来的时频分析方法,结合了重排算法的思想,可以获得较高的时频分辨率,同时可以实现信号的重构。
文中基于CWT和重排算法系统地介绍了SSWT的方法原理,并通过示例对其时频分析效果和重构效果进行了分析。
另外,针对与SSWT算法思想类似的几种改进和推广算法,如:压缩短时傅里叶变换、二阶压缩短时傅里叶变换以广义同步压缩变换等,文中对其方法原理一一进行了介绍,并用模型信号和实际地震信号进行了分析对比。
由于SSWT以CWT为基础,因此也一样受测不准原理限制,针对这一问题,本文将互补集合经验模态分解(Complementary Empirical Mode Decomposition,CEEMD)与SSWT结合,首先利用CEEMD将信号自适应分解为一系列的经验模态分量(Intrinsic Mode Function,IMF),然后根据各个分量频率范围采用不同的压缩小波系数,最后将各个分量的时频结果相加得到原信号的时频谱结果,从而改善SSWT的时频分辨率。
地震信号是典型的非平稳信号,SSWT可以获得良好的时频表征,因此该方法是对地震信号进行处理分析的有效工具。
文中基于该方法主要研究了以下几个方面的具体应用:基于SSWT的谱模拟反褶积提高地震资料分辨率;基于SSWT的Q估计和反Q补偿衰减地震信号;基于SSWT的随机噪声压制以及利用SSWT进行低频阴影检测。
通过模型和实际资料测试,并与其他方法对比,证明了该时频分析方法在地震资料处理中应用的有效性和优越性。
关键词:时频分析;同步压缩小波变换;提高分辨率;去噪;储层预测Synchrosqueezing Wavelet Transform and ItsApplication in Seismic Data ProcessingZhang Yan(School of Geosciences)Directed by Prof. Li ZhenchunAbstractSynchrosqueezing Wavelet Transform is a time-frequency analysis method developed on the basis of Wavelet Transform (CWT). Combining with the idea of Reassignment Method (RM), it can obtain higher time-frequency resolution and signal reconstruction at the same time.In this paper, the principle of SSWT is systematically introduced based on CWT and RM, and the effect of time-frequency analysis and reconstruction results are analyzed through examples. In addition, several improvements and generalizations similar to those of the SSWT algorithm, such as: synchrosqueezing short-time Fourier transform, second-order synchrosqueezing transform and generalized synchrosqueezing transform, etc. Introduced and compared using the model signal and the actual seismic signal.Since the SSWT is based on CWT, it is also subject to the principle of unqualified measurement. To solve this problem, this paper combines Complementary Empirical Mode Decomposition (CEEMD) with SSWT, and first uses CEEMD to decompose signals adaptively. For a series of empirical modal components (IMF), then use different compression wavelet coefficients according to the frequency range of each component, and finally add the time-frequency results of each component to obtain the time-frequency spectrum of the original signal, thereby improving the SSWT. Time-frequency resolution.Seismic signals are typical non-stationary signals. SSWT can obtain good time-frequency characterization. Therefore, this method is an effective tool for processing and analyzing seismic signals. Based on this method, the paper mainly studied the following applications: spectral modeling deconvolution based on SSWT to improve the resolution of seismic data; SSWT-based Q-estimation and anti-Q compensation for attenuated seismic signals; and SSWT-based noise suppression and utilization The SSWT performs low-frequency shadow detection. Through the model and real data tests, and compared with other methods, the validity andsuperiority of this time-frequency analysis method in seismic data processing are proved.Key words: time-frequency analysis; Synchrosqueezing Wavelet Transform; improving resolution; Denoising; Reservoir prediction.目录第一章绪论 (1)1.1选题的目的与意义 (1)1.2国内外研究现状 (1)1.3论文的研究内容及成果 (3)第二章同步压缩小波变换 (5)2.1常用时频分析方法 (5)2.1.1短时傅里叶变换 (5)2.1.2 连续小波变换 (6)2.1.3 广义S变换 (8)2.1.4 Wigner Ville分布及平滑伪Wigner Ville 分布 (9)2.1.5 时频分析方法效果对比分析 (11)2.2 SSWT (17)2.2.1 时频谱重排 (17)2.2.2 SSWT的基本原理 (18)2.3 SSWT时频分析及重构示例 (21)2.3.1 模型信号SSWT示例 (21)2.3.2实际地震信号SSWT示例 (23)2.4 小结 (25)第三章SSWT的推广及改进方法 (26)3.1 压缩短时傅里叶变换 (26)3.1.1 方法原理 (26)3.1.2 模型信号时频表征及重构示例 (27)3.1.3 实际地震信号时频表征及重构示例 (28)3.2 二阶压缩短时傅里叶变换 (30)3.2.1 方法原理 (30)3.2.2 模型信号示例 (31)3.2.3 实际地震信号示例 (32)3.3 广义同步压缩变换 (34)3.3.1 广义解调 (34)3.3.2 广义同步压缩变换的原理 (35)3.3.3 模型信号示例 (37)3.4 小结 (39)第四章基于CEEMD的同步压缩小波变换 (41)4.1 CEEMD (41)4.1.1 CEEMD及算法流程 (41)4.1.2 CEEMD分解测试 (43)4.2 基于CEEMD分解的同步压缩小波变换 (46)4.2.1 方法原理 (46)4.2.2 模型信号测试 (49)4.2.3 实际地震信号测试 (50)4.3 小结 (51)第五章SSWT在地震数据处理中的应用 (53)5.1 基于SSWT的时变谱模拟反褶积提高地震资料分辨率 (53)5.1.1 谱模拟反褶积方法原理 (53)5.1.2 基于SSWT的谱模拟反褶积 (54)5.1.3 实际地震资料测试 (57)5.2 基于SSWT的Q提取及反Q补偿 (59)5.2.1 Q提取及反Q补偿原理 (59)5.2.2 基于SSWT的Q提取及反Q补偿模型测试 (61)5.2.3 实际地震资料测试 (68)5.3 基于SSWT压制随机噪声 (70)5.3.1 方法原理 (70)5.3.2 模型信号测试 (71)5.3.3 实际地震资料测试 (73)5.4 基于SSWT的谱分解低频阴影检测 (75)5.4.1 模型资料测试 (75)5.4.2 实际地震资料测试 (77)5.5 小结 (79)结论与讨论 (80)参考文献 (81)攻读硕士期间取得的学术成果 (86)致谢 (87)中国石油大学(华东)硕士学位论文第一章绪论1.1选题的目的与意义地震波在地下介质中传播时,会发生吸收衰减及散射等现象,这都和频率相关,这导致接受到的地震波时频关系较为复杂,为典型的非平稳信号。
如何使用小波变换进行信号特征提取信号特征提取是信号处理领域中的一个重要任务,它可以帮助我们从复杂的信号中提取出有用的信息。
而小波变换作为一种有效的信号分析工具,被广泛应用于信号特征提取中。
本文将介绍如何使用小波变换进行信号特征提取,并探讨其在实际应用中的优势和限制。
一、小波变换简介小波变换是一种时频分析方法,它可以将信号分解成不同尺度和频率的小波系数。
与傅里叶变换相比,小波变换具有更好的时域和频域局部性。
小波变换通过对信号进行连续或离散的小波分解,得到小波系数,从而实现信号的特征提取和分析。
二、小波变换的优势1. 多分辨率分析能力:小波变换可以将信号分解成不同尺度的小波系数,从而提供了多尺度的信号分析能力。
这使得小波变换在处理具有不同频率成分的信号时具有更好的适应性。
2. 时域和频域局部性:小波变换具有时域和频域局部性,能够更好地捕捉信号的瞬态特征和局部频率变化。
这使得小波变换在处理非平稳信号时具有优势,例如生物信号、地震信号等。
3. 信息压缩能力:小波变换可以通过对小波系数的阈值处理,实现信号的信息压缩。
这对于存储和传输大量信号数据时非常有用,可以减少数据量并保留重要的特征信息。
三、小波变换的应用小波变换在信号特征提取中有广泛的应用,下面以几个具体的应用领域为例进行介绍。
1. 生物医学信号处理:小波变换可以用于生物医学信号的特征提取,如心电图(ECG)信号的QRS波群检测、脑电图(EEG)信号的睡眠分期等。
通过对小波系数的分析,可以提取出与特定疾病或状态相关的特征,为医学诊断和监测提供支持。
2. 图像处理:小波变换可以用于图像的特征提取和压缩。
通过对图像的小波分解,可以提取出不同尺度和方向的纹理特征,用于图像分类、目标检测等任务。
同时,小波变换还可以实现图像的压缩编码,减少图像数据的存储和传输量。
3. 振动信号分析:小波变换可以用于振动信号的故障诊断和预测。
通过对振动信号进行小波分解,可以提取出与故障特征相关的频率成分和能量分布,从而实现对机械设备的故障检测和健康状态评估。
小波变换在地震勘探中的应用地震勘探是一种常用的地质勘探方法,它通过观测地震波在地下的传播和反射来获取地下结构信息。
在地震勘探中,小波变换被广泛应用于地震数据的处理和解释。
小波变换是一种数学工具,它可以将信号分解成不同频率的成分,从而提供更详细和准确的地下结构信息。
首先,小波变换可以用于地震数据的去噪。
地震数据通常包含大量的噪声,这些噪声会干扰地震波的传播和反射,从而影响地下结构的解释。
通过应用小波变换,可以将地震数据分解成不同频率的成分,然后根据频率的特性选择合适的阈值进行去噪。
这样可以有效地去除噪声,提高地震数据的质量。
其次,小波变换可以用于地震数据的压缩和压缩感知。
地震数据通常具有大量的冗余信息,而小波变换可以将信号分解成不同频率的成分,从而提供了一种有效的压缩方法。
通过选择合适的小波基函数和分解层数,可以将地震数据压缩到较小的存储空间中,同时保留重要的地下结构信息。
此外,小波变换还可以与压缩感知理论相结合,通过选择少量的测量样本和适当的重建算法,实现对地震数据的高效压缩和重建。
此外,小波变换还可以用于地震数据的频谱分析和频率域处理。
地震数据的频谱特性可以提供地下结构的频率分布信息,从而帮助解释地下构造和岩性。
通过应用小波变换,可以将地震数据转换到频率域,然后进行频谱分析和滤波处理。
这样可以提取地震数据的频率特征,帮助解释地下结构的频率分布和变化规律。
最后,小波变换还可以用于地震数据的时间-频率分析和时频域处理。
地震数据的时间-频率特性可以提供地下结构的时变信息,从而帮助解释地震波的传播和反射过程。
通过应用小波变换,可以将地震数据转换到时频域,然后进行时间-频率分析和时频滤波处理。
这样可以提取地震数据的时变特征,帮助解释地下结构的时变规律和动态过程。
综上所述,小波变换在地震勘探中具有广泛的应用。
它可以用于地震数据的去噪、压缩和压缩感知,频谱分析和频率域处理,以及时间-频率分析和时频域处理。
通过应用小波变换,可以提高地震数据的质量和分辨率,从而提供更详细和准确的地下结构信息。
地震波形识别与特征提取方法探讨地震是地球内部能量释放的一种表现,其波动会引起地下或地表的振动,导致严重的破坏和人员伤亡。
因此,地震波形识别与特征提取是地震预警、震级、震源定位以及地震工程等领域的重要研究内容。
本文将探讨地震波形识别与特征提取的方法。
地震波形识别是指确定地震波形属于地震事件的类型,如地壳地震、火山地震等。
对于波形的识别,可以采用时域和频域分析相结合的方法。
时域分析主要通过观察波形的波形图、时刻图、统计量、信号的均方根等特征来确定地震类型。
频域分析则是通过将波形进行傅里叶变换,将波形转换为频谱,进而观察频谱的能量分布、主频、频率带宽等特征来判断地震类型。
目前,常用的地震波形识别方法有人工分类、模式识别、机器学习等。
特征提取是在地震波形识别基础上,进一步分析波形中的关键信息。
常用的特征有时域特征、频域特征、小波变换特征。
时域特征包括振幅、持续时间、起伏性等,通过对波形的统计学指标进行分析,可以获得波形的基本特征。
频域特征则是通过对波形进行频率分析,提取频率域上的信息,如主频、频谱带宽等。
小波变换特征是一种能够同时获得时频信息的方法,可以将时域信号转换为时频域信号,进而提取波形的频谱特征。
除了传统的特征提取方法,近年来,深度学习技术在地震波形识别与特征提取方面也得到了广泛应用。
深度学习通过构建多个隐层并进行逐层训练,能够自动学习波形的特征表示,提高地震波形识别的准确性。
常用的深度学习方法包括卷积神经网络、循环神经网络等。
在地震波形识别与特征提取的研究中,也存在一些挑战和问题。
首先,地震波形数据的获取和处理较为困难,需要大量的监测设备和专业知识。
其次,地震波形具有时变性、非线性、噪声扰动等特点,对算法的稳定性和鲁棒性提出了要求。
此外,由于地震波形识别与特征提取中所涉及的数据量大且复杂,需要高效的算法和计算资源支持。
综上所述,地震波形识别与特征提取在地震预警、震级、震源定位以及地震工程等领域具有重要的应用前景。