下载文档原格式
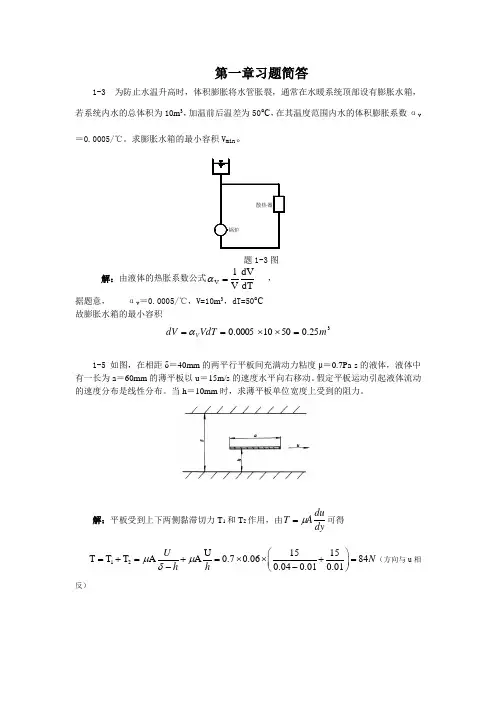
第一章习题简答1-3 为防止水温升高时，体积膨胀将水管胀裂，通常在水暖系统顶部设有膨胀水箱，若系统内水的总体积为10m 3，加温前后温差为50°С，在其温度范围内水的体积膨胀系数αv＝0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解：由液体的热胀系数公式dTdVV 1V =α ， 据题意， αv ＝0.0005/℃，V=10m 3，dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图，在相距δ＝40mm 的两平行平板间充满动力粘度μ＝0.7Pa·s 的液体，液体中有一长为a ＝60mm 的薄平板以u ＝15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h ＝10mm 时，求薄平板单位宽度上受到的阻力。
解：平板受到上下两侧黏滞切力T 1和T 2作用，由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭（方向与u 相反）1-7 温度为20°С的空气，在直径为2.5cm 的管中流动，距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少？解：温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系，且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250，c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ （与课本后的答案不一样。
第一章 绪论1-1 空气的密度31.165kg/m ρ=，动力粘度51.8710Pa s μ-=⨯⋅，求它的运动粘度ν。
解：由ρμ=v 得，55231.8710Pa s 1.6110m /s 1.165kg/m v μρ--⨯⋅===⨯ 1-2 水的密度3992.2kg/m ρ=，运动粘度620.66110m /s v -=⨯，求它的动力粘度μ。
解：由ρμ=v 得，3624992.2kg/m 0.66110m /s 6.5610Pa s μρν--==⨯⨯=⨯⋅ 1-3 一平板在油面上作水平运动，如图所示。
已知平板运动速度V ＝lm/s ，板与固定边界的距离δ＝5mm ，油的粘度0.1Pa s μ=⋅，求作用在平板单位面积上的粘滞阻力。
解：假设板间流体中的速度分布是线性的，则板间流体的速度梯度为13d 1m/s 200s d 510mu V y δ--===⨯ 由牛顿内摩擦定律d d u yτμ=，可得作用在平板单位面积上的粘滞阻力为 -1d 0.1Pa s 200s 20Pa d u yτμ==⋅⨯= 1-4 有一个底面积为40cm ×60cm 矩形木板，质量为5kg ，以0.9m/s 的速度沿着与水平面成30倾角的斜面匀速下滑，木板与斜面之间的油层厚度为1mm ，求油的动力粘度。
解：建立如下坐标系，沿斜面向下方向为x 轴的正方向，y 轴垂直于平板表面向下。
设油膜内速度为线性分布，则油膜内的速度梯度为：330.9m /s 0.910110mu y -∂==⨯∂⨯1s - 由牛顿内摩擦定律知，木板下表面处流体所受的切应力为：30.910u yτμμ∂==⨯∂ Pa 木板受到的切应力大小与τ相等，方向相反，则匀速下滑时其受力平衡方程为：30.9100.40.659.8sin 30μ︒⨯⨯⨯=⨯从而可得油的动力粘度：0.1134Pa s μ=⋅1-5 上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩M 的表达式。
习题【1】1-1 解：已知：120t =℃，1395p kPa '=，250t =℃ 120273293T K =+=，250273323T K =+= 据p RT ρ=，有：11p RT ρ'=，22p RT ρ'= 得：2211p T p T '='，则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解：受到的质量力有两个，一个是重力，一个是惯性力。
重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-3 解：已知：V=10m 3，50T ∆=℃，0.0005V α=℃-1根据1V V V Tα∆=⋅∆，得：30.000510500.25m V V V T α∆=⋅⋅∆=⨯⨯=1-4 解：已知：419.806710Pa p '=⨯，52 5.884010Pa p '=⨯，150t =℃，278t =℃ 得：1127350273323T t K =+=+=，2227378273351T t K =+=+= 根据mRTp V=，有：111mRT p V '=，222mRT p V '=得：421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯，即210.18V V =体积减小了()10.18100%82%-⨯=G ＝mg自由落体： 加速度a ＝g1-5 解：已知：40mm δ=，0.7Pa s μ=⋅，a =60mm ，u =15m/s ，h =10mm根据牛顿内摩擦力定律：u T Ayμ∆=∆ 设平板宽度为b ，则平板面积0.06A a b b =⋅= 上表面单位宽度受到的内摩擦力：1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ，方向水平向左 下表面单位宽度受到的内摩擦力：2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ，方向水平向左 平板单位宽度上受到的阻力：12216384N τττ=+=+=，方向水平向左。
第一章习题答案选择题（单选题）1.1 按连续介质的概念，流体质点是指：（d ）（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。
1.2 作用于流体的质量力包括：（c ）（a ）压力；（b ）摩擦阻力；（c ）重力；（d ）表面张力。
1.3 单位质量力的国际单位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。
1.4 与牛顿内摩擦定律直接有关的因素是：（b ）（a ）剪应力和压强；（b ）剪应力和剪应变率；（c ）剪应力和剪应变；（d ）剪应力和流速。
1.5 水的动力黏度μ随温度的升高：（b ）（a ）增大；（b ）减小；（c ）不变；（d ）不定。
1.6 流体运动黏度ν的国际单位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。
1.7 无黏性流体的特征是：（c ）（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RT p=ρ。
1.8 当水的压强增加1个大气压时，水的密度增大约为：（a ）（a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。
1.9 水的密度为10003kg/m ，2L 水的质量和重量是多少？ 解： 10000.0022m V ρ==⨯=（kg ）29.80719.614G mg ==⨯=（N ）答：2L 水的质量是2 kg ，重量是19.614N 。
1.10 体积为0.53m 的油料，重量为4410N ，试求该油料的密度是多少？ 解： 44109.807899.3580.5m G g V V ρ====（kg/m 3） 答：该油料的密度是899.358 kg/m 3。
1.11 某液体的动力黏度为0.005Pa s ⋅，其密度为8503/kg m ，试求其运动黏度。
第一章 流体及其物理性质1－1 已知油的重度为7800N/m 3，求它的密度和比重。
又，0.2m 3此种油的质量和重量各为多少？已已知知：：γ＝7800N/m 3；V ＝0.2m 3。
解析：(1) 油的密度为 3kg/m 79581.97800===gγρ； 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρN 15602.07800=⨯==V G γ 1－2 已知300L(升)水银的质量为4080kg ，求其密度、重度和比容。
已已知知：：V ＝300L ，m ＝4080kg 。
解析：水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为3N/m 13341681.913600=⨯==g ργ水银的比容为 kg /m 10353.7136001135-⨯===ρv1－3 某封闭容器内空气的压力从Pa 提高到Pa ，温度由20℃升高到78℃，空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少？减少的百分比又为多少？已已知知：：p 1＝Pa ，p 2＝Pa ，t 1＝20℃，t 2＝78℃，R ＝287.06J/k g ·K 。
解析：由理想气体状态方程(1－12)式，得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v vv 每kg 空气的体积比原有体积减少了0.664m 3；减少的百分比为80％。
1－4 图示为一水暖系统，为了防止水温升高时体积膨胀将水管胀裂，在系统顶部设一膨胀水箱，使水有膨胀的余地。
《工程流体力学》课后习题答案孔珑第四版第2章流体及其物理性质 (5)2-1 (5)2-3 (5)2-4 (7)2-5 (7)2-6 (8)2-7 (8)2-8 (9)2-9 (9)2-11 (10)2-12 (10)2-13 (11)2-14 (11)2-15 (12)2-16 (13)第3章流体静力学 (14)3-1 (14)3-2 (14)3-3 (15)3-5 (15)3-6 (16)3-9 (16)3-21 (20)3-22 (21)3-23 (22)3-25 (22)3-27 (22)第4章流体运动学及动力学基础 (24)4-2 (24)4-5 (24)4-6 (25)4-8 (25)4-11 (26)4-12 (26)4-14 (27)4-22 (28)4-24 (28)4-26 (30)第6章作业 (30)6-1 (30)6-3 (31)6-7 (31)6-10 (31)6-12 (32)6-17 (33)第2章流体及其物理性质2-1已知某种物质的密度ρ=2.94g/cm3，试求它的相对密度d。
【2.94】解：ρ=2.94g/cm3=2940kg/m3，相对密度d=2940/1000=2.942-2已知某厂1号炉水平烟道中烟气组分的百分数为，α(CO2)=13.5%α(SO2)=0.3%，α(O2)=5.2%，α(N2)=76%，α(H2O)=5%。
试求烟气的密度。
解：查课表7页表2-1，可知ρ(CO2)=1.976kg/m3，ρ(SO2)=2.927kg/m3，ρ(O2)=1.429kg/m3，ρ(N2)=1.251kg/m3，ρ(H2O)=1.976kg/m3，ρ(CO2)=1.976kg/m3，3ρ=∑i iαρ=341kg/m.12-3上题中烟气的实测温度t=170℃，实测静计示压强Pe=1432Pa，当地大气压Pa=100858Pa。
试求工作状态下烟气的密度和运动粘度。
【0.8109kg/m3，2.869×10-5㎡∕s】解：1）设标准状态下为1状态，则p1=101325pa，T1=273K，ρ1=1.341kg/m3工作状态下为2状态，则p2=p a-p e=100858-1432=99416pa，T2=273+170=443K，则根据理想气体状态方程，可知带入数值，可得工作状态下ρ2=0.8109kg/m32）运动粘度，及课本14页例题2-4题比较先求出每一种气体在170℃时的动力粘度，利用苏士兰公式，课本12页。
1-2 一盛水封闭容器从空中自由下落，则器内水体质点所受单位质量力等于多少 解：受到的质量力有两个，一个是重力，一个是惯性力。
重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-5 如图，在相距δ＝40mm 的两平行平板间充满动力粘度μ＝0.7Pa·s 的液体，液体中有一长为a ＝60mm 的薄平板以u ＝15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h ＝10mm 时，求薄平板单位宽度上受到的阻力。
解：平板受到上下两侧黏滞切力T 1和T 2作用，由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭（方向与u 相反）1-9 某圆锥体绕竖直中心轴以角速度ω＝15rad/s 等速旋转，该锥体与固定的外锥体之间的间隙δ＝1mm ，其间充满动力粘度μ＝0.1Pa ·s 的润滑油，若锥体顶部直径d ＝0.6m ，锥体的高度H ＝0.5m ，求所需的旋转力矩M 。
题1-9图解：取微元体，微元面积：θππcos 22dhr dl r dA ⋅=⋅= 切应力： θπσωμμτcos 2rdh r dA dy du dA dT ⋅=⋅=⋅= 微元阻力矩： dM=dT·r阻力矩：2-12 圆柱形容器的半径cm R 15=，高cm H 50=，盛水深cm h 30=，若容器以等角速度ω绕z 轴旋转，试求ω最大为多少时不致使水从容器中溢出。
解：因旋转抛物体的体积等于同底同高圆柱体体积的一半，因此，当容器旋转使水上升到最高时，旋转抛物体自由液面的顶点距容器顶部h’= 2(H-h)= 40cm等角速度旋转直立容器中液体压强的分布规律为0222p gz r p +⎪⎪⎭⎫⎝⎛-=ωρ对于液面，p=p 0 , 则gr z 222ω=，可得出22r gz =ω 将z=h ’,r=R 代入上式得s R gh /671.1815.04.08.92'222=⨯⨯==ω2-13装满油的圆柱形容器，直径cm D 80=，油的密度3/801m kg =ρ，顶盖中心点装有真空表，表的读数为Pa 4900，试求：（1）容器静止时，作用于顶盖上总压力的大小和方向；（2）容器以等角速度120-=s ω旋转时，真空表的读数值不变，作用于顶盖上总压力的大小和方向。
解：（1）N A p P 24628.0449002=⨯⨯=⋅=π方向竖直向下（2）如图建立直角坐标系，根据C gz r p +⎪⎪⎭⎫⎝⎛-=222ωρ在O 点,r=0,Z=0,p=-4900Pa,代入上式可得，C=-4900Pa令Z=0得4900222-=r p ωρ则 N rdr r rdr p P D39772)49002(224.0022=⋅-=⋅=⎰⎰πωρπ 方向竖直向上2-14 顶盖中心开口的圆柱形容器半径为m R 4.0=，高度为m H 7.0=，顶盖重量为N G 50=，装入325.0m V =的水后以匀角速度110-=s ω绕垂直轴转动，试求作用在顶盖螺栓组上的拉力。
题2-14图解：如图建立坐标系m R V h h R V 5.04.025.0222=⨯==⇒=πππ 旋转形成的抛物体的体积应等于容器内没装水部分的体积，则()()'2'212222h h H R r h H R h r -=⇒-=ππ 将z=h’，ω=10s -1, ()'222h h H R r -=代入自由表面方程为g r z 222ω=可得()m g h H R g h H R h 571.08.95.07.04.01010100'2=-⨯⨯=-=-=则 ()m h h H R r 335.0571.02.04.02'222=⨯⨯=-=等角速旋转直立容器中液体压强分布规律为0222p gz r p +⎪⎪⎭⎫⎝⎛-=ωρ由于容器的顶盖中心开口，则p 0=0(本题均指相对压强)将ω=10s -1，r=0.3， z=h’=0.571m ， p 0=0代入上式得)596.550(22022-=+⎪⎪⎭⎫ ⎝⎛-=r p gz r p ρωρNG P F Nrdr rrdr rrdr p P 55.1315055.18155.181)596.550(22)596.550(24.0335.024.0335.04.0335.02=-=-==-=⋅-=⋅=⎰⎰⎰πρπρπ2-17 宽为1M ，长为AB 的矩形闸门，倾角为45°，左侧水深H=3 H=2,试用图解法求作用于闸门上的水静压力及其作用点解：1m b =，45α︒=，13m h =，12m h =压力分为两部分：()()21211129.8100032116.932sin 452sin 45h h P S b g h h b kN ρ︒︒⨯⨯-⨯-=⋅=-⋅⋅==⨯ 作用方向垂直于闸门指向右。
作用点：12120.943sin 45h h y m ︒-== ()()222129.81000322127.72sin 45sin 45h P S b g h h b kN ρ︒︒⨯⨯-⨯⨯=⋅=-⋅⋅== 作用方向垂直于闸门指向右。
作用点：1221 2.83sin 452sin 45h h y m ︒︒=-⋅= 总压力大小：12 6.9327.7234.65P P P kN =+=+= 总压力作用方向垂直于闸门指向右。
根据合力矩定理：1122Py P y P y =+ 有作用点：11226.930.9427.72 2.83 2.4534.65P y P y y m P +⨯+⨯===2-19 金属的矩形平板闸门，门高m h 3=，宽m b 1=，由两根工字钢横梁支撑，挡水面于闸门顶边齐平，如要求两横梁所受的力相等，两横梁的位置21,y y 应为多少。
题2-19图解：先求出闸门所受的水静压力和作用点()()mbh h bh h A y I y y b gh A gh P C C C D x C 2135.112315.1212221332=⨯⨯⨯+=+=+===ρρ横梁所受力b gh b gh P P P 2122121412ρρ==== 则 mh h y hh 414.133222323222111=⨯=⨯=== 则由力矩平衡可得2211y P y P Py M D +==m y y y D 586.2414.122212=-⨯=-=∴2-24 封闭容器水面的绝对压强20/37.137m kN p =，容器左侧开m 22⨯的方形孔，覆以盖板AB ，当大气压2/07.98m kN p a =时，求作用于此板上的水静压力及作用点。
ρg （h 1-h y x题2-24图解：()()()()()mA y I y y y kNA gh P m h h mgp p h C C C D e c c 05.0260sin 3412/2222522348.934232460sin 2'48.907.9837.137'2310=⨯︒+⨯=⋅=-==⨯⨯+⨯==+=⨯+=︒+==-=-=ρρ故水静压力的作用点位于距离形心C 0.05m 的下方。
2-29某圆柱体的直径m d 2=，长m l 5=，放置于︒60的斜面上，求作用于圆柱体上的水平和铅直分压力及其方向。
解：水平方向分力大小：kN hl gh A gh P c x c x 5.2451218.9=⨯⨯⨯=⋅==ρρ 方向水平向右铅直方向分力大小：kN l h d g gV P z 12052131218.923)2(212=⨯⎪⎪⎭⎫⎝⎛⨯+⨯⨯⨯=⋅⎥⎦⎤⎢⎣⎡+⋅==ππρρ 方向铅直向上3-16 高层楼房煤气立管B 、C 两个供煤气点各供应s m Q /02.03=的煤气量。
假设煤气的密度为3/6.0m kg ，管径50mm ，压强损失AB 段用2321v ρ计算,BC 段用2422v ρ,假定C 点要求保持余压为2/300m N ，求A 点酒精（3/806m kg =酒ρ）液面应有的高差（空气密度为3/2.1m kg ）。
题3-16图解：由题意可求得s m d Q v sm d Q v /18.1005.0402.04/37.2005.04202.0422222211=⨯===⨯⨯==ππππ取断面1-1、2-2，列出伯努利方程mm m g p h Paz z g p v v p p p v p z z g v p a l l a 6.440446.08.980635232608.9)6.02.1(218.106.04237.206.03)37.2018.10(26.0300)()()(22)()(21222212212122212122212211==⨯===⨯⨯--⨯⨯+⨯⨯+-+=---+-+=++=--++--ρρρρρρρρ3-17锅炉省煤器的进口处测得烟气负压O mmH h 215.10=，出口负压O mmH h 2220=。
如炉外空气3/2.1m kg =ρ，烟气的平均3/6.0m kg ='ρ，两测压断面高差H=5m ，试求烟气通过省煤器的压强损失。
题3-17图解：本题要应用气流以相对压强表示的伯努利方程。
由进口断面1-1至出口断面2-2列伯努利方程p v p z z g v p a ∆++=--++2')()(2'22212211ρρρρ式中10.0 1059 807102.97Pa p =-⨯=- 20.029 807196.14Pa p =-⨯=-v 1=v 2故 102.979.81(1.20.6)(05)196.14p -+⨯-⨯-=-+∆ 得Δ63.74Pa p =3-18 图为矿井竖井和横向坑道相连，竖井高为200m ，坑道长为300m ，坑道和竖洞内气温保持恒定C t ︒=15，密度3/18.1m kg =ρ，坑外气温在清晨为C ︒5，30/29.1m kg =ρ，中午为C ︒20，30/16.1m kg =ρ，问早午空气的气流流向及气流速v 的大小。
假定总的损失292v ρ。
题3-18图解：因为空气是由高温区向低温区流动，所以早上空气是由坑内流向坑外，下午则是由坑外流向坑内。
取断面1-1、2-2，列出伯努利方程292)()(222222120211v v p z z g v p ρρρρρ++=--++早上:2920)()(002222120v v z z g ρρρρ++=--++sm v v v /05.6218.19218.10)0200(8.9)18.129.1(0022222=⨯++=-⨯⨯-++解得中午: 2920)()(002222120v v z z g ρρρρ++=--++sm v v v /58.2218.19218.10)0200(8.9)18.116.1(0022222=⨯++=-⨯⨯--+解得3-22求水流对1m 宽的挑流坎AB 作用的水平分力和铅直分力。
