二次函数中和角有关的存在性问题

二次函数与三角形的存在性问题一、预备知识1、坐标系中或抛物线上有两个点为P （x1，y ），Q （x2，y ）(1)线段对称轴是直线2x 21x x +=(2)AB 两点之间距离公式：221221)()(y y x x PQ -+-=中点公式：已知两点()()2211y ,x Q ,y ,x P ，则线段PQ 的中点M 为⎪⎭⎫ ⎝⎛++222121y y ,x x 。

2、两直线的解析式为11b x k y +=与 22b x k y +=如果这两天两直线互相垂直，则有121-=⋅k k3、平面内两直线之间的位置关系：两直线分别为：L1：y=k1x+b1 L2：y=k2x+b2（1）当k1=k2，b1≠b2 ，L1∥L2（2）当k1≠k2， ，L1与L2相交（3）K1×k2= -1时， L1与L2垂直二、三角形的存在性问题探究：三角形的存在性问题主要涉及到的是等腰三角形，等边三角形，直角三角形（一）三角形的性质和判定：1、等腰三角形性质：两腰相等，两底角相等，三线合一（中线、高线、角平分线）。

判定：两腰相等，两底角相等，三线合一（中线、高线、角平分线）的三角形是等腰三角形。

2、直角三角形性质：满足勾股定理的三边关系，斜边上的中线等于斜边的一半。

判定：有一个角是直角的三角形是直角三角形。

3、等腰直角三角形性质：具有等腰三角形和等边三角形的所以性质，两底角相等且等于45°。

判定：具有等腰三角形和等边三角形的所以性质的三角形是等腰直角三角形4、等边三角形性质：三边相等，三个角相等且等于60°，三线合一，具有等腰三角形的一切性质。

判定：三边相等，抛物线或坐标轴或对称轴上三个角相等，有一个角是60°的等腰三角形是等边三角形。

总结：（1）已知A 、B 两点，通过“两圆一线”可以找到所有满足条件的等腰三角形，要求的点（不与A 、B 点重合）即在两圆上以及两圆的公共弦上（2）已知A 、B 两点，通过“两线一圆”可以找到所有满足条件的直角三角形，要求的点（不与A 、B 点重合）即在圆上以及在两条与直径AB 垂直的直线上。

二次函数背景下的相似三角形存在性问题
二次函数背景下的相似三角形存在性问题是中考数学常考的题型，在考试中一般出现在压轴题的位置，综合性强，难度略大。

这篇文章主要来讨论下二次函数背景下的相似三角形存在性问题的解题思路方法及应用举例。

【模型解读】
在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．
【相似判定】
判定1：三边对应成比例的两个三角形是相似三角形；
判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；
判定3：有两组角对应相等的三角形是相似三角形．
以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题．
【题型分析】
通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．
【思路总结】
根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！
所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．
然后再找：
思路1：两相等角的两边对应成比例；
思路2：还存在另一组角相等．
事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．
一、如何得到相等角？
二、如何构造两边成比例或者得到第二组角？
搞定这两个问题就可以了．
【例题】
【分析】
综上所述，点P的坐标为（3，2）或（3，9）．
【总结】
【练习】
声明：文章图文来源网络，意在分享，仅限交流学习使用，如有分享不当或侵权，请联系删除。

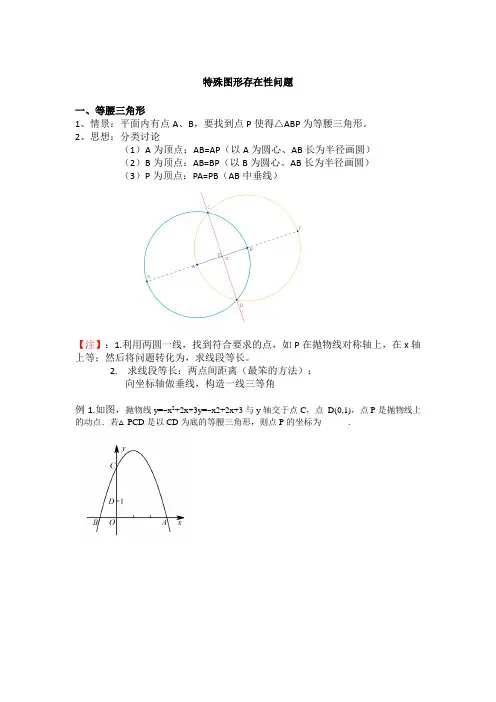
特殊图形存在性问题一、等腰三角形1、情景：平面内有点A、B，要找到点P使得△ABP为等腰三角形。

2、思想：分类讨论（1）A为顶点：AB=AP（以A为圆心、AB长为半径画圆）（2）B为顶点：AB=BP（以B为圆心、AB长为半径画圆）（3）P为顶点：PA=PB（AB中垂线）【注】：1.利用两圆一线，找到符合要求的点，如P在抛物线对称轴上，在x轴上等；然后将问题转化为，求线段等长。

2.求线段等长：两点间距离（最笨的方法）；向坐标轴做垂线，构造一线三等角例1.如图，抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C，点D(0,1)，点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为______．练习1.如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A,B 两点，A点在原点的左侧，B点的坐标为(3,0)，与y轴交于C(0,−3)点，点P是直线BC下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．练习2、已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．练习3.如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣x+1与y轴交于点D．（1）求抛物线的解析式；（2）证明：△DBO∽△EBC；（3）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．练习4.如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点，与y轴交于点C(0,−3)，其顶点为D．(1)求该抛物线的解析式，并用配方法把解析式化为y=a(x−h)2+k的形式；(2)动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM,BM，当t为何值时，△OMB为等腰三角形？练习5.如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n （m＜n）分别是方程x2﹣2x﹣3=0的两根．（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E 两点（点D在y轴右侧），连接OD、BD．①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标．25．（10分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过原点O，与x轴交于点A（5，0），第一象限的点C（m，4）在抛物线上，y轴上有一点B（0，10）．（Ⅰ）求抛物线的解析式及它的对称轴；（Ⅱ）点P（0，n）在线段OB上，点Q在线段BC上，若OP＝2BQ，且P A＝QA．求n 的值；（Ⅲ）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．19-红桥一模25．（10分）如图，抛物线y＝x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A，B，且B点的坐标为（2，0）．（1）求该抛物线的解析式．（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．(17河北一模)25(10分）如图，己知抛物线y=x2+bx+c图象经过点A（﹣1，0），B（0，﹣3），抛物线与x轴的另一个交点为C．（1）求这个抛物线的解析式：（2）若抛物线的对称轴上有一动点D，且△BCD为等腰三角形（CB≠CD），试求点D的坐标；二、直角三角形1.情景：平面内有点A、B，要找到点P使得△ABP为直角三角形2.思想：分类讨论（1）A为顶点：∠A（过A做垂线）（2）B为顶点：∠B（过B做垂线）（3）P为顶点：∠C（AB为直径的圆）【注】1.等腰直角三角形，只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A，B与x 轴交于点E，F且B，E两点的坐标分别为B(2，32)E(−1，0)(1)求二次函数的解析式；(2)在抛物线上是否存在点Q，使△QBF为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．练习1.如图，抛物线y=x2+bx+3顶点为P，且分别与x轴、y轴交于A、B两点，点A在点P的右侧，tan∠ABO=13(1)求抛物线的对称轴和PP的坐标．(2)在抛物线的对称轴上是否存在这样的点D，使△ABD为直角三角形？如果存在，求点D 的坐标；如果不存在，请说明理由．例2.如图，抛物线y=−x2+bx+c与x轴相交于AB两点，与y 轴相交与点C，且点B与点CC 的坐标分别为(3,0)，C(0,3)，点M是抛物线的顶点．(1)求二次函数的关系式(2)在MB上是否存在点P，过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由练习2.如图，在平面直角坐标系中，直线y=−13x+2交x轴点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E(−1,0)，并与直线相交于A、B两点．(1)求抛物线的解析式（关系式）；(2)过点A作AC⊥AB交x轴于点C，求点C的坐标；(3)除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．练习3.如图，抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．（1）求抛物线的解析式；（2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．（3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．（18东丽-一模）25.如图，在平面直角坐标系中，点A、B的坐标分别为（1，1）、（1，2），过点A、B分别作y轴的垂线，垂足为D、C，得到正方形ABCD，抛物线y=x2+bx+c经过A、C两点，点P为第一象限内抛物线上一点（不与点A重合），过点P分别作x轴y轴的垂线，垂足为E、F，设点P的横坐标为m，矩形PFOE与正方形ABCD重叠部分图形的周长为l．（1）直接写出抛物线所对应的函数表达式．（2）当矩形PFOE的面积被抛物线的对称轴平分时，求m的值．（3）当m＜2时，求L与m之间的函数关系式．（4）设线段BD与矩形PFOE的边交于点Q，当△FDQ为等腰直角三角形时，直接写出m的取值范围．三、平行四边形存在性问题类型一：1.情景：一直平面内三点A、B、C，求一点P使四边形ABCP为平行四边形2.思想：分类讨论（1）以AC为对角线：ABCP1（2）以AB为对角线：ACBP3（3）以BC为对角线：ACP2B【注】找到P点后，用平行四边形的判定定理，求等长线段，或利用等角度、平行线求坐标即可。

中考数学几何模型第二十四节:二次函数相等角存在性问题438.二次函数面积定值相等角存在性问题(初三)如图,已知点A(―1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式:(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.439.二次函数内心在x轴上相等角存在性问题(初三)如图,已知:抛物线y=x2+bx+c与直线1交于点A(―1,0),C(2,―3),与x轴另一交点为B.(1)求抛物线的解析式(2)在抛物线上找一点P,使△ACP的内心在x轴上,求点P的坐标;(3)M是抛物线上一动点,过点M作x轴的垂线,垂足为N,连接BM.在(2)的条件下,是否存在点M,使∠MBN=∠APC?若存在,请求出点M的坐标;若不存在,请说明理由.440.二次函数角度相等四边形面积最大值(初三)x+3的图象与x轴交于点A,与y轴交于点B,点C的坐标为(―2,0),如图,在平面直角坐标系x0y中,一次函数y=―12抛物线经过A,B,C三点(1)求抛物线的解析式;(2)直线AD与y轴负半轴交于点D,且∠BAO=∠DAO,求证:OB=OD(3)在(2)的条件下,若直线AD与抛物线的对称轴1交于点E,连接BE,在第一象限内的抛物线上是否存在一点P,使四边形BEAP的面积最大?若存在,请求出点P的坐标及四边形BEAP面积的最大值;若不存在,请说明理由.441.二次函数面积定值二倍角存在性问题(初三)如图，抛物线y=ax2+bx+c经过A(―1,0)、B(4,0)、C(0,2)三点,点D(x,y)为抛物线上第一象限内的一个动点.(1)求抛物线所对应的函数表达式;(2)当△BCD的面积为3时,求点D的坐标;(3)过点D作DE⊥BC,垂足为点E,是否存在点D,使得△CDE中的某个角等于∠ABC的2倍？若存在，求点D的横坐标；若不存在，请说明理由.442.二次函数相等角存在性问题讨论(初三)如图,已知二次函数y=―x2+bx+c的图象经过点A(―1,0),B(3,0),与y轴交于点C.(1)求抛物线的解析式(2)抛物线上是否存在点P,使∠PAB=∠ABC,若存在请直接写出点P的坐标.若不存在,请说明理由.443.二次函数相等角存在性问题线段比值的定值(初三)已知,抛物线y=ax2+bx+c经过A(―1,0)、B(3,0)、C(0,3)三点,点P是抛物线上一点.(1)求抛物线的解析式:(2)当点P位于第四象限时,连接AC,BC,PC,若∠PCB=∠ACO,求直线PC的解析式;的值是否为定值?若是,请求出(3)如图2,当点P位于第二象限时,过P点作直线AP,BP分别交y轴于E,F两点,请问CECF此定值;若不是,请说明理由.444.二次函数铅垂定理面积最大值相等角存在性问题(初三)如图，已知抛物线y=ax2+bx+c与两坐标轴相交于点A(―1,0)、B(3,0)、C(0,3)，D是抛物线的顶点,E是线段AB的中点.(1)求抛物线的解析式,并写出D点的坐标;(2)F(x,y)是抛物线上的动点:①当x>1,y>0时,求△BDF的面积的最大值;②当∠AEF=∠DBE时,求点F的坐标.445.二次函数将军饮马最小值相等角存在性问题(初三)如图,直线y=―x+3与x轴、y轴分别交于B、C两点,抛物线y=―x2+bx+c经过点B、C,与x轴另一交点为A,顶点为D.(1)求抛物线的解析式;(2)在x轴上找一点E,使EC+ED的值最小,求EC+ED的最小值;(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出P点坐标;若不存在,请说明理由.446.二次函数相等角存在性问题动点翻折问题(初三)如图,二次函数y=x2+bx+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,拋物线过点C(1,0),且顶点为D,连接AC、BC、BD、CD.(1)填空:b=________(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD=∠ACB,求点P的坐标;(3)点E在直线AC上,点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG.当点F在x轴上时,直接写出AG的长.447.二次函数铅垂定理面积最大值相等角存在性问题(初三)如图,已知抛物线y=ax2+bx+5经过A(―5,0),B(―4,―3)两点,与x轴的另一个交点为C,顶点为D,连接CD.(1)求该抛物线的表达式;(2)点P为该拋物线上一动点(与点B、C不重合),设点P的横坐标为t.①当点P在直线BC的下方运动时,求△PBC的面积的最大值;②该拋物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.答案438【解】(1)设抛物线的解析式为y=a(x+1)(x―3),将C(0,1)代入得―3a =1,解得:a =―13,∴拋物线的解析式为y =―13x 2+23x +1.(2)如图,过点P 作PD ⊥x,交BC 于点D.设直线BC 的解析式为y =kx +b,则{3k +b =0b =1,解得:k =―13,∴直线BC 的解析式为y =―13x +1.设点P (x,―13x 2+23x +1),则D (x,―13x +1)∴PD =(―13x 2+23x +1)―(―13x +1)=―13x 2+x,∴S △PBC =12OB ⋅DP =12×3×(―13x 2+x )=―12x 2+32x.又∵S △PBC =1,∴―12x 2+32x =1,整理得:x 2―3x +2=0,解得:x =1或x =2,∴点P 的坐标为(1,43)或(2,1).(3)存在.作△ABC 的外接圆E,与x 轴下方对称轴的交点就是所求的Q 点,连接QC 、BQ,弦BC 所对的圆周角相等,即∠BQC =∠BAC .∵A(―1,0),C(0,1),∴OC =OA =1∴∠BAC =45∘.∵∠BQC =∠BAC =45∘,则∠CEB =90∘.设⊙E 的半径为x,则Rt △CEB 中,由勾股定理可知CM 2+BE 2=BC 2,即2x 2=10,解得:x =5(负值舍去),∵AC 的垂直平分线的为直线y =―x,AB 的垂直平分线为直线x =1,∴点E 为直线y =―x 与x =1的交点,即E(1,―1),∴Q 的坐标为(1,―1―5).439【解】(1)把点A(―1,0),C(2,―3)代入y =x 2+bx +c,得到方程组:{0=1―b +c ―3=4+2b +c ,解得{b =―2c =―3,∴抛物线的解析式为y =x 2―2x ―3;(2)作点C 关于x 轴的对称点C 1,则C 1(2,3),连接AC 1并延长与抛物线交于点P,由图形的对称性可知P 为所求的点,设直线AC 1的解析式为y =mx +n,由题意得:{0=―m +n 3=2m +n ,解得:{m =1n =1,∴直线AC 1的解析式为y =x +1,将直线和拋物线的解析式联立得:{y =x +1y =x 2―2x ―3,解得{x=―1y=0(舍去)或{x=4y=5,∴P(4,5);(3)存在点M,理由如下:已知A(―1,0),P(4,5),由两点距离公式可得:AP=(―1―4)2+(0―5)2=52,同理可求得AC=32,PC=217,∴AP2+AC2=PC2,∠PAC=90∘,∴tan ∠APC=ACAP =35,∵∠MBN=∠APC,∴tan ∠MBN=tan ∠APC,∴MNBN =35,设点M(m,m2―2m―3),则|m2―2m―3||3―m|=35(m≠3),解得m=―25或m=―85,当m=―25时,m2―2m―3=(―25)2―2×(―25)―3=―5125,∴M(―25,―5125),当m=―85,m2―2m―3=(―85)2―2×(―85)―3=―6925,∴M(―85,6925),∴综上所述,M的坐标为(―25,―5125),(―85,6925).440【解】(1)令y=0,则―12x+3=0,解得x=6,令x =0,则y =3,∴A(6,0),B(0,3),设抛物线的解析式为y =ax 2+bx +c,把A,B,C 三点坐标代入解析式,得:{36a +6b +c =0c =34a ―2b +c =0,解得:{a =―14b =1c =3,∴抛物线的解析式为y =―14x 2+x +3;(2)证明:∵在平面直角坐标系xOy 中,∴∠BOA =∠DOA =90∘,在△BOA 和△DOA 中,{∠BOA =∠DOAOA =OA ∠BAO =∠DAO,∴△BOA≅△DOA (ASA),∴OB =OD,(3)存在,理由如下:如图,过点E 作EM ⊥y 轴于点M,∵y =―14x 2+x +3=―14(x ―2)2+4,∴抛物线的对称轴是直线x =2,∴E 点的横坐标是2,即EM =2,∵B(0,3),∴OB =OD =3,∴BD =6,∵A(6,0),∴OA =6,∴S △ABE =S △ABD ―S △DBE =12×6×6―12×6×2=12,设点P 的坐标为(t,―14t 2+t +3),连接PA,PB,过点P 作PN ⊥x 轴丁点H 1,交直线AB 于点N,过点B 作BH 2⊥PN 于点H 2,∴N (t,―12t +3),∴PN =―14t 2+t +3―(―12t +3)=―14t 2+32t,∵AH 1+BH 2=OA =6,S △ABP =S △NBP +S △ANP =12PN ∙BH 2+12PN ⋅AH 1=12PN ⋅OA,∴S △ABP =12×6(―14t 2+32t )=―34(t ―3)2+274,∵―34<0,抛物线开口向下,函数有最大值,∴当t =3时,△BPA 面积的最大值是274,此时四边形BEAP 的面积最大,∴四边形BEAP 的面积最大值为274+12=754,∴当P 点坐标是(3,154)时,四边形BEAP 面积的最大值是754.441【解】(1)将A(―1,0)、B(4,0)、C(0,2)代入y =ax 2+bx +c 得:{a ―b +c =016a +4b +c =0c =2,解得{a =―12b =32c =2故抛物线的解析式为y =―12x 2+32x +2.(2)如图1,过D 作DG ⊥x 轴,与BC 交于K 点,由B(4,0)、C(0,2)可得直线BC 的解析式为y =―12x +2,设D (x,―12x 2+32x +2),K (x,―12x +2)∴DK =―12x 2+32x +2―(―12x +2)=―12x 2+2x∴S △BCD =12×0OB ×DK =12×4×(―12x 2+2x )=―x 2+4x =3,解得:∴x =1或3,∵当x =1时,y =3,当x =3时,y =2,∴点D 的坐标为(1,3)或(3,2).(3)存在,分两种情况考虑:①当∠DCE =2∠ABC 时,如图2,取点F(0,―2),连接BF.∵OC =OF,OB ⊥CF,∴∠ABC =∠ABF ,∴∠CBF =2∠ABC.∵∠DCB =2∠ABC ,∴∠DCB =∠CBF,∴CD//BF.∵点B(4,0),F(0,―2),∴直线BF 的解析式为y =12x ―2,∴直线CD 的解析式为y =12x +2.联立直线CD 及抛物线的解析式成方程组得:{y =12x +2y =―12x 2+32x +2,解得:{x =0y =2(舍去),{x =2y =3,∴点D 的坐标为(2,3);②当∠CDE =2∠ABC 时,过点C 作CN ⊥BF 于点N,交OB 于H.作点N 关于BC 的对称点P,连接NP 交BC 于点Q,如图3所示.∵∠OCH =90∘―∠OHC,∠OBF =90∘―∠BHN ，∠OHC =∠BHN在△OCH与△OBF中{∠OOH=∠BOF∠OCH=∠OBF,∴△OCH∽△OBF,∴OHOF =OCOB,即OH2=24∴OH=1,H(1,0).设直线CN的解析式为y=kx+n(k≠0),:∵C(0,2),H(1,0),∴{n=2k+n=0,解得{k=―2 n=2,∴直线CN的解析式为y=―2x+2.联立直线BF及直线CN成方程组得:{y=12x―2y=―2x=2,解得:{x=85y=―65,∴点N的坐标为(85,―65).∵点B(4,0),C(0,2),∴直线BC的解析式为y=-12x+2.∵NP⊥BC,且点N(85,-65),∴直线NP的解析式为y=2x-225.联立直线BC及直线NP成方程组得:{y=-12x+2y=2x-225,解得:{x=6425y=1825,∴点Q的坐标为(6425,1825).∵点N(85,-65),点N,P关于BC对称,∴点P的坐标为(8825,6625).∵点C(0,2),P(8825,6625),∴直线CP 的解析式为y =211x +2.将y =211x +2代入:y =-12x 2+32x +2整理,得:11x 2-29x =0,解得:x 1=0(舍去),x 2=2911,∴点D 的横坐标为2911.综上所述:存在点D,使得△CDE 的某个角恰好等于∠ABC 的2倍,点D 的横坐标为2或2911.442.【解】(1)根据题意得{-1-b +c =0-9+3b +c =0,解得{b =2c =3.故抛物线的解析式为y =-x 2+2x +3;(2)分两种情况,如图中的P1和P2:①易知,二次函数y =-x 2+2x +3的对称轴是直线x =1,当x =0时,y =3,则C(0,3),点C 关于对称轴的对应点P 1(2,3),②AP 2//BC 时,满足题意,设直线BC 的解析式为y =kx +3,则3k +3=0,解得k =-1.则直线BC 的解析式为y =-x +3,设与BC 平行的直线AP 2的解析式为y =-x +m,把A(-1,0)代入得:则1+m =0,解得m =-1.则与BC 平行的直线AP 2的解析式为y =-x -1,联立拋物线解析式得:{y =-x -1y =-x 2+2x +3,解得{x =4y =-5,{x =-1y =0(舍去).P 2(4,-5).综上所述,P 1(2,3),P 2(4,-5).443.【解】(1)将A(-1,0)、B(3,0)、C(0,3)代入y =ax 2+bx +c,∴{a -b +c =09a +3b +c =0c =3,∴{a =-1b =2c =3,∴y =-x 2+2x +3(2)如图,过点B 作MB ⊥CB 交于点M,过点M 作MN ⊥x 轴交于点N,∵A(-1,0)、C(0,3),B(3,0),∴OA =1,OC =3,BC =32,∴tan ∠ACO =13,∵∠PCB =∠ACO,∴tan ∠BCM =13=BM BC=BM 32∴BM =2,∵OB =OC,∴∠CBO =45∘,∴∠NBM =45∘,∴MN =NB =1,∴M(2,-1),设直线CM 的解析式为y =kx +b,∴{b =32k +b =-1,∴{k =-2b =3,∴直线PC 的解析式为y =-2x +3;(3)CE CF 的值是为定值13.理由如下:设P (t,-t 2+2t +3),设直线AP 的解析式为y =k 1x +b 1,把A(-1,0),P (t,-t 2+2t +3)代入得:∴{tk 1+b 1=-t 2+2t +3-k 1+b 1=0,∴{k 1=3-t b 1=3-t ,∴直线AP 的解析式为y =(3-t)x +(3-t),∴E(0,3-t),∴CE =EO -CO =3-t -3=-t,设直线BP 的解析式为y =k 2x +b 2,把B(3,0)、P (t,-t 2+2t +3)代入得:∴{k 2t +b 2=-t 2+2t +33k 2+b 2=0,∴{k 2=-t -1b 2=3t +3,∴直线BP 的解析式为:y =(-t -1)x +3t +3,∴F(0,3t +3),∴OF =3t +3∴CF =CO -OF =3-(3t +3)=-3t,∴CE CF =13,∴CE CF 的值是为定值13.444.【解】(1)将A(-1,0)、B(3,0)、C(0,3)代入y =ax 2+bx +c,{a -b +c =09a +3b +c =0c =3,解得:{a =-1b =2c =3,∴抛物线的解析式为y =-x 2+2x +3.∵y =-x 2+2x +3=-(x -1)2+4,∴顶点D 的坐标为(1,4)(2)①过点F 作FM ⊥x 轴,交BD 于点M,如图1所示.设直线BD 的解析式为y =mx +n(m ≠0),将(3,0)、(1,4)代入y =mx +n,{3m +n =0m +n =4,解得:{m =-2n =6,∴直线BD 的解析式为y =-2x +6.∵点F 的坐标为(x,-x 2+2x +3),∴点M 的坐标为(x,-2x +6),(1<x <3)∴FM =-x 2+2x +3-(-2x +6)=-x 2+4x -3,∴S △BDF =12FM ⋅(x B -x D )=(-x 2+4x -3)×1=-(x -2)2+1.∵-1<0,∴当x =2时,S △BDF 取最大值,最大值为1.②过点E 作EN//BD 交y 轴于点G1,交抛物线于点F 1,在y 轴负半轴取OG2=OG1,连接EG2,射线EG2交抛物线于点F 2,如图2,F1和F2足满足条件的F 点.∵EF 1//BD,∴∠AEF 1=∠DBE.∵OG1=OG2,EO ⊥G1G2,∴∠AEF 2=∠AEF 1=∠DBE.∵E 是线段AB 的中点,A(-1,0),B(3,0),∴点E 的坐标为(1,0).设直线EF1的解析式为y=-2x+b1,将E(1,0)代入y=-2x+b1,得-2+b1=0,解得:b1=2,∴直线EF1的解析式为y=-2x+2.联立直线EF1、抛物线解析式成方程组,{y=-2x+2y=-x2+2x+3,解得:{x=2-5y=25-2,或{x=2+5y=-25-2(舍去),∴点F1的坐标为(2-5,25-2).当x=0时,y=-2x+2=2,∴点Gl的坐标为(0,2),∴点G2的坐标为(0,-2).同理,可求出直线EF2的解析式为y=2x-2.联立直线EF2、抛物线解析式成方程组,{y=2x-2y=-x2+2x+3,解得:{x=-5y=-25-2,或{x=5y=25-2(舍去),∴点F2的坐标为(-5,-25-2).综上所述:当∠AEF=∠DBE时,点F的坐标为(2-5,25-2)或(-5,-25-2).445.【解】(1)直线y=-x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0)、(0,3),将点B、C的坐标代入二次函数表达式得:{-9+3b+c=0c=3,解得:{b=2c=3,故抛物线的表达式为:y=-x2+2x+3,(2)如图1,作点C关于x轴的对称点C',连接CD交x轴于点E,则此时EC+ED为最小,∵抛物线的顶点D坐标为(1,4),点C'(0,-3),将C'、D的坐标代入一次函数表达式并解得:直线C'D的表达式为:y=7x-3,当y=0时,x=3,7故点E(3,0),由两点距离公式可得:DC'=52,则EC+ED的最小值为DC'=52;7(3)设BC与对称轴交于点M,则∠AMB=2∠BMN=∠OCB,以点M为圆心,MA为半径作圆,交对称轴与点P1、P2,∴∠AMB=∠APP1B,此时P1就是x轴上方,符合题意的P点,作点P1关于x轴的对称点P2,此时P2就是x轴下方符合题意的P点.易知∠CBO=45∘,∴△BMN是等腰直角三角形。

二次函数中与角有关的存在性问题与角有关的存在性问题包括相等角的存在性、二倍角或半角的存在性，其他倍数关系角的存在性等，解决这类问题我们通常利用以下知识点去构造相关角：①平行线的同位角、内错角相等；②等腰三角形的等边对等角；③相似三角形对应角相等；④全等三角形对应角相等；⑤三角形的外角定理等。

然后利用解直角三角形、相似三角形边的比例关系作为计算工具去计算求解，难度相对较大，需要同学们灵活运用，融会贯通。

【类型一 相等角的存在性问题】（一）.利用平行线、等腰三角形构造相等角例1 如图，直线33+-=x y 与x 轴、y 轴分别交于A ，B 两点，抛物线c bx x y ++-=2与直线y =c 分别交y 轴的正半轴于点C 和第一象限的点P ，连接PB ，得BOA PCB ≌△△（O 为坐标原点）。

若抛物线与x 轴正半轴交点为点F ，设M 是点C ，F 间抛物线上的一点（包括端点），其横坐标为m . （1）直接写出点P 的坐标和抛物线的解析式. （2）求满足POA MPO ∠=∠的点M 的坐标.解：(1)易得点P 坐标为（3，4），抛物线解析式为432++-=x x y .(2) ①当点M 在线段OP 上方时，∵CP ∥x 轴，∴当点C 、M 重合时，∠MPO=∠POA ，∴点M 的坐标为（0，4）；②当点M 在线段OP 下方时，在x 轴正半轴取点D ，连接DP ，使得DO=DP ，此时∠DPO=∠POA.设点D 坐标为（n ，0），则DO=n ，()16322+-=n DP ，∴()16322+-=n n ，解得：n=625，∴点D 坐标为⎪⎭⎫⎝⎛0625，. 设直线PD 解析式为b kx y +=，代入得：7100724+-=x y .联立抛物线解析式得⎪⎭⎫⎝⎛49124,724M 综上所述：点M 的坐标为（0，4）或⎪⎭⎫⎝⎛49124,724（二）.利用相似三角形构造相等角例2 如图，抛物线c bx x y ++=221与x 轴交于A 、B 两点，与y 轴交于点C ，其对称轴交抛物线于点D ，交x 轴于点E ，已知OB=OC=6. （1）求抛物线的解析式及点D 的坐标；（2）连接BD ，F 为抛物线上一动点，当EDB FAB ∠=∠时，求点F 的坐标；解：（1）因为OB=OC=6，所以B （6，0），C ()6,0-， 将B、C点坐标代入解析式，得()8221622122--=--=x x x y ， 所以点D 的坐标为（2，—8）（2）如图1，过F 作FG ⊥x 轴于点G ，设⎪⎭⎫ ⎝⎛--6221,F 2x x x ，则FG=62212--x x ，AG=x +2，当EDB FAB ∠=∠时，且B ED GA ∠=∠F ，所以BDE FAG ∽△△，所以FGAGEB DE =，即262212482=--+=x x x ， 当点F 在x 轴上方时，则有12422--=+x x x ，解得x=—2（舍去）或x=7，此时F 点的坐标为⎪⎭⎫ ⎝⎛297，；当点F 在x 轴下方时，则有）（12422---=+x x x ，解得x=—2（舍去）或x=5，此时F 点的坐标为⎪⎭⎫⎝⎛-275，，,综上可知点F 的坐标为⎪⎭⎫ ⎝⎛297，或⎪⎭⎫ ⎝⎛-275，.【类型二二倍角或半角的存在性问题】（一）.二倍角的构造方法如图，已知α∠，我们可以利用等腰三角形和外角定理去构造α2，在BC 边上找一点D，使得BD=AD，则α2ADC=∠.这样我们就构造出了二倍角，接下来利用三角函数（一般用正切）计算就可以了。

二次函数综合--角度存在性问题【题型解读】二次函数综合中的角度问题是大部分地区全卷的压轴题，具有较好的区分度和选拔功能，此类试题不仅可以考查二次函数与平面几何的基础知识，还可以考查数形结合、分类讨论等数学思想方法，以及阅读理解能力、收集处理信息能力、运用数学知识探究问题的能力等.解题关键是，充分挖掘题目中的隐含条件，构造角，利用解直角三角形或相似进行计算求解.【主要类型】1.相等角的存在性，主要形式为基于动点构造某个角使其与特定已知角相等2.二倍角的存在性，主要形式为基于动点构造某个角使其等于特定已知角的2倍3.半角的存在性，主要形式为基于动点构造某个角使其等于特定已知角的一半【方法总结】角度存在性问题主要解题突破口在于构造相关角，主要有以下几种构造方法：⑴构造相等角的方法①利用平行线的性质或者等腰三角形的性质构造相等角②利用相似三角形构造相等角⑵构造二倍角的方法⑶构造半角的方法【典型例题】1．如图，已知直线BC的解析式为y＝﹣x+3，与x轴，y轴交于点B，C．抛物线y＝ax2+bx+3过A（﹣1，0），B，C三点，D点为抛物线的顶点，抛物线的对称轴与x轴交于点E，连接BD，CD．（1）求二次函数及直线CD的解析式；（2）点P是线段CD上一点（不与点C，D重合），当△BCP的面积为时，求点P的坐标．（3）点F是抛物线上一点，过点F作FG⊥CD交直线CD于点G，当∠CFG＝∠EDB 时，请直接写出点F的坐标．2．如图，已知二次函数y＝ax2+x+b的图象经过点A（﹣3，0）和点B（0，4），∠BAO 的平分线分别交抛物线和y轴于点C，D．点P为抛物线上一动点，过点P作x轴的垂线交直线AC于点E，连接PC．（1）求二次函数的解析式；（2）当以点P，C，E为顶点的三角形与△ADO相似时，求点P的坐标；（3）设点F为直线AC上一点，若∠BFD＝∠ABO，请直接写出点F的坐标．3．如图，在平面直角坐标系中，一次函数y＝x﹣2的图象分别交x、y轴于点A、B，抛物线y＝x2+bx+c经过点A、B，点P为第四象限内抛物线上的一个动点．（1）求此抛物线对应的函数表达式；（2）如图1所示，过点P作PM∥y轴，分别交直线AB、x轴于点C、D，若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似，求点P的坐标；（3）如图2所示，过点P作PQ⊥AB于点Q，连接PB，当△PBQ中有某个角的度数等于∠OAB度数的2倍时，请直接写出点P的横坐标．4．如图，在平面直角坐标系中，直线y＝x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c经过AB两点，与x轴的另一个交点为C．（1）直接写出点A和点B的坐标．（2）求抛物线的解析式．（3）D为直线AB上方抛物线上一动点．①连接DO交AB于点E，若DE：OE＝3：4，求点D的坐标；②是否存在点D，使得∠DBA的度数恰好是∠BAC的2倍？如果存在，直接写出点D的坐标；如果不存在，请说明理由．5．如图，在平面直角坐标系中，O为坐标原点，抛物线y＝ax2+bx+4（a≠0）经过点A（﹣8，0）、B（2，0），与y轴交于点C，点D是AB中点，连接CD．点P是抛物线上一点．（1）求a、b的值；（2）若S△CDP＝S△CDO，求点P的横坐标；（3）过点P作直线CD的垂线，垂足为E，若∠CPE＝∠CDO，求点P的横坐标．。

第22章二次函数中的存在性问题-重难点题型总结【】【题型1 二次函数中直角三角形存在性问题】【例1】（2021•罗湖区校级模拟）如图，已知抛物线y＝﹣x2+2x+3与x轴交于点A、B，与y轴交于点C，点P是抛物线上一动点，连接PB，PC．（1）点A的坐标为，点B的坐标为；（2）如图1，当点P在直线BC上方时，过点P作PD上x轴于点D，交直线BC于点E．若PE＝2ED，求△PBC的面积；（3）抛物线上存在一点P，使△PBC是以BC为直角边的直角三角形，求点P的坐标．【变式1-1】（2021春•望城区校级月考）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2+bx+c与x 轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C（0，3），连接AC，点P为第二象限抛物线上的动点．（1）求a、b、c的值；（2）连接P A、PC、AC，求△P AC面积的最大值；（3）在抛物线的对称轴上是否存在一点Q，使得△QAC为直角三角形，若存在，请求出所有符合条件的点Q的坐标；若不存在，请说明理由．【变式1-2】（2021•长沙模拟）如图，抛物线y＝﹣x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为B（3，0）．C（0，3），点M是抛物线的顶点．点P为线段MB上一个动点，过点P作PD⊥x轴于点D，若OD＝m．（1）求二次函数解析式；（2）设△PCD的面积为S，试判断S有最大值或最小值？若有，求出其最值，若没有，请说明理由；（3）在MB上是否存在点P，使△PCD为直角三角形？若存在，请写出点P的坐标；若不存在，请说明理由．【变式1-3】（2021•长沙模拟）如图，抛物线y＝ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）直接写出点C的坐标，并求出△ABC的面积；（3）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；（4）若点M在直线BH上运动，点N在x轴上运动，是否存在以点C、M、N为顶点的三角形为等腰直角三角形？若存在，请直接写出此时点M的坐标，若不存在，请说明理由．【题型2 二次函数中等腰三角形存在性问题】【例2】（2020秋•曾都区期末）如图，抛物线y＝ax2+4x+c经过A（﹣3，﹣4），B（0，﹣1）两点，点P是y轴左侧且位于x轴下方抛物线上一动点，设其横坐标为m．（1）直接写出抛物线的解析式；（2）将线段AB绕点B顺时针旋转90°得线段BD（点D是点A的对应点），求点D的坐标，并判断点D是否在抛物线上；（3）过点P作PM⊥x轴交直线BD于点M，试探究是否存在点P，使△PBM是等腰三角形？若存在，求出点m的值；若不存在，说明理由．【变式2-1】（2020秋•云南期末）如图，直线y=−12x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B，C和点A（﹣1，0）．（1）求B，C两点的坐标．（2）求该二次函数的解析式．（3）若抛物线的对称轴与x轴的交点为点D，则在抛物线的对称轴上是否存在点P，使△PCD是以CD 为腰的等腰三角形？如果存在，直接写出点P的坐标；如果不存在，请说明理由．【变式2-2】（2021•南充）如图，已知抛物线y＝ax2+bx+4（a≠0）与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线x=5 2．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ．在y轴上是否存在点F，得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．【变式2-3】（2021•建华区二模）综合与探究如图，在平面直角坐标系中，直线y＝﹣3x﹣3与x轴交于点A，与y轴交于点C．抛物线y＝x2+bx+c经过A、C两点，且与x轴交于另一点B（点B在点A右侧）．（1）求抛物线的解析式及点B坐标；（2）设该抛物线的顶点为点H，则S△BCH＝；（3）若点M是线段BC上一动点，过点M的直线ED平行y轴交x轴于点D，交抛物线于点E，求ME 长的最大值及点M的坐标；（4）在（3）的条件下：当ME取得最大值时，在x轴上是否存在这样的点P，使得以点M、点B、点P 为顶点的三角形是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．【题型3 二次函数中平行四边形存在性问题】【例3】（2020秋•元阳县期末）如图，直线y=−12x+c与x轴交于点A（﹣3，0），与y轴交于点C，抛物线y=12x2+bx+c经过点A，C，与x轴的另一个交点为B（1，0），连接BC．（1）求抛物线的函数解析式．（2）M为x轴的下方的抛物线上一动点，求△ABM的面积的最大值．（3）P为抛物线上一动点，Q为x轴上一动点，当以B，C，Q，P为顶点的四边形为平行四边形时，求点P的坐标．【变式3-1】（2020秋•泰山区期末）如图，抛物线y=12x2+bx+c经过点A（﹣4，0），点M为抛物线的顶点，点B在y轴上，且OA＝OB，直线AB与抛物线在第一象限交于点C（2，6），如图．（1）求直线AB和抛物线的表达式；（2）在y轴上找一点Q，使得△AMQ的周长最小，在备用图中画出图形并求出点Q的坐标；（3）在坐标平面内是否存在点N，使以点A、O、C、N为顶点且AC为一边的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【变式3-2】（2021春•雨花区期末）如图，已知抛物线y＝ax2+bx+c的对称轴为直线x＝﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．（1）求抛物线的解析式；（2）若点P从点B出发，沿着射线BC运动，速度每秒√2个单位长度，过点P作直线PM∥y轴，交抛物线于点M．设运动时间为t秒．①在运动过程中，当t为何值时，使（MA+MC）（MA﹣MC）的值最大？并求出此时点P的坐标．②若点N同时从点B出发，向x轴正方向运动，速度每秒v个单位长度，问：是否存在t使点B，C，M，N构成平行四边形？若存在，求出t，v的值；若不存在，说明理由．【变式3-3】（2021•北碚区校级模拟）如图1，在平面直角坐标系中，抛物线y＝ax2+bx﹣6与x轴交于A，C（﹣6，0）两点（点A在点C右侧），交y轴于点B，连接BC，且AC＝4．（1）求抛物线的解析式．（2）若P是BC上方抛物线上不同于点A的一动点，连接P A，PB，PC，求当S△PBC−12S△P AC有最大值时点P的坐标，并求出此时的最大值．（3）如图2，将原抛物线向右平移，使得点A刚好落在原点O，M是平移后的抛物线上一动点，Q是直线BC上一动点．当A，M，B，Q组成的四边形是平行四边形时，请直接写出此时点Q的坐标．【题型4 二次函数中菱形存在性问题】【例4】（2020秋•巴南区期末）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C．（1）求b，c的值；（2）如图1，点P为直线BC上方抛物线上的一个动点，设点P的横坐标m．当m为何值时，△PBC的面积最大？并求出这个面积的最大值．（3）如图2，将该抛物线向左平移2个单位长度得到新的抛物线y＝a1x2+b1x+c1（a1≠0），平移后的抛物线与原抛物线相交于点D，点M为直线BC上的一点，点N是平面坐标系内一点，是否存在点M，N，使以点B，D，M，N为顶点的四边形为菱形，若存在，请直接写出点M的坐标；若不存在，请说明理由．【变式4-1】（2021•湘潭）如图，一次函数y=√33x−√3图象与坐标轴交于点A、B，二次函数y=√33x2+bx+c图象过A、B两点．（1）求二次函数解析式；（2）点B关于抛物线对称轴的对称点为点C，点P是对称轴上一动点，在抛物线上是否存在点Q，使得以B、C、P、Q为顶点的四边形是菱形？若存在，求出Q点坐标；若不存在，请说明理由．【变式4-2】（2021春•无棣县月考）如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A、B两点，B点的坐标为（3，0），与y轴交于点C（0，﹣3），点P是直线BC下方抛物线上的一个动点．（1）求二次函数解析式；（2）连接PO，PC，并将△POC沿y轴对折，得到四边形POP'C．是否存在点P，使四边形POP'C为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．【变式4-3】（2020秋•南岸区期末）如图，在平面直角坐标系xOy中，二次函数y＝x2+bx+c的图象与x轴交于点A（4，0）和B（﹣1，0），交y轴于点C．（1）求二次函数y＝x2+bx+c的表达式；（2）将点C向右平移n个单位得到点D，点D在该二次函数图象上．点P是直线BD下方该二次函数图象上一点，求△PBD面积的最大值以及此时点P的坐标；（3）在（2）中，当△PBD面积取得最大值时，点E是过点P且垂直于x轴直线上的一点．在该直角坐标平面内，是否存在点Q，使得以点P，D，E，Q四点为顶点的四边形是菱形？若存在，直接写出满足条件的点Q的坐标；若不存在，请说明理由．【题型5 二次函数中矩形存在性问题】【例5】（2021春•九龙坡区校级期末）如图1，若二次函数y＝﹣x2+3x+4的图象与x轴交于点A、B，与y轴交于点C，连接AC、BC．（1）求三角形ABC的面积；（2）若点P是抛物线在一象限内BC上方一动点，连接PB、PC，是否存在点P，使四边形ABPC的面积为18，若存在，求出点P的坐标；若不存在，说明理由；（3）如图2，若点Q是抛物线上一动点，在平面内是否存在点K，使以点B、C、Q、K为顶点，BC为边的四边形是矩形？若存在，请直接写出点K的坐标；若不存在，请说明理由．【变式5-1】（2021•齐齐哈尔）综合与探究如图，在平面直角坐标系中，抛物线y＝ax2+2x+c（a≠0）与x轴交于点A、B，与y轴交于点C，连接BC，OA＝1，对称轴为直线x＝2，点D为此抛物线的顶点．（1）求抛物线的解析式；（2）抛物线上C、D两点之间的距离是2√2；（3）点E是第一象限内抛物线上的动点，连接BE和CE，求△BCE面积的最大值；（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．【变式5-2】（2021春•杏花岭区校级月考）如图，在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．（2）若点P为直线BC下方抛物线上一动点，当点P运动到某一位置时，△BCP的面积最大，求△BCP 的最大面积及此时点P的坐标；（3）点M为抛物线对称轴上一动点，点N为坐标平面内一点，若以点B，C，M，N为顶点的四边形是矩形，直接写出点M的坐标．【变式5-3】（2021•北碚区校级模拟）如图，已知抛物线y＝ax2+bx﹣4与x轴交于A，B两点，与y轴交于点C，且点A的坐标为（﹣2，0），直线BC的解析式为y=12x﹣4．（2）如图1，过点A作AD∥BC交抛物线于点D（异于点A），P是直线BC下方抛物线上一点，过点P作PQ∥y轴，交AD于点Q，过点Q作QR⊥BC于点R，连接PR．求△PQR面积的最大值及此时点P 的坐标．（3）如图2，点C关于x轴的对称点为点C′，将抛物线沿射线C′A的方向平移2√5个单位长度得到新的抛物线y′，新抛物线y′与原抛物线交于点M，原抛物线的对称轴上有一动点N，平面直角坐标系内是否存在一点K，使得以D，M，N，K为顶点的四边形是矩形？若存在，请直接写出点K的坐标；若不存在，请说明理由．【题型6 二次函数中正方形存在性问题】【例6】（2021•渝中区校级二模）在平面直角坐标系xOy中，抛物线y＝ax2+bx+3与y轴交于点C，与x 轴交于A，B两点（点A在点B的左侧），其中A（﹣2，0），并且抛物线过点D（4，3）．（1）求抛物线的解析式；（2）如图1，点P为直线CD上方抛物线上一点，过P作PE∥y轴交BC于点E，连接CP，PD，DE，求四边形CPDE面积的最值及点P的坐标；（3）如图2，将抛物线沿射线CB方向平移得新抛物线y＝a1x2+b1x+c1（a1≠0），是否在新抛物线上存在点M，在平面内存在点N，使得以A，C，M，N为顶点的四边形为正方形？若在，直接写出此时新抛物线的顶点坐标，若不存在，请说明理由．【变式6-1】（2020秋•高明区期末）如图，抛物线y＝x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y 轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．（1）求该抛物线的函数表达式；（2）点Q在该抛物线的对称轴上，若△ACQ是以AC为腰的等腰三角形，求点Q的坐标；（3）若P为BD的中点，过点P作PF⊥x轴于点F，G为抛物线上一动点，GM⊥x轴于点M，N为直线PF上一动点，当以F、M、G、N为顶点的四边形是正方形时，直接写出点M的坐标．【变式6-2】（2021•合川区校级模拟）如图，在平面直角坐标系．xOy中，直线y＝x﹣4与x轴交于点A，与y轴交于点B，过A，B两点的抛物线交x轴于另一点C（﹣2，0）．（1）求抛物线解析式；（2）如图1，点F是直线AB下方抛物线上一动点，连接F A，FB，求出四边形F AOB面积最大值及此时点F的坐标．（3）如图2，在（2）问的条件下，点Q为平面内y轴右侧的一点，是否存在点Q及平面内任意一点M 使得以A，F，Q，M为顶点的四边形是正方形？若存在，直接写出点Q的坐标；若不存在，说明理由．【变式6-3】（2021•海南模拟）如图，平面直角坐标系中，抛物线y＝ax2+bx+c交x轴于A（﹣3，0），B （4，0），交y轴于点C（0，4）．（1）求抛物线的函数表达式；（2）直线y=34x+94与抛物线交于A、D两点，与直线BC交于点E．若点M（m，0）是线段AB上的动点，过点M作x轴的垂线，交抛物线于点F，交直线AD于点G，交直线BC于点H．①当S EOG=12S△AOE时，求m的值；②在平面内是否存在点P，使四边形EFHP为正方形？若存在，请求出点P的坐标，若不存在，请说明理由．。

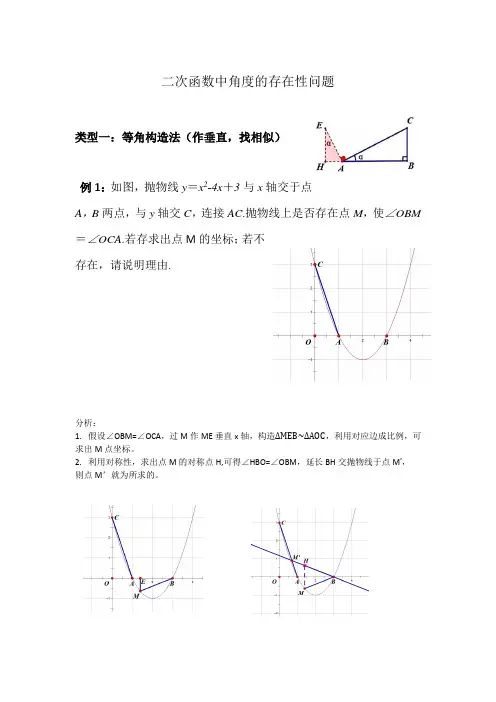
二次函数中角度的存在性问题类型一：等角构造法（作垂直，找相似）例1：如图，抛物线y＝x2-4x＋3与x轴交于点A，B两点，与y轴交C，连接AC.抛物线上是否存在点M，使∠OBM ＝∠OCA.若存求出点M的坐标；若不存在，请说明理由.分析：1.假设∠OBM=∠OCA，过M作ME垂直x轴，构造∆MEB~∆AOC，利用对应边成比例，可求出M点坐标。

2.利用对称性，求出点M的对称点H,可得∠HBO=∠OBM，延长BH交抛物线于点M’，则点M’就为所求的。

类型二：2倍角构造法（作垂直平分线，构造等腰三角形，则外角就为已知角的两倍）例2.如图，直线y＝-3x＋3与x轴交于点A，与y轴交于点B，抛物线y＝-x2＋bx＋c经过点A，B．抛物线上是否存在点M，使直线AM与y轴所夹锐角是∠ABO的2倍？若存在，请求出点M的坐标；若不存在，请说明理由.分析：1.作AB的垂直平分线CD,交y轴于点D,则构造等腰三角形BDA，所以∠ODA=2∠OBA，延长AD交抛物线于点M，则联立解析式可求点M坐标。

2.利用对称性可求点M的对称点H（或者求D点的对称点），则延长AH交抛物线于M’。

类型三：半角构造法（作角平分线或向外延长作等腰三角形）例3：如图，抛物线交x 轴于A ，C 两交y 轴于点B ，连接AB .抛物线上是否存在点M ，使∠ACM ＝？若存在，请求出点M 的坐标；若不存在，请说明理由.分析：方法1：作∠OAB 的J 角平分线AE ，求出E 点坐标及AE 解析式。

过点C 作CM ∥AE ，则∠MCA=∠OAE=∠OAB ，则点M 就为所求作的。

然后利用对称性，可求点M ’.4x 31x 31y 2+--=BAO ∠2121方法2：延长OA 至D ，使AD 等于AB ，构造等腰三角形BAD,则∠ADB=∠OAB ，过C 点作CM ∥BD,则点M 就为所求作的。

然后一样利用对称性求出点M ’。

21。

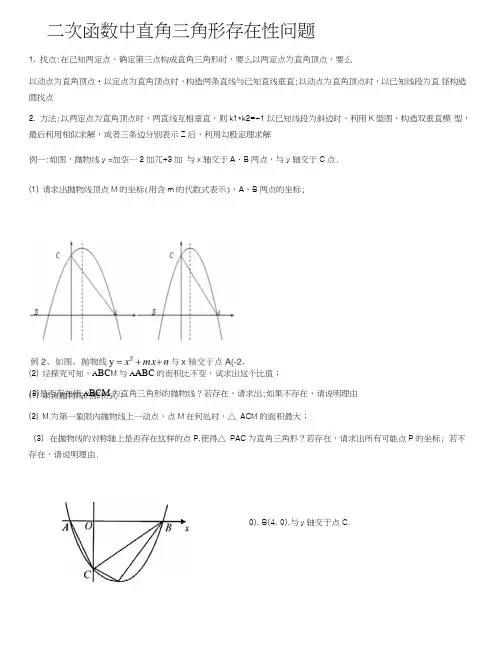
二次函数中直角三角形存在性问题1. 找点:在己知两定点，确定第三点构成直角三角形时，要么以两定点为直角顶点，要么以动点为直角顶点•以定点为直角顶点时，构造两条直线与已知直线垂直;以动点为直角顶点时，以已知线段为直 径构造圆找点2. 方法:以两定点为直角顶点时，两直线互相垂直，则k1*k2=-1以已知线段为斜边时，利用K 型图，构造双垂直模 型，最后利用相似求解，或者三条边分别表示Z 后，利用勾股定理求解例一:如图，抛物线y =加空一2加兀+3加 与x 轴交于A 、B 两点，与y 轴交于C 点.(1) 请求出抛物线顶点M 的坐标(用含m 的代数式表示)，A 、B 两点的坐标;(2) 经探究可知，A BC M 与A ABC 的而积比不变，试求出这个比值；(1) 求该抛物线的解析式； (2) M 为第一象限内抛物线上一动点，点M 在何处时，△ ACM 的面积最大；(3) 在抛物线的对称轴上是否存在这样的点P,使得△ PAC 为直角三角形？若存在，请求出所有可能点P 的坐标; 若不存在，请说明理由.(3)是否存在使A BCM 为直角三角形的抛物线？若存在，请求出;如果不存在，请说明理由0), B(4, 0),与y 轴交于点C.练习：1.如图.C知抛物线y=ar±bx+c (a«)的顶点M在第一象限，抛物线bx轴相交FA、B两点(点A 住点B的左边),f jy轴交万点C, O为唯标原点，如果ZkABM是何角二角形，AB=2, OM= J5(1)求点M的坐标;(2)求抛物线y=ax2+bx+c的解析式；(3)在抛物线的对称轴匕是否存在点P,使W APAC为直角三角形？若存在.请求出所有符合条件的点P 的坐标：若不存在•请说明理由.2.如图，抛物线y =〒一2加兀(m>0)与x轴的另一个交点为A,过P(l, -m)作PM丄x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.(1)若m二2,求点A和点C的坐标；(2)令m>l,连接CA,若AACP为直角三角形，求m的值；(3)在坐标轴上是否存在点E,使得APEC是以P为直角顶点的等腰直角三角形？若存在，求出点E的坐标；若不存在，请说明理由.3.如图，抛物线y =衣+分+2与x轴交于点A(l, 0)和B(4, 0).(1)求抛物线的解析式；(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点，FC〃x轴，与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形，求点C的坐标；(3)在(2)的条件下，抛物线的对称轴上是否存在点P,使AOCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由.4、在平面直角坐标系中，抛物线y = ++仗一1)兀一比与直线y二kx+1交于A, B两点，点A在点B的左侧.(1)如图1,当k二1吋，直接写出A, B两点的坐标；(2)在(1)的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求岀AABP面积的最大值及此时点P 的坐标；(3)如图2,抛物线y =兀2+仗_1)兀一比(k>0)与x轴交于点C、D两点(点C在点D的左侧)，在直线y二kx+1 使得Z0QC=90° ?若存在，请求出此吋k的值；若不存在，请说明理由.5.如图，直线y=x+2与抛物线y = ajc^-bx^6 (a#0)相交于A (2, 2)和B(4, m),点P是线段AB上异于A、B的动点，过点P作PC丄x轴于点D,交抛物线于点C.(1)求抛物线的解析式；(2)是否存在这样的P点，使线段PC的长有最大值，若存在，求出这个最大值；若不存在，请说明理由;(3)求厶PAC为直角三角形时点P的坐标.6、如图，抛物线y = ci^+bx+c经过A(-3, 0)、C(0, 4),点B在抛物线上，。

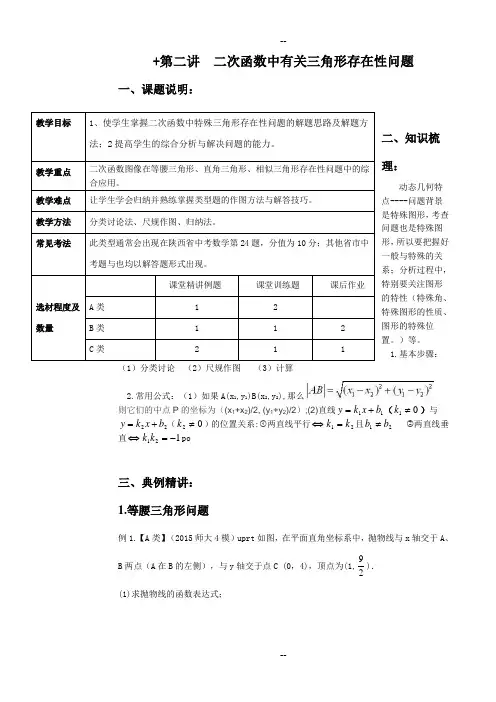
+第二讲 二次函数中有关三角形存在性问题一、课题说明：二、知识梳理：动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）等。

1.基本步骤：（1）分类讨论 （2）尺规作图 （3）计算 2.常用公式：（1）如果A(x 1,y 1)B(x 2,y 2),那么则它们的中点P 的坐标为（(x 1+x 2)/2, (y 1+y 2)/2）;(2)直线11b x k y +=（01≠k ）与22b x k y +=（02≠k ）的位置关系:①两直线平行⇔21k k =且21b b ≠ ②两直线垂直⇔121-=k k po三、典例精讲： 1.等腰三角形问题例1.【A 类】（2015师大4模）uprt 如图，在平面直角坐标系中，抛物线与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C (0，4)，顶点为(1,29)． (1)求抛物线的函数表达式；教学目标1、使学生掌握二次函数中特殊三角形存在性问题的解题思路及解题方法；2提高学生的综合分析与解决问题的能力。

教学重点 二次函数图像在等腰三角形、直角三角形、相似三角形存在性问题中的综合应用。

教学难点 让学生学会归纳并熟练掌握类型题的作图方法与解答技巧。

教学方法 分类讨论法、尺规作图、归纳法。

常见考法此类型通常会出现在陕西省中考数学第24题，分值为10分；其他省市中考题与也均以解答题形式出现。

选材程度及数量课堂精讲例题课堂训练题课后作业A 类 1 2B 类 1 1 2C 类211(2)设抛物线的对称轴与x 轴交于点D ，试在对称轴上找出点P ，使△CDP 为等腰三角形，请直接写出满足条件的所有点P 的坐标；【教法参考】（1）.分类讨论：分类标准：讨论顶角的位置或者底边的位置例如：本题第二问：在抛物线上找一点p ，使得P D C 、、三点构成等腰三角形，则可分成以下几种情况：（1）当C ∠为顶角时，CP CD = （2）当D ∠为顶角时，DP DC = （3）当P ∠为顶角时，PD PC =(2).尺规作图：两圆一线（①当C ∠为顶角时，以C 为圆心CD 为半径画圆，与对称轴交点即为所求点P ，②当D ∠为顶角时，以D 为圆心DC 为半径画圆，与对称轴交点即为所求点P ，③当P ∠为顶角时，线段DC 的垂直平分线与对称轴交点即为所求点P 。

第2 讲：角度的存在性问题【例1】如图，在平面直角坐标系两点，与y 轴交于点C（0, 2）；1）求抛物线的表达式；2）求证：CAO BCO ；3）若点P 是抛物线上的一点，且PCB ACB BCO ，求直线CP的表达式．1 2 5 4参考答案】（1）y x2x 2 ；（ 2）证明略；（ 3）y x 2或y 2 ．2 2 3思路点拨1．设求抛物线的交点式比较简便．2．第（ 2）题求两个锐角的正切值相等，可以得到两个锐角相等．3．第（ 3）题先把 3个角的关系，转化为∠ PCB＝∠ 2，再按点 P与 CB的位置关系分两种情况讨论．满分解答（1）因为抛物线与 x轴交于 A（1, 0）、 B（4, 0）两点，所以 y＝a（x－1）（x－4）．代入点 C（0, 2），得a 1．2所以抛物线的表达式为y 1（x 1）（x 4）＝1 x2 5x 2．2 2 22）如图 2，tan∠CAO＝OC＝2．如图 3，tan∠BCO＝OB＝4＝2，所以∠ CAO ＝∠ BCO ．xOy 中，抛物线y ax2bx c与x 轴交于A(1,0) 、B(4,0)（3）如图 2，图 3，由于∠ CAO ＝∠ BCO ，根据等角的余角相等，得∠ 1＝∠2． 因为∠ PCB ＋∠ ACB ＝∠ BCO ，所以∠ PCB ＝∠ BCO －∠ ACB ＝∠ 1＝∠2． ∠PCB 存在两种情况：7 10P （73,190） ． 例 2】已知在直角坐标系中，抛物线 y ax交 x 轴于点 B ，点 P 在抛物线上，且位于抛物线对称轴的右侧； 1）当 AB BD 时（如图），求抛物线的表达式；2）在第（ 1）小题的条件下，当 DP ∥ AB 时，求点 P 的坐标；13）点 G 在对称轴 BD 上，且 AGB ABD ，求△ ABG 的面积．2①如图 4，当点 P 在CB 的右侧时，由∠ PCB ＝＝∠ 2，得 CP//x 轴． 此时直线 CP 的解析式为 y ＝ 2．②如图 5，当点 P 在 CB 的左侧时，设 CP 与x 轴交于点 D ． 由∠ PCB ＝∠ 2，得 DC ＝DB ．33x 3．所以 D (3,0) ．22考点伸展如果第（ 3）题的条件不变，求点 P 的坐标．第一种情形，如图 4，当 CP//x 轴时，点 C 关于抛物线的对称轴 5x 5对称，所以 P(5,2) ．第二种情形，如图 6，设 P （x,1x 2 5x 2）．22 3 2作 PE⊥y 轴于 E ，那么ODCO CO ．所以CE21 25 2 (2 x 22x 2)解得 x ＝ 0，或 x 7．所以228ax 3 （a 0） 与 y 轴交于点 A ，顶点为 D ，其参考答案】 1) y1x 2 x 3 ；(2) (10, 1) ；(3)82设 D （x, 0），根据 DC 2＝DB 2，列方程 x 2＋22＝ （4－ x ）2．解得思路点拨1．抛物线的解析式中隐含了对称轴（点B）和点 A 的坐标，根据 AB＝ BD 求出点 D 的坐标，再代入解析式求待定系数 a ．2．看着 1∠ ABD ，结合 BA ＝ BD ，不由得让人联想起“三线合一” ．23．以∠ ABD 为外角，构造等腰三角形 BAG ，BG ＝BA ，这样就满足∠ ABD ＝2∠ AGB ． 4．根据对称性，∠ AGB 的顶点 G 存在两种情况．满分解答由 y ＝ax 2－8ax ＋3，可得 A(0, 3)，抛物线的对称轴为直线 x ＝4． B(4, 0)， AB ＝ 5．当 BD ＝ AB ＝ 5时， D(4, 5)．考点伸展(1) 所以 将点 D (4, 5)代入 y ＝ax 2－8ax ＋3，得1a 1 ．所以8y 1 x 2x 3 ． 82) 如图 2，作 PE ⊥ BD 于 E ． 设点 P 的坐标为 (x, 1x 28OA OB当 DP //AB 时， ED EP 所以 ED3EP ．x 3) ．解方程 5 ( 1x 2x 3) 3(x 4)， 84整理，得 x 2－14x ＋ 40＝0． 所以 x ＝10，或 x ＝4(与点 D 重合，舍去) ．所以 P (10,1) ．2(3)如图 3，在 DB 的延长线上截取 BG ＝BA ＝ 5，那么∠ AGB＝∠1 又因为∠ABD ＝∠ AGB ＋∠ BAG ，所以此时∠ AGB ＝ ∠ABD ．2BAG ． 此时 如S △ABG ＝ 10．4，作 AH⊥BD 于H ，点 G 关于直线 AH 的对称点为G′， BG′＝BH＋ G′H＝11．此时 S △那么 G ′H ＝GH ＝8． 图5图3图4第( 3)题也可以从∠ ABD 的平分线开始思考： 如图 5，作∠ ABD 的平分线与 y 轴交于点 C ．因为∠ 1＝∠ 2，∠ 1＝∠ C ，所以∠ 2＝∠ C ．所以 AC ＝ AB ＝ 5．过点 A 作 BC 的平行线交抛物线的对称轴于点 G ，那么四边形 CAGB 是平行四边形．1所以∠ 1＝∠ G ，BG ＝ AC ＝ 5．所以∠ AGB ＝ ∠ ABD ．此时 S △ABG ＝10．2求点 G ′的过程同上．【例 3】在平面直角坐标系中，抛物线 y 3x 2bx c 与y 轴角于点 A(0,3) ，与 x 轴的正半轴交于点5B(5,0) ，点 D 在线段 OB 上，且 OD 1，联结 AD 、将线段 AD 绕着点 D 顺时针旋转 90 得到线段 DE过点 E 作直线 l x 轴，垂足为 H ，交抛物线于点 F ． ( 1)求这条抛物线的解析式； ( 2)联结 DF ，求 cot EDF 的值；( 3)点 G 在直线 l 上，且 EDG 45 ，求点 G 的坐标．满分解答由 D(1, 0)、 F(4, 3)、E(4, 1)，可得∠ DFE ＝45°，DF ＝3 2 ，EF ＝2．参考答案： 1)32 x 5 12x32) cot EDF3) E (4,6)或(4, 3)．3x 轴交于点 B(5, 0)，设 y (x 5)(x m) ，53 3 2 121．所以 y (x 5)(x 1) x 2 x 3 ．5 5 5(2)如图 2，由△ AOD ≌△ DHE ，得 DH ＝AO ＝3，EH ＝DO ＝1．所以 E(4,1)．1) 因为抛物线与代入点 A(0, 3)， 得－ 3m ＝ 3 ．所以 m ＝－如图 3，作 EM⊥DF 于 M，那么 EM＝FM＝2 ．在 Rt△DEM 中，EM＝2，DM＝DF－FM＝2 2 ，所以 DE＝10．所以cos∠EDF ＝DM＝ 2 2＝ 2 5DE 10 52图(3)符合条件的点 G 有两个：①如图 4，当点 G在 DE 上方时，所以 ED2＝EF·EG．所以 10＝2EG．②如图 5，当 G′在DE下方时，△ GDG ′是直角三角形．此时 DH2＝HG·HG′．所以9＝ 6HG ′．所以 HG′＝3．此时G′(4, 3)．由∠EDG＝∠ EFD ＝ 45°，∠ DEG是公共角，可得△ EDG ∽△EFG ．所以 EG＝5．此时 G(4, 6)．x例4】已知顶点为A（2, 1）的抛物线经过点B（0,3），与x 轴交于C 、D 两点（点C 在点D 的左侧）； 1）求这条抛物线的表达式；2）联结AB 、BD 、DA ，求△ ABD 的面积；3）点P在x轴正半轴上，如果A PB 45 ，求点P的坐标．参考答案：（ 1）y x24x 3 ；（2）3；（3）（3 6,0）．满分解答（1）设抛物线的顶点式为 y＝a（x－2）2－1，代入点 B（0, 3），得 a＝1．所以这条抛物线的解析式为 y＝（x－2）2－1＝ x2－ 4x＋3．（2）由 y＝ x2－ 4x＋ 3＝（x－ 1）（x－ 3），得 C（1, 0）， D（3, 0）．如图 2，由 A（2,－1）、B（0, 3）、D（3, 0），可得∠ BDO ＝ 45°，∠ ADO＝45°， BD＝3 2，AD＝2．所以 S△ABD ＝1AD BD ＝12 3 2 ＝ 3．22（3）如图 3，以 AB 为斜边构造等腰直角三角形 GAB，以 G 为圆心、 GB 为半径画圆，与 x 轴交于点 P（圆与 x 轴右侧的一个交点），根据同弧所对的圆周角等于圆心角的一半，可知∠APB＝ 45°．如图 4，由△ BMG≌△ GNA，得 BM＝GN，MG＝NA．设 G（m, n），那么 m＝n＋1，3－n＝m－2．解得 m＝3，n＝2．所以 G（3, 2）．设 P（x, 0）．根据 GB2＝GP2，列方程 32＋12＝（x－3）2＋ 22．解得（3 6,0），或（3 6,0）（这是圆与 x 轴左侧的交点的横坐标，此时∠ APB＝135°）．所以点P 的坐标为（3 6,0）．【裴文通老师和顾晓琴老师提供的解法】 因为∠ BDO ＝ 45°＝∠ 1＋∠ 3，∠ APB ＝45°＝∠ 2＋∠ 3，∠ ADO ＝45°＝∠ 2＋∠4， 所以∠ 1＝∠2，∠3＝∠ 4．所以△ PBD ∽△ APD ．所以 DP DA．于是DP 2＝DA ·DB ＝ 2 3 2 ＝6．DB DP所以DP ＝ 6，OP ＝3 6 ．所以P （36,0） ．【例 5】已知在平面直角坐标系 xOy 中，二次函数 y x 2 mx n 的图像经过点 A（3,0） ， 且与 y 轴相交于点 C ；（ 1）求这个二次函数的解析式并写出其图像顶点 D 的坐标； （ 2）求 CAD 的正弦值；（3）设点 P 在线段 DC 的延长线上，且 PAO CAD ，求点 P 的坐标．图2 图3 图4B(m,m 1) ，图2图3Ox2 9 3m n 0 1）将 A （3,0）、B （m, m ＋1）两点分别代入 y ＝－ x 2＋ mx ＋ n ，得n m 1.解得m ＝2，n ＝3．所以y ＝－ x 2＋2x ＋3＝－（x －1）2＋4．所以C （0, 3），顶点 D （1, 4）． （2）如图 2，作 DE ⊥y 轴于 E ．由A(3, 0)、C(0, 3)、 D(1, 4)，可得∠ ACO ＝∠DCE ＝45°，AC ＝ 3 2，DC＝ 2．所以∠ ACD ＝ 90°．所以 AD 2＝AC 2＋DC 2＝18＋2＝20．所以 AD ＝2 5． 所以tan ∠CAD ＝ DC＝ 2＝1，sin ∠CAD ＝ DC＝ 2＝ 10．AC 3 2 3 AD 2 5 10（3）直线 CD 的解析式为 y ＝ x ＋ 3，于是可设 P （x, x ＋ 3）． 作PH ⊥x 轴于H ，当∠ PAO ＝∠ CAD 时，由 tan ∠PAO ＝tan ∠CAD ，得 PH 1．AH 3①当P 在x 轴上方时，x 3 1．解得 x 3．此时 P （ 3,3）（如图 2所示）．3 x 3 2 2 2 ②当P 在x 轴下方时， （x 3） 1．解得x ＝－ 6．此时 P （－6,－3）（如图3所示）．参考答案：（1） y x 22x 3，顶点 （1,4） ；满分解答2) 10 ；10333)( 23,32)，( 6, 3)．图2图3【例 6】 如图，在平面直角坐标系中 xOy 中，抛物线 y x 2 bx c 与 x 轴相交于点 A （-1,0） 和点 B ，与 y 轴相交于点 C （0,3），抛物线的顶点为点 D ，联结 AC 、BC 、DB 、DC ． （ 1）求这条抛物线的表达式及顶点 D 的坐标； （ 2）求证： △ACO ∽△DBC ；（ 3）如果点 E 在 x 轴上，且在点 B 的右侧，∠ BCE= ∠ ACO，求点 E 的坐标 ．满分解答（1）由抛物线 y ＝－x 2＋bx ＋c 与 x 轴相交于点 A （－1, 0），设 y ＝－（x ＋1）（x －m ）． 代入点 C （0, 3） ，得 m ＝ 3．所以 y ＝－ （x ＋1）（x －3）＝－（x 2－2x －3）＝－x 2＋2x ＋3＝－ （x －1）2＋4． 所以点 B 的坐标为 （3, 0），顶点 D 的坐标为 （1, 4） ．（2）如图 2，由 B （3, 0）、C （0, 3）、D （1, 4），可知 B 、C 两点间的水平距离、竖直距离都是3，C 、D两点间的水平距离、竖直距离都是 1．因此 BC 、DC 与 y 轴的夹角都是 45°．tan ∠DBC ＝ DC＝ 2＝ 1． BC 3 2 3由 A(－1, 0)、 C(0, 3)，得 OA ＝1， OC ＝ 3，所以 tan ∠ACO ＝ OC 所以∠ ACO ＝∠ DBC ．所以△ ACO ∽△ DBC ．（3）设 CE 与 BD 交于点 G ．由∠ BCE ＝∠ ACO ＝∠ DBC ，得 GB ＝ GC ． 于是可得 CG 是 Rt △DBC 斜边上的中线，点 G 是 BD 的中点．所以 G （2, 2）．所以∠ BCD ＝ 90°，2）略；x3)E(6,0) ．2达标检测【 1】如图，抛物线y ax2bx 5( a 0)经过点A(4, 5) ，与x轴的负半轴交于点B，与y 轴交于点C ，且OC 5OB ，抛物线的顶点为D ．( 1)求这条抛物线的表达式；(2)联结AB、BC、CD、DA ，求四边形ABCD的面积；( 3)如果点E 在y 轴的正半轴上，且BEO A BC ，求点E 的坐标．参考答案】解： ( 1)∵抛物线y ax2bx 5与y 轴交于点C，∴C(0, 5)，∴ OC5．∵OC 5OB，∴OB 1．又点B在x轴的负半轴上，∴B( 1,0)．∵抛物线经过点A(4, 5)和点B( 1,0) ，16a 4b 5 5 a 1 2∴ ，解得．∴这条抛物线的表达式为y x24x 5 ．a b 5 0 b 4(2)由y x24x 5，得顶点D 的坐标是(2, 9)．联结AC ．∵点A的坐标是(4, 5) ，点C的坐标是(0, 5)，11又S ABC 2 4 5 10，S ACD 2 4 4 8，∴ S四边形ABCD S ABC S ACD 18．3)过点C作CH AB ，垂足为点H ．15216∵S ABC 1AB CH 10， AB 5 2， ∴CH 2 2．2在 Rt BCH 中， BHC 90 ， BC 26 ， BH BC 2 CH 2 3 2 ；∴ tan CBHC B H H23．在 Rt BOE 中， BOE 90 ， tan BEOBO，EO，∵ BEO ABC ，BO EO 2，得 EO 3∴点 E 的坐标为 (0, 3)．2】如图，抛物线 y=x 2+bx+5与x 轴交于点 A 与 B （5,0） 点，与 y 轴交于点 C ，抛物线的顶点为点 P ． 1）求抛物线的表达式并写出顶点 P 的坐标；2）在 x 轴上方的抛物线上有一点 D ，若 ?ABD ? ABP ，试求点 D 的坐标； 3）设在直线 BC 下方的抛物线上有一点 Q ，若S DBCQ = 15 ，试写出点 Q 坐标．满分解答（1）将点 B （5, 0）代入 y ＝x 2＋bx ＋5，得．解得 b ＝－ 6． 所以 y ＝x 2－6x ＋5＝－（x －3）2－4，顶点 P 的坐标为 （3,－4）．2）如图 2，作 DN ⊥x 轴于 N ．设抛物线的对称轴与 x 轴交于点 M ． 由 tan ∠ABD ＝ tan∠ ABP，得DN PMBN BM2x 26x 5 4参考答案： （ 1） y x 26x 5 ， P （3, 4） ； 2) D( 1,12) ； (3) Q(2, 3)或(3, 4)．2．5 x 23）由 B （5, 0）、C （0, 5），可知 BC ＝5 2，直线 BC 与 x 轴负半轴的夹角为 45°设点 D 的坐标为 （x, x 2－ 6x ＋ 5），那么图3设BC 边上的高为 h ，那么 S △BCQ＝ 15 2h ＝15．解得 h 3 2 ．2如图3，设y 轴上点 C 下方的点 G 到直线BC 的距离GH ＝ 3 2，那么 CG ＝6，G （0,－1）．练习 1】如图，在平面直角坐标系 xOy 中，抛物线 y ax 2 bx 1经过点 A （2, 1） ，它的对称轴与 x 轴 相交于点 B ；（ 1）求点 B 的坐标；（ 2）如果直线 y x 1与此抛物线的 对称轴交于点 C 、与抛物 线在对称轴右 侧交于点 D ，且 BDC ACB ，求此抛物线的表达式．过点 G 作BC 的平行线与抛物线的交点就是要求的点 Q ，这条直线为 y ＝－ x － 1．解方程组y2x 1, 得x 2,或x 3,y x 26x 5, y3, y4.所以 Q （2,－3）或（3,－4）．5 10参考答案】(1)B(1,0)；(2) y 53x2 130x 1．满分解答1)将点 A(2,－1)代入 y＝ax2＋bx－1，得 1－＝ 4a＋ 2b－1．所以 b＝－ 2a．抛物线的对称轴 x＝b＝2a＝1．所以点 B 的坐标为 (1, 0)．2a 2a(2)如图 2，由 y＝x＋ 1，得 C(1, 2)．所以 BC＝2．由A(2,－1)、B(1, 0)，得BA 2 ，∠ 2＝45°因为直线 y＝x＋1 与坐标轴的夹角为 45°，由此可知∠ 1＝ 45°．所以∠ 1＝∠ 2．根据等角的邻补角相等，可知∠ DCB＝∠ CBA．当∠ BDC＝∠ ACB时，△ DCB ∽△ CBA．所以DC CB，即CB BA 所以DC 2 2 ．因此 D、C 两点间的水平距离、竖直距离都是将点 D(3, 4)代入 y＝ax2－2ax－1，得 4＝9a－6a－1．解得所以抛物线的表达式是y 5x2 10 x 1．33DC 2．2 2．2．所以 D(3, 4)．。

二次函数中的十二大存在性问题【题型1二次函数中等腰三角形的存在性问题】【题型2二次函数中直角三角形的存在性问题】【题型3二次函数中等腰直角三角形的存在性问题】【题型4二次函数中全等三角形的存在性问题】【题型5二次函数中平行四边形的存在性问题】【题型6二次函数中菱形的存在性问题】【题型7二次函数中矩形的存在性问题】【题型8二次函数中正方形的存在性问题】【题型9二次函数中面积问题的存在性问题】【题型10二次函数中线段问题的存在性问题】【题型11二次函数中角度问题的存在性问题】【题型12二次函数中最值问题的存在性问题】【题型1二次函数中等腰三角形的存在性问题】1(2023春·甘肃张掖·九年级校考期中)如图甲，直线y=-x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A，顶点为P．(1)求该抛物线的解析式；(2)当0<x<3时，在抛物线上求一点E，使△CBE的面积有最大值(图乙、丙供画图探究)，并求出最大面积及E点的坐标．(3)在该抛物线的对称轴上是否存在点M，使以C、P、M为顶点的三角形为等腰三角形？若存在，请求出所符合条件的点M的坐标；若不存在，请说明理由；1(2023春·广西贵港·九年级统考期末)如图，抛物线y=ax2+3x+c a≠0和与x轴交于点A-2,0点B，与y轴交于点C0,8，点P为直线BC上方抛物线上的动点，连接CP，PB，直线BC与抛物线的对称轴l交于点E．(1)求抛物线的解析式；(2)求△BCP的面积最大值；(3)点M是抛物线的对称轴l上一动点．是否存在点M，使得△BEM为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．2(2023春·山西晋城·九年级校考期末)如图1，抛物线y=ax2+bx+3与x轴交于A-1,0两，B4,0点，与y轴交于点C，顶点为D．点P是直线BC上方抛物线上的一个动点，过点P作PE⊥x轴于点E，交直线BC于点Q．(1)求抛物线的表达式；(2)求线段PQ的最大值；(3)如图2，过点P作x轴的平行线交y轴于点M，连接QM．是否存在点P，使得△PQM为等腰三角形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．3(2023•沙坪坝区校级模拟)如图1，抛物线y=ax2+bx+2(a≠0)交x轴于点A(-1，0)，点B(4，0)，交y轴于点C．连接BC，过点A作AD∥BC交抛物线于点D(异于点A)．(1)求抛物线的表达式；(2)点P是直线BC上方抛物线上一动点，过点P作PE∥y轴，交AD于点E，过点E作EG⊥BC于点G，连接PG．求△PEG面积的最大值及此时点P的坐标；(3)如图2，将抛物线y=ax2+bx+2(a≠0)水平向右平移32个单位，得到新抛物线y1，在y1的对称轴上确定一点M，使得△BDM是以BD为腰的等腰三角形，请写出所有符合条件的点M的坐标，并任选其中一个点的坐标，写出求解过程．【题型2二次函数中直角三角形的存在性问题】1(2023春·四川广安·九年级校考期中)如图，已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2)，B(0,-2)，其对称轴为直线x=52，C0,1 2为y轴上一点，直线AC与抛物线交于另一点D．(1)求抛物线的函数表达式；(2)试在线段AD下方的抛物线上求一点E，使得△ADE的面积最大，并求出最大面积；(3)在抛物线的对称轴上是否存在一点F，使得△ADF是直角三角形？如果存在，求点F的坐标；如果不存在，请说明理由．1(2023春·辽宁盘锦·九年级校考期中)如图，已知直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=-x2+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．(1)求抛物线的解析式；(2)在第三象限内，F为抛物线上一点，以A、E、F为顶点的三角形面积为3，求点F的横坐标；(3)点P是对称轴上的一动点，是否存在某一点P使P、B、C为顶点的三角形是以BC为直角边的直角三角形？若存在，请直接写出所有符合条件的P点坐标；不存在，说明理由．2(2023春·广东梅州·九年级校考期中)已知二次函数y=x2+bx+c的图象经过A(-2,5)，B(-1,0)，与x轴交于点C．(1)求这个二次函数的解析式；(2)点P直线AC下方抛物线上的一动点，求△PAC面积的最大值；(3)在抛物线对称轴上是否存在点Q，使△ACQ是直角三角形？若存在，直接写出点Q的坐标，若不存在，请说明理由．3(2023春·甘肃金昌·九年级统考期中)平面直角坐标系中，抛物线y=a(x-1)2+92与x轴交于A，B(4，0)两点，与y轴交于点C．(1)求抛物线的解析式，并直接写出点A，C的坐标；(2)在抛物线的对称轴上是否存在点P，使△BCP是直角三角形？若存在，请直接写出点P的坐标，若不存在，请说明理由；(3)如图，点M是直线BC上的一个动点，连接AM，OM，是否存在点M使AM+OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；【题型3二次函数中等腰直角三角形的存在性问题】1(2023春·山西阳泉·九年级统考期末)综合与探究：在平面直角坐标系中，抛物线y=ax2+bx-2与x轴交于点A-1,0作平行于x轴的直线l，直线l与抛物线y，与y轴交于点C，过动点D0,m和点B4,0=ax2+bx-2相交于点E，F．(1)求抛物线的表达式；(2)求m的取值范围；(3)直线l上是否存在一点P，使得△BCP是以BC为直角边的等腰直角三角形？若存在，求m的值；若不存在，请说明理由．1(2023春·福建漳州·九年级校考期中)如图①，已知抛物线y=ax2+bx+3的图象经过点B1,0，与y 轴交于点A，其对称轴为直线l：x=2，过点A作AC∥x轴交抛物线于点C，∠AOB的角平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m．(1)求抛物线的解析式；(2)若动点P在直线OE下方的抛物线上，连接PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；(3)如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．2(2023春·湖南湘西·九年级统考期末)如图，在平面直角坐标系中，直线y =-x +3交x轴于点B ，交y 轴于点C ，直线AD 交x 轴于点A ，交y 轴于点D ，交直线BC 于点E -12，72，且CD =1．(1)求直线AD 解析式；(2)点P 从B 点出发沿线段BA 方向以1个单位/秒的速度向终点A 运动(点P 不与A ，B 两点重合)，设点P 的运动时间为t ，则是否存在t ，使得△AEP 为等腰直角三角形？若存在，请求出t 的值，若不存在，请说明理由；(3)在(2)的条件下，点P 出发的同时，点Q 从C 点出发沿射线CO 方向运动，当点P 到达终点时，点Q 也停止运动，连接AQ ，PQ ，设△APQ 的面积为S ，S 与t 的函数关系式为S =32t 2-12t +2120≤t <1a t -1 t -7 1<t <7，其图象如图2所示，结合图1、图2的信息，请求出a 的值及当△APQ 的面积取得最大值时AQ 的长．3(2023春·北京通州·九年级统考期末)如图，抛物线y1=ax2-2x+c的图象与x轴交点为A和B，与y 轴交点为D0,3，与直线y2=-x-3交点为A和C．(1)求抛物线的解析式；(2)在直线y2=-x-3上是否存在一点M，使得△ABM是等腰直角三角形，如果存在，求出点M的坐标，如果不存在请说明理由．(3)若点E是x轴上一个动点，把点E向下平移4个单位长度得到点F，点F向右平移4个单位长度得到点G，点G向上平移4个单位长度得到点H，若四边形EFGH与抛物线有公共点，请直接写出点E的横坐标x E的取值范围．【题型4二次函数中全等三角形的存在性问题】1(2023·陕西咸阳·统考三模)如图，抛物线y=14x2-2x+3与x轴交于A、B两点，抛物线的顶点为C，对称轴为直线l，l交x轴于点D．(1)求点A、B、C的坐标；(2)点P是抛物线上的动点，过点P作PM⊥y轴于点M，点N在y轴上，且点N在点M上方，是否存在这样的点P、N，使得以点P、M、N为顶点的三角形与△BCD全等，若存在，请求出点P、N的坐标；若不存在，请说明理由．1(2023·甘肃陇南·统考一模)如图，抛物线y=x2+bx+c与x轴交于A-1,0，B两点，与y轴交于点C0,-3．(1)求抛物线的函数解析式；(2)已知点P m,n在抛物线上，当-1≤m<3时，直接写出n的取值范围；(3)抛物线的对称轴与x轴交于点M，点D坐标为2,3，试问在该抛物线上是否存在点P，使△ABP与△ABD全等？若存在，请求出所有满足条件的P点的坐标；若不存在，请说明理由．2(2023·陕西咸阳·统考三模)如图，抛物线y=14x2-2x+3与x轴交于A，B两点，抛物线的顶点为C，对称轴为直线l，l交x轴于点D．(1)求点A、B、C的坐标；(2)点P是抛物线上的动点，过点P作PM⊥y轴于点M，点N在y轴上，且点N在点M上方，是否存在这样的点P、N，使得以点P、M、N为顶点的三角形与△BCD全等，若存在，请求出点P、N的坐标；若不存在，请说明理由．3(2023·内蒙古通辽·统考中考真题)如图，在平面直角坐标系中，抛物线y=ax2+bx+c(a≠0)的顶点为B(2，1)，且过点A(0，2)，直线y=x与抛物线交于点D，E(点E在对称轴的右侧)，抛物线的对称轴交直线y=x于点C，交x轴于点G，EF⊥x轴，垂足为F，点P在抛物线上，且位于对称轴的右侧，PQ⊥x轴，垂足为点Q，△PCQ为等边三角形(1)求该抛物线的解析式；(2)求点P的坐标；(3)求证：CE=EF；(4)连接PE，在x轴上点Q的右侧是否存在一点M，使△CQM与△CPE全等？若存在，试求出点M的坐标；若不存在，请说明理由．[注：3+22=(2+1)2]．【题型5二次函数中平行四边形的存在性问题】1(2023春·云南临沧·九年级统考期末)如图，抛物线y=ax2+bx-3与x轴交于A-1,0两点，、B3,0与y轴交于点C．(1)求抛物线的解析式；(2)若点D是抛物线上的一点，当△ABD的面积为10时，求点D的坐标；(3)点P是抛物线对称轴上的一点，在抛物线上是否存在一点Q，使得以B、C、P、Q为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．1(2023春·山东东营·九年级校考期末)如图，已知抛物线y=ax2+bx+3与x轴交于A-1,0、B3,0两点，与y轴交于点C，连接BC．(1)求抛物线的解析式；(2)若点P为线段BC上的一动点(不与B、C重合)，PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求点P的坐标；(3)在(2)的条件下，当△BCM的面积最大时，点D是抛物线的对称轴上的动点，在抛物线上是否存在点E，使得以A、P、D、E为顶点的四边形为平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由．2(2023春·重庆梁平·九年级统考期末)如图1，在平面直角坐标系中，抛物线y=-2x2+4x+6与y轴交于点A，与x轴交于点E，B(E在B的左侧)．(1)如图2，抛物线的顶点为点Q，求△BEQ的面积；(2)如图3，过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点(点P在AC上方)，作PD 平行于y轴交AB于点D、交AC于点F，当点P在何位置时，PD+CF最大？求出最大值；(3)在(2)条件下，当PD+CF最大时，将抛物线y=-2x2+4x+6沿着射线AB平移，使得抛物线经过点C，此时得到新抛物y ，点N是原抛物线对称轴上一点，在新抛物线y 上是否存在一点M，使以点A，D，M，N为顶点的四边形为平行四边形，若存在，请直接写出点M的所有坐标，若不存在，请说明理由．3(2023春·重庆江北·九年级重庆十八中校考期末)如图1，抛物线y=ax2+bx+3a≠0与x轴正半轴交于点A，B，与y轴正半轴交于点C，且OC=OB=3OA，点D为抛物线的顶点．(1)求该抛物线的函数表达式；(2)点P为直线BC下方该抛物线上任意一点，点E为直线BC与该抛物线对称轴的交点，求△PBE面积的最大值；(3)如图2，将该抛物线沿射线CB的方向平移22个单位后得到新抛物线y ，新抛物线y 的顶点为D ，过(2)问中使得△PBE面积为最大时的点P作平行于y轴的直线交新抛物线y 于点M．在新抛物线y 的对称轴上是否存在点N，使得以点P，D ，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【题型6二次函数中菱形的存在性问题】1(2023春·重庆云阳·九年级校联考期中)如图1，抛物线y=ax2+bx+c(a≠0)与x轴相交于点A、B(点B在点A左侧)，与y轴相交于点C(0,3)．已知点A坐标为(1,0)，△ABC面积为6．(1)求抛物线的解析式；(2)点P是直线BC上方抛物线上一动点，过点P作直线BC的垂线，垂足为点E，过点P作PF∥y轴交BC于点F，求△PEF周长的最大值及此时点P的坐标：(3)如图2，将该抛物线向左平移2个单位长度得到新的抛物线y ，平移后的抛物线与原抛物线相交于点D，点M为直线BC上的一点，点N是平面坐标系内一点，是否存在点M，N，使以点B，D，M，N为顶点的四边形为菱形，若存在，请直接写出点M的坐标；若不存在，请说明理由．1(2023春·甘肃庆阳·九年级统考期末)如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C0,-3，点P是直线BC下，点A在原点的左侧，点B的坐标为3,0方的抛物线上一动点．(1)求这个二次函数的表达式．(2)连接PO、PC，并把△POC沿CO所在直线翻折，得到四边形POP C，那么是否存在点P，使四边形POP C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．(3)当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的面积．点，抛物线y=-x2+bx+c经过点B，且与x轴交于点C(2,0)．(1)求该抛物线的解析式；(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，四边形OAMB的面积为S，求S与m的函数表达式，并求出S的最大值；(3)若点P在平面内，点Q在直线AB上，平面内是否存在点P使得以O，B，P，Q为顶点的四边形是菱形．若存在，求出点P的坐标；若不存在，请说明理由．点，抛物线y=-x2+bx+c经过点B，且与x轴交于点C(2,0)．(1)求该抛物线的解析式；(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，四边形OAMB的面积为S，求S与m的函数表达式，并求出S的最大值；(3)若点P在平面内，点Q在直线AB上，平面内是否存在点P使得以O，B，P，Q为顶点的四边形是菱形．若存在，求出点P的坐标；若不存在，请说明理由．【题型7二次函数中矩形的存在性问题】1(2023春·浙江湖州·九年级统考期末)如图，在平面直角坐标系xOy中，O为坐标原点，抛物线y=a(x+3)(x-1)(a>0)与x轴交于A，B两点(点A在点B的左侧)．(1)求点A与点B的坐标；(2)若a=13，点M是抛物线上一动点，若满足∠MAO不大于45°，求点M的横坐标m的取值范围．(3)经过点B的直线l：y=kx+b与y轴正半轴交于点C．与抛物线的另一个交点为点D，且CD=4BC．若点P在抛物线对称轴上，点Q在抛物线上，以点B，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．1(2023·山东东营·东营市胜利第一初级中学校考三模)已知抛物线y=ax2+bx-4a≠0交x轴于点A4,0和点B-2,0，交y轴于点C．(1)求抛物线的解析式；(2)如图，点P是抛物线上位于直线AC下方的动点，过点P分别作x轴、y轴的平行线，交直线AC于点D，交x轴于点E，当PD+PE取最大值时，求点P的坐标及PD+PE最大值．(3)在抛物线上是否存在点M，对于平面内任意点N，使得以A、C、M、N为顶点且AC为一条边的四边形为矩形，若存在，请直接写出M、N的坐标，不存在，请说明理由．2(2023春·内蒙古通辽·九年级校考期中)如图，抛物线y=ax2+bx+3交x轴于A(3,0),B(-1,0)两点，交y轴于点C．(1)求抛物线的解析式和对称轴．SΔABC，求R的坐标．(2)若R为第一象限内抛物线上点，满足SΔRAC=12(3)若点P在抛物线的对称轴上，点Q是平面直角坐标系内的任意一点，是否存在点P使得A、C、P、Q为顶点的四边形是矩形，若存在，请直接写出所有符合条件的点P的坐标．3(2023春·广东江门·九年级校考期末)如图，在平面直角坐标系中，已知抛物线y=ax2+bx-2a≠0、B两点，交y轴于点C，其对称轴为x=1.5，交x轴于A-1，0(1)求该抛物线的函数解析式；(2)P为第四象限内抛物线上一点，连接PB，过点C作CQ∥BP交x轴于点Q，连接PQ，求△PBQ面积的最大值及此时点P的坐标．(3)在(2)的条件下，将抛物线y=ax2+bx-2a≠0向右平移经过点Q，得到新抛物线，点E在新抛物线的对称轴上，是否在平面内存在一点F，使得以A、P、E、F为顶点的四边形是矩形？若存在，直接写出点F的坐标；若不存在，请说明理由．【题型8二次函数中正方形的存在性问题】1(2023·辽宁阜新·阜新实验中学校考一模)如图，在平面直角坐标系中，抛物线y=ax2+bx-3与x轴交于A(-1,0)，B(3,0)两点，与y轴交于点C，点P为抛物线上的动点．(1)求该抛物线的函数表达式；(2)点D为直线y=x上的动点，当点P在第四象限时，求四边形PBDC面积的最大值及此时点P的坐标；(3)已知点E为x轴上一动点，点Q为平面内任意一点，是否存在以点P，C，E，Q为顶点的四边形是以PC为对角线的正方形，若存在，请直接写出点Q的坐标，若不存在，请说明理由．1(2023·陕西西安·校考模拟预测)如图，已知拋物线y=-x2+2x+c与x轴交于点A3,0，B与y轴交于点C．(1)求c的值及该抛物线的对称轴；(2)若点D在直线AC上，点E是平面内一点．是否存在点E，使得以点A,B,D,E为顶点的四边形为正方形？若存在，请求出点E的坐标；若不存在，请说明理由．2(2023·山西晋中·山西省平遥中学校校考模拟预测)如图，二次函数y=-x2+2x+3的图象与x轴交于A，B两点(点A在点B左侧)，与y轴交于点C．连接BC．点P是抛物线第一象限内的一个动点，设点P的横坐标为m，过点P作直线PD⊥x轴于点D．交BC于点E．过点P作BC的平行线，交y轴于点M．(1)求A，B，C三点的坐标，并直接写出直线BC的函数表达式；(2)在点P的运动过程中，求使四边形CEPM为菱形时，m的值；(3)点N为平面内任意一点，在(2)的条件下，直线PM上是否存在点Q使得以P，E，Q，N为顶点的四边形是正方形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．3(2023·江西赣州·统考一模)已知二次函数C1：y=mx2-2mx+3(m≠0)．(1)有关二次函数C1的图象与性质，下列结论中正确的有．(填序号)①二次函数C1的图象开口向上；②二次函数C1的图象的对称轴是直线x=1；③二次函数C1的图象经过定点(0，3)和(2，3)；④函数值y随着x的增大而减小．(2)当m=1时，①抛物线C1的顶点坐标为；②将抛物线C1沿x轴翻折得到抛物线C2，则抛物线C2的表达式为；(3)设抛物线C1与y轴相交于点E，过点E作直线l∥x轴，与抛物线C1的另一交点为F，将抛物线C1沿直线l翻折，得到抛物线C3，抛物线C1，C3的顶点分别记为P，Q．是否存在实数m，使得以点E，F，P，Q为顶点的四边形为正方形？若存在，请求出m的值；若不存在，请说明理由．【题型9二次函数中面积问题的存在性问题】1(2023春·四川广安·九年级统考期末)如图1，抛物线y=ax2+bx+3经过A1,0两点，交y轴于,B3,0点C．(1)求抛物线的函数解析式．(2)在抛物线的对称轴上是否存在一点M，使得△ACM的周长最小？若存在，求出点M的坐标；若不存在，请说明理由．S△BCA，请直接写出点P的横坐(3)如图2，连接BC，若在BC下方的抛物线上存在一点P，使得S△BCP=12标．1(2023春·江西九江·九年级校考期中)如图，已知二次函数L1：y=x2+bx+c与x轴交于A、B两点，A点坐标(-1，0)，B点坐标(3,0)，与y轴交于点C，直线L2：y=x+n经过点A．(1)求二次函数L1的表达式及顶点P的坐标；(2)二次函数L3与二次函数L1关于X轴对称，直线L2与二次函数L3相交于A、D两点．①直接写出二次函数L3的表达式；②求出D点的坐标；③在直线L2上半部分的二次函数L3上，是否存在一点M，使得△AMD的面积最大？若存在，请求出M坐标，并求出最大面积．2(2023春·山东东营·九年级东营市实验中学校考期中)如图，抛物线y=ax2+bx+c a≠0与y轴交于点C0,4．，点B4,0，与x轴交于A-2,0(1)求抛物线的解析式；(2)若点M是抛物线上的一动点，且在直线BC的上方，当S△MBC取得最大值时，求点M的坐标；(3)在抛物线上是否存在点P，使三角形ABP的面积为12？若存在，直接写出点P的坐标；若不存在，请说明理由．3(2023春·福建泉州·九年级统考期末)如图，在平面直角坐标系xOy中，顶点为E1，4的抛物线y= ax2+bx+c与x轴从左到右依次交于A，B两点，与y轴的交点为C0，3，P是抛物线对称轴右侧图象上的一点，且在x轴的上方．(1)求此抛物线的解析式；(2)若直线BP与抛物线对称轴交于点D，当BD-CD取得最大值时，求点P的坐标；(3)若直线BC与抛物线对称轴交于点F，连接PC，PE，PF，记△PCF，△PEF的面积分别为S1，S2，判断2S1+S2是否存在最大值．若存在，求出最大值；若不存在，请说明理由．【题型10二次函数中线段问题的存在性问题】1(2023春·内蒙古巴彦淖尔·九年级校考期中)如图1，抛物线y=ax2+bx+c a≠0与x轴交于A-8,0．点E是第二象限内抛物线上的一个动点，设点E的横坐标 两点，与y轴交于点D0,4，C2,0为n，过点E作直线EB⊥x轴于点B，作直线AD交EB于点F．(1)求该抛物线的解析式；(2)如图1，当△EFD是以FD为底边的等腰三角形时，求点E的坐标；(3)如图2，连接CD，过点E作直线l∥CD，交y轴于点H，连接BH．试探究：在点E运动的过程中，是否存在点E，使得FD=BH，若存在，请求出点E的坐标；若不存在，请说明理由．1(2023春·四川南充·九年级统考期中)如图，平面直角坐标系中的Rt△AOB和Rt△COD全等，直角边OB、OD在x轴上．已知点C的坐标为4，2，过A、C两点的直线分别交x轴、y轴于点E、F，抛物线y=ax2+bx+c经过O、A、C三点．(1)写出点A的坐标并求该抛物线的函数解析式；(2)点G为抛物线上位于线段OC所在可直线上方部分的一动点，求G到直线OC的最大距离和此时点G 的坐标；(3)点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM的边AM与边BP相等？若存在，求出此时点P的坐标；若不存在，请说明理由．2(2023春·云南曲靖·九年级统考期末)已知抛物线y=x2+bx+c与x轴交于点A-1,0两，B3,0点，与y轴交于点C，连接BC．(1)求抛物线的解析式；(2)在抛物线上是否存在点M，使得B、C两点到直线AM的距离相等，如果存在，求出点M的坐标，如果不存在，请说明理由；(3)点P为x轴上一动点，以P为旋转中心，把线段BC逆时针旋转90°，得到线段GH，其中点B的对应点为点G，当抛物线的对称轴刚好经过GH中点时，求此时点P的坐标．3(2023春·安徽阜阳·九年级校考期末)如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=-2与x轴交于点C，直线y=-2x+1经过抛物线上一点B2,m，且与y轴．直线x=-2分别交于点D、E．(1)求m的值及该抛物线对应的函数关系式；(2)①判断△CBE的形状，并说明理由；②判断CD与BE的位置关系；(3)若P x,y是该抛物线上的一个动点，是否存在这样的点P，使得PB=PE？若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由．【题型11二次函数中角度问题的存在性问题】1(2023春·辽宁葫芦岛·九年级统考期末)如图，在平面直角坐标系中，已知抛物线y=-x2+bx+c与x轴交于A，B4,0在抛物线上，点P是抛物线上一动点．两点，与y轴交于点C，点D3,4(1)求该抛物线的解析式；(2)如图1，连接OD，若OP平分∠COD，求点P的坐标；(3)如图2，连接AC，BC，抛物线上是否存在点P，使∠CBP+∠ACO=45°？若存在，请直接写出点P的坐标；若不存在，请说明理由．1(2023春·内蒙古鄂尔多斯·九年级统考期末)如图，直线y=-x+3与x轴、y轴分别交于B、C两点，抛物线y=-x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D．(1)求抛物线的解析式；(2)在第四象限的抛物线上是否存在一点M，使△MBC的面积为27？若存在，求出M点坐标；若不存在，请说明理由．(3)在抛物线的对称轴上是否存在一点P，使得∠APB=∠OCB？若存在，求出P点坐标；若不存在，请说明理由．2(2023春·江苏盐城·九年级统考期末)如图，抛物线y=12x2+mx+n与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A-4,0,C0,-2．(1)求抛物线的函数表达式；(2)点E是线段AC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDAF的面积最大?求出四边形CDAF的最大面积及此时E点的坐标；(3)在y轴上是否存在点P，使得∠OAP+∠OAC=60°？若存在，请直接写出P点的坐标，若不存在，请说明理由．3(2023春·浙江湖州·九年级统考期末)如图，在平面直角坐标系中，直线y=12x-2与x轴交于点A，与y轴交于点C，抛物线y=12x2+bx+c经过A，C两点，与x轴的另一交点为点B，点P为抛物线上的一个动点．(1)求抛物线的函数表达式；(2)当△ACP的面积与△ABC的面积相等时，求点P的坐标；(3)是否存在点P，使得∠ACP=∠ABC-∠BAC，若存在，请直接写出点P的横坐标；若不存在，请说明理由．【题型12二次函数中最值问题的存在性问题】1(2023春·甘肃庆阳·九年级统考期中)如图，已知抛物线y=38x2-34x-3与x轴的交点为点A、D(点A在点D的右侧)，与y轴的交点为点C．(1)直接写出A、D、C三点的坐标；(2)在抛物线的对称轴上找一点M，使得MD+MC的值最小，并求出点M的坐标；(3)设点C关于抛物线对称轴的对称点为点B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由．1(2023春·浙江宁波·九年级校考期中)对于给定的两个函数，任取自变量x 的一个值，当x <0时，它们对应的函数值互为相反数；当x ≥0时，它们对应的函数值相等，我们称这样的两个函数互为“伴随”函数．例如：一次函数y =x -3，它的“伴随”函数为y =-x +3x <0 x -3x ≥0 ．(1)已知点M -2，1 在一次函数y =-mx +1的“伴随”函数的图象上，求m 的值．(2)已知二次函数y =-x 2+4x -12．①当点A a ，32 在这个函数的“伴随”函数的图象上时，求a 的值．②当-3≤x ≤3时，函数y =-x 2+4x -12的“伴随”函数是否存在最大值或最小值，若存在，请求出最大值或最小值；若不存在，请说明理由．。

课题：二次函数中直角三角形的存在性问题教学目标：知识与技能1、 知道并会推导三垂直性质，能正确找出对应边，能准确写出三垂直中的对应边成比例.2、 准确掌握平面直角坐标系中三垂直性质使用条件和操作程序.过程与方法通过对平面直角坐标系中不同位置的直角三角形活动探究出构造三垂直性质应如何添加辅助线，并会利用三垂直性质解决二次函数中直角三角形的存在性问题.情感态度与价值观通过对解析几何产生的背景介绍及三垂直性质在二次函数中直角三角形存在性问题的应用感受数形结合思想的重要性及意义；通过对不确定直角顶点的直角三角形存在性问题的解决，感受分类思想在学习中的必要性.教学重点：探究如何构造三垂直模型，并会利用三垂直性质解决直角三角形的存在性问题.教学难点：探究使用三垂直性质的操作程序.教学过程：一、 情景设计讲述解析几何产生的背景，说明数形结合思想的重要性， 引出课题。

二、 预习思考),(1b x ),(2b x ),(1y a ),(2ya1、如图1，水平线上各点的___坐标相同，水平线上的两点间的距离等于_______________________________。

2、如图2，竖直线上各点的___坐标相同，竖直线上的两点间的距离等于_______________________________。

3、 如何设函数图像上的动点坐标？如何设二次函数对称轴上的动点坐标？教学要点1、 分组提问，调动学生积极性.2、 引导学生由图找答案，并用自己的语言叙述结论.3、 对学生的结论补充强调.三、 探索问题问题1：(1) 图3是什么模型？(2) 该模型的已知条件是什么？结论是什么？你可以证明你的结论吗？(3) 图3、图4的已知条件和结论的区别与联系是什么？教学要点1、问题1的设置是对本节课的应用知识点重点巩固，可齐声回答.2、教师分析：三垂直模型还可看作，已知一直角三角形，过其直角顶点在直角三角形的外部做一条直线，并过直角三角形的另外两个顶点引上述直线的垂线段.问题2：(1) 如果需要求一条线段的长，你希望在坐标系中是什么样的线段？(2) 如果平面直角坐标系中随意放置了一个直角三角形，过其直角顶点在其外部做一条什么方向的直线，能保证构成的三垂直模型中相似的两个直角三角形的四条直角边不是水平方向就是竖直方向？(3) 总结在平面直角坐标系中构造三垂直模型的操作步骤. 教学要点1、针对（1），能预料到学生的答案是竖直方向或水平方向，如果不是这个答案，再继续询问他们的结论的理由.2、对于（2），教师引导学生在平面直角坐标系中画出任意三角形，并让学生观察、尝试符合要求的直线.3、教师引导学生总结平面直角坐标系中构造三垂直模型操作步骤.4、教师课件展示详细操作步骤.（1）平面直角坐标系中构造三垂直模型的操作步骤.（2）过另外两个顶点向水平线或竖直线作垂线段（3）根据条件求出各点坐标及四条直角边长度（4）根据对应边相等或成比例，列出四条直角边之间的数量关系，进而求出未知数，求出动点坐标问题3：例、（2015本溪）如图，抛物线 （ ≠0）经过点A （2，0），点B （3，3）（1）求抛物线的解析式并直接写出它的对称轴；（2）点P 是抛物线对称轴上一点，当△ABP 是直角三角形时，请求出所有符合条件的点P 坐标．教学要点1、学生回答解决第（1）问的方法，学生完成（1）解答过程，教师巡视指导并讲评2、教师引导：（1）构造三垂直模型需要有一个直角，谁是Rt △ABP 的直角呢？（生：不知道）bx ax y +=2a（2）怎么办？（生：分类讨论）（3）分几类？是哪几类？（生：3类，分别是当∠ABP=90°，当∠APB=90°，∠BAP=90°）3、师生共同探究当∠ABP=90°时的情况解：如图，当∠ABP=90°时，过点P作PM⊥BC交BC的延长线于点M，设点P（1，a），则M(3，a)，C（3，0）∴PM=3-1=2，MB=a-3，BC=3，AC=3-2=1∵∠MPB+∠MBP=90°，∠MBP+∠ABC=90°，∴∠MPB=∠ABC，又∵∠PMB=∠ACB=90°∴△PM B∽△BCA∴PM/MB=BC/AC,2/(a-3)=3/1解得：a=11/3∴点P（1，11/3）4、剩下两种情况，让学生小组讨论，并找两位学生上台分别讲解，主讲学生可以自己需要选择要不要带小帮手，之后师生共同点评总结.四、课堂小结通过本节课的学习，你有什么收获？五、课后作业除了利用三垂直性质解决二次函数中直角三角形的存在性问题，你还有其它的方法吗？并试用你想到的方法解决今天的例题.教学反思：本节课是二次函数中直角三角形的存在性问题，此类问题通常在河南中招卷中作为压轴题出现，一般是23题的第（2）问或第（3）问，其知识覆盖面较广，综合性较强，是数形结合思想及分类思想的典型题。

中考数学二次函数存在性问题及参考答案中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图，把抛物线 $y=x^2$ 向左平移1个单位，再向下平移4个单位，得到抛物线 $y=(x-h)^2+k$。

所得抛物线与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D。

1）写出h、k的值；2）判断△ACD的形状，并说明理由；3）在线段AC上是否存在点M，使△AOM∽△ABC？若存在，求出点M的坐标；若不存在，说明理由。

2.如图，已知抛物线经过A（$-2,0$），B（$-3,3$）及原点O，顶点为C。

1）求抛物线的解析式；2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；3）P是抛物线上的第一象限内的动点，过点P作PM⊥x 轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由。

二、二次函数中面积的存在性问题3.如图，抛物线 $y=ax^2+bx$ （$a>0$）与双曲线$y=\frac{k}{x}$ 相交于点A，B。

已知点B的坐标为（$-2,-2$），点A在第一象限内，且 $\tan\angle AOX=4$。

过点A作直线AC∥x轴，交抛物线于另一点C。

1）求双曲线和抛物线的解析式；2）计算△ABC的面积；3）在抛物线上是否存在点D，使△ABD的面积等于△ABC的面积。

若存在，请写出点D的坐标；若不存在，请说明理由。

4.如图，抛物线 $y=ax^2+c$ （$a>0$）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（$-2,0$），B（$-1,-3$）。

1）求抛物线的解析式；2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；3）在第（2）问的结论下，抛物线上的点P使$\triangle PAD=4\triangle ABM$ 成立，求点P的坐标。

㊀㊀㊀㊀㊀数学学习与研究㊀２０２３ ０４基于核心素养的数学课堂教学基于核心素养的数学课堂教学㊀㊀㊀ 二次函数中与角有关的存在性问题 专题教学设计与思考Һ陈煜舟㊀（苏州市沧浪中学校，江苏㊀苏州㊀２１５００７）㊀㊀ʌ摘要ɔ‘义务教育数学课程标准（２０２２年版）“颁布后， 如何将核心素养真正落实到课堂教学中 成了诸多教师㊁学者热烈讨论的话题．本文通过 二次函数中与角有关的存在性问题 这节专题课的教学，以小见大，将数学思想渗透于学生的数学活动中，以培养学生的数学核心素养，让学生学有所得．文章应用新课标引领教育新生态，采用 巧设问题，体验由繁化简；对比探究，悟得方法优劣；变化局部，调动类比思维；探本寻源，发展建模素养；以编促学，统筹知识全局 等策略，旨在将核心素养真正落实到数学课堂，让学生在分析和思考问题的过程中感悟转化㊁对比㊁类比等数学思想方法，提炼出思维精华，发展建模素养，在开放性的问题中打破知识的壁垒，建立联系，从而通过教学活动实现数学教育的育人功能．ʌ关键词ɔ数学活动；数学思维；核心素养一㊁新课标引领教育新生态２０２２年４月２１日，教育部颁布了‘义务教育数学课程标准（２０２２年版）“，标志着我国以核心素养为导向的新一轮课程改革拉开了序幕．从 双基 到 三维目标 ，再到现在以 核心素养 为本位，数学教学把核心素养的培育作为主要教学目标，使义务教育呈现出新的面貌，也使数学学科独特的育人价值不断地体现出来．初中阶段，学生的数学学习需要掌握很多显性的表层知识，如一些概念㊁性质㊁公式等．新课标更加关注数学思维的形成㊁活动经验的积累㊁理想信念和价值观的引领，让学生在与周围环境产生相互作用时具备良好的数学核心素养．接下来，笔者以 二次函数中与角有关的存在性问题 这节专题课的教学为例，阐述如何将核心素养的培养贯彻到数学教学中．这堂课重点解决下面的问题：如图１，已知抛物线ｙ＝－２３ｘ２＋４３ｘ＋２交ｘ轴于Ａ，Ｂ两点（点Ａ在点Ｂ右边），交ｙ轴于点Ｃ，点Ｐ在抛物线上运动．在抛物线上是否存在点Ｐ（在ＡＣ上方），使得øＡＣＰ＝４５ʎ？若存在，求点Ｐ的坐标；若不存在，请说明理由．图１二㊁核心素养落地数学课堂（一）巧设问题，体验由繁化简首先，学生会画一个草图了解点Ｐ的大致位置（如图２），但经过尝试会发现直接求点Ｐ的坐标比较复杂．因此，教师抛出一个简单清晰的问题 点Ｐ的位置在哪里 ，以合适的问题引导学生观察点Ｐ的位置：点Ｐ在抛物线上，也在直线ＣＰ上．这便让学生意识到：要求点Ｐ的坐标，可以先求直线ＣＰ的解析式．这是解决该问题最关键的一步．图２教师鼓励学生将最终转化而成的问题写下来以明确解题目标，即解决该问题的第一步可以转化为：如图３，在平面直角坐标系中，已知一次函数ｙ＝－２３ｘ＋２分别交ｘ轴㊁ｙ轴于Ａ，Ｃ两点，将直线ＡＣ绕点Ｃ逆时针旋转４５ʎ，求旋转后的直线ｌ１的解析式．图３这一巧妙的设计开拓了学生的思路，使学生能通过观察点的位置主动推理出解决问题的方法．因此，教师应通过巧设问题引导学生分解㊁转化综合问题，为学生提供思维的阶梯．按照上述解题思路，大问题分解成了相对简单的小问题，由难到易，由繁化简．教师应有意识地向学生揭示这里利用了转化的数学思想，将数学思想加以明确．（二）对比探究，悟得方法优劣在求旋转后的直线解析式时可以发现只有一个点Ｃ的坐标是已知的，因此还需确定这条直线上另一点的坐标．那么如何选取这个点呢？教师让学生合作讨论后再分享各自的做法．有的小组提出：过点Ａ向ｌ１作垂线，交ｌ１于点Ｄ（如图４），然后求垂足Ｄ的坐标；也有小组认为：过点Ａ向ＡＣ作垂线，交ｌ１于点Ｄ（如图５），然后求点Ｄ的坐标．还有一些㊀㊀㊀㊀数学学习与研究㊀２０２３ ０４类似的方法这里不一一赘述．图４㊀㊀㊀图５接着，教师引导学生回忆求点的坐标的常用方法：向ｘ轴或ｙ轴作垂线．学生马上联想到可通过构造 ｋ型全等 求出点Ｄ的坐标．为了更好地让学生感受 构造 这一数学方法，教师请学生将解题方法进行对比，可以发现两种方法都构造了 ｋ型全等 ，即把倾斜着的难以解决的线段转化为横平竖直的线段，从而转移了线段长度，求出了点的坐标，这是一种大家常用的化斜为直的构造方法．但两种方法有繁易之分，所以教师进一步请学生分析两种方法的不同之处：图４中的解题过程比较烦琐，需要设未知数，图５可直接求解．教师继续引导：造成这种区别的主要原因是什么呢？学生通过观察发现，图４中由于点Ｄ未知，ＲｔәＥＤＣ与ＲｔәＦＡＤ的直角边都是未知的，所以需要设未知数；而图５中点Ａ是已知的，ＲｔәＡＯＣ的两条直角边都已知，因此可以直接求解．两种思路的比较让学生感悟到：在解决此类问题时，应尽可能地选择以已知点为直角顶点构造 ｋ型全等 ．在这一过程中，学生由浅入深㊁由表及里，在对比中主动地 悟 出解决这个问题的好方法．教师的启发引导㊁小组的相互合作㊁班级的分享互动，改变了传统的 教师教，学生学 的教学模式，构建了以学生为中心的课堂．（三）变化局部，调动类比思维教师将 旋转４５ʎ 改为 旋转一个正切值为１２的角度，即ｔａｎøＡＣＰ＝１２，其余条件及问题不变．虽然旋转角度不是特殊角，但正切值确定，øＡＣＰ的度数相当于是已知的，因而这是一道与旋转角为４５ʎ一脉相承的题目．考虑到正切值的利用应该放在直角三角形中，学生经过观察㊁分析能迅速类比得出此类问题的解决思路，依然可以作垂直构造 ｋ型相似 ，并且模仿较简单的辅助线构造方法，即以点Ａ为直角顶点构造 ｋ型相似 ．角度的一般化同时带来了 ｋ型全等 到 ｋ型相似 的变化，教师通过列举一个一般化的例子，调动起学生的类比思维，让学生在以后接触到其他一般化的角度时也能得心应手地解题，这为后续归纳解题步骤做好了铺垫．（四）探本寻源，发展建模素养此时，学生对本节课的第一个难点有了初步的理解，但是教师不需要急着展开后面的内容，应该给予学生充分的时间，小结解决问题的步骤，归纳图形的共同属性．教师引导学生观察图形中的已知信息：直线ＡＣ是已知的，点Ａ，Ｃ为已知点，旋转角度α也是已知的．列举出已知信息之后，教师请学生思考要求的是什么，并将已知信息与所求内容用语言组织起来，进行口头完整叙述．问题是： 已知直线ＡＣ绕点Ｃ旋转一个角度α，其中点Ａ，Ｃ是已知点，旋转角度α已知，如何求旋转后的直线解析式？ 解法是： 应该尽可能以已知点Ａ为直角顶点构造 ｋ型相似 ，再求点Ｄ的坐标，最后求直线解析式．将思维的结果用文字语言表达出来，可以帮助学生梳理解题脉络，并锻炼他们的表达能力，也能辅助教师及时获得学情，让教师了解学生是否观点明确㊁条理清晰，是否具有丰富的数学语言系统，从而调整教学策略．为了将信息多方面地呈现给学生，教师请学生用图示的方法明确解题思路，进一步把抽象的文字语言转化为具体㊁直观的图示信息（如图６）．图６接下来，教师带领学生 回头 看课堂开始时提出的问题．通过前后比较，学生能够很容易找出两幅图关联的地方，即有两条相同的直线，因此可将求二次函数上动点的坐标转化为求抛物线与直线的交点．至此，这个问题便迎刃而解．这时，教师就可顺势引出本节课研究的专题 二次函数中与角有关的存在性问题 ．自然的过渡强化了学生的解题思路：对于这类二次函数中与角有关的存在性问题，需要先求旋转后的直线解析式．接下来，教师请学生完善图６的步骤（如图７）．图７就如初中数学一开始先学习具体的有理数加减乘除㊁再学习用字母表示数一样，学生总能慢慢地从特殊的数据处理中得出具有普遍意义的结论．在本节课上，教师通过具体的语言归纳以及直观的图示两种策略，让学生对于这类问题的解决脉络逐渐清晰化，建立起这类题目的解题模型，达到对这类问题的深度认知目标，将知识尽快地转化为学生的能力．㊀㊀㊀㊀㊀数学学习与研究㊀２０２３ ０４（五）以编促学，统筹知识全局在应用部分，教师让学生模仿例题，合作编题，并讨论解决．具体过程如下：教师：这个角度可以为４５ʎ，在相同的题目条件下，根据我们研究的内容，还可以怎样编题呢？生１：在抛物线上是否存在点Ｐ（在ＡＣ上方），使得øＡＣＰ＝３０ʎ？若存在，求点Ｐ的坐标；若不存在，请说明理由．生２：在抛物线上是否存在点Ｐ（在ＡＣ上方），使得ｔａｎøＡＣＰ＝１２？若存在，求点Ｐ的坐标；若不存在，请说明理由．生３：在抛物线上是否存在点Ｐ，使得ｔａｎøＡＣＰ＝１２若存在，求点Ｐ的坐标；若不存在，请说明理由．如果学生很难提出问题，那么教师可以加以引导：在这个图像中，已经有一个特殊的角，是øＢＣＯ，它的正切值为１２，你觉得这个问题还可以怎样变化？生４：问题也可以改成：在抛物线上是否存在点Ｐ，使得øＡＣＰ＝øＢＣＯ？若存在，求点Ｐ的坐标；若不存在，请说明理由．教师在此处可进行适当的停顿，并引导学生发现这是一道什么类型的题目，从而引导学生总结出：对于二次函数中一个角等于已知角的问题，也可以用类似的方法求解．由角相等也可以联想到相似，所以也会有学生做下面的联想．生５：在抛物线上是否存在点Ｐ，过点Ｐ作ＰＤʅＡＣ，垂足为Ｄ，使得әＣＰＤʐәＣＢＯ？若存在，求点Ｐ的坐标；若不存在，请说明理由．生６：在抛物线上是否存在点Ｐ，过点Ｐ作ＰＤʅＡＣ，垂足为Ｄ，使得әＣＰＤ与әＣＢＯ相似？若存在，求点Ｐ的坐标；若不存在，请说明理由．思维比较发散的学生也能想到更换角的顶点．生７：在抛物线上是否存在点Ｐ，使得øＣＡＰ＝øＢＣＯ？若存在，求点Ｐ的坐标；若不存在，请说明理由．生８：在抛物线上是否存在点Ｐ，使得øＡＣＰ＝øＡＣＯ？若存在，求点Ｐ的坐标；若不存在，请说明理由．在这种情况下，ＡＣ是øＯＣＰ的平分线，所以也可以利用角平分线加平行推导出等腰三角形来解决．一题多解的具体方法可以留给学生课后思考．如果此时学生觉得提问题有难度，那么教师可以继续引导学生思考：两个角还可能有什么关系？是互余㊁互补或两倍角吗？生９：在抛物线上是否存在点Ｐ，使得øＰＣＡ与øＣＡＯ互余？若存在，求点Ｐ的坐标；若不存在，请说明理由．这一环节实际上检验的是学生对这类问题是否真正建立起了数学模型，即是否都能转化为今天课堂开始时提出的问题．开放性的编题活动促使学生全身心地参与课堂活动，让学生在自己创造性的思考以及聆听他人想法的过程中感受这类问题的特点，强化了对这类问题的认知，突破了 就题论题 的弊端．以后碰到类似的问题时，学生就能迅速将新问题转化为旧问题，自身的数学思维得以提升．教师的例题是一个 纲 ，学生通过讨论将一个问题进行发散，将已有的知识进行串联㊁积累㊁加工，主动地进行一种更高难度的思维活动，是一种立足于整体的学习．在这一过程中，教师只需要扮演点拨者的角色，在学生有困难的时候帮助其将知识点牵桥搭线，建立起宏观的数学观念．课堂最后，教师拓展布置了一道题： 在相同的条件下，在第四象限是否存在点Ｐ，点Ｑ在ＰＢ的延长线上，满足øＣＢＱ＝øＣＡＢ＋４５ʎ？若存在，求点Ｐ的坐标；若不存在，请说明理由． 这道题也涉及两个角度之间的关系，改编自一道中考题．学生通过课后思考巩固本节课所学知识及思想方法，链接了中考．同时，教师可以通过这道题检验学生的习得情况，对学生今日所学做出评价．三㊁数学活动变革学科育人‘义务教育数学课程标准（２０２２年版）“坚持了以往课标中对于数学基本属性的描述，即 数学是研究数量关系和空间形式的科学 ，还明确提出： 数学源于对现实世界的抽象，通过对数量和数量关系㊁图形和图形关系的抽象，得到数学的研究对象及其关系；基于抽象结构，通过对研究对象的符号运算㊁形式推理㊁模型构建等，形成数学的结论和方法，帮助人们认识㊁理解和表达现实世界的本质㊁关系和规律．数学不仅是运算和推理的工具，还是表达和交流的语言．数学承载着思想和文化，是人类文明的重要组成部分．以这节专题课作为 数学 的典型代表，学生学会了如何解决这类问题，在分析图形的过程中感悟到了转化㊁对比㊁类比等数学思想方法，同时经历了文字语言㊁图形语言的抽象归纳过程，提炼出思维精华，发展了建模素养，最后在开放性的问题中打破了知识的壁垒，建立了联系．这些真实㊁深刻的数学活动让学生的学习变得更有价值，学生在潜移默化中感悟到数学是什么，具备了认识世界的一种 眼光 ㊁思考世界的一种 方式 ㊁表达世界的一种 语言能力 ．正如著名的数学家波利亚所说， 完善的思想方法犹如北极星 ，许多人通过它找到了正确道路，从 解题 学会 解决问题 ，从 做题 学会 做人做事 ，以期学生之所学终身受用．ʌ参考文献ɔ［１］义务教育数学课程标准修订组．聚焦核心素养㊀指向学生发展：义务教育数学课程标准（２０２２年版）解读［Ｊ］．基础教育课程，２０２２（１０）：１２－１８．［２］史宁中．核心素养统领的数学教育：‘义务教育数学课程标准（２０２２年版）“修订的理念与要点［Ｊ］．小学教学（数学版），２０２２（０７）：４－１２．［３］陈华忠．‘义务教育数学课程标准（２０２２年版）“ 新 在何处［Ｊ］．课程教材教学研究（小教研究），２０２２（０７）：７－１０．。