当前位置：文档之家 › 指派模型【数学建模】

指派模型【数学建模】

  • 格式：doc
  • 大小：26.00 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

441指派问题

441指派问题

一、指派问题的标准形式及其数学模型
指派问题的标准形式（以人和事为例）
n个人做n件事，并且要求每人必须而且只做
一件事。设第i人做第j件事的费用为 Cij（i,j
＝1，2……，n)，使总费用最少。因此，我们可得
指派问题的系数
c c 11 12 c1n
矩阵
c
(cij)n n
c c 21 22
c
2
n
cn1cn 2
cnn
对于问题的每个可行解，可用解矩阵
X 11 X 12 X 1n
X
( Xij)n
n
X
21
X 22
X
2n
Xn1
Xn2 Xnn
来表示。
为了建立标准指派问题的数学模型，我们引入n²个 0－1变量。并且得到该问题的数学模型。
1 xij
0
若指派第i人做第j事 若不指派第i人做第j事
5
Xij 1
i1
5
Xij 1
j1
Xij
0或1
j 1,2, ,5 i 1,2, ,5 i, j 1,2, ,5
（i, j 1,2, , n)
二、匈牙利解法
匈牙利法基于下面的价值系数矩阵：
（cij）=
c11 c12 … c1n c21 c22 … c2n ……………….
cn1 cn2 … cnn
22
16
1) 对没有加圈零元素的行打√号；
2) 对所有打√号行的含Ø零元素的列打√号；
3) 再对已打√号的列中含加圈零元素的行打√ 号；
4) 重复2）和3），直到再也不能找到可以打 √号行或列为止；
5) 对没有打√号的行画一横线，对打√号的列 画一竖线，这样就得到能覆盖所有零元素 的最少直线数目的直线集合。

指派问题

指派问题
√ 运筹学
STEP 4: 调整
GO TO STEP 1
45 0 40 65 45 55 55 0 0 5 0 45 0 55 60 55 45 45 0 45
√ √
0 20 40 √ 60 √ 95 √
运筹学
45 0 40 65 45 55 55 0 0 5 0 45 0 55 60 55 45 45 0 45
M ≥ m cij ), bij = M − cij ax(
则有
∑∑b x = ∑∑(M −c )x
i=1 j =1 ij ij n i=1 j =1 n ij n n i=1 j =1 i=1 j =1
n
n
n
n
ij n n
= M∑∑xij − ∑∑cij xij = nM − ∑∑cij xij
i=1 j =1
运筹学
32a 12a 0 0 0 0 640a 0 48a 176a 96a 0 8a 56a 26a 0
运筹学
32a 12a 0 0 0 0 640a 0 48a 176a 96a 0 8a 56a 26a 0
√ √
0 20 40 √ 60 √ 95 √
运筹学
50 0 45 65 50 55 60 0 0 0 0 40 0 50 60 50 45 40 0 40
0 20 35 55 90
运筹学
0 0 (xij ) = 0 1 0
指派问题
Assignment Problems
指派问题（分配问题）
1. 指派问题及其数学模型 2. 求解指派问题的匈牙利法 3. 非标准指派问题的求解 4. 指派问题的应用举例

指派问题的匈牙利法

指派问题的匈牙利法
√
l =m=4 < n=5
2 ◎0 4 2 4 2 5 Ø0 3 ◎0 4 1 ◎0 1 3 4 Ø0 3 5 1 ◎0 2 3 0Ø 5
1 0 3 1 3 2 6 0 3 0 4 2 0 1 3 3 0 2 4 0 0 3 3 0 5
1 0 3 1 3 1 ◎0 3 1 3 √
2 6 0 3 0 2 6 ◎0 3 Ø0 √
（5）若◎ 元素旳数目m 等于矩阵旳阶数n，那么这指 派问题旳最优解已得到。若m < n, 则转入下一步。
第三步：作至少旳直线覆盖全部0元素。 (1)对没有◎旳行打√号； (2)对已打√号旳行中全部含Ø元素旳列打√号； (3)再对打有√号旳列中含◎ 元素旳行打√号；
(4)反复(2)，(3)直到得不出新旳打√号旳行、列为止； (5)对没有打√号旳行画横线，有打√号旳列画纵线， 这就得到覆盖全部0元素旳至少直线数 l 。l 应等于m， 若不相等，阐明试指派过程有误，回到第二步(4)，另 行试指派；若 l＝m < n，须再变换目前旳系数矩阵， 以找到n个独立旳0元素，为此转第四步。
0
3
8
5
圈零划零
0 8 0 5
11 0 9 4
2 3 4 0
0
38
5
得最优解
将圈起旳零改为1，其他元素改为0，即得 最优解如下
0 0 1 0
（xij
)
0 0
1 0
0 0
0 1
1 0 0 0
最小总时间为22。
再看一例
祈求解如下矩阵体现旳指派问题
12 7 9 7 9
8
9
6
6
6
7 17 12 14 9
将时间矩阵C旳每一行都减去相应行旳最小元素 和每一列都减去相应列旳最小元素，使每一行 和每一列都具有零；

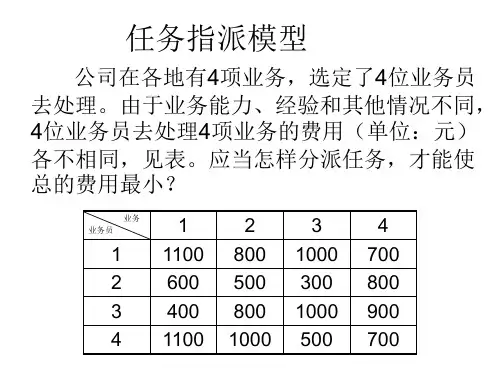
任务指派模型

任务指派模型
业务 业务员
1 2 3 4
1 1100 600 400 1100
2 800 500 800 1000
3 1000 300 1000 500
4 700 800 900 700
解
这是一个最优指派问题，引入如下变量：
1, xij = 0,
分派第 i个人做第 j项业务 不分派第 i个人做第 j项业务
业务业务斜11008001000700600500300800400800100090011001000500700分派第7个人做第项业务o不分派第个人做第项业务设矩阵儿皿为指派矩阵其中di刀为第istaxjj1234xfj
任务指派模型
公司在各地有4项业务，选定了4位业务员 去处理。由于业务能力、经验和其他情况不同， 4位业务员去处理4项业务的费用（单位：元） 各不相同，见表。应当怎样分派任务，才能使 总的费用最小？
设矩阵 A4×4为指派矩阵，其中 a (i, j )为第 i 个业务员 做第
j 项业务的业务费，则可以建立如下模型
min Z = ∑∑ aij xij
i =1 xij = 1, j = 1,2,3,4 i =1 4 s.t. ∑ xij = 1, i = 1,2,3,4 j =1 xij = 0或1，i, j = 1,2,3,4

运筹学__指派问题

运筹学__指派问题
(i 1, ,4; j 1, ,4)
则该指派问题的数学模型为：
min z 2x11 15x12 13x13 4x14 L 11x43 9x44
4
xij
1
(i 1,L
, 4)
∑xij=1 (i=1,2,3,4) 表示第i人只能完成一项任务
j1
s.t.
4
xij
1
( j 1,L
, 4)
i1
xij=1 (j=1,2,3,4) 表示第0或1
(i，j 1,L
, 4)
满足约束条件的解称为可行解， 可写成矩阵形式，叫作解矩阵。
如本例的一个可行解矩阵（但不一定是最优解）
0 1 0 0
xij
0 1
0 0
1 0
0 0
0 0 0 1
指派问题的解矩阵应具有如下特点：
在实际中经常会遇到这样的问题，
有n 项不同的任务， 需要n 个人分别完成其中的一项，
但由于任务的性质和各人的专长不同， 因此各人去完成不同的任务的效率 （或花费的时间或费用）也就不同。 于是产生了一个问题: 应指派哪个人去完成哪项任务，
使完成 n 项任务的总效率最高（或所需时间最少），
这类问题称为指派问题或分派问题。
二 匈牙利算法
思路 算法原理 算法步骤
（一） 思路
匈牙利法基于这样一个明显的事实： 如果在m阶效率矩阵中，所有元素cij≥0， 而其中有m个位于不同行不同列的一组0元素， 则在解矩阵中，只要令对应于这些0元素位置的 xij＝1，其余的xij＝0，就得到最优解。 此时的最优解为０
•如效率矩阵为 •恰有4个不同行 不同列的0系数
2. 指派问题数学模型—一般形式
设[cij]表示指派问题的效率矩阵，令

指派问题

指派问题

xij
0或1
i 1,, m
j 1,, m i, j 1,m
分配模型的标准形
如果一个分配模型满足以下三个条件： 1)目标要求为min 2)系数矩阵(cij)为n阶方阵 3)系数矩阵中所有元素cij≥0,且为常数
则称它为分配模型的标准形.
分配模型的标准形的特点:
含有n×n个变量,n+n个约束方程,所有变量均为0-1变量.
0; （2）如果人多事少，增加一些虚拟“事”，虚拟“事”做事的费用系数也取 为0； 3）一个人可做几件事的指派问题 可将某个人化作同样几个“人”接受指派，这几个“人”做同一件事的费用 系数一样。 4）某事一定不能由某人做的指派问题
可将相应的费用系数取为足够大的数M。
指派问题 assignment problem
①从只有一个0元素的行（列）的0元素开始，给这 个0元素加圈，记作◎，这表示对这行所代表的人 ，只 有一种任务可分派。然后划去◎所在列（行）的其它0 元素 ，记作，这表示这列所代表的任务已分派完， 不必再考虑别人了。
②给只有一个0元素的列(行)的元素加圈，记作◎； 然后划去◎所在的行的其它0元素，即作。
工厂1 工厂2 工厂3 工厂4
产品1 58 75 65 82
产品2 69 50 70 55
产品3 180 150 170 200
产品4 260 230 250 280
指派问题 assignment problem
得到两个最优解
1
1
X (1)＝
1
，X (2)＝
1
1 1
1
1
有两个最优方案
第一种方案：第一个工厂加工产品1，第二工厂加工产品3， 第三个工厂加工产品4，第四个工厂加工产品2；

指派问题

指派问题

第二步：找出矩阵每列的最小元素，再分别从每列中减去， 第二步：找出矩阵每列的最小元素，再分别从每列中减去，有
0 11 122 202 0 11 22 22 25 0 100 180 25 0 0 0 ⇒ 0 5 105 185 0 5 5 5 27 0 145 225 27 0 45 45
表5-34 工作 人员 甲 乙 丙 丁 A 85 95 82 86 B 92 87 83 90 C 73 78 79 80 D 90 95 90 88
x11 x X = 21 x31 x41
x12 x22 x32 x42
x13 x23 x33 x43
x14 x24 x34 x44
指派问题 assignment problem
min 58 75 65 82 69 50 70 55 180 150 170 200 260 58 230 50 ⇒ 250 65 280 55
0 11 122 202 25 0 100 180 0 5 105 185 27 0 145 225
6 17 17 0 0 0 0 0 0 0 45 45
第五步：覆盖所有零最少需要 条直线 表明矩阵中存在4个 条直线， 第五步：覆盖所有零最少需要4条直线，表明矩阵中存在 个 不同行不同列的零元素．容易看出4个 不同行不同列的零元素．容易看出 个“0”的位置 的位置
( 0 ) 30 0 × 32 6 17 17 × ( 0) 0 0 × 0 ( 0) 0 ( 0) 45 45 ( 0 ) 30 × 0 32 6 17 17 × 0 ( 0) 0 × ( 0) 0 0 ( 0) 45 45

指派问题和匈牙利法

指派问题和匈牙利法

2015-6-16
汇报提纲
一、指派问题的数学模型 二、匈牙利法 三、实例分析
三、实例分析
实例分析
有一份中文说明书，需译成英、日、德、俄四种文字，分别记作E、 J、G、R。现有甲、乙、丙、丁四人，将中文说明书译成不同语种的说 明书，所需的时间如表所示。问应指派何人去完成何种工作，使所需时
间最少？
第四步 进一步变换，得到最优解
（1）在未划线的元素中找最小者，设为 δ ； （2）在未被直线覆盖的各元素减去 δ ； （3）对两条直线交叉点覆盖的元素加上 δ ； （4）只有一条直线覆盖的元素保持不变 ；
(0)
11 2 0
8
(0)
2
5
5
4
0 6 13 0
0
5
3
4
3 (0) 0 11 4 5
11 0
或竖直线)数恰好为m条。
（3） 如果在价值系数矩阵中，位于不同行或不同列的零元素的个 数与价值系数矩阵(Cij)n×n的阶数相同，则显然只要令对应于这些 零元素位置的Xij=1，其余的Xij=0，则此解就是问题的最优解。
8
二、匈牙利法
匈牙利法的求解步骤
第一步 第二步 第三步 第四步 变换价值系数矩阵，使各行各列中都出现0元素； 选取0元素； 以最少数目的直线覆盖矩阵中所有0元素； 进一步变换，得到最优解。
(0) 11 2 0
8 (0)
2 5
5 4
3 (0) 0 11 4 5
此例中括起的0元素只有三个，小于矩阵阶数4，故需转第 三步。
2015-6-16
三、实例分析
第三步 以最少数目的直线覆盖矩阵中所有0元素
； ； ； 行上所有的0元素对应的列打 （1）对没有括起的行打 （2）对打 （3）对打

第4章 线性整数规划_指派问题

第4章 线性整数规划_指派问题

由此可见，最优分配方案所对应的原效应矩阵中元素值之 和，等于进行变换过程中行和列所加减数字的代数和(加为 负，减为正) 。此例中目标函数S的最小值即为：
n
n
n
S ui v j
i 1 j 1
n
n
由于上式后面两项均为常数，且指派问题的约束条件与效 率矩阵无关，故由 [ c ij ] 确定的指派问题与 [ c ij ] 的指派问 题有相同的最优解。证毕。
14
匈牙利法
该定理是对指派问题进行同解变换的依据。 定理 3：若矩阵 A 的元素可分成 0与非 0 两部分，则覆盖 0元 素的最少直线数等于位于不同行、不同列的 0元素 的最大个数。 所谓用直线覆盖是指用一条横线划去矩阵的一行元素或用 一条竖线划去一列元素，划去的元素就称为被覆盖。这个 定理实际上回答了这样一个问题：至少要多少条直线(横线 和竖线)才能覆盖矩阵A中的所有0元素?
0 8 7 5 11 0 10 4 2 3 5 0 0 11 9 5
0 8 11 0 2 3 0 11 2 5 5 4 0 0 4 5
S1+S2＝21+5＝26
19
匈牙利法
(2) 第二步：为了给每个教师分配一个任务，以实现完整的任 务分配，希望每行每列只有一个零元素，现在有的行或列 超过一个零元素，如何分配呢？这需要用检验的办法决定 取舍。 先进行行检验，如图 l 所示。碰到 每行只有一个 0 元素的先打△，有 两个 0 元素不作记号，例如第一行 只有一个0，就在0处打△，这就表 示把第一门课 ( 微积分 )分配给教师 Al ，因此，对第一列其它的 0 元素 打×；同理第二行打一个△；第三 行有两个0，不作记号。
0 13 4 0

关于运输问题与指派问题的建模及其求解【精选文档】

关于运输问题与指派问题的建模及其求解【精选文档】

关于运输问题与指派问题的建模及其求解【精选文档】(文档可以直接使用，也可根据实际需要修改使用,可编辑推荐下载）关于运输问题与指派问题的建模及其求解考生名单：石琦、程培培、曾凯、桑佳丽、王菁、薛苗苗、郝园、付长宇、孙丽媛、杜晓宇问题：某公司决定使用三个有生产余力的工厂进行四种新产品的生产。

下面表中给出了每种产品在不同工厂中的单位成本，以及各工厂每天生产的每种产品的数量，每种产品每天的需求量。

每家工厂都可以制造这些产品，除了工厂2不能生产产品3以外。

现在需要决定的是在哪个工厂生产哪种产品，可使总成本最小。

产品生产的有关数据（1）如果允许产品的生产分解，请建模并求解。

（2）如果不允许产品的生产分解，请建模并求解。

分析：（1）如果允许产品的生产分解，可以将生产产品问题看作运输问题来求解。

三个工厂1、2、3的总产量为78+70+40=188；四种产品1、2、3、4的总需求量为：25+35+30+40=115.由于总产量大于总需求量，所以该问题是一个供大于求的运输问题。

①决策变量设x ij为工厂i生产产品j的数量（i=1,2,3; j=1,2,3,4）。

②目标函数本问题的目标函数是使得总成本最小。

即Min z=41x11+27x12+28x13+24x14+40x21+29x22 +23x24+38x31+30x32+27x33+22x34③约束条件根据上表可以写出此问题的约束条件ⅰ各厂产量（生产能力）限制工厂1：x11+x12+x13+x14≤78工厂2：x21+x22+x23+x24≤70工厂3：x31+x32+x33+x34≤40ⅱ各种产品需求量的约束产品1：x11+x21+x31=25产品2：x12+x22+x32=35产品3：x13+x23+x33=30产品4：x14+x24+x34=40ⅲ由于工厂2不能生产产品3，所以x23=0ⅳ非负：x ij≥0；（i=1,2,3; j=1,2,3,4）。

所以该供大于求的运输问题的线性规划模型如下：Min z=41x11+27x12+28x13+24x14+ 40x21+29x22 +23x24+38x31+30x32+27x33+22x34s.t.{x11+x12+x13+x14≤78 x21+x22+x23+x24≤70 x31+x32+x33+x34≤40 x11+x21+x31=25 x12+x22+x32=35 x13+x23+x33=30 x14+x24+x34=40 x23=0x ij≥0；（i=1,2,3; j=1,2,3,4）（2）如果不允许产品的生产分解，可以将该问题视为指派工厂生产产品问题，工厂可以看作指派问题中的人，产品则可以看作需要完成的工作（任务）。

5.5指派问题

5.5指派问题

15 12 A1
15
12
A1'
14 10 A2
14
10
A2'
8 7 A3
8 7 A3'
上面的系数矩阵有6行5列，为了使“人”和“事”的数目相同， 引入一件虚拟的事B6，使之成为标准指派问题的系数矩阵：
B1 B2 B3 B4 B5 B6
4 8 4 8 7 9 7 9 6 9 6 9
7 15 12 0 A1
确定独立0元素的方法：当n较小时，可用观察法、或试探法； 当n较大时，可按下列顺序进行 • 从只有一个0元素的行（列）开始，给这个0元素加圈，记作， 然后划去所在的列（行）的其它0元素，记作。 •给只有一个0元素的列（行）的0加圈，记作，然后划去所 在行的0元素，记作。 •反复进行，直到系数矩阵中的所有0元素都被圈去或划去为止。
•如遇到行或列中0元素都不只一个（存在0元素的闭回路）， 可任选其中一个0元素加圈，同时划去同行和同列中的其它0 元素。被划圈的0元素即是独立的0元素。
3.作最少数目的直线，覆盖所有0元素（目的是确定系数矩 阵的下一个变换），可按下述方法进行 1） 对没有的行打“✓”号； 2）在已打“✓”号的行中，对 所在列打“✓” 3）在已打“✓”号的列中，对所在的行打“✓”号； 4）重复2）3），直到再也找不到可以打“✓”号的行或列为止； 5）对没有打“✓”的行划一横线，对打“✓”的列划一纵线，这样 就得到覆盖所有0元素的最少直线数。
若某个人可做几件事，则可将该人看做相同的几个人来接受指 派。这几个人作同一件事的费用系数当然都一样。 • 某事一定不能由某人作的指派问题
若某事一定不能由某个人做，则可将相应的费用系数取做足够 大的数M。
例3：对于例2的指派问题，为了保证工程质量，经研究 决定，舍弃公司A4和A5，而让技术力量较强的建设公司A1， A2，A3参加招标承建，根据实际情况，可允许每家建设公司 承建一项或二项工程。求使总费用最少的指派方案。

4.5 指派问题

4.5 指派问题

23
OR:SM
五、非标准指派问题
工作
例：现有4份工作，6个人应聘，由
1 2 3 4 56
人
于个人的技术专长不同，他们承担
1 12 7 9 7 0 0
各项工作所需时间如下表所示，且
2 7 17 12 14 0 0
规定每人只能做一项工作，每一项
3 15 14 6 6 0 0
工作只能由一个人承担，试求使总
75 50 150 230 50 25 0 100 180
65 70 170 250 65 0 5 105 185
82 55 200 280 55 27 0 145 225
然后找出矩阵每列的最小元素，再分别从每列中减去，有：
0 11 122 202 0 11 22 22
25
0
100
180
25
运筹学--管理科学方法
李军
桂林电子科技大学商学院
第四章 整数规划
内S容ub提ti要tle
问题背景与数学描述
一般
的ILP
分枝定界法 原理
求解 割平面法
步骤
整数
规划 特殊的ILP
0-1规划 指派问题
进一步讨论
建模 求解 特点分析
整数规划应用
今天要研究 的内容？
2
2013-5-29
2
引例1：趣味问题
( 0) 6 17 17
30 ×0 ( 0) ×0
×0 ×0 ×0 (0)
32
( 0)
45
45
(0 ) 6 17 17
或 30 ×0 ×0 (0)
×0 ×0 (0) ×0
32
( 0)
45
45

3.4指派问题(经典运筹学)

3.4指派问题(经典运筹学)

n
ci1 xi1
ci 2 xi 2
cin xin
cn1xn1 cn2 xn2 cnn xnn b
cc1211
c12 c22
c1n c2n
C
ci1 cn1
ci2 cn2
cin
-b
cnn
min Z Z b
c11 c21
x11 x21
c12 x12 c22 x22
i=1,2, …,n; j=1,2, …,n
Z表示总费用
12…j …n
1 c11 c12 c1 j c1n 2 c21 c22 c2 j c2n … i ci1 ci2 cij cin …
n cn1 cn2 cnj cnn
指派问题模型：
min Z
cij xij
c11 c21
c12 c22
c1n c2n
C
ci1 cn1
b
ci2 b cn2
cin b cnn
min Z
c11x11 c21x21
ccZ1222xx1222bcc12nnxx1n2
n
ci1xi1
ci 2
xi 2
cin
xin
cn1xn1 cn2 xn2 cnn xnn b
xi1 xi2 xij xin 1
s.tLeabharlann x1jx2j
xij
i=1,2, …,n
xnj 1
j=1,2, …,n
xij 0,1 i 1,2,, n; j 1,2,, n
cc1211
c12 c22
c1n c2n
C
ci1 cn1
ci 2 cn2
cin
-b
cnn

(四)指派问题的Excel建模求解

(四)指派问题的Excel建模求解

（四）指派问题的Excel建模求解
实验目的:掌握在Excel中建立指派问题模型和求解的方法
实验内容:
利用Excel“规划求解”求解下述运输问题。

（如果“工具”菜单没有显示“规划求解”子菜单，可到“加载宏”下加载。

在本实验室选择安装路径：D:\tool_bak\office2003\PRO11.MSI ）
内容：求解教材P110页的例2（具体题目如下）：
有一份中文说明书，需译成英、日、德、俄四种文字。

现有甲、乙、丙、丁四人。

他们将中文说明书翻译成不同语种的说明书所需时间如表1所示。

问应指派何人去完成何工作，使所需总时间为最少？
实验步骤
第一步建模依次在相应的单元格内输入数据和公式，建模如图1
注：Sumproduct()函数：在给定的几组数组中，将数组间对应的元素相乘，并返回乘积之和。

图1指派问题的Excel模型
第二步设置规划求解参数如图2和图3，其中，“选项”中选取“假定非负”和“采用线性模型”，其它采用默认选项，如图
图2 规划求解参数设置
（注：“二进制”的输入在下图中选择“bin”即可）
图3 选项设置
第三步求解设置完毕后，单击图2中“求解”按钮，出现如图4规划求解结果对话框
图4 规划求解结果对话框
如图4所示，共提供3类报告，选择你想要的报告，单击确定按钮，完成运算，最后计算结果如图5
图5 计算结果。

指派问题

指派问题

0 1 X＝ 0 0
1 0 0 0
0 0 0 1
0 0 1 、丁 做第三项, 最高总分Z＝92＋95＋90＋80＝357
人数和工作数不相等的指派问题
• 像处理不平衡运输问题那样，根据情况，虚设人，或者虚设 工作任务。虚设人完成工作的费用以及任何人完成虚设工作 的费用取零（理解为这些费用实际不会发生）。这样一来， 便可将人数和工作数不相等的指派问题转化为标准形式的指 派问题。
2 2 0 0
0 1 2 1
0 0 0 1
• 步骤三：找出独立零元素。
4 ◎ 0 2 0 Φ
2 ◎ 0 Φ 0 2 1 Φ 0 0 2 ◎ 0 Φ 0 1 1 ◎
4 Φ 0 2 0 ◎
2 ◎ 0 Φ 0 2 1 ◎ 0 0 2 Φ 0 ◎ Φ 0 1 1
' M cij ，其中 M max cij ，则 令 cij
1i , j n
n
n
i 1 j 1
' ' z cij xij (M cij xij ) M xij cij xij Mn z ' i 1 j 1 i 1 j 1 i 1 j 1 i 1 j 1
• 找独立0元素，常用的步骤为：
从只有一个0元素的行开始，给该行中的0元素加圈，记作◎ 。
然后划去◎ 所在列的其它0元素，记作Ø ；这表示该列所代 表的任务已指派完，不必再考虑别人了。依次进行到最后一 行。
从只有一个0元素的列开始（画Ø的不计在内），给该列中的0
元素加圈，记作◎；然后划去◎ 所在行的0元素，记作Ø ， 表示此人已有任务，不再为其指派其他任务了。依次进行到 最后一列。

指派问题(含非标准指派问题)

指派问题(含非标准指派问题)

第五章 整数规划§1 整数规划的数学模型及特点要求一部分或全部决策变量必须取整数值得规划问题称为整数规划。

其模型为：Max(或min)z=∑=nj jj xc 1s.t ⎪⎪⎩⎪⎪⎨⎧=≥=≥=≤∑=nj nj i ij ij xx x n j x m i b x a ,,,2,10,2,1),(211若要求决策变量只能取值0或1的整数规划称为0-1型整数线性规划。

§5 指 派 问 题 一． 指派问题的标准形式及数学模型在现实生活中，有各种性质的指派问题。

例如，有若干项工作需要分配给若干人（或部门）来完成；有若干项合同需要选择若干个投标者来承包；有若干班级需要安排在各教室上课等等。

诸如此类的问题，它们的基本要求是在满足特定的指派要求条件下，使指派方案的总体效果最佳。

由于指派问题的多样性，有必要定义指派问题的标准形式。

指派问题的标准形式（以人和事为例）是：有n 个人和n 件事，已知第i 个人作第j 件事的费用为),2,1,(n j i c ij =，要求确定人和事之间的一一对应的指派方案，是完成这n 件事的总费用最少。

为了建立标准指派问题的数学模型，引入2n 个0-1变量：⎩⎨⎧=10ij x这样，问题的数学模型可写成 ∑∑===ni nj ij ijx cz 11min （5.1）s.t ⎪⎪⎪⎩⎪⎪⎪⎨⎧======∑∑==n j i x n i x n j x ij n j ij ni ij ,2,1,1,0,2,11,2,1111 （5.3）其中，（5.1）表示每件事必优且只有一个人去做，（5.2）表示每个人必做且只做一件事。

注：○1 指派问题是产量（i a ）、销量（j b ）相等，且i a =j b =1，i ，j=1,2,…n 的运输中部分或全部取整数 若指派第i 人作第j 件事若不指派第i 人作第j 事i ，j=1,2,…n（5.2）（5.4）问题。

○2 有时也称ijc 为第i 个人完成第j 件工作所需的资源数，称之为效率系数（或价值系数）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

指派模型 宋海洲 一：指派问题 设有n个人被分配去做n件工作，规定每
个人只做一件工作，每件工作只由一个人做。已
知第i个人做第j件工作的效率（时间或费用)为 ，并假设 。 ?问：应
如何分配才能使总效率（总时间或总费用）最高？ 引进变量 设 建立模型 分
析 这是线性规划模型； 也是整数规划模型；0-1规划模型； 更是运输模型。 共
有n*n个变量，实际上只需找n个变量为1即可，因此这是高度退化的线性规划
模型。 例1 设有5个人被分配去做5件工作，规定每个人只做一件工作，每件
工作只由一个人做。已知第i个人做第j件工作的费用如下表所示。问：应
如何分配工作才能使总费用最省？ 二：匈牙利法 定义：指派问题的效益矩阵：
效益矩阵的性质 定理1：从效益矩阵C的第k行（或第k列）的每一个元素中
减去一个常数a得到的矩阵C’所表示的指派问题具有相同的最优解。（ C’称
缩减效益矩阵） 定义：如果这些0元素分布在效益矩阵的不同的行和不同的列
上，则称这些0元素为独立的0元素。 定理2：若方阵的一部分元素为0，一部
分元素不为0，则覆盖方阵内所有0元素的最少直线数，等于矩阵中独立的0元
素的最多个数（匈牙利：konig） 积和式 定义： 积和式的性质 按行展开性； 转
置不变性； 换行不变性； 倍法变换增倍性； 单行可加性； Laplace法则。 补
矩阵 定义： 匈牙利法解指派模型算法 第一步：将原指派问题的效益矩阵C进
行变换得矩阵CC，使得CC的各行各列均出现0元素，其方法是： （1）从效益
矩阵C的每行元素减去该行最小元素； （2）在从所得的效益矩阵的每列元素减
去该列最小元素。 第二步：计算CC的补矩阵D,计算D的积和式per(D)。 判断
per(D)是否不等于0，如果per(D)不等于0，转第五步； 如果per(D)等于0，
转第三步。 第三步： （1）在CC中找0元素最少的一排（行或列），选中其中
一个0，记为0，将该0所在的行及列划去。 （2）对上述划去一行及一列的矩
阵，重复（1）的做法。 „„. 一共得到m个0 。(m n) 记下这m个0 所在的
行号i1,i2,„,im及列号j1,j2,„,jm. (则CC所有的0或0必在i1,i2,„,im
行中或在j1,j2,„,jm中） (3)①：在 CC中找出不在i1,i2,„,im行的0，记
下他们的列号r1,r2,„;并将这些列划竖线； ②：在划去竖线的CC中找出不含
0的列的0，记下他们的行号s1,s2,„;并将这些列划横线； 重复① ②，则这
些直线构成覆盖方阵CC内所有零元素的最少直线。 第四步：调整CC ,使之增
加一些0，为此按如下方法进行： （1）在没有直线覆盖的元素中，找出最小元
素x; （2）在未划线的行减去最小元素x； （3）在划线的列加上最小元素x；
得到新的CC，返回第二步。 第五步： （1）在CC中找0元素最少的一排（行
或列），选中其中一个0，记为0，将该0所在的行及列划去。 （2）对上述划去
一行及一列的矩阵，重复（1）的做法。 „„. 一共得到n个0 。 （3）将n
个0 所在位置对应的变量赋“1”，其他变量赋“0”，得到最优解。 例2：用匈
牙利法求解例1 第一步：将原指派问题的效益矩阵C进行变换 第二步：计算
CC的补矩阵D,计算D的积和式per(D)。 第三步： （1）在CC中找0元素最
少的一排（行或列），选中其中一个0，记为0，将该0所在的行及列划去。 （2）
对上述划去一行及一列的矩阵，重复（1）的做法。 „„.。一共得到4个0 。
(4 n=5) 记下这4个0 所在的行号1，2，3，5。 （3）在 CC中找出不在1，
2，3，5行的0(不是0 ）的列号2，并将第2列划竖线，在CC划去竖线后剩下
的0划横线；则这些直线构成覆盖方阵CC内所有零元素的最少直线:（下一页）
第四步：调整CC ,使之增加一些0，为此按如下方法进行： （1）在没有直线覆
盖的元素中，找出最小元素x=1; （2）在未划线的行减去最小元素x； （3）在
划线的列加上最小元素x； 得到新的CC，返回第二步。 返回第二步：计算
CC的补矩阵D,计算D的积和式per(D)=0。再进行第三步得： 返回第四步：
调整CC ,使之增加一些0，为此按如下方法进行： （1）在没有直线覆盖的元素
中，找出最小元素x=1; （2）在未划线的行减去最小元素x； （3）在划线的列
加上最小元素x； 得到新的CC， 返回第二步，此时per(D)~=0,转第五步
得： 三：极大指派问题
模型： 令Cij’=maxCij-Cij,则模型等价为： 四：不平衡指派问题 令
令 模型转化为： * * 工作 人 a b c d e 甲 乙 丙 丁 戊
7 9 8 7 4 5 12 5 3 6 9 7 4 6 7 8 11 6 9 5 11 9 8 6 11