自动控制原理第三章时域分析

自动控制原理经典考试题目整理第三章-第四章第三章时域分析法一、自测题1．线性定常系统的响应曲线仅取决于输入信号的______________和系统的特性，与输入信号施加的时间无关。

2．一阶系统1/（TS+1）的单位阶跃响应为。

3．二阶系统两个重要参数是，系统的输出响应特性完全由这两个参数来描述。

4．二阶系统的主要指标有超调量MP%、调节时间ts和稳态输出C(∞)，其中MP%和ts是系统的指标，C(∞)是系统的指标。

5．在单位斜坡输入信号的作用下，0型系统的稳态误差ess=__________。

6．时域动态指标主要有上升时间、峰值时间、最大超调量和__________。

7．线性系统稳定性是系统__________特性，与系统的__________无关。

8．时域性能指标中所定义的最大超调量Mp的数学表达式是__________。

9．系统输出响应的稳态值与___________之间的偏差称为稳态误差ess。

10．二阶系统的阻尼比ξ在______范围时，响应曲线为非周期过程。

11．在单位斜坡输入信号作用下，Ⅱ型系统的稳态误差ess=______。

12．响应曲线达到超调量的________所需的时间，称为峰值时间tp。

13．在单位斜坡输入信号作用下，I型系统的稳态误差ess=__________。

14．二阶闭环控制系统稳定的充分必要条件是该系统的特征多项式的系数_____________。

15．引入附加零点，可以改善系统的_____________性能。

16．如果增加系统开环传递函数中积分环节的个数，则闭环系统的稳态精度将提高，相对稳定性将________________。

17．为了便于求解和研究控制系统的输出响应，输入信号一般采用__________输入信号。

18．当系统的输入具有突变性质时，可选择阶跃函数为典型输入信号。

（）19．暂态响应是指当时间t趋于无穷大时，系统的输出状态。

（）20．在欠阻尼0＜ζ＜1情况下工作时，若ζ过小，则超调量大。

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t 25.1e 0125.0)t (k -=，试求系统闭环传递函数)s (Φ。

解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 设某高阶系统可用下列一阶微分方程)t (r )t (r )t (c )t (c T +τ=+∙∙近似描述，其中，1)T (0<τ-<。

试求系统的调节时间s t 。

解 设单位阶跃输入ss R 1)(=当初始条件为0时有：1T s 1s )s (R )s (C ++τ= 1Ts T s 1s 11Ts 1s )s (C +τ--=⋅++τ=∴ T/t e T T 1)t (h )t (c -τ--== T )0(h τ=，1)(h =∞，20T T )]0(h )(h [05.0τ-=-∞=∆求 s tT/t s s e TT 1)0(h )]0(h )(h [95.0)t (h -τ--=+-∞= 3T 05.ln0T t s ==∴3-2 一阶系统结构如图所示。

要求单位阶跃输入时调节时间4.0t s ≤s （误差带为5%），稳态 输出为2，试确定参数21k ,k 的值。

解 由结构图写出闭环系统传递函数1k k sk 1k k s k sk k 1s k )s (212211211+=+=+=Φ闭环增益2k 1k 2==Φ， 得：5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==，得：15k 1≥。

3-4 在许多化学过程中，反应槽内的温度要保持恒定， 下图（a ）和（b ）分别为开环和闭环温度控制系统结构图，两种系统正常的K 值为1。

解 （1）对（a ）系统： 1s 1011s 10K )s (G a +=+=， 时间常数 10T =632.0)T (h = （a ）系统达到稳态温度值的63.2%需要10秒；对（b ）系统：1s 10110101100101s 10100)s (b+=+=Φ， 时间常数 10110T = 632.0)T (h = （b ）系统达到稳态温度值的63.2%需要0.099秒。

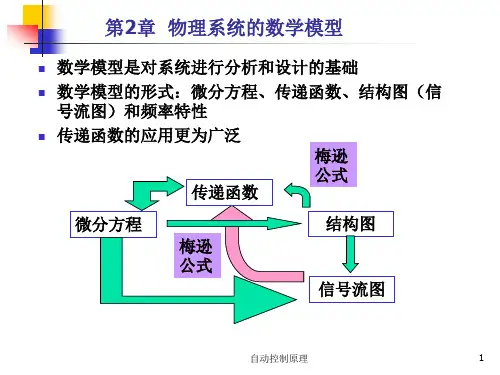
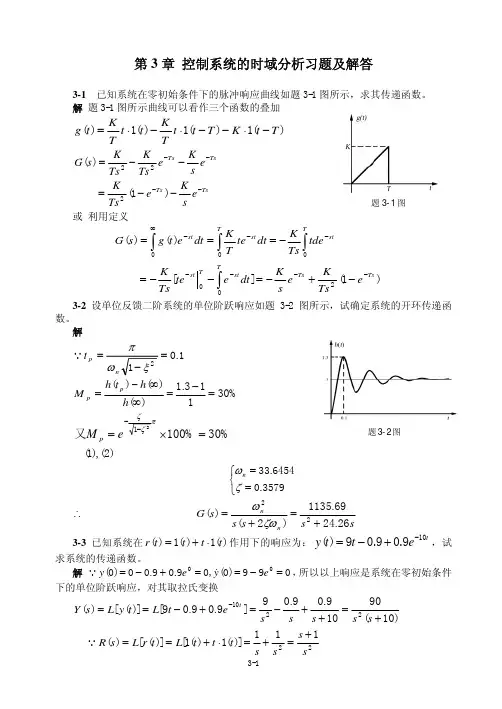
第3章　自动控制系统的时域分析1．设单位反馈系统的开环传递函数分别为试确定使闭环系统稳定的开环增益K的数值范围（注意，K≠K*）。

解：（1）根据系统的开环传递函数可得闭环系统的特征方程为利用劳斯稳定判据来判定系统的稳定性，列出劳斯表如下所示：表3-1故使闭环系统稳定的增益K*的范围为故使闭环系统稳定的开环增益K的数值范围：（2）根据系统的开环传递函数可得系统的特征方程为利用劳斯稳定判据来判定系统的稳定性，列出劳斯表如下所示：表3-2欲使闭环系统稳定的增益K*的范围为故使闭环系统稳定的开环增益K的数值范围：K不存在。

2．给定典型二阶系统的设计指标：超调量σ％≤5％，调节时间，峰值时间试确定系统极点配置的区域，以获得预期的响应特性。

解：依题意综合以上条件可画出满足要求的特征根区域如图3-1中阴影部分所示。

图3-13．已知系统特征方程式如下，试求系统在s 右半平面的根数及虚根值。

解：（1）列出劳斯表如下所示：表3-3由于表中第一列元素的符号有两次改变，故系统在s 右半平面的根数为2，无虚根。

（2）列出劳斯表如下：表3-4由于表中第一列元素的符号有两次改变，故系统在s右半平面的根数为2，无虚根。

MATLAB 文本及仿真结果如下：MATLAB 程序：exe307.m系统的特征根为：4．仅靠调整参数无法稳定的系统，称为结构不稳定系统。

图3-2为液位控制系统结构图。

试判断该系统是否属于结构不稳定系统？若是，提出消除结构不稳的有效措施。

图3-2 液位控制系统结构图解：令，则闭环特征方程为由稳定性必要条件知，不论如何改变T m 和K 均不能使系统稳定，故该系统属结构不稳定系统。

可考虑采用如下两种措施：（1）用反馈K H 包围有积分的环节，如图3-3（a ）和（b ）所示。

①若采用图3-3（a ）方案，则闭环特征方程变为图3-3用反馈包围有积分的环节由赫尔维茨或劳斯稳定判据知，适当选择参数T m ，K ，K H 满足不等式：可使闭环系统稳定。

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解 Φ()()./(.)s L k t s ==+00125125 3-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ••+=+()()()()τ近似描述，其中，1)(0<-<τT 。

试证系统的动态性能指标为 T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=τln 693.0t T r =22. T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解 设单位阶跃输入ss R 1)(= 当初始条件为0时有：11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 当 t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; Tt TT d-⎪⎭⎫ ⎝⎛-=-τln 2ln ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求t r （即)(t c 从1.0到9.0所需时间)当 Tt eTT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt eTT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s eTT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [ln TT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。