氘光谱实验报告

氢氘灯光谱实验报告【实验目的】1.了解平面光栅单色仪的结构与使用方法。

2.验证氢同位素的存在。

用光栅光谱仪测量氢、氘原子光谱巴耳末线系的前四对谱线波长（4100～6500A左右），计算氢氘里德伯常数。

M M ,计算质子与电子的质量比。

3.通过实验，计算氢和氘的原子核质量比/D H【实验原理】1.氢、氘原子光谱氢原子光谱是最简单、最典型的原子光谱。

用电激发氢放电管（氢灯）中的稀薄氢气（压力在102 Pa左右），可得到线状氢原子光谱。

瑞士物理学家巴尔未根据实验结果给出氢原子光谱在可见光区域的经验公式=式中为氢原子谱线在真空中的波长，＝364.57 nm 是一经验常数；n取3,4,5等整数。

若用波数表示，则变为==()式中称为氢的里德伯常数。

根据玻尔理论，对氢和类氢原子的里德伯常数的计算，得=式中M为原子核质量，m为电子质量，e为电子电荷，c 为光速，h 为普朗克常数，为真空介电常数，Z为原子序数。

当时，可得出相当于原子核不动时的里德伯常数（普适的里德伯常数）所以对于氢，有这里是氢原子核的质量。

由此可知，通过实验测得氢的巴尔末线系的前几条谱线的波长，可求得氢的里德伯常数。

里德伯常数是重要的基本物理常数之一，对它的精密测量在科学上有重要意义，目前它的推荐值为=10973731.568549(83)谱线符号波长(nm)658.280486.133434.047410.174397.007388.906383.540379.791377.063375.015值得注意的是，计算和时，应该用氢谱线在真空中的波长，而实验是在空气中进行的，所以应将空气中的波长转换成真空中的波长。

即真空=空气＋，氢巴尔末线系前6 条谱线的修正值如表所示。

氢谱线0.181 0.136 0.121 0.116 0.112 0.1102.关于/同一元素的不同同位素且有不同的核质量和电荷分布，由此引起原子光谱波长的微小差别称为“同位素位移”。

实验氢-氘原子光谱原子光谱的测定与分析，为量子理论的建立提供了坚实的实验基础。

1885年巴尔末（J. J. Balmer ）总结出了氢光谱线的经验公式。

1913年玻尔（N. Bohr ），1925年，海森伯（W.Heisenberg ）建立起他们的理论都是建筑在原子光谱的测量基础之上的。

现在，无论在工业生产部门还是在科学研究领域，原子光谱的观察、测定和分析都是研究原子结构、物质分析的重要方法之一。

在物理学、化学化工、材料、生命科学领域内有广泛的实际应用。

一 实验目的1．掌握WPG-100型平面光栅摄谱仪的工作原理和使用方法，学习摄谱、识谱和谱线测量等光谱研究的基本技术。

2．通过所测得的氢（氘）原子光谱在可见和近紫外区的波长（误差小于0.5Å），验证巴耳末公式并准确测出氢（氘）的里德伯常数。

3．测量氢、氘同位素位移，求出质子与电子的质量比。

二 实验原理1．原子的激发与辐射原子内部的不同能量状态称为能级。

处于基态的原子可以吸收能量而跃迁到较高的能量状态，这个过程称为原子的激发。

原子也可以从较高的能级退到较低的能级或基态而放出能量，如果放出的能量取辐射形式，那么放出的能量就成为一个光子的能量hv ，这个过程称为原子的辐射。

要使原子发光必须先将它激发，原子激发的方式通常分为碰撞激发和光激发两种。

具有一定能量的电子、原子、分子与某原子相碰撞而使后者激发称为碰撞激发；原子吸收一个光子引起的激发称为光激发，即光的吸收过程。

本实验采用碰撞激发，它又分为热激发和电场引起的碰撞激发两种形式，前者指在高温下各原子有较大的运动速度，相互碰撞而产生激发，本实验的铁光谱就是这种方式产生的。

电场引起的碰撞激发是带电粒子在电场作用下加速运动，与原子发生非弹性碰撞使原子激发，氢（氘）光谱就是采用这种方式产生的。

2．氢原子光谱的实验规律早在原子理论建立以前人们就积累了有关原子光谱的大量实验数据，发现氢原子光谱可用一个普通的公式表示，即⎪⎭⎫ ⎝⎛-=2211~n m R v （1）其中：m 取1、2、3、4、5等正整数，每一个m 值对应一个光谱线系，如当m=2时便得到谱线在可见光和近紫外区的巴耳末线系；n 取m+1、m+2、m+3、…等正整数，每一个n 值对应一条谱线；R 称为里德伯常数。

实验六 原子光谱实验—氢氘光谱的测量一、 实验目的（1）熟悉光栅光谱仪的基本原理，了解它的性能和使用方法。

（2）熟悉测量氢-氘和其他原子光谱的方法。

（3）计算氢和氘原子核的质量比。

（4）了解并观察钠、汞原子的主要光谱线。

二、 实验原理（1） 测量公式的导出：根据玻尔（Bohr ）原子理论，一个电子绕正电荷为Ze 、质量为M z 的原子核作圆周运动时，其能量是量子化的，可表示为2Z 22220242n1R hcZ n 1h )4(Z e 2E -=πεμπ-= （6-0） 其中ZZ M m mM +=μ 为核与电子的折合质量，ZZ 32042Z Z 32042Z M m 11R M m 11c h )4(me 2M m M c h )4(me 2R +=+πεπ=+πεπ=∞ 称为里德堡（Rydberg ）常数，ε0为真空介电常数，m 为电子质量，h 和c 分别为普朗克常数和真空中的光速，n=1，2，3…，称为能级量子数，而常数1-32042m 10973731ch )4(me 2R =πεπ=∞ 为忽略原子核运动时（即认为原子核质量M Z 趋于无穷）的里德堡常数。

当原子从高能级向低能级跃迁时，便辐射出光子，并满足能量守恒：)m1n 1(hcZ R h 222Z --=ν 其中ν为光子频率，n 为上能级量子数，m 为下能级量子数。

对于氢原子，Z=1，并且对于落在可见区的巴耳末线系m=2（参见图6-0），此时发射出的光谱以波数表示为)n141(Rc1~2H-=ν=λ=νn= 3，4，5，…（6-1）图6-0 氢原子能级图其中R H为氢原子的里德堡常数：HHH32423242HMm11RMmmMch)4(e2ch)4(e2R+=+πεπ=πεμπ=∞（6-2）同理，对于氢的同位素氘，设核的质量为M D，其里德堡常数为DDMm11RR+=∞（6-3）将式（6-3）除以式（6-2），有DHHDMm1Mm1RR++=解出M D/M H，得)1RR(mM1RRMMHDHHDHD--=（6-4）式中M H/m为氢原子核质量与电子质量之比，采用公认值1836.5。

专题实验1 光谱的测量与分析1.1 氢（氘）原子光谱原子光谱是建立量子理论的实验基础。

1885年，巴尔末（J. J. Balmer ）根据已有的观测结果，提出氢光谱线的经验公式。

波尔（N. Bohr ）1913年2月看到这一公式，3月6日就建立了氢原子理论；海森堡（W. Heisenberg ）在1925年提出量子力学理论也是基于原子光谱的实验成就；光谱的精细结构使人们认识到核外电子的运动状态除了存在主能级量子化以外，还有亚能级量子化。

1932年，尤里（H. C. Urey ）将3 liter 液态氢在低压下缓慢蒸发至1 ml 后，注入放电管，拍摄其巴尔末线系光谱，发现在普通氢（氕）每条谱线的短波侧都出现一条弱的伴线，从而证实了氘的存在。

这是原子核质量差异导致里德伯常数发生变化的结果，称为同位素移位。

对于重核，同位素移位并不明显，但是中子数不同会引起核自旋发生改变，光谱结构还是会复杂化，这就是所谓的超精细结构。

今天，原子光谱仍然是研究原子结构的重要方法。

一、实验目的（1）了解光栅光谱仪等常见光谱分析仪器的原理和使用方法； （2）通过测量巴尔末线系的谱线波长，计算氘的里德伯常数。

二、实验原理原子虽然是元素的最小单元，但还具有复杂的核式内部结构，核外是绕核运动的电子。

α粒子散射实验肯定了原子的核式结构，而对核外结构的认识则是从光谱研究开始的。

光谱记录了电磁辐射随波长变化的强度分布，是研究原子结构的重要手段。

通过测量原子发光光谱中各谱线的波长，可以推算出原子的能级结构，从而得到有关原子微观结构的信息。

光谱主要指发射光谱或吸收光谱。

发射光谱是由发光体直接产生的光谱，例如，由炽热的固体、液体和高压气体发光形成的连续光谱和由稀薄气体或者金属蒸汽发光形成的明线光谱都属于发射光谱。

吸收光谱则是连续光谱中某些波长的光被物质吸收后产生的光谱。

吸收光谱中的每条暗线都与物质的特征谱线相对应。

在所有的元素中，氢的原子结构最简单，从氢原子明线光谱理解原子的核外结构也最直观。

氢氘原子光谱实验报告氢氘原子光谱实验报告引言：光谱实验是物理学和化学学科中一项重要的实验技术，通过观察和分析物质发射、吸收光的特性，可以揭示物质的组成、结构以及性质等信息。

本次实验旨在通过研究氢氘原子的光谱特性，深入了解原子结构和能级跃迁的规律。

实验方法：实验采用了经典的光谱仪装置，包括光源、光栅、光谱仪和探测器等。

首先，我们将氢氘气体注入光谱仪中，利用光源激发氢氘原子，使其发射特定波长的光。

然后，通过光栅的衍射作用，将光分散成不同波长的光谱线。

最后，使用探测器记录光谱线的强度和位置。

实验结果：在实验过程中，我们观察到了氢氘原子发射光谱的多个谱线。

根据经验公式和已知的光谱线数据，我们可以推导出氢氘原子的能级结构。

在可见光区域，我们观察到了红、黄、绿、蓝等不同颜色的谱线。

这些谱线对应着不同的能级跃迁，从而揭示了氢氘原子内部电子的运动规律。

讨论：通过对氢氘原子光谱的研究，我们可以得到一些有趣的结论。

首先，我们发现氢氘原子的能级结构与氢原子类似，但存在一些微小的差异。

这是由于氘原子的质量稍大，从而导致了能级的微小变化。

其次，我们发现氢氘原子的光谱线相对较宽，这与氘原子的自旋和核自旋耦合有关。

这种耦合导致了能级的分裂，从而使得光谱线变宽。

此外，我们还观察到了氢氘原子的吸收光谱。

当我们通过光源照射氢氘原子时，一部分光被吸收，导致光谱线的减弱或消失。

通过分析吸收光谱，我们可以得到氢氘原子在不同波长下的吸收截面，从而研究原子与光的相互作用。

结论：通过对氢氘原子光谱的实验研究，我们深入了解了原子的能级结构和能级跃迁的规律。

同时，我们也发现了氢氘原子与光的相互作用的一些特性。

这些研究成果对于理解原子结构、光谱分析以及相关应用具有重要意义。

总结：光谱实验是一项重要的实验技术，通过观察和分析物质发射、吸收光的特性，可以揭示物质的组成、结构以及性质等信息。

本次实验通过研究氢氘原子的光谱特性，深入了解了原子结构和能级跃迁的规律。

氢（氘）原子光谱实验报告1、实验目的1.熟悉实实验仪器的用法。

2.求里德伯常数。

2、实验原理原子光谱是线光谱，光谱的排列的规律不同，反映出原子结构的不同，研究原子结构的基本方法之一是进行光谱分析。

3、实验内容1.用汞灯对光栅光谱仪进行定标，保存谱线。

2.测量氢（氘）光谱的谱线，通过“寻峰”求出巴耳末系前 3~4 条谱线的波长。

保存谱图，计算各谱线的里德伯常数RH（RD），然后求平均值。

3.计算普适里德伯常数 R∞，并与推荐值比较，求相对误差。

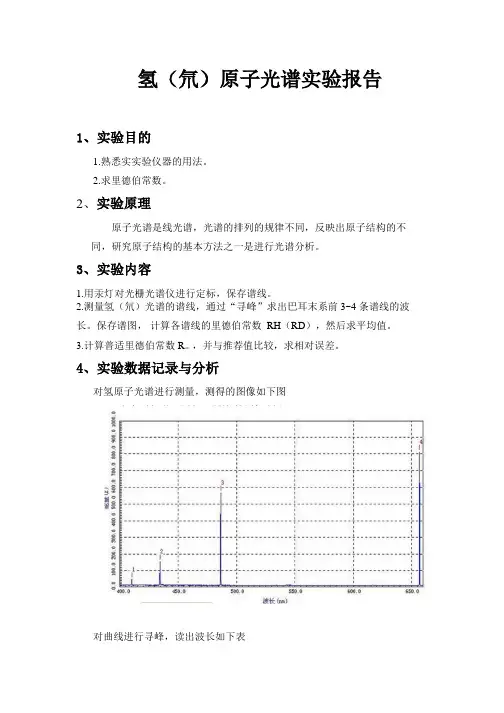
4、实验数据记录与分析对氢原子光谱进行测量，测得的图像如下图对曲线进行寻峰，读出波长如下表谱线HδHγHβHα光谱波长/nm 410.4 434.6 486.5 656.8 谱线相对能量47.1 457.3 566.1 812.2利用波长的修正值计算真空中氢原子的波长：谱线HδHγHβHα光谱波长/nm 410.4 434.6 486.5 656.8 △ι(nm) 0.116 0.121 0.136 0.181 真空中谱波长410.5 434.7 486.6 657.0 /nm可以计算出里德伯常数谱线HδHγHβHα410.5 434.7 486.6 657.0 真空中谱波长/nmn 6 5 4 6 里德伯常数1.096 1.095 1.096 1.096/107m-1经过计算得R=1.00054*1.096*107m-1=1.096* 107m-1而R推荐值是R∞＝10973731.568549(83)/m，故相对误差为=（1.097-1.096）/1.097=0.06%4.实验结果讨论与心得1实验中由于氢光源的寿命有限，注意在不用时关闭灯源。

2实验过程中突然谱线很乱，怎么调节都调节不行，可能原因是灯源出现问题，换一个氢灯，实验恢复正常。

3实验中噪音可能对实验产生一定的误差。

4.任何实测谱线都有一定的宽度，主要是由以下原因造成的：1) 由海森伯不确定原理，∆E∆t>h，由于测量时间是有限的，故测得的能级有一定展宽。

实验四 氢（氘）原子光谱原子光谱的观测，为量子理论的建立提供了坚实的实验基础。

光谱线的超精细结构曾被认为是不同的同位素发射的谱线。

但现在认为，超精细结构是单一的同位素的光谱线由原子核的自旋而引起的复杂结构，而不同的同位素的光谱差别则称为“同位素移位”。

氢原子同位素移位是可以准确算出的。

1932年尤里（H.C.Urey ）等人用3m 凹面衍射光栅拍摄巴耳末（J.J.Balmer ）线系的光谱，发现在αH 、βH 、γH 和δH 的短波一侧均有一条弱的伴线，测量这些伴线的波长并在实验误差范围内与计算结果比较，从而证实了重氢H 2（氘）的存在。

一、实验目的 （1） 通过测量氢和氘谱线的波长，计算氢与氘的原子核的质量比H D M M /以及里德伯（J.R.Rydberg ）常量)(D H R R 。

（2）加深对氢光谱规律和同位素位移的认识，理解精确测量的重要意义。

（3）掌握WGD-8A 组合式光栅光谱仪的原理和使用方法，并学会用光谱进行分析。

二、 实验原理原子光谱是线光谱，光谱排列的规律不同，反映出原子结构的不同，研究原子结构的基本方法之一是进行光谱分析。

氢原子光谱由许多谱线组成，在可见光区的谱线系是巴耳末系，其代表线为αH 、βH 、γH 、δH …，这些谱线的间隔和强度都向着短波方向递减，并满足下列规律：422-=n n B λ （1） 式中n nm B ,56.364=为正整数。

当6,5,4,3=n 时，上式分别给出αH 、βH 、γH 、δH 各谱线波长，（1）式是瑞士物理学家巴耳末根据实验结果首先总结出来的，故称为巴耳末公式。

若用波数λν/1~=表示谱线，则（1-1）式改写为：⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=22221211214~n R n B H ν（2）式中B R H /4=为里德伯常量，n 取整数。

根据玻尔（Bohr N .）理论对氢原子和类氢原子的里得伯常量计算（诸圣麟，1979），有：Mm R R e /1+=∞ （3） 式中e m 为电子质量，M 为原子核质量。

氢氘原子光谱实验报告氢氘原子光谱实验报告引言：光谱实验是物理学中一项重要的实验，通过对物质发射或吸收光的特性进行研究，可以得到物质的结构和性质信息。

本次实验旨在研究氢氘原子的光谱特性，探究其能级结构和能级跃迁的规律。

实验方法：实验采用了氢氘原子光谱仪，该仪器能够将光分解成不同波长的光谱，并通过测量光的强度，得到不同波长光的发射或吸收情况。

实验过程中，我们使用了氢氘原子的气体样品，将其放入光谱仪中，并通过调节仪器的参数，如入射光强度、波长范围等，获取所需的光谱数据。

实验结果：在实验中，我们观察到了氢氘原子在可见光区域的发射光谱。

通过对光谱图的分析，我们发现了一系列明显的发射峰，这些峰代表了氢氘原子的不同能级跃迁。

根据经验公式和理论计算，我们得到了这些能级跃迁对应的波长和能量差。

讨论：根据实验结果，我们可以得出氢氘原子的能级结构和能级跃迁规律。

氢氘原子的能级结构由一系列离散的能级组成，这些能级之间的跃迁会导致特定波长的光的发射或吸收。

这与玻尔模型和量子力学理论的预测一致。

此外，我们还观察到了氢氘原子的光谱中存在一些弱的发射峰，这些峰可能来自于其他能级跃迁或者与氢氘原子相互作用导致的能级变化。

这些弱的发射峰的研究对于理解氢氘原子的复杂行为和相互作用具有重要意义。

结论：通过氢氘原子光谱实验，我们成功地研究了氢氘原子的能级结构和能级跃迁规律。

实验结果与理论预测相符，验证了量子力学理论在描述原子光谱中的有效性。

此外，我们还发现了一些未知的发射峰，这为进一步研究氢氘原子的行为提供了新的线索。

总结：光谱实验是一种重要的手段，可以揭示物质的结构和性质。

本次氢氘原子光谱实验通过观察氢氘原子发射光谱，研究了其能级结构和能级跃迁规律。

实验结果与理论预测相符，验证了量子力学理论的有效性。

未来的研究可以进一步探究氢氘原子的复杂行为和相互作用，并应用于其他领域的研究和应用中。

实验目的：本实验旨在通过氢氘光谱的测量，研究氢和氘的光谱特性，探究原子光谱的发射线和吸收线规律。

实验装置：氢氘光谱仪：包括氢氘光源、光栅、光电倍增管等。

实验台：用于支撑和安装实验装置。

实验步骤：准备工作：确保实验装置正常工作，调整光栅的角度和位置，保证光线能够正常通过。

放置氢氘光源：将氢氘光源安装在适当位置，使得光线能够经过光栅。

调整光栅：通过调整光栅的角度和位置，使得光线经过光栅后能够产生衍射现象，并形成光谱。

测量光谱：使用光电倍增管接收经过光栅衍射的光线，并将光信号转换成电信号。

使用电子仪器记录和测量各个波长的光谱强度。

数据处理：根据实验测量的数据，绘制氢氘光谱图谱，并分析不同波长对应的光谱线。

实验结果：根据实验测量得到的数据，绘制了氢氘光谱图谱。

光谱图谱上显示了氢氘在不同波长处的发射线和吸收线。

通过对光谱的分析，可以观察到不同电子能级跃迁引起的特定波长的发射或吸收现象。

讨论与结论：通过本实验，我们观察到了氢氘的光谱特性，并绘制了光谱图谱。

根据光谱图谱分析，我们可以得出氢和氘的光谱线的规律和特点。

这些光谱线的存在与原子的能级结构和电子跃迁有关，进一步验证了原子光谱的发射和吸收现象。

实验中可能遇到的误差和改进方法：光栅调整误差：光栅的角度和位置调整可能存在误差，影响光谱的质量和精度。

可以通过精确的光栅调整和校准来改进。

光电倍增管的噪音和漂移：光电倍增管可能受到噪音和漂移的干扰，影响测量结果的准确性。

可以使用更高质量的光电倍增管或进行信号滤波和校正来改进。

总结：通过本实验，我们成功测量了氢氘的光谱特性，观察到了发射线和吸收线的存在，并对其进行了分析。

实验结果有助于进一步了解原子光谱的特点和原子结构的研究。

此实验对于深入理解光谱学和原子物理学有重要意义。

氢（氘）原子光谱光谱线系的规律与原子结构有内在的联系，因此，原子光谱是研究原子结构的一种重要方法。

1885年巴尔末总结了人们对氢光谱的测量结果，发现了氢光谱的规律，提出了著名的巴尔末公式，氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础。

1932年尤里根据里德伯常数随原子核质量不同而变化的规律，对重氢赖曼线系进行摄谱分析，发现氢的同位素——氘的存在。

通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一，成为检验原理论可靠性的标准和测量其它基本物理常数的依据。

【实验目的】1． 熟悉光栅光谱仪的性能与用法。

2． 用光栅光谱仪测量氢（氘）原子光谱巴尔末县系的波长，求里德伯常数。

【实验原理】原子光谱是线光谱，光谱排列的规律不同，反映出原子结构的不同，研究原子结构的基本方法之一是进行光谱分析。

氢（氘）原子光谱是最简单、最典型的原子光谱。

瑞士物理学家巴尔末根据实验结果给出氢原子光谱在可见光区域的经验公式为：422:-=n n B Hλ式中H λ为氢原子谱线在真空中的波长，nm B 56.364=， 5,4,3=n 。

若用波数λν1~=表示谱线，则（？-1）式可改写为： ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=222222121121441~n R n B n n B H ν 式中H R 为里德伯常数。

根据波尔理论，可得出氢和类氢原子的里德伯常数为：()()Mm 1R M m 1mc h 4z e 2ch 4z e 2R 32044320442z +=+⋅==∞πεππεμπ 其中：M 为原子核质量，m 为电子质量，e 为电子电荷，C 为光速，h 为普朗克常数，0ε为真空介电常数，z 为原子序数。

当∞→M 时，可得里德伯常数为：()ch z me R 32044242πεπ=∞里德伯常数∞R 是重要的基本物理常数之一，对它的精密测量在科学上有重要意义，它的公认值为：1m 568549.10973731R -∞=。

氢与氘原子光谱实验报告一、实验背景和目的原子光谱是研究原子结构的重要工具，而氢与氘原子光谱实验则是探究氢和氘这两种轻元素原子结构及光谱特性的重要手段。

本实验旨在通过观察氢与氘原子光谱，学习原子光谱的基本原理，理解原子能级的跃迁原理，并比较不同原子光谱的差异。

二、实验原理与方法原子光谱的产生原理是基于原子能级的跃迁。

当原子受到外部能量激发时，原子中的电子会从低能级跃迁到高能级，当电子从高能级返回到低能级时，会释放出一定波长的光。

通过测定这些光的波长，我们可以确定原子的能级结构。

本实验采用激光激发原子光谱法。

具体方法是将氢或氘原子置于一个电场中，通过激光束照射，当激光能量与原子能级差相匹配时，原子会被激发并放射出光子。

通过测量这些光子的波长，我们可以得到原子的光谱。

三、操作过程准备实验器材：氢或氘原子、激光器、单色仪、光电倍增管、电源等。

将氢或氘原子置于电场中，调整激光器的波长，使激光能量与原子能级差相匹配。

打开激光器，照射氢或氘原子，并调整激光器的功率，使原子产生明显的光谱。

通过单色仪测量光子的波长，并记录数据。

重复步骤2-4多次，以获取足够的数据进行分析。

四、实验数据与分析通过实验，我们得到了氢与氘原子光谱的数据。

通过对比氢与氘原子的光谱，我们可以发现它们在波长和强度上存在差异。

这表明不同元素的原子具有不同的能级结构和光谱特性。

通过分析数据，我们可以使用Rydberg公式等理论公式来计算原子的能级和光谱波长。

通过比较理论计算与实验数据的差异，我们可以评估实验的准确性。

同时，我们还可以讨论影响实验结果的可能参数，例如激光功率、电场强度等。

五、误差来源和计算在本实验中，可能存在以下误差来源：激光器波长稳定性：如果激光器波长不稳定，将导致激发的原子数目减少，影响实验结果。

可以通过采用稳频激光器来减小此误差。

电场强度：电场强度不均匀可能导致原子激发效率不一致，影响光谱强度。

可以通过优化电场分布来减小此误差。

氘原子光谱姓名：王静 学号：PB07210457一、实验目的：本实验以氘原子光谱为研究对象，研究获得同位素光谱的实验方法、分析方法及其在微观测量中的应用。

二、实验原理：根据玻尔理论，原子的能量是量子化的，即具有分立的能级。

当电子从高能级跃迁到低能级时，原子释放出能量，并以电磁波形式辐射。

氢和类氢原子的巴耳末线系对应光谱线波数为)121()1()4(222320242nm m c h Z e m Zee -+=πεπσ ————（1） 其中mZ 为原子核质量，me 为电子质量，e 为电子电荷，h 为普朗克常数，ε0为真空介电常数，c 为光速，Z 为原子序数。

因此类氢原子的里德伯常数可写成)1(1)4(2320242Zee Z m m ch Z e m R +⋅=πεπ ————（2） 若∞→Z m ，即假定原子核不动，则有c h Z e m R e 320242)4(2πεπ=∞ ————（3） 因此)1(ZeZ m m R R +=∞————（4） 由此可见，RZ 随原子核质量mZ 变化，对于不同的元素或同一元素的不同同位素R Z 值不同。

mZ 对RZ 影像很小，因此氢和它的同位素的相应波数很接近，在光谱上形成很难分辨的双线或多线。

设氢和氘的里德伯常数分别为RH 和RD ，氢、氘光谱线的波数σH 、σD 分别为⎪⎭⎫ ⎝⎛-=22121n R H H σ n=3,4,5… ————（5） ⎪⎭⎫ ⎝⎛-=22121n R D Dσ n=3,4,5… ————（6）氢和氘光谱相应的波长差为)1()1()1(DH H D H H H D H D H R R-=-=-=-=∆λσσλλλλλλλ———— （7）因此，通过实验测得氢和氘的巴耳末线系的前几条谱线的谱长及其波长差，可求得氢与氘的里德伯常数RH 、RD 。

根据式（4）有⎪⎪⎭⎫⎝⎛+=∞H e H m m R R 1/————（8）⎪⎪⎭⎫ ⎝⎛+=∞D e D m m R R 1/————（9） 其中mH 和mD 分别为氢和氘原子核的质量。

氢氘原子光谱实验报告氢氘原子光谱实验报告一、引言光谱实验是研究光的波动和粒子性质的重要手段之一，对于深入了解原子结构和化学反应机理至关重要。

氢和氘原子光谱实验是一项经典的实验，通过研究氢和氘原子发射的光谱线，可以揭示出原子的结构和特性，为量子力学提供了有力支持。

本实验旨在通过观察氢氘原子的光谱现象，得出对应原子能级的信息，进一步深入研究原子的性质。

二、实验方法1. 实验仪器：使用光谱仪和不同波长的光源，例如氢氘灯。

2. 实验过程：a. 将氢氘灯与光谱仪连接，调整光谱仪，确保其工作在最佳状态。

b. 通过调节仪器，使光源尽可能均匀地照射到光谱仪上。

c. 观察并记录下每个波长下的光谱现象，特别注意氢氘原子产生的谱线。

三、实验结果通过实验观察和记录，我们得到了如下实验结果：1. 在可见光波段，氢和氘原子表现出不同的光谱线，具有各自特征的谱线分布。

2. 氢原子的光谱线位于可见光谱中的红、绿、蓝三个区域，其中最明显的是红色和蓝色的谱线。

3. 氘原子的光谱线与氢原子相比，在波长上发生了较大的位移，整体往长波方向移动。

四、数据分析与讨论1. 通过对实验结果的观察，我们可以得出结论，不同的原子具有不同的光谱线，这表明了原子的结构和能级分布与光谱现象的关系。

2. 氢原子的光谱线表现出离散特性，这与波尔模型相符，即氢原子的电子只存在于特定的能级上，能级之间的跃迁会导致相应波长的光谱线出现。

而氘原子的光谱线位移说明了核子质量的影响。

3. 光谱实验的结果与理论模型相吻合，这进一步验证了波尔模型的正确性，并为原子结构研究提供了更加深入的理论支持。

五、实验结论通过本次氢氘原子光谱实验，我们得出了以下结论：1. 氢原子和氘原子在可见光谱中具有各自特征的光谱线分布。

2. 氢原子的光谱线呈现出离散特性，与波尔模型相符。

3. 氘原子的光谱线位移较大，与核子质量的差异有关。

4. 光谱实验结果与理论模型相吻合，为原子结构研究提供了有效支持。

氢氘光谱实验报告氢氘光谱实验报告引言光谱学是研究物质与电磁辐射相互作用的科学。

氢氘光谱实验是光谱学中的重要实验之一，通过观察氢氘原子在不同波长的光照射下的发射和吸收现象，可以了解原子内部结构和能级分布的信息。

本实验旨在通过测量氢氘原子在可见光范围内的光谱，探索其能级结构和能级间的跃迁。

实验装置和原理实验装置主要包括氢氘光源、光栅、光电倍增管和光谱仪。

当氢氘原子受到激发后，会发射出特定波长的光线，形成光谱线。

光栅的作用是将光线分散成不同波长的光谱，而光电倍增管则用于检测和放大光信号。

实验步骤1. 将氢氘光源接通电源，使其开始发光。

2. 调节光栅的角度，使得光线能够通过光栅并被分散。

3. 将光电倍增管与光栅对准，使得光线能够被光电倍增管接收。

4. 使用光谱仪观察和记录光电倍增管输出的光谱图像。

实验结果通过实验，我们观察到了氢氘原子在可见光范围内的光谱线。

根据光谱图像，我们可以看到一系列明亮的谱线，每条谱线对应着氢氘原子的一个能级跃迁。

讨论与分析1. 能级结构根据实验结果，我们可以推测氢氘原子的能级结构。

氢氘原子的能级由电子的能量决定，而电子的能量与其所处的能级有关。

每条光谱线对应着一个能级跃迁，从高能级到低能级的跃迁会释放出特定波长的光线。

通过测量光谱线的波长，我们可以计算出氢氘原子不同能级之间的能量差。

2. 能级间距氢氘原子的能级间距可以通过测量光谱线的波长来计算。

根据波长和光的速度，我们可以使用公式λ = c / ν计算出光的频率，进而计算出能级间距。

通过实验数据的分析，我们可以得到氢氘原子能级间距的近似数值。

3. 能级跃迁不同的能级跃迁对应着不同的光谱线。

通过观察光谱图像，我们可以推测氢氘原子的能级跃迁规律。

根据量子力学理论，我们知道能级跃迁是由电子的能量变化引起的。

因此，通过研究光谱线的强度和位置，我们可以进一步了解氢氘原子内部电子的能级分布和跃迁过程。

结论通过氢氘光谱实验，我们成功地观察到了氢氘原子在可见光范围内的光谱线。

一、实验目的1. 通过氢氘谱实验，了解氢和氘原子的光谱特性，掌握光谱分析的基本方法。

2. 测量氢和氘原子的巴耳末系发射光谱的波长，计算里德伯常数。

3. 掌握WGD-8A型组合式多功能光栅光谱仪的使用方法。

二、实验原理氢原子光谱是量子力学发展的重要基础，通过研究氢原子的光谱，可以了解原子的能级结构和跃迁规律。

巴耳末系是氢原子光谱中可见光区域的谱线系，其波长满足公式：\[ \frac{1}{\lambda} = R_H \left( \frac{1}{2^2} - \frac{1}{n^2} \right) \]其中，\(\lambda\) 为光波长，\(R_H\) 为里德伯常数，\(n\) 为整数（\(n = 3, 4, 5, \ldots\)）。

氘原子是氢的同位素，其原子核质量略大于氢原子核。

因此，氘原子的光谱与氢原子光谱有一定的相似性，但里德伯常数略有差异。

三、实验仪器1. 氢氘灯2. WGD-8A型组合式多功能光栅光谱仪3. 狭缝4. 光栅5. 摄谱仪6. 滤光片7. 望远镜8. 光电倍增管四、实验步骤1. 将氢氘灯安装于光谱仪的光源位置，调整狭缝宽度，使光通过狭缝。

2. 将光栅光谱仪的入射狭缝与狭缝对齐，调整光栅角度，使光谱仪的出射狭缝与光栅垂直。

3. 将滤光片插入光谱仪的光路中，选取适当的波长范围。

4. 将望远镜对准光谱仪的出射狭缝，调整望远镜的焦距，使光谱清晰。

5. 使用光电倍增管记录光谱数据，测量氢和氘原子的巴耳末系发射光谱的波长。

6. 根据测量结果，计算氢和氘原子的里德伯常数。

五、实验结果1. 氢原子的巴耳末系发射光谱波长：- \( \lambda_1 = 656.3 \, \text{nm} \)- \( \lambda_2 = 486.1 \, \text{nm} \)- \( \lambda_3 = 434.0 \, \text{nm} \)- \( \lambda_4 = 410.1 \, \text{nm} \)2. 氘原子的巴耳末系发射光谱波长：- \( \lambda_1 = 656.5 \, \text{nm} \)- \( \lambda_2 = 486.2 \, \text{nm} \)- \( \lambda_3 = 434.1 \, \text{nm} \)- \( \lambda_4 = 410.2 \, \text{nm} \)3. 氢原子的里德伯常数：\( R_H = 1.097 \times 10^7 \, \text{m}^{-1} \)4. 氘原子的里德伯常数：\( R_D = 1.097 \times 10^7 \, \text{m}^{-1} \)六、误差分析1. 光栅光谱仪的分辨率有限，导致测量结果存在一定的误差。

物理仿真实验氢氘光谱拍摄实验报告范本实验目的学习和掌握物理仿真实验中的氢氘光谱拍摄实验，了解氢、氘的原子光谱的产生机理，掌握氢氘原子光谱的基本特征，培养实验操作技能和实验数据分析能力。

实验原理原子光谱原子光谱是指原子在受到外部能量激发后，向外发射光的过程。

根据普朗克和德布罗意的量子理论，能量的传递都是以量子形式进行的，原子从高能级到低能级跃迁的过程中，会释放出能量的多少与跃迁能级的差有关，并且对应这个特定能级差的光子就会被释放出来，其频率和波长与能级差相关。

氢氘光谱的产生机理在氢氘原子中，电子的跃迁可以产生一系列的发射谱线，称为氢氘光谱。

从能级差的大小可以分类为巴尔末系或布吕姆斯特德系。

其中巴尔末系是指跃迁的两个能级至少有一个是基态，而布吕姆斯特德系是指跃迁的两个能级均不是基态。

实验步骤1.打开VirtualLab软件，选择进入“原子物理学”实验；2.选择“原子发光和吸收”实验，进入实验面板；3.将曝光时间调整为5秒，将取样率调整为50，选择“多谱线数目：1”；4.调整初始化状态，在“氢谱线/氘谱线”按钮处选择氢/氘原子，点击“初始化”；5.点击“曝光”按钮，等待实验结束；6.点击“保存谱线数据”按钮，进行数据保存。

实验结果与分析根据实验步骤，我们得到了氢氘原子光谱的数据，并进行分析。

实验结果我们得到了以下氢氘光谱数据：谱线编号波长（nm）能级差（eV）1 656.28 1.892 486.13 3.033 434.05 3.474 410.17 3.89分析与讨论我们观察到，在氢谱线中，波长最长的谱线（谱线1）的波长为656.28nm，相应的能级差为1.89eV，对应着巴尔末系，表示一个电子从第3能级跃迁回第2能级。

其他3个谱线（谱线2-4）是布吕姆斯特德系，表示电子在不同的高能级跃迁到低能级。

在氘谱线中，我们观察到的谱线与氢谱线相比较，波长变短了。

这是因为氘原子具有比氢原子更大的质量，电子围绕氘原子运动的速度比氢原子更慢，所以处于一个较少的能级，等级差也相应变小。

实验五 氢、氘原子光谱实验一、实验目的1．学习使用WGD-8A 型组合式多功能光栅光谱仪测谱的方法。

2．测定氢原子巴尔末系前几条谱线的波长，验证巴尔末公式。

3．测定氢同位素氘谱线位移，计算氢、氘雷德堡常数，计算电子与质子的质量比，计算氢、氘的核质量比。

二、实验原理1672年牛顿证明了白光是由各种色光复合而成的，因而色光在性质上比白光更简单。

1800年赫谢尔发现了红外辐射，1801年李特和沃拉斯顿发现了紫外辐射，1815年夫朗和费发现了太阳光谱中的锐黑线。

随着人们对各种光谱现象的深入研究，逐渐加深了对物质结构的认识，从而进入了原子的世界。

从这个意义上说，现代的量子力学是在光谱学的摇篮里长大的。

值得一提的是，氢光谱的研究成果在原子结构理论的产生过程中起过巨大的作用。

氢原子的光谱是最简单的光谱，它有相互独立的光谱系，其中只有一个线系在可见光区，即巴尔末（Johann Balmer 瑞士的中学教师）线系，其中比较明亮的谱线有四条如图1： 各谱线波长如下；H α ～656.28 nm H β ～486.13 nm H γ ～434.05 nm H δ ～410.18 nm这些谱线的波长的倒数很有规律n=3、4、5，…υ~ 称为波数，R 是雷德堡常数。

以后又继续发现了氢的一系列线系：赖曼（Lgman ）系 远紫外 n=2、3、4…帕邢（Paschen ）系 近红外 n=4、5、6…布拉开（Brackett ）系 红外 n=5、6、7…普芳德（Pfund ）系 红外 n=6、7、8…)121(~122nR -==υλ)111(~22nR -=υ)131(~22n R -=υ)141(~22n R -=υ)151(~22nR -=υ这些已知的氢原子光谱，可以用一个普遍的公式表示，就是广义巴尔未公式： m 、n = 1、2、3…n ＞m（1）现在，在普通的实验室里人们观察到的谱线可达到相应于m=6，n=7的水平，在射电天文望远镜的观测中已经接收到相应于m ＝158， n=159的1651兆赫谱线。