带金属销钉的波导带通滤波器的设计
- 格式:pdf
- 大小:442.73 KB
- 文档页数:5

带通滤波器的设计和实现随着科技的不断发展和应用场景的不断拓宽,信号处理在各个领域中扮演着重要的角色。
而滤波器作为信号处理的重要组成部分,其设计和实现对于信号处理的效果起到至关重要的作用。
本文将详细介绍带通滤波器的设计原理和实现方法。
一、带通滤波器的基本概念带通滤波器是一种对信号进行频率选择的滤波器,它能够将某一频率范围内的信号通过,而将其他频率范围内的信号抑制或削弱。
在信号处理中,常常需要对特定频率范围的信号进行提取或滤除,此时带通滤波器的应用便显得尤为重要。
二、带通滤波器的设计原理1. 滤波器的传输函数滤波器的传输函数是描述滤波器输入和输出之间关系的数学表达式。
带通滤波器的传输函数通常采用有理函数形式,例如巴特沃斯、切比雪夫等形式。
2. 频率响应带通滤波器的频率响应描述了滤波器对不同频率信号的处理效果。
通常采用幅度响应和相位响应两个参数来描述频率响应。
3. 滤波器的阶数滤波器的阶数表示滤波器的复杂程度,阶数越高,滤波器的频率选择性越强。
根据实际需求和应用场景,选择合适的滤波器阶数非常重要。
三、带通滤波器的实现方法1. 模拟滤波器的实现模拟滤波器是指基于传统电子电路的滤波器实现方法。
常见的模拟滤波器包括RC滤波器、RL滤波器、LC滤波器等。
模拟滤波器的设计需要考虑电路参数和元器件选择等因素,涉及到模拟电路设计的相关知识。
2. 数字滤波器的实现数字滤波器是指利用数字信号处理技术实现的滤波器。
常见的数字滤波器包括FIR滤波器、IIR滤波器等。
数字滤波器的实现采用离散系统的理论分析和数字信号处理算法的设计,需要掌握相关的数学知识和算法掌握。
四、带通滤波器的应用案例带通滤波器在实际应用中有着广泛的应用场景。
例如,在音频处理中,可以利用带通滤波器实现音乐频谱的提取和信号的降噪;在图像处理中,可以利用带通滤波器进行图像边缘检测和图像增强等处理;在通信系统中,带通滤波器可以用于信号调制和解调等关键环节。
五、总结本文对带通滤波器的设计原理和实现方法进行了详细介绍,并给出了相关的应用案例。
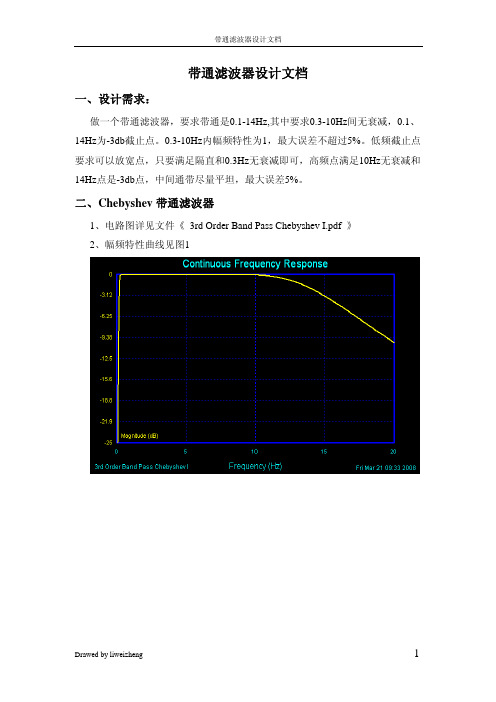
带通滤波器设计文档一、设计需求:做一个带通滤波器,要求带通是0.1-14Hz,其中要求0.3-10Hz间无衰减,0.1、14Hz为-3db截止点。
0.3-10Hz内幅频特性为1,最大误差不超过5%。
低频截止点要求可以放宽点,只要满足隔直和0.3Hz无衰减即可,高频点满足10Hz无衰减和14Hz点是-3db点,中间通带尽量平坦,最大误差5%。
二、Chebyshev带通滤波器1、电路图详见文件《3rd Order Band Pass Chebyshev I.pdf 》2、幅频特性曲线见图1图1 三阶Chebyshev I滤波器幅频特性曲线说明:1)、0.3~10HZ之间满足波动幅度<5%2)、3dB带宽点落在0.19HZ和14.9HZ点3)、具有很好的隔直功能、带通特性4)、需求分析中只对幅频特性做了要求,因而放宽对相频特性的要求5)、电容、电阻值均为理想计算值,未代入实际配置值3、传输函数3、利用低通和高通级联3.1 Butterworth低通滤波器1、电路图详见文件《6th Order Low Pass Butterworth.pdf 》2、幅频特性曲线见图2图2 六阶Butterworth低通滤波器幅频特性曲线说明:1)、0.3~10HZ之间满足波动幅度<5%。
2)、3dB带宽点落在14HZ点。
3)、具有很好的低通特性4)、需求分析中只对幅频特性做了要求,因而放宽对相频特性的要求5)、电容、电阻值均为理想计算值,未代入实际配置值3、传输函数3.2 Butterworth高通滤波器1、电路图详见文件《4th Order High Pass Butterworth.pdf 》2、幅频特性曲线见图3图3 四六阶Butterworth高通滤波器幅频特性曲线说明:1)、0.3~10HZ之间满足波动幅度<5%。
2)、3dB带宽点落在0.1HZ点。
3)、具有很好的高通特性4)、需求分析中只对幅频特性做了要求,因而放宽对相频特性的要求5)、电容、电阻值均为理想计算值,未代入实际配置值3、传输函数。

带通滤波器设计1. 引言在信号处理中,滤波器是一种重要的工具,用于去除或改变信号的特定频率成分。
带通滤波器是一种常用的滤波器,它可以传递一定范围内的频率成分,而抑制其他频率成分。
本文将介绍带通滤波器的基本原理和设计方法。
2. 带通滤波器的原理带通滤波器是一种频率选择性滤波器,它可以传递一定范围内的频率信号,而将其他频率信号抑制。
其基本原理是利用滤波器的频率响应特性,对输入信号进行滤波处理。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联连接而成。
低通滤波器用于抑制高于截止频率的频率成分,而高通滤波器用于抑制低于截止频率的频率成分,从而实现带通滤波效果。
3. 带通滤波器的设计方法带通滤波器的设计通常包括以下几个步骤:在设计带通滤波器之前,需要确定滤波器的一些规格参数,包括中心频率、通带宽度、阻带宽度等。
这些参数决定了滤波器的性能和应用范围。
步骤二:选择滤波器的类型常见的带通滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
根据具体的应用要求和设计指标,选择适合的滤波器类型。
步骤三:计算滤波器的阶数滤波器的阶数决定了滤波器的陡峭程度和相频特性。
根据设计要求和滤波器类型,计算滤波器的阶数。
步骤四:确定滤波器的传输函数根据滤波器的类型和阶数,使用滤波器设计方法计算滤波器的传输函数。
常用的设计方法包括频率折叠法、零极点法等。
根据滤波器的传输函数,采用模拟滤波器的设计方法,设计滤波器的电路结构和参数。
常用的设计方法包括电压法、电流法等。
步骤六:数字滤波器的设计对于数字信号处理系统,需要将模拟滤波器转换为数字滤波器。
常用的设计方法包括脉冲响应法、频率采样法等。
根据系统的采样率和滤波器的性能要求设计数字滤波器。
4. 带通滤波器的应用带通滤波器在信号处理领域有着广泛的应用。
例如,音频处理中常用带通滤波器对音频信号进行频率选择性处理,去除噪声和杂音。
图像处理中常用带通滤波器对图像进行频率域滤波,增强或抑制特定频率成分,实现图像增强、去噪等功能。

带通滤波器毕业设计带通滤波器毕业设计引言:在现代电子技术的发展中,滤波器是一种非常重要的电子元件。
它可以对信号进行处理,去除杂波和干扰,从而提高信号的质量。
而在电子工程师的毕业设计中,设计一个带通滤波器是一项常见的任务。
本文将介绍带通滤波器的原理、设计方法以及实际应用。
一、带通滤波器的原理带通滤波器是一种能够通过一定频率范围内的信号,而削弱其他频率信号的电子元件。
其原理是利用电容、电感和电阻等元件的组合,形成一个能够选择性地通过一定频率范围内信号的电路。
带通滤波器可以分为主动滤波器和被动滤波器两种类型。
主动滤波器采用了运算放大器等主动元件,能够提供放大和反馈功能,从而实现更精确的频率选择。
被动滤波器则只采用了电容、电感和电阻等被动元件,其频率响应相对较简单。
二、带通滤波器的设计方法1. 确定设计要求:在设计带通滤波器时,首先需要明确设计要求,包括通带范围、阻带范围、通带衰减和阻带衰减等参数。
这些参数将决定滤波器的性能和适用场景。
2. 选择滤波器类型:根据设计要求,选择适合的滤波器类型。
常见的带通滤波器类型有Butterworth滤波器、Chebyshev滤波器和Elliptic滤波器等。
它们在通带和阻带的衰减特性、相位响应等方面有所不同,因此需要根据具体需求进行选择。
3. 计算元件数值:根据选择的滤波器类型和设计要求,计算滤波器中各个元件的数值。
这包括电容、电感和电阻等元件的数值选择,以及元件的连接方式和拓扑结构。
4. 仿真和优化:通过电子设计自动化软件,进行滤波器的仿真和优化。
根据仿真结果,对滤波器的性能进行评估和调整,以达到设计要求。
5. 实际制作和测试:根据设计结果,制作实际的滤波器电路,并进行测试和验证。
测试结果将反馈给设计者,以便对设计进行进一步改进和优化。
三、带通滤波器的应用带通滤波器在电子领域有着广泛的应用。
以下是几个常见的应用场景:1. 语音信号处理:在通信系统中,带通滤波器可以用于去除语音信号中的噪声和杂音,提高通信质量。

信号与系统带通滤波器设计学生姓名:***学号:03班级:14光伏设计任务书目录设计目的要求 (7)设计原理 (7)设计内容 (8)1. 连续输入信号产生 (8)2.抽样、频谱分析 (11)3.带通滤波器设计 (12)4.滤波结果 (13)5.总程序 (14)使用函数说明 (17)结果分析 (17)设计心得 (17)一、设计目的要求要求产生一个连续信号,包含低频、中频、高频分量,对其进行采样,进行频谱分析,并设计带通滤波器对信号进行滤波处理,观察滤波后信号的频谱;1.熟悉有关采样,频谱分析的理论知识,对信号作频谱分析;2.熟悉有关滤波器设计理论知识,选择合适的滤波器技术指标,设计带通滤波器对信号进行滤波,对比分析滤波前后信号的频谱;3.实现信号频谱分析和滤波等有关Matlab函数;4.写出基本原理,有关程序,得到的图表,结果分析,总结;二、设计原理1.利用MATLAB软件产生一个包含低频、中频、高频分量的连续信号;2.对信号进行抽样,进行频谱分析;1时域采样奈奎斯特采样定理:为了避免产生混叠现象,能从抽样信号无失真地恢复出原信号,抽样频率必须大于或等于信号频谱最高频率的两倍;本设计中信号最高频率是300Hz,抽样频率采用1200Hz;2频谱分析:频谱分析是指对信号进行频域谱的分析,观察其频域的各个分量的功率大小,其理论基础是傅立叶变换,现在一般采用数字的方法,也就是将时域信号数字化后做FFT,可以得到频域的波形;3.带通滤波器滤波的工作原理现代生活中,为了滤除谐波干扰,获得所需要的高精度的模拟信号,经常要用到滤波器对信号进行滤波;典型的模拟滤波器有巴特沃斯Butterworth滤波器、切比雪夫Chebyshev滤波器和椭圆Ellipse滤波器等;其中,巴特沃斯滤波器又叫最平坦响应滤波器,顾名思义,它的响应最为平坦,通带内没有波纹,其频率响应在通带和阻带中都是单调的,且在靠近零频处最平坦,而在趋向阻带时衰减单调增大,巴特沃斯响应能够最大化滤波器的通带平坦度;该响应非常平坦,非常接近DC信号,然后慢慢衰减至截止点为-3dB,最终逼近-20ndB/decade的,其中n为滤波器的;特别适用于应用,其对于维护增益的平坦性来说非常重要;本次课程设计将使用巴特沃斯带通滤波器对信号进行滤波;滤波器的结构框图如下图1 所示:图1 滤波器的结构框图相对于低通滤波器的通带频率为0,w,带通滤波器的通带频率问为w1,w2,带通滤波器是指某一频率范围内的频率分量能通过,但将其他范围的频率分量衰减到极低水平的滤波器,信号通过线性系统后,其输出就是输入信号和系统冲激响应的卷积;从频域分析来看,信号通过线性系统后,输出信号的频谱将是输入信号的频谱与系统传递函数的乘积;除非输入信号为常数,否则输出信号的频谱将不同于输入信号的频谱,信号中某些频率成分较大的模滤波后这些频率成分将得到加强,而另外一些频率成分很小甚至为零的模,这部分频率分量将被削弱或消失;因此,带通滤波系统的作用相当于对输入信号的频谱进行加权;带通滤波器的频率响应图如下图2;图2 带通滤波器的频率响应图三、设计内容本次设计中利用双线性变换法和buttord 、butter 这两个函数直接设计数字滤波器;设定巴特沃斯带通数字滤波器指标:通带范围为:150-350Hz,阻带上限为:400HZ,阻带下限为100Hz,通带最大衰减pα=2dB,阻带最小衰减为sα=30dB,采样频率为fsa=1200Hz;设计步骤为:1. 首先产生一个连续输入信号,包含中频f=200Hz,高频f=500Hz,低频f=30Hz 分量; 1程序代码 f1=30; f2=200; f3=500; t=1:100/2000;采样 1200HZ连续混合信号带通滤波器输出x1=sin2pitf1;figure1;subplot2,1,1;plotx1; %绘制x1t的图形xlabel't';ylabel'x1t';title'连续信号';grid;x2=sin2pitf2;subplot2,1,2;plotx2; %绘制x2t的图形xlabel't';ylabel'x2t';title'连续信号';grid;x3=sin2pitf3;figure2;subplot2,1,1;plotx3; %绘制x3t的图形xlabel't';ylabel'x3t';title'连续信号';grid;x=sin2pitf1+sin2pitf2+sin2pitf3;subplot2,1,2;plotx; %绘制xt的图形xlabel't';ylabel'xt';title'连续信号';grid;2程序运行结果如图3:图3 包含低频、中频、高频分量的连续信号的波形图2.对连续输入信号进行采样,进行频谱分析;1程序代码:n=1:100;t=n/2000X=fftx,512;w=0:255/2561000;x=sin2pitf1+sin2pitf2+sin2pitf3;figure3;stemx; %绘制xn的图形xlabel'n';ylabel'xn';title'数字信号';grid;figure4;plotw,absX1:256; %绘制频谱图xlabel'Hz';ylabel'频率响应幅度';title'频谱图';grid;2程序运行结果如图4、图5:图4 连续信号抽样结果波形图图5 连续信号进行抽样后的频谱图3.根据设定要求设计带通滤波器;1程序代码:fp=100 300;fs=50 350;ap=2;as=30;fsa=2000;wp=fp/fsa2;ws=fs/fsa2;n,wn=buttordwp,ws,ap,as;B,A=buttern,wn;H,w=freqzB,A,512;figure5;subplot2,1,1;plotw2000/2pi,absH; %绘制带通频谱图xlabel'Hz';ylabel'频率响应幅度';title'带通滤波器';grid;subplot2,1,2;plotw/pi,angleH;xlabel'Hz';ylabel'angel';title'相位特性';grid;2程序运行结果如图6:图6 带通滤波器的频率响应和相位特性曲线4.对信号进行滤波1程序代码:y=filterB,A,x;figure8;subplot2,1,1;ploty;xlabel't';ylabel'xt';title'连续信号';grid;Y=ffty,512;w=0:255/2561000;subplot2,1,2;plotw,absY1:256; %绘制频谱图xlabel'Hz';ylabel'频率响应幅度';title'频谱图';grid;2程序运行结果如图7:图7 滤波后信号时域和频域波形图5.总程序代码f1=30;f2=200;f3=500;t=1:100/2000;x1=sin2pitf1;figure1;subplot2,1,1;plotx1; %绘制xt的图形xlabel't';ylabel'x1t';title'连续信号';grid;x2=sin2pitf2;subplot2,1,2;plotx2; %绘制x2t的图形xlabel't';ylabel'x2t';title'连续信号';grid;x3=sin2pitf3;figure2;subplot2,1,1;plotx3; %绘制x3t的图形xlabel't';ylabel'x3t';title'连续信号';grid;x=sin2pitf1+sin2pitf2+sin2pitf3;subplot2,1,2;plotx; %绘制xt的图形xlabel't';ylabel'xt';title'连续信号';grid;n=1:100;t=n/2000X=fftx,512;w=0:255/2561000;x=sin2pitf1+sin2pitf2+sin2pitf3;figure3;stemx; %绘制xn的图形xlabel'n';ylabel'xn';title'数字信号';grid;figure4;plotw,absX1:256; %绘制频谱图xlabel'Hz';ylabel'频率响应幅度';title'频谱图';grid;fp=100 300;fs=50 350;ap=2;as=30;fsa=2000;wp=fp/fsa2;ws=fs/fsa2;n,wn=buttordwp,ws,ap,as;B,A=buttern,wn;H,w=freqzB,A,512;figure5;subplot2,1,1;plotw2000/2pi,absH; %绘制带通频谱图xlabel'Hz';ylabel'频率响应幅度';title'带通滤波器';grid;subplot2,1,2;plotw/pi,angleH;xlabel'Hz';ylabel'angel';title'相位特性';grid;y=filterB,A,x;figure8;subplot2,1,1;ploty;xlabel't';ylabel'xt';title'连续信号';grid;Y=ffty,512;w=0:255/2561000;subplot2,1,2;plotw,absY1:256; %绘制频谱图xlabel'Hz';ylabel'频率响应幅度';title'频谱图';grid;四、带通滤波器设计中使用函数计算幅值函数:abs;计算相位角函数:angle;设定图像显示窗口函数:figure,如:figure1,figure2;分割figure,创建子坐标系函数:subplot;在图形底层显示格点,便于参照比对函数:grid;Butterworth设计带通滤波器 B,A = BUTTERN,Wn,N为阶数,Wn与Fs有关;模拟滤波器的频率响应函数:freqs;数字滤波器的频率响应函数:freqz;实现滤波函数:Filter对于离散序列,MATLAB用stem 命令实现其绘制五、结果分析设计过程中,首先产生连续输入信号,包含中频f=200Hz,高频f=500Hz,低频f=30Hz分量,然后对其进行采样,利用傅里叶变换进行频谱分析,并由带通滤波器的参数设计带通滤波器对信号进行滤波处理,对应带通滤波器的通带范围是100,300,从运行结果图中可以看出,经过带通滤波器滤波后信号对应的频率为原信号中的中频分量f=200Hz;对比波形如下图8:a 滤波前信号波形图b 滤波后波形图图8 滤波前后信号波形对比图由上述结果显示,在误差允许的范围内实验结果与理论结果相同;出现误差的原因:在设计滤波器的参数时并不是十分的准确,在不同计算机上运行MATLAB时会有一定的偶然误差,从而导致实验误差的存在;六、设计心得此次带通滤波器的课程设计,我们是用三个信号分别为高、中、低频相结合产生一个连续的输入信号,以巴特沃斯滤波器为原型设计出带通滤波器,继而用这个带通滤波器对连续的输入信号进行滤波,产生一个带通输出;由课本上知识已知,一个理想的滤波器是物理不可实现的,肯定会有一些误差,应该做的就是尽量减小误差,去跟理想逼近;在此次课程设计中,就是运用这个原理进行设计,希望设计出的滤波器尽量逼近理想情况;一个理想的带通滤波器应该有平稳的通带,同时限制所有通带外频率的波通过,而实际上,并不能完全实现这种理想的状态,所以我们设计时,一遍遍地改变设计参数,继而调试运行,查看调试出的图形结果,使它能尽量的逼近理想滤波器;课程设计过程中,我最大的收获就是对MATLAB有了更深刻的认识,以前对这个软件只是有一点点的理解,平时做实验时接触了一下下,但是在这一周内,通过不断地接触、应用、与同学讨论、查课外资料等等途径,现在可以说用起它来基本上是可以得心应手了;这段时间内,通过对这个软件的接触,我深感于MATLAB强大的功能,它不仅具有高效的计算能力、灵活的图形处理能力、简单易懂的编程语言,更重要的是它对图形有超强的逼近模仿能力,应用起来非常方便;对于每次的实验,由于时间有限,我总是处在有很多疑问的状态,得不到及时的解答,而这次的课程设计,历时一周,让我有充分的时间去思考、去查阅相关资料、和同学讨论,并询问了相关的代课老师,真正的学到了好多东西,也是少有的几次真正透彻地理解了其原理、不再存在未解决的疑问的设计;设计过程中,我们也遇到了很多问题;起初用的是椭圆滤波器为原型来设计这个需要的带通滤波器,因为椭圆滤波器对带通来说有较多的优点;根据设计参数的要求,和我以前对这个滤波器的认识,我得出了初步的设计结果,所以有了设计结果之后再回顾过来,我们存在好多问题无法解决,查阅了相关书籍还是有一些疑问存在;最终,我决定放弃这个方案,改用对带通来说也能很逼近的巴特沃斯滤波器;不过虽然是学过的东西,要真正做起来,也并没那么简单;了解了巴特沃斯滤波器所有的参数特性以后,结合题目的要求,一遍遍地修改拟定的参数,使得最后滤波的结果能尽量的最逼近理想结果;经过多次的修改之后,终于定下了它最后需要的参数,设计出了能力范围之内的最理想的滤波器,并选择了不会产生失真的符合要求的连续输入信号,经过调试运行之后,最后的设计结果都在控制范围之内;。

带通滤波器设计指南通滤波器是一种常见的电子电路,它可以通过选择某个频率范围内的信号而削弱或排除其他频率的信号。
通滤波器常用于信号处理、通信系统和音频设备中。
本文将为读者提供一个通滤波器设计指南,帮助大家理解通滤波器的原理和设计过程。
通滤波器的基本原理是基于信号在电路中传递时的频率响应。
通滤波器可分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四种类型。
低通滤波器允许低频信号通过,而削弱或阻断高频信号;高通滤波器则允许高频信号通过,削弱或阻断低频信号。
带通滤波器通过选择某个频率范围内的信号而削弱其他频率的信号;带阻滤波器则排除某个频率范围内的信号。
设计通滤波器时,首先需要确定需要滤除或保留的频率范围。
根据具体应用,选择适当的滤波器类型。
然后,需要确定滤波器的阻带衰减和过渡带宽要求,并考虑滤波器的性能要求和成本约束。
通滤波器的设计过程可以分为以下几个步骤:1. 确定滤波器类型和频率范围:根据应用需求,选择合适的滤波器类型,如低通、高通、带通或带阻滤波器。
确定所需滤波的频率范围。
2. 选择滤波器的拓扑结构:滤波器的拓扑结构决定了滤波器的性能和特性。
常见的滤波器拓扑结构包括RC滤波器、RL滤波器、LC滤波器和激励器滤波器等。
3. 计算滤波器参数:根据滤波器的频率范围和性能要求,计算滤波器的参数,如截止频率、阻带衰减、过渡带宽等。
这些参数可以通过传递函数、频率响应或其他滤波器参数来计算得出。
4. 选择滤波器元件:根据计算得出的滤波器参数,选择合适的电阻、电容或电感元件。
这些元件的选择要考虑到它们的频率响应、功率容纳能力和成本。
5. 滤波器的仿真和调试:使用电子电路仿真工具,如SPICE软件,对设计的滤波器进行仿真和调试。
可以通过改变滤波器的元件值、调整滤波器的参数来优化滤波器的性能。
6. 制造和测试:根据设计图纸,制造滤波器电路。
通过测试滤波器电路的性能,检验滤波器是否满足设计要求。
如果需要,可以对滤波器电路进行调整和修改。


滤波器的设计流程与步骤滤波器是一种电子器件或电路,用于改变信号的频率特性。
在电子领域,滤波器被广泛应用于信号处理、通信系统、音频设备等方面。
设计一个滤波器需要遵循一定的流程与步骤,本文将介绍滤波器设计的一般流程,并详细探讨每个步骤的具体内容。
第一步:需求分析在滤波器设计之前,首先需要明确设计滤波器的需求。
这包括确定滤波器的类型(如低通、高通、带通、带阻等),频率范围、阻带衰减要求、插入损耗限制等。
需求分析阶段的目标是明确设计滤波器所需的功能和性能规格。
第二步:选择滤波器结构根据需求分析的结果,根据不同的滤波器类型和频率范围,选择适合的滤波器结构。
常见的滤波器结构包括RC滤波器、LC滤波器、激励响应滤波器、数字滤波器等。
选择滤波器结构时需要综合考虑设计的难度、性能指标和实际应用需求。
第三步:确定滤波器规格在选择滤波器结构后,需要进一步确定滤波器的规格。
这包括确定滤波器的阶数、各个截止频率的具体数值、通带和阻带的设定等。
可以利用相关的数学模型、理论计算或者实验手段来确定滤波器规格。
第四步:设计滤波器设计滤波器是滤波器设计流程的核心步骤。
根据滤波器的结构和规格,运用电路理论、数学模型等手段进行滤波器的具体设计。
这包括计算和选择滤波器元件的数值、确定元件的合适布局和连接方式,以及优化设计,以满足设计要求。
第五步:仿真与分析在设计完成后,进行滤波器的仿真和分析是十分重要的。
这可以通过使用模拟电路仿真软件、信号处理工具等进行。
通过仿真结果,可以评估滤波器的性能是否满足设计要求,并进行必要的调整和优化。
第六步:原型制作与测试设计完成后,需要制作滤波器的实际原型,并进行测试和验证。
这可以通过PCB设计和制作、元器件的选取和组装等方式完成。
通过实际测试,可以验证滤波器的性能指标,并进行必要的调整和改进。
第七步:性能验证与优化通过对原型滤波器的测试结果进行分析和评估,可以判断滤波器是否满足设计要求。
若不满足,则需要针对具体问题进行调整和优化。

带通滤波器的设计报告设计报告:带通滤波器一、引言:二、设计原理:带通滤波器的工作原理是只允许特定频率范围的信号通过滤波器。
其设计的关键在于确定带通滤波器的中心频率和带宽。
常见的带通滤波器包括主动滤波器和被动滤波器,其中主动滤波器采用放大器和运算放大器等主动元件工作,而被动滤波器则主要由电容器和电感器等被动元件组成。
三、设计步骤:1.确定滤波器的中心频率和带宽:根据实际需求,选择需要通过的频率范围,然后计算出滤波器的中心频率和带宽。
2.选择滤波器的类型:根据设计要求,选择适合的滤波器类型,如二阶巴特沃斯滤波器、椭圆滤波器等。
3.计算滤波器的参数:根据选择的滤波器类型,计算出所需的电阻、电容和电感等参数数值。
4.组装滤波器电路:根据计算结果,组装相应的电路,包括放大器、电容和电感等元件,构成带通滤波器。
5.进行实验验证:使用信号发生器提供输入信号,通过示波器观察滤波器的输出情况,验证滤波器的设计效果。
四、实现过程中的问题及解决方案:1.参数计算问题:参数计算是滤波器设计中的重要步骤,对滤波器性能有直接影响。
解决方法是通过查阅资料或使用相关软件进行计算,同时根据实际需求进行调整。
2.元件选型问题:选择适合的电容器和电感器等元件也是滤波器设计中的关键步骤。
解决方法是根据设计要求选择合适的元件,考虑其额定参数和价格等因素。
3.实验验证问题:在实验过程中可能会遇到输出信号不稳定、频率失真等问题。
解决方法是检查电路连接是否正确,调整电源参数和放大器增益等,确保滤波器正常工作。
五、总结:通过本次带通滤波器的设计过程,我们深入了解了带通滤波器的原理和设计步骤。
在实践中遇到的问题都得到了解决,并且通过实验验证了滤波器的设计效果。
带通滤波器在电子电路设计中具有广泛的应用,本设计报告对于滤波器设计感兴趣的读者将会提供有用的参考和指导。

金属同轴腔滤波器设计金属同轴腔滤波器设计摘要近年来随着移动通信导航技术和电子对抗的快速发展对现有微波元器件的需求和性能的改进都提出了很高的要求同轴腔体带通滤波器作为微波带通滤波器中应用最广的一种滤波器具有功率容量大插入损耗低寄生通带远等特点在现代无线通信数字电视广播卫星导航遥测遥感和雷达等系统中得到了广泛的应用本文对同轴腔体带通滤波器做了详细的分析分析讨论了同轴谐振腔的电磁特性主要包括谐振频率谐振腔的耦合结构和外部品质因数等利用响应函数得到腔体之间的耦合系数应用三维全波仿真软件分析了腔体结构参数与耦合系数和耦合窗的关系最后论文给出了同轴腔滤波器设计实例测试结果性能良好符合设计指标要求关键词微波滤波器带通滤波器同轴谐振腔全波仿真分析With the rapid development of mobile communication system the quality of microwave components is becoming more and more important As a microwave band-pass filter coaxial cavity filter is widely applied in modern wireless communication and radar systems for its high power capacity low insertion loss and far spurious pass-bandBased on the research of coaxial filter the electromagnetic properties of coaxial cavity resonator are proposed in the paper including resonant frequency coupling structure and external Q of the cavities The coupling coefficient of filter can be getting by utilizing response function The width of coupling windows and in-putout-put coupling lines are acquired by full wave simulation and optimization At last a coaxial cavity filter is designed and measured which has perfect performances and is satisfied with the technical specificationsKey Words microwave filter band-pass filter coaxial resonator full wave simulation一绪论 111 前言 112 常见的滤波器形式 113 国内外发展现状 3二滤波器的基本概念521 滤波函数 522 微波滤波器参数 623 低通滤波器到带通滤波器的转换7 三同轴腔带通滤波器的设计831 滤波器的设计步骤832 滤波器的设计方法8com 前言8com 设计指标9com 参数计算933 仿真与测试10com 仿真10com 实物加工与测试12总结14参考文献15一绪论11 前言随着通信广播雷达测量遥感空间技术和电子对抗技术等的逐步发展从米波段一直到毫米波段以至更广阔的波段上微波滤波器在雷达信号处理通信等不同电路系统的传输变换处理和收发中有广泛应用[1]随着导航技术和移动通信电子对抗的快速发展同时对改善现有器件的性能和对未开发的微波元器件提出更高更严谨的需求是必要的尤其是在无线电通信频率资源日益紧张的今天不同通信系统能够获得的频率范围越来越窄从而使得对于无源器件尤其是那些前端使用毫米波微波收发信机的器件的性能优劣提出了更高层次的要求为的是前端系统降低对信号的衰减使不同的干扰信号得到抑制另外由于新工艺新材料的逐步发展以及迅速发展的半导体先进技术新的RF模块不断不出现使得研制毫米波微波RF有源电路的周期渐渐缩短且高度集成小体积的电路正在逐步发展[2]因此研制小体积高性能的无源器件减少设计无源器件的周期是目前毫米波微波通信等相关领域的重要步骤之一1915年在德国 K W Wagner 创新发明了一种以新的滤波器设计方法--瓦特纳滤波器与此同时在美国G A Canbell则开创了另一种知名的设计方法--图像参数法间隔两年LC滤波器在两国分别由两位科学家发明出来1918年第一个多路复用系统在美国问世自此以后科研人员便开始积系统而全面的对使用集总元件电容和电感的滤波器进行理论研究随着滤波器的设计理论不断的深入研究材料领域的不断发展以及工作频率的日益升高使得由原先的集总参数元件滤波器的设计逐渐扩展到分布参数元件滤波器的设计[3]1939年P D Richtmeyer报道了介电滤波器因为当时材质的温度稳定性不够高这样就导致该种滤波器不足以应用于实际直到1970年左右因为陶瓷材料有较快的发展介电滤波器在实际中应用也随即得到了较快的发展目前20世纪年代出现的高温度临界超导材料被认为很大可能应用于设计出极小尺寸和极低损耗的新颖滤波器并且现在已经在商业和军事领域使用[4]12 常见的滤波器形式在现代无线电系统中包括各种移动通信电子对抗雷达系统等的发展同时促进了微波器件的发展其中微波滤波器是现代毫米波微波通信技术中一个极其重要的部分[5]是毫米波微波系统中不可缺少的器件其性能的优劣往往会直接影响整个通信系统的质量近年来随着滤波器结构的不断发展与更新因为应用环境的不同伴随出现了各种不同结构的滤波器1 集总参数滤波器根据滤波器原型电路最简单最直接的结构是采用集总参数的电感电容元件直接搭建滤波器电路可以采用分立元件也可以采用集成电路集总参数滤波器的元件Q值较低[6]在10GHz频段的Q值大约为100-200这比较适合于低频信号的滤波由于现代移动通讯频率都比较高所以很少采用这类滤波器2 微带线带状线滤波器众所周知布参数传输线可以等效为电感或电容因此选用合理尺寸的传输线组合可以构成滤波器电路最为常用的是微带线和带状线结构可以很方便地制成印制板造成本低廉[7]在结构设计上主要有三种方式梳状线线卡线这类滤波器的特点是结构紧凑阻带宽容易制造缺点是Q值低10GHz时Q值为150-200插入损耗大滤波特性一般适用于小功率滤波场合一些小功率指标要求低的的干线放大器中有使用3 同轴腔体滤波器腔体滤波器因其通带插入损耗低阻带抑制性高承受较大功率调谐方便等特点在通信系统中也应用广泛[8]其中同轴腔体具有高Q值损耗特性电磁屏蔽和小尺寸等优异特点但是如果在10GHz以上使用时由于其物理尺寸很微小所以制作精度很难达到同轴腔形式的带通滤波器广泛应用于雷达通信等系统按照腔体结构不同一般分为标准同轴腔方腔同轴等4 波导滤波器波导型滤波器是一种经常使用的无源微波滤波器特别是在高频段大功率的天线馈电系统中波导型滤波器能够发挥巨大的作用波导腔体带通滤波器本质是一种选择频率电路应用在雷达电子战通信等设备的微波设备中它易于连接馈电装置适合应用于较高功率的情况下并且具有良好的性能在信号的电平较小时它一般都是用在8GHz到100GHz的范围内[9]这种滤波器的主要功能应用是在通频带插入损耗和失真较小的情况下使阻带的选择性能够得到足够的提供比如说在使用微波接收机时不需要的带外信号被带通滤波器滤除掉为了使前段噪声的特性得到保持在使用微波发射机时不需要的频率谱被滤波器减小使得发射机的噪声不能传递到接收机在不同的微波多工器上此种滤波器也得到应用但是它最大的缺点是其尺寸大小显然比其他可应用在微波段的谐振器大随着微波技术的迅猛发展天线系统日趋复杂对波导型滤波器的需求更大范围更广同时也对其性能提出更高要求5 介质滤波器介质滤波器分为两种一种TEM模式它和传输线型滤波器原理相同只不过尺寸更小在400NHz-5GHz频率范围内的Q值为200-800其插入损耗比较大滤波特性也比较差一般只在性能要求低的中频滤波中采用另一种为TE01δ模介质滤波器其Q值非常高10GHz的Q值可以达到10000以上900MHz时的Q值约为22000这种滤波器兼有小尺寸和低损耗的特点[10]直到现在TE01δ模介质滤波器仍然是国际学术界研究非常活跃的课题并且已经在卫星通讯移动通讯中获得了成功的应用随着技术的不断进步和工艺材料的不断改进TE01δ模介质滤波器在电气性能上远远超过了以往任何滤波器的水平在大容量移动通讯系统中为了充分利用频率资源相邻信道或收发通道频率间隔非常小如果采用传统滤波器其损耗大得难以接收如两个相邻CDMA载频的滤波合路则必须采用介质滤波合路方式才能做到既有效抑制相邻信号所谓干扰又能不增加太多的插入损耗可以预见在未来的3G系统中TE01δ模介质滤波器将会得到大量的应用在下一代移动通信的基站中对基站的重量和体积都有十分严格的控制因此必须减小滤波器的重量和体积与此同时不能降低滤波器的性能在工艺材料和微波技术发展至今的情况下制造这些微波滤波器选用高Q值低损耗具有一定介电常数的陶瓷材料加载介质谐振腔是一种必然经过理论和实践方面的长期努力和积累已经将这种介质谐振腔滤波器应用在移动通信系统中而且会有很好的前景伴着滤波器技术的不断完善其他各种新型滤波器如SAW滤波器陶瓷介质滤波器SIR滤波器微波有源器件等也开始应用于各种通信系统中[11]13 国内外发展现状20年代初出现的载波电话系统使得在电信领域内引发了一场伟大的技术革命从而迎来了电信历史的新纪元它的快速发展促成了在检出信号和特定频带提取的新兴技术的发展这种技术慢慢的发展成为现在的滤波器技术从电信早期的发展中可以看出电路中滤波器发挥着极其重要的作用而且随着通信技术不断的发展而取得进展早期耦合谐振器滤波器的综合理论基于Cohn的研究成果主要针对同步调谐的级联谐振器滤波器设计这种结构的传输零点在无限远处只能实现切比雪夫或巴特沃斯型响应并未涉及广义切比雪夫型响应1970年Atia和Wiiliams提出了可实现有限频率传输零点的耦合谐振器滤波器综合通用理论[12]根据该理论通过解析方法可以得到小于四阶的耦合谐振器滤波器耦合拓扑结构国外最早解决办法主要有以Cameron在1999年提出来的相似变换Amari在2000年提出的优化法为代表两条技术路径前者基于矩阵旋转理论通过一系列矩阵相似变换在保证耦合矩阵特征值和特征向量不变的前提下将不需要的矩阵元素消零但这种方法仅限于特定耦合拓扑结构折叠规范型后来一些学者在此基础上给出了常见的拓扑结构的耦合矩阵旋转方法该方法计算效率高精度高但是不同结构需要不同的旋转顺序和步骤并不能得到任意拓扑结构的耦合矩阵因此结合多种方法对滤波器拓扑结构进行综合已是大势所趋国内有报道采用遗传算法优化提取耦合谐振器滤波器的耦合矩阵近年来J S HongM J LancansterMing Yu等也在微波滤波器与双工器的综合方面做出非常重要的贡献[1314]七十年代初期我国的老一代微波专家甘本祓吴万春等在前人研究的基础上对微波滤波器的设计理论和方法进行了补充和完善为我国微波滤波器的研究奠定了良好的基础80年代中后期的研究相关文献报道较少90年代有见零星报道进入21世纪后这已经在国内成为研究热点中国空间技术研究院的吴须大研究员对同轴腔滤波器与微放电腔体滤波器与低气压放电等问题进行了细致的分析[15]电子科技大学的贾宝富西安电子科技大学的梁昌洪李刚等在微波滤波器双工器和多工器研制上做出了一些探索并取得了一系列的成果二滤波器的基本概念21 滤波函数理想的低通滤波器的衰减特性如图21 a 所示即在ω=0到ω1的频率范围内衰减为零称为通带在ωω1的范围内频率衰减为∞称为阻频带Ω为角频率大小ω1称之为截止频率大小显而易见有限个元件数目的电抗网络的频率衰减特性必是一个连续函数必然不会在某一固定的频率上突变像这种理想的滤波特性是无法用有限个元件的电抗网络来实现而实际中的滤波器只能通过逼近函数来逼近理想滤波器的衰减特性所以在滤波器综合设计时第一步是要确定一个无限接近理想频率衰减特性的滤波函数然后再依据第一步得到的逼近函数综合出具体的电路结构实用中有三种滤波函数使用最广泛各对应的滤波器称为最平坦型切比雪夫型和椭圆函数型滤波器它们的衰减特性如图 21 b c d 所示理想特性 b 最大平坦型逼近c 切比雪夫型逼近d 椭圆函数型逼近图2-1 常用逼近函数最大平坦型响应最大平坦型低通原型滤波函数为2-1它有四个指标参数通带内的最大衰减用LAr表示截止频率ω1阻带内的最小衰减用LAs表示以及阻带的边频用ωs表示为了让获得的梯形电路通用于对各不相同的ω1和ωs的低通滤波器可以使用归一化的频率于是其衰减函数为 2-2综合低通滤波器过程为首先通过四个指标参数LArω1LAsωs确定常数ε和n从而可以求得需要的滤波函数再次根据第一步得到的这个函数利用前面介绍的网络综合法来确定低通滤波器原型的梯形电路各元件值和结构ε是当ω1时计算通带内的最大衰减LAr得到的即n可以通过带外最小衰减获得2-3切比雪夫型响应切比雪夫的低通原型滤波函数为2-4切比雪夫函数多项式为Tn ω在ω 01之间是余弦函数因此衰减在ω 01之间出现的时等波纹的变化在ω 1时Tn 1 1LAr达到其最大值即2-52-6LAr是波纹幅度ε是波纹的因数在通频带内最小的衰减频率为零而当ω 1时即阻带内时Tn ω是一个双曲余弦函数若在阻频带ωs上阻频带的衰减为LAs则有2-7椭圆函数响应由图21 d 可见由于椭圆函数滤波器的阻带衰减极点不全在无限远处因而用这种滤波器可得到很陡的截止率图中LAr是通带最大衰减LAs是阻带最小衰减ω1是通带带边频率ωs是阻带带边频率考虑n阶椭圆函数型低通变换器衰减特性得到2-8其中Fn是含有模为K的函数22 微波滤波器参数1带宽Bandwidth通带的3dB带宽flowfhigh2中心频率fc或f03截止频率下降沿3dB点频率4插入损耗insertion loss当滤波器与设计要求的负载连接通带中心衰减5带内波纹绝对衰减Absolute attenuation阻带中最大衰减dB6品质因数uality factor中心频率与3dB带宽之比7反射损耗Return loss23 低通滤波器到带通滤波器的转换要依据低通的滤波器设计出一个带通的滤波器它的截止频率是ω1和ω2频率需要进行较复杂的变换使低通原型滤波器的频率变量ω’与带通滤波器的频率变量ω符合下面公式2-9式中ω2是带通滤波器高端的截止频率ω1是其低端的截止频率ω0为中心频率通常令ω2-ω1称为该滤波器中的通频带ω2-ω1 ω0称为该滤波器中的相对通频带W2-10 根据母型低通滤波器换算带通滤波器电路元件变得更加复杂母型滤波器的电感应改为LC串联电路它的电感Lk和电容Ck与母型的电感保持以下关系2-11 2-12母型滤波器的电容应改为LC并联电路它的电容Ck1 和电感Lk1 与母型的电容保持以下关系2-13 和都可以从母型低通滤波器的元件表上查得三同轴腔带通滤波器的设计31 滤波器的设计步骤滤波器的设计步骤为1 确定滤波器的类型和实现方式根据技术指标要求确定滤波器的类型和实现方式包括低通高通带通还是带阻的确定使用何种逼近函数模型体实现形式选择用微带线同轴线还是用波导等实现2 确定滤波器的阶数n根据技术指标要求逼近函数模型确定滤波器的阶数n主要取决于带内插损带外抑制以及所选择的衰减逼近函数模型即元件数n是由衰减特性曲线决定的可以通过查表可以得到也可以通过一些公式计算得到3 查表得到低通滤波器原型的各元件值其余三种滤波器可以从低通滤波器原型通过函数转换得到一般滤波器都是对称设计的也就是说知道一半的元件值就可以了4 使用电路仿真软件仿真使用电路仿真软件仿真是为了优化电路各元件的值5 使用场仿真软件仿真场仿真和实际相差较小所以一般都会使用仿真软件来确定最终的设计6 实物加工与调试32 滤波器的设计方法com 前言滤波器的设计当前有两种不同的出发点一种出发点是镜象参数法这种方法是过去人们一直用来设计滤波器的经典办法此方法的好处是它理论依据很简单但在分析的过程中不会考虑到外接负载对滤波器的影响是它的缺点本文主要采用另外一种方法故镜象参数法不作详细介绍另一种出发点是综合法又称为插入损耗法此方法是近些年以来采用的很普遍的设计方法此方法的步骤是依据需求的技术参数得到插入损耗Li与频率ω的所决定的关系函数再依据这个关系函数推导出具体的相应的电路结构因此第二种方法是第一种方法的相反过程此方法应用网络理论推求出具体的电路反之镜象参数法是根据已知的电路参数拼凑出符合要求的电路结构设计准确是第二种方法的最突出优点并且设计时将外界负载时的影响已经考虑进去从而不用进行多次试探因为要用到比较难的网络理论这就使设计难度增大这是它的缺点尽管如此因为只要设计出满足指定参数要求的母型滤波器以后的设计步骤就成了简单的读图查表和使用数学方法数据将换算即可相比较镜象参数法综合法要比其更加实用com 设计指标设计指标通带频率1785-1800MHz fL--fU插入损耗≤20dB回波损耗≥15dB带外抑制1700-1755MHz 30dB1805-1830MHz≥20dB1830MHz≥30dB输入功率50W工作温度范围-3575℃接口类SMA F 特性阻抗50Ωcom 参数计算经过带通滤波器到低通原型的变换可以得到低通原型的带外抑制3-1由低通原型的带外抑制要求可以得到滤波器的级数n3-2根据技术指标由以上公式算得n 5由低通原型滤波器的级数n 求解其集总参数电路中各元件的归一化值根据公式算得元件的归一化值如表31所示表3-1 元件归一化值g0g1g2g3g4g5g610000137121146819750137121146810000由低通原型中各元件的归一化值求解同轴腔体之间各耦合系数以及端口的有载Q值根据公式由技术指标要求得到K12 K45 00067K23 K34 00051QL 13704由滤波器级数指标要求f0和耦合系数MR确定腔体物理结构以及耦合腔体开窗的尺寸33 仿真与测试com 仿真1单腔1 建立本征模求解模型图3-1 单腔模型图表3-2 单腔模型尺寸单位mm腔高腔宽腔长内圆柱半径外圆柱半径内圆柱高外圆柱高82627523759792 仿真图3-2 谐振频率与谐振柱高度关系曲线由图3-2可知当h 790mm时谐振频率f0 17925GHz 2双腔1 建立本征模求解模型图3-3 双腔模型图2 仿真图3-4 窗口宽度与耦合系数的关系曲线从图3-4得出w12 940时K12 00051w12 882时K12 00067 由仿真计算得到的数据如表3-3所示表3-3 尺寸图单位mm12腔L12W12H12X12K12w12R12r1227526830006788237223腔L23W23 H23 X23 K23 w23 R23 R23 275 2683 00051 940 37234腔L34 W34 H34 X34 K34 w34r34 275 2683 00051 940 37245腔L45 W45 H45 X45 K45 w45 R45 r45 275 26800067882372说明表3-3中LWH为单腔的长宽高X是腔与腔之间的壁厚rR分别是圆柱腔的内外半径com 实物加工与测试1 实物根据仿真结果加工制作了如图3-5所示的实物图3-5 滤波器实物图图3-5中1是滤波器输入端2是耦合窗口调谐螺钉3是腔体调谐螺钉4是固定螺钉5是滤波器输出端2根据加工的实物在网络分析仪上进行调试其测试结果如图3-6所示设计目标为通带17851800MHz内S21≥-20dB回波损耗IL≥15dB带外抑制18051830MHz≤-20dB17001755MHz或1830MHz≤-30dB实测结果为通带内S21为-12dB 回波损耗IL为18dB带外抑制18051830MHz为-25dB17001755MHz为-34dB1830MHz为-359dB经过以上分析可知实际测试结果完全符合设计目标要求总结滤波器是现代移动通信等领域不可或缺的基本器件其性能的优劣往往会直接影响整个通信系统的质量在采用各种形式的滤波器中带通滤波器是所有滤波器中使用最多最重要也是最难设计的一种滤波器本论文设计的是18GHz同轴腔带通滤波器前两章介绍了滤波器的研究现状和基本概念理论第三章详细阐述了同轴腔带通滤波器的设计步骤和方法通过参数计算得出了滤波器的阶数理论耦合系数和品质因数由Ansoft HFSS软件仿真出了和理论计算相对应的谐振频率f0和耦合窗口宽度w12等参数并由最终的仿真优化结果设计出了符合技术要求的同轴腔带通滤波器经过网络分析仪调试属于可以应用于实际的合格滤波器通过本次论文设计使我对滤波器的设计和HFSS软件的应用有了较深入的了解为以后在这方面的深入学习奠定了基础参考文献[1] 姚毅等调谐微波滤波器的腔间耦合结构研究[J]微波学报 1994 01 12-15[2] 姜宇等基于HFSS密度测量同轴谐振腔磁耦合环优化设计[J]哈尔滨商业大学学报2010 05 10-14[3] 吴微微波滤波器综合技术的研究[D]西安电子科技大学 2008211-220[4] 贾守礼同轴腔体带通滤波器的研究[D]大连海事大学 2011198-210[5] 姚毅腔体滤波器中侧面耦合孔的等效模型[J]四川轻化工学院学报1994 04 6-8[6] 薛欣同轴腔滤波器机电耦合研究及双圆极化天线设计[D]西安电子科技大201077-85[7] 杨皎皎TD-SCDMA准椭圆函数腔体带通滤波器的设计[D]西安电子科技大学 2007157-163[8] 熊莹霞可调腔体带通滤波器的研究与设计[D]华东师范大学200588-102[9] 王一凡等广义切比雪夫滤波器等效电路参数的提取[J]真空电子技术2007 01 10-13[10] 邓贤进等微波腔体滤波器的快速设计及仿真[J]微波学报2006 04 13-15[11] 郑泽国800MHZ同轴腔体双工器的研制[D]西安科技大学 201165-80[12] 吴边无线通信中微波滤波器的比较设计法与应用研究[D]西安电子科技大学20089208-214[13] 甘本袚等现代微波滤波器的结构与设计[M]上册北京科学出版社 1974[14] 甘本袚等现代微波滤波器的结构与设计[M]下册北京科学出版社 1974[15] 吴须大等同轴腔滤波器与微放电[J]空间电子技术20008 4 6-9。


一文教你设计一个带通滤波器
带通滤波器是一个太宽泛的概念了,窄带的宽带的,LC/微带/同轴/波导/介质的。
各种花样的谐振器,各种花样的耦合结构。
但不管如何变化,有两个概念始终无法避开;谐振和耦合,各种设计方法也都是为了如何准确的确定谐振频率和谐振器间的耦合量。
各种技术进步也都是为了找到更小,Q值更高的谐振结构。
同时自己为什幺这幺喜欢滤波器,滤波器是微波的一个基础器件,在前人的论文中已经证明了任何宽带匹配网络都是滤波器结构,自己对微波的感觉也从这个器件中获益良多。
· 一个波导同轴转换是一个滤波器结构
· 一个极化转换器是一个滤波器结构
· 一个OMT是一个滤波器结构
· 一个功分器也可以是一个滤波器结构
· 甚至一个天线也是一个滤波器结构(实现了50欧和自由空间阻抗的匹配)
· 你也可以把滤波器和衰减器结合起来设计一个均衡器
当通过大量的实践,有了大量不同结构的谐振结构和耦合结构的概念,我们在微波有源产品设计中你可以感觉到信号可能会从那些地方窜来窜去,你可以让你的链路更加干净有序。
未来一段时间计划总结一下有价值的滤波器设计理念,今天用一个5阶1805MHz~1880MHz的同轴梳线滤波器的例子来说明如何设计一个简单的带通滤波器。
1.带通滤波器的设计步骤
一个带通滤波器应该遵循以下设计步骤:。


带通滤波器的设计和优化在电子领域中,滤波器是一种重要的电路组件,用于去除信号中的杂波和噪声,同时保留感兴趣的频率成分。
其中,带通滤波器是一种常见的滤波器类型,可以通过选择性地通过一定范围内的频率信号。
本文将介绍带通滤波器的设计和优化技巧。
一、带通滤波器的基本原理带通滤波器通常由低通滤波器和高通滤波器级联而成。
低通滤波器将低于某个截止频率的信号通过,而高通滤波器则将高于某个截止频率的信号通过。
两者的级联形成了带通滤波器,只有位于截止频率范围内的信号能够通过。
二、带通滤波器的设计步骤1. 确定设计需求:根据实际应用的要求,确定带通滤波器的通带范围、截止频率、通带波纹和阻带衰减等指标。
2. 选择滤波器类型:根据设计需求选择合适的滤波器类型,常见的有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
3. 计算滤波器阶数:滤波器的阶数决定了其频率响应的陡峭程度,阶数越高,衰减越大。
根据设计需求和滤波器类型,计算出合适的阶数。
4. 计算滤波器元件数值:根据滤波器的阶数和类型,利用标准滤波器元件数值表,计算出所需的电感和电容数值。
5. 组装滤波器电路:按照计算得到的元件数值,组装滤波器电路。
6. 进行仿真和测试:使用电子设计自动化软件进行滤波器的仿真分析,验证设计的性能指标是否满足要求。
之后,进行实际的电路测试,进一步优化和调整。
三、带通滤波器的优化技巧1. 阻带衰减的优化:提高阻带的衰减能力,可以更好地抑制不需要的频率成分,增强滤波器的性能。
2. 降低通带波纹:通带波纹会引入额外的误差,可以通过增加滤波器的阶数或采用更复杂的滤波器结构来减小通带波纹的幅度。
3. 减小滤波器的尺寸和功耗:在实际应用中,滤波器的尺寸和功耗也是需要考虑的因素。
通过优化电路结构和选择合适的元件,可以在不影响性能的前提下减小滤波器的尺寸和功耗。
4. 噪声抑制的优化:在信号处理中,对噪声的抑制能力也是重要的指标。
通过对滤波器元件的选择和电路布局的优化,可以提高滤波器对噪声的抑制能力。

带通滤波器课程设计一、课程目标知识目标:1. 学生能够理解带通滤波器的基本原理,掌握其频率响应特性。
2. 学生能够掌握带通滤波器的传递函数、幅频特性及相频特性。
3. 学生能够了解带通滤波器的设计方法,包括切比雪夫、巴特沃斯等滤波器的设计。
技能目标:1. 学生能够运用所学知识,使用电路仿真软件(如Multisim、LTspice等)设计简单的带通滤波器电路。
2. 学生能够分析实际电路中带通滤波器的性能,并进行调试和优化。
3. 学生能够通过实验,观察并验证带通滤波器的频率响应特性。
情感态度价值观目标:1. 学生通过学习带通滤波器,培养对电子电路的兴趣和热情,增强学习动力。
2. 学生在团队协作中,学会沟通、交流,培养合作精神和集体荣誉感。
3. 学生能够认识到带通滤波器在实际应用中的重要性,增强理论联系实际的意识。
课程性质:本课程为电子技术基础课程,以理论与实践相结合的方式进行教学。
学生特点:学生为高二年级电子技术爱好者,具备一定的电子电路基础知识和实践能力。
教学要求:注重理论教学与实践操作相结合,培养学生动手能力和创新能力,提高学生分析问题和解决问题的能力。
将课程目标分解为具体的学习成果,以便后续的教学设计和评估。
二、教学内容1. 带通滤波器原理及其数学描述- 滤波器的基本概念和分类- 带通滤波器的定义和频率响应特性- 带通滤波器的传递函数、幅频特性及相频特性分析2. 带通滤波器设计方法- 切比雪夫滤波器设计原理及方法- 巴特沃斯滤波器设计原理及方法- 其他类型带通滤波器设计方法简介3. 带通滤波器电路分析与仿真- 使用Multisim、LTspice等软件进行带通滤波器电路设计与仿真- 分析实际电路中带通滤波器的性能,并进行调试和优化- 验证带通滤波器频率响应特性的实验方法4. 带通滤波器应用案例及拓展- 带通滤波器在通信、音频等领域的应用案例介绍- 带通滤波器的创新设计思路及发展趋势- 学生拓展实践项目:设计一个特定应用场景下的带通滤波器教学内容安排与进度:第1周:带通滤波器原理及其数学描述第2周:带通滤波器设计方法第3周:带通滤波器电路分析与仿真第4周:带通滤波器应用案例及拓展本教学内容根据课程目标,结合教材章节内容进行科学、系统地组织,旨在帮助学生掌握带通滤波器的基本原理、设计方法和实际应用。

摘要滤波是信号处理中一种最基本但十分重要的技术,利用滤波,可以从复杂的信号中提取所需的信号,抑制不需要的信号。
所谓滤波器,就是对已知激励,可以在时间域或频域产生规定响应的网络,要使滤波器能够提取有用信号,要求滤波器对信号与噪声有不同的增益,对有用信号尽量无失真放大,而对噪声尽量衰减。
根据其冲击响应函数的时域特性将滤波器为FIR(有限长冲击响应)和IIR(无限长冲击响应)。
按信号处理的方式分类,滤波器可分为模拟滤波器和数字滤波器。
本文介绍了两部分,一部分是硬件电路,设计有源带通模拟滤波器,并按照一定的指标来设计;另一部分是用matlab实现FIR数字滤波器的结构,通过matlab GUI设计实现界面,显示FIR和IIR数字滤波器的时域和频域波形。
GUI 是 Graphical User Interface 的简称,即图形用户界面。
GUI 是一种结合计算机科学、美学、心理学、行为学,及各商业领域需求分析的人机系统工程,强调人—机—环境三者作为一个系统进行总体设计。
关键字:滤波;信号;有源带通滤波器;matlab GUIAbstractFiltering is the signal processing in a basic but very important technology, the use of filtering, the desired signal can be extracted from the complex signal, it use to suppress unwanted signals. What is filter, is known to inspire, in the time domain or frequency domain response to the arising network, make the filter be able to extract the useful signal, filters is the signal and noise gain, as far as possible without distortion of the useful signal amplification, attenuation of the noise as much as possible. According to the time domain characteristics of the impulse response function of the filter FIR (finite-length impulse response) and IIR (infinite-long impact response). Signal processing classification, the filter can be divided into analog filters and digital filters.This article describes the two parts, the hardware circuit design active band-pass analog filter, and according to certain indicators; another part of the structure of the FIR digital filter using matlab GUI design interface, display the FIR and IIR digital filters in time domain and frequency domain waveforms. GUI is a Graphical User Interface, referred to as the graphical user interface. The GUI is a combination of computer science, aesthetics, psychology, behavioral science, human-machine systems engineering and commercial areas of demand analysis, emphasizing the man - machine - environment among the overall design as a system. Keywords: filtering; signal; active band-pass filter; Matlab GUI;桂林电子科技大学实训(论文)报告用纸第1 页共1 页目录引言 (1)1 带通滤波器的硬件设计方案 (1)1.1滤波器的分类 (1)1.2滤波器的参数 (2)1.3带通滤波器的特点 (2)1.4带通滤波器的方案选择 (2)1.5电路方案选取 (3)1.5.1电路原理图 (3)1.5.2 PCB图 (4)1.6电路工作原理 (4)1.7芯片介绍 (5)1.7.1 NE5532特点 (5)1.7.2 NE5532引脚图 (5)1.8硬件电路软件设计 (6)1.8.1 软件设计电路图 (6)1.8.2 软件设计参数分析 (6)1.9调试 (7)2 数字滤波器软件设计 (8)2.1FIR滤波器的设计 (8)2.1.1 FIR滤波器的特点 (8)2.1.2FIR滤波器的设计 (10)2.2 IIR滤波器的设计 (11)2.2.1IIR滤波器的特点 (11)2.2.2 IIR滤波器的设计 (11)2.3FIR和IIR滤波器的实现过程 (12)3 用MATLAB GUI实现FIR数字滤波器的界面设计 (13)3.1FIR数字滤波器界面设计 (13)3.2结果与显示 (14)4 实训总结 (16)谢辞 (18)参考文献: (19)附录一 (20)附录二 (23)引言数字滤波器因其精度高、可靠性好、灵活性大等优点,在语音信号处理、信号频谱估计、信号去噪、无线通信中的数字变频以及图像处理等工程实际应用中都很广泛。

带通滤波器设计步骤带通滤波器设计步骤1、根据需求选择合适的低通滤波器原型2、把带通滤波器带宽作为低通滤波器的截止频率,根据抑制点的频率距离带通滤波器中心频点距离的两倍作为需要抑制的频率,换算抑制频率与截止频率的比值,得出m 的值,然后根据m 值选择低通滤波器的原型参数值。
滤波器的时域特性任何信号通过滤波器都会产生时延。
Bessel filter 是特殊的滤波器在于对于通带内的所有频率而言,引入的时延都是恒定的。
这就意味着相对于输入,输出信号的相位变化与工作的频率是成比例的。
而其他类型的滤波器(如Butterworth, Chebyshev,inverse Chebyshev,and Causer )在输出信号中引入的相位变化与频率不成比例。
相位随频率变化的速率称之为群延迟(group delay )。
群延迟随滤波器级数的增加而增加。
模拟滤波器的归一化归一化的滤波器是通带截止频率为w=1radian/s, 也就是1/2πHz 或约0.159Hz 。
这主要是因为电抗元件在1弧度的时候,描述比较简单,XL=L, XC=1/C ,计算也可以大大简化。
归一化的无源滤波器的特征阻抗为1欧姆。
归一化的理由就是简化计算。
Bessel filter特征:通带平坦,阻带具有微小的起伏。
阻带的衰减相对缓慢,直到原理截止频率高次谐波点的地方。
原理截止频率点的衰减具有的经验公式为n*6dB/octave ,其中,n 表示滤波器的阶数,octave 表示是频率的加倍。
例如,3阶滤波器,将有18dB/octave 的衰减变化。
正是由于在截止频率的缓慢变化,使得它有较好的时域响应。
Bessel 响应的本质截止频率是在与能够给出1s 延迟的点,这个点依赖于滤波器的阶数。
逆切比雪夫LPF 原型参数计算公式(Inverse Chebyshev filterparameters calculate equiations ))(cosh )(cosh 11Ω=--Cn n 其中 1101.0-=A Cn , A 为抑制频率点的衰减值,以dB 为单位;Ω为抑制频率与截止频率的比值例:假设LPF 的3dB 截止频率为10Hz,在15Hz 的频点需要抑制20dB,则有:95.91020*1.0==Cn ;Ω=15/10=1.51.39624.0988.2)5.1(cosh )95.9(cosh 11===--n ,因此,滤波器的阶数至少应该为4图1 3阶逆切比雪夫LPF 结构如果用Ks 表示需要抑制频点的衰减dB 数,(说明:输入输出阻抗相等的情况下使用下面的公式)。

波导滤波器的制作与调试(2)波导金属柱滤波器
保罗·韦德; 张鹏宇(编译)
【期刊名称】《《电子制作》》
【年(卷),期】2012(000)011
【摘要】除了最简单的微波系统,在几乎所有的微波应用中,我们都需要利用滤
波器来抑制规定频段范围外的辐射及其可能产生的干扰信号。
对于大多数业余爱好者来说,一般会重复他人的设计方法。
一个结构过于简单的滤波器所能实现的性能是有限的,如果滤波器的结构较为复杂,对它的理解分析、制作或调试也会更困难。
但如果使用合适的仿真软件,同时配备较为齐全的实验设备,我们其实可以设计出结构简单、但同时性能优异的波导滤波器。
【总页数】6页(P28-33)
【作者】保罗·韦德; 张鹏宇(编译)
【作者单位】
【正文语种】中文
【中图分类】TN713
【相关文献】
1.基于十字连通形环形谐振腔金属-介质-金属波导的折射率传感器和滤波器 [J],
祁云平;张雪伟;周培阳;胡兵兵;王向贤
2.基于金属-电介质-金属波导结构的等离子体滤波器的数值研究 [J], 杨韵茹;关建
飞
3.波导滤波器的制作与调试(1)滤波器的概述 [J], 保罗·韦德(Paul Wade,
W1GHZ); 张鹏宇(编译)
4.波导滤波器的制作与调试(3)消逝模波导滤波器 [J], 保罗·韦德; 张鹏宇(编译)
5.基于波导设计软件的基片集成波导滤波器组的快速设计方法 [J], 杨书奎;刘飞;吴团锋
因版权原因,仅展示原文概要,查看原文内容请购买。