5.5 控制系统的相对稳定性
- 格式:ppt
- 大小:254.50 KB
- 文档页数:11


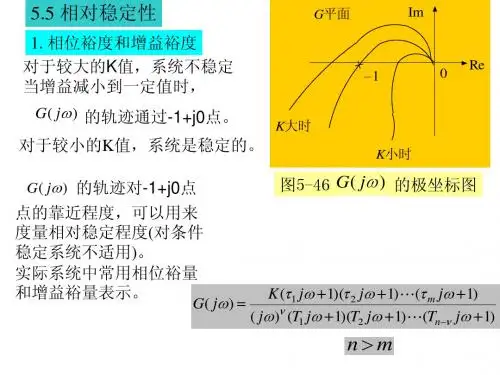



控制系统稳定性控制控制系统的稳定性是指在系统输入和干扰的作用下,系统输出能够保持在一定范围内,并且不会发生剧烈的波动或不稳定的情况。
稳定性是控制系统设计和优化中的重要考虑因素,它直接关系到系统的性能和可靠性。
一、稳定性的基本概念在控制系统中,稳定性可以分为两类:绝对稳定性和相对稳定性。
绝对稳定性是指当系统的任何初始条件和参数变化都不会引起系统的输出超出一定范围,系统始终保持稳定。
相对稳定性是指系统在参数变化或干扰作用下,虽然会有一定的波动或震荡,但最终输出会趋于稳定。
二、稳定性判断的方法常用的判断控制系统稳定性的方法有两种:时域方法和频域方法。
1. 时域方法时域方法是通过分析系统的状态方程或差分方程来判断系统的稳定性。
常用的判断方法有:极点位置判据、Nyquist稳定性判据、Hurwitz 稳定性判据等。
极点位置判据是指通过分析系统极点的位置来判断系统的稳定性。
当系统的所有极点的实部都小于零时,系统是稳定的。
Nyquist稳定性判据是将控制系统的开环传递函数绘制在复平面上,通过分析曲线的轨迹来判断系统的稳定性。
Hurwitz稳定性判据是通过分析系统特征方程的Jacobi矩阵行列式来判断系统的稳定性。
2. 频域方法频域方法是通过分析系统的频率响应来判断系统的稳定性。
常用的判断方法有:Bode稳定性判据、Nyquist稳定性判据等。
Bode稳定性判据是通过分析系统的频率响应曲线的相角和幅值来判断系统的稳定性。
当系统幅值曲线超过0dB的频率点相角为-180°时,系统是稳定的。
三、控制系统稳定性的控制方法为了保证控制系统的稳定性,通常采取以下方法进行控制:1. 增加稳定裕度稳定裕度是指系统在保持稳定的前提下,对参数变化或负载波动的容忍能力。
通过增加稳定裕度,可以提高系统的鲁棒性和可靠性。
常用的方法有:采用PID控制器、增加系统正反馈等。
2. 优化控制器参数优化控制器参数是通过对系统的传递函数进行分析和调节,使系统的性能指标达到最优。
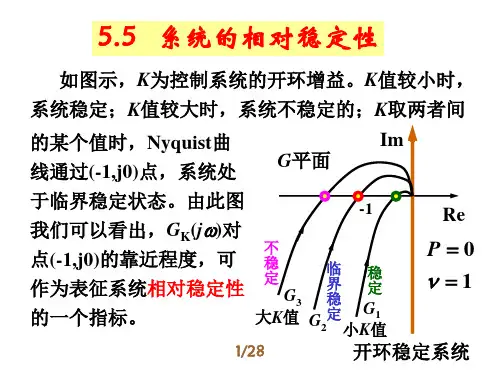




实验三控制系统的稳定性分析控制系统的稳定性是指系统在受到外部扰动或内部变化时,是否能保持原有的稳态或稳定的性能。
稳定性是控制系统设计和分析的重要指标之一,它直接影响系统的性能和可靠性。
本实验将介绍控制系统稳定性的分析方法和稳定性判据。
一.控制系统的稳定性分析方法1.传递函数法:传递函数是表示控制系统输入与输出之间关系的数学表达式,通过分析和求解传递函数的特征根,可以判断系统的稳定性。
在传递函数中,特征根的实部和虚部分别代表了系统的衰减和振荡性能,根据特征根的位置可以得到稳定、不稳定和临界稳定等几种情况。
2.极点分布法:极点分布是指控制系统的特征根在复平面上的位置分布。
通过绘制极点图可以直观地判断系统的稳定性。
一般来说,稳定系统的极点都位于左半复平面,而不稳定系统的极点则位于右半复平面。
3. Nyquist稳定性判据:Nyquist稳定性判据是通过绘制Nyquist曲线来判断系统的稳定性。
Nyquist曲线是将控制系统的特征根的位置映射到复平面上形成的闭合曲线,通过分析Nyquist曲线的形状和位置可以判断系统的稳定性。
4. Routh-Hurwitz稳定性判据:Routh-Hurwitz稳定性判据是基于特征多项式的系数和正负性进行判断的方法。
通过构造一个特征方程的判别矩阵,可以判断系统的稳定性。
如果判别矩阵的所有元素都大于0,则系统是稳定的。
二.控制系统的稳定性判据1.传递函数法:通过求解传递函数的特征根,判断特征根的实部和虚部是否满足系统稳定的条件。
特征根的实部必须小于0,而虚部可以等于0。
2.极点分布法:绘制控制系统的极点图,判断极点是否位于左半复平面。
如果所有极点都在左半平面,则系统是稳定的。
3. Nyquist稳定性判据:绘制Nyquist曲线,通过分析曲线的形状和位置来判断系统的稳定性。
如果曲线不经过原点或环绕原点的次数为0,则系统是稳定的。
4. Routh-Hurwitz稳定性判据:构造特征方程的判别矩阵,通过判别矩阵的元素是否都大于0来判断系统的稳定性。