小尺度桩波浪力计算

波浪力计算公式波浪力是描述海浪对海岸或其他结构物的冲击力的物理量。

它是指海浪作用于单位长度海岸线或结构物上的力量。

波浪力的计算公式可以使用斯托克斯公式来表示。

斯托克斯公式是描述波浪力计算的经典公式，它基于假设波浪是理想的正弦波。

根据斯托克斯公式，波浪力可以表示为：F = 0.5 * ρ * g * H^2 * L其中，F是波浪力，ρ是水的密度，g是重力加速度，H是波高，L 是波长。

波浪力的计算公式可以帮助我们了解海浪对海岸线或其他结构物的冲击程度。

通过计算波浪力，我们可以评估海岸线的稳定性，预测海岸侵蚀的风险，设计合适的防护工程等。

在海岸工程中，波浪力的计算是一个重要的任务。

通过对波浪力的计算，可以确定合适的海岸保护结构的尺寸和类型。

根据波浪力的大小，我们可以选择适当的海岸防护工程，如堤防、防波堤、海堤等，以减轻海浪对海岸的冲击。

除了海岸工程，波浪力的计算在海洋工程和海洋能利用领域也具有重要意义。

在海洋工程中，波浪力的计算可以用于设计海上平台、船舶和海洋结构物的稳定性。

在海洋能利用领域，波浪力的计算可以用于评估波浪能量的潜力和设计波浪能发电设备。

波浪力的计算公式是基于理想的正弦波假设。

然而，在实际情况中，海浪往往是复杂的，包含多种频率和方向的波浪成分。

因此，在实际应用中，需要考虑更复杂的波浪模型和数值方法来计算波浪力。

波浪力的计算公式是描述海浪对海岸线或其他结构物冲击力的重要工具。

它可以帮助我们评估海岸侵蚀的风险，设计合适的海岸防护工程，以及评估海洋工程和海洋能利用的可行性。

通过深入研究波浪力的计算公式，我们可以更好地理解海洋与人类活动的相互作用，保护海岸环境，促进可持续发展。

波浪力计算公式引言：在海洋工程中，波浪力是一个重要的参数，用于估计波浪对结构物的作用力。

波浪力的计算可以通过波浪力计算公式来实现。

本文将介绍波浪力计算公式的原理和应用，并探讨波浪力计算的相关问题。

一、波浪力计算公式的原理波浪力计算公式是根据波浪理论和结构动力学原理推导出来的。

其基本原理是根据波浪的特性和结构物的几何形状，通过计算波浪作用下的压力和力矩，进而得到波浪力的大小和方向。

二、常用的波浪力计算公式1. Morison公式：Morison公式是最常用的波浪力计算公式之一，适用于波浪作用下的柱状结构物。

该公式基于马克思-赫茨伯格(Morison)定律，考虑了波浪作用下的惯性力和阻力。

其表达式为：F = 0.5 * ρ * Cd * A * (dV/dt) + ρ * Cp * A * V * |V|其中，F为波浪力，ρ为水的密度，Cd和Cp分别为阻力系数和惯性系数，A为结构物的横截面积，V为波浪速度，dV/dt为波浪加速度。

2. Goda公式：Goda公式是一种改进的波浪力计算公式，适用于不规则波浪作用下的结构物。

该公式考虑了波浪的频率谱和结构物的响应特性，能更准确地估计波浪力。

其表达式为：F = ∫∫ (0.5 * ρ * Hs * g * S(f) * A * R(f)^2 * |H(f)|^2 * cos(θ))^0.5 df dθ其中，F为波浪力，ρ为水的密度，Hs为波浪高度，g为重力加速度，S(f)为波浪频率谱密度函数，A为结构物的横截面积，R(f)为结构物的响应函数，H(f)为波浪高度频谱密度函数，θ为波浪方向。

三、波浪力计算的应用波浪力计算公式广泛应用于海洋工程中的结构设计和安全评估。

通过计算波浪力，可以评估结构物的稳定性和安全性，为结构物的设计和施工提供依据。

例如，在海上风电场中，需要计算波浪力来评估风机基础的稳定性；在海岸工程中，需要计算波浪力来评估海堤的稳定性。

四、波浪力计算的相关问题1. 如何确定阻力系数和惯性系数？阻力系数和惯性系数是波浪力计算公式中的重要参数，可以通过试验或数值模拟来确定。

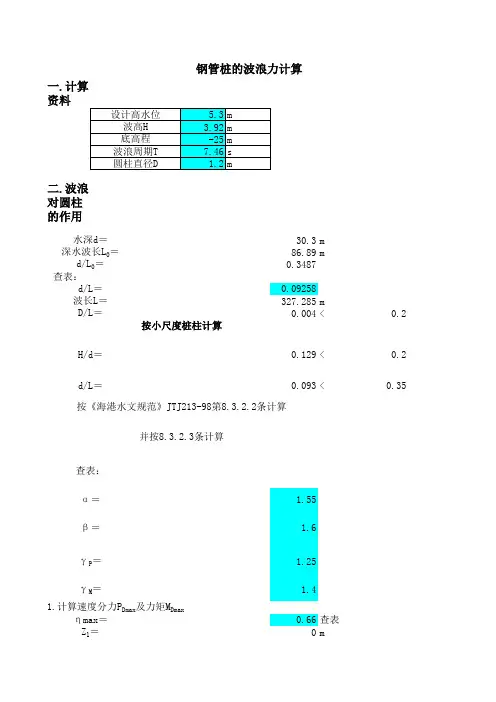
由Morison方程计算桩基平台的波浪力实例：有一桩基平台，平台的支撑结构由四根直径D=6.0m的圆柱组成。

平台设计工作水深d=40m，设计波高H=10m，设计周期T=10.4s。

试确定每根桩柱最大水平波浪力和作用点的位置，以及四根桩柱的最大水平合波力和最大水平合波力矩。

基本数据：设计水深d=40m 海水密度ρ=1.025×103kg/m3设计波高H=10.0m 桩柱直径D=6.0m设计波周期T=10.4s 桩柱之间距l=30.0m有波长计算公式：L=（gT2/2π）thkd=155.8115m波数k=2π/L=0.0403相对水深d/L=0.2567波陡H/L=0.0642相对桩径D/L=0.0385 (小直径桩)质量系数C M＝2.0拖拽力系数C D=1.0桩柱相对间距l/D=5选用群桩系数K=1.0计算：选用Ariy波理论，利用Ｍatlab编写进行计算。

（1）得到单根桩柱的最大水平拖拽力F HDmax,最大水平惯性力F HImax, 最大水平拖拽力矩M HDmax, 最大水平惯性力矩M HImax,见表1.表1 单桩水平方向最大拖拽力、惯性力及力矩（2）单桩最大水平波浪力F Hmax及最大水平波浪力矩M Hmax的计算。

因为F HImax =2622.8 kN >2F HDmax=2×673.05kN=1346.10 kN,所以单桩柱的最大水平波浪力F Hmax= F HImax=2622.8 kN因为M HImax =61438 kN﹒m >2M HDmax=2×21197 kN.m =42394 kN﹒m,所以单桩柱的最大水平波浪力M Hmax= M HImax=61438 kN﹒m因此，单桩柱发生最大水平波浪力F Hmax=和最大水平波浪力矩M Hmax的相位角在θ=π/2处。

最大水平波浪力作用点距海底的距离：e= M Hmax/ F Hmax=23.425m（3）计算不同相位θ时，前桩柱的水平波浪力F H和水平波力矩M H分别为：F H= F HDmax cosθ|cosθ|+ F HImax sinθ=673.05 cosθ|cosθ|+2622.8sinθM H= M HDmax cosθ|cosθ|+ M HImax sinθ=21197 cosθ|cosθ|+61438 sinθ计算结果列于表2.(4)利用表中数据绘制出前桩柱水平波浪力F H 随波浪相位角θ的变化曲线I 以及水平波浪力矩M H 随波浪相位角θ的变化曲线I （图1-2）。

波浪对桩柱作用力的计算分析港口码头、跨海桥梁、海洋工程中经常遇到波浪力对桩柱的作用，水中的桩柱结构所受的水平力主要来自波浪的作用。

对于一般的桩柱结构，当桩柱的直径D与波浪的波长L的比值D/L<0.2时，称此结构为小尺度结构物；当D/L>0.2时，则称为大尺度结构物[1]。

港口码头、跨海桥梁、海洋工程常用的桩柱结构，一般为小尺度结构物，因此本文重点探究小尺度结构物的波浪力计算。

1 波浪力的计算方法国内外对波浪力的计算理论相差不大，都是基于Morison公式[2]內对波浪力的计算主要有《海港水文规范》规定的方法，国外对波浪力的计算有美国的API、挪威的DNV等标准提出的方法。

基于Morison理论的波浪力计算公式如下：（公式-1）（公式-2）（公式-3）上式中：PD是波浪力的速度分力（也叫拖曳力）；PI是波浪力的惯性分力；CD是速度力系数；CM是质量力系数；D是桩柱直径；dz是桩柱上每一小分段的长度；A是桩柱的断面积。

u、u/t——分别为水质点轨道运动的水平速度和水平加速度；是圆频率；t是时间，当波峰通过柱体中心线时t=0；H、T分别是波高和波周期。

美国的API规范给出拖曳力系数取0.6～1.0，惯性力系数取2.0。

国内的《海港水文规范》给出拖曳力系数取1.2，惯性力系数取2.0。

《海港水文规范》提出的拖曳力系数和惯性力系数比较适合我国的情况，因此本文以《海港水文规范》给出拖曳力系数1.2、惯性力系数2.0进行波浪力计算。

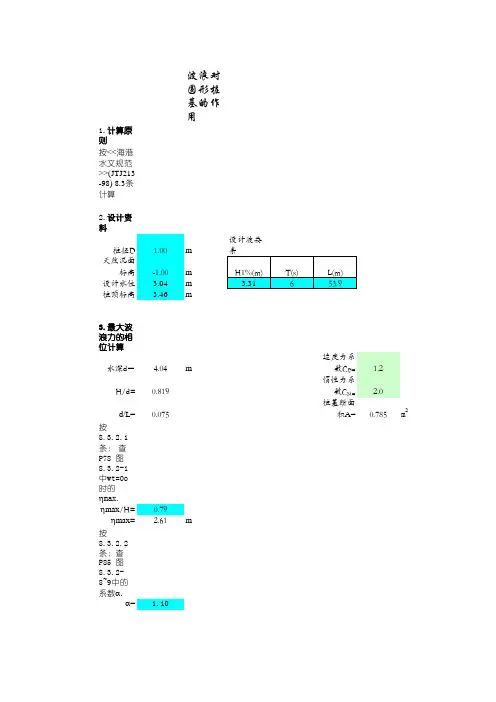
2 波浪力随高度和时间的变化趋势本文模拟了一个我国东部沿海的项目的桩基，该项目水深10m，采用垂直的钢管桩，桩体直径2.5m。

计算海浪的波长72m，波高3.9m，波周期7.8s。

采用Excel对周期T内的各时间点、沿桩柱各高度的拖曳力和惯性力的分力分别进行计算，然后用数值积分的方法将各分力沿桩柱高度进行积分，得出各时间点作用在桩柱上的波浪力的合力。

为考察波浪力随桩体高度变化趋势，按照公式1～3，将桩体在平均海平面以上分为10等份，在平均海平面以上分为2等份，进行拖曳力和惯性力计算。

波浪力计算公式引言：波浪力是指波浪对于物体施加的力量，它是海洋工程中一个重要的参数。

通过对波浪力进行准确的计算，可以帮助我们设计和构建海洋结构物，预测其受力情况，从而确保结构的安全性和稳定性。

本文将介绍波浪力的计算公式及其应用。

一、波浪力的定义波浪力是波浪作用在物体上的力量，它的大小与波浪的高度、周期、波浪传播方向以及物体的形状和尺寸等因素有关。

波浪力的计算是海洋工程中的一个重要问题，也是一项挑战性的任务。

二、波浪力的计算公式波浪力的计算公式可以用以下公式表示：F = 0.5 * ρ * g * H^2 * L其中，F为波浪力，ρ为水的密度，g为重力加速度，H为波浪高度，L为波长。

三、波浪力的应用波浪力的计算在海洋工程中有着广泛的应用。

例如，在设计海洋平台、堤坝、海底管道等结构物时，需要考虑波浪对这些结构物施加的力量。

通过使用波浪力计算公式，可以预测结构物在不同波浪条件下的受力情况，从而指导工程设计和施工过程。

在海洋工程中，波浪力的计算还可以用于预测海洋结构物的疲劳寿命。

由于波浪力是结构物受力的主要因素之一，通过对波浪力进行准确的计算，可以评估结构物的疲劳损伤程度，为结构物的维护和修复提供依据。

波浪力的计算还可以应用于海洋能利用领域。

波浪能和潮汐能是海洋能资源中的两个重要组成部分。

通过准确计算波浪力，可以评估波浪能装置的性能和效益，为海洋能的开发和利用提供科学依据。

四、波浪力计算的挑战和改进尽管波浪力的计算公式已经相对成熟，但在实际应用中仍然存在一些挑战。

例如，波浪力的计算需要准确测量波浪的高度、周期和波长等参数，这对于海洋工程来说是一项技术难题。

另外，波浪力的计算还需要考虑波浪与结构物之间的相互作用，这也增加了计算的复杂性。

为了解决这些问题，研究人员正在不断改进波浪力的计算方法。

一方面，他们致力于改进波浪参数的测量技术，例如利用遥感技术和数值模拟方法来获取更准确的波浪参数。

另一方面，他们还在研究波浪与结构物之间的相互作用机理，以提高波浪力计算的准确性。

基于ABAQUS的小尺度桩柱波浪力计算方法引言桩柱作为深水海域中结构物的主要支撑方式，受到波浪力的作用，往往会引发破坏，导致结构的失稳。

针对这种情况，需要对波浪力进行准确的计算，并通过结构模拟分析方法进行评估，以提高深水海域工程的安全性。

本文基于ABAQUS有限元分析软件，介绍一种小尺度桩柱波浪力计算方法。

桩柱波浪力计算方法桩柱受到波浪力的作用主要是由于波浪通过水流对由桩柱搭建的结构物产生的冲击作用，同时还会产生摩擦力和涡流力。

由于波浪对结构物的影响会随着深度的增加而逐渐减弱，因此在进行波浪力计算时，需要考虑深度因素。

针对桩柱受到波浪力后产生的应力、位移及损伤情况，我们通常选择采用有限元方法来进行分析。

ABAQUS作为广泛应用于结构仿真研究的软件，可以很好的满足这一需求。

具体而言，桩柱波浪力计算可采用以下方法：1. 设定研究区域首先，需要确定桩柱所在深度和桩柱周边水域的研究范围。

通常，我们可以通过UG软件等CAD工具来建立三维模型，然后进行网格划分。

2. 建立并计算波浪力针对建立好的模型，需要将波浪的力引入其中，通过计算波浪作用的瞬时冲击力来得出桩柱所受的力系。

在确定波浪力之前，需要先考虑波峰、波谷及周期等参数的选取。

3. 加载波浪力到模型中ABAQUS软件中提供了多种载荷方式，针对波浪力，我们通常采用瞬态动态载荷的方式进行模拟。

这种模拟可以模拟出波浪对结构物造成的瞬间载荷，相对于稳态载荷下的静力测试来说，更能模拟出结构物真正所受的波浪力。

4. 分析研究模型应力、位移及损伤情况最后，我们需要采用ABAQUS提供的后处理工具，对模拟得到的应力、位移及损伤情况进行分析，以确定桩柱的稳定性以及结构物的安全系数。

总结桩柱波浪力计算方法是深水海域工程研究中的重要内容。

基于ABAQUS有限元分析软件的小尺度桩柱波浪力计算方法，能够准确地计算桩柱受到波浪力后的应力、位移及损伤情况，有助于提高深水海域工程的安全性。

波浪桩刚度计算公式首先，我们需要考虑波浪作用下桩身的弯矩和剪力。

波浪作用下的水力压力可以通过伯努利方程计算得到，即：P=0.5*ρ*g*H^2其中，P为波浪作用下的水力压力，ρ为水的密度，g为重力加速度，H为波高。

当波浪通过桩身时，将会产生弯矩M和剪力V。

根据静力平衡的原理，我们可以得到：M=P*hV=P*A其中，h为桩身其中一截面离开水面的高度，A为桩身其中一截面的净面积。

现在，我们开始推导波浪桩刚度的计算公式。

在推导中，我们假设波浪桩为弹性材料，并忽略桩的自重和背注力。

首先，我们假设桩身在波浪作用下的变形为弯曲变形。

根据弯曲理论，桩身在弯曲作用下的变形可以由以下公式计算得到：δ=M*L^2/(2*E*I)其中，δ为桩身的纵向变形，L为桩身的长度，E为桩身材料的弹性模量，I为桩身截面的惯性矩。

由于我们忽略了桩身的自重和背注力，所以这里的弯曲变形只是由波浪作用产生的变形。

接下来，我们需要将变形表达式中的弯矩M和剪力V用波浪力P表示。

根据前面的推导，我们可以得到：M=P*h=0.5*ρ*g*H^2*hV=P*A=0.5*ρ*g*H^2*A将上述表达式代入弯曲变形的计算公式中，我们可以得到波浪桩的刚度计算公式：δ=(0.5*ρ*g*H^2*h*L^2)/(2*E*I)根据公式可以看出，波浪桩的刚度与波高H的平方成正比，与桩身离开水面的高度h、桩身长度L、截面净面积A、材料的弹性模量E和截面的惯性矩I都有关系。

需要注意的是，上述的刚度计算公式只是一个简化的理论模型，它假设桩身变形是弯曲变形，并忽略了其他因素的影响。

在实际应用中，刚度的计算需要考虑更多的因素，如桩身的支承方式、土壤的力学特性、波浪的频率和形态等。

因此，在实际工程中，一般需要结合实测数据和经验公式来确定波浪桩的刚度。

桩基结构物波浪力的工程计算方法桩基结构物在海洋工程中具有举足轻重的地位，而波浪力是影响桩基结构物稳定性和安全性的关键因素之一。

因此，对桩基结构物波浪力的工程计算方法进行研究，对保障海洋工程的安全性和稳定性具有重要意义。

本文将围绕桩基结构物波浪力的工程计算方法展开讨论，旨在明确计算方法及其在实际工程中的应用。

桩基结构物波浪力是指海洋工程中桩基结构物受到海浪作用产生的力。

这种力的产生主要源于海浪的冲击力、海流力和重力等多种因素。

波浪力的计算公式通常根据物理力学原理进行推导，是桩基结构设计中的重要参数。

在实际工程中，波浪力的计算方法大致可分为经验法和理论法两类。

经验法主要依据实际工程数据进行拟合计算，而理论法则是基于物理力学理论进行计算。

有限元法是一种常用的数值计算方法，适用于各种复杂的工程问题。

在桩基结构物波浪力的计算中，有限元法可以将桩基和周围介质视为离散的单元体，通过对单元体进行力学分析，得到每个单元体上的力与位移关系，最终得到整个结构的应力与变形。

模拟法是通过计算机模拟海浪对桩基结构物的作用过程，从而得到结构物所受的波浪力。

这种方法需要建立海浪模型和桩基结构物模型，通过设定不同的海浪条件和结构物参数，进行大量模拟计算，最终得到不同条件下的波浪力。

为了说明上述计算方法的有效性和可行性，我们选取了一个实际案例进行详细的分析和验证。

该案例为某海上风电场桩基结构物，基础形式为单桩基础。

我们运用有限元法对该结构物进行了建模，并对其在不同海浪条件下的波浪力进行了模拟计算。

计算结果表明，在相同的海浪条件下，有限元法与模拟法得到的波浪力结果相近，证明了这两种计算方法的可靠性。

同时，通过对比分析，我们发现有限元法在处理复杂边界条件和多因素耦合问题上具有更大的优势。

本文对桩基结构物波浪力的工程计算方法进行了系统的探讨，分别介绍了经验法和理论法两种计算思路，并详细推导了其中的公式和理论。

通过实例分析和验证，说明这些方法在计算桩基结构物波浪力上的有效性和可行性。

波浪对桩柱作用力的计算波浪对桩柱作用力的计算是海洋工程中重要的研究内容。

波浪在桩柱上的作用力分为水平力和垂直力两种，其中垂直力对桩柱的稳定性影响较大。

本文将介绍波浪对桩柱作用力的计算方法及其对海洋工程的应用。

一、波浪对桩柱垂直力的计算波浪对桩柱垂直力的计算可以采用线性水波理论或非线性水波理论。

线性水波理论是一种经验公式，适用于波高小于1/7水深的情况。

非线性水波理论考虑了波浪的非线性因素，适用于波高大于1/7水深的情况。

1. 线性水波理论线性水波理论最早由Stokes提出，其公式表达如下：$$F=ρgh\cdot A$$其中，F为波浪垂直力，ρ为水密度，g为重力加速度，h为波高，A为横截面积。

Stokes公式的前提条件是波高比较小，海洋工程中较少使用。

2. 非线性水波理论非线性水波理论与线性水波理论相比，考虑了波浪的非线性因素，因此更加准确。

非线性水波理论中最常用的是Mild-Slope equation，其公式表达如下：$$F=\frac{1}{g}(\frac{∂P}{∂z})$$其中，F为波浪垂直力，g为重力加速度，P为波浪压力，z为水深。

Mild-Slope equation适用于海洋深度较大的海域，且波浪高度不太受深度影响的情况。

二、波浪对桩柱水平力的计算波浪对桩柱水平力的计算较为复杂，需要考虑波浪和桩柱之间的摩擦力和慣性力等因素。

常用的计算方法有Morison方程、Barracuda方程和Strip Theory等。

1. Morison方程Morison方程是目前海洋工程中最常用的波浪和桩柱的作用力计算方法。

该方法将桩柱的作用力分为二阶谐波力和非二阶谐波力。

其中，二阶谐波力对于波高较小的海域较为准确，而非二阶谐波力对于波高较大的海域较为准确。

Morison方程的公式表达如下：$$F_{x}=ρC_{d}D_{p}V(t)^{2}+ρC_{m}D_{p}ẋ(t)+F_{xN}$$$$F_{y}=ρC_{d}D_{p}V(t)^{2}+ρC_{m}D_{p}ẏ(t)+F_{yN}$$其中，Fx和Fy分别为水平力和横向力，ρ为水密度，Cd 为Morison方程中的阻力系数，Dp为桩柱直径，V(t)为波浪速度，Cm为Morison方程中的惯性系数，ẋ(t)和ẏ(t)分别为桩柱在水平和垂直方向上的速度，FxN和FyN分别为非二阶谐波力。

小尺寸双柱式桥墩波浪力的数值分析柳春光;李璐璐;张士博【期刊名称】《水利与建筑工程学报》【年(卷),期】2016(014)005【摘要】Morison 方程适用于小直径孤立柱的波浪力计算，对于双柱式桥墩的波浪力计算已不能直接采用 Morison 方程。

为了能利用 Morison 方程求解双柱式桥墩的波浪力，定义了双柱式桥墩前柱、后柱及整体结构的波浪力干扰系数。

采用线性波浪理论，利用推板式造波方法模拟线性波，将 ANSYS Workbench平台作为 FLUENT 和 ANSYS 的数据传递平台，对深水环境下双柱式桥墩受到的波浪力以及波浪场作用下双柱式桥墩的结构变形进行单向流固耦合数值模拟。

数值模拟结果表明，双柱式桥墩前、后柱波浪力的干扰系数在一定柱距范围内均随柱距的增大近似的成线性增大，当柱距超过一定值后趋于稳定。

由于双柱间存在相位差，双柱墩波浪力的总干扰系数以及双柱墩的结构变形却随着双柱中心距的增大而减小。

这些变化曲线为实际工程中深水桥梁双柱式桥墩的波浪荷载计算提供了一种更为简便的算法。

【总页数】7页(P6-12)【作者】柳春光;李璐璐;张士博【作者单位】大连理工大学建设工程学部，辽宁大连 116024; 大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024;大连理工大学建设工程学部，辽宁大连 116024;大连理工大学建设工程学部，辽宁大连 116024【正文语种】中文【中图分类】U442.55【相关文献】1.软土场地上双柱式桥墩-桩-土相互作用体系地震反应特性的数值分析 [J], 李冬来;熊巨华2.拼装式双柱桥墩梁-柱接头的抗震验算方法 [J], 陈兴冲;田琪;孙杰3.拼装式双柱桥墩梁-柱接头抗震能力的评估 [J], 陈兴冲;虞庐松;田琪4.中、英、美规范计算小尺寸桩(柱)波浪荷载的对比 [J], 杨艺平; 杨佳岩5.波浪作用对单柱式桥墩地震反应特性的影响 [J], 白德贵;陈国兴;王志华因版权原因，仅展示原文概要，查看原文内容请购买。