桩土相互作用模型分析及土弹簧的刚度确定

公路桩基土弹簧计算方法一、引言公路桩基是公路工程中常见的基础形式之一，用于支撑桥梁、隧道、边坡等结构。

而基础的稳定性则取决于基土的性质以及其与桩基之间的相互作用。

在公路桩基设计中，弹簧计算方法被广泛应用于桩基土的力学性能分析和设计。

二、弹簧模型弹簧模型是一种简化的模型，将基土与桩基之间的相互作用力看作是一组弹簧的作用。

在这个模型中，基土和桩基分别被看作是相互连接的弹簧，其刚度可以通过试验或经验公式来确定。

三、基土弹簧刚度的计算基土弹簧的刚度可以通过试验数据或经验公式来计算。

其中，试验数据是最直接、准确的刚度计算方法。

通过在实验室或现场进行试验，可以获得基土在不同荷载下的应力-应变关系曲线，进而计算出基土的刚度参数。

另一种计算方法是利用经验公式，根据基土的工程性质和试验数据进行拟合。

这些经验公式基于大量试验数据的统计分析，可以较好地反映基土的力学性能。

然而，由于基土的性质在不同地区和工程中存在差异，因此在使用经验公式时需要注意其适用范围。

四、桩基弹簧刚度的计算桩基弹簧的刚度计算与基土弹簧类似，可以通过试验数据或经验公式来确定。

在试验中，通过在桩基上施加荷载并测量其位移，可以计算出桩基的刚度参数。

而经验公式则根据桩基的几何形状和材料性质进行拟合，以得到刚度参数。

五、弹簧模型的应用在公路桩基土弹簧计算中，弹簧模型被广泛应用于分析桩基在不同荷载下的变形和应力分布。

通过建立弹簧模型，可以计算出桩基和基土之间的相互作用力，进而评估桩基的稳定性和承载能力。

弹簧模型的应用可以通过有限元方法、解析方法或其他数值方法来实现。

其中，有限元方法是一种常用的数值计算方法，通过将桩基土系统离散为多个小单元，并建立相应的刚度矩阵，可以计算出桩基和基土之间的相互作用力和变形情况。

六、案例分析以某公路桥梁的桩基为例，假设桩基为直径为1m、长度为20m的钢筋混凝土桩。

根据现场试验数据和经验公式，得到基土的刚度为1×10^6 N/m，桩基的刚度为2×10^6 N/m。

桩-土-桩相互作用有限元接触分析摘要：桩土体作为一个共同工作的系统，广泛存在于土木工程实践中，是典型的接触问题之一，对桩-土-桩相互作用的研究也是工程十分关心的，其中桩身摩阻力的分布更是关键所在。

本文基于有限元数值分析方法软件对此进行了深入研究。

关键词：有限单元法；接触非线性；桩土相互作用；桩侧摩阻力中图分类号：TU43 文献标识码：A 文章编号：1006-4311（2010）11-0108-020 引言桩土相互作用问题的实质是固体力学中不同介质的接触问题，具体表现为材料非线性、接触非线性等。

目前，有限单元法是解决复杂空间结构静、动力问题、弹塑性问题最有效的数值方法之一。

本文对桩土相互作用中接触问题进行分析时主要采用接触非线性有限元法，利用ABAQUS有限元软件进行研究。

1 ABAQUS软件概述ABAQUS是功能强大的有限元法软件[1,2]，提供了广泛的功能且使用起来十分简明。

对于非线性分析，ABAQUS能自动选择合适的荷载增量和收敛精度，且拥有十分丰富的、可模拟任意实际形状的单元库。

2 ABAQUS桩土接触分析中需解决的问题2.1 单元类型的选择在接触模拟中采用二阶单元会引起接触面上等效节点力的计算出现混淆，因此接触面两侧的单元一般不宜采用二阶单元，只能采用线性单元。

2.2 主从接触面的建立可以通过定义接触面（surface）来模拟接触问题，本文所涉及的桩土体之间的接触面主要有两类：①桩侧单元构成的柔性接触面（桩侧土体表面）或刚性接触面（桩表面）；②桩底土体一般采用节点构成的接触面，选取桩底土体节点时，不包含己定义在柔性接触面上的节点。

在模拟过程中，接触方向总是主面的法线方向，从面上的节点不会穿越主面，但主面上的节点可以穿越从面。

一般遵循以下原则：①应选择刚度较大的面作为主面，对于刚度相似的两个面，应选择网格较粗的面作为主面；②主面不能是由节点构成的面，并且必须是连续的；③如果接触面在发生接触的部位有很大的凹角或尖角，应该将其分别定义为两个面；④如果两个接触面之间的相对滑动小于接触面单元尺寸的20%，选用小滑动，否则选用有限滑动。

用MIDAS模拟桩-土相互作用（“m法”确定土弹簧刚度）迈达斯技术2009年05月1、引言土与结构相互作用的研究已有近60～70年的历史，待别是近30年来，计算机技术的发展为其提供了有力的分析手段。

桩基础是土建工程中广泛采用的基础形式之一，许多建于软土地基上的大型桥梁结构往往都采用桩基础，桩-土动力相互作用又是土-结构相互作用问题中较复杂的课题之一。

至今已有不少关于桩基动力特性的研究报告，国外研究人员也提出了许多不同的桩-土动力相互作用计算方法。

从研究成果的归类来看，理论上主要有离散理论和连续理论及两者的结合，解决的方法一般有集中质量法、有限元法、边界元法和波动场法。

60～70年代，美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法，目前已在国外得到了广泛的应用。

集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体，来建立整体耦联的地震振动微分方程组进行求解。

该模型假定桩侧土是Winkler连续介质。

以半空间的Mindlin静力基本解为基础，将桩-土体系的质量按一定的厚度简化并集中为一系列质点，离散成一理想化的参数系统。

并用弹簧和阻尼器模拟土介质的动力性质，形成一个包括地下部分的多质点体系。

土弹簧刚度的确定，除考虑使用较为精确的有限元或边界元方法外，较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规中土弹簧的计算方法。

我国公路桥涵地基与基础设计规(JTG D63-2007)用的“m法”计算方法和参数选取方面比Penzien的方法要简单和方便，且为国广大工程师所熟.“m法”的基本原理是将桩作为弹性地基梁，按Winkler假定（梁身任一点的土抗力和该点的位移成正比）求解。

但是，由于桩-土相互作用的实验数据不足，土的物性取值有时亦缺乏合理性，在确定土弹簧的刚度时，仍有不少问题未能很好解决。

特别是，“m法”中m的取值对弹簧刚度的计算结果影响很大，且不能反映地震波的频率特性和强度带来的影响。

1 用MIDAS模拟桩-土相互作用（“m法”确定土弹簧刚度）北京迈达斯技术有限公司2009年05月1、引言土与结构相互作用的研究已有近60～70年的历史，待别是近30年来，计算机技术的发展为其提供了有力的分析手段。

桩基础是土建工程中广泛采用的基础形式之一，许多建于软土地基上的大型桥梁结构往往都采用桩基础，桩-土动力相互作用又是土-结构相互作用问题中较复杂的课题之一。

至今已有不少关于桩基动力特性的研究报告，国内外研究人员也提出了许多不同的桩-土动力相互作用计算方法。

从研究成果的归类来看，理论上主要有离散理论和连续理论及两者的结合，解决的方法一般有集中质量法、有限元法、边界元法和波动场法。

60～70年代，美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法，目前已在国内外得到了广泛的应用。

集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体，来建立整体耦联的地震振动微分方程组进行求解。

该模型假定桩侧土是Winkler连续介质。

以半空间的Mindlin静力基本解为基础，将桩-土体系的质量按一定的厚度简化并集中为一系列质点，离散成一理想化的参数系统。

并用弹簧和阻尼器模拟土介质的动力性质，形成一个包括地下部分的多质点体系。

2 土弹簧刚度的确定，除考虑使用较为精确的有限元或边界元方法外，较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规范中土弹簧的计算方法。

我国公路桥涵地基与基础设计规范(JTG D63-2007)用的“m法”计算方法和参数选取方面比Penzien 的方法要简单和方便，且为国内广大工程师所熟.“m法”的基本原理是将桩作为弹性地基梁，按Winkler假定（梁身任一点的土抗力和该点的位移成正比）求解。

但是，由于桩-土相互作用的实验数据不足，土的物性取值有时亦缺乏合理性，在确定土弹簧的刚度时，仍有不少问题未能很好解决。

特别是，“m法”中m的取值对弹簧刚度的计算结果影响很大，且不能反映地震波的频率特性和强度带来的影响。

桩周土体静阻力模型分析及在打桩中的应用1概述在运用波动方程法预测桩的可打入性及单桩极限承载力中，桩周土体静力模型的合理选择是个极其重要的问题。

土体的静力特性远非线弹性、理想弹塑性能简单描述，而非线性、非弹性、弹塑性等模型可较好地描述。

因此，改良土体静力模型及其计算参数确实定方法，是进一步完善波动方程分析法的一个非常重要方面。

桩侧摩阻力的发挥一般是桩体和土体之间的剪切破坏,也可能是桩体带着部分土体，土体间的剪切破坏，而桩端阻力的发挥有的是刺入破坏，有的是压剪破坏［1］。

由此可知，桩侧土主要承受剪切变形，而桩端土体变形主要是压缩，而且不能承受拉应力，桩侧土体和桩端土体的变形和破坏机理是截然不同的。

文献［2］通过室内剪切试验，测得不同法向压力下，钢和混凝土材料分别与土之间的摩阻力与剪切位移的关系曲线，用以描述桩、土间的荷载传递特性。

结果说明摩阻力和剪切位移呈非线性关系，而且符合双曲线方程。

汉森(Hansen).瑞典桩基委员会和ISSMFE提案也都曾假定压载试验的荷载-位移(P-S)曲线为双曲线［3］。

曹汉志［4］通过试桩发现实测到的荷载传递曲线可近似用双曲线来描述。

王幼青、张克绪［5］等人通过分析71根桩的压载试验的荷载-位移(P-S)曲线，得到S/P-S的线性回归的相关系数的平均值为O.9976,这说明桩的荷载-位移（p-S）曲线完全可近似用双曲线关系来拟和。

但该文中不分桩侧土体、桩端土体，均采用双曲线模型来模拟，模型中参数完全基于桩的静载荷试验值，不易推广。

由上述土力学理论及室内、室外试验结果，都说明在静荷载作用下桩周土体表现出非线性特性，并可用双曲线来描述荷载与位移的关系。

但基于桩侧土体和桩底土体的变形及破坏机制不一样，而且桩端土不能承受拉力的特点，因此,桩侧与桩端土体静力模型应用不同的模型来描述。

为简化起见，文中桩侧土体静摩阻力与剪切位移的模型采用双曲线关系，桩端土体仍采用理想弹塑性模型来描述（即同Smith法[6]）o2桩周土体模型2.1改良的桩侧土体模型在动力打桩过程中，桩侧土体单元i在时刻t时所发挥的静阻力和动阻力分别由非线性弹簧（双曲线）和缓冲壶组成的模型来模拟。

水平地震作用下桩—土—上部结构弹塑性动力相互作用分析一、本文概述《水平地震作用下桩—土—上部结构弹塑性动力相互作用分析》这篇文章主要探讨了水平地震作用对桩—土—上部结构体系的影响，并详细分析了这一复杂系统在地震作用下的弹塑性动力相互作用。

本文旨在深入理解地震时桩—土—上部结构体系的动态行为，为工程实践提供理论依据和指导，以提高结构的抗震性能。

本文首先介绍了地震作用下桩—土—上部结构体系的研究背景和意义，阐述了国内外在该领域的研究现状和发展趋势。

接着，文章对桩—土—上部结构体系的弹塑性动力相互作用进行了理论分析，包括桩土相互作用、地震波的传播与散射、结构的动力响应等方面。

在理论分析的基础上，本文进行了数值模拟和实验研究。

通过建立合理的数值模型，模拟了不同地震波作用下的桩—土—上部结构体系的动态响应过程，得到了结构的地震反应特性和破坏模式。

同时，结合实验数据，验证了数值模拟的有效性，并对模拟结果进行了深入分析。

本文总结了地震作用下桩—土—上部结构弹塑性动力相互作用的研究成果，指出了现有研究的不足和未来研究方向。

文章强调了在实际工程中应考虑桩土相互作用的影响，合理设计抗震结构，以提高结构的整体抗震性能。

通过本文的研究，可以为工程师和科研人员提供有益的参考，推动桩—土—上部结构体系抗震设计方法的改进和完善，为保障人民生命财产安全和提高建筑行业的可持续发展水平做出贡献。

二、桩—土—上部结构相互作用的基本理论桩—土—上部结构的相互作用是一个复杂且关键的动力学问题，涉及到地震波传播、土壤动力学、结构动力学等多个领域。

在水平地震作用下，土壤对桩的约束和桩对土壤的支撑形成了相互作用力，这些力通过桩传递到上部结构，进而影响整个系统的动力响应。

桩—土相互作用的理论基础主要是基于土的动力学特性和桩土之间的接触关系。

土壤在地震作用下的行为受到其本身的物理特性（如密度、弹性模量、泊松比等）和动力特性（如阻尼比、剪切波速等）的影响。

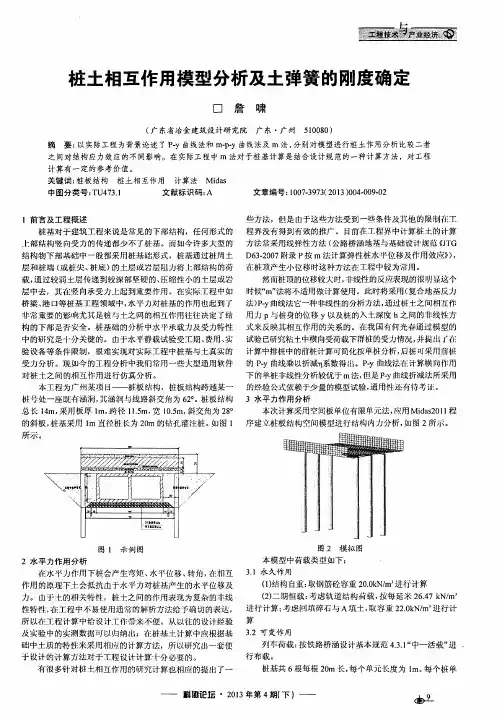
等代土弹簧刚度ks 计算参照《土力学与基础工程》(赵明华主编)中的“地基土横向抗力系数的比例系数m 值”,桩的计算宽度可按下式计算,且:d b 21≤:当时m d 0.1≥ )1(1+=d kk b f当时m d 0.1∠ )5.05.1(1+=d kk b f当桩m d 0.1∠､单排桩或116.0h L ≥的多排桩K=1.0对的多排桩116.0h L 11226.01h L b b k •-+= 式中:1b —桩的计算宽度(m) d —桩径或垂直于水平外力作用方向桩的宽度(m)f k —桩形状换算系数,视水平力作用面(垂直于水平力作用方向)而定,圆形或圆端截面9.0=f k ;矩形截面0.1=f k ;对圆端形与矩形组合截面da k f 1.01-= k —桩间相互影响系数;1L —平行于水平力作用方向的桩间净距;梅花形布桩时,若相邻两排桩中心距c 小于(d+1)m 时,可按水平力作用面各桩间的投影距离计算｡1h —地面或局部冲刷线以下桩的计算埋入深度,可取1h =3(d+1),但不得大于地面或局部冲刷线以下桩入土深度h .2b —平行于水平力作用方向的一排桩的桩数n 有关系数,当n=1时,2b =1.0;n=2时,2b =0.6;n=3时,2b =0.5;n≧4时,2b =0.45;采用式-1公式计算土弹簧刚度ks ｡mz ab k s 1= 式-1式中:a ——计算位置所处的土层厚度,取每个单元长度a=1.0m ｡z ——计算位置土层深度m ——水平地基抗力系数M 值列表 地基土质情况M 值(KN/m 4) 0.1≥L I 的粘性土,淤泥 1000~20005.00.1≥L I 的粘性土,粉砂 2000~400005.0≥L I 的粘性土,中､细沙 4000~60000 L I 的粘性土,粗砂 6000~10000砾石､砾砂､碎石､卵石10000~20000 L 位大于10mm 时,取表中较小值｡上海南浦大桥纵向地震反应分析2007-05-07 16:17上海南浦大桥纵向地震反应分析范立础袁万城胡世德(同济大学)【摘要】本文采用克拉夫(CIough)拟静力位移的概念,建立包括柱周土弹簧在内的结构多点激振增量动力平衡方程,并考虑了拉索､塔和辅助墩预应力拉索支座的非线性,对上海南浦大桥进行了考虑桩一土一结构相互作用和行波效应的纵向水平地震反应分析｡一､前言上海南浦大桥是一座双塔双素面斜拉桥,跨径为76.5十94.5十423.0十94.5十76.5m ｡除二个主塔外,主跨两侧对称布置锚固墩和辅助墩｡主塔为H型门式塔架,主梁和主塔间无支座连接,仅有挡块限制梁的横向摆动,属漂浮体系,主梁采用工型钢板梁与混凝土桥面结合的复合结构,主梁和锚固墩之间除设有盆式橡胶支座外,另有预埋钢筋锚固,辅助墩采用预应力拉索支座,该支座允许梁自由下沉0.12m｡斜拉索呈扇形布置,在塔的两侧各有21对,中间另有一对0号索,故每个主塔有43对斜拉索｡主塔基础为98根直径0.914m､长度51.1m的钢管桩群｡主桥桥面宽为30.3m,其中行车道宽25.0m,二侧各设宽2.675m人行道｡引桥邻孔为预应力混凝土简支梁,通过牛腿搁置在斜拉桥边孔梁端上作为压重｡主桥布置示意见图1｡本文对南浦大桥纵向水平地层反应分析,考虑了索､塔和顶应力拉索支座的非线性,并分析了行波效应和桩一土一结构相互作用的影响｡二､南浦大桥动力计算模式和地震输入(一)动力计算模式本文仅讨论南浦大桥纵向水平地震反应,故采用平面杆系力学模式(图2),其中模式I考虑塔根固结,模式Ⅱ考虑桩一土一结构相互作用｡其中斜拉索自重引起垂度的非线性采用等效弹性模量的概念来处理;梁､塔柱单元的非线性是用截面的轴力弯距相互作用图作为屈服面(图3a),并在计算时程中每一步迭代循环之后修改切线刚度短阵和几何刚度短阵(P—△效应);作者已推导了弹塑性切线刚度矩阵;辅助墩处的预应力拉索采用图3b所示的力与位移关系来描述(在此,△1=0,△2=0.12m)｡处理桩一土一结构相互作用时,土壤的非线性特征是控制土动力作用的重要因素｡作者利用Kause1有关土一结构相互作用中主要非线性和次要非线性的概念,并结合桩基轿梁的具体情况,研究了在桩基桥梁结构相互作用中使用这一概念的可行性,并提出了大路桥梁结构非线性地震反应分析,可等价作为一维非线性场地地震反应分析与考虑桩周土弹性约束作用的多点激振下的桥梁结构非线性地震反应分析的方法｡因此,当采用自由场地地震分析结果输入时,桩周土的约束作用可用土弹簧来描述,其等代土弹簧杆单元的刚度由土介质的m值计算(所使用的土层的m 值有实测数据为依据),其定义为:式中a为土层的厚度;bp为该土层在垂直于计算模式所在平面的方向上的宽度,常取为桩计算宽度,按照规范有关规定取值｡等代土弹簧杆长度为1,弹性模量为E(任选),则面积为:为了减少力学模式的节点数,本模式采用三索并一索的处理,但在辅助墩上和相应锚索与尼索不予并索｡(二)地震输人南浦大桥桥址由上海地震局进行了地震危险性分析,提供了主桥东塔(位于浦东)和西塔(位于浦西)的基岩地震波三组,由同济大学结构理论研究所进行了覆盖土层的地震反应分析,提供了三组沿覆盖各土层沿深度变化的地震波,浦东与浦西有差别,图4所示为其中—组的浦东与浦西沿深度各土层地震波加速度峰值的变化情况｡对动力计算模式Ⅱ,考虑覆盖土层的自由场运动作为桩一土一结构力学模式的输入激励,即采用每组地震波,用沿桩深所在各土层的多点激励的办法求解｡本文只引用第三组地震波的计算结果作为讨论的依据｡对塔根固结的计算模式Ⅰ,采用每组波的地表波作为地震输入｡此外,还采用了E1—Centro 波的南北分量来分析南浦大桥的行波效应问题｡三､多点激振动力平衡方程桥梁结构在各支承处受到地面运动的作用,其运动方程为:基于拟静力位移的的概念,多点激振下的总结构反应位移可分离为动力反应位移和拟静力位移,可表示为:上式采用逐步积分法求出节点的动力位移及加速度增量,节点的总位移为节点的动力位移与拟静力位移之和｡每一步单元内力亦是动力位移量引起的内力与拟静力位移引起的内力之和｡四､南浦大桥地震反应分析为了分桥各种情况对漂浮体系的南浦大桥地震反应的影响,作者曾对十余种工况作了分桥对比,限于篇幅,本文只介绍主要的六种工况的分析结果,这六种工况的特点列于表l｡计算结果择要列于表2—表4､图5—图7｡从分析结果看,1､2工况均取塔根固结模式,采用第三组地震波的地表彼作为输入(浦东与浦西不相同),其拟静力反应很小,其原因是浦东和浦西不同地震波的地表被波形比较相似,而且其加速度峰值亦较接近｡4､5工况采用E1—Centro波作为输入,并考虑不计相位差和计入相位差(以1秒计)作比较,结果是当计入相位差影响时,浦东塔根截面弯矩减少了11.3%,浦西塔根截面弯矩减少了30%;浦东塔顶相对水平位移减少了20%,右塔顶相对水平位移减少了12.1%｡因此,对漂浮体系的斜拉桥来说,考虑行波效应对塔顶相对水平位移和塔根截面弯矩都是有益的｡但跨中竖向位移增加了208%,这是应该注意的｡从工况1､3情况分析,预应力拉索支承的使用,相对于竖向采用刚性杆约束来说,对塔顶水平位移反应影响很小,但对浦东塔根截面弯矩反应减少37%,对浦西塔根截面弯矩反应增加了16.5%,而对跨中竖向位移反应增加了315.3%,可见,预应力拉索支座的使用使漂浮体系斜拉桥地震反应有明显的变化,在抗震设计中应予注意｡采用桩一土一结构相互作用模式与塔根固结模式相比,地震反应普遍增大,其中浦东塔相截面弯矩增加了49.6%,右塔塔根截面弯矩增加了47.7%,浦东塔顶相对水平位移增加了36.5%,浦西塔顶水平相对位移增加了37.8%,跨中竖向位移由塔根固结模式的0.0119m增加到0.1378m｡究其原因,主要是由于地震波沿桩深度有一梯度变化,因而桩及其承台除受到地震波的平动分量外,还要受到摇摆分量｡由此可见,对深桩基础的漂浮体系斜拉桥,若不考虑桩一土一结构的相互作用,而取简化的塔根固结的计算模式,其结果是偏小的,会降低抗震设防要求｡从多种工况分析表明,上海南浦大桥的主桥结构的地震作用下是很安全的。

1 用MIDAS模拟桩-土相互作用（“m法”确定土弹簧刚度）北京迈达斯技术有限公司2009年05月1、引言60～70年代，美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法，目前已在国内外得到了广泛的应用。

集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体，来建立整体耦联的地震振动微分方程组进行求解。

该模型假定桩侧土是Winkler连续介质。

以半空间的Mindlin静力基本解为基础，将桩-土体系的质量按一定的厚度简化并集中为一系列质点，离散成一理想化的参数系统。

并用弹簧和阻尼器模拟土介质的动力性质，形成一个包括地下部分的多质点体系。

土弹簧刚度的确定，除考虑使用较为精确的有限元或边界元方法外，较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规范中土弹簧的计算方法。

我国公路桥涵地基与基础设计规范(JTG D63-2007)用的“m法”计算方法和参数选取方面比Penzien 的方法要简单和方便，且为国内广大工程师所熟.“m法”的基本原理是将桩作为弹性地基梁，按Winkler假定（梁身任一点的土抗力和该点的位移成正比）求解。

但是，由于桩-土相2 互作用的实验数据不足，土的物性取值有时亦缺乏合理性，在确定土弹簧的刚度时，仍有不少问题未能很好解决。

特别是，“m法”中m的取值对弹簧刚度的计算结果影响很大，且不能反映地震波的频率特性和强度带来的影响。

本次介绍的土弹簧的模拟是采用规范中的“m法”确定土的地基系数C（m的取值根据土的物性而定）,再由其算出土弹簧的水平刚度。

2、采用“m”法，确定土弹簧刚度桩在横轴向荷载作用下桩身的内力和位移计算，国内外学者提出了许多方法。

目前较为普遍的是桩侧土采用文克尔假定，通过求解挠曲微分方程，再结合力的平衡条件，求出桩各部位的内力和位移，该方法称为弹性地基梁法。

以文克尔假定为基础的弹性地基梁法从土力学观点看是不够严密的，但其基本概念明3确，方法简单，所得结果一般较安全，在国内外工程界得到广泛应用。

地下结构时程分析的桩基等代弹簧参数分析发表时间：2019-08-19T10:45:26.937Z 来源：《防护工程》2019年10期作者：黄国发[导读] 基于三维有限元模型时程分析结果，论证了桩基等代弹簧动力参数的有效性，可为后续类似工程设计问题提供参考。

上海市政交通设计研究院有限公司上海 200030摘要：本文以郑州某三层地下空间的结构三维抗震时程分析为背景，就桩基等代弹簧的刚度、阻尼等静动力参数进行了计算分析和确定。

基于三维有限元模型时程分析结果，论证了桩基等代弹簧动力参数的有效性，可为后续类似工程设计问题提供参考。

关键词：地下空间；结构抗震；时程分析；等代弹簧；1、引言对于较复杂的地下结构，时程分析法是非常适合的抗震分析手段。

其中结构-土体相互作用参数是时程分析法的关键因素之一。

桩-土相互作用的考虑是结构-土体相互作用分析的重要内容，存在两种处理方式[1]，一是将桩基作为结构的一部分，对桩基施加非线性弹簧，但是一般勘察报告不提供全面的动力参数；二是将桩作为结构的约束作用，采用多自由度等代弹簧来简化替代，基于一定的假设计算等代弹簧的静动力参数，郑一峰等[1]证明这种简化处理方法可满足工程精度要求。

2、工程背景本文背景工程，采用一柱一桩设计，由于勘察报告中参数不全面，若将桩基作为结构的一部分，其动力参数的确定存在较大难度，故动力时程分析时将桩基简化为非线性弹簧施加在桩顶与结构连接处，以此反映桩-土相互作用的非线性动力特性。

按规范要求，本工程结构仅考虑水平地震作用，但考虑大面积侧壁土体的约束，将忽略转动弹簧分量，本文就桩基等代弹簧的刚度及阻尼模型参数的确定过程进行分析。

3、桩基等代弹簧参数的确定3.1 竖向拉压弹簧刚度竖向等代弹簧，其拉压刚度不等，受压时有桩侧摩擦弹簧和桩底受压弹簧。

本工程桩侧摩擦弹簧刚度确定，根据抗浮工况中，假定合适的位移目标(10mm)，通过迭代计算确定, 弹簧刚度=单桩抗拔力特征值/位移；迭代确定其中短桩的摩擦弹簧刚度ks=171460 kN/m，长桩的摩擦弹簧刚度kL=328420 kN/m。

桩一土相互作用集中质量模型的土弹簧刚度计算方法篇一：桩一土相互作用集中质量模型的土弹簧刚度计算方法桩一土相互作用集中质量模型的土弹簧刚度计算方法桩一土相互作用集中质量模型的土弹簧刚度计算方法桩一土相互作用集中质量模型的土弹簧刚度计算方法孙利民刘东潘龙王君杰（同济大学桥梁工程系）[摘要]本文针对桥梁柱一土相互作用问题分析法中,如何合理地确定土弹簧的刚度和土体的变形的课题进行分析计算。

研究了不同地震强度下上弹簧刚度的变化特性，并将的方法和桥梁设计规范中的"法'计算结果进行比较，为桩一土相互作用问题的理论分析和参数选取提供重要的手段和依据。

关键词桩一土相互作用土弹簧刚度土体位移模型法一、引言对于城市高架桥梁、大跨桥梁等桩承重要工程结构，除保证其上部结构的抗震安全性外，在遭受大地震作用时避免其基础受损也十分重要。

近几年国外发生的大地震（如日本神户地震等）的震害表明，坐落在软弱土层上的桥梁桩基的震害十分突出，桩土相互作用这一课题又引起了人们的重视。

对于基础坐落在软弱土层上的桥梁结构来说，在地震发生时，桥梁上部结构的惯性力将通过基础反馈给地基，使地基产生局部变形。

同时，地基自身也会因地震力作用而发生变形，反过来影响上部结构的反应。

这即所谓地基一结构系统的相互作用。

考虑地基一结构系统的相互作用的影响，不仅可以更准确地掌握桥梁上部结构的地震反应，对于正确计算土中基础的内力和变形也十分必要。

土与结构相互作用的研究已有近60～70年的历史，待别是近30年来，计算机技术的发展为其提供了有力的分析手段。

桩基础是土建工程中广泛采用的基础形式之一，许多建于软土地基上的大型桥梁结构往往都采用桩基础，桩一土动力相互作用又是土一结构相互作用问题中较复杂的课题之一。

至今已有不少关于桩基动力特性的研究报告，国内外研究人员[1-8]也提出了许多不同的桩一土动力相互作用计算方法。

从研究成果的归类来看，理论上主要有离散理论和连续理论及两者的结合，解决的方法一般有集中质量法、有限元法、边界元法和波动场法。

桩土相互作用研究综述1 桩土相互作用的研究现状桩土相互作用问题属于固体力学中不同介质的接触问题,表现为材料非线性(混凝土、土为非线性材料)、接触非线性(桩土接触面在复杂受荷条件下有黏结、滑移、张开、闭合4形态)等,是典型的非线性问题。

为了能够全面地评价桩土的相互作用问题,通常需要确定桩、土体各自的应力和应变以及接触区域处位移和应力分布的数据,对影响桩土相互作用的各因素进行全面研究。

研究桩土相互作用问题需要考虑的因素有:(a)土的变形特征;(b)桩的变形特征;(c)桩的埋置深度;(d)时间效应(土的固结和蠕变);(e)外部荷载的形式(静载或动载);(f)施工顺序(即开挖、排水以及基础和上部结构施工各个阶段的影响)。

目前桩土相互作用的研究方法主要有理论分析法和试验方法。

1.1理论分析方法理论分析方法分为经典理论分析方法和数值分析方法。

1.1.1经典理论分析法(1)弹性理论法。

以Poulos方法为代表。

假定桩和土为弹性材料,土的杨氏模量ES或为常数或随深度按某一规律变化。

由轴向荷载下桩身的压缩求得桩的位移,由荷载作用于半无限空间内某一点所产生的Mindlin位移解求得桩周土体的位移。

假定桩土界面不发生滑移,即可求得桩身摩阻力和桩端力的分布,进而求得桩的位移分布。

如果假定Mindlin位移解在群桩的情况下仍旧适用,则弹性理论法可以被推广至群桩的相互作用分析中。

(2)剪切位移法。

以Cooke等为代表。

根据线性问题的叠加原理,可将剪切位移法推广到群桩的桩土相互作用分析中。

Nogami等基于上述思想再把每根桩分成若干段并考虑地基土分层特性,得到比Mindlin公式积分大为简化的数值计算方程组。

剪切位移法的优点是在竖向引入一个变化矩阵,可方便考虑层状地基的性况,均质土不需对桩身模型进行离散,分析群桩时不依赖于许多共同作用系数,便于计算。

(3)荷载传递法。

荷载传递法本质为地基反力法。

根据求取传递函数手段的不同,可将传递函数法分为Seed等提出的位移协调法和佐腾悟等提出的解析法。

桩一土相互作用集中质量模型的土弹簧刚度计算方法篇一：用MIDAS模拟桩土相互作用用MIDAS模拟桩-土相互作用（“m法”确定土弹簧刚度）北京迈达斯技术有限公司 2009年05月 11、引言土与结构相互作用的研究已有近60～70年的历史，待别是近30年来，计算机技术的发展为其提供了有力的分析手段。

桩基础是土建工程中广泛采用的基础形式之一，许多建于软土地基上的大型桥梁结构往往都采用桩基础，桩-土动力相互作用又是土-结构相互作用问题中较复杂的课题之一。

至今已有不少关于桩基动力特性的研究报告，国内外研究人员也提出了许多不同的桩-土动力相互作用计算方法。

从研究成果的归类来看，理论上主要有离散理论和连续理论及两者的结合，解决的方法一般有集中质量法、有限元法、边界元法和波动场法。

60～70年代，美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法，目前已在国内外得到了广泛的应用。

集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体，来建立整体耦联的地震振动微分方程组进行求解。

该模型假定桩侧土是Winkler连续介质。

以半空间的Mindlin静力基本解为基础，将桩-土体系的质量按一定的厚度简化并集中为一系列质点，离散成一理想化的参数系统。

并用弹簧和阻尼器模拟土介质的动力性质，形成一个包括地下部分的多质点体系。

2 土弹簧刚度的确定，除考虑使用较为精确的有限元或边界元方法外，较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规范中土弹簧的计算方法。

我国公路桥涵地基与基础规范(JTG D63-2007)用的“m 法”计算方法和参数选取方面比Penzien的方法要简单和方便，且为国内广大工程师所熟. “m法”的基本原理是将桩作为弹性地基梁，按Winkler假定（梁身任一点的土抗力和该点的位移成正比）求解。

但是，由于桩-土相互作用的实验数据不足，土的物性取值有时亦缺乏合理性，在确定土弹簧的刚度时，仍有不少问题未能很好解决。

桩土相互作用模型分析及土弹簧的刚度确定桩基地基相互作用在工程领域中是一个非常重要的研究方向。

如何分析桩土相互作用，确定土弹簧的刚度，已经成为研究者们长期以来的研究方向。

本文将着重介绍桩土相互作用模型的分析以及土弹簧刚度的确定方法。

一、桩土相互作用模型分析桩土相互作用的分析是一个很复杂的问题，需要考虑很多因素，例如桩的形状、尺寸、材质、荷载作用方式以及土体的本构模型等等。

因此，建立一个合适的桩土相互作用模型是非常重要的。

常用的桩土相互作用模型主要包括刚性桩模型、柔性桩模型、弹性桩-地基模型和弹塑性桩-地基模型等。

具体模型的选择应根据实际工程情况进行合理选择。

在选择模型的同时，还需要考虑模型的精度和适用范围。

1. 刚性桩模型刚性桩模型是一种假设桩完全刚性的模型，桩与土体之间不存在变形，荷载沿着桩轴线方向传递。

该模型的应用比较广泛，特别是在短桩和单桩承载力计算中。

但是，刚性桩模型忽略了桩与土体之间的变形，因此在一些长桩、柔性桩及复杂荷载情况下，其结果可能需要进行修正。

2. 柔性桩模型柔性桩模型是一种假设桩的刚度较小，桩与土体间存在较大变形的模型。

因此，在该模型中，桩遭受荷载后，桩柄会发生变形，从而引起桩端和土体的变形。

这种模型适用于长桩或软土等复杂工程情况的分析。

但是，柔性桩模型的计算较为复杂，同时模型误差也较大。

3. 弹性桩-地基模型弹性桩-地基模型是一种假设桩和土体都是均质的弹性体的模型。

该模型假设桩和土体在弹性阶段的反应服从弹性理论，可以较好地反映桩与土体之间的相互作用关系。

其应用比较广泛，适用于一些较小荷载的工程应用。

4. 弹塑性桩-地基模型弹塑性桩-地基模型是一种新的桩土相互作用模型，既考虑了弹性行为，也考虑了土体的塑性行为。

该模型能够比较准确地反映桩与土体之间的相互作用关系。

其应用范围广泛，特别适用于长桩和承载力较大的复杂应力场中的计算分析。

二、土弹簧的刚度确定在桩土相互作用中，土弹簧承担着承载荷载的重要作用。

桩一土相互作用集中质量模型的土弹簧刚计算方法篇一：桩一土相互作用集中质量模型的土弹簧刚度计算方法桩一土相互作用集中质量模型的土弹簧刚度计算方法桩一土相互作用集中质量模型的土弹簧刚度计算方法桩一土相互作用集中质量模型的土弹簧刚度计算方法孙利民刘东潘龙王君杰（同济大学桥梁工程系）[摘要]本文针对桥梁柱一土相互作用问题PushOver分析法中, 如何合理地确定土弹簧的刚度和土体的变形的课题进行分析计算。

研究了不同地震强度下上弹簧刚度的变化特性，并将Penzien的方法和桥梁设计规范中的 "m法'计算结果进行比较，为桩一土相互作用问题的理论分析和参数选取提供重要的手段和依据。

关键词桩一土相互作用土弹簧刚度土体位移 Penzien模型 m法一、引言对于城市高架桥梁、大跨桥梁等桩承重要工程结构，除保证其上部结构的抗震安全性外，在遭受大地震作用时避免其基础受损也十分重要。

近几年国外发生的大地震（如日本神户地震等）的震害表明，坐落在软弱土层上的桥梁桩基的震害十分突出，桩土相互作用这一课题又引起了人们的重视。

对于基础坐落在软弱土层上的桥梁结构来说，在地震发生时，桥梁上部结构的惯性力将通过基础反馈给地基，使地基产生局部变形。

同时，地基自身也会因地震力作用而发生变形，反过来影响上部结构的反应。

这即所谓地基一结构系统的相互作用。

考虑地基一结构系统的相互作用的影响，不仅可以更准确地掌握桥梁上部结构的地震反应，对于正确计算土中基础的内力和变形也十分必要。

土与结构相互作用的研究已有近60～70年的历史，待别是近30年来，计算机技术的发展为其提供了有力的分析手段。

桩基础是土建工程中广泛采用的基础形式之一，许多建于软土地基上的大型桥梁结构往往都采用桩基础，桩一土动力相互作用又是土一结构相互作用问题中较复杂的课题之一。

至今已有不少关于桩基动力特性的研究报告，国内外研究人员[1-8]也提出了许多不同的桩一土动力相互作用计算方法。