高二第一讲
- 格式:doc
- 大小:586.00 KB
- 文档页数:6

高二英语第一讲GOALS: 1. 定语从句的讲解; 2.定语从句的训练;3.历届高考英语单项选择题定语从句精选。
“介词+关系代词”引导的定语从句关系代词在定语从句中作介词宾语时,从句常常由“介词+关系代词”引出。
①The school (which / that) he once studied in is very famous.=The school in which he once studied is very famous.②Tomorrow I’ll bring here the magazine (which / that) you asked for.=Tomorrow I’ll bring here the magazine you asked.③This is the boy (whom / who / that) I played tennis with yesterday.=This is the boy I played tennis with yesterday.注意:1.含有介词的短语动词一般不拆开,介词仍放在短语动词的后面。
如:look for, look after, take care of 等。
This is the watch (which / that) I am looking for. (正)This is the watch for which I am looking. (误) 2.若介词放在关系代词前,关系代词指人时只可用whom,不可用who, that;关系代词指物时只可用which,不可用that。
关系代词是所有格时用whose。
The man with whom you talked just now is my neighbor. (正)The man with that / who you talked just now is my neighbor. (误)关系副词引导的定语从句1. when 指时间,在定语从句中作时间状语。


2024年秋季学期,高二年级开学第一课主题班会的主题是“互相了解”。
在这场班会中,我们将帮助同学们更好地认识彼此,增进相互之间的了解和信任,以此为基础,更好地展开我们的高中学习生活。
本次班会的教案大致分为以下三个部分:
第一部分:自我介绍
在这个部分,我们将为同学们提供一个自我介绍的机会,让他们了解自己班级中的其他同学。
在介绍时,需要同学们提供自己的姓名、家庭情况、兴趣爱好等。
通过这些信息,同学们可以了解彼此,找到共同点,建立联系。
在介绍完毕后,我们将组织一些小游戏,加深同学们之间的联系和了解。
第二部分:班级风采展示
在这个部分,我们将邀请每个班级代表,展示自己班级的风采。
可以是班级文化、班级条幅、班级logo等,只要是代表班级的东西都可以。
通过这个展示,同学们可以了解自己班级的特点和文化,也可以更好地了解自己班级的同学们。
第三部分:团队建设小讲堂
在这个部分,我们将邀请一位专业的讲师,为同学们讲解团队建设的理论和实践。
通过这个讲座,同学们可以了解团队拼图、瓶颈关卡等团队建设的实践方法,了解如何更好地协作和合作。
在讲座结束后,我们将结合班级实际情况,组织同学们进行团队建设小方案的设计和制定。
通过这场班会,我们希望同学们可以更好地认识自己的班级和同学,了解团队建设的理论和实践,更好地开始我们的高中学习生活。
同时,我们也希望同学们可以积极参与,展现自己的风采和特点,为班级建设做出自己的贡献。



第1讲空间向量及其运算新课标要求1.经历由平面向量推广到空间向量的过程,了解空间向量的概念。
2.经历由平面向量的运算及其法则推广到空间向量的过程。
3.掌握空间向量的线性运算。
4.掌握空间向量的数量积。
知识梳理1.空间向量的概念与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量,空间向量的大小叫做空间向量的长度或模,空间向量用字母a,b,c ...表示.2.几个常见的向量零向量长度为0的向量叫做零向量单位向量模为1的向量叫做单位向量相反向量与向量a 长度相等而方向相反的向量,叫做a 的相反向量,记做-a 共线向量如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量。
我们规定:零向量与任意向量平行.相等向量方向相同且模相等的向量叫做相等向量3.向量的线性运算交换律:+=+a b b a ;结合律:()();()()λμλμ+=+=a b +c a +b c a a ;分配律:();()λμλμλλλ+=++=+a a a a b a b .4.共面向量平行于同一平面的向量,叫做共面向量.5.空间向量的数量积||||cos ,⋅=<>a b a b a b 零向量与任意向量的数量积为0.名师导学知识点1空间向量的有关概念【例1-1】(咸阳期末)已知是空间的一个单位向量,则的相反向量的模为A.1B.2C.3D.4【分析】本题考查了向量的基础知识,根据向量模的概念求解即可;【解答】解:因为是空间的一个单位向量,所以的相反向量的模,故选A.【变式训练1-1】(龙岩期末)在平行六面体中,与向量相等的向量共有A.1个B.2个C.3个D.4个【分析】本题考查了相等向量及其平行六面体的性质,考查了推理能力与计算能力,属于基础题.利用相等向量及其平行六面体的性质即可得出.【解答】解:如图所示,与向量的相等的向量有以下3个:故选C.知识点2空间向量的线性运算【例2-1】(泰安期末)如图所示,在长方体中,O为AC的中点.化简:________;用,,表示,则________.【分析】本题考查空间向量的线性运算,属于基础题.利用化简即可;将分解为,继而进行正交分解即可.【解答】解:..【例2-2】(河西区期末)在三棱锥中,,,,D为BC的中点,则A. B.C. D.【分析】本题考查空间向量的加减运算,属于基础题.若D为BC的中点,则,根据向量的减法法则即可得到答案.【解答】解:依题意得,故选A.【变式训练2-1】(东湖区校级一模)在空间四边形ABCD中,M,G分别是BC,CD的中点,则A. B. C. D.【分析】本题考查了空间向量的加减运算及数乘运算,属于基础题.根据题意,将进行转化,即可得解.【解答】解:.【变式训练2-2】(随州期末)如图,已知长方体,化简下列向量表达式,并在图中标出化简结果的向量.;.【解析】解:..向量,如图所示.知识点3共面向量【例3-1】(珠海期末)已知A,B,C三点不共线,点M满足.,,三个向量是否共面点M是否在平面ABC内【解析】解,,,向量,,共面.由知向量,,共面,又它们有共同的起点M,且A,B,C三点不共线,,A,B,C四点共面,即点M在平面ABC内.【变式训练3-1】(日照期末)如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且,.求证:向量,,共面.【解析】证明:因为M在BD上,且,所以.同理.所以.又与不共线,根据向量共面的充要条件可知,,共面.知识点4空间向量的数量积【例4-1】(溧阳市期末)已知长方体中,,,E为侧面的中心,F为的中点试计算:.【解析】解:如图,设,,,则,,....【变式训练4-1】(兴庆区校级期末)如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求:.【解析】解,..,.,,.名师导练A组-[应知应会]1.(台江区校级期末)长方体中,若,,,则等于A. B.C. D.【分析】本题考查空间向量的运算,属基础题.根据空间向量的运算法则求解即可.【解答】解:,故选C.2.(秦皇岛期末)若空间四边形OABC的四个面均为等边三角形,则的值为A. B. C. D.0【分析】本题主要考查了空间向量的运算、向量的数量积、向量垂直的判定,属于中档题.先求出向量的数量积,由它们的数量积为0判断,所以向量的夹角为,由此得出结论.【解答】解:,空间四边形OABC的四个面为等边三角形,,,,,,故选D.3.(定远县期末)给出下列几个命题:向量,,共面,则它们所在的直线共面;零向量的方向是任意的;若,则存在唯一的实数,使.其中真命题的个数为A.0B.1C.2D.3【分析】本题主要考查命题的真假判断与应用,比较基础.利用向量共面的条件判断.利用零向量的性质判断.利用向量共线的定理进行判断.【解答】解:假命题.三个向量共面时,它们所在的直线或者在平面内或者与平面平行;真命题.这是关于零向量的方向的规定;假命题.当,则有无数多个使之成立.故选B .4.(葫芦岛期末)在下列条件中,使M 与A 、B 、C 一定共面的是A.;B.;C.D.【分析】本题考查空间向量基本定理,考查学生分析解决问题的能力,属于基础题.利用空间向量基本定理,进行验证,对于C ,可得,,为共面向量,从而可得M 、A 、B 、C四点共面.【解答】解:对于A ,,无法判断M 、A 、B 、C 四点共面;对于B ,,、A 、B 、C 四点不共面;C 中,由,得,则,,为共面向量,即M 、A 、B 、C 四点共面;对于D ,,,系数和不为1,、A 、B 、C四点不共面.故选C .5.(多选)(点军区校级月考)已知1111ABCD A B C D -为正方体,下列说法中正确的是()A .221111111()3()A A A D AB A B ++= B .1111()0A C AB A A -=C .向量1AD 与向量1A B的夹角是60︒D .正方体1111ABCD A B C D -的体积为1||AB AA AD【分析】本题考查的是用向量的知识和方法研究正方体中的线线位置关系及夹角与体积.用到向量的加法、减法、夹角及向量的数量积,研究了正方体中的线线平行、垂直,异面直线的夹角及正方体的对角线的计算、体积的计算.【解答】解:由向量的加法得到:111111A A A D A B A C ++= , 221113AC A B =,∴22111()3()AC A B = ,所以A 正确;1111A B A A AB -= ,11AB A C ⊥,∴110A C AB =,故B 正确;1ACD ∆ 是等边三角形,160AD C ∴∠=︒,又11//A B D C ,∴异面直线1AD 与1A B 所成的夹角为60︒,但是向量1AD 与向量1A B的夹角是120︒,故C 不正确;1AB AA ⊥ ,∴10AB AA = ,故1||0AB AA AD =,因此D 不正确.故选:AB .6.(都匀市校级期中)空间的任意三个向量,,,它们一定是________向量填“共面”或“不共面”.【分析】正确理解共面向量定理是解题的关键.由于可用向量,线性表示,即可判断出空间中的三个向量,,是否是共面向量.【解答】解:可用向量,线性表示,由空间中共面向量定理可知,空间中的三个向量,,一定是共面向量.7.(池州模拟)给出以下结论:两个空间向量相等,则它们的起点和终点分别相同;若空间向量,,满足,则;在正方体中,必有;若空间向量,,满足,,则.其中不正确的命题的序号为________.【分析】本题考查的知识点是空间相等的定义,难度不大,属于基础题.根据相向相等的定义,逐一分析四个结论的真假,可得答案.【解答】解:若两个空间向量相等,则它们方向相同,长度相等,但起点不一定相同,终点也不一定相同,故错误;若空间向量,,满足,但方向不相同,则,故错误;在正方体中,与方向相同,长度相等,故,故正确;若空间向量,,满足,,则,故正确;故答案为.8.(未央区校级期末)O为空间中任意一点,A,B,C三点不共线,且3148OP OA OB tOC=++,若P,A,B,C四点共面,则实数t=.【分析】利用空间向量基本定理,及向量共面的条件,即可得到结论.【解答】解:由题意得,3148OP OA OB tOC=++,且P,A,B,C四点共面,∴31148t++=18t∴=,故答案为:18.9.(天津期末)在正四面体P ABC-中,棱长为2,且E是棱AB中点,则PE BC的值为.【分析】如图所示,由正四面体的性质可得:PA BC⊥,可得:0PA BC=.由E是棱AB中点,可得1()2PE PA PB=+,代入PE BC,利用数量积运算性质即可得出.【解答】解:如图所示,由正四面体的性质可得:PA BC⊥,可得:0PA BC=.E是棱AB中点,∴1()2PE PA PB=+,∴1111()22cos12012222PE BC PA PB BC PA BC PB BC=+=+=⨯⨯⨯︒=-.故答案为:1-.10.(三明期中)如图所示,在正六棱柱中化简,并在图中标出表示化简结果的向量化简,并在图中标出表示化简结果的向量.【解析】解:.,在图中表示如下:.在图中表示如下:11.(都匀市校级期中)如图所示,在四棱锥中,底面ABCD为平行四边形,,,底面求证:.【解析】证明:由底面ABCD为平行四边形,,,知,则.由底面ABCD ,知,则.又,所以,即.12.(西夏区校级月考)如图所示,平行六面体1111ABCD A B C D -中,E 、F 分别在1B B 和1D D 上,且11||||3BE BB =,12||||3DF DD =(1)求证:A 、E 、1C 、F 四点共面;(2)若1EF xAB y AD z AA =++ ,求x y z ++的值.【分析】(1)利用向量三角形法则、向量共线定理、共面向量基本定理即可得出.(2)利用向量三角形法则、向量共线定理、共面向量基本定理即可得出.【解答】(1)证明: 1111111212()()3333AC AB AD AA AB AD AA AA AB AA AD AA AB BE AD DF AE AF =++=+++=+++=+++=+.A ∴、E 、1C 、F 四点共面.(2)解: 111211()333EF AF AE AD DF AB BE AD DD AB BB AB AD AA =-=+-+=+--=-++ ,1x ∴=-,1y =,13z =,13x y z ∴++=.B 组-[素养提升]1.(多选)(三明期中)定义空间两个向量的一种运算||||sin a b a b a =<⊗ ,b > ,则关于空间向量上述运算的以下结论中恒成立的有()A .a b b a=⊗⊗ B .()()a b a b λλ=⊗⊗ C .()()()a b c a c b c +=+⊗⊗⊗ D .若1(a x = ,1)y ,2(b x = ,2)y ,则1221||a b x y x y =-⊗【分析】A 和B 需要根据定义列出左边和右边的式子,再验证两边是否恒成立;C 由定义验证若a b λ= ,且0λ>,结论成立,从而得到原结论不成立;D 根据数量积求出cos a < ,b > ,再由平方关系求出sin a < ,b > 的值,代入定义进行化简验证即可.【解答】解:对于A ,||||sin a b a b a =<⊗ ,b > ,||||sin b a b a b ==<⊗ ,a > ,故a b b a =⊗⊗ 恒成立;对于:()(||||sin B a b a b a λλ=<⊗ ,)b > ,()||||||sin a b a b a λλλ=<⊗ ,b > ,故()()a b a b λλ=⊗⊗ 不会恒成立;对于C ,若a b λ= ,且0λ>,()(1)||||sin a b c b c b λ+=+<⊗ ,c > ,()()||||sin a c b c b c b λ+=<⊗⊗ ,||||sin c b c b >+< ,(1)||||sin c b c b λ>=+< ,c > ,显然()()()a b c a c b c +=+⊗⊗⊗ 不会恒成立;对于D ,cos a < ,1212||||x x y y b a b +>= ,sin a < ,b >= ,即有||||||a b a b a ==⊗=1221||x y x y ===-.则1221||a b x y x y =-⊗ 恒成立.故选:AD .。

高二地理第一课讲课稿范文同学们,今天我们开始学习高二地理的第一课——自然地理环境。
在这门课程中,我们将了解地球的自然环境对我们人类的影响,以及如何合理利用和保护这个环境。
首先,让我们来了解一下自然地理环境的概念。
自然地理环境指的是地球上的各种自然要素,包括地形、水和气候等。
这些自然要素相互作用,形成了我们居住的环境。
地形是指地球表面的形状和高低变化,它对地球上的水文过程、气候和植被分布等都有着重要影响。
水是地球上最重要的自然资源之一,它分布广泛,包括海洋、湖泊、河流和冰川等形式。
气候则是地球表面的气候现象的总和,包括温度、降水、风向和风速等。
自然地理环境对我们人类的影响是十分巨大的。
首先,地形的不同导致了不同的人类活动方式和生产方式。
对于山地地区来说,由于地势陡峭,土地资源相对有限,农业生产不利,因此这些地区往往以畜牧业和林业为主要产业。
而平原地区由于土地肥沃,农田资源丰富,适宜农业生产。
其次,水资源的分布不均匀也影响着人们的生活和经济发展。
在水资源丰富的地区,人们可以通过农田灌溉和发电等方式合理利用水资源。
然而,水资源缺乏的地区则需要制定节约用水的政策,确保人们的生活需求。
对于自然地理环境的合理利用和保护是我们每个人的责任。
合理利用自然地理环境意味着我们要根据各个地区的特点,制定适合当地的发展策略,确保资源的可持续利用。
同时,我们也需要加强对自然地理环境的保护意识,合理利用资源、减少污染、保护生物多样性。
只有这样,我们才能保持地球的健康和可持续发展。
总结起来,自然地理环境是地球上各种自然要素相互作用的结果。
它对我们人类的生产、生活和经济发展都有着重要影响。
我们应该了解自然地理环境的特点,合理利用资源、保护环境,为地球的可持续发展做出贡献。
谢谢大家!。

高二文科语文上学期开学第一课教案设计思路:第一课非常重要,学生从高一向高二迈进,动力没有高一时候足了,压力却又不像高三那么大,这时候就要求学生要有毅力。
这节课关系到新学期同学们对语文学习的热情和兴趣,要重温高一时对他们的要求。
一定要精心准备,一炮打响,让学生在观念上重新认识语文课的不可替代的价值,并从此“死心塌地”的爱上语文。
这便是语文教学成功的第一步——甚至是一多半了。
此外,不使学生掌握学习语文的方法,学生就难以自觉主动地学习语文,其结果很可能就会误认为学习语文就是在上语文课的时候学语文课本,从而跳不出语文课本,跳不出语文课堂,最终学下去就是越学越不得法,越学越枯燥。
所以,第一节不忙于讲新课,而主要是调动学习兴趣,讲明语文学习的理念,介绍学习方法,明确要求等等。
关于语文学习的价值、意义、重要性——对高二的学生也要讲,而且要大讲特讲,要让学生对语文产生前所未有的好感,让他们明白:语文学习除了关乎其前途命运,更关乎其生命质量。
有一种“大语文”的认识,树立学习是一种自觉的意识。
1、应考:不论高考怎么改革,语文也稳居榜首——永远的“三分之一”。
2、交际工具:立身处世之本,建功立业之基。
3、素养:文化传承、积淀,形成民族强大向心力凝聚力的“磁核”。
4、人格形成:是精神的建筑师、心灵的守护神,生命的别名。
教学过程:一、聊天1、又一个暑假过去了,这个暑假你过得充实吗?介绍老师在暑假里培训的收获:阅读与写作在高中语文学习中的重要性。
2、新学期开始了,回顾过去,你在语文学习方面积累了什么经验?还有什么困惑?需要老师的什么帮助?(目的:相互了解)二、投影材料朗读几篇考场作文,并展示阅卷老师的评分和评语,请学生说说感受。
(目的:使学生高度重视语文,尤其是写作与阅读)三、方法介绍引言:清代王国维也曾经说过,古今成大事业者必须经过三种境界:“昨夜西风凋碧树,独上高楼,望尽天涯路”,此第一境也;“衣带渐宽终不悔,为伊消得人憔悴”,此第二境也;“众里寻她千百度,蓦然回首,那人却在灯火阑珊处”,此第三境也。

第一讲交变电流的产生和描述【学习目标】1.理解交变电流的产生原理,会推导出电动势的瞬时值。
2.会判断在中性面和平行面位置各个物理量的区别。
3.会结合物理情景和图像分析“四值”,并且进行简单的计算问题。
【知识点一】交变电流定义:大小和方向都随时间作周期性变化的电流叫交流电。
【例】下图中画出了六种电流随时间变化的图像.这六个图中的电流,都随时间t作周期性变化,其中属于交流电的是________,属于正弦式交流电的是________.【知识点二】正、余弦交流电:1.产生:强度和方向都随时间作周期性变化的电流叫交流电。
矩形线圈在匀强磁场中,绕垂直于匀强磁场的线圈的对称轴作匀速转动时,产生正弦(或余弦)交流电动势。
当外电路闭合时形成正弦(或余弦)交流电流。
2.变化规律:(1)中性面:与磁感线垂直的平面。
平行面(也叫垂直于中性面的位置):与磁感线平行的平面。
(2)正弦交流电的函数表达式若n 匝面积为S 的线圈以角速度ω绕垂直于磁场方向的轴匀速转动,从中性面开始计时,其函数形式为t NBS e ωωsin =,用ωNBS E m =表示电动势最大值,则有t E e m ωsin =。
若与外电阻R 串联,则其电流大小为i =e R =E mR sin ωt =I m sin ωt ,电压大小为u =U m ·sin ωt =RE mR +r sin ωt 。
(3)线圈平面与中性面重合时,S ⊥B ,Φ最大,ΔΦΔt=0,e =0,i =0,电流方向将发生改变,电动势的瞬时值表达式:e t m =εω·s i n ,感应电流的瞬时值表达式:i I t m =·s i n ω. (4)线圈平面与中性面垂直时,S ∥B ,Φ=0,ΔΦΔt最大,e 最大,i 最大,电流方向不改变,电动势的瞬时值表达式:et m =εω·c o s ,感应电流的瞬时值表达式:i I t m =·c o s ω。

高二开学第一课主题班会教案5篇20xx高二开学第一课主题班会教案第一篇主题:“诚信”主题班会教学目的:1.让同学了解诚信。
2.使同学在生活中做到诚信。
实施步骤:一、由班长朗诵一段话,引入班会课主题。
诚恳,即忠诚狡猾,不隐瞒自己的真实思想,不掩饰自己的真实感情,不说谎,不作假,不为不行告人的目的而欺瞒别人。
守信,就是讲信用,讲信誉,信守承诺,忠实于自己担当的义务,答应了别人的事肯定要去做。
忠诚地履行自己担当的义务是每一个现代公民应有的职业品质。
由于《中同学日产行为规范》中特殊规定:中同学应当守信,答应别人做的事要按时做到,做不到时表示歉意。
我们今日的班会课主题:诚恳守信。
二、主持人:21世纪是信息社会,信息化浪潮汹涌而至,加速推动前进信息化进程已成历史必定,而社会的全面信息化又是建立在良好的社会诚信体系之上,没有诚信,信息化无从谈起。
那什么是诚信?诚,即真诚、诚恳;信,即遵守承诺、讲信用。
诚信的基本含义是受诺、践约、无欺。
通俗表述,就是说狡猾话、办狡猾事、做狡猾人。
人生活在社会中,总要和他人。
处理这种关系必需遵守肯定的规章,有章必循,有诺必践;否则,个人就失去了立身之本,社会就失去了运行之规。
诚恳守信是中华民族的传统美德。
几千年来,“一诺千金”的佳话不绝于史,广为流传。
三、由同学------为大家叙述《曾子杀猪》的故事。
在我国古代就有许多诚信的小故事,如“曾参杀猪”示诚信。
曾参,春秋末期鲁国出名的思想家、儒学家,是孔子门生中七十二贤之一。
他博学多才,且非常注意修身养性,德行高尚。
有一次,他的妻子要到集市上办事,年幼的儿子吵着要去。
曾参的妻子不愿带儿子去,便对他说:你在家好好玩,等妈妈回来,将家里的猪杀了煮肉给你吃。
儿子听了,特别愉快而兴奋,不再吵着要去集市了。
这话本是哄儿子说着玩的,过后,曾参的妻子便忘了。
不料,曾参却真的把家里的一头猪杀了。
妻子从集市上回来后,生气地对丈夫说:我是哄儿子说着玩的,你怎么就真把猪杀了呢?曾参说:孩子是不能哄骗的!他不懂事,还没有辨别力量,接触到的是父母,所以什么都跟父母学。

第01讲 空间向量与立体几何知识点1 空间向量的有关概念1.在空间,把具有方向和大小的量叫做空间向量,空间向量的大小叫做空间向量的长度或模.注:数学中讨论的向量与向量的起点无关,只与大小和方向有关,只要不改变大小和方向,空间向量可在空间内任意平移,故我们称之为自由向量。
2. 表示法:(1)几何表示法:空间向量用有向线段表示,有向线段的长度表示空间向量的模(2)字母表示法:用字母表示,若向量a 的起点是A ,终点是B ,则a 也可记作AB →,其模记为|a |或|AB →|. 3.几类特殊的空间向量 名称 定义表示法 零向量 规定长度为0的向量叫做零向量 记为0 单位模为1的向量叫做单位向量|a|=1或【考点目录】【知识梳理】知识点2 空间向量的线性运算(一)空间向量的加减运算共起点的两边为邻边作平行四边形,共起点对角线为和共起点,连终点,方向指向被减向量a+b=b+aλa的长度是a的长度的|λ|倍μa)=(λμ)a知识点3 共线向量与共面向量1.共线向量与共面向量的区别 //0a b b ≠()使得a b λ=;(2)存在唯一实数λ,使得0a b b λ≠=(),则//a b .注意:0b ≠不可丢掉,否则实数就不唯一.―→―→―→1、空间一点实数对→数对(,,)x y z ,使得对空间中任意一点(OP xOA yOB zOC x+=++其中共面向量定理的用途:⇒λ利用向量的线性运算即可,但一定要注意所表示的向量必须有一个公共点。
2.直线l 的方向向量如图O ∥l ,在直线l 上取非零向量a ,设P 为l 上的任意一点,则∥λ∥R 使得OP ―→=λa. 定义:把与a 平行的非零向量称为直线l 的方向向量.知识点4 空间向量的夹角定义如图,已知两个非零向量a ,b ,在空间任取一点O ,作OA →=a ,OB →=b ,则∥AOB 叫做向量a ,b 的夹角,记作〈a ,b 〉范围 0≤〈a ,b 〉≤π向量垂直 如果〈a ,b 〉=π2,那么向量a ,b 互相垂直,记作a ∥b知识点5 空间向量的数量积运算1.(1)空间向量的数量积已知两个非零向量a ,b ,则|a ||b |cos 〈a ,b 〉叫做a ,b 的数量积,记作a ·b ,即a ·b =|a ||b |·cos 〈a ,b 〉.零向量与任意向量的数量积为0,即0·a =0.注:a b ⋅等于a 的长度a 与b 在a 的方向上的投影b cos a,b 〈〉的乘积.(2)运算律数乘向量与数量积的结合律(λa )·b =λ(a ·b ),λ∥R交换律 a ·b =b ·a 分配律a ·(b +c )=a ·b +a ·c2.投影向量及直线与平面所成的角(1)如图∥,在空间,向量a 向向量b 投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b 共线的向量c ,c =|a |cos 〈a ,b 〉b|b |,向量c 称为向量a 在向量b 上的投影向量.类似地,可以将向量a 向直线l 投影(如图∥).(2)如图∥,向量a 向平面β投影,就是分别由向量a 的起点A 和终点B 作平面β的垂线,垂足分别为A ′,B ′,得到向量A ′B ′——→,向量A ′B ′——→称为向量a 在平面β上的投影向量.这时,向量a ,A ′B ′——→的夹角就是向量a 所在直线与平面β所成的角.知识点6 空间向量数量积运算律及性质1、数量乘积的运算律:()1a b b a ⋅=⋅; ()2()()()a b a b a b λλλ⋅=⋅=⋅; ()3()a b c a c b c +⋅=⋅+⋅.2、若a ,b 为非零向量,e 为单位向量,则有()1e a a e a cos a,e ⋅=⋅=〈〉;()20a b a b ⊥⇔⋅=;()3()()a b a b a b a b a b ⎧⎪⋅=⎨-⎪⎩与同向与反向,2a a a ⋅=,a a a =⋅;()4a b cos a,b a b ⋅〈〉=;()5a b a b ⋅≤.知识点7 空间向量基本定理1.定理如果三个向量a ,b ,c 不共面,那么对任意一个空间向量p ,存在唯一的有序实数组(x ,y ,z ),使得p =xa+yb+zc .其中{a ,b ,c }叫做空间的一个基底,a ,b ,c 都叫做基向量.如果p =xa+yb+zc ,则称xa+yb+zc 为p 在基底{a ,b ,c }下的分解式. 2.空间向量的正交分解(1)单位正交基底:空间的一个基底中的三个基向量两两垂直,且长度都为1,常用{i ,j ,k }表示. (2)正交分解:由空间向量基本定理可知,对空间中的任意向量a ,均可以分解为三个向量xi ,yj ,zk ,使a =xi +yj +zk .像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量正交分解.知识点8 空间向量基本定理应用1、证明平行、共面问题(1)对于空间任意两个向量a ,b (b ≠0),a ∥b 的充要条件是存在实数λ,使a =λb .(2) 如果两个向量a ,b 不共线,那么向量p 与向量a ,b 共面的充要条件是存在唯一的有序实数对(x ,y ),使p =xa +yb .(3)直线平行和点共线都可以转化为向量共线问题;点线共面可以转化为向量共面问题.2、求夹角、证明垂直问题 (1)θ为a ,b 的夹角,则cos θ=a ·b|a ||b |. (2)若a ,b 是非零向量,则a ∥b ∥a ·b =0. 3、求距离(长度)问题 ||a =a ·a ( ||AB →=AB →·AB→ ).知识点9 空间直角坐标系1.空间直角坐标系(1)空间直角坐标系:在空间选定一点O 和一个单位正交基底{i ,j ,k },以O 为原点,分别以i ,j ,k 的方向为正方向,以它们的长为单位长度建立三条数轴:x 轴、y 轴、z 轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz .(2)相关概念:O 叫做原点,i ,j ,k 都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy 平面、Oyz 平面、Ozx 平面,它们把空间分成八个部分. 注意点:(1)基向量:|i |=|j |=|k |=1,i ·j =i ·k =j ·k =0.(2)画空间直角坐标系Oxyz 时,一般使∥xOy =135°(或45°),∥yOz =90°.(3)建立的坐标系均为右手直角坐标系.在空间直角坐标系中,让右手拇指指向x 轴的正方向,食指指向y 轴的正方向,如果中指指向z 轴的正方向,则称这个坐标系为右手直角坐标系. 2.空间一点的坐标、向量的坐标 (1)空间点的坐标在空间直角坐标系Oxyz 中,i ,j ,k 为坐标向量,对空间任意一点A ,对应一个向量OA →,且点A 的位置由向量OA →唯一确定,由空间向量基本定理,存在唯一的有序实数组(x ,y ,z ),使OA →=xi +yj +zk .在单位正交基底{i ,j ,k }下与向量OA →对应的有序实数组(x ,y ,z ),叫做点A 在空间直角坐标系中的坐标,记作A (x ,y ,z ),其中x 叫做点A 的横坐标,y 叫做点A 的纵坐标,z 叫做点A 的竖坐标.注:空间直角坐标系中坐标轴、坐标平面上的点的坐标特点(2)空间点的对称问题∥空间点的对称问题可类比平面直角坐标系中点的对称问题,要掌握对称点的变化规律,才能准确求解.∥对称点的问题常常采用“关于谁对称,谁保持不变,其余坐标相反”这个结论. (3)空间向量的坐标向量的坐标:在空间直角坐标系Oxyz 中,给定向量a ,作OA →=a ,由空间向量基本定理,存在唯一的有序实数组(x ,y ,z ),使a =xi +yj +zk .有序实数组(x ,y ,z )叫做a 在空间直角坐标系Oxyz 中的坐标,可简记作a =(x ,y ,z ).知识点10 空间向量的坐标运算1.空间向量的坐标运算法则设向量a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),λ∥R ,那么(1)空间向量运算的坐标表示与平面向量的坐标表示完全一致.(2)设A (x 1,y 1,z 1),B (x 2,y 2,z 2),则AB →=(x 2-x 1,y 2-y 1,z 2-z 1).即一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.(3)运用公式可以简化运算:(a ±b )2=a 2±2a ·b +b 2;(a +b )·(a -b )=a 2-b 2. (4)向量线性运算的结果仍是向量,用坐标表示;数量积的结果为数量.2.空间向量相关结论的坐标表示设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),则有(1)平行关系:当b ≠0时,a ∥b ∥a =λb ∥a 1=λb 1,a 2=λb 2,a 3=λb 3(λ∥R); (2)垂直关系:a ∥b ∥a ·b =0∥a 1b 1+a 2b 2+a 3b 3=0.(3)|a|=a ·a =a 21+a 22+a 23.(4)cos 〈a ,b 〉=a ·b|a ||b |=a 1b 1+a 2b 2+a 3b 3a 21+a 22+a 23·b 21+b 22+b 23. 3.空间两点间的距离公式在空间直角坐标系中,设P 1(x 1,y 1,z 1),P 2(x 2,y 2,z 2). (1)P 1P 2――→=(x 2-x 1,y 2-y 1,z 2-z 1).(2)P 1P 2=|P 1P 2――→|=(x 2-x 1)2+(y 2-y 1)2+(z 2-z 1)2. (3)若O (0,0,0),P (x ,y ,z ),则|OP →|=x 2+y 2+z 2.知识点11 空间中点、直线和平面的向量表示1.空间直线的向量表示式设A 是直线上一点,a 是直线l 的方向向量,在直线l 上取AB →=a ,设P 是直线l 上任意一点, (1)点P 在直线l 上的充要条件是存在实数t ,使AP →=ta ,即AP →=tAB →.(2)取定空间中的任意一点O ,点P 在直线l 上的充要条件是存在实数t .使OP →=OA →+ta . (3)取定空间中的任意一点O ,点P 在直线l 上的充要条件是存在实数t ,使OP →=OA →+tAB →.2.空间平面的向量表示式∥如图,设两条直线相交于点O ,它们的方向向量分别为a 和b ,P 为平面α内任意一点,由平面向量基本定理可知,存在唯一的有序实数对(x ,y ),使得OP →=xa +yb .∥如图,取定空间任意一点O ,空间一点P 位于平面ABC 内的充要条件是存在实数x ,y ,使OP →=OA →+xAB →+yAC →.我们把这个式子称为空间平面ABC 的向量表示式.∥由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.如图,直线l ∥α,取直线l 的方向向量a ,我们称向量a 为平面α的法向量.给定一个点A 和一个向量a ,那么过点A ,且以向量a 为法向量的平面完全确定,可以表示为集合{P |a ·AP →=0}.知识点12 空间平行、垂直关系的向量表示知识点13 空间距离及向量求法设u 为直线l 的单位方向向量,A ∥l ,P ∉l ,AP―→=a ,向量AP ―→在直线l 上的投影向量为AQ ―→(AQ ―→=(a ·u )u .), 则PQ =|AP ―→|2-|AQ ―→|2=a 2-a ·u2―→知识点14 空间角及向量求法成锐角的余角.两平面的夹角平面α与平面β相交,形成四个二面角,把不大于π2的二面角称为这两个平面的夹角.设平面α与平面β的夹角为θ,两平面α,β的法向量分别为n 1,n 2,则cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|(1)两个平面的夹角的范围是⎣⎡⎦⎤0,π2(2)两平面的夹角是两法向量的夹角或其补角.考点一 空间向量及其线性运算1.(2022·重庆·高二期末)在长方体1111ABCD A B C D -中,1BA BC CC ++=( ) A .11D BB .1D BC .1DBD .1BD2.(2022·湖南益阳·高二期末)在四面体OABC 中,,,,OA a OB b OC c M ===为OA 的中点,N 为棱BC 上的点,且2BN NC =,则MN =( )A .112233a b c -++B .112233a b c --C .121233a b c -++D .111222a b c -++3.(2022·陕西商洛·高二期末(理))在平行六面体1111ABCD A B C D -中,点P 在1A C 上,且1114A P AC =,若1AP xAA yAB zAD =++,则x y z ++=( )A .34B .1C .54D .744.(2022·福建师大附中高二期末)如图所示,在平行六面体ABCD -A 1B 1C 1D 1中,M 为A 1C 1与B 1D 1的交点.若AB a =,AD b =,1AA c =,则下列向量中与BM 相等的向量是( ).【考点剖析】A .1122-++a b cB .1122a b c ++C .1122a b c --+D .1122a b c -+考点二 共线问题5.(2022·全国·高二期末)已知空间向量a ,b ,且2AB a b =+,56BC a b =-+,72CD a b =-,则一定共线的三点是( ) A .、、A B CB .BCD 、、C .A BD 、、D .A C D 、、6.(2022·山西吕梁·高二期末)在平行六面体1111ABCD A B C D -中,点P 在1A C 上,若1311444AP AA AB AD =++,则11A PAC =( ) A .13B .34C .14D .237.(2022·上海松江·高二期末)设O ABC -是正三棱锥,1G 是ABC 的重心,G 是1OG 上的一点,且13OG GG =,若OG xOA yOB zOC =++,则(),,x y z 为( )A .111,,444⎛⎫ ⎪⎝⎭B .333,,444⎛⎫ ⎪⎝⎭C .111,,333⎛⎫ ⎪⎝⎭D .222,,333⎛⎫ ⎪⎝⎭考点三 共面问题8.【多选】(2022·广东江门·高二期末)若{,,}a b c 构成空间的一个基底,则下列向量共面的是( ) A .,,a b a a b -+ B .,,b c b b c -+ C .,,a b c a b -+D .,,a b a b c c +++9.(2022·山东·巨野县第一中学高二期末)对于空间一点O 和不共线三点A ,B ,C ,且有623OP OA OB OC =++,则( )A .O ,A ,B ,C 四点共面 B .P ,A ,B ,C 四点共面 C .O ,P ,B ,C 四点共面D .O ,P ,A ,B ,C 五点共面10.(2022·上海市建平中学高二期末)已知A 、B 、C 、D 、E 是空间中的五个点,其中点A 、B 、C 不共线,则“DE 平面ABC ”是“存在实数x 、y ,使得DE x AB y AC =+的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件11.(2022·福建厦门·高二期末)已知{},,a b c 是空间的一个基底,AB a b =+,AC a c =+,AD b c λ=+,若,,,A B C D 四点共面.则实数λ的值为( )A .1-B .0C .1D .212.(2022·江西·临川一中高二期末(理))已知空间向量()2,1,a m =-,()1,1,2b =-,()1,2,2c t =-,若a ,b ,c 共面,则m +2t =( )A .-1B .0C .1D .-613.(2022·全国·高二期末)已知(2,1,3)PA =-,(1,2,3)PB =-,(7,6,)PC λ=,若P ,A ,B ,C 四点共面,则λ=___________.考点四 空间向量基本定理14.(2022·重庆长寿·高二期末)如图,在斜棱柱1111ABCD A B C D -中,AC 与BD 的交点为点M ,AB a =,AD b =,1AA c =,则1MC =( )A .1122a b c ++B .1122---a b cC .1122-++a b cD .1122a b c --+15.(2022·天津市第九十五中学益中学校高二期末)在四棱锥P ABCD -中,底面ABCD 是正方形,E 为PD 中点,若PA a =,PB b =,PC c =,则BE =( )A .131222a b c ++B .111222a b c --C .131222a b c -+D .131222a b c +-16.(2022·河南郑州·高二期末(理))已知三棱锥O —ABC ,点M ,N 分别为线段AB ,OC 的中点,且OA a =,OB b =,OC c =,用a ,b ,c 表示MN ,则MN 等于( )A .()12c a b -- B .()12b ac -- C .()12a cb -- D .()12c a b ++ 17.(2022·江苏无锡·高二期末)定义:设{}123,,a a a 是空间的一个基底,若向量123p xa ya za =++,则称有序实数组(),,x y z 为向量p 在基底{}123,,a a a 下的坐标.已知{},,a b c 是空间的单位正交基底,{},,2a b a b a c +-+是空间的另一个基底,若向量p 在基底{},,2a b a b a c +-+下的坐标为()1,2,3.(1)求向量p 在基底{},,a b c 下的坐标; (2)求向量p 在基底{},,a b c 下的模.考点五 空间向量的数量积及其性质的应用18.(2022·广西钦州·高二期末(理))如图,正四棱柱是由四个棱长为1的小正方体组成的,AB 是它的一条侧棱,128,,P P P ⋯是它的上底面上其余的八个点,则集合{},1,2,,8i x x AB AP i =⋅=⋯的元素个数( )A .1B .2C .4D .819.(2022·福建省华安县第一中学高二期末)三棱锥A BCD -中,2AB AC AD ===,2BAD π∠=,3BAC π∠=,则AB CD ⋅=______.20.(2022·河南焦作·高二期末(理))已知在四面体ABCD 中,236AB AC AD ===,3BAC CAD DAB π∠=∠=∠=,则BC BD ⋅=______.21.(2022·河南新乡·高二期末(理))已知空间向量()0,1,2AB =-,2AC =,2,3AB AC π=,则AB BC ⋅=( )A .5B 5C .5D 522.(2022·北京昌平·高二期末)已知正三棱锥-P ABC 的底面ABC 的边长为2,M 是空间中任意一点,则()MA MB MC ⋅+的最小值为( )A .32-B .1-C .D .12-23.(2022·江苏省扬州市教育局高二期末)如图,平行六面体1111ABCD A B C D -的底面ABCD 是边长为1的正方形,且1160A AD A AB ∠=∠=︒,12AA =,则线段1AC 的长为( )AB C D .24.(2022·江苏宿迁·高二期末)四面体ABCD 中,2,90,2===∠=︒⋅=-AB AC AD BAD AB CD ,则BAC ∠=( )A .30︒B .45︒C .60︒D .90︒25.(2022·福建厦门·高二期末)在四面体OABC 中,OA OB OC ==,60AOB AOC ∠==︒,90BOC ∠=︒,则OB 与AC 所成角的大小为( ) A .30°B .60°C .120°D .150°26.(2022·全国·高二期末)已知()0,0,0O ,()1,2,3A ,()2,1,2B ,()1,1,2P ,点Q 在直线OP 上运动,当QA QB ⋅取最小值时,点Q 的坐标是______27.【多选】(2022·湖北黄冈·高二期末)棱长为2的正方体1111ABCD A B C D -的侧面11ABB A (含边界)内有一动点P ,则( )A .若1111,1B P mB B nB A m n =++=,则 1110B P B D ⋅= B .若11(01)A P A B λλ=<<,则110C P BD ⋅= C .若()11111111,22B P PA A E AC AD ==+,则 1123E B P A⋅=- D .若()1111112A E AC A D =+,则存在非零向量1B P 使111B P A E ⋅=-考点六 空间向量的运算的坐标表示(一)空间向量坐标的基本运算28.(2022·内蒙古乌兰察布·高二期末(理))已知向量()()2,1,3,1,1,2a b =-=-,则2a b +=( )A .B .()4,1,1-C .()5,1,4-D29.(2022·重庆九龙坡·高二期末)在空间直角坐标系中,若(1,1,0)A ,1(2,0,1)2AB =--,则点B 的坐标为( ) A .(3,1,﹣2)B .(-3,1,2)C .(-3,1,-2)D .(3,-1,2)30.(2022·福建宁德·高二期末)已知()1,2,3A ,()4,5,9B ,13AC AB =,则AC 的坐标为______. 31.(2020·陕西·绥德中学高二期末(理))若(1,1,0)a =,(1,0,2)b =- ,则与a b +同方向的单位向量是_______. 32.【多选】(2022·福建三明·高二期末)已知正方体1111ABCD A B C D -的棱长为2,建立如图所示的空间直角坐标系Dxyz ,则( )A .点1C 的坐标为(2,0,2)B .()12,2,2C A =--C .1BD 的中点坐标为(1,1,1) D .点1B 关于y 轴的对称点为(-2,2,-2)(二)空间向量平行的坐标运算33.(2022·河南焦作·高二期末(理))已知向量()2,1,1a x =---,()2,,2b x x =-,且//a b ,则x 的值为( ) A .2-B .1C .1-或2D .1或2-34.(2022·浙江·杭州四中高二期末)已知向量()1,1,0a =-,()1,0,2b =,且ka b +与2a b -互相平行,则k =( ) A .114-B .15C .35D .12-35.(2022·北京昌平·高二期末)已知(,2,6)a x =-是直线1l 的方向向量,(1,,3)b y =-是直线2l 的方向向量.若直线12l l ∥,则x y +=________.36.(2022·重庆长寿·高二期末)已知()1,2,1u =是直线l 的方向向量,()2,,2v y =为平面α的法向量,若l α⊥,则y 的值为( )A .2-B .12-C .14D .4(三)空间向量垂直的坐标运算37.(2022·广东广州·高二期末)已知向量(1,3,2)a →=-,(2,,4)b m →=--,若a b →→⊥,则实数m 的值是___________. 38.【多选】(2022·福建福州·高二期末)已知空间向量()()1,,2,2,1,2a k k b =+-=-,且a b ⊥,则 ( ) A .6k =-B .6k =C .3b =D .9b =39.(2022·河北保定·高二期末)已知()2,1,3a =-,()1,2,1b =-,若()b a b λ⊥+,则实数λ=______.40.(2022·黑龙江·哈尔滨工业大学附属中学校高二期末(文))已知向量a →=(1,1,k),b →=(−1,0,−1),c →=(0,2,1),且向量2a b -与c 互相垂直,则k 的值是( ) A .1 B .2- C .3- D .4-(四)空间向量模长的坐标运算41.(2021·湖北·黄石市有色第一中学高二期末)若点(1,1,2)A -,(0,3,0)B ,(1,0,1)C -点D 在z 轴上,且AD BC ⊥则||=AD ______.42.(2022·天津市滨海新区塘沽第一中学高二期末)已知向量()2,1,3a →=-,()1,1,b x =-,若a →与b →垂直,则2a b →→+=___________.43.(2022·江苏·南京市大厂高级中学高二期末)向量(),1,1a x =,()1,,1b y =,()2,4,2c =-,且a c ⊥,//b c ,则2a b +=______.44.(2022·江苏·沭阳如东中学高二期末)已知(1,21,0),(3,,)a t t b t t =--=,则||b a -的最小值( )A B C .143D (五)空间向量夹角的坐标运算45.(2022·吉林辽源·高二期末)已知空间向量(3,22)a =-,b 是单位向量,1213a b -=,则向量a 与b 的夹角为______.46.(2022·全国·高二期末)若向量(1,,)a λλ=,(2,1,1)b =-,a ,b 夹角为钝角,则λ的取值范围是______. 47.(2022·江苏淮安·高二期末)如图,在四棱锥P -ABCD 中,底面ABCD 为正方形,P A ⊥平面ABCD ,PA AB =,M 为PC 上一动点,PM tPC =,若⊥BMD 为钝角,则实数t 可能为( )A .15B .14 C .13D .1248.(2022·广东江门·高二期末)若两个单位向量(,,0),(,0,)OA m n OB n p ==与向量(1,1,1)OC =的夹角都等于π4,则cos AOB ∠=__________.(六)空间向量投影的坐标运算49.(2022·上海金山·高二期末)在空间直角坐标系O xyz - 中,已知向量()1,0,3a =,则a 在x 轴上的投影向量为________.50.(2022·天津天津·高二期末)已知空间向量()1,0,1=a ,()2,1,2b =-,则向量a 在向量b 上的投影向量的坐标是__________.51.(2022·广东惠州·高二期末)已知()0,1,1a =,()0,1,0b =,则a 在b 上的投影向量为( )A .1B C .()0,1,0D .110,,22⎛⎫ ⎪⎝⎭考点七 空间向量在立体几何平行、垂直问题中的应用(一)平行问题52.(2022·黑龙江·哈尔滨工业大学附属中学校高二期末(文))如图,已知四棱锥V ABCD -的底面是矩形,VD ⊥平面,222,,,ABCD AB AD VD E F G ===分别是棱,,AB VC CD 的中点.(1)求证:EF ⊥平面VAD ;(2)求平面AVE 与平面VEG 夹角的大小.53.(2022·安徽滁州·高二期末)如图,在多面体ABCDEF 中,AD ⊥平面ABC ,AD //BE //CF ,且AD =1,BE =5,CF =3,⊥ABC 是边长为2的正三角形,G 是AB 的中点.(1)求证:CG //平面DEF ;(2)求二面角E DF A --的余弦值.(二)垂直问题54.(2022·安徽省宿州市第二中学高二期末)如图,边长为2的等边PCD 所在的平面垂直于矩形ABCD 所在的平面,BC =M 为BC 的中点.(1)证明:AM PM ⊥;(2)求平面P AM 与平面ABCD 的夹角的大小;(3)求点D 到平面AMP 的距离.55.(2022·福建福州·高二期末)如图,在正四棱柱1111ABCD A B C D -中,已知2AB AD ==,15AA =,E ,F 分别为1DD ,1BB 上的点,且11DE B F ==.(1)求证:BE ⊥平面ACF :(2)求点B 到平面ACF 的距离.56.(2022·湖北恩施·高二期末)在三棱台ABC -A 1B 1C 1中,C 1C ⊥平面ABC ,AB ⊥BC ,且AB =BC =C 1C =2A 1B 1,O 为AC 的中点,P 是C 1C 的中点.(1)证明:平面A 1BC ⊥平面POB ;(2)求二面角B 1-A 1B -C 的余弦值.(三)综合问题57.(2022·浙江·杭州四中高二期末)已知平面β法向量为()3,1,5m =-,直线l 的方向向量为()6,2,10n =--,则( )A .l 与β平行B .l 与β垂直C .l 与β相交但不垂直D .以上都不对58.【多选】(2022·广东深圳·高二期末)直三棱柱111ABC A B C 中,1,,,,CA CB CA CB CC D E M ⊥==分别为11B C ,11,CC AB 的中点,点N 是棱AC 上一动点,则( )A .对于棱AC 上任意点N ,有1MN BC ⊥B .棱AC 上存在点N ,使得MN ⊥面1BC NC .对于棱AC 上任意点N ,有MN 面1A DED .棱AC 上存在点N ,使得MN DE ∥59.(2022·北京房山·高二期末)如图,正方体1111ABCD A B C D -中,P 是1A D 的中点,则下列说法正确的是( )A .直线PB 与直线1A D 垂直,直线PB ∥平面11B D CB .直线PB 与直线1DC 平行,直线PB ⊥平面11AC DC .直线PB 与直线AC 异面,直线PB ⊥平面11ADC BD .直线PB 与直线11B D 相交,直线PB ⊂平面1ABC考点八 空间角的计算60.(2022·广东江门·高二期末)在直三棱柱111ABC A B C 中,1190,,BCA D F ∠=︒分別是1111,A B AC 的中点,1BC CA CC ==,则1BD 与1AF 所成角的正弦值是( )A B .12 C D 61.(2022·贵州六盘水·高二期末(理))如图是正方体的平面展开图,则在这个正方体中:⊥BM 与ED 平行⊥BM 与CE 垂直⊥CE 与平面ABCD ⊥CN 与BM 所成角为60︒以上四个命题中,正确命题的序号是( )A .⊥⊥B .⊥⊥C .⊥⊥D .⊥⊥62.(2022·黑龙江·双鸭山一中高二期末)如图,在四棱锥S ABCD -中,底面ABCD 为等腰梯形,AD BC ∥,60DAB ∠=,SA ⊥面ABCD ,22SA AD BC ===,点F 为线段SD 中点(1)求证:CF 面SAB ;(2)求异面直线FC 与BD 所成角的大小.63.【多选】(2022·山东·巨野县第一中学高二期末)已知在直三棱柱111ABC A B C 中,底面是一个等腰直角三角形,且1AB BC BB ==,E 、F 、G 、M 分别为1111B C A B AB BC ,,,的中点.则( )A .1GB 与平面11ACC A B .1AB 与1BC 所成角为3π C .1//A M 平面EFBD .平面1AB C ⊥平面1A MC64.(2022·河南南阳·高二期末(理))如图,四边形ABEF 为直角梯形,//AF BE 且BE EF ⊥,CDFE 为正方形,且平面CEFD ⊥平面ABEF ,22EF AF BE ===,13AP AB =,23DQ DC =,则PQ =______,直线PQ 与平面ACD 所成角的正弦值为______.65.(2022·福建省仙游县度尾中学高二期末)如图,在三棱锥-P ABC 中,PAC △是正三角形,AC BC ⊥,2,AC BC PB ===D 是AB 的中点.(1)证明:AC PD ⊥;(2)求直线BC 与平面PAB 所成角的正弦值.66.(2022·甘肃·测试·编辑教研五高二期末(理))如图,在直三棱柱111ABC A B C 中,AC BC ⊥,2AC BC ==,13CC =,点D ,E 分别在棱1AA ,1CC 上,且1AD =,2CE =,M 为棱11A B 的中点.(1)求证:11C M B D ⊥;(2)求直线AB 与平面1DB E 所成角的正弦值.67.(2022·四川绵阳·高二期末(理))如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD ⊥,//BC AD ,2PA AB BC ===,4=AD ,E 为棱PD 的中点,F 是线段PC 上一动点.(1)求证:平面PBC ⊥平面PAB ;(2)若直线BF 与平面ABCD F EA D --的余弦值.(三)平面与平面所成的角(二面角)68.(2022·青海玉树·高二期末(理))如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,2PA AB =,正方形ABCD 的对角线交于点O .(1)求证:BD ⊥平面P AC ;(2)求二面角P BD C --的余弦值.69.(2022·云南曲靖·高二期末)如图所示,AE ⊥平面ABCD ,四边形AEFB 为矩形,,BC AD BA AD ⊥,224AE AD AB BC ====.(1)求证:CF ⊥平面ADE ;(2)求平面CDF 与平面AEFB 所成锐二面角的余弦值.70.(2022·广东中山·高二期末)如图,在四棱锥P ABCD -中,底面四边形ABCD 为直角梯形,π2DAB ∠=,π3ABC ∠=,22AB DC ==,PD PA =CD PD ⊥.(1)求证:平面PAD ⊥平面ABCD ;(2)求平面APB 和平面PBC 的夹角大小.71.(2022·浙江省杭州第九中学高二期末)如图,在三棱锥-P ABC 中,AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,BM BC λ=,且二面角M PA C --为30°,求λ的值.考点九 空间距离的计算(一)点到直线的距离72.(2022·吉林白山·高二期末)已知(3,1,0)A ,(5,2,2)B ,(2,0,3)C ,则点C 到直线AB 的距离为( )A .3BC .D73.(2022·安徽省宿州市第二中学高二期末)已知直线l 经过点()211A ,,,且()101n =,,是l 的方向向量,则点()432P ,,到l 的距离为( )A .12BCD 74.(2022·青海海东·高二期末(理))在正方体1111ABCD A B C D -中,6,3,,AB AB AE PF ==分别是线段11,A C BB 的中点,则点P 到直线EF 的距离是( )A B .125 C D .185(二)点到平面的距离、直线到平面的距离、平面到平面的距离75.(2022·上海市奉贤中学高二期末)经过原点的平面α的一个法向量为(3,1,2)n =,点A 坐标为(0,1,0),则点A 到平面α的距离为______.76.(2022·青海·海南藏族自治州高级中学高二期末(理))设正方体1111ABCD A B C D -的棱长为4,则点1C 到平面1A BD 的距离是( )A B C D77.(2022·江苏·南京师大附中高二期末)在矩形ABCD 中,2==AD AB E 是线段AD 的中点,将⊥ABE 沿BE 折起到⊥PBE 位置(如图),点F 是线段CP 的中点.(1)求证:DF ⊥平面PBE :(2)若二面角P BE C --的大小为2π,求点A 到平面PCD 的距离. 78.(2022·浙江省杭州第九中学高二期末)若两平行平面α、β分别经过坐标原点O 和点()2,1,1A ,且两平面的一个法向量为()1,0,1n =-,则两平面间的距离是______.(三)异面直线的距离79.(2022·福建·厦门外国语学校高二期末)如图,在正方体1111ABCD A B C D -中,AB =1,M ,N 分别是棱AB ,1CC 的中点,E 是BD 的中点,则异面直线1D M ,EN 间的距离为______.80.(2022·浙江宁波·高二期末)如图,正四棱锥P ABCD -的棱长均为2,点E 为侧棱PD 的中点.若点M ,N 分别为直线AB ,CE 上的动点,则MN 的最小值为______.81.(2022·全国·高二期末)在如图所示实验装置中,正方形框架的边长都是1,且平面ABCD ⊥平面ABEF ,活动弹子,M N 分别在正方形对角线AC ,BF 上移动,则MN 长度的最小值是___________.考点十 空间向量与立体几何的综合问题82.【多选】(2022·广东茂名·高二期末)(多选)如图,在长方体1111ABCD A B C D -中,11AA =,AB AD ==E 是侧面11AA D D 的中心,F 是底面ABCD 的中心,以A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则( )A .EF 是单位向量B .三棱锥1A BCD -外接球的表面积为7πC .直线EF 与1A CD .//EF 平面1A BC83.【多选】(2022·辽宁辽阳·高二期末)在空间直角坐标系O xyz -中,(1,0,0),(1,2,2),(0,0,2)---A B C ,则( )A .3⋅=OC ABB .点B 到平面AOC 的距离是2C .异面直线OC 与ABD .点O 到直线AB 84.【多选】(2022·江苏南通·高二期末)在平行六面体1111ABCD A B C D -中,1AB AD AA ==,1160A AB A AD DAB ∠∠∠===,点P 在线段1BC 上,则( ) A .1AP B C ⊥B .P 到11A B 和CD 的距离相等C .AP 与11A BD .AP 与平面ABCD所成角的正弦值最大为13 一、单选题 1.(2022·江苏扬州·高二期中)如图,在平行六面体1111ABCD A B C D -中,M 为AC 和BD 的交点,若AB a =,AD b =,1AA c =,则下列式子中与1MB 相等的是( )A .1122-+a b cB .1122a b c +- C .1122a b c -++ D .1122--+a b c 2.(2022·河北·石家庄二十三中高二阶段练习)设直线1l 、2l 的方向向量分别为a ,b ,能得到12l l ⊥的是( ) A .(1,2,2)a =-,(2,4,4)b =-B .(2,2,1)a =-,(3,2,10)b =-C .(1,0,0)a =,(3,0,0)b =-D .(2,3,5)a =-,(2,3,5)b =3.(2022·全国·高二专题练习)如图所示,空间四边形ABCD 中,点G 为BCD △的重心,E ,F ,H 分别为边CD ,AD 和BC 的中点,则1132AG BE CA ++的化简结果为( )A .AFB .AHC .AED .CF4.(2021·全国·高考真题(理))在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角【过关检测】为( )A .π2B .π3C .π4D .π65.(2022·湖北·武汉市第十七中学高二期中)在正四面体D ABC -中,点E 在棱AB 上,满足2AE EB =,点F 为线段AC 上的动点,则( )A .存在某个位置,使得DE BF ⊥B .存在某个位置,使得π4FDB ∠= C .存在某个位置,使得直线DE 与平面DBFD .存在某个位置,使得平面DEF 与平面DAC二、多选题 6.(2022·广东·普宁市华侨中学高二阶段练习)如图所示,平行六面体1111ABCD A B C D -中,11111A C B D O ⋂=,以顶点A 为端点的三条棱长都为1,且1160BAD DAA BAA ∠=∠=∠=︒,则下列结论正确的是( )A.1BD B .1//CO 平面1BDA C .1AA 与平面ABCDD .四棱锥1B ABCD -7.(2022·全国·高二专题练习)已知直三棱柱111ABC A B C 中,AB BC ⊥,1AB BC BB ==,O 为1A C 的中点.点P 满足1BP BC λ=,其中[0,1]λ∈,则( )A .对[0,1]λ∀∈时,都有11A P OB ⊥B .当13λ=时,直线1A P 与AB 所成的角是30° C .当12λ=时,直线1A P 与平面111A B CD .当12λ=时,直线1A P 与1OB 相交于一点Q ,则112PQ QA = 三、填空题8.(2022·重庆·四川外国语大学附属外国语学校高二阶段练习)在平行六面体1111ABCD A B C D -中,用向量AB ,AD ,1AA 表示1D B =______.9.(2022·江西南昌·高二期末(理))已知正四面体ABCD 中,E ,F 分别是线段BC ,AD 的中点,点G 是线段CD 上靠近D 的四等分点,则直线EF 与AG 所成角的余弦值为______.四、解答题10.(2022·全国·高二课时练习)如图,在三棱柱111ABC A B C 中,AB ⊥平面11BB C C ,122AB BB BC ===,1BC E 为11A C 的中点.(1)求证:1C B ⊥平面ABC ;(2)求点A 到平面BCE 的距离.11.(2022·辽宁实验中学高二阶段练习)如图,在平行六面体1111ABCD A B C D -中,1160A AD A AB BAD ∠=∠=∠=︒,2AB AD ==,11AA =,点P 为线段BC 中点.(1)求1D P ;(2)求直线1AB 与1D P 所成角的余弦值.12.(2022·广东·顺德一中高二阶段练习)如图,在三棱柱111ABC A B C 中,1CC ⊥平面ABC ,,,D E F 分别为111,,AA AC A C 的中点,AB BC ==12AC AA ==.(1)求证:AC ⊥平面BEF ;(2)求二面角1B CD C 的余弦值; 13.(2022·天津·静海一中高二阶段练习)如图,⊥AE 平面ABCD ,//CF AE ,//AD BC ,AD AB ⊥,2AE BC ==,1AB AD ==,87CF =,则(1)求BD 与EC 所成角的余弦值;(2)求直线CE 与平面BDE 所成角的正弦值; (3)求平面EBD 与平面BDF 的夹角的余弦值.。

第1讲地球与地球仪考点展示素养目标地球的形状和大小。
纬线和纬度、经线和经度、东西半球和南北半球的划分、经纬网的作用。
知识:知道地球的形状和大小,掌握经纬网的特点。
技能:能利用有关数据,说明地球的形状和大小;能够利用经纬网进行区域定位、方向辨别、估算距离等。
素养:结合经纬网图,从区域认知的角度进行区域定位,判断区域特征。
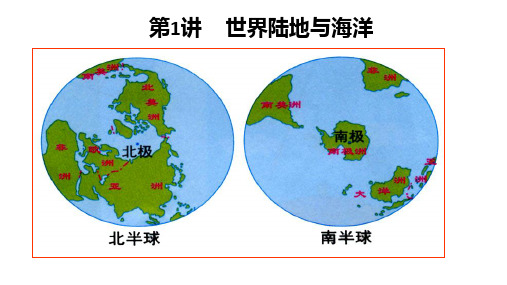
地球的形状和大小__________________________________[读图思考]如何描述地球的形状和大小?1.形状地球的赤道半径略大于极半径,故其形状特点是两极稍扁、赤道略鼓的椭球体。
2.大小平均半径6_371千米;赤道周长约4万千米;表面积约5.1 亿平方千米。
经纬网___________________________________________________[读图思考]纬线有哪些特点?在地图上如何辨别南北纬度?[读图思考]经线有哪些特点?在地图上如何辨别东西经度?1.纬线和纬度(1)纬线:与地轴垂直并且环绕地球一周的圆圈。
每一条纬线构成纬线圈,长度自赤道向两极递减,并且指示东西方向。
(2)纬度:从赤道向南、向北各分为90°。
赤道以北为北纬,用“N”表示,赤道以南为南纬,用“S”表示。
北纬的度数越向北越大,南纬的度数越向南越大。
(3)低、中、高纬地区的划分:以30°、60°纬线为界,将地球划分为低、中、高纬地区。
2.经线和经度(1)经线:连接南北两极并且与纬线垂直相交的半圆。
每一条经线的长度相等,并且指示南北方向。
(2)经度:从本初子午线向东、向西各分为180°。
以东为东经,用“E”表示,以西为西经,用“W”表示。
东经度向东度数增大,西经度向西度数增大。
(3)东、西半球的分界线:20°W和160°E经线组成的经线圈。
1.读下图,回答下列问题。
(1)图1中A点的地理坐标是______________,所属的半球是________________,与B 点的距离约为__________,所属的纬度带是__________。

第1讲地球和地球仪一.地球的形状1.盖天说:在我国,早在二千多年前的周朝,就存在着一种“天圆如张盖、地方如棋局”的盖天说。
2.浑天说:地球不是孤零零地悬在空中的,而是浮在水上,后来又有发展,认为地球浮在气中,因此有可能回旋浮动,这就是“地有四游”的朴素地动说的先河。
浑天说认为全天恒星都布于一个“天球”上,而日月五星则附丽于“天球”上运行,这与现代天文学的天球概念十分接近。
3.球体(1)古希腊学者亚里士多德根据月食的景象分析认为: 月球被地影遮住的部分的边缘是圆弧型的,所以地球是球体或近似球体。
(2)在海上看远处行驶来的船,最先看到的是桅杆,然后才看到船体,这证明地球是球体。
(3)麦哲伦还通过一次航海,进一步用事实证明了地球是球体。
4.实际形状:地球是一个两极稍扁、赤道略鼓的不规则球体。
通过实测和分析,人们终于得到确切的数据:地球的平均赤道半径为6378.38千米,极半径为6356.89千米。
测量还发现,北极地区约高出18.9米,南极地区则低下24-30米。
看起来,地球形状像一只梨子:它的赤道部分鼓起,是它的“梨身”;北极有点放尖,像个“梨蒂”;南极有点凹进去,像个“梨脐”……因此,地球被叫做“梨形地球”。
确切地说,地球是个三轴椭球体。
二.地球的大小地球的平均半径是6371千米。
最大周长约4万千米,表面积约5.1亿平方千米。
三.地球仪1.地轴:假想的轴,与地球北端交点为北极点,南端交点为南极点。
2.形状:正球体。
地球的赤道半径比极半径长21km ,如果按照比例制作一个半径为1米的地球仪,那么赤道半径仅仅比极半径长了大约3mm ,凭肉眼无法察觉出来,因此在制作地球仪的时候总是将它做成球体。
四.纬线和经线1.纬度(1)定义:指某点与地球球心的连线和地球赤道面所成的线面角(线面角)。
(2)数值范围:0°~90°。
(3)读数变化:向北增大是北纬,用字母“N”表示,向南增大是南纬,用字母“S”表示。


Be the change you want to see in the world.——《越狱》第一讲Grammar + Reading总纲(一)Parts of sentences(句子成分)1.主语I love you.(主语从句)2.谓语He went away.3.宾语I love you.(宾语从句)4.表语He is a teacher.(表语从句)句子成分 5.补语宾语补足语He asked me to leave.I was asked to leave.6.定语He is a good teacher.(定语从句)7.状语He went abroad yesterday.(状语从句)8.同位语Mr. Lee, our teacher, is coming.(同位语从句)9.插入语By the way, he will go to school.(二)Kinds of sentences(句子种类)I.简单句(五种构成方式)1.主谓(主语+不及物动词)2.主谓宾(主语+及物动词+宾语)3.主系表(主语+连系动词+表语)(必须记住五组连系动词)4.主谓双宾(主语+及物动词+间接宾语+直接宾语)(1)间接宾语后置,我们可以通过加入介词(to或for)来将间接宾语后置。
(2)当两个宾语都是代词时,通常将间接宾语后置。
Give it to me.5.主谓宾宾补(主语+及物动词+宾语+宾语补足语(宾语的动作或状态) )(1)形容词做宾语补足语使(2)名词或名词短语做宾语补足语:(3)非谓做宾语补足语只须记住感观动词和使役动词的短语II.并列句:两个或以上简单句用以下四种方法连接1.并列连词(and, so, or, but, yet) He is young, and he is good.(Make) Greater efforts, and you will succeed2.分号:He is young ; he is good.3.—:Try some of this juice-perhaps you'll like it.4.两个插入语for example:I have many good friends, for example, Tom is one of them.that is:He seldom helps others, that is, he is so selfish.III.主从复合句:两个或以上简单句用从句连词连接。
IV.并列复合句:(三)Numeral(数词)1.普通分数one third, two thirds, a half, a quarter, 3 quarters + ofI.分数 2.百分数thirty percent+ of百分之三十的3.具体分数one in four=one out of four四个中的一个1.确定基数词: one, two, three…(1) three boys (2) three of us (3) three of my students2.不确定基数词: many, few, a few, several, little, a little, some, any…II.基数词(1) many boys (2) many of them (3) many of my students3.单位基数词dozen, score, hundred, thousand, million, billion(1) three dozen eggs, many dozen eggs(2) three dozen of the eggs, many dozen of those eggs(3) dozens of, scores of, tens of, millions of, billions of, tens of thousands ofIII.序数词:first, second, third, fifth, eighth, ninth, twelfth, twentieth, hundredth(用法见冠词)IV.数词短语(1)every few days 每几天1.频率(2)every other day=every two days=every second day每两天(每隔一天)(3)every three days=every third day每三天(每隔两天)(1)enough>plenty of + Ns/Nu2.许多(2)lots of=a lot of=a mass of=masses of=a quantity of=quantities of+ Ns/Nu(3)a number of=a good (great) many=many +Ns=many a + Nc(4)a great deal of=an amount of=amounts of + Nu3.越来越多的an increasing number of=a growing number of=more and more4.各种各样的a variety of=different kinds of + Ns/Nu5.大多数的the majority of = most (of the) + Ns/Nu≠少数的the minority of+ Ns/NuV.英语没有量词on his first visit to China(四)Agreement(主谓一致)1. both A and B: Both time and tide wait for no man.I. A and B 2.表示两个人,物或事: What I love and what I hate are none of your business.(1) The famous singer and dancer is coming.3.表示一个人,物或事(2) Every (each/no) boy and every (each/no) girl is good.(3) When and where to meet is not decided.B以A为主:He as well as his friends is going abroad.单独做主语 1.指人: All but one were here just now.指物: All he has done is right.IV.集体名词 1.强调整体: My class is a good one.V.二合一名词 1.单独做主语: My trousers are new.is what I want.VI.单复同形的名词 1. Every means has been tried to prevent pollution.VII. the +形容词或分词表示一类: The old are wise.(the old, the dying垂死者, the employing雇佣者, the employed被雇佣者)(the police ,the Chinese , the English, the French)VIII.分数和the rest of以中心名词为主: The rest of the students are fond of computer games.1. There be: There is a book and two pens on the desk.IX.靠近原则2.平行词组:Not only Tom but also his parants are kind to me(either..or../neither...nor.../whether...or.../).3. A or B: One boy or his friends are to come.1. One hundred years is a long time.X. Time/Money/Distance 2. One million dollars is a large sum.3. Two thousand miles is a long way.XI.倒装句要认准主语 1. Between the two windows hangs a picture.2. What he needs is more money, while what I need are more books. XII.固定词组(1)One of his books is very good.1. one of (2)He is one of the boys who like English. (定语从句)(3)He is the (only)one of the boys who likes English. (定语从句)(1) a quantity of Ns/Nu +is, large quantities of Ns/Nu +are2.数量(2) a number of+ Ns+ are, the number of +Ns +is(3) an amount of Nu+ is, large amounts of Nu+ are3. one and a half apples +is=one apple and a half +is4. more than one +is5. many a boy +is6. we each +are=each of us +is7.加减乘除算式+is8 The 2008 Olympic Games are to be held in Beijing.9. This kind (sort/type) of man is good.= Men of this kind (sort/type) are good.10. My collection of stamps is very wonderful.(五)插入语1. (much/greatly) to one’s surprise=to one’s (great) surprise (shock, joy, delight, knowledge)2. 否则otherwise=or else≠or(连词)3. 然而nevertheless≠while(连词)4. 因此therefore=thus=as a result≠(and) so(连词)5. 但是6. 就我所能/知/见so(as) far as I can/know/see; 就…而言so(as) far as sb./sth. is concerned7. 另外also=again=besides=in addition=what’s more=moreover=more than that同时(in the) meanwhile (meantime) = at the same time进一步(甚至)further more≠even(副词)8. 一方面,另一方面on one hand…on the other hand=for one thing…for another (thing)…=firstly…secondly(互换)9. 相反instead=rather=in turn≠从反方面看on the contrary10.实际上as a matter of fact=in (actual) fact =actually11.更糟的to make matters worse= what’s worse still=what’s worse= worse still=worse than that12.最后/终于finally=eventually =in the end<at last13.现在nowadays=for the time being=at present=presently14.那以后(ever)after (that)=afterwards=from then on=later(on) +did那以后(ever) since (then) +have(had) done15.突然suddenly=all of a sudden=all at once≠刹那间(一瞬间)in a flash16.确切地说namely=or rather =or≠换言之that is (to say )= in other words =ie17.俗话说as a saying goes18.多半/大多数情况下more often (than not)=in most cases=for the most part19.例如for example=for instance20.等等and so on=and so forth=etc.21.in that case在那种情况下≠in case 以防万一≠in case (that)万一(连词)≠in case of 万一(介词)22..in general;in particular特别地;on the whole整体上;in detail细节上in short简言之;in a word总之;in common共同;in common with与…相同(介词)23.after all毕竟(终究);at all(1)一点都不(2)究竟,above all最重要的是;first先(then然后);first of all=firstly第一(secondly…其次)at first起初;(all) in all=altogether=in total总共24.on earth=in the world (1)究竟(2)在世界上, on the earth在地球上, in the earth在地里。