三角函数公式--个人整理

三角函数公式大全三角函数是数学中非常重要的一个分支，广泛应用于物理学、工程学、计算机科学等多个领域。

下面为大家带来一份三角函数公式大全。

一、基本三角函数1、正弦函数（sin）：在直角三角形中，一个锐角的正弦是它的对边与斜边的比值。

即 sinA ＝ a ／ c （其中 A 为锐角，a 为 A 的对边，c 为斜边）。

2、余弦函数（cos）：一个锐角的余弦是它的邻边与斜边的比值。

即 cosA ＝ b ／ c （其中 b 为 A 的邻边）。

3、正切函数（tan）：一个锐角的正切是它的对边与邻边的比值。

即 tanA ＝ a ／ b 。

二、同角三角函数基本关系1、平方关系：sin²A ＋ cos²A ＝ 1 。

2、商数关系：tanA ＝ sinA ／ cosA 。

三、诱导公式1、终边相同的角的三角函数值相等：sin(2kπ ＋ A) ＝ sinA ，cos(2kπ ＋ A) ＝ cosA ，tan(2kπ ＋ A) ＝ tanA （k ∈ Z）。

2、关于 x 轴对称：sin(A) ＝ sinA ，cos(A) ＝ cosA ，tan(A) ＝tanA 。

3、关于 y 轴对称：sin(π A) ＝ sinA ，cos(π A) ＝ cosA ，tan(π A) ＝ tanA 。

4、关于原点对称：sin(π ＋ A) ＝ sinA ，cos(π ＋ A) ＝ cosA ，tan(π ＋ A) ＝ tanA 。

5、 90°相关：sin(π/2 A) ＝ cosA ，cos(π/2 A) ＝ sinA 。

四、两角和与差的三角函数公式1、两角和的正弦：sin(A ＋ B) ＝ sinAcosB ＋ cosAsinB 。

2、两角差的正弦：sin(A B) ＝ sinAcosB cosAsinB 。

3、两角和的余弦：cos(A ＋ B) ＝ cosAcosB sinAsinB 。

4、两角差的余弦：cos(A B) ＝ cosAcosB ＋ sinAsinB 。

三角函数公式大全及记忆口诀一、正弦函数（sine function）公式：1. 正弦函数的定义：在直角三角形中，正弦函数是对边与斜边之比，表示为sinθ。

2. 正弦函数的基本关系式：sinθ = 对边 / 斜边3. 弦函数的平方和恒等式：sin²θ + cos²θ = 1二、余弦函数（cosine function）公式：1. 余弦函数的定义：在直角三角形中，余弦函数是邻边与斜边之比，表示为cosθ。

2. 余弦函数的基本关系式：cosθ = 邻边 / 斜边3. 弦函数与余弦函数的关系：cosθ = sin(90° - θ)三、正切函数（tangent function）公式：1. 正切函数的定义：在直角三角形中，正切函数是对边与邻边之比，表示为tanθ。

2. 正切函数的基本关系式：tanθ = 对边 / 邻边3. 弦函数与正切函数的关系：tanθ = sinθ / cosθ四、余切函数（cotangent function）公式：1. 余切函数的定义：在直角三角形中，余切函数是邻边与对边之比，表示为cotθ。

2. 余切函数的基本关系式：cotθ = 邻边 / 对边3. 弦函数与余切函数的关系：cotθ = 1 / tanθ = cosθ / sinθ五、正割函数（secant function）公式：1. 正割函数的定义：在直角三角形中，正割函数是斜边与邻边之比，表示为secθ。

2. 正割函数的基本关系式：secθ = 斜边 / 邻边= 1 / cosθ六、余割函数（cosecant function）公式：1. 余割函数的定义：在直角三角形中，余割函数是斜边与对边之比，表示为cscθ。

2. 余割函数的基本关系式：cscθ = 斜边 / 对边= 1 / sinθ七、和差公式：1. 正弦函数和差公式：sin(θ±φ) = sinθcosφ ± cosθsinφ2. 余弦函数和差公式：cos(θ±φ) = cosθcosφ ∓ sinθsinφ3. 正切函数和差公式：tan(θ±φ) = (tanθ ± tanφ) / (1 ∓tanθtanφ)八、倍角公式：1. 正弦函数倍角公式：sin2θ = 2sinθcosθ2. 余弦函数倍角公式：cos2θ = cos²θ - sin²θ = 2cos²θ - 1= 1 - 2sin²θ3. 正切函数倍角公式：tan2θ = (2tanθ) / (1 - tan²θ)九、半角公式：1. 正弦函数半角公式：sin(θ/2) = ±√[(1 - cosθ) / 2]2. 余弦函数半角公式：cos(θ/2) = ±√[(1 + cosθ) / 2]3. 正切函数半角公式：tan(θ/2) = ±√[(1 - cosθ) / (1 +cosθ)]十、和差化积公式：1. 正弦函数和差化积公式：sinθ ± sinφ = 2sin[(θ ±φ)/2]cos[(θ ∓ φ)/2]2. 余弦函数和差化积公式：cosθ + cosφ = 2cos[(θ +φ)/2]cos[(θ - φ)/2]3. 正切函数和差化积公式：tanθ ± tanφ = sin(θ ± φ) /cosθcosφ以上是三角函数的常用公式。

三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ,记：22y x r +=， 正弦函数：r y=αsin 余弦函数：r x =αcos 正切函数：x y =αtan余切函数：y x =αcot 正割函数：xr=αsec余割函数：yr=αcsc二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割,左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ,1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角,终边相同的角的同一三角函数的值相等:sin（2kπ＋α）＝sinα cos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanα cot（2kπ＋α)＝cotα (其中k∈Z) 公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin（π＋α）＝－sinα cos（π＋α）＝－cosα tan（π＋α）＝tanα cot（π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系： sin（－α）＝－sinα cos（－α）＝cosα tan(－α）＝－tanα cot（－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin（π－α）＝sinα cos（π－α）＝－cosα tan（π－α）＝－tanα cot(π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系:sin（απ-2）＝cosα cos（απ-2）＝sinα tan（απ-2）＝cotα cot（απ-2）＝tanα公式六:απ+2与α的三角函数值之间的关系:sin（απ+2）＝cosα cos（απ+2）＝－sinαtan(απ+2)＝－cotα cot（απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系：sin(απ-23）＝－cosα cos（απ-23）＝－sinαtan（απ-23)＝cotα cot（απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin(απ+23）＝－cosα cos（απ+23）＝sinαtan（απ+23）＝－cotα cot（απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin（2π－α)＝－sinα cos(2π－α）＝cosα tan（2π－α)＝－tanα cot（2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

最全的三角函数公式三角函数是数学中一个重要的概念，广泛应用于几何、物理和工程等领域。

在本文中，我将为您介绍最全的三角函数公式，包括基本公式、倒数公式、和角公式、和差公式、倍角公式、半角公式、和积公式、和商公式以及其他一些特殊的三角函数公式。

一、基本公式1. 正弦公式：sinθ = 对边/斜边2. 余弦公式：cosθ = 邻边/斜边3. 正切公式：tanθ = 对边/邻边二、倒数公式1. 余切公式：cotθ = 邻边/对边2. cosec公式：cscθ = 1/sinθ3. sec公式：secθ = 1/cosθ三、和角公式1. 正弦和：sin(α+β) = sinαcosβ + cosαsinβ2. 余弦和：cos(α+β) = cosαcosβ - sinαsinβ3. 正切和：tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)四、差角公式1. 正弦差：sin(α-β) = sinαcosβ - cosαsinβ2. 余弦差：cos(α-β) = cosαcosβ + sinαsinβ3. 正切差：tan(α-β) = (tanα - tanβ)/(1 + tanαtanβ)五、倍角公式1. 正弦倍角：sin2θ = 2sinθcosθ2. 余弦倍角：cos2θ = cos²θ - sin²θ3. 正切倍角：tan2θ = 2tanθ/(1 - tan²θ)六、半角公式1. 正弦半角：sin(θ/2) = ±√[(1 - cosθ)/2]2. 余弦半角：cos(θ/2) = ±√[(1 + cosθ)/2]3. 正切半角：tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)] （其中分母不等于0）七、和积公式1. 正弦和积：sin(α+β) = 2sin(α/2)cos(β/2)2. 余弦和积：cos(α+β) = 2cos(α/2)cos(β/2)3. 正切和积：tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)八、和商公式1. 正弦和商：sin(α+β) = sinαcosβ + cosαsinβ/cosαcosβ - sinαsinβ2. 余弦和商：cos(α+β) = cosαcosβ - sinαsinβ/cosαcosβ + sinαsinβ3. 正切和商：tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)九、其他特殊公式1. 倍角余弦1：cos2θ = 1 - 2sin²θ2. 倍角余弦2：cos²θ = （1 + cos2θ）/23. 倍角正弦：sin2θ = 2sinθcosθ4. 差角正切：tan(α-β) = (tanα - tanβ)/(1 + tanαtanβ)这些三角函数公式是三角学中最基本且最重要的公式。

(完整版)三角函数公式表1. 正弦函数 (sin):定义：正弦函数是直角三角形中对边与斜边的比值。

公式：sin(θ) = 对边 / 斜边范围：1 ≤ sin(θ) ≤ 1特殊值：sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义：余弦函数是直角三角形中邻边与斜边的比值。

公式：cos(θ) = 邻边 / 斜边范围：1 ≤ cos(θ) ≤ 1特殊值：cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义：正切函数是直角三角形中对边与邻边的比值。

公式：tan(θ) = 对边 / 邻边范围：tan(θ) 可以取任意实数值特殊值：tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在（无穷大）4. 余切函数 (cot):定义：余切函数是直角三角形中邻边与对边的比值。

公式：cot(θ) = 邻边 / 对边范围：cot(θ) 可以取任意实数值特殊值：cot(0°) 不存在（无穷大）, cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义：正割函数是直角三角形中斜边与邻边的比值。

公式：sec(θ)= 1 / cos(θ)范围：sec(θ) 可以取任意实数值特殊值：sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在（无穷大）6. 余割函数 (csc):定义：余割函数是直角三角形中斜边与对边的比值。

三角函数的公式大全1、两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)2、倍角公式tan2A = 2tanA/(1-tan² A)Sin2A=2SinA•CosACos2A = Cos^2 A–Sin² A=2Cos² A—1=1—2sin^2 A3、三倍角公式sin3A = 3sinA-4(sinA)³;cos3A = 4(cosA)³ -3cosAtan3a = tan a • tan(π/3+a)• tan(π/3-a)4、半角公式sin(A/2) = √{(1–cosA)/2}cos(A/2) = √{(1+cosA)/2}tan(A/2) = √{(1–cosA)/(1+cosA)}cot(A/2) = √{(1+cosA)/(1-cosA)} ?tan(A/2) = (1–cosA)/sinA=sinA/(1+cosA) 5、和差化积sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB6、积化和差sin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)]7、诱导公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2-a) = cos(a)cos(π/2-a) = sin(a)sin(π/2+a) = cos(a)cos(π/2+a) = -sin(a)sin(π-a) = sin(a)cos(π-a) = -cos(a)sin(π+a) = -sin(a)cos(π+a) = -cos(a)tgA=tanA = sinA/cosA8、万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]²}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]²}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}9、其它公式a•sin(a)+b•cos(a) = [√(a²+b²)]*sin(a+c) [其中，tan(c)=b/a] a•sin(a)-b•cos(a) = [√(a²+b²)]*cos(a-c) [其中，tan(c)=a/b] 1+sin(a) = [sin(a/2)+cos(a/2)]²;1-sin(a) = [sin(a/2)-cos(a/2)]²;10、其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)11、双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tg h(a) = sin h(a)/cos h(a)12、公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）= sinαcos（2kπ＋α）= cosαtan（2kπ＋α）= tanαcot（2kπ＋α）= cotα13、公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα14、公式三：任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα15、公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα16、公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα17、公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= cotαcot（π/2-α）= tanαsin（3π/2+α）= -cosαcos（3π/2+α）= sinαtan（3π/2+α）= -cotαcot（3π/2+α）= -tanαsin（3π/2-α）= -cosαcos（3π/2-α）= -sinαtan（3π/2-α）= cotαcot（3π/2-α）= tanα√表示根号,包括{……}中的内容18、三角函数记忆口诀三角函数是函数，象限符号坐标注。

三角函数公式大全1.三角函数的基本定义：- 正弦函数：sinθ = 对边/斜边- 余弦函数：cosθ = 邻边/斜边- 正切函数：tanθ = 对边/邻边- 余切函数：cotθ = 1/tanθ- 正割函数：secθ = 1/cosθ- 余割函数：cscθ = 1/sinθ2.三角函数的周期性：- 正弦函数的周期为2π：sin(θ+2π) = sinθ- 余弦函数的周期为2π：cos(θ+2π) = cosθ- 正切函数的周期为π：tan(θ+π) = tanθ3.三角函数的平方和差公式：- 正弦函数的平方和差公式：sin(A±B) = sinAcosB ± cosAsinB - 余弦函数的平方和差公式：cos(A±B) = cosAcosB ∓ sinAsinB - 正切函数的平方和差公式：tan(A±B) = (tanA ± tanB)/(1 ∓tanAtanB)4.三角函数的倍角公式：- 正弦函数的倍角公式：sin2θ = 2sinθcosθ- 余弦函数的倍角公式：cos2θ = cos²θ - sin²θ- 正切函数的倍角公式：tan2θ = (2tanθ)/(1 - tan²θ)5.三角函数的半角公式：- 正弦函数的半角公式：sin(θ/2) = ±√((1 - cosθ)/2)- 余弦函数的半角公式：cos(θ/2) = ±√((1 + cosθ)/2)- 正切函数的半角公式：tan(θ/2) = ±√((1 - cosθ)/(1 +cosθ))6.三角函数的和差化积公式：- 正弦函数的和差化积公式：sinA + sinB = 2sin((A+B)/2)cos((A-B)/2)- 余弦函数的和差化积公式：cosA + cosB = 2cos((A+B)/2)cos((A-B)/2)- 正弦函数的差化积公式：sinA - sinB = 2cos((A+B)/2)sin((A-B)/2)- 余弦函数的差化积公式：cosA - cosB = 2sin((A+B)/2)sin((A-B)/2)7.其他重要公式：- 三角函数的平方公式：sin²θ + cos²θ = 1- 三角函数的倒数公式：sin(π/2 - θ) = cosθ，cos(π/2 - θ) = sinθ，tan(π/2 - θ) = cotθ- 三角函数的和差化差公式：cos(A-B) = cosAcosB + sinAsinB，cos(A+B) = cosAcosB - sinAsinB这些是三角函数中一些重要的公式，对于理解和应用三角函数有很大的帮助。

三角函数公式大全三角函数是数学中的重要概念，广泛应用于各个领域。

本文将为您介绍一些常用的三角函数公式，以及它们的应用。

一、正弦函数公式1. 正弦函数定义：在直角三角形中，对于任意角A，正弦函数的值定义为：sin(A) = 对边 / 斜边。

2. 正弦函数的基本性质：- 周期性：sin(A) = sin(A + 2πk)，其中k为整数。

- 奇偶性：sin(-A) = -sin(A)。

- 平移性：sin(A + π) = -sin(A)。

二、余弦函数公式1. 余弦函数定义：在直角三角形中，对于任意角A，余弦函数的值定义为：cos(A) = 邻边 / 斜边。

2. 余弦函数的基本性质：- 周期性：cos(A) = cos(A + 2πk)，其中k为整数。

- 奇偶性：cos(-A) = cos(A)。

- 平移性：cos(A + π) = -cos(A)。

三、正切函数公式1. 正切函数定义：在直角三角形中，对于任意角A，正切函数的值定义为：tan(A) = 对边 / 邻边。

2. 正切函数的基本性质：- 周期性：tan(A) = t an(A + πk)，其中k为整数。

- 奇偶性：tan(-A) = -tan(A)。

- 平移性：tan(A + π) = tan(A)。

四、余切函数公式1. 余切函数定义：在直角三角形中，对于任意角A，余切函数的值定义为：cot(A) = 邻边 / 对边。

2. 余切函数的基本性质：- 周期性：cot(A) = cot(A + πk)，其中k为整数。

- 奇偶性：cot(-A) = -cot(A)。

- 平移性：cot(A + π) = cot(A)。

五、正割函数和余割函数公式1. 正割函数定义：在直角三角形中，对于任意角A，正割函数的值定义为：sec(A) = 斜边 / 邻边。

2. 余割函数定义：在直角三角形中，对于任意角A，余割函数的值定义为：csc(A) = 斜边 / 对边。

综上所述，我们介绍了正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数的基本定义及性质。

三角函数所有公式大全三角函数是数学中的重要概念，它在几何学、物理学、工程学等领域都有着广泛的应用。

本文将为大家详细介绍三角函数的所有公式，包括正弦函数、余弦函数、正切函数等，希望能够帮助大家更好地理解和掌握三角函数的知识。

一、正弦函数。

正弦函数是三角函数中的一种，通常用sin表示。

在直角三角形中，正弦函数的定义是：对于一个角为θ的直角三角形，正弦函数的值等于对边与斜边的比值，即sinθ=对边/斜边。

在数学中，正弦函数的周期是2π，其图像是一条周期性波动的曲线。

正弦函数的常用公式包括：1. 正弦函数的和差化积公式：sin(a±b) = sinacosb ± cosasinb。

2. 正弦函数的倍角公式：sin2a = 2sinacosb。

3. 正弦函数的半角公式：sin(a/2) = ±√((1-cos a)/2)。

二、余弦函数。

余弦函数是三角函数中的另一种，通常用cos表示。

在直角三角形中，余弦函数的定义是：对于一个角为θ的直角三角形，余弦函数的值等于邻边与斜边的比值，即cosθ=邻边/斜边。

余弦函数的周期也是2π，其图像是一条周期性波动的曲线。

余弦函数的常用公式包括：1. 余弦函数的和差化积公式：cos(a±b) = cosacosb ∓ sinasinb。

2. 余弦函数的倍角公式：cos2a = cos^2a sin^2a。

3. 余弦函数的半角公式：cos(a/2) = ±√((1+cos a)/2)。

三、正切函数。

正切函数是三角函数中的另一种，通常用tan表示。

在直角三角形中，正切函数的定义是：对于一个角为θ的直角三角形，正切函数的值等于对边与邻边的比值，即tanθ=对边/邻边。

正切函数的周期是π，其图像是一条周期性波动的曲线。

正切函数的常用公式包括：1. 正切函数的和差化积公式：tan(a±b) = (tana±tanb)/(1∓tanatanb)。

(完整版)三角函数公式汇总介绍三角函数是数学中重要的概念，可用来描述角的性质和在各个学科中的应用。

三角函数包括正弦（sin）、余弦（cos）、正切（tan）等，它们之间存在一系列的基本关系和公式。

本文档将详细介绍常见的三角函数公式，以帮助读者更好地理解和应用三角函数。

正弦函数（sin）定义正弦函数是一个周期为2π的周期函数，定义域为实数集，值域为[-1, 1]。

公式1. 正弦函数的周期性公式为：sin(x + 2kπ) = sin(x)，其中 k ∈ Z。

2. 正弦函数的关系公式有：- 反正弦函数：x = arcsin(y)，其中 y ∈ [-1, 1]。

- 正弦函数的平方和公式：sin^2(x) + cos^2(x) = 1。

余弦函数（cos）定义余弦函数是一个周期为2π的周期函数，定义域为实数集，值域为[-1, 1]。

公式1. 余弦函数的周期性公式为：cos(x + 2kπ) = cos(x)，其中 k ∈Z。

2. 余弦函数的关系公式有：- 反余弦函数：x = arccos(y)，其中 y ∈ [-1, 1]。

- 余弦函数的平方和公式：sin^2(x) + cos^2(x) = 1。

正切函数（tan）定义正切函数是一个周期为π的周期函数，定义域为实数集。

公式1. 正切函数的周期性公式为：tan(x + kπ) = tan(x)，其中 k ∈ Z。

2. 正切函数的关系公式有：- 反正切函数：x = arctan(y)，其中 y ∈ R。

其他三角函数公式1. 余切函数（cot）与正切函数的关系式：cot(x) = 1/tan(x)。

2. 正割函数（sec）与余弦函数的关系式：sec(x) = 1/cos(x)。

3. 余割函数（csc）与正弦函数的关系式：csc(x) = 1/sin(x)。

应用领域三角函数广泛应用于工程、物理、计算机图形学等领域。

例如，在三角形的计算中，可以利用正弦、余弦、正切等函数来求解各种角度和边长。

三角函数公式大全一、正弦函数公式。

正弦函数是最基本的三角函数之一，其公式如下：sinθ = 对边/斜边。

其中，θ为角度，对边为与角度θ相对的直角三角形的边长，斜边为直角三角形的斜边长度。

正弦函数的图像是一个周期性的波动曲线，具有一定的对称性和周期性。

二、余弦函数公式。

余弦函数是另一个重要的三角函数，其公式如下：cosθ = 邻边/斜边。

其中，θ为角度，邻边为与角度θ相邻的直角三角形的边长，斜边为直角三角形的斜边长度。

余弦函数的图像也是一个周期性的波动曲线，与正弦函数的图像有一定的相似性。

三、正切函数公式。

正切函数是三角函数中的另一个重要概念，其公式如下：tanθ = 对边/邻边。

其中，θ为角度，对边为与角度θ相对的直角三角形的边长，邻边为与角度θ相邻的直角三角形的边长。

正切函数的图像也是一个周期性的波动曲线，但与正弦函数和余弦函数的图像有着明显的不同。

四、三角函数的基本关系。

在学习三角函数时，还需要了解三角函数之间的基本关系，如正弦函数与余弦函数、正切函数与余切函数之间的关系。

这些关系可以通过三角恒等式来表示，如sin^2θ + cos^2θ = 1，tanθ = sinθ/cosθ等。

五、三角函数的诱导公式。

三角函数的诱导公式是指通过某个角的正弦、余弦、正切等函数值，来推导其他角的正弦、余弦、正切等函数值的公式。

例如，利用角度为θ的正弦函数值，可以求得角度为π/2-θ的余弦函数值，从而得到诱导公式sin(π/2-θ) = cosθ。

六、三角函数的图像和性质。

除了掌握三角函数的公式外，还需要了解三角函数的图像和性质。

正弦函数、余弦函数、正切函数等在坐标平面上的图像特点，以及它们的周期、对称性、增减性等性质都是非常重要的。

七、三角函数在实际问题中的应用。

三角函数在实际问题中有着广泛的应用，如在航海、测量、建筑等领域都需要用到三角函数的知识。

掌握三角函数公式和性质，能够帮助我们更好地解决实际问题。

总结。

高中数学-三角函数公式大全新课程高中数学三角公式汇总一、任意角的三角函数在角α的终边上任取一点P(x,y)，记r=x²+y²。

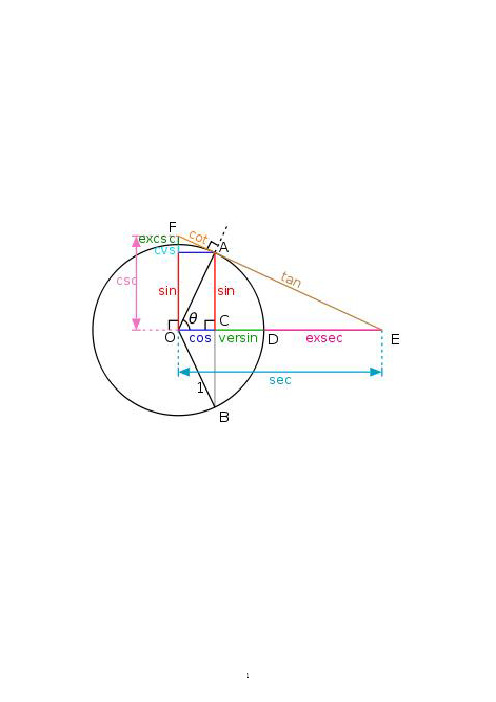
正弦：sinα=y/r余弦：cosα=x/r正切：tanα=y/x余切：cotα=x/y正割：secα=r/x余割：cscα=r/y注：我们还可以用单位圆中的有向线段表示任意角的三角函数。

如图，与单位圆有关的有向线段MP、OM、AT分别叫做角α的正弦线、余弦线、正切线。

二、同角三角函数的基本关系式倒数关系：sinα·cscα=1，cosα·secα=1，tanα·cotα=1.商数关系：tanα=sinα/cosα，cotα=cosα/sinα。

平方关系：sin²α+cos²α=1，1+tan²α=sec²α，1+cot²α=csc²α。

三、诱导公式⑴α+2kπ(k∈Z)、-α、π+α、π-α、2π-α的三角函数值，等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号。

（口诀：函数名不变，符号看象限）⑵π/3+α、-π/3+α、π-α、-π+α的三角函数值，等于α的异名函数值，前面加上一个把α看成锐角时原函数值的符号。

（口诀：函数名改变，符号看象限）四、和角公式和差角公式sin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβcos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)五、二倍角公式sin2α=2sinα·cosαcos2α=cos²α-sin²α=2cos²α-1=1-2sin²α…(※)tan2α=2tanα/(1-tan²α)二倍角的余弦公式(※)有以下常用变形：（规律：降幂扩角，升幂缩角）1+cos2α=2cos²α1-cos2α=2sin²α1+sin2α=(sinα+cosα)²1-sin2α=(sinα-cosα)²cos2α=(1+cos2α)/(1-cos2α)sin2α=(1-cos2α)/2tanα=sin2α/(1+cos2α)万能公式告诉我们，任何单角的三角函数都可以用半角的正切来表示。

三角函数公式大全一、基本定义及性质1. 正弦函数（sin）：sin A = 对边 / 斜边cos A = 临边 / 斜边tan A = 对边 / 临边余切函数（cot）：cot A = 临边 / 对边2.零度三角函数：sin 0° = 0, cos 0° = 1, tan 0° = 0, cot 0° = ∞3.π/6弧度三角函数：sin (π/6) = 1/2, cos (π/6) = √3/2, tan (π/6) = 1/√3, cot (π/6) = √34.π/4弧度三角函数：sin (π/4) = √2/2, cos (π/4) = √2/2, tan (π/4) = 1, cot (π/4) = 15.π/3弧度三角函数：sin (π/3) = √3/2, cos (π/3) = 1/2, tan (π/3) = √3, cot (π/3) = 1/√36.相反角关系：sin (-A) = -sin A, cos (-A) = cos A, tan (-A) = -tan A, cot (-A) = -cot A7.90°三角函数：sin 90° = 1, cos 90° = 0, tan 90° = ∞, cot 90° = 08.π/2弧度三角函数：sin (π/2) = 1, cos (π/2) = 0, tan (π/2) = ∞, cot (π/2) = 09.倒数关系：sin (π - A) = sin A, cos (π - A) = -cos A, tan (π - A) = -tan A, cot (π - A) = -cot A10.余角关系：sin (π/2 - A) = cos A, cos (π/2 - A) = sin A, tan (π/2 -A) = cot A, cot (π/2 - A) = tan A二、和差与倍角公式1.和差公式：sin (A ± B) = sin A cos B ± cos A sin Bcos (A ± B) = cos A cos B ∓ sin A sin Btan (A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B)2.二倍角公式：sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)三、万能角公式（三角函数的倒数、减角公式、二倍角公式的推广形式）1.正弦函数倒数公式：csc A = 1 / sin A2.余弦函数倒数公式：sec A = 1 / cos A3.正切函数倒数公式：cot A = 1 / tan A4.减角公式：sin (A - B) = sin A cos B - cos A sin Bcos (A - B) = cos A cos B + sin A sin Btan (A - B) = (tan A - tan B) / (1 + tan A tan B)5.二倍角公式推广形式：sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)四、积和差公式1.积公式：sin A sin B = (1/2)[cos(A-B) - cos(A+B)]cos A cos B = (1/2)[cos(A-B) + cos(A+B)]sin A cos B = (1/2)[sin(A-B) + sin(A+B)]2.差公式：sin A - sin B = 2 cos[(A+B)/2] sin[(A-B)/2]cos A - cos B = -2 sin[(A+B)/2] sin[(A-B)/2]sin A + sin B = 2 sin[(A+B)/2] cos[(A-B)/2]cos A + cos B = 2 cos[(A+B)/2] cos[(A-B)/2]五、其他重要性质1. 正弦函数的周期：2π，即sin (x + 2π) = sin x余弦函数的周期：2π，即cos (x + 2π) = cos x2.正弦函数的奇偶性：sin (-x) = -sin x，即 sin 函数是奇函数sin (π + x) = -sin x，即 sin 函数是周期为2π的周期函数3.余弦函数的奇偶性：cos (-x) = cos x，即 cos 函数是偶函数cos (π + x) = -cos x，即 cos 函数是周期为2π的周期函数4.正弦函数和余弦函数的间接关系：sin^2 x + cos^2 x = 1。

三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ,记：22y x r +=， 正弦函数：ry=αsin 余弦函数：r x =αcos 正切函数：x y =αtan余切函数：y x =αcot 正割函数：xr=αsec 余割函数：yr=αcsc 二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割,左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ,1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角,终边相同的角的同一三角函数的值相等:sin （2kπ＋α）＝sinα cos（2kπ＋α）＝cosαtan （2kπ＋α）＝tanα cot（2kπ＋α)＝cotα (其中k ∈Z) 公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin （π＋α）＝－sinα cos（π＋α）＝－cosα tan （π＋α）＝tanα cot（π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系： sin （－α）＝－sinα cos（－α）＝cosα tan(－α）＝－tanα cot（－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin （π－α）＝sinα cos（π－α）＝－cosα tan （π－α）＝－tanα cot(π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系:sin （απ-2）＝cosα cos（απ-2）＝sinα tan （απ-2）＝cotα cot（απ-2）＝tanα公式六:απ+2与α的三角函数值之间的关系:sin （απ+2）＝cosα cos（απ+2）＝－sinαtan(απ+2)＝－cotα cot（απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系： sin(απ-23）＝－cosα cos（απ-23）＝－sinαtan （απ-23)＝cotα cot（απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin(απ+23）＝－cosα cos（απ+23）＝sinαtan （απ+23）＝－cotα cot（απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin （2π－α)＝－sinα cos(2π－α）＝cosα tan （2π－α)＝－tanα cot（2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ，记：22y x r +=，正弦函数：r y =αsin 余弦函数：r x =αcos 正切函数：x y=αtan 余切函数：y x =αcot 正割函数：xr=αsec 余割函数：y r =αcsc 二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ，1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）＝sinα cos （2kπ＋α）＝cosαtan （2kπ＋α）＝tanα cot （2kπ＋α）＝cotα (其中k ∈Z)公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin （π＋α）＝－sinα cos （π＋α）＝－cosα tan （π＋α）＝tanα cot （π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系：sin （－α）＝－sinα cos （－α）＝cosα tan （－α）＝－tanα cot （－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin （π－α）＝sinα cos （π－α）＝－cosα tan （π－α）＝－tanα cot （π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系：sin （απ-2）＝cosα cos （απ-2）＝sinα tan （απ-2）＝cotα cot （απ-2）＝tanα公式六：απ+2与α的三角函数值之间的关系：sin （απ+2）＝cosα cos （απ+2）＝－sinα tan （απ+2）＝－cotα cot （απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系： sin （απ-23）＝－cosα cos （απ-23）＝－sinαtan （απ-23）＝cotα cot （απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin （απ+23）＝－cosα cos （απ+23）＝sinαtan （απ+23）＝－cotα cot （απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin （2π－α）＝－sinα cos （2π－α）＝cosα tan （2π－α）＝－tanα cot （2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值，等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

倒数关系：tanα ·cotα=1sinα ·cscα=1cosα ·secα=1cosα/sinα=cotα=cscα/secα1+cot^2(α)=csc^2(α)tan α *cot α=1一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=（2tanA）/（1-tan^2(A)）万能公式sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))半角公式sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ双曲函数sh a = [e^a-e^(-a)]/2ch a = [e^a+e^(-a)]/2th a = sin h(a)/cos h(a)sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= cotαcot（π/2-α）= tanα三角函数的诱导公式（六公式）公式一sin(-α) = -sinαtan (-α)=-tanα公式二sin(π/2-α) = cosαcos(π/2-α) = sinα公式三sin(π/2+α) = cosαcos(π/2+α) = -sinα公式四sin(π-α) = sinαcos(π-α) = -cosα公式五sin(π+α) = -sinαcos(π+α) = -cosα公式六tanA= sinA/cosAtan（π/2+α）=－cotαtan（π/2－α）=cotαtan（π－α）=－tanαtan（π+α）=tanα诱导公式记背诀窍：奇变偶不变，符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))²]cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²] tanα=2tan(α/2)/[1-(tan(α/2))²]其它公式(1) (sinα)^2+(cosα)^2=1（平方和公式）(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2(4)对于任意非直角三角形，总有tanA+tanB+tanC=tanAtanBtanC(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)（sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)(seca)^2+(csca)^2=(seca)^2(csca)^2和差化积及积化和差用还原法结合上面公式可推出（换(a+b)/2与(a-b)/2）两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π－arccosxarctan(-x)=-arctanxarccot(-x)=π－arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2，π/2〕时，有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=xx〉0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)三角函数求导：(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)基本求导公式⑴ 0)(='C （C 为常数）⑵ 1)(-='n n nx x ；一般地，1)(-='αααx x 。

三角函数公式 tgA=tanA =a acos sin cotA=1/tanA cscA=1/sinA secA=1/cosA两角和与差的公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanBtanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+倍角公式 tan2A =A tan 12tanA2- sin2A=2sinA •cosAcos2A = cos 2A-sin 2A=2cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A Acos 1sin +和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2ba - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2ba - tana+tanb=b a b a cos cos )sin(+积化和差sina ·sinb = -21[cos(a+b)-cos(a-b)] cosa ·cosb = 21[cos(a+b)+cos(a-b)]sina ·cosb = 21[sin(a+b)+sin(a-b)] cosa ·sinb = 21[sin(a+b)-sin(a-b)] 万能公式 sina=2)2(tan 12tan2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 其它公式a •sina+b •cosa=)b (a 22+×sin(a+c) [其中tanc=a b] a •sin(a)-b •cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a)2 1-sin(a) = (sin 2a -cos 2a)2任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα正弦定理a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径余弦定理b²=a²+c²-2accosB 注：角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[tan(a+b)/2]/[tan(a-b)/2]}3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1配方公式1±sinθ=[sin(θ/2)±cos(θ/2)]21+cosθ=2cos²(θ/2)1-cosθ=2sin²(θ/2)。