较难初一数学题

1、小明有100元，他买了一本书花了x元，买了一个笔记本花了（30-x）元，最后他还剩下20元。

根据这些信息，他一共花了多少元？
A. 50元
B. 70元
C. 80元（答案）
D. 90元
2、一个矩形的长是宽的3倍，如果矩形的面积是75平方米，那么它的宽是多少米？
A. 5米（答案）
B. 10米
C. 15米
D. 20米
3、小红和小华一起做作业，小红用了1小时，小华用了40分钟。

如果他们在同一时间开始，那么小红比小华多用了几分钟？
A. 10分钟
B. 20分钟（答案）
C. 30分钟
D. 40分钟
4、一个数的三分之一加5等于这个数的四分之一加10，这个数是多少？
A. 10
B. 15
C. 20（答案）
D. 25
5、一列火车以每小时60公里的速度行驶，如果它需要行驶300公里，那么它需要多少小时？
A. 4小时
B. 5小时（答案）
C. 6小时
D. 7小时
6、一个正方形的周长是40厘米，那么它的边长是多少厘米？
A. 5厘米
B. 10厘米（答案）
C. 15厘米
D. 20厘米
7、小明有10个苹果，他分给小红和小华，每人得到的苹果数量相同。

每人得到多少个苹果？
A. 3个
B. 4个
C. 5个（答案）
D. 6个
8、一个长方体的长、宽、高分别是5厘米、4厘米和3厘米，它的体积是多少立方厘米？
A. 30立方厘米
B. 40立方厘米
C. 50立方厘米
D. 60立方厘米（答案）。

一、 初一数学上册精选难题二、 选择题1．以下各组数据为长度的三条线段，能组成三角形的是A ．1，2，3B ．1，4，3C ．5，9，5D ．2，7，3 2．下列事件中，是确定的事件为（ ）A 、掷一枚骰子6点朝上B 、买一张电影票，座位号是偶数C 、黑龙江冬天会下雪D 、从装有3个红球和2个白球的口袋中，摸出一个球是红球 3．为了了解某地区初一年级4500名学生的体重情况，从中抽取了500名学生的体重，就这个问题来说，下面说法中正确的是A ．样本容量是500B ．每个学生是个体C ．500名学生是所抽取的一个样本D ．4500名学生是总体 4．下列条件中，不能判定△ABC ≌△A ′B ′C ′，的是（ ）A ．∠A=∠A ，∠C=∠C ，AC=A ′C ′B ．∠B=∠B ，BC=B ′C ′，AB=A ′B ′C ．∠A=∠A ′=80°，∠B=60°，∠C ′=40°，AB=A ′B ′D ．∠A=∠A ，BC=B ′C ′，AB=A ′B ′ 5．如图，若AD ∥B C ，则A ．∠DAC=∠BCAB ．∠BAC=∠DCAC ．∠DAC=∠BACD ．∠B+∠BCD=180° 6.下列计算正确的是（ ）A 、x 2+x 3=x 5B 、x 2•x 3=x 6C 、(-x 3)2= -x 6D 、x 6÷x 3=x 37．如图，在5×5方格纸中，将图①中的三角形乙平移到图②中所示位置，与三角形拼成一个长方形，那么，下面的平移方法中，正确的是（ ）A ．先向上平移3格，再向左平移l 格B ．先向上平移2格，再向左平移1格C ．先向上平移3格，再向左平移2格D ．先向上平移2格，再向左平移2格8. 下列条件中，不能判定三角形全等的是（ ）A ．三条边对应相等B ．两边和一角对应相等C ．两角的其中一角的对边对应相等D ．两角和它们的夹边对应相等 9．下列乘法中，不能运用平方差公式进行运算的是（ ）A 、(x +a )(x -a )B 、(b +m )(m -b )C 、(-x -b )(x -b )D 、(a+b )(-a -b )10．如图，在△ABC 中，AD ⊥BC 于点D ，BD=CD ，若BC=6，AD=5，则图中阴影部分的面积为A ．30B ．15C ．7．5D ．611. 从数字2,3，4中任取两个不同的数字，其积不小于8，发生的概率是( ) A31 B 32 C 61 D 21 12.火车站和汽车站都为旅客提供打包服务，如果长、宽、高分别为x 、y 、z 的箱子按如图所示的方式打包，则打包带的长至少为（ ） A 、z y x 1044++ B 、z y x 32++C 、z y x 642++D 、z y x 686++13. .如图，下列条件中，不能判断直线l1∥l2的是（）A、∠1=∠3B、∠2=∠3C、∠4=∠5D、∠2+∠4=180°(第13图) 14．一学员在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来的方向相同，这两次拐弯角度可能是（）A、第一次向右拐50°，第二次向左拐130°B、第一次向左拐30°，第二次向右拐30°C、第一次向右拐50°，第二次向右拐130°D、第一次向左拐50°，第二次向左拐130°15. 将一张矩形的纸对折，然后用笔尖在上面扎出“B”，再把它铺平，你可见到（）16.下列图象中,哪个图象能大致刻画在太阳光的照射下,太阳能热水器里面的水的温度与时间的关系.( )0 时间0 时间0 时间0A B C D17.给出下列图形名称：（1）线段（2）梯形（3）等腰三角形（4）平行四边形（5）长方形，在这五种图形中是轴对称图形的有（）（A）1个（B）2个（C）3个（D）4个二、填空题1.多项式x2y-2xy+3的是次项式，二次项的系数是.2.近似数0.055万精确到位，有个有效数字，用科学记数法表示记作。

七年级上册数学难题及答案1. 若干学生住若干间房间，如果每间住4人，则有20人没有地方住，如果每间房住8人，则有一间只有4人住，问共有多少个学生？2.甲对乙说：“你给我100元，我的钱将比你多1倍。

”乙对甲说：“你只要给我10元，我的钱将比你多5倍。

”问甲乙两人各有多少元钱？3.小王和小李从AB两地，相向而行，80分钟后相遇，小王先出发60分钟后小李在出发，40分钟后相遇，问小李和小王单独走完这段距离需要多长时间？4.一天，猫发现前面20米的地方有只老鼠，立即去追，同时，老鼠也发现了猫，马上就跑。

猫每秒跑7米，用了10秒追上老鼠。

老鼠每秒跑多少米？5.一项工程，甲单独做10天完成，乙单独做6天完成。

先由甲先做2天，然后甲乙合作，问：甲乙合作还需要多少天完成工作？6.某商场经销一种商品,由于进货时价格比原来进价降低了6.4%,使得利润率增加了8个百分点,求经销这种商品原来的利润率是多少?7.某商场购进甲，乙两种商品50件，甲种商品进价每件35元，利润率是20%，乙种商品的进价每件20元，利润率是15%，共获利278元，问甲乙两种商品各购进了多少件？8.时钟从9点走到9点25分,时针转过的角度是？分针转过的角度是？9.现有某位储户按零存整取的存款方式每月存入500元，存期为3年，存入时三年期零存整取方式的月利率为1.725‰。

此储户在期满时应得的本息和是多少元？参考答案1.设有x间宿舍每间住4人，则有20人无法安排所以有4x+20人每间住8人，则最后一间不空也不满所以x-1间住8人，最后一间大于小于8所以0<(4x+20)-8(x-1)<80<-4x+28<8 乘以-1，不等号改向-8<4x-28<0加上28 20<4x<28 除以4 5<x<7x是整数所以x=6 4x+20=44所以有6间宿舍，44人2.设甲原有x元，乙原有y元．x+100=2*(y-100) 6*(x-10)=y+10 x=40 y=1703.解：设小王的速度为x,小李的速度为y根据：路程=路程，可列出方程：80(x+y)=60x+40(x+y)解得y=1\2x 设路程为单位1，则：80（1\2x+x)=1 解得x=1\120 所以y=1\240所以小王单独用的时间：1*1\120=120(分)小李单独用的时间：1*1\240=240(分)4.解：设老鼠每秒跑X米7*10=10X+20 10X=70-20 X=5 答：老鼠每秒跑5米。

一、填空。

1．如果下降5米，记作－5米，那么上升4米记作（）米；如果＋2千克表示增加2千克，那么－3千克表示（）。

2．海平面的海拔高度记作0m，海拔高度为＋450米，表示（），海拔高度为－102米，表示（）。

3．如果把平均成绩记为0分，＋9分表示比平均成绩（），－18分表示（），比平均成绩少2分，记作（）。

4．＋8.7读作（），－25 读作（）。

5．数轴上所有的负数都在0的（）边，所有正数都在0的（）边。

6．在数轴上，从表示0的点出发，向右移动3个单位长度到A点，A点表示的数是（）；从表示0的点出发向左移动6个单位长度到B点，B点表示的数是（）。

7．比较大小。

－7○ －5 1.5○52 0○－2.4 －3.1○3.1二、判断。

1．零上12℃（＋12℃）和零下12℃（－12℃）是两种相反意义的量。

………（）2．数轴上左边的数比右边的数小。

………………………………………………（）3．在8.2、－4、0、6、－27中，负数有3个。

…………………………………（）三、选择。

（将正确答案的序号填在括号里）。

1．规定10吨记为0吨，11吨记为＋1吨，则下列说法错误的是（）。

A、8吨记为－8吨B、15吨记为＋5吨C、6吨记为－4吨D、＋3吨表示重量为13吨2．以明明家为起点，向东走为正，向西走为负。

如果明明从家走了＋30米，又走了－30米，这时明明离家的距离是（）米。

A、30B、－30C、60D、03．数轴上，－12 在－18 的（）边。

A、左B、右C、北D、无法确定4．一种饼干包装袋上标着：净重（150±5克），表示这种饼干标准的质量是150克，实际每袋最少不少于（）克。

A、155B、150C、145D、160四、按要求完成下面各题。

1．请你把这些数填入相应的圈里。

36、－9 、0.7、＋20.4、－56 、100、－13、－261、＋4.8、1092．写出A、B、C、D、E、F点表示的数。

3．在数轴上表示下列各数。

初一上册数学题目大全难题
以下是一些初一上册数学难题，供您参考：
1. 小明和小红沿着400米的环形跑道练习跑步，他们同时从同一点出发，同向而行，小明每秒跑米，小红每秒跑米。

经过多少秒，小红比小明多跑一圈？
2. 有一根长为10米的绳子，用它来围成一个长方形，怎样围才能使这个长方形的面积最大？最大面积是多少？
3. 某班学生计划在植树节当天种植80棵树苗，上午种了总数的
$\frac{3}{8}$，下午种的树苗数是上午的$\frac{3}{4}$。

这一天他们按计划种下了多少棵树苗？
4. 一个数的倒数是它本身，这个数是多少？
5. 已知$x = 5$，$y = 2$，且$x - y = -$$(x - y)$，求$x^{2} + xy +
y^{2}$的值。

6. 下列计算正确的是（）
A. $7a - a = 6$
B. $a^{2} \cdot a^{4} = a^{6}$
C. $a^{6} \div a^{2} = a^{3}$
D. $2a^{-2} = \frac{1}{4a^{2}}$
7. 下列各式中正确的是（）
A. $3a + 2b = 5ab$
B. $5a^{2} - 2b^{2} = 3$
C. $a + ( - 3b) = - 2ab$
D. $- (a - b) = - a + b$
8. 下列各式中正确的是（）
A. $a^{6} \div a^{2} = a^{3}$
B. $a^{2} \cdot a^{4} = a^{6}$
C. $3a^{2} - 2a^{2} = 1$
D. $a^{2} + b^{2} = (a + b)^{2}$。

初一数学较难题型汇总 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN综合二一选择题1．如果一个有理数的绝对值是5，那么这个数一定是（）A 5B -5C -5或5D 以上都不对2中国古代问题：有甲、乙两个牧童，甲对乙说：“把你的羊给我一只，我的羊数就是你的羊数的2倍”。

乙回答说：“最好还是把你的羊给我一只，我们羊数就一样了”。

若设甲有x只羊，则下列方程正确的是（）A．)2(21-=+xx B．)1(23-=+xxC．)3(21-=+xx D．1211++=-xx3实数a，b在数轴上的对应点如图所示，则下列不等式中错误．．的是（）A．0ab>B．0a b+<C．1ab<D．0a b-<4．如图，是一个几何体从正面、左面、上面看得到的平面图形，下列说法错误的是( )A．这是一个棱锥 B．这个几何体有4个面C．这个几何体有5个顶点 D．这个几何体有8条棱5．如果a＜0，－1＜b＜0，则a，ab，2ab按由小到大的顺序排列为（）A．a＜ab＜2ab B．a＜2ab＜ab C．ab＜2ab＜a D．2ab＜a＜ab 6．如果xy3=，)1(2-=yz，那么x－y＋z等于（）A．4x－1 B．4x－2 C．5x－1 D．5x－27．如图1，把一个长为m、宽为n的长方形（m n>）沿虚线剪开，拼接成图2，成为在一角去掉一个小正方形后的一个大正方形，则去掉的小正方形的边长为（）A．2m n-B．m n- C．2mD．2n8、某品牌手机的进价为1200元，按原价的八折出售可获利14%，则该手机的原售价为（ ）A ．1800元B ．1700元C ．1710元D ．1750元9．某商店有两个进价不同的计算器都卖了80元，其中一个赢利60％，另一个亏本20％，在这次买卖中，这家商店 （ ） A.不赔不赚 B.赚了10元 C.赔了10元 D.赚了50元 10钟表在8:25时，时针与分针的夹角是（ ）度 A.101.5 B.102.5 C.120 D.125 11如图的几何体，从左面看到的是（ ）DC B A12将下列图形画在硬纸片上，剪下并折叠后能围成三棱柱的是（ ） A ．B ．C ．D ．13. 小王利用计算机设计了一个计算程序，输入和输出的数据如下表：输入 ······ 1 2 3 4 5······ 输出······12 25 310 417 526······那么，当输入数据是8时，输出的数据是（ ） A ．618 B ．638 C ．658D ．678mnnn14．如图，点A 位于点O 的 方向上。

初一数学练习题（难度较大）一．选择题1．如果a,b,c 是非零数，且a+b+c=0,那么abcabc c c b b c a +++的所有可能的值为（ ） （A ） 0 （B ） 1或-1 （C ） 2或-2 （D ） 0或-22．某种商品若按标价的八折出售，可获利20%，若按原价出售，可获利（ ）A 、25%B 、40%C 、50%D 、66.7%3．把一个正方形分割成n 个小正方形（n>1），则n 不可能取（ ）A 、4B 、5C 、8D 、94．一个立方体的六个面上标着连续的整数， 若相对的两个面上所标之数的差相等，则 这六个数的和是（ ）A 、116B 、117C 、118D 、1195．甲、乙、丙三人比赛象棋，每局比赛后，若是和棋，则这两人继续比赛，直到分出胜负，负者退下，由另一人与胜者比赛。

比赛若干局后，甲胜4局、负2局；乙胜3局、负3局。

若丙负3局，那么丙胜（ ）（A ）0局 （B ）1局 （C ）2局 （D ）3局6．有一种游戏，一枚棋子第一次只能进入第一关，然后每次可以向前进一步或二步，那么从开始到第六关可以有（ ）种走法A 、 5B 、6C 、7D 、8二．填空题1．今天是星期一，从今天算起，第20031111...1个是星期_____________2．汽车以每小时72千米的速度笔直地开向寂静的山谷，驾驶员按一声喇叭，4秒后听到回响，已知声音的速度是每秒340米，听到回响时汽车离山谷听距离是_________米3．某市居民生活用电基本价格为每度0.40元，若每月用电量超过60度，超出部分按基本电价的70%收费，若某户居民六月份的电费平均每度0.36元，则6月份共用电__________度，应交电费__________元。

4．甲、乙、丙、丁四个数之和等于－90，又甲数减－4，乙数加－4，丙数乘－4，丁数除－4所得的值彼此相等，则四个数中最大的一个数比最小的一个数大___________.5．假期学校组织360名师生外出旅游，某客车出租公司有两种大客车可供选择：甲种客车每辆车有40个座，租金400元；乙种客车每辆车有50个座，租金480元。

一、填空。

1．如果下降5米，记作－5米，那么上升4米记作（）米；如果＋2千克表示增加2千克，那么－3千克表示（）。

2．海平面的海拔高度记作0m，海拔高度为＋450米，表示（），海拔高度为－102米，表示（）。

3．如果把平均成绩记为0分，＋9分表示比平均成绩（），－18分表示（），比平均成绩少2分，记作（）。

4．＋8.7读作（），－25 读作（）。

5．数轴上所有的负数都在0的（）边，所有正数都在0的（）边。

6．在数轴上，从表示0的点出发，向右移动3个单位长度到A点，A点表示的数是（）；从表示0的点出发向左移动6个单位长度到B点，B点表示的数是（）。

7．比较大小。

－7○ －5 1.5○52 0○－2.4 －3.1○3.1二、判断。

1．零上12℃（＋12℃）和零下12℃（－12℃）是两种相反意义的量。

………（）2．数轴上左边的数比右边的数小。

………………………………………………（）3．在8.2、－4、0、6、－27中，负数有3个。

…………………………………（）三、选择。

（将正确答案的序号填在括号里）。

1．规定10吨记为0吨，11吨记为＋1吨，则下列说法错误的是（）。

A、8吨记为－8吨B、15吨记为＋5吨C、6吨记为－4吨D、＋3吨表示重量为13吨2．以明明家为起点，向东走为正，向西走为负。

如果明明从家走了＋30米，又走了－30米，这时明明离家的距离是（）米。

A、30B、－30C、60D、03．数轴上，－12 在－18 的（）边。

A、左B、右C、北D、无法确定4．一种饼干包装袋上标着：净重（150±5克），表示这种饼干标准的质量是150克，实际每袋最少不少于（）克。

A、155B、150C、145D、160四、按要求完成下面各题。

1．请你把这些数填入相应的圈里。

36、－9 、0.7、＋20.4、－56 、100、－13、－261、＋4.8、1092．写出A、B、C、D、E、F点表示的数。

3．在数轴上表示下列各数。

初一抽考数学试卷及参考解析（较难）一．选择题（每题3分，共30分）1．在四边形ABCD中,假如AD∥BC,A=60,则D的度数( D )A.是60B.是120C.60或120D.不能确定2．第四象限内一点A到x轴的距离是3,到y轴的距离是5,则点A的坐标是( D )A.(3,5)B.(5,3)C.(-3,5)D.(5,-3)3．假如一元一次不等式组无解,则a的取值范畴是( D )A.aB.aC.aD.a54．下列方程组中，与方程组的解不同的方程组是（ C ）5．若1与2互补，2与3互余，则1与3的关系为( C )A.3B. 1=1803C.1= 903D.以上都不对6．现有边长相等的正三角形、正方形、正六边形、正八边形的地砖，假如选择其中的两种铺满地面，那么选择的两种地砖形状不可能的是（ C ）A.正三角形与正方形B.正三角形与正六边形C.正方形与正六边形D.正方形与正八边形7．点P（m-1，2m+1）在第二象限，则m的取值范畴是（B ）A．m＞-1/2或m＞1 B．-＜m＜1 C．m＜1 D．m＞-1/28. 已知关于x的不等式组的整数解共有6个，则m的取值范畴是（D ）A．-5＜m＜B．-5-4 C．-5＜m-4 D．-5m＜-49. 若关于x的不等式组的解集为x＞-1，则n的值为（B ）A．3 B．-3 C．1 D．-110. 某所中学现有学生4200人，打算一年后初中在校生增加8%，高中在校生增加11%，如此全校学生将增加10%，则这所中学现在的初中在校生和高中在校生人数分别是（ A ）A．1400人和2800人B．1900人和2300人C．2800人和1400人D．2 300人和1900人二.填空题（每题3分，共30分）11. 把命题能够被6整除的数一定能被3整除改写为假如那么的形式是：假如一个数能够被6整除，那么那个数一定能被3整除.12.关于x﹑y的二元一次方程组的解也是二元一次方程2x+3y=8的一个解,则k的值是1 .13. 三角形的两边为7cm和5cm，则该三角形周长C的取值范畴是14＜C＜24 .14.如图所示，将△ABC沿着DE翻折，若2=70，则B= 35 度．15.小马虎在进行多边形的内角和运算时，加掉了一个角，结果得到那个多边形的内角和为2021度，则加掉的那个角的度数为：148 .16.如图，△ABC中，ABC=50，ACB=80，AD平分BAC，EFBC于E，则F= 15 . 17. 如图，AM，CM分别平分BAD和BCD. B=40，D=30，则M= 35 度.18.点A、B分别在x、y轴上移动,BE平分ABy，EB与OAB的平分线交于点C,则C = 45 度．第14题图第16题图第17题图第18题图9.若2x-y-2z=0，x+2y-11z=0（xyz0）则代数式的值为1 .20. 用若干辆载重为8吨的汽车运一批物资，若每辆汽车只装4吨，则剩下20吨物资；若每辆汽车装满8吨，则最后一辆汽车不满也不空，则共有6 辆汽车；三、解答题（共60分）23.（8分）非直角△ABC中，A=45，高BD和高CE所在的直线交于点H，求BHC的度数.解：BHC=45或135（每个4分）24. （8分）如图，△ABC中，角平分线AD、BE、CF相交于点H，过H点作HGAC，垂足为G，求证：AHE=CHG.证明：∵AD、BE、CF为△ABC的角平分线，可设BAD=CAD=x，ABE=CBE=y，BCF=ACF=z，则2x+2y+2z=180，即x+y+z=90，在△AHB中，∵AHE是△AHB的外角，AHE=BAD+ABE=x+y=90-z，在△CHG中，CHG=90-z，AHE=CHG．25. （8分）假如将点P绕定点M旋转180后与点Q重合，那么称点P与点Q关于点M对称，定点M叫做对称中心.现在，M是线段PQ的中点.如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0）.点列P1、P2、P3、中的相邻两点都关于△ABO的一个顶点对称：点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，.对称中心分别是A、B，O，A，B，O，，且这些对称中心依次循环.已知点P1的坐标是（1，1），⑴试求出点P2、P7、P100的坐标. ⑵观看⑴的结果，假如M1（x1，y1）、M2（x2，y2）中点为M，试表示点M的坐标.解：⑴P2的坐标是（1，-1），P7的坐标是（1，1），P100的坐标是（1，-3）．（6分）⑵M（）（8分）26. （10分）正在修建的某条公路招标，现有甲乙两个工程队，若甲乙合作24天能够完成，需要费用120万元；若甲单独做20天后剩下的工程由乙做，还需40天完成，如此需费用110万元，问：⑴甲、乙两队单独完成此项工程各需多少天？⑵甲乙两队单独完成此项工程各需费用多少万元？⑶若甲乙两队同时开工，且要使工程总费用不超过100万元，则乙队至少需要工作多少天？解：⑴设甲、乙各需x、y天完成，解得，甲、乙两队单独完成此项工程各需30、120天. （4分）⑵设甲、乙两队各需a、b万元，解得，4.530=135万元、0.5120=60万元甲乙两队单独完成此项工程各需费用135、60万元. （7分）⑶设乙队至少需要t天.0.5t+ 4.5100，解得t56，乙队至少需要工作56天. （10分）27. （12分）为了爱护环境，某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备，共花费资金54万元，且每台乙型设备的价格是每台甲型设备价格的75%，实际运行中发觉，每台甲型设备每月能处理污水200吨，每台乙型设备每月能处理污水160吨，且每年用于每台甲型设备的各种爱护费和电费为1万元，每年用于每台乙型设备的各种爱护费和电费为1.5万元.今年该厂二期工程立即完成，产生的污水将大大增加，因此该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理，预算本次购买资金不超过84万元，估量二期工程完成后每月将产生许多于1 300吨污水.⑴请你运算每台甲型设备和每台乙型设备的价格各是多少万元？⑵请你求出用于二期工程的污水处理设备的所有购买方案；⑶若两种设备的使用年限都为10年，请你说明在⑵的所有方案中，哪种购买方案的总费用最少？（总费用＝设备购买费＋各种爱护费和电费）解：⑴设每台甲型设备和每台乙型设备的价格各是x、y万元，解得，每台甲型设备和每台乙型设备的价格各是12、9万元. （3分）⑵设二期工程需甲型a台，乙型b台，，解得，a=1、2、3、4，即购买甲型1台，乙型7台；甲型2台，乙型6台；甲型3台，乙型5台；甲型4台，乙型4台. （8分）⑶设总费用为W万元W=12a+9(8-a)+10a+1.5(8-a)10= -2a+192要练说，得练听。

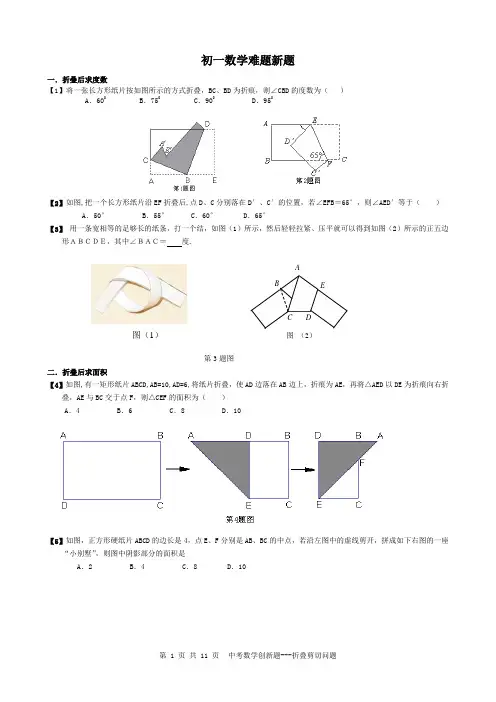
初一数学难题新题一．折叠后求度数【1】将一张长方形纸片按如图所示的方式折叠，BC 、BD 为折痕，则∠CBD 的度数为（ ）A ．600B ．750C ．900D ．950【2】如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置，若∠EFB ＝65°，则∠AED ′等于（ ） A ．50° B ．55° C ．60° D ．65°【3】 用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝ 度.二．折叠后求面积【4】如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AE 与BC 交于点F ，则△CEF 的面积为（ ） A ．4B ．6C ．8D ．10【5】如图，正方形硬纸片ABCD 的边长是4，点E 、F 分别是AB 、BC 的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是A ．2B ．4C ．8D ．10图（1）第3题图CDEBA图 （2）【6】如图a ，ABCD 是一矩形纸片，AB ＝6cm ，AD ＝8cm ，E 是AD 上一点，且AE ＝6cm 。

操作：（1）将AB 向AE 折过去，使AB 与AE 重合，得折痕AF ，如图b ；（2）将△AFB 以BF 为折痕向右折过去，得图c 。

则△GFC 的面积是（ ）A.1cm 2B.2 cm 2C.3 c m 2D.4 cm 2三．折叠后求长度【7】如图，已知边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折叠，使点A 落在BC 边上的点D 的位置，且ED BC ⊥，则CE 的长是（ ） （A ）10315- （B ）1053- （C ）535- （D ）20103-四．折叠后得图形 【8】将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）A ．矩形B ．三角形C ．梯形D ．菱形【9】在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是（ ）A. B. C. D.【10】小强拿了张正方形的纸如图（1），沿虚线对折一次如图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是( )E A A ABB B CC C GD D D FF F图a图b图c第6题图ABCDEF 第7题图第8题图第9题图【11】如图，把矩形ABCD 对折，折痕为MN （图甲），再把B 点叠在折痕MN 上的处。

初一数学习题难题精选初一是学生学习的重要阶段，数学作为一门基础学科，在学习过程中也是不可或缺的。

但是，在学习初一数学的过程中，常常会遇到一些难题，这些难题有时候甚至让学生望而却步。

下面我将为大家介绍几道初一数学难题，帮助大家更好地掌握这门学科。

难题一：田地分配问题某地有一块长方形的田地，需要将它划分为4块。

其中，第一块是长10米，宽8米，第二块是长12米，宽8米，第三块是长8米，宽15米，第四块是长7米，宽10米。

请问，该田地的面积是多少？解法：首先可以将这块田地划分成两个小长方形。

其中，第一个长方形的面积是10米*8米=80平方米，第二个长方形的面积是(12-10)*8=16平方米。

然后，将第二个长方形再分成两个小长方形，即一个长7米，宽8米的长方形和一个长5米，宽8米的长方形。

其中，第三块面积是8米*15米=120平方米，第四块面积是7米*10米=70平方米。

综上所述，该田地的面积是80+16+120+70=286平方米。

难题二：解方程已知方程2x+1=5，求x的值。

解法：将2x+1=5式中的1挪到等式左边，得到2x=5-1=4，再将2挪到等式右边，得到x=4/2=2，则x的值为2。

难题三：几何中的三线共点定理已知在三角形ABC中，AD、BE和CF三条线段交于一点O，求证：当且仅当AO、BO和CO三条线段通过三角形的同一顶点时，三线才共点。

解法：首先，我们容易知道，当三线通过三角形同一个点时，它们自然就共点了。

而想要证明当三线共点时，它们必须同时通过三角形同一顶点时，可以采用反证法。

即，假设有三条线段AD、BE和CF满足这三条线段交于一点O，但是AO、BO和CO没有同时通过三角形的同一顶点。

那么，根据欧拉定理，我们可以得知三角形ABC不是一个正三角形，也不是一个等腰三角形。

于是，我们可以在三角形ABC的内部选取一个点P，做出AP、BP、CP连线。

由于AO、BO、CO不通过三角形同一顶点，所以我们可以假设P和O不重合。