人教版数学八年级下册第17章 勾股定理 单元习题 含答案

第17章勾股定理一．选择题（共10小题）1．下列结论中，错误的有（）①在Rt△ABC中，已知两边长分别为3和4，则第三边的长为5；②△ABC的三边长分别为AB，BC，AC，若BC2+AC2＝AB2，则∠A＝90°；③在△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形；④若三角形的三边长之比为3：4：5，则该三角形是直角三角形；A．0个B．1个C．2个D．3个2．如图，将一副三角板如图放置，如果DB＝2，那么点E到BC的距离为（）A．﹣1 B．3﹣C．2﹣2 D．+13．如图，在△ABC中，∠ACB＝90°，CD⊥AB于D，若AC＝2，BC＝，则CD为（）A．B．2 C．D．34．如图，将△ABC放在正方形网格中（图巾每个小正方形边长均为1）点A，B，C恰好在网格图中的格点上，那么∠ABC的度数为（）A．90°B．60°C．45°D．30°5．如图，已知数轴上点P表示的数为﹣1，点A表示的数为1，过点A作直线l垂直于PA，在l上取点B，使AB＝1，以点P为圆心，以PB为半径作弧，弧与数轴的交点C所表示的数为（）A．B．C．D．6．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D．已知AB＝15，Rt△ABC的周长为15+9，则CD的长为（）A．5 B．C．9D．67．如图，设小方格的面积为1，则图中以格点为端点且长度为的线段有（）A．2条B．3条C．4条D．5条8．如图，已知在Rt△ABC中，E，F分别是边AB，AC上的点，AE＝AB，AF＝AC，分别以BE、EF、FC为直径作半圆，面积分别为S1，S2，S3，则S1，S2，S3之间的关系是（）A．S1+S3＝2S2 B．S1+S3＝4S2C．S1＝S3＝S2 D．S2＝（S1+S3）9．如图，有一个池塘，其底面是边长为10尺的正方形，一个芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′．则这根芦苇的长度是（）A．10尺B．11尺C．12尺D．13尺10．一云梯AB长25米，如图那样斜靠在一面墙上，云梯底端离墙7米，如果云梯的顶端下滑了4米，那么它的底端在水平方向滑动BB'的长是（）A．10米B．8米C．6米D．4米二．填空题（共6小题）11．若△ABC的三边长分别为a，b，c．下列条件：①∠A＝∠B﹣∠C；②a2＝（b+c）（b﹣c）；③∠A：∠B：∠C＝3：4：5；④a：b：c＝5：12：13．其中能判断△ABC是直角三角形的是（填序号）．12．已知，△ABC的三边长分别为：2，，，则△ABC的面积是．13．如图，BD为△ABC的中线，AB＝10，AD＝6，BD＝8，△ABC的周长是．14．若8，a，17是一组勾股数，则a＝．15．如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8．AD平分∠BAC交BC边于点D，则BD＝．16．如图，在四边形ABCD中，AD∥BC，∠B＝90°，AD＝8cm，AB＝6cm，BC＝10cm，点Q 从点A出发以1cm/s的速度向点D运动，点P从点B出发以2cm/s的速度向C点运动，P、Q两点同时出发，其中一点到达终点时另一点也停止运动．若DP≠DQ，当t＝s 时，△DPQ是等腰三角形．三．解答题（共6小题）17．如图，在Rt△ABC中，∠B＝90°．点D为BC边上一点，线段AD将Rt△ABC分为两个周长相等的三角形．若CD＝2，BD＝6，求△ABC的面积．18．如图，在△ABC中，AB＝AC，△ABC的高BH，CM交于点P．（1）求证：PB＝PC．（2）若PB＝5，PH＝3，求AB．19．已知：如图，在△ABC中，CD⊥AB，垂足为点D，AC＝20，BC＝15，DB＝9．（1）求CD的长．（2）求AB的长．20．平面直角坐标系中如果任意两点A、B的坐标分别为（x1，y1）、（x2，y2），则A、B两点之间的距离可表示为|AB|＝；在平面直角坐标系中．（1）若点C的坐标为（3，4），O为坐标原点，则C、O两点之间的距离为．（2）若点E（﹣2，3）、F（4，﹣5），求E、F两点之间的距离．21．如图，正方形网格的每个小方格都是边长为1的正方形，△ABC的顶点都在格点上．（1）分别求出AB，BC，AC的长；（2）试判断△ABC是什么三角形，并说明理由．22．阅读下列材料：小明遇到一个问题：在△ABC中，AB，BC，AC三边的长分别为、、，求△ABC 的面积．小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．参考小明解决问题的方法，完成下列问题：（1）图2是一个6×6的正方形网格（每个小正方形的边长为1）．①利用构图法在答卷的图2中画出三边长分别为、、的格点△DEF；②计算①中△DEF的面积为；（直接写出答案）（2）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，正方形PRDE，连接EF．①判断△PQR与△PEF面积之间的关系，并说明理由．②若PQ＝，PR＝，QR＝3，直接．．写出六边形AQRDEF的面积为．参考答案一．选择题（共10小题）1．解：①在Rt△ABC中，已知两边长分别为3和4，则第三边的长为5或，错误；②△ABC的三边长分别为AB，BC，AC，若BC2+AC2＝AB2，则∠C＝90°，错误；③在△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形，正确；④若三角形的三边长之比为3：4：5，则该三角形是直角三角形，正确；故选：C．2．解：作EF⊥BC于F，设EF＝x，则BF＝x，BE＝x，CE＝2x，则AC＝，AE＝﹣x，则（﹣x）2+（）2＝（2x）2，x2+2x﹣6＝0，解得x1＝3﹣，x2＝﹣3﹣（舍去）．故点E到BC的距离为3﹣．故选：B．3．解：在Rt△ABC中，AC＝2，BC＝，根据勾股定理得：AB＝＝3，∵△ABC中，∠C＝90°，CD⊥AB，∴S△ABC＝AC•BC＝AB•CD，即AC•BC＝AB•CD，∴CD＝＝2，故选：B．4．解：由勾股定理得：AC2＝12+22＝5，BC2＝12+32＝10，AB2＝12+22＝5，∴AB＝AC，AC2+AB2＝BC2，∴△ACB是等腰直角三角形，∴∠ABC＝45°，故选：C．5．解：PB＝，∴PB＝PC，∴OC＝PC﹣1＝﹣1，∴点C的数为﹣1，故选：B．6．解：如图所示：∵Rt△ABC的周长为15+9，∠ACB＝90°，AB＝15，∴AC+BC＝9，AC2+BC2＝AB2＝152＝225，∴（AC+BC）2＝（9）2，即AC2+2AC×BC+BC2＝405，∴2AC×BC＝405﹣225＝180，∴AC×BC＝90，∵AB×CD＝AC×BC，∴CD＝＝＝6；故选：D．7．解：∵＝，∴是直角边长为2，3的直角三角形的斜边，如图所示，AB，CD，BE，DF的长都等于；故选：C．8．解：∵在Rt△ABC中，AE＝AB，AF＝AC，∴AE＝BE，AF＝CF，EF2＝AE2+AF2，∴EF2＝BE2+CF2．∴π•EF2＝π•（BE2+CF2），即S2＝（S1+S3）．∴S1+S3＝4S2．故选：B．9．解：设芦苇长AB＝AB′＝x尺，则水深AC＝（x﹣1）尺，因为边长为10尺的正方形，所以B'C＝5尺在Rt△AB'C中，52+（x﹣1）2＝x2，解之得x＝13，即水深12尺，芦苇长13尺．故选：D．10．解：由题意可得：AB＝25m，OB＝7m，则OA＝＝24（m），当云梯的顶端下滑了4米，则A′O＝24﹣4＝20（m），故OB′＝＝15（m），则BB′＝CB′﹣BC＝（15﹣7）m＝8m．答：它的底部在水平方向滑动了8米，故选：B．二．填空题（共6小题）11．解：∵∠A＝∠B﹣∠C，∴∠A+∠C＝∠B，∵∠A+∠C+∠B＝180°，∴∠B＝90°，∴△ABC是直角三角形，故①符合题意；∵a2＝（b+c）（b﹣c）∴a2+c2＝b2，∴△ABC是直角三角形，故②符合题意；∵∠A：∠B：∠C＝3：4：5，∠A+∠B+∠C＝180°，∴∠A＝45°，∠B＝60°，∠C＝75°，∴△ABC不是直角三角形，故③不符合题意；∵a：b：c＝5：12：13，∴a2+b2＝c2，∴△ABC是直角三角形，故④符合题意；故答案为：①②④．12．解：∵△ABC的三边长分别为：2，，，∴22+（）2＝（）2，∴△ABC是直角三角形，斜边为，∴△ABC的面积为＝，故答案为：．13．解：∵AB＝10，AD＝6，BD＝8，∴AB2＝AD2+BD2＝100，∴△ABD是直角三角形且AD⊥BD．又BD为△ABC的中线，∴AB＝BC＝10，AD＝CD＝6．∴，△ABC的周长＝AB+BC+AD＝2AB+2AD＝20+12＝32．故答案是：32．14．解：①a为最长边，a＝＝，不是正整数，不符合题意；②17为最长边，a＝＝15，三边是整数，能构成勾股数，符合题意．故答案为：15．15．解：作DE⊥AC于E，如图所示：∵∠B＝90°，AB＝6，BC＝8．∴DB⊥AB，AC＝＝10，∵AD平分∠BAC，DE⊥AC，∴DE＝DB，在Rt△AED和Rt△ABD中，，∴Rt△AED≌Rt△ABD（HL），∴AE＝AB＝6，∴CE＝AC﹣AE＝4，设DE＝DB＝x，则CD＝8﹣x，在Rt△CDE中，由勾股定理得：x2+42＝（8﹣x）2，解得：x＝3，∴BD＝3；故答案为：3．16．解：由运动知，AQ＝t，BP＝2t，∵AD＝8，BC＝10，∴DQ＝AD﹣AQ＝（8﹣t）（cm），PC＝BC﹣BP＝（10﹣2t）（cm），∵△DPQ是等腰三角形，且DQ≠DP，∴①当DP＝QP时，∴点P在DQ的垂直平分线上，∴AQ+DQ＝BP，∴t+（8﹣t）＝2t，∴t＝，②当DQ＝PQ时，如图，Ⅰ、过点Q作QE⊥BC于E，∴∠BEQ＝∠OEQ＝90°，∵AD∥BC，∠B＝90°，∴∠A＝∠B＝90°，∴四边形ABEQ是矩形，∴EQ＝AB＝6，BE＝AQ＝t，∴PE＝BP﹣BE＝t，在Rt△PEQ中，PQ＝＝，∵DQ＝8﹣t∴＝8﹣t，∴t＝，∵点P在边BC上，不和C重合，∴0≤2t＜10，∴0≤t＜5，∴此种情况符合题意，即t＝或s时，△DPQ是等腰三角形．故答案为：或．三．解答题（共6小题）17．解：根据题意可知，△ACD与△ADB的周长相等，∴AC+CD+AD＝AD+BD+AB．∴AC+CD＝BD+AB．∵CD＝2，BD＝6，∴AC+2＝6+AB，BC＝CD+BD＝8，∴AC＝AB+4，设AB＝x，则AC＝4+x．在Rt△ABC中，AB2+BC2＝AC2，∴x2+82＝（x+4）2．∴x2+64＝16+x2+8x．∴x＝6．∵经检验，x＝6为原方程的解，∴原方程的解为x＝6．∴．18．（1）证明：∵AB＝AC，∴∠ABC＝∠ACB．∵BH，CM为△ABC的高，∴∠BMC＝∠CHB＝90°．∴∠ABC+∠BCM＝90°，∠ACB+∠CBH＝90°．∴∠BCM＝∠CBH．∴PB＝PC．（2）解：∵PB＝PC，PB＝5，∴PC＝5．∵PH＝3，∠CHB＝90°，∴CH＝4．设AB＝x，则AH＝x﹣4．在Rt△ABH中，∵AH2+BH2＝AB2，∴（x﹣4）2+（5+3）2＝x2．∴x＝10．即AB＝10．19．解：（1）∵CD⊥AB，∴∠CDB＝∠CDA＝90°，在Rt△BCD中，∵BC＝15、DB＝9，∴CD＝＝＝12；（2）在Rt△ACD中，∵AC＝20、CD＝12，∴AD＝＝＝16，则AB＝AD+DB＝16+9＝25．20．解：（1）∵O为原点，∴O坐标为（0，0），∵点C的坐标为（3，4），∴CO＝＝5，故答案为：5；（2）∵点E（﹣2，3）、F（4，﹣5），E、F两点之间的距离可表示为|EF|＝，∴EF＝＝＝10．21．解：（1），，；（2）△ABC是直角三角形，理由如下：∵，AC2＝52＝25，∴AB2+BC2＝AC2，∴△ABC是直角三角形．22．解：（1）①如图所示：②△DEF的面积为4×5﹣×2×3﹣×2×4﹣×2×5＝8；（2）①如图3，△PEF的面积为6×2﹣×1×6﹣×1×3﹣×3×2＝，△PQR的面积为×3×3＝，∴△PQR与△PEF面积相等；②六边形AQRDEF的面积为（）2+++（）2＝13+9+10＝32．故答案为：8；32．。

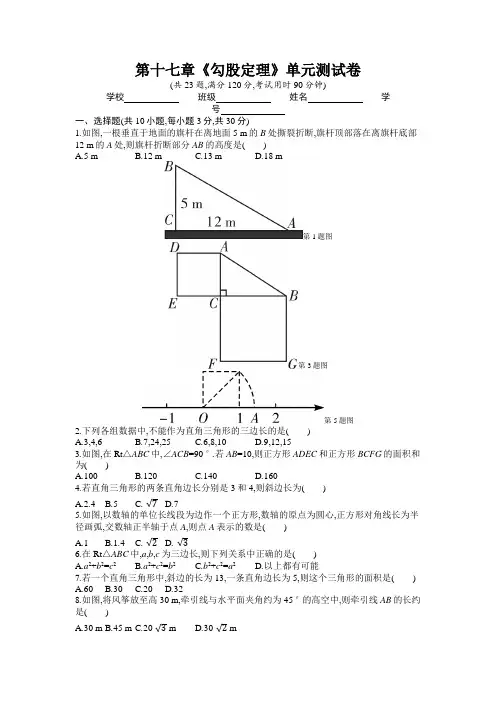
第十七章《勾股定理》单元测试卷(共23题,满分120分,考试用时90分钟)学校班级姓名学号一、选择题(共10小题,每小题3分,共30分)1.如图,一根垂直于地面的旗杆在离地面5 m的B处撕裂折断,旗杆顶部落在离旗杆底部12 m的A处,则旗杆折断部分AB的高度是()A.5 mB.12 mC.13 mD.18 m第1题图第3题图第5题图2.下列各组数据中,不能作为直角三角形的三边长的是()A.3,4,6B.7,24,25C.6,8,10D.9,12,153.如图,在Rt△ABC中,∠ACB=90°.若AB=10,则正方形ADEC和正方形BCFG的面积和为()A.100B.120C.140D.1604.若直角三角形的两条直角边长分别是3和4,则斜边长为()A.2.4B.5C.√7D.75.如图,以数轴的单位长线段为边作一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是()A.1B.1.4C.√2D.√36.在Rt△ABC中,a,b,c为三边长,则下列关系中正确的是()A.a2+b2=c2B.a2+c2=b2C.b2+c2=a2D.以上都有可能7.若一个直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是()A.60B.30C.20D.328.如图,将风筝放至高30 m,牵引线与水平面夹角约为45°的高空中,则牵引线AB的长约是()A.30 mB.45 mC.20√3 mD.30√2 m第8题图第9题图第10题图9.(跨学科融合)如图,在物理实验课上,小明将长为8 cm的橡皮筋放置在水平面上,固定两端A和B,然后把中点C垂直向上拉升3 cm至点D,则橡皮筋被拉长了()A.3 cmB.2 cmC.6 cmD.4 cm10.如图所示的一块地,已知∠ADC=90°,AD=12 m,CD=9 m,AB=25 m,BC=20 m,则这块地的面积为()A.96 m2B.204 m2C.196 m2D.304 m2二、填空题(共5小题,每小题3分,共15分)11.如图,两个正方形的面积分别是100和36,则字母B所代表的正方形的面积是.第11题图第13题图12.若△ABC的三边长满足a2=b2+c2,则△ABC是直角三角形且∠=90°.13.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了步路(假设2步为1米),却踩伤了花草.14.如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长等于.第14题图第15题图15.(数学文化)如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AH=6,EF=2,那么AB的长等于.三、解答题(一)(共3小题,每小题8分,共24分)16.如图,根据所给条件,求BC的长.17.如果三角形的三边长分别为√2,√6,2,那么这个三角形是直角三角形吗?。

第17章勾股定理一．选择题（共10小题）1．已知点A的坐标为（2，﹣1），则点A到原点的距离为（）A．3B．C．D．12．满足下列条件的三角形中，不是直角三角形的是（）A．三内角的度数之比为1：2：3B．三内角的度数之比为3：4：5C．三边长之比为3：4：5D．三边长的平方之比为1：2：33．一个直角三角形两条直角边的长分别为5，12，则其斜边上的高为（）A．B．13C．6D．254．有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了下图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是（）A．1B．2018C．2019D．20205．历史上对勾股定理的一种证法采用了下列图形：其中两个全等的直角三角形边AE、EB 在一条直线上．证明中用到的面积相等关系是（）A．S△EDA＝S△CEBB．S△EDA+S△CEB＝S△CDBC．S四边形CDAE＝S四边形CDEBD．S△EDA+S△CDE+S△CEB＝S四边形ABCD6．校园内有两棵树，相距12米，一棵树高为13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞（）A．10米B．11米C．12米D．13米7．如图，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要（）A．4米B．5米C．7米D．10米8．如图，在△ABC中，∠C＝90°，AC＝2，点D在BC上，∠ADC＝2∠B，AD＝，则BC的长为（）A．﹣1B．+1C．﹣1D．+19．△ABC是某市在拆除违章建筑后的一块三角形空地．已知∠C＝90°，AC＝30米，AB ＝50米，如果要在这块空地上种植草皮，按每平方米草皮a元计算，那么共需要资金（）A．600a元B．50a元C．1200a元D．1500a元10．放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是200米/分，小红用3分钟到家，小颖4分钟到家，小红和小颖家的直线距离为（）A．600米B．800米C．1000米D．1400米二．填空题（共7小题）11．在Rt△ABC中，∠C＝90°，BC＝12，AC＝9，则AB＝．12．有一个直角三角形的两边为4、5，要使三角形为直角三角形，则第三边等于．13．如图，在数轴上，点A、B表示的数分别为0、2，BC⊥AB于点B，且BC＝1，连接AC，在AC上截取CD＝BC，以A为圆心，AD的长为半径画弧，交线段AB于点E，则点E 表示的实数是．14．观察下列式子：当n＝2时，a＝2×2＝4，b＝22﹣1＝3，c＝22+1＝5n＝3时，a＝2×3＝6，b＝32﹣1＝8，c＝32+1＝10n＝4时，a＝2×4＝8，b＝42﹣1＝15，c＝42+1＝17…根据上述发现的规律，用含n（n≥2的整数）的代数式表示上述特点的勾股数a＝，b＝，c＝．15．如图，正方形网格中，点A，B，C，D均在格点上，则∠ACD+∠BDC＝°．16．如果三角形的两个内角α与β满足2α+β＝90°，那么我们称这样的三角形为“准互余三角形”．如图在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D为BC边上一点，若△ABD为“准互余三角形”，则BD的长为．17．如图，四边形ABCD中，AD∥BC，∠BCD＝90°，AB＝BC+AD，∠DAC＝45°，E为CD上一点，且∠BAE＝45°，若CD＝4，则DE长为．三．解答题（共5小题）18．如图，△ABC中，∠ACB＝90°，AB＝，求斜边AB上的高CD．19．如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图1中，画一个三角形，使它的三边长都是有理数；（2）在图2中，画一个直角三角形，使它们的三边长都是无理数；（3）在图3中，画一个正方形，使它的面积是10．20．某消防队进行消防演练，在模拟现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12米，即AD＝BC＝12米，此时建筑物中距地面12.8米高的P 处有一被困人员需要救援，已知消防云梯的车身高AB是3.8米．为此消防车的云梯至少应伸长多少米？21．一架方梯AB长13米，如图，斜靠在一面墙上，梯子底端离墙OB为5米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了3米，那么梯子的底端在水平方向滑动了几米？22．这是某商场自动扶梯示意图，若将扶梯AC水平放置，则刚好与AB一样长．已知扶梯高度CE＝5cm，CD＝1cm，求扶梯AC的长．参考答案一．选择题（共10小题）1．C．2．B．3．A．4．D．5．D．6．D．7．C．8．D．9．A．10．C．二．填空题（共7小题）11．15．12．3或．13．﹣1．14．2n，n2﹣1，n2+1．15．90．16．或．17．．三．解答题（共5小题）18．解：∵∠ACB＝90°，AB＝，∴AC＝＝，∵×AB•CD＝×AC•BC∴CD＝＝＝．19．解：（1）三边分别为：3、4、5 （如图1）；（2）三边分别为：、2、（如图2）；（3）画一个边长为的正方形（如图3）．20．某消防队进行消防演练，在模拟现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12米，即AD＝BC＝12米，此时建筑物中距地面12.8米高的P 处有一被困人员需要救援，已知消防云梯的车身高AB是3.8米．为此消防车的云梯至少应伸长多少米？解：由题意可知：AB＝CD＝3.8米，AD＝12米，PC＝12.8米，∠ADP＝90°，∴PD＝PC﹣CD＝9米，在Rt△ADP中，AP＝＝15米，答：此消防车的云梯至少应伸长15米．21．解：（1）∵AO⊥DO，∴AO＝＝＝12（m），（2）∵AA′＝3m，∴A′O＝AO﹣AA′＝9m，∴OB′＝＝＝，∴BB′＝OB′﹣OB＝﹣5＝2﹣5（m），∴梯子的底端在水平方向滑动了2﹣5米．22．解：设AC的长为x米，∵AC＝AB，∴AB＝AC＝x米，∵EB＝CD＝1米，∴AE＝（x﹣1）米，在Rt△ACE中，AC2＝CE2+AE2，即：x2＝52+（x﹣1）2，解得：x＝13，答：扶梯AC的长为13米．。

八年级数学下册《第十七章-勾股定理》单元测试卷及答案(人教版)一 选择题(每小题3分 共30分)1. 如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组数是( )A. √2 √3 √5B. 1.5C. 32 42 52D. 1 22. 点A(−3,−4)到原点的距离为( )A. 3B. 4C. 5D. 73. 有一个直角三角形的两边长分别为3和4，则第三边的长为( )A. 5B. √7C. √5D. 5或√74．如果直角三角形两直角边的比为5∶12， 则斜边上的高与斜边的比为（ ） A 60∶13B 5∶12C 12∶13D 60∶1695. 若一直角三角形两边长分别为12和5 则第三边长为（ ） A ．13 B ．13或C ．13或15D ．156．一个圆桶底面直径为24cm ，高32cm ，则桶内所能容下的最长木棒为（ ）A ．20cmB ．50cmC ．40cmD ．45cm7．如图 小明准备测量一段水渠的深度 他把一根竹竿AB 竖直插到水底 此时竹竿AB 离岸边点C 处的距离米．竹竿高出水面的部分AD 长0.5米 如果把竹竿的顶端A 拉向岸边点C 处 竿顶和岸边的水面刚好相齐 则水渠的深度BD 为（ ）A ．2米B ．2.5米C ．2.25米D ．3米1.5CD8.如图， “赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形 已知大正方形面积为25 (x +y)2=49 用x y 表示直角三角形的两直角边(x >y) 下列选项中正确的是( )A. 小正方形面积为4B. x 2+y 2=5C. x 2−y 2=7D. xy =249.如图，在△ABC 中 ∠C =90° AC =4 BC =2.以AB 为一条边向三角形外部作正方形 则正方形的面积是( )A. 8B. 12C. 18D. 2010.如图 在Rt △ABC 中 ∠ACB =90° AC =3 BC =4 BE 平分∠ABC CD ⊥AB 于D BE 与CD 相交于F 则CF 的长是( )A. 1B. 43C. 53D. 2二 填空题（每题3分 共24分）11．若一个三角形的三边之比为5：12：13 且周长为60cm 则它的面积为_____cm 2． 12．如图所示 所有的四边形都是正方形 所有的三角形都是直角三角形 其中最大的正方形的边长为7cm 正方形A B C 的面积分别是28cm 210cm 214cm 则正方形D 的面积是___________2cm ．13．在ABC中90C∠=︒AB=5 则222AB AC BC++=______．14.如图在△ABC中∠ABC=90° 分别以BC AB AC为边向外作正方形面积分别记为S1S2,S3若S2=4 S3=6则S1=__________.15.方程思想如图在Rt△ABC中∠C=90° BC=6cm AC=8cm 按图中所示方法将△BCD沿BD折叠使点C落在AB边的点C’处那么△ADC’的面积是_____cm2. 16．如图一架秋千静止时踏板离地的垂直高度DE＝0.5m将它往前推送1.5m（水平距离BC＝1.5m）时秋千的踏板离地的垂直高度BF＝1m秋千的绳索始终拉直则绳索AD的长是m．17．如图小明利用升旗用的绳子测量学校旗杆BC的高度他发现绳子刚好比旗杆长11米若把绳子往外拉直绳子接触地面A点并与地面形成30°角时绳子末端D距A点还有1米那么旗杆BC的高度为米．18．在△ABC中AB＝AC＝5 BC＝6．若点P在边AC上移动则BP的最小值是．三、解答题(满分46分,19题6分20 21 22 23 24题每题8分)19.小明将一副三角板如图所示摆放在一起发现只要知道其中一边的长就可以求出其它各边的长若已知CD=2求AC的长．20.如图折叠长方形的一边AD使点D落在边BC的点F处已知AB=8cm BC=10cm求(1)FC的长．(2)EF的长．21 (8分)如图已知∠ADC=90°AD=8 CD=6 AB=26 BC=24．（1）证明：△ABC是直角三角形．（2）请求图中阴影部分的面积．22．如图 在长方形中 点在边上 把长方形沿直线折叠 点落在边上的点处。

第17章勾股定理一．选择题（共10小题）1．下列各组数是勾股数的是（）A．2，3，4 B．0.3，0.4，0.5C．7，24，25 D．，，2．△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（）A．a2+b2＝c2B．a＝5，b＝12，c＝13C．∠A：∠B：∠C═3：4：5 D．∠A＝∠B+∠C3．如图，长方形ABCD中，AB＝3，AD＝1，AB在数轴上，若以点A为圆心，AC的长为半径作弧交数轴于点M，则点M表示的数为（）A．﹣1 B．﹣1 C．2 D．4．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC＝4，BC＝6，将四个直角三角形中边长为4的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（）A．56 B．24 C．64 D．325．如图，点E在正方形ABCD的边AB上，若EB＝1，EC＝2，那么正方形ABCD的面积为（）A．B．3 C．D．56．勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出（）A．直角三角形的面积B．最大正方形的面积C．较小两个正方形重叠部分的面积D．最大正方形与直角三角形的面积和7．如图，今年第9号台风利奇马”过后，市体育中心附近一棵大树在高于地面3米处折断，大树顶部落在距离大树底部4米处的地面上，那么树高是（）A．7m B．8m C．9m D．12m8．将一根长为25厘米的筷子置于底面直径为5厘米，高为12厘米的圆柱形水杯中，设筷子露在杯子外的长为h厘米，则h的取值范围是（）A．12≤h≤13 B．11≤h≤12 C．11≤h≤13 D．10≤h≤129．如图，已知1号、4号两个正方形的面积和为7，2号、3号两个正方形的面积和为4，则a，b，c三个正方形的面积和为（）A．11 B．15 C．10 D．2210．如图，高速公路上有A、B两点相距25km，C、D为两村庄，已知DA＝10km，CB＝15km．DA ⊥AB于A，CB⊥AB于B，现要在AB上建一个服务站E，使得C、D两村庄到E站的距离相等，则AE的长是（）km．A．5 B．10 C．15 D．25二．填空题（共6小题）11．如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8．AD平分∠BAC交BC边于点D，则BD＝．12．如图，有赵爽弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3＝27，S3＝1，则S1的值是．13．观察下列各式：32+42＝52；82+62＝102；152+82＝172；242+102＝262；…；你有没有发现其中的规律？请用你发现的规律写出接下来的式子：．14．如图，有一块田地的形状和尺寸如图所示，则它的面积为．15．如图，某自动感应门的正上方A处装着一个感应器，离地AB＝2.5米，当人体进入感应器的感应范同内时，感应门就会自动打开．一个身高1.6米的学生CD正对门，缓慢走到离门1.2米的地方时（BC＝1.2米），感应门自动打开，则AD＝米．16．如图，△ABC是边长为12cm的正三角形，动点P从A向B以2cm/s匀速运动，同时动点Q从B向C以1cm/s匀速运动，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t秒，则t＝时，△PBQ为直角三角形．三．解答题（共5小题）17．如图，已知在四边形ABCD中，AB＝20cm，BC＝15cm，CD＝7cm，AD＝24cm，∠ABC＝90°．（1）连结AC，求AC的长；（2）求∠ADC的度数；（3）求出四边形ABCD的面积18．分析探索题：细心观察如图，认真分析各式，然后解答问题．OA22＝（）2+1＝2 S1＝；OA32＝（）2+1＝3 S2＝；OA42＝（）2+1＝4 S3＝…（1）请用含有n（n为正整数）的式子表示S n＝；（2）推算出OA10＝．（3）求出S12+S22+S32+…+S102的值．19．《中华人民共和国道路交通管理条例》规定：小汽车在城市街道上的行驶速度不得超过70千米/时，如图，一辆小汽车在某城市街道直道上行驶，某一时刻刚好行驶到路对面车速检测仪A（观测点）正前方30米处的C处，过了2秒钟后，测得小汽车与车速检测仪间的距离为50米，问：这辆小汽车超速了吗？（参考数据转换：1m/s＝3.6km/h）20．如图1，在△ABC中，∠B＝22.5°，AC＝5，AD是BC边上的高，AB的垂直平分线交AB 于点E，交BC于点F．（1）判别AD与DF的数量关系并证明；（2）过F点作FG⊥AC于点G，交AD于点O（如图2），若OD＝3，求BC的长度．21．如图，在Rt△ABC中，AB＝3，BC＝4，动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q 的运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止运动，连接PQ，设它们的运动时间为t（t＞0）秒．（1）设△CBQ的面积为S，请用含有t的代数式来表示S；（2）线段PQ的垂直平分线记为直线l，当直线l经过点C时，求AQ的长．参考答案一．选择题（共10小题）1．解：A、22+32≠42，故此选项错误；B、0.3，0.4，0.5不是正整数，故此选项错误；C、72+242＝252，故此选项正确；D、（）2+（）2≠（）2，同时它们也不是正整数，故此选项错误．故选：C．2．解：A、∵a2+b2＝c2，∴∠C＝90°，即△ABC是直角三角形，故本选项不符合题意；B、∵a＝5，b＝12，c＝13，∴a2+b2＝c2，∴∠C＝90°，即△ABC是直角三角形，故本选项不符合题意；C、∵∠A：∠B：∠C＝3：4：5，∴最大角∠C＝×180°≠90°，∴△ABC是直角三角形，故本选项符合题意；D、∵∠A＝∠B+∠C，∠A+∠B+∠C＝180°，∴∠A＝90°，即△ABC是直角三角形，故本选项不符合题意；故选：C．3．解：∵AB＝3，AD＝1，∴AC＝＝，∵点A为圆心，AC的长为半径作弧交数轴于点M，AM＝AC＝，∵A点表示﹣1，∴M点表示的数为：﹣1，故选：A．4．解：依题意，设“数学风车”中的四个直角三角形的斜边长为x，则x2＝82+62＝100所以x＝10所以“数学风车”的周长是：（10+4）×4＝56．故选：A．5．解：∵四边形ABCD是正方形，∴∠B＝90°，∴BC2＝EC2﹣EB2＝22﹣12＝3，∴正方形ABCD的面积＝BC2＝3．故选：B．6．解：设直角三角形的斜边长为c，较长直角边为b，较短直角边为a，由勾股定理得，c2＝a2+b2，阴影部分的面积＝c2﹣b2﹣a（c﹣b）＝a2﹣ac+ab＝a（a+b﹣c），较小两个正方形重叠部分的宽＝a﹣（c﹣b），长＝a，则较小两个正方形重叠部分底面积＝a（a+b﹣c），∴知道图中阴影部分的面积，则一定能求出较小两个正方形重叠部分的面积，故选：C．7．解：根据勾股定理可知：折断的树高＝＝5米，则这棵大树折断前的树高＝3+5＝8米．故选：B．8．解：当筷子与杯底垂直时h最大，h最大＝25﹣12＝13cm．当筷子与杯底及杯高构成直角三角形时h最小，如图所示：此时，AB＝＝＝13cm，故h＝25﹣13＝12cm．故h的取值范围是12cm≤h≤13cm．故选：A．9．解：利用勾股定理可得S a＝S1+S2，S b＝S2+S3，S c＝S3+S4，∴S a+S b+S c＝S a＝S1+S2+S2+S3+S3+S4＝7+4+4＝15．故选：B．10．解：设AE＝x，则BE＝25﹣x，由勾股定理得：在Rt△ADE中，DE2＝AD2+AE2＝102+x2，在Rt△BCE中，CE2＝BC2+BE2＝152+（25﹣x）2，由题意可知：DE＝CE，所以：102+x2＝152+（25﹣x）2，解得：x＝15km．所以，E应建在距A点15km处．故选：C．二．填空题（共6小题）11．解：作DE⊥AC于E，如图所示：∵∠B＝90°，AB＝6，BC＝8．∴DB⊥AB，AC＝＝10，∵AD平分∠BAC，DE⊥AC，∴DE＝DB，在Rt△AED和Rt△ABD中，，∴Rt△AED≌Rt△ABD（HL），∴AE＝AB＝6，∴CE＝AC﹣AE＝4，设DE＝DB＝x，则CD＝8﹣x，在Rt△CDE中，由勾股定理得：x2+42＝（8﹣x）2，解得：x＝3，∴BD＝3；故答案为：3．12．解：∵八个直角三角形全等，四边形ABCD，EFGH，MNKT是正方形，∴CG＝NG，CF＝DG＝NF，∴S1＝（CG+DG）2＝CG2+DG2+2CG•DG＝GF2+2CG•DG，S2＝GF2，S3＝（NG﹣NF）2＝NG2+NF2﹣2NG•NF，∴S1+S2+S3＝GF2+2CG•DG+GF2+NG2+NF2﹣2NG•NF＝3GF2＝27，∴GF2＝9，∴S2＝9，∵S3＝1，∴S1的值是17．故答案为17．13．解：根据规律，下一个式子是：352+122＝372．14．解：作辅助线：连接AB，因为△ABD是直角三角形，所以AB＝＝＝5，因为52+122＝132，所以△ABC是直角三角形，则要求的面积即是两个直角三角形的面积差，即×12×5﹣×3×4＝30﹣6＝24．15．解：如图，过点D作DE⊥AB于点E，∵AB＝2.5米，BE＝CD＝1.6米，ED＝BC＝1.2米，则AE＝AB﹣BE＝2.5﹣1.6＝0.9（米）．在Rt△ADE中，由勾股定理得到：AD＝＝＝1.5（米）故答案是：1.5．16．解：∵△ABC是等边三角形，∴AB＝BC＝6cm，∠A＝∠B＝∠C＝60°，当∠PQB＝90°时，∠BPQ＝30°，∴BP＝2BQ．∵BP＝12﹣2x，BQ＝x，∴12﹣2x＝2x，解得x＝3；当∠QPB＝90°时，∠PQB＝30°，∴BQ＝2PB，∴x＝2（12﹣2x），解得x＝．答：3或秒时，△BPQ是直角三角形．故答案为3或．三．解答题（共5小题）17．解：（1）连接AC，在Rt△ABC中，∠ABC＝90°，∵AB＝20cm，BC＝15cm，∴由勾股定理可得：AC＝cm；（2）∵在△ADC中，CD＝7cm，AD＝24cm，∴CD2+AD2＝AC2，∴∠ADC＝90°；（3）由（2）知，∠ADC＝90°，∴四边形ABCD的面积＝，18．解：（1）+1＝n+1Sn＝（n是正整数）；故答案是：；（2）∵OA12＝1，OA22＝（）2+1＝2，OA32＝（）2+1＝3，OA42＝（）2+1＝4，∴OA12＝，OA2＝，OA3＝，…∴OA10＝；故答案是：；（3）S12+S22+S32+…+S102＝（）2+（）2+（）2+…+（）2＝（1+2+3+ (10)＝．即：S12+S22+S32+…+S102＝．19．解：在Rt△ABC中，AC＝30m，AB＝50m，由勾股定理可得：BC＝＝40（m），∴小汽车的速度为v＝40÷2＝20（m/s）＝20×3.6（km/h）＝72（km/h），∵72（km/h）＞70（km/h），∴这辆小汽车超速行驶．答：这辆小汽车超速了．20．（1）AD＝DF，理由如下：证明：如图1，连结AF，∵EF是AB的垂直平分线，∴BF＝AF，∴∠BAF＝∠B＝22.5°，∴∠AFD＝45°，∵AD是BC边上的高，∴△AFD是等腰直角三角形，∴AD＝DF；（2）解：∵FG⊥AC，AD⊥BC，∴∠FGC＝∠ADF＝90°，∠GFC+∠C＝90°，∠DAC+∠C＝90°，∴∠GFC＝∠DAC，∵AD＝DF，∴△ODF≌△CDA，∴OD＝CD＝3，在Rt△ACD中，由勾股定理得AD＝＝＝4，连结AF，在Rt△ADF中，AD＝DF＝4，∴AF＝＝＝4，∴BF＝AF＝4，∴BC＝BF+DF+CD＝4+4+3＝7+4．21．解：（1）如图1，当0＜t≤3时，BQ＝t，BC＝4，∴S＝×4×t＝2t；如图2，当3＜t≤5时，，AQ＝t﹣3，则BQ＝3﹣（t﹣3）＝6﹣t，∴S＝×4×（6﹣t）＝12﹣2t；（2）连接CQ，如图3，∵QP的垂直平分线过点C，∴CP＝CQ，∵AB＝3，BC＝4，∴AC＝＝＝5，∴42+t2＝（5﹣t）2，解得t＝；或42+（6﹣t）2＝（5﹣t）2，显然不成立；∴AQ＝3﹣＝．。

第17章勾股定理一．选择题（共10小题）1．下列说法中正确的是（）A．已知a，b，c是三角形的三边，则a2+b2＝c2B．在直角三角形中两边和的平方等于第三边的平方C．在Rt△ABC中，∠C＝90°，所以a2+b2＝c2D．在Rt△ABC中，∠B＝90°，所以a2+b2＝c22．下列各组线段中的三个长度：①9，12，15；②7，24，25；③32，42，52；④3a，4a，5a（a＞0）；⑤m2﹣n2，2mn，m2+n2（m，n为正整数，且m＞n）其中可以构成直角三角形的有（）A．5组B．4组C．3组D．2组3．下列数据中不能作为直角三角形的三边长是（）A．1，1，B．1，，C．，， D．，，4．如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，则BC边长的高为（）A．B．C．D．5．如图，四边形ABCD中，AC⊥BD于O，AB＝3，BC＝4，CD＝5，则AD的长为（）A．1 B．3C．4 D．26．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，AD＝AC，点D在AB上，AF⊥CD交于点E，交CB于点F，则CF的长是（）A．2.5 B．2 C．1.8 D．1.57．在平面直角坐标系中，已知点A（1，1）和B（4，5），则线段AB 的长是（）A．3 B．5 C．4 D．38．一个正方体物体沿斜坡向下滑动，其截面如图所示．正方形DEFH 的边长为2米，∠B＝90°，AB＝8米，BC＝6米．当正方形DEFH 运动到什么位置，即当AE＝（）米时，有DC2＝AE2+BC2．A．2 B．2.5 C．3.4 D．3.69．如图，在2×2的正方形网格中，每个小正方形边长为1，点A、B、C均为格点，以点A为圆心，AB长为半径作弧，交格线于点D，则以B、C、D为顶点的三角形面积为（）A．B．C．D．10．如图，在△ABC中，AB＝2，∠C＝45°，高AD＝6，则△ABC 的面积为（）A．12 B．24 C．36 D．48二．填空题（共5小题）11．在△ABC中，a2+b2＝25，ab＝12，且c＝5，则最大边上的高是．12．如图，一块形如“z”字形的铁皮，每个角都是直角，且AB＝BC ＝EF＝GF＝1，CD＝DE＝GH＝AH＝3，则AF＝．13．如图，由四个相同直角三角形与中间一个正方形拼成一个大正方形，大正方形边长为13cm，小正方形边长为7cm．则每个三角形较短直角边为．14．一颗大树在一次强烈的地震中于离树根B处4米的C处折断倒下（如图），树顶A落在离树根B处3米，则大树AB的原长为米．15．如图，一架长25m的云梯，斜靠在墙上，云梯底端在点A处离墙7米，如果云梯的底部在水平方向左滑动8米到点B处，那么云梯的顶端向下滑了m．三．解答题（共5小题）16．如图，A（﹣2，3），B（4，3），C（﹣1，﹣3）（1）点C到x轴的距离为．（2）△ABC的三边长为：AB＝，AC＝，BC＝．（3）当点P在y轴上，且△ABP的面积为6时，点P的坐标为：．17．已知△ABC中，BC＝m﹣n（m＞n＞0），AC＝2，AB＝m+n．（1）求证：△ABC是直角三角形；（2）当∠A＝30°时，求m，n满足的关系式．18．如图，某斜拉桥的主梁AD垂直于桥面MN于点D，主梁上两根拉索AB、AC长分别为13米、20米．（1）若拉索AB⊥AC，求固定点B、C之间的距离；（2）若固定点B、C之间的距离为21米，求主梁AD的高度．19．定义：若三角形三个内角的度数分别是x、y和z，满足x2+y2＝z2，则称这个三角形为勾股三角形．（1）根据上述定义，“直角三角形是勾股三角形”是真命题还是假命题；（2）已知一勾股三角形三个内角从小到大依次为x、y和z，且xy ＝2160，求x+y的值；（3）如图，△ABC中，AB＝，BC＝2，AC＝1+，求证：△ABC 是勾股三角形．20．如图，已知在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝16，D是AC上的一点，CD＝3，点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动．设点P的运动时间为t．连结AP．（1）当t＝3秒时，求AP的长度（结果保留根号）；（2）当△ABP为等腰三角形时，求t的值；（3）过点D做DE⊥AP于点E．在点P的运动过程中，当t为何值时，能使DE＝CD？参考答案一．选择题（共10小题）1．C．2．B．3．D．4．C．5．B．6．D．7．B．8．C．9．D．10．B．二．填空题（共5小题）11．2.4．12．5．13．5．14．8．15．13．三．解答题（共5小题）16．解：（1）∵C（﹣1，﹣3），∴点C到x轴的距离为3；（2）∵A（﹣2，3）、B（4，3）、C（﹣1，﹣3），∴AB＝4﹣（﹣2）＝6，AC ＝＝，BC＝＝；（3）∵点P在y轴上，当△ABP的面积为6时，∴P到AB的距离为：6÷（×6）＝2，故点P的坐标为（0，1）或（0，5）．故答案为：3；6，，；（0，1）或（0，5）．17．解：（1）∵BC＝m﹣n（m＞n＞0），AC＝2，AB＝m+n，∴AC2+CB2＝（m﹣n）2+4mn＝m2+n2﹣2mn+4mn＝m2+n2+2mn＝（m+n）2＝AB2．∴∠C＝90°．∴△ABC是为直角三角形；（2）∵∠A＝30°，∴＝＝，∴m＝3n．18．解：（1）∵AB⊥AC，∴∠BAC＝90°，∵AB、AC长分别为13米、20米，∴BC＝＝＝m，答：固定点B、C之间的距离为m；（2）∵BC＝21，∴BD＝21﹣CD，∵AD⊥BC，∴AB2﹣BD2＝AC2﹣CD2，∴132﹣BD2＝202﹣（21﹣BD）2，∴BD＝5，∴AD＝＝＝12．19．（1）解：“直角三角形是勾股三角形”是假命题；理由如下：∵对于任意的三角形，设其三个角的度数分别为x°、y°和z°，若满足x2+y2＝z2，则称这个三角形为勾股三角形，∴无法得到，所有直角三角形是勾股三角形，故是假命题；（2）解：由题意可得：，解得：x+y＝102；（3）证明：过B作BH⊥AC于H，如图所示：设AH＝xRt△ABH中，BH＝，Rt△CBH中，（）2+（1+﹣x）2＝4，解得：x＝，∴AH＝BH＝，HC＝1，∴∠A＝∠ABH＝45°，∴tan∠HBC＝＝＝，∴∠HBC＝30°，∴∠BCH＝60°，∠B＝75°，∴452+602＝752∴△ABC是勾股三角形．20．解：（1）根据题意，得BP＝2t，PC＝16﹣2t＝16﹣2×3＝10，AC＝8，在Rt△APC中，根据勾股定理，得AP＝＝＝2．答：AP的长为2．（2）在Rt△ABC中，AC＝8，BC＝16，根据勾股定理，得AB＝＝＝8若BA＝BP，则 2t＝8，解得t＝4；若AB＝AP，则BP＝32，2t＝32，解得t＝16；若PA＝PB，则（2t）2＝（16﹣2t）2+82，解得t＝5．答：当△ABP为等腰三角形时，t的值为4、16、5．（3）若P在C点的左侧，CP＝16﹣2t．AP＝20﹣2t（20﹣2t）2＝（16﹣2t）2+82解得：t＝5，若P在C点的右侧，CP＝2t﹣16．AP＝2t﹣12；（2t﹣12）2＝（2t﹣16）2+82解得：t＝11答：当t为5或11时，能使DE＝CD．。

人教版数学八年级下册第17章勾股定理单元测试卷含答案一．选择题（共6小题）1．已知直角三角形两边的长为6和8，则此三角形的周长为（）A．24 B．14+2C．24或14+2D．以上都不对2．下列各组数能构成勾股数的是（）A．2，，B．12，16，20 C．，，D．32，42，523．在△ABC中，AB＝AC＝10，BD是AC边上的高，DC＝2，则BD等于（）A．2B．4 C．6 D．84．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3．若S1+S2+S3＝60，则S2的值是（）A．12 B．15 C．20 D．305．如图，一根垂直于地面的旗杆在离地面5m处撕裂折断，旗杆顶部落在离旗杆底部12m 处，旗杆折断之前的高度是（）A．5 m B．12 m C．13 m D．18 m6．如图，小明准备测量一段水渠的深度，他把一根竹竿AB竖直插到水底，此时竹竿AB离岸边点C处的距离CD＝1.5米．竹竿高出水面的部分AD长0.5米，如果把竹竿的顶端A 拉向岸边点C处，竿顶和岸边的水面刚好相齐，则水渠的深度BD为（）米．A．2 B．2.5 C．2.25 D．3二．填空题（共5小题）7．已知三角形三边长分别是6，8，10，则此三角形的面积为．8．若8，a，17是一组勾股数，则a＝．9．已知甲、乙两人在同一地点出发，甲往东走4km，乙往南走了3km，这时甲、乙两人相距km．10．勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC＝90°，AB＝3，AC＝4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为．11．如图，在数轴上，点A、B表示的数分别为0、2，BC⊥AB于点B，且BC＝1，连接AC，在AC上截取CD＝BC，以A为圆心，AD的长为半径画弧，交线段AB于点E，则点E表示的实数是．三．解答题（共6小题）12．如图，在边长为c的正方形中，有四个斜边为c的全等直角三角形，已知其直角边长为a，b．利用这个图试说明勾股定理．13．如图在四边形ABCD中，AB＝BC＝2，CD＝3，DA＝1，且∠B＝90°，求∠DAB的度数．14．我们学习了勾股定理后，都知道“勾三、股四、弦五”．观察：3、4、5；5、12、13；7、24、25；9、40、41；…，发现这些勾股数的勾都是奇数，且从3起就没有间断过．（1）请你根据上述的规律写出下一组勾股数：；（2）若第一个数用字母n（n为奇数，且n≥3）表示，那么后两个数用含n的代数式分别表示为和，请用所学知识说明它们是一组勾股数．15．如图，在等腰△ABC中，AB＝AC，BC＝5．点D为AC上一点，且BD＝4，CD＝3．（1）求证：BD⊥AC；（2）求AB的长．16．如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）．（1）用这样的两个三角形构造成如图（2）的图形（B，E，C三点在一条直线上），利用这个图形，求证：a2+b2＝c2（2）当a＝1，b＝2时，将其中一个直角三角形放入平面直角坐标系中（如图（3）），使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合．①请在坐标轴上找一点C，使△ABC为等腰三角形．写出一个满足条件的在x轴上的点的坐标：；写出一个满足条件的在y轴上的点的坐标：，这样的点有个．17．如图，已知△ABC中，∠B＝90°，AB＝8cm，BC＝6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．（1）当t＝2秒时，求PQ的长；（2）求出发时间为几秒时，△PQB是等腰三角形？（3）若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．参考答案一．选择题（共6小题）1．解：设Rt△ABC的第三边长为x，①当8为直角三角形的直角边时，x为斜边，由勾股定理得，x＝＝10，此时这个三角形的周长＝6+8+10＝24；②当8为直角三角形的斜边时，x为直角边，由勾股定理得，x＝＝＝2，此时这个三角形的周长＝6+8+2＝14+2，故选：C．2．解：A、22+（）2＝（）2，但不是正整数，故选项错误；B、122+162＝202，能构成直角三角形，是整数，故选项正确；C、（）2+（）2≠（）2，不能构成直角三角形，故选项错误；D、（32）2+（42）2≠（52）2，不能构成直角三角形，故选项错误．故选：B．3．解：∵AB＝AC＝10，CD＝2，∴AD＝10﹣2＝8，∵BD是AC边上的高，∴∠BDA＝90°，由勾股定理得：BD＝＝＝6，故选：C．4．解：设每个小直角三角形的面积为m，则S1＝4m+S2，S3＝S2﹣4m，因为S1+S2+S3＝60，所以4m+S2+S2+S2﹣4m＝60，即3S2＝60，解得S2＝20．故选：C．5．解：旗杆折断后，落地点与旗杆底部的距离为12m，旗杆离地面5m折断，且旗杆与地面是垂直的，所以折断的旗杆与地面形成了一个直角三角形．根据勾股定理，AB＝＝13m，所以旗杆折断之前高度为BC+AB＝13m+5m＝18m．故选：D．6．解：设BD的长度为xm，则AB＝BC＝（x+0.5）m，在Rt△CDB中，1.52+x2＝（x+0.5）2，解得x＝2．故选：A．二．填空题（共5小题）7．解：∵62+82＝102，∴此三角形为直角三角形，∴此三角形的面积为：×6×8＝24．故答案为：24．8．解：①a为最长边，a＝＝，不是正整数，不符合题意；②17为最长边，a＝＝15，三边是整数，能构成勾股数，符合题意．故答案为：15．9．解：如图，∵∠AOB＝90°，OA＝4km，OB＝3km∴AB＝＝5km．10．解：如图，延长AB交KF于点O，延长AC交GM于点P，所以，四边形AOLP是正方形，边长AO＝AB+AC＝3+4＝7，所以，KL＝3+7＝10，LM＝4+7＝11，因此，矩形KLMJ的面积为10×11＝110．故答案是：110．11．解：∵BC⊥AB，∴∠ABC＝90°，∵AB＝2，BC＝1，∴AC＝＝，∵CD＝BC，∴AD＝AC﹣CD＝﹣1，∵AE＝AD，∴AE＝﹣1，∴点E表示的实数是﹣1．故答案为：﹣1．三．解答题（共6小题）12．解：∵大正方形面积为：c2，直角三角形面积为ab，小正方形面积为：（a﹣b）2，所以c2＝4×ab+（a﹣b）2，即c2＝a2+b2，在每个直角边为a、b而斜边为c的直角三角形中，这个式子就是勾股定理．13．解：如右图所示，连接AC，∵∠B＝90°，AB＝BC＝2，∴AC＝＝2，∠BAC＝45°，又∵CD＝3，DA＝1，∴AC2+DA2＝8+1＝9，CD2＝9，∴AC2+DA2＝CD2，∴△ACD是直角三角形，∴∠CAD＝90°，∴∠DAB＝45°+90°＝135°．故∠DAB的度数为135°．14．解：（1）11，60，61；（2）后两个数表示为和，∵，，∴．又∵n≥3，且n为奇数，∴由n，，三个数组成的数是勾股数．故答案为：11，60，61．15．（1）证明：∵CD＝3，BC＝5，BD＝4，∴CD2+BD2＝9+16＝25＝BC2，∴△BCD是直角三角形，∴BD⊥AC；（2）解：设AD＝x，则AC＝x+3．∵AB＝AC，∴AB＝x+3．∵∠BDC＝90°，∴∠ADB＝90°，即（x+3）2＝x2+42，解得：x＝，∴AB＝+3＝．16．解：（1）由图可得，×（a+b）（a+b）＝ab+c2+ab，整理得＝，∴a2+2ab+b2＝2ab+c2，∴a2+b2＝c2．（2）一个满足条件的在x轴上的点的坐标：（﹣1，0）；一个满足条件的在y轴上的点的坐标：（0，2+），这样的点有 4个．故答案为：（﹣1，0）；（0，2+），4．17．（1）解：（1）BQ＝2×2＝4cm，BP＝AB﹣AP＝8﹣2×1＝6cm，∵∠B＝90°，PQ＝＝＝2（cm）；（2）解：根据题意得：BQ＝BP，即2t＝8﹣t，解得：t＝；即出发时间为秒时，△PQB是等腰三角形；（3）解：分三种情况：①当CQ＝BQ时，如图1所示：则∠C＝∠CBQ，∵∠ABC＝90°，∴∠CBQ+∠ABQ＝90°，∠A+∠C＝90°，∴∠A＝∠ABQ∴BQ＝AQ，∴BC+CQ＝11，∴t＝11÷2＝5.5秒．②当CQ＝BC时，如图2所示：则BC+CQ＝12∴t＝12÷2＝6秒．③当BC＝BQ时，如图3所示：过B点作BE⊥AC于点E，则BE＝＝＝4.8（cm）∴CE＝＝3.6cm，∴CQ＝2CE＝7.2cm，∴BC+CQ＝13.2cm，∴t＝13.2÷2＝6.6秒．由上可知，当t为5.5秒或6秒或6.6秒时，△BCQ为等腰三角形．。

人教版数学八年级下册第17章勾股定理单元练习题一．选择题（共10小题）1．在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，下列条件中，能判断△ABC是直角三角形的是（）A．a＝2，b＝3，c＝4 B．a：b：c＝C．∠A+∠B＝2∠C D．∠A＝2∠B＝3∠C2．如图，正方形网格中的△ABC，若小方格边长为1，则△ABC的形状为（）A．直角三角形B．锐角三角形C．钝角三角形D．以上答案都不对3．下列是勾股数的有（）①3，4，5 ②5、12、13 ③9，40，41④13、14、15 ⑤⑥11、60、61A．6组B．5组C．4组D．3组4．若等腰三角形的腰长为13，底边长为10，则底边上的高为（）A．6 B．7 C．9 D．125．如图，在△ABC中，AB＝8，BC＝10，AC＝6，则BC边上的高AD为（）A．8 B．9 C．D．106．如图，在边长为1个单位长度的小正方形网格中，点A、B都是格点（即网格线的交点），则线段AB的长度为（）A．3B．5 C．6 D．47．已知点A的坐标为（2，﹣1），则点A到原点的距离为（）A．3 B．C．D．18．在平面直角坐标系中，O是坐标原点，点A（3，2），点P（m，0）（m＜6），若△POA是等腰三角形，则m可取的值最多有（）A．2个B．3个C．4个D．5个9．如图，以数轴的单位长度线段为边作一个正方形，以1为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（）A．1 B．﹣1 C．1﹣D．10．已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长为（）A．4 B．16 C．D．4或二．填空题（共9小题）11．如图，某会展中心在会展期间准备将高5m，长13m，宽2m的楼道上铺地毯，已知地毯每平方米18元，请你帮助计算一下，铺完这个楼道至少需要元钱．12．如图，三角形ABC中，∠ACB＝90°，AC＝3，BC＝4，P为直线AB上一动点，连接PC，则线段PC的最小值是．13．如图，在一次暴风灾害中，一棵大树在离地面2米处折断，树的另一部分倒地后与地面成30°角，那么这棵树折断之前的高度是米．14．一个无盖的圆柱形杯子的展开图如图所示，现将一根长18cm的吸管放在杯子中，则吸管露在杯子外面的部分至少有cm．15．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b，若ab＝8，大正方形的面积为25，则小正方形的边长为．16．如图，△ABC中，AC＝5，BC＝12，AB＝13，以AB为直径的半圆过点C，再分别以BC、AC为直径向上作三个半圆，则阴影部分面积为．17．如图，已知四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝13，DA＝12，则四边形ABCD的面积等于．18．如图，在Rt△ABC中，∠ACB＝90°，AB＝7.5cm，AC＝4.5cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为t秒，当△ABP为等腰三角形时，t的取值为．19．如图，AB＝AC，则数轴上点C所表示的数为．三．解答题（共6小题）20．如图，在锐角三角形ABC中，AB＝13，AC＝15，点D是BC边上一点，BD＝5，AD＝12，求BC的长度．21．如图，正方形网格的每个小方格都是边长为1的正方形，△ABC的顶点都在格点上．（1）分别求出AB，BC，AC的长；（2）试判断△ABC是什么三角形，并说明理由．22．如图，四边形ABCD中，AB＝20，BC＝15，CD＝7，AD＝24，∠B＝90°．（1）判断∠D是否是直角，并说明理由．（2）求四边形ABCD的面积．23．如图，一架长25米的梯子，斜靠在竖直的墙上，这时梯子底端离墙7米．（1）此时梯子顶端离地面多少米？（2）若梯子顶端下滑4米，那么梯子底端将向左滑动多少米？24．如图：Rt△ABC斜边BC的中垂线交AB边于点E，若AC＝3，BC＝5，求AE的长．25．（1）如图（1），分别以Rt△ABC三边为直径向外作三个正方形，其面积分别用S1，S2，S3表示，写出S1，S2，S3之间关系．（不必证明）（2）如图（2），分别以Rt△ABC三边为边向外作三个半圆，其面积分别用S1，S2，S3表示，确定它们的关系证明；（3）如图（3），分别以Rt△ABC三边为边向外作正三角形，其面积分别用S1，S2，S3表示，确定它们的关系并证明．参考答案与试题解析一．选择题（共10小题）1．【解答】解：A、22+32≠42，不符合勾股定理的逆定理，不能够判断△ABC是直角三角形，不符合题意；B、（）2+（）2＝（）2，符合勾股定理的逆定理，能够判断△ABC是直角三角形，符合题意；C、∠A+∠B＝2∠C，此时∠C＝60°，不能够判断△ABC是直角三角形，不符合题意；D、∠A＝2∠B＝3∠C，那么∠A＝（）°、∠B＝（）°、∠C＝（）°，△ABC不是直角三角形，不符合题意．故选：B．2．【解答】解：∵正方形小方格边长为1，∴BC＝＝5，AC＝＝，AB＝＝，在△ABC中，∵AB2+AC2＝5+20＝25，BC2＝25，∴AB2+AC2＝BC2，∴△ABC是直角三角形．故选：A．3．【解答】解：①32+42＝52，是勾股数；②52+122＝132，是勾股数；③92+402＝412，是勾股数；④132+142≠152，不是勾股数；⑤不是正整数，不是勾股数；⑥112+602＝612，是勾股数；故是勾股数的有4组．故选：C．4．【解答】解：如图：AB＝AC＝13，BC＝10．△ABC中，AB＝AC，AD⊥BC；∴BD＝DC＝BC＝5；Rt△ABD中，AB＝13，BD＝5；由勾股定理，得：AD＝＝＝12．故选：D．5．【解答】解：∵AB＝8，BC＝10，AC＝6，∴62+82＝102，∴△ABC是直角三角形，∠BAC＝90°，则由面积公式知，S△ABC＝AB•AC＝BC•AD，∴AD＝．故选：C．6．【解答】解：由勾股定理得：AB＝＝5；故选：B．7．【解答】解：点A的坐标为（2，﹣1）到原点O的距离：OA＝＝．故选：C．8．【解答】解：由勾股定理得：OA＝＝，如图所示：OA＝OP有2个、AP＝OA有1个（不符合题意舍去）、AP＝OP有1个，一共2+1＝3（个）．则m可取的值最多有3个．故选：B．9．【解答】解：∵正方形的边长为1，∴BC＝＝，∴AC＝，即|A﹣1|＝，故点A表示1﹣．故选：C．10．【解答】解：当3和5都是直角边时，第三边长为：＝；当5是斜边长时，第三边长为：＝4．故选：D．二．填空题（共9小题）11．【解答】解：由勾股定理，AC＝＝＝12（m）．则地毯总长为12+5＝17（m），则地毯的总面积为17×2＝34（平方米），所以铺完这个楼道至少需要34×18＝612元．故答案为：612．12．【解答】解：作CP⊥AB于P，由垂线段最短可知，此时PC最小，由勾股定理得，AB＝＝＝5，S△ABC＝×AC×BC＝×AB×PC，即×3×4＝×5×PC，解得，PC＝，故答案为：．13．【解答】解：∵一棵大树在离地面2米处折断，树的另一部分倒地后与地面成30°角，如图，可知：∠ACB＝90°，AC＝2米，∠ABC＝30°，∴AB＝2AC＝4米，∴折断前高度为2+4＝6（米）．故答案为6．14．【解答】解：由题意可得：杯子内的筷子长度为：＝15，则筷子露在杯子外面的筷子长度为：18﹣15＝3（cm）．故答案为：3．15．【解答】解：由题意可知：中间小正方形的边长为：a﹣b，∵每一个直角三角形的面积为：ab＝×8＝4，∴4×ab+（a﹣b）2＝25，∴（a﹣b）2＝25﹣16＝9，∴a﹣b＝3，故答案是：3．16．【解答】解：∵52+122＝169＝132，∴△ABC是直角三角形，S阴影＝π（）2+π（）2﹣[π（）2﹣×5×12]＝30．故答案为：30．17．【解答】解：连接AC，∵∠ABC＝90°，AB＝3，BC＝4，∴AC＝＝＝5，在△ACD中，AC2+CD2＝25+144＝169＝AD2，∴△ACD是直角三角形，∴S四边形ABCD＝AB•BC+AC•CD＝×3×4+×5×12＝36．故答案为：36．18．【解答】解：在Rt△ABC中，BC2＝AB2﹣AC2＝7.52﹣4.52＝36，∴BC＝6（cm）；①当AB＝BP＝7.5cm时，如图1，t＝＝3.75（秒）；②当AB＝AP＝7.5cm时，如图2，BP＝2BC＝12cm，t＝6（秒）；③当BP＝AP时，如图3，AP＝BP＝2tcm，CP＝（6﹣2t）cm，AC＝4.5cm，在Rt△ACP中，AP2＝AC2+CP2，所以4t2＝4.52+（6﹣2t）2，解得：t＝，综上所述：当△ABP为等腰三角形时，t＝3.75或t＝6或t＝．故答案为：3.75或6或．19．【解答】解：由勾股定理得，AB＝＝，∴AC＝，∵点A表示的数是﹣1，∴点C表示的数是﹣1．故答案为：﹣1．三．解答题（共6小题）20．【解答】解：在△ABD中，∵AB＝13，BD＝5，AD＝12，∴BD2+AD2＝52+122＝169，AB2＝132＝169，∴BD2+AD2＝AB2∴∠ADB＝∠ADC＝90°，在Rt△ACD中，由勾股定理得，∴BC＝BD+CD＝5+9＝14．21．【解答】解：（1），，；（2）△ABC是直角三角形，理由如下：∵，AC2＝52＝25，∴AB2+BC2＝AC2，∴△ABC是直角三角形．22．【解答】解：（1）连接AC，∵∠B＝90°，∴AC2＝BA2+BC2＝400+225＝625，∵DA2+CD2＝242+72＝625，∴AC2＝DA2+DC2，∴△ADC是直角三角形，即∠D是直角；（2）∵S四边形ABCD＝S△ABC+S△ADC，∴S四边形ABCD＝AB•BC+AD•CD＝×20×15+×24×7＝234．23．【解答】解：（1）∵AB＝25米，BE＝7米，梯子距离地面的高度AE＝＝24米．答：此时梯子顶端离地面24米；（2）∵梯子下滑了4米，即梯子距离地面的高度CE＝（24﹣4）＝20米，∴BD+BE＝DE＝＝＝15，∴DE＝15﹣7＝8（米），即下端滑行了8米．答：梯子底端将向左滑动了8米．24．【解答】解：连接CE，由勾股定理得，AB＝＝＝4，∵DE是BC的中垂线，∴EC＝EB＝4﹣AE，由勾股定理得，AC2+AE2＝EC2，即32+AE2＝（4﹣AE）2，解得，AE＝．25．【解答】解：（1）S2+S3＝S1，由三个四边形都是正方形则：∵S3＝AC2，S2＝BC2，S1＝AB2，∵三角形ABC是直角三角形，∴AC2+BC2＝AB2，∴S2+S3＝S1．（2）∵S3＝AC2，S2＝BC2，S1＝AB2，∵三角形ABC是直角三角形，∴AC2+BC2＝AB2，∴S2+S3＝S1．（3）∵S1＝AB2，S2＝BC2，S3＝AC2，∵三角形ABC是直角三角形，∴AC2+BC2＝AB2，∴S2+S3＝S1．。

第十七章勾股定理一、选择题1.在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲移到一边，花朵齐及水面，已知红莲移动的水平距离为2米，这里的水深为()A． 1.5米B． 2米C． 2.5米D． 1米2.如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6.其中S1＝16，S2＝45，S5＝11，S6＝14，则S3＋S4等于()A． 86B． 64C． 54D． 483.如图表示的是一个十字路口，O是两条公路的交点，点A、B、C、D表示的是公路上的四辆车，若OC＝8 cm，AC＝17 cm，AB＝5 cm，BD＝10m，则C，D两辆车之间的距离为()A． 5 mB． 4 mC． 3 mD． 2 m4.如图是由三个棱长均为1的正方体箱子堆积而成的几何体，在底端的顶点A处有一只蚂蚁，它想吃到顶端的顶点B处的食物，则它沿该几何体表面爬行的最短路程等于()A．B． 2＋1C．D． 55.如图，长方体的透明玻璃鱼缸，假设其长AD＝80 cm，高AB＝60 cm，水深为AE＝40 cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG＝60 cm；一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵，则小动物爬行的最短路线长为()A． 40 cmB． 60 cmC． 80 cmD． 100 cm6.三角形三边长为6、8、10，那么最长边上的高为()A． 6B． 4.5C． 4.8D． 87.如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2 m，梯子的顶端B到地面的距离为7 m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3 m，同时梯子的顶端B下降至B′，那么BB′()A．小于1 mB．大于1 mC．等于1 mD．小于或等于1 m8.如图，一根垂直于地面的旗杆在离地面5 m处撕裂折断，旗杆顶部落在离旗杆底部12 m处，旗杆折断之前的高度是()A． 5 mB． 12 mC． 13 mD． 18 m二、填空题9.直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为________．10.一个三角形的三边长之比为5∶12∶13，它的周长为120，则它的面积是________．11.如图，分别以△ABC的三边为直径向外作3个半圆，它们的面积分别为4、5、9，则△ABC________直角三角形．(填“是”或“不是”)12.如图，AD＝8，CD＝6，∠ADC＝90°，AB＝26，BC＝24，该图形的面积等于________．13.中国古代的数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位．尤其是三国时期的数学家赵爽，不仅最早对勾股定理进行了证明，而且创制了“勾股圆方图”，开创了“以形证数”的思想方法．在图1中，小正方形ABCD的面积为1，如果把它的各边分别延长一倍得到正方形A1B1C1D1，则正方形A1B1C1D1的面积为________；再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2(如图2)，如此进行下去，得到的正方形AnBnCnDn的面积为________(用含n的式子表示，n为正整数)．14.如图，四边形ABCD中，AB⊥AD于A，AB＝8，AD＝8，BC＝7，CD＝25，则四边形ABCD的面积为__________．15.如图，以直角△ABC的三边向外作正方形，其面积分别为S1，S2，S3且S1＝4，S2＝8，则S3＝________.16.在△ABC中，已知AB＝BC＝CA＝4 cm，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C 运动，速度为1 cm/s；点Q沿CA、AB向终点B运动，速度为2 cm/s，设它们运动的时间为x(s)，当x＝__________，△BPQ是直角三角形．三、解答题17.如图所示的一块地，AD＝9 m，CD＝12 m，∠ADC＝90°，AB＝39 m，BC＝36 m，求这块地的面积．18.如图，在B港有甲、乙两艘渔船，若甲船沿北偏东60°方向以每小时8海里速度前进，乙船沿南偏东某方向以每小时15海里速度全速前进，2小时后甲船到M岛，乙船到P岛，两岛相距34海里，你知道乙船沿那个方向航行吗？19.在△ABC中，AB＝15，BC＝14，AC＝13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．20.为了弘扬“社会主义核心价值观”，乐至县政府在广场树立公益广告牌，如图所示，为固定广告牌，在两侧加固钢缆，已知钢缆底端D距广告牌立柱距离CD为3米，从D点测得广告牌顶端A点和底端B点的距离分别是5米和3米．(1)求公益广告牌的高度AB；(2)求∠BDC的度数．21.阅读与应用：阅读以下材料，并按要求完成相应的任务．中国最早的一部数学著作－－《周髀算经》的开头，记载着一段周公向商高请教数学知识的对话：周公问：“我听说您对数学非常精通，我想请教一下：天没有梯子可以上去，地也没法用尺子去一段一段丈量，那么怎样才能得到关于天地的数据呢？”商高回答说：“数的产生来源于对方和圆这些形体的认识，其中有一条原理：当直角三角形‘矩’得到的一条直角边‘勾’等于3，另一条直角边‘股’等于4的时候，那么它的斜边‘弦’就必定是5.这个原理是大禹在治水的时候就总结出来的呵．”任务：(1)上面周公与商高的这段对话，反映的数序原理在数学上叫做__________定理；(2)请你利用以上数学原理解决问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，求问题中葛藤的最短长度是多少尺．答案解析1.【答案】A【解析】设水深为h米，则红莲的高(h＋1)米，且水平距离为2米，则(h＋1)2＝22＋h2，解得h＝1.5.故选A.2.【答案】C【解析】如图1，S1＝AC2，S2＝AB2，S3＝BC2，∵BC2＝AB2－AC2，∴S2－S1＝S3，如图2，S4＝S5＋S6，∴S3＋S4＝45－16＋11＋14＝54.故选C.3.【答案】D【解析】在Rt△AOC中，∵OA2＋OC2＝AC2，∴OA＝＝＝15(m)，∴OB＝OA＋AB＝20 m，在Rt△BOD中，∵BD2＝OB2＋OD2，∴OD＝＝＝10(m)，∴CD＝OD－OC＝2 m，故选D.4.【答案】A【解析】如图所示，由图可知，AB＝＝.故选A.5.【答案】D【解析】如图所示作点A关于BC的对称点A′，连接A′G交BC与点Q，小虫沿着A→Q→G的路线爬行时路程最短．在直角△A′EG中，A′E＝80 cm，EG＝60 cm，∴AQ＋QG＝A′Q＋QG＝A′G＝＝100 cm.∴最短路线长为100 cm.故选D.6.【答案】C【解析】∵62＋82＝102，∴这个三角形是直角三角形，∴最长边上的高为6×8÷10＝4.8.故选C.7.【答案】A【解析】在直角三角形AOB中，因为OA＝2，OB＝7，由勾股定理，得AB＝，由题意可知AB＝A′B′＝，又OA′＝3，根据勾股定理得OB′＝，∴BB′＝7－＜1.故选A.8.【答案】D【解析】旗杆折断后，落地点与旗杆底部的距离为12 m，旗杆离地面5 m折断，且旗杆与地面是垂直的，所以折断的旗杆与地面形成了一个直角三角形．根据勾股定理，折断的旗杆为＝13 m，所以旗杆折断之前高度为13 m＋5 m＝18 m.故选D.9.【答案】6【解析】∵直角三角形斜边长是5，一直角边的长是3，∴另一直角边长为＝4.该直角三角形的面积S＝×3×4＝6.10.【答案】480【解析】设三边的长是5x,12x,13x，则5x＋12x＋13x＝120，解得x＝4，则三边长是20,48,52.∵202＋482＝522，∴三角形是直角三角形，∴三角形的面积是×20×48＝480.11.【答案】是【解析】由分别以△ABC的三边为直径向外作3个半圆，它们的面积分别为4、5、9，得BC2＋AC2＝AB2，则△ABC是直角三角形．12.【答案】96【解析】连接AC，在Rt△ACD中，AD＝8，CD＝6，∴AC＝＝＝10，在△ABC中，∵AC2＋BC2＝102＋242＝262＝AB2，∴△ABC为直角三角形；∴图形面积为S△ABC－S△ACD＝×10×24－×6×8＝96.13.【答案】55n【解析】已知小正方形ABCD的面积为1，则把它的各边延长一倍后，△AA1B1的面积是1，新正方形A1B1C1D1的面积是5，从而正方形A2B2C2D2的面积为5×5＝25＝52，…正方形AnBnCnDn的面积为5n.14.【答案】84＋96【解析】连接BD，∵AB⊥AD，∴∠A＝90°，∴BD＝24，∵BC2＋BD2＝72＋242＝625＝252＝CD2，∴△CBD为直角三角形，∴S四边形ABCD＝S△ABD＋S△BCD＝×8×8＋×24×7＝96＋84.15.【答案】12【解析】∵△ABC直角三角形，∴BC2＋AC2＝AB2，∵S1＝BC2，S2＝AC2，S3＝AB2，S1＝4，S2＝8，∴S3＝S1＋S2＝12.16.【答案】2或【解析】根据题意，得BP＝t cm，CQ＝2t cm，BQ＝(8－2t) cm，若△BPQ是直角三角形，则∠BPQ＝90°或∠BQP＝90°，①当∠BPQ＝90°时，Q在A点，CQ＝CA＝4 cm，4÷2＝2(s)；②当∠BQP＝90°时，∵∠B＝60°，∴∠BPQ＝90°－60°＝30°，∴BQ＝BP，即8－2t＝t，解得t＝，故当t＝2或秒时，△BPQ是直角三角形．17.【答案】解连接AC，则在Rt△ADC中，AC2＝CD2＋AD2＝122＋92＝225，∴AC＝15，在△ABC中，AB2＝1521，AC2＋BC2＝152＋362＝1521，∴AB2＝AC2＋BC2，∴∠ACB＝90°，∴S△ABC－S△ACD＝AC·BC－AD·CD＝×15×36－×12×9＝270－54＝216.答：这块地的面积是216平方米．【解析】连接AC，运用勾股定理逆定理可证△ACD，△ABC为直角三角形，可求出两直角三角形的面积，此块地的面积为两个直角三角形的面积差．18.【答案】解BM＝8×2＝16海里，BP＝15×2＝30海里，在△BMP中，BM2＋BP2＝256＋900＝1156，PM2＝1156，BM2＋BP2＝PM2，∴∠MBP＝90°，180°－90°－60°＝30°，故乙船沿南偏东30°方向航行．【解析】先根据路程＝速度×时间，求出BM，BP的长，再根据勾股定理的逆定理得到∠MBP＝90°，进一步即可求解．19.【答案】解如图，在△ABC中，AB＝15，BC＝14，AC＝13，设BD＝x，则CD＝14－x，由勾股定理，得AD2＝AB2－BD2＝152－x2，AD2＝AC2－CD2＝132－(14－x)2，故152－x2＝132－(14－x)2，解之得x＝9.∴AD＝12.∴S△ABC＝BC·AD＝×14×12＝84.【解析】根据题意利用勾股定理表示出AD2的值，进而得出等式求出答案．20.【答案】解(1)在直角三角形ADC中，AC ＝＝＝4(m)，在直角三角形BDC中，BC ＝＝＝3(m)，故AB＝AC－BC＝1(米)，答：公益广告牌的高度AB的长度为1 m；(2)∵在直角三角形BDC中，BC＝CD＝3 m，∴△DBC是等腰直角三角形，∴∠BDC＝45°.【解析】(1)直接利用勾股定理得出AC的长，进而得出BC的长即可得出AB的长；(2)利用已知结合(1)中所求得出△DBC是等腰直角三角形，进而得出答案．21.【答案】解(1)上面周公与商高的这段对话，反映的数序原理在数学上叫做勾股定理；故答案是勾股；(2)如图，一条直角边(即枯木的高)长20尺，另一条直角边长5×3＝15(尺)，因此葛藤长为＝25(尺)．答：问题中葛藤的最短长度是25尺．【解析】(1)根据勾股定理的概念填空；(2)这种立体图形求最短路径问题，可以展开成为平面内的问题解决，展开后可转化下图，所以是个直角三角形求斜边的问题，根据勾股定理可求出．。

人教版八年级下册数学第十七章勾股定理含答案一、单选题(共15题，共计45分)1、我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形，得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理.如图，若a＝4，b＝6，则该直角三角形的周长为（）A.18B.20C.24D.262、已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,则△ABC的形状为( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形3、如图，是由一连串的直角三角形演化而成，其中OA1＝A1A2＝…＝A7A8＝1，若将图形继续演化，第n 个直角三角形△OA n A n+1 的面积是（）A. B. C. D.4、如图，四边形ABCD中，DC∥AB，BC＝1，AB＝AC＝AD＝2，则BD的长为（）A. B. C.3 D.25、直角三角形有一条直角边为6，另两条边长是连续偶数，则其斜边中线长为( )A.5B.10C.8D.166、在⊙O中，弦AB的长为2 cm，圆心O到AB的距离为1cm，则⊙O的半径是（）A.2B.3C.D.7、下列长度的三条线段，能组成直角三角形的是（）A.3，4，8B.5，6，10C.5，5，11D.5，12，138、如图，直线与反比例函数的图象相交于A、B两点，线段的中点为点C，过点C作x轴的垂线，垂足为点D.直线过原点O和点C.若直线上存在点，满足，则的值为（）A. B.3或 C. 或 D.39、如图，在Rt△ABC中，∠C=90°，D为AC上一点，且DA=DB=5，又△DAB的面积为10，那么△ABC的面积是（）A.14B.15C.16D.10、平面直角坐标系中，点P（2，0）平移后对应的点为Q（5，4），则平移的距离为（）A.3B.4C.5D.711、如图，在四边形ABCD中，∠DAB=∠BCD=90°，分别以四边形的四条边为边向外作四个正方形，若S1+S4=100，S3=36，则S2=（）A.136B.64C.50D.8112、已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）A.25海里B.30海里C.35海里D.40海里13、如图，在由边长为1个单位长度的小正方形组成的网格中，点A， B都是格点，则线段AB的长为（）A.5B.6C.7D.214、如图，的顶点在边长为1的正方形网格的格点上，于，则的长为（）A. B. C. D.15、在Rt△ABC中，，则AB的长是（）A. B.2 C.1 D.二、填空题(共10题，共计30分)16、如图，已知中，为直径，平分，弦，则半径的为________ .17、如图，在Rt△ABC中，∠C＝90°，将△ABC绕点C顺时针旋转90°得到△A′B′C，M、M′分别是AB、A′B′的中点，若AC＝8，BC＝6，则线段MM′的长为________.18、如图，正方形ABCD，AC、BD交于点O，点E、F分别在AB、BC上，且∠EOF=90°，则下列结论①AE=BF，②OE=OF，③BE+BF=AD，④AE2+CF2=2OE2中正确的有________（只写序号）19、为了推广城市绿色出行，小蓝车公司准备在十圩港沿岸AB段建设一个共享单车停放点，该路段附近有两个广场C和D（如图），CA⊥AB于A、DB⊥AB于B，AB=4km，CA=2km，DB=1km．则停放点E应建在距点A________km处，才能使它到两广场的距离相等．20、如图，AB=AC，则数轴上点C所表示的数为________.21、在矩形ABCD中，AB=6，BC=8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是________．22、如图，在正方形纸片中，是的中点，将正方形纸片折叠，点落在线段上的点处，折痕为. 若，则的长为________.23、如图，Rt△ABC中，∠B=90°，AB=4，BC=3，AC的垂直平分线DE分别交AB，AC于D，E两点，则CD的长为________．24、如图，直线AB与⊙O切于点A，⊙O的半径为2，若∠OBA=30°，则AB的长为________.25、一个等边三角形的边长等于4cm，则这个三角形的面积等于________．三、解答题(共5题，共计25分)26、如图所示，△ABC和△AEF为等边三角形，点E在△ABC内部，且E到点A，B，C的距离分别为3，4，5，求∠AEB的度数．27、如图，四边形ABCD中，∠C=90°，BD平分∠ABC，AD=3，E为AB上一点，AE=4，ED=5，求CD的长．28、如图，某地方政府决定在相距50km的A、B两站之间的公路旁E点，修建一个土特产加工基地，且使C、D两村到E点的距离相等，已知DA⊥AB于A，CB⊥AB于B，DA=30km，CB=20km，那么基地E应建在离A站多少千米的地方？29、某条道路限速如图，一辆小汽车在这条道路上沿直线行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方的C处，过了后，小汽车到达B处，此时测得小汽车与车速测检测仪间的距离为，这辆小汽车超速了吗？30、如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=10，DA= ，求BD的长．参考答案一、单选题(共15题，共计45分)1、C2、D3、C4、B5、A6、A7、D8、A9、C11、B12、D13、A14、C15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)28、29、。

人教版数学八年级下册第十七章勾股定理单元测试卷一、单选题（共10题；共20分）1.下列说法：①无理数分为正无理数，零，负无理数；②-4是16的平方根；③如果a，b，c为一组勾股数，那么4a，4b，4c仍是勾股数；④任何实数都有立方根，其中正确的有（）A. 4B. 3C. 2D. 12.若一个直角三角形的三边分别为a、b、c，a2＝144，b2＝25，则c2＝（）A. 169B. 119C. 169或119D. 13或253.如图，∠B＝∠ACD＝90°；AD=13；CD=12；BC=3，则AB的长为（）A. 4B. 5C. 8D. 104.下列各组数是勾股数的是（）A. 12、15、18B. 6、8、12C. 4、5、6D. 7、24、255.一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处．若M，N两点相距100海里，则∠NOF的度数为（）A. 50°B. 60°C. 70°D. 90°6.如图以数轴的单位长线段为边作一个正方形，以数轴的原点为旋转中心，将过原点的对角线顺时针旋转，使对角线的另一端点落在数轴正半轴的点处，则点表示的数是（）A. B. C. D.7.图1是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图2所示，两支脚OC=OD=10分米，展开角∠COD=60°，晾衣臂0A=OB=10分米，晾衣臂支架HG=FE=5分米，HO=FO=4分米。

当∠AOC=90°，且OB∥CD时，线段OG与OE的长分别为( )A. 3和7B. 3和C. 3和2+D. 和2+8.如图，圆柱形容器高为18cm，底面周长为32cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好也在杯内壁，离杯上沿2cm与蜂蜜正相对的点A处，则蚂蚁从内壁A处到达内壁B处的最短距离为（）A. 13cmB. cmC. 2 cmD. 20cm9.如图，在△ABC中，AB=AC，∠BAC=60°，BC=2，AD⊥BC于D，点F是AB的中点，点E在AD边上，则BE+EF的最小值是( )A. 1B.C. 2D.10.如图，小江同学把三角尺含有60°角的一端以不同的方向穿入进另一把三角尺(含有45°角)的孔洞中。

人教版八年级数学下册《第十七章勾股定理》单元测试题一．选择题（共10小题，满分40分，每小题4分）1．已知一个直角三角形的两直角边长分别为5和12，则第三边长的平方是（）A．169B．119C．13D．1442．在Rt△ABC中，∠B＝90°，BC＝1，AC＝2，则AB的长是（）A．1B．C．2D．3．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A，B，C，D的边长分别是4，9，1，4，则最大正方形E的面积是（）A．18B．114C．194D．3244．如图是一个直角三角形，它的未知边的长x等于（）A．13B．C．5D．5．如图，在平面直角坐标系中，点A，B的坐标分别为（﹣6，0），（0，8），以点A为圆心，以AB长为半径画弧，交x轴正半轴于点C，则点C的坐标为（）A．（10，0）B．（0，4）C．（4，0）D．（2，0）6．以下列三个数据为三角形的三边，其中能构成直角三角形的是（）A．2，3，4B．4，5，6C．5，12，13D．5，6，77．下列各组数据中，不是勾股数的是（）A．3，4，5B．7，24，25C．8，15，17D．5，7，98．满足下列条件的△ABC，不是直角三角形的是（）A．b2﹣c2＝a2B．a：b：c＝3：4：5C．∠C＝∠A﹣∠B D．∠A：∠B：∠C＝9：12：159．如图，在Rt△ABC中，∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”，当AC＝4，BC＝2时，则阴影部分的面积为（）A．4B．4πC．8πD．810．如图，这是用面积为24的四个全等的直角三角形△ABE，△BCF，△CDG和△DAH拼成的“赵爽弦图”，如果AB＝10，那么正方形EFGH的边长为（）A．1B．2C．2D．4二．填空题（共4小题，满分20分，每小题5分）11．平面直角坐标系上有点A（﹣3，4），则它到坐标原点的距离为．12．一个直角三角形的两条直角边长分别为3，4，则第三边为．13．如图，每个小正方形边长为1，A、B、C是小正方形的顶点，则AB2＝，∠ABC＝°．14．已知两线段的长分别是5cm、3cm，则第三条线段长是时，这三条线段构成直角三角形三．解答题（共9小题，满分90分）15．在△ABC中，∠ACB＝90°，AC＝5，AB＝BC+1，求Rt△ABC的面积．16．如图，在△ADC中，∠C＝90°，AB是DC边上的中线，∠BAC＝30°，若AB＝6，求AD的长．17．如图，某人划船横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B25m，结果他在水中实际划了65m，求该河流的宽度．18．如图，在△ABC中，AB＝20，AC＝15，BC＝25，AD⊥BC，垂足为D．求AD，BD的长．19．如图，在Rt△ABC中，∠C＝90°，AC＝30cm，BC＝21cm，动点P从点C出发，沿CA方向运动，动点Q从点B出发，沿BC方向运动，如果点P，Q的运动速度均为1cm/s．那么运动几秒时，它们相距15cm？20．如图，在△ABC中，AD⊥BC，AB＝10，BD＝8，∠ACD＝45°．（1）求线段AD的长；（2）求△ABC的周长．21．在△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C所对的边．（1）若b＝2，c＝3，求a的值；（2）若a：c＝3：5，b＝16，求△ABC的面积．22．如图所示，四边形ABCD ，∠A ＝90°，AB ＝3m ，BC ＝12m ，CD ＝13m ，DA ＝4m ．（1）求证：BD ⊥CB ； （2）求四边形ABCD 的面积；（3）如图2，以A 为坐标原点，以AB 、AD 所在直线为x 轴、y 轴建立直角坐标系，点P 在y 轴上，若S△PBD＝S 四边形ABCD ，求P 的坐标．23．如图，一艘轮船以30km /h 的速度沿既定航线由西向东航行，途中接到台风警报，某台风中心正以20km /h 的途度由南向北移动，距台风中心200km 的圆形区域（包括边界）都属台风影响区．当这艘轮船接到台风警报时，它与台风中心的距离BC ＝500km ，此时台风中心与轮船既定航线的最近距离BA ＝300km ． （1）如果这艘轮船不改变航向，那么它会不会进入台风影响区？（2）如果你认为这艘轮船会进入台风影响区，那么从接到警报开始，经过多长时间它就会进入台风影响区？（3）假设轮船航行速度和航向不变，轮船受到台风影响一共经历了多少小时？人教版八年级数学下册《第十七章勾股定理》单元测试题参考答案与试题解析一．选择题（共10小题，满分40分，每小题4分）1．【解答】解：第三边长的平方是52+122＝169．故选：A．2．【解答】解：在Rt△ABC中，∠B＝90°，BC＝1，AC＝2，∴AB＝＝＝，故选：B．3．【解答】解：根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1＝42+92，S2＝12+42，则S3＝S1+S2，∴S3＝16+81+1+16＝114．故选：B．4．【解答】解：∵x＝＝，故选：B．5．【解答】解：∵点A，B的坐标分别为（﹣6，0），（0，8），∴OA＝6，OB＝8，在Rt△AOB中，由勾股定理得：AB＝＝10，∴AC＝AB＝10，∴OC＝10﹣6＝4，∴点C的坐标为（4，0），故选：C．6．【解答】解：A、22+32≠42，故不能构成直角三角形；B、42+52≠62，故不能构成直角三角形；C、52+122＝132，故能构成直角三角形；D、52+62≠72，故不能构成直角三角形．故选：C．7．【解答】解：A、32+42＝52，能构成直角三角形，是整数，故错误；B、72+242＝252，能构成直角三角形，是整数，故错误；C、82+152＝172，构成直角三角形，是正整数，故错误；D、52+72≠92，不能构成直角三角形，故正确；故选：D．8．【解答】解：b2﹣c2＝a2则b2＝a2+c2△ABC是直角三角形；a：b：c＝3：4：5，设a＝3x，b＝4x，c＝5x，a2+b2＝c2，△ABC是直角三角形；∠C＝∠A﹣∠B，则∠B＝∠A+∠C，∠B＝90°，△ABC是直角三角形；∠A：∠B：∠C＝9：12：15，设∠A、∠B、∠C分别为9x、12x、15x，则9x+12x+15x＝180°，解得，x＝5°，则∠A、∠B、∠C分别为45°，60°，75°，△ABC不是直角三角形；故选：D．9．【解答】解：由勾股定理得，AB2＝AC2+BC2＝20，则阴影部分的面积＝×AC×BC+×π×（）2+×π×（）2﹣×π×（）2＝×2×4+×π××（AC2+BC2﹣AB2）＝4，故选：A．10．【解答】解：∵正方形EFGH的面积＝正方形ABCD的面积﹣4S＝102﹣4×24＝4，△ABE∴正方形EFGH的边长＝2，故选：C．二．填空题（共4小题，满分20分，每小题5分）11．【解答】解：∵点A（﹣3，4），∴它到坐标原点的距离＝＝5，故答案为：5．12．【解答】解：由勾股定理得：第三边为：＝5，故答案为：5．13．【解答】解：连接AC．根据勾股定理可以得到：AB2＝12+32＝10，AC2＝BC2＝12+22＝5，∵5+5＝10，即AC2+BC2＝AB2，∴△ABC是等腰直角三角形，∴∠ABC＝45°．故答案为：10，45．14．【解答】解：当第三条线段为直角边时，5cm为斜边，根据勾股定理得，第三条线段长为＝4cm；当第三条线段为斜边时，根据勾股定理得，第三条线段长为＝cm．故答案为4或cm．三．解答题（共9小题，满分90分）15．【解答】解：如图所示：设AB＝x，则BC＝x﹣1，故在Rt△ACB中，AB2＝AC2+BC2，故x2＝52+（x﹣1）2，解得；x＝13，即AB＝13．∴BC＝12，∴S＝•AC•BC＝×5×12＝30．△ABC16．【解答】解：在Rt△ABC中，∠C＝90°，∠BAC＝30°，AB＝6，∴BC＝AB＝3，在Rt△ABC中，AC＝＝3，∵AB是DC边上的中线，∴DB＝BC＝3，所以CD＝6，在Rt△ACD中，AD＝＝＝3．答：AD的长是317．【解答】解：根据图中数据，由勾股定理可得：AB＝＝＝60（米）．∴该河流的宽度为60米．18．【解答】解：∵AB2+AC2＝202+152＝625＝252＝BC2，∴△ABC是直角三角形，∵S＝×AB×AC＝×BC×AD，△ACB∴15×20＝25×AD，∴AD＝12，由勾股定理得：BD＝＝16．19．【解答】解：设运动x秒时，它们相距15cm，则CP＝xcm，CQ＝（21﹣x）cm，依题意有x2+（21﹣x）2＝152，解得x1＝9，x2＝12．故运动9秒或12秒时，它们相距15cm．20．【解答】解：（1）∵AD⊥BC，∴∠ADB＝90°．在Rt△ABD中，∠ADB＝90°，AB＝10，BD＝8，∴AD＝＝6．（2）∵AD⊥BC，∠ACD＝45°，∴△ACD为等腰直角三角形，又∵AD＝6，∴CD＝6，AC＝6，＝AB+BD+CD+AC＝24+6．∴C△ABC21．【解答】解：（1）∵△ABC中，∠C＝90°，b＝2，c＝3，∴a＝＝；（2）∵a：c＝3：5，∴设a＝3x，c＝5x，∵b＝16，∴9x2+162＝25x2，解得：x＝4，∴a＝12，∴△ABC的面积＝×12×16＝96．22．【解答】（1）证明：连接BD．∵AD＝4m，AB＝3m，∠BAD＝90°，∴BD＝5m．又∵BC ＝12m ，CD ＝13m ， ∴BD 2+BC 2＝CD 2． ∴BD ⊥CB ；（2）四边形ABCD 的面积＝△ABD 的面积+△BCD 的面积＝×3×4+×12×5 ＝6+30 ＝36（m 2）．故这块土地的面积是36m 2；（3）∵S △PBD ＝S 四边形ABCD ，∴•PD •AB ＝×36，∴•PD ×3＝9， ∴PD ＝6，∵D （0，4），点P 在y 轴上， ∴P 的坐标为（0，﹣2）或（0，10）．23．【解答】解：（1）根据题意得：轮船不改变航向，轮船会进入台风影响区； （2）如图所示：设x 小时后，就进入台风影响区，根据题意得出： CE ＝30x 千米，BB ′＝20x 千米， ∵BC ＝500km ，AB ＝300km ，∴AC ＝＝＝400（km ），∴AE ＝400﹣30x ，AB ′＝300﹣20x ， ∴AE 2+AB ′2＝EB ′2，即（400﹣30x ）2+（300﹣20x ）2＝2002，解得：x 1＝≈8.3，x 2＝≈19.3，∴轮船经8.3小时就进入台风影响区；（3）由（2）知，从8.3小时到19.3小时轮船受到台风影响， ∴轮船受台风影响的时间＝19.3﹣8.3＝11（小时），答：轮船受到台风影响一共经历了11小时．。

八年级数学下册《第十七章勾股定理》单元测试卷及答案(人教版)一、单选题1．我国古代算书《九章算术》中第九章第六题是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深葭长各几何？你读懂题意了吗？请回答水深______尺，葭长_____尺.解：根据题意，设水深OB＝x尺，则葭长OA'＝（x+1）尺.可列方程正确的是（）A．x2+52 ＝（x+1）2B．x2+52 ＝（x﹣1）2C．x2+（x+1）2 ＝102D．x2+（x﹣1）2＝522．如图，Rt△ABC中，∠BAC=90°，AB=AC，D、E为BC边上两点，∠DAE=45°，过A 点作AF⊥AE，且AF=AE，连接DF、BF.下列结论：①△ABF≌△ACE，②AD平分∠EDF；③若BD=4，CE=3，则AB=6√2；④若AB=BE，S△ABD=12S△ADE，其中正确的个数有（）A．1个B．2个C．3个D．4个3．在△ABC中，AB=10，AC=17，BC边上的高AD=8，则△ABC的面积为（）A．72B．84C．36或84D．72或844．如图，在△ABC中，△C＝90°，以A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于12MN长为半径画弧，两弧交于点O，作射线AO，交BC于点E．已知CE＝3，BE＝5，则AC的长为（）A．8B．7C．6D．55．如图，已知钓鱼竿AC的长为10m，露在水面上的鱼线BC长为6m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC转动到AC′的位置，此时露在水面上的鱼线B′C′为8m，则BB′的长为（）A．1m B．2m C．3m D．4m6．有一个边长为1的正方形，以它的一条边为斜边，向外作一个直角三角形，再分别以直角三角形的两条直角边为边，向外各作一个正方形，称为第一次“生长”（如图1）；再分别以这两个正方形的边为斜边，向外各自作一个直角三角形，然后分别以这两个直角三角形的直角边为边，向外各作一个正方形，称为第二次“生长”（如图2）……如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是（）A．1B．2020C．2021D．20227．如图，直线l上有三个正方形A、B、C，若正方形A、C的边长分别为4和6，则正方形B的面积为（）A．26B．49C．52D．648．要焊接一个如图所示的钢架，需要的钢材长度是（）A．(3√5+7)m B．(5√3+7)m C．(7√5+3)m D．(3√7+5)m9．如图，某超市为了吸引顾客，在超市门口离地高4.5m的墙上，装有一个由传感器控制的门铃A，如①图所示，人只要移至该门铃5m及5m以内时，门铃就会自动发出语音“欢迎光临”.如②图所示，一个身高1.5m的学生走到D处，门铃恰好自动响起，则BD的长为（）A．3米B．4米C．5米D．7米10．如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC 绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（）A．√2B．√2+1C．1﹣√2D．﹣√2二、填空题11．如图，在△ABC中，∠A=90°，AB=AC，点D为AB中点，过点B作BE⊥CD交CD的延长线于点E，BE=2，CD=5，则DE=．12．如图，在Rt△ABC中，AB=BC=4，以AB为边作等边三角形ABD，使点D与点C在AB同侧，连接CD，则CD=．13．如图，已知Rt△ABC，△C=90°，BD是角平分线，BD=5，BC=4，则D点到AB的距离是。

人教版八年级数学下册第十七章《勾股定理》单元测试题（含答案）1．下列四组数据，不是勾股数的是（）A．3，4，5 B．5，6，7 C．6，8，10 D．9，40，41 2．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，BE平分∠ABC，CD⊥AB于D，BE 与CD相交于F，则CF的长是（）A．1 B．C．D．23．等腰三角形的周长为36，其底边上的高为6，则其面积为（）A．216 B．96 C．48 D．324．下列命题中真命题的个数（）（1）已知直角三角形面积为4，两直角边的比为1：2，则它的斜边为5；（2）直角三角形的最大边长为26，最短边长为10，则另一边长为24；（3）在直角三角形中，两条直角边长为n2﹣1和2n，则斜边长为n2+1；（4）等腰三角形面积为12，底边上的底为4，则腰长为5．A．1个B．2个C．3个D．4个5．已知锐角△ABC的三边长恰为三个连续整数，AB＞BC＞CA，若边BC上的高为AD，则BD ﹣DC＝（）A．3 B．4 C．5 D．66．已知直角三角形的周长是2+，斜边是2，则该三角形的面积是（）A．B．C．D．17．已知△ABC中，AB＝17，AC＝10，BC边上的高AD＝8，则边BC的长为（）A．21 B．15 C．6 D．以上答案都不对8．如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH＝EB ＝3，AE＝4，则BC+AC的长是（）A．7 B．8 C．D．9．△ABC中，AB＝AC＝5，BC＝8，点P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC 于点E，则PD+PE的长是（）A．4.8 B．4.8或3.8 C．3.8 D．510．已知一个直角三角形的三边的平方和为1800cm2，则斜边长为（）A．30 cm B．80 cm C．90 cm D．120 cm11．如图，△ABC三条边AC＝20cm，BC＝15cm，AB＝25cm，CD⊥AB，则CD＝cm．12．如图，已知CD＝3，AD＝4，∠ADC＝90°，BC＝12，AB＝13．则图中阴影部分的面积＝．13．如图，在Rt△ABC中，∠B＝90°，AC的垂直平分线DE分别交AB，AC于D，E两点，若AB＝4，BC＝3，则CD的长为．14．如图所示，△ABC的顶点A、B、C在边长均为1的正方形网格的格点上，BD⊥AC于D，则BD的长＝．15．如图，在△ABC中，∠C＝90°，AC＝2，点D在BC上，∠ADC＝2∠B，AD＝，则△ABC的面积为．16．已知△ABC是边长为6的等边三角形，点E在直线AB上，AB＝AE，在直线BC上取点D，若ED＝EC，则CD的长为．17．如图△ABC中，∠D＝90°，C是BD上一点，已知CB＝9，AB＝17，AC＝10，则DC的长是，AD＝．18．如图，在四边形ABCD中，AD∥BC，∠B＝60°，E为AB的中点，EC⊥AB，若AD＝2，AB ＝6．则CD的长度为．19．在平面直角坐标系中，已知A（﹣3，0），B（0，4），C（1，m），当△ABC是直角三角形时，m的值为．20．如图，在Rt△ABC中，∠ACB＝90°，AD平分∠BAC，DE⊥AB于E，若AC＝3cm，AB＝5cm，则DE＝cm．21．如图，在四边形ABCD中，AB＝AD＝8，∠A＝60°，∠ADC＝150°，四边形ABCD的周长为32．（1）求∠BDC的度数；（2）四边形ABCD的面积．22．如图，在Rt△ABC中，∠ABC＝90°，AB＝20，BC＝15，点D为AC边上的动点，点D 从点C出发，沿边CA往A运动，当运动点A时停止，若设点D运动的时间为t秒，点D 运动的速度为每秒2个单位长度．（1）当t＝2时，CD＝，AD＝；（请直接写出答案）（2）当t＝时，△CBD是直角三角形；（请直接写出答案）（3）求当t为何值时，△CBD是等腰三角形？并说明理由．23．已知△ABC中，AB＝AC，CD⊥AB于点D．（1）若∠A＝36°，求∠DCB的度数；（2）若AB＝10，CD＝6，求BC的长．24．一架方梯长25米，如图，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？25．已知某开发区有一块四边形的空地ABCD，如图所示，现计划在空地上种植草皮，经测量∠A＝90°，AB＝3m，BC＝12m，CD＝13m，DA＝4m．（1）若每平方米草皮需要200元，问要多少投入？（2）若BE⊥DC，垂足为E，求BE的长．26．如图：正方形网格中每个小方格的边长为1，且点A、B、C均为格点．（1）求△ABC的面积；（2）通过计算判断△ABC的形状；．（3）求AB边上的高．27．如图，△ABC中，∠C＝90°，AB＝10cm，BC＝6cm，若动点P从点C开始，按C→A→B →C的路径运动，且速度为每秒1cm，设出发的时间为t秒．（1）出发2秒后，求△ABP的周长；（2）当t为几秒时，BP平分∠ABC；（3）问t为何值时，△BCP为等腰三角形？参考答案1．解：A、因为32+42＝52，属于勾股数；B、因为52+62≠72，不属于勾股数；C、因为62+82＝102，属于勾股数；D、因为92+402＝412，属于勾股数；故选：B．2．解：过点E作EG⊥AB于点G，如图：∵CD⊥AB于D，∴EG∥CD，∴∠GEB＝∠EFC，∵在Rt△ABC中，∠ACB＝90°，∴EC⊥CB，又∵BE平分∠ABC，EG⊥AB，∴EG＝EC．在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，∴AB＝5．在Rt△EBC和Rt△EBG中，，∴Rt△EBC≌Rt△EBG（HL），∠CEB＝∠GEB，BG＝BC＝4，∴∠CEB＝∠EFC，AG＝AB﹣BG＝5﹣4＝1，∴CF＝CE．设CF＝EG＝EC＝x，则AE＝3﹣x，在Rt△AEG中，由勾股定理得：（3﹣x）2＝x2+12，解得x＝∴CF的长是．故选：B．3．解：设等腰三角形的腰长是x，根据周长可以表示出其底边是（36﹣2x）．根据等腰三角形的三线合一，得底边的一半是（18﹣x），根据勾股定理得：x2＝62+（18﹣x）2，解得：x＝10，则底边＝36﹣2x＝16，根据三角形的面积公式即可计算：×6×16＝48．故选：C．4．解：（1）设两直角边的长分别为x，2x，∵x•2x＝4，解得x＝2，∴直角三角形两直角边的长分别为2，4，∴斜边长＝＝2，故本小题错误；（2）∵直角三角形的最大边长为26，最短边长为10，∴另一边长＝＝24，故本小题正确；（3）∵在直角三角形中，两条直角边长为n2﹣1和2n，∴斜边长＝＝n2+1，故本小题正确；（4）设等腰三角形底边上的高为h，∵等腰三角形面积为12，底边上的底为4，∴×4h＝12，解得h＝6，∴腰长＝＝2，故本小题错误．故选：B．5．解：设BC＝n，则有AB＝n+1，AC＝n﹣1，因为AB2﹣BD2＝AC2﹣CD2，所以（n+1）2﹣（n﹣1）2＝（BD﹣CD）n，所以BD﹣CD＝4，故选：B．6．解：设直角三角形的两直角边分别为a、b（a＞b），则满足，解得2ab＝2，则ab＝1，所以这个三角形的面积为S＝ab＝．故选：C．7．解：在直角三角形ABD中，根据勾股定理，得BD＝15；在直角三角形ACD中，根据勾股定理，得CD＝6．当AD在三角形的内部时，BC＝15+6＝21；当AD在三角形的外部时，BC＝15﹣6＝9．则BC的长是21或9．故选：D．8．解：∵AD⊥BC，CE⊥AB，∠AHE＝∠CHD，∴∠EAH＝∠ECB，又EH＝EB，∴△AEH≌△CEB．∴BC＝AH＝5，EC＝AE＝4，∴AC＝4，∴BC+AC＝5+4．故选：C．9．解：过A点作AF⊥BC于F，连接AP，∵△ABC中，AB＝AC＝5，BC＝8，∴BF＝4，∴△ABF中，AF＝＝3，∴×8×3＝×5×PD+×5×PE，12＝×5×（PD+PE）PD+PE＝4.8．故选：A．10．解：设直角三角形的两直角边分别为acm，bcm，斜边为ccm，根据勾股定理得：a2+b2＝c2，∵a2+b2+c2＝1800，∴2c2＝1800，即c2＝900，则c＝30cm．故选：A．11．解：∵202+152＝252，∵AC2+BC2＝AB2，∴△ACB是直角三角形，∵S△ACB＝AC•BC＝AB•CD，∴AC•BC＝AB•CD，20×15＝25•CD，CD＝12．故答案为：12．12．解：由勾股定理可知：AC＝＝＝5，又∵AC2+BC2＝52+122＝132＝AB2，∴△ABC是直角三角形故所求面积＝S△ABC﹣S△ACD＝×5×12﹣×3×4＝30﹣6＝24，故答案为：24．13．解：∵DE是AC的垂直平分线，∴CD＝AD，∴AB＝BD+AD＝BD+CD，设CD＝x，则BD＝4﹣x，在Rt△BCD中，CD2＝BC2+BD2，即x2＝32+（4﹣x）2，解得x＝．故答案为：．14．解：△ABC的面积＝×BC×AE＝2，由勾股定理得，AC＝＝，则××BD＝2，解得BD＝．故答案为：．15．解：∵∠ADC＝2∠B，∠ADC＝∠B+∠BAD，∴∠B＝∠DAB，∴DB＝DA＝，在Rt△ADC中，DC＝＝＝1，∴BC＝+1．∴△ABC的面积＝AC•BC＝+1；故答案为：+1．16．解：分两种情况：①当点E在BA延长线上时，过点E作EF⊥BC于F，则Rt△BEF中，∠BEF＝30°，∵AB＝AE＝6，∴AE＝4，∴BF＝BE＝（4+6）＝5，∵BC＝6，∴CF＝6﹣5＝1，∵ED＝EC，EF⊥CD，∴CD＝2CF＝2；②当点E在线段AB上时，过E作EF⊥BC于F，则Rt△BEF中，∠BEF＝30°，∴BF＝BE＝（AB﹣AE）＝1，∵BC＝6，∴CF＝6﹣1＝5，∵ED＝EC，EF⊥CD，∴CD＝2CF＝10．综上所述，CD的长为2或10．故答案为：2或10．17．解：设CD＝x，则BD＝BC+CD＝9+x．在△ACD中，∵∠D＝90°，∴AD2＝AC2﹣CD2，在△ABD中，∵∠D＝90°，∴AD2＝AB2﹣BD2，∴AC2﹣CD2＝AB2﹣BD2，即102﹣x2＝172﹣（9+x）2，解得：x＝6，即CD＝6，∴AD2＝102﹣62＝64，∴AD＝8．故答案为：6，8．18．解：过A点作AF⊥BC于F，过D点作DG⊥BC于G，则四边形AFGD是矩形，∵在Rt△AFB中，∠B＝60°，AB＝6，∴∠BAF＝30°，∴BF＝×6＝3，∴AF＝＝3，∴DG＝3，∵AD＝2，∴FG＝2，∴CG＝BC﹣BF﹣FG＝1，∴在Rt△CGD中，CD＝＝2．故答案为：2．19．解：①A是直角顶点，（﹣3﹣0）2+（0﹣4）2+（﹣3﹣1）2+（0﹣m）2＝（0﹣1）2+（m﹣4）2，解得m＝﹣3；②B是直角顶点，（﹣3﹣0）2+（0﹣4）2+（0﹣1）2+（m﹣4）2＝（﹣3﹣1）2+（0﹣m）2，解得m＝；③C是直角顶点，（﹣3﹣1）2+（0﹣m）2+（0﹣1）2+（m﹣4）2＝（﹣3﹣0）2+（0﹣4）2，解得m＝2．故当△ABC是直角三角形时，m的值为﹣3或或2．故答案为：﹣3或或2．20．解：∵∠ACB＝90°，AC＝3cm，AB＝5cm，∴BC＝＝4，∴Rt△ABC的面积为：×3×4＝6，∵AD平分∠BAC，DE⊥AB，∠ACB＝90°，∴DE＝DC，∴×AC×CD+×AB×DE＝6，解得，DE＝cm，故答案为：．21．解：（1）∵AB＝AD＝8cm，∠A＝60°，∴△ABD是等边三角形，∵∠ADC＝150°∴∠BDC＝150°﹣60°＝90°；（2）∵△ABD为正三角形，AB＝8cm，∴其面积为××AB×AD＝16，∵BC+CD＝32﹣8﹣8＝16，且BD＝8，BD2+CD2＝BC2，解得BC＝10，CD＝6，∴直角△BCD的面积＝×6×8＝24，故四边形ABCD的面积为24+16．22．解：（1）t＝2时，CD＝2×2＝4，∵∠ABC＝90°，AB＝20，BC＝15，AD＝AC﹣CD＝25﹣4＝21；（2）①∠CDB＝90°时，S△ABC＝AC•BD＝AB•BC，即×25•BD＝×20×15，解得BD＝12，所以CD＝＝＝9，t＝9÷2＝4.5（秒）；②∠CBD＝90°时，点D和点A重合，t＝25÷2＝12.5（秒），综上所述，t＝4.5或12.5秒；故答案为：（1）4，21；（2）4.5或12.5秒；（3）①CD＝BD时，如图1，过点D作DE⊥BC于E，则CE＝BE，CD＝AD＝AC＝×25＝12.5，t＝12.5÷2＝6.25；②CD＝BC时，CD＝15，t＝15÷2＝7.5；③BD＝BC时，如图2，过点B作BF⊥AC于F，则CF＝9，CD＝2CF＝9×2＝18，t＝18÷2＝9，综上所述，t＝6.25或7.5或9秒时，△CBD是等腰三角形．23．解：（1）在△ABC中，∵AB＝AC，∠A＝36°，∵CD⊥AB于点D，∴∠DCB＝90°﹣72°＝18°；（2）∵△ABC中，AB＝AC，CD⊥AB于点D，AB＝10，CD＝6，∴AC＝AB＝10．设BD＝x，则AD＝10﹣x，在Rt△ACD中，∵AC2＝CD2+AD2，即102＝62+（10﹣x）2，解得x＝2．在Rt△BCD中，∵BC2＝CD2+BD2，即BC2＝62+22＝40，∴BC＝＝2．24．解：（1）根据勾股定理：梯子距离地面的高度为：＝24米；（2）梯子下滑了4米，即梯子距离地面的高度为A'B＝AB﹣AA′＝24﹣4＝20，根据勾股定理得：25＝，解得CC′＝8．即梯子的底端在水平方向滑动了8米．25．（1）解：连接BD，在Rt△ABD中，BD2＝AB2+AD2＝32+42＝52，在△CBD中，CD2＝132，BC2＝122，而122+52＝132，即BC2+BD2＝CD2，即∠DBC＝90°，S四边形ABCD＝S△BAD+S△DBC＝•AD•AB+DB•BC，＝×4×3+×12×5＝36．所以需费用36×200＝7200（元）．（2）作BE⊥CD，垂足为E，在Rt△DBC中，由于BD•BC＝CD•BE，即BE＝＝．26．解：（1）△ABC的面积＝4×4﹣×4×2﹣×2×1﹣×3×4＝5；（2）由勾股定理得：AC2＝42+22＝20，BC2＝22+12＝5，AB2＝32+42＝25，∴AC2+BC2＝AB2，∴△ABC是直角三角形，∠ACB＝90°；（3）∵AC＝＝2，BC＝，△ABC是直角三角形，∴AB边上的高＝＝＝2．27．解：（1）∵∠C＝90°，AB＝10cm，BC＝6cm，∴有勾股定理得AC＝8cm，动点P从点C 开始，按C→A→B→C的路径运动，且速度为每秒1cm∴出发2秒后，则CP＝2cm，那么AP＝6cm．∵∠C＝90°，∴由勾股定理得PB＝2cm∴△ABP的周长为：AP+PB+AB＝6+10+2＝（16+2）cm；（2）如图2所示，过点P作PD⊥AB于点D，∵BP平分∠ABC，∴PD＝PC．在Rt△BPD与Rt△BPC中，，∴Rt△BPD≌Rt△BPC（HL），∴BD＝BC＝6 cm，∴AD＝10﹣6＝4 cm．设PC＝x cm，则PA＝（8﹣x）cm在Rt△APD中，PD2+AD2＝PA2，即x2+42＝（8﹣x）2，解得：x＝3，∴当t＝3秒时，AP平分∠CAB；（3）若P在边AC上时，BC＝CP＝6cm，此时用的时间为6s，△BCP为等腰三角形；若P在AB边上时，有两种情况：①若使BP＝CB＝6cm，此时AP＝4cm，P运动的路程为12cm，所以用的时间为12s，故t＝12s时△BCP为等腰三角形；②若CP＝BC＝6cm，过C作斜边AB的高，根据面积法求得高为4.8cm，根据勾股定理求得BP＝7.2cm，所以P运动的路程为18﹣7.2＝10.8cm，∴t的时间为10.8s，△BCP为等腰三角形；③若BP＝CP时，则∠PCB＝∠PBC，∵∠ACP+∠BCP＝90°，∠PBC+∠CAP＝90°，∴∠ACP＝∠CAP，∴PA＝PC ∴PA＝PB＝5cm∴P的路程为13cm，所以时间为13s时，△BCP为等腰三角形．∴t＝6s或13s或12s或 10.8s时△BCP为等腰三角形．。

第十七章勾股定理一、选择题1.铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160 cm，某厂家生产符合该规定的行李箱，已知行李箱的高为30 cm，长与宽的比为3∶2，则该行李箱的长的最大值为()A． 26 cmB． 52 cmC． 78 cmD． 104 cm2.由以下三边不能组成直角三角形的是()A． 5,13,12B． 2,3，C． 4,7,5D． 1，，3.如图，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是()A．CD、EF、GHB．AB、EF、GHC．AB、CD、GHD．AB、CD、EF4.下列命题中是假命题的是()A．△ABC中，若∠B＝∠C－∠A，则△ABC是直角三角形B．△ABC中，若a2＝(b＋c)(b－c)，则△ABC是直角三角形C．△ABC中，若∠A∶∠B∶∠C＝3∶4∶5，则△ABC是直角三角形D．△ABC中，若a∶b∶c＝5∶4∶3，则△ABC是直角三角形5.在下列条件中：①∠A＋∠B＝∠C，②∠A∶∠B∶∠C＝1∶2∶3，③∠A＝90°－∠B，④∠A＝∠B＝∠C中，能确定△ABC是直角三角形的条件有()A． 1个B． 2个C． 3个D． 4个6.已知一个直角三角形的两直角边长分别为3和4，则斜边长是()A． 5B．C．D．或57.长方体敞口玻璃罐，长、宽、高分别为16 cm、6 cm和6 cm，在罐内点E处有一小块饼干碎末，此时一只蚂蚁正好在罐外壁，在长方形ABCD中心的正上方2 cm处，则蚂蚁到达饼干的最短距离是多少cm.()A． 7B．C． 24D．8.如图：一个长、宽、高分别为4 cm、3 cm、12 cm的长方体盒子能容下的最长木棒长为()A． 11 cmB． 12 cmC． 13 cmD． 14 cm9.如图，要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道，则平板车的长最多为()A． 2B． 2C． 4D． 410.已知在Rt△ABC中，∠C＝90°，AC＝2，BC＝3，则AB的长为()A． 4B．C．D． 5二、填空题11.如下图，在Rt△ABC中，∠B＝90°，BC＝15，AC＝17，以AB为直径作半圆，则此半圆的面积为________．12.等腰△ABC中，AB＝AC＝5，△ABC的面积为10，则BC＝________.13.如图，△ABC中，D是AC边上的一点，AD＝9，BD＝12，BC＝13，CD＝5，那么△ABC的面积是__________．14.甲船以每小时16海里的速度从港口A出发向北偏东50°的方向航行，乙船以每小时12海里的速度同时从港口A出发向南偏东方向航行，离开港口2小时后两船相距40海里，则乙船向南偏东________方向航行．15.如图，△AOB是等腰三角形，OA＝OB，点B在x轴的正半轴上，点A的坐标是(1,1)，则点B的坐标是________．16.如图，四边形ABCD中，AD＝3，AB＝4，BC＝12，CD＝13，∠A＝90°，计算四边形ABCD的面积__________．17.如图，在等腰△ABC中，AD是角平分线，E是AB的中点，已知AB＝AC＝15 cm.BC＝18 cm，则△ADE的周长是________ cm.18.如图，在Rt△ABC中，∠B＝90°，AC的垂直平分线DE分别交AB，AC于D，E两点，若AB＝4，BC＝3，则CD的长为________．19.在△ABC中，∠C＝90°，AC＝6，BC＝8，点D是斜边AB的中点，连接CD，则CD长为________．20.如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在AB上，AD＝AC，AF⊥CD交CD 于点E，交CB于点F，则CF的长是________．三、解答题21.如图，在△ABC中，∠ACB＝90°，BC＝15，AC＝20，CD是高．(1)求AB的长；(2)求△ABC的面积；(3)求CD的长．22.东明县是鲁西南的化工基地，有东明石化集团，洪业化工集团，玉皇化工集团等企业，化学工业越来越成为东明县经济的命脉，化工厂里我们会经常看到如图储存罐，根据需要，在圆柱形罐的外围要安装小梯子，如果油罐的底面半径为6米，高24米，梯子绕罐体半圆到达罐顶，则梯子至少要多长？23.如图，在Rt△ABC中，∠BAC＝90°，AD是中线，AE是高，AC＝6，AD＝5，求AE的长．24.如图，在△ABC中，AC＝AB，底边BC＝10，点D是腰AB上一点，且CD＝8，BD＝6，求△ABC的周长．25.如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13米，此人以0.5米每秒的速度收绳，10秒后船移动到点D的位置，问船向岸边移动了多少米？(假设绳子是直的，结果保留根号)26.如图，一幢居民楼与马路平行且相距9米，在距离载重汽车41米处(图中B点位置)就会受到噪音影响，试求在马路上以4米/秒速度行驶的载重汽车，给这幢居民楼带来多长时间的噪音影响？若影响时间超过25秒，则此路禁止该车通行，那么载重汽车可以在这条路上通行吗？27.如图，△ABC中，AC＝13，AB＝12，BC＝5，CD是△ABC的角平分线，DE⊥AC于E，连结EB.(1)求证：∠ABC＝90°；(2)求证：∠CBE＝∠CEB.28.如图，在8×8网格纸中，每个小正方形的边长都为1.(1)已知点A在第四象限，且到x轴距离为1，到y轴距离为5，求点A的坐标；(2)在(1)的条件下，已知点B(a＋1，－2a＋10)，且点B在第一、三象限的角平分线上，判断△OAB 的形状．答案解析1.【答案】C【解析】设长为3a cm，宽为2a cm.由题意30＋3a＋2a≤160，解得a≤26，∴a的最大值为26,3a＝78，∴该行李箱的长的最大值为78 cm，故选C.2.【答案】C【解析】A.∵52＋122＝132，∴此三角形是直角三角形，不符合题意；B．∵22＋()2＝32，∴此三角形是直角三角形，不符合题意；C．∵42＋52≠72，∴此三角形不是直角三角形，符合题意；D．∵12＋()2＝()2，∴此三角形是直角三角形，不符合题意；故选C.3.【答案】B【解析】设小正方形的边长为1，则AB2＝22＋22＝8，CD2＝22＋42＝20，EF2＝12＋22＝5，GH2＝22＋32＝13.因为AB2＋EF2＝GH2，所以能构成一个直角三角形三边的线段是AB、EF、GH.故选B.4.【答案】C【解析】A.∠B＋∠A＝∠C，所以∠C＝90°，所以△ABC是直角三角形，故本选项不符合题意．B．若a2＝(b＋c)(b－c)，所以a2＋c2＝b2，所以△ABC是直角三角形，故本选项不符合题意．C．若∠A∶∠B∶∠C＝3∶4∶5，最大角为75°，故本选项符合题意．D．若a∶b∶c＝5∶4∶3，则△ABC是直角三角形，故本选项不符合题意．故选C.5.【答案】C【解析】①因为∠A＋∠B＝∠C，则2∠C＝180°，∠C＝90°，所以△ABC是直角三角形；②因为∠A∶∠B∶∠C＝1∶2∶3，设∠A＝x，则x＋2x＋3x＝180，x＝30°，∠C＝30°×3＝90°，所以△ABC是直角三角形；③因为∠A＝90°－∠B，所以∠A＋∠B＝90°，则∠C＝180°－90°＝90°，所以△ABC是直角三角形；④因为∠A＝∠B＝∠C，所以三角形为等边三角形．所以能确定△ABC是直角三角形的有①②③共3个．故选C.6.【答案】A【解析】设斜边长为c，由勾股定理可得：c2＝32＋42，则c＝5，故选A.7.【答案】B【解析】①若蚂蚁从平面ABCD和平面CDFE经过，蚂蚁到达饼干的最短距离如图1：H′E＝＝＝7，②若蚂蚁从平面ABCD和平面BCEH经过，则蚂蚁到达饼干的最短距离如图2：H′E＝＝.故选B.8.【答案】C【解析】∵侧面对角线BC2＝32＋42＝52，∴CB＝5 m，∵AC＝12 m，∴AB＝＝13(m)，∴空木箱能放的最大长度为13 m，故选C.9.【答案】C【解析】设平板手推车的长度为x米，当x为最大值，且此时平板手推车所形成的△CBP为等腰直角三角形．连接PO，与BC交于点N.∵直角通道的宽为2m，∴PO＝4 m，∴NP＝PO－OO＝4－2＝2(m)．又∵△CBP为等腰直角三角形，∴AD＝BC＝2CN＝2NP＝4(m)．故选C.10.【答案】C【解析】在Rt△ABC中，∠C＝90°，AC＝2，BC＝3，由勾股定理，得AB＝＝＝；故选C.11.【答案】8π【解析】在Rt△ABC中，AB＝＝＝8，所以S半圆＝×42＝8π.12.【答案】2或4【解析】作CD⊥AB于D，则∠ADC＝∠BDC＝90°，△ABC的面积＝AB·CD＝×5×CD＝10，解得CD＝4，∴AD＝＝＝3；分两种情况：①等腰△ABC为锐角三角形时，如图1所示：BD＝AB－AD＝2，∴BC＝＝＝2；②等腰△ABC为钝角三角形时，如图2所示：BD＝AB＋AD＝8，∴BD＝＝＝4；综上所述：BC的长为2或4.。