八年级上册数学思维导图

如果一个句子没有对某一件事情做出任何判断，那么它就不是命题 由一个基本事实或定理直接推出的定理，叫做这个基本事实或定理的推论
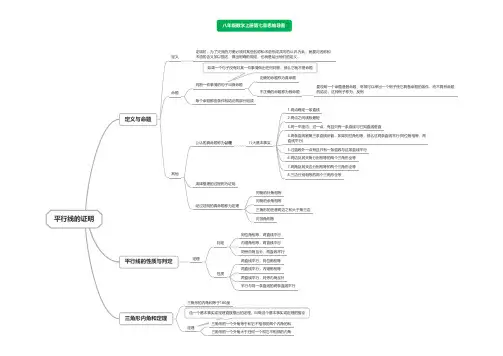
平行线的证明
定义与命题 定义证明时，为了交流的方便必须对某些名称和术语形成共同的认识.为此，就要对名称和术语的含义加以描述，做出明确的规定，也就是给出他们的定义.
命题
判断一件事情的句子叫做命题 每个命题都由条件和结论两部分组成 正确的命题称为真命题
不正确的命题称为假命题
要说明一个命题是假命题，常常可以举出一个例子使它具备命题的条件，而不具有命题
的结论，这种例子称为，反例 其他
公认的真命题称为公理八大基本事实 1.两点确定一条直线
2.两点之间线段最短
3.同一平面内，过一点，有且只有一条直线与已知直线垂直
4.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行(同位角相等，两直线平行)
5.过直线外一点有且只有一条直线与这条直线平行
6.两边及其夹角分别相等的两个三角形全等
7.两角及其夹边分别相等的两个三角形全等
8.三边分别相等的两个三角形全等演绎推理的过程称为证明
经过证明的真命题称为定理 同角的补角相等
同角的余角相等
三角形的任意两边之和大于第三边
对顶角相等 平行线的性质与判定 定理 判定同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
性质 两直线平行，同位角相等
两直线平行，内错角相等
两直线平行，同旁内角互补
平行与同一条直线的两条直线平行
三角形内角和定理 三角形的内角和等于180度
定理三角形的一个外角等于和它不相邻的两个内角的和
三角形的一个外角大于任何一个和它不相邻的内角。

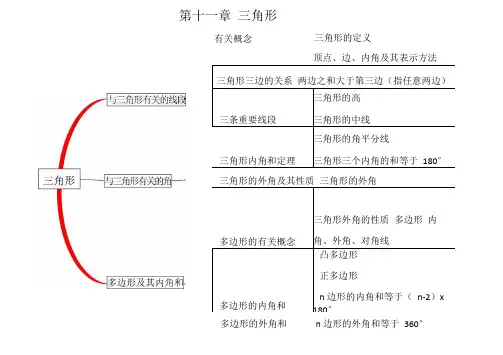
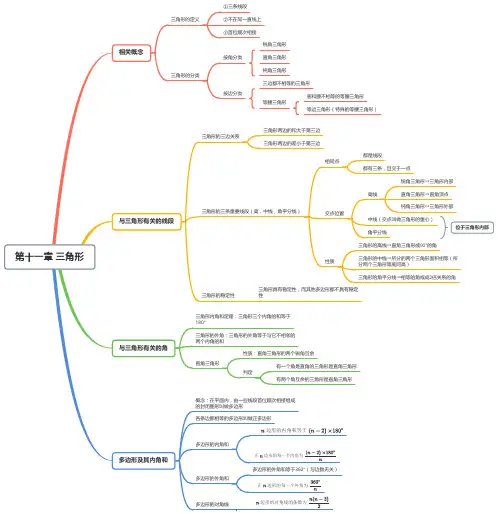
第十一章三角形
有关概念三角形的定义
三角形三边的关系两边之和大于第三边（指任意两边）
三条重要线段三角形的高三角形的中线
三角形内角和定理三角形的角平分线
三角形三个内角的和等于180°
三角形的外角及其性质三角形的外角
多边形的有关概念三角形外角的性质多边形内角、外角、对角线
多边形的内角和
凸多边形
正多边形
n 边形的内角和等于（n-2）x 180°
顶点、边、内角及其表示方法
多边形的外角和n 边形的外角和等于360°
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章二次根式
满足下列两个特点的二次根式，叫最简二次
根式.
1)被开方数不含分母，分母中不含二次
根式；
2)被开方数中不含开得尽方的因数或因
式. 定义：式子(a≥0)叫做二次根式
(a≥0)是一个非负数
最简二次根式(a≥0)
二次根式
二次根式性质
a≥0,b>0)
二次根式的
除法
(a≥0,b≥0)
二次根式
的混合运算运算
(a≥0,b>0)
二次根式的
加减
二次根式加减是，可以先将二次根式化成
最简二次根式，再合并同类二次根式
第十七章勾股定理
第十八章平行四边形
第十九章一次函数
第二十章数据的分析。

你现在的努力要对得起别人对你的好！
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。

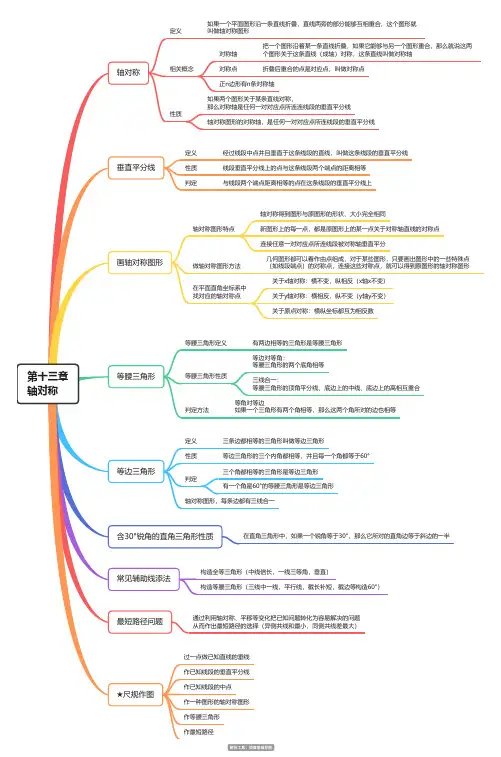
第十三章轴对称轴对称定义如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形相关概念对称轴把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线（成轴）对称，这条直线叫做对称轴对称点折叠后重合的点是对应点，叫做对称点正n边形有n条对称轴性质如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连连线段的垂直平分线轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线垂直平分线定义经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线性质线段垂直平分线上的点与这条线段两个端点的距离相等判定与线段两个端点距离相等的点在这条线段的垂直平分线上画轴对称图形轴对称图形特点轴对称得到图形与原图形的形状、大小完全相同新图形上的每一点，都是原图形上的某一点关于对称轴直线的对称点连接任意一对对应点所连线段被对称轴垂直平分做轴对称图形方法几何图形都可以看作由点组成，对于某些图形，只要画出图形中的一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形在平面直角坐标系中找对应的轴对称点关于x轴对称：横不变，纵相反（x轴x不变）关于y轴对称：横相反，纵不变（y轴y不变）关于原点对称：横纵坐标都互为相反数等腰三角形等腰三角形定义有两边相等的三角形是等腰三角形等腰三角形性质等边对等角：等腰三角形的两个底角相等三线合一：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合判定方法等角对等边如果一个三角形有两个角相等，那么这两个角所对的边也相等等边三角形定义三条边都相等的三角形叫做等边三角形性质等边三角形的三个内角都相等，并且每一个角都等于60°判定三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形轴对称图形，每条边都有三线合一含30°锐角的直角三角形性质在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半常见辅助线添法构造全等三角形（中线倍长，一线三等角，垂直）构造等腰三角形（三线中一线，平行线，截长补短，截边等构造60°）最短路径问题通过利用轴对称、平移等变化把已知问题转化为容易解决的问题从而作出最短路径的选择（异侧共线和最小，同侧共线差最大）★尺规作图过一点做已知直线的垂线作已知线段的垂直平分线作已知线段的中点作一种图形的轴对称图形作等腰三角形作最短路径。

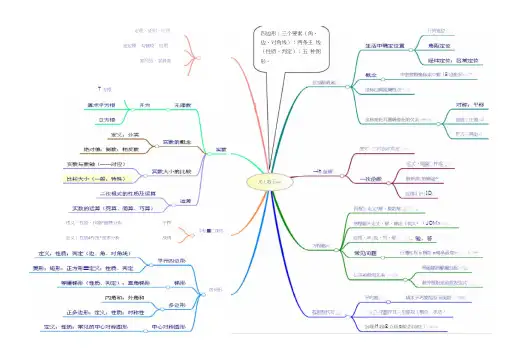
八年级上册数学思维导图第一章一、数学思维导图的概念与作用1.1 数学思维导图的定义数学思维导图是一种以图形的形式来表达数学概念和思维关系的工具。

它通过将各个概念以节点的形式表示，并用连线表示概念之间的关系，帮助学生理清数学知识的结构框架，并促进理解和记忆。

1.2 数学思维导图的作用•帮助学生理解和记忆数学知识的结构关系，促进知识的整体性理解。

•帮助学生发现数学知识之间的联系和规律，培养抽象思维和逻辑推理能力。

•帮助学生发展创造性思维，拓展解题思路和方法。

•培养学生形象思维，提高数学思维的直观性和准确性。

•培养学生的自主学习能力，让学生学会制作和运用思维导图。

二、数学思维导图的制作方法2.1 选择适当的绘图工具常见的数学思维导图制作工具有手绘、纸笔、黑板、电脑绘图软件等。

根据自己的喜好和制作要求选择合适的工具。

2.2 组织结构首先确定要表达的主题，并将主题放在导图中央，作为核心概念。

然后根据核心概念，逐步展开各个相关的分支，用连线将它们与核心概念相连。

2.3 标题和关键词每个节点旁边都应标明标题和关键词，以方便概念的理解和记忆。

标题应简洁明了，关键词要准确概括该节点的内容。

2.4 层次关系和连接方式节点之间的层次关系可以用数字或字母标号表示，也可以用不同的线型或颜色表示。

连接方式可以使用直线、曲线或箭头等，以准确表达节点之间的关系。

三、数学思维导图的应用实例3.1 整式的展开公式整式的展开公式是初中数学中的重要知识点之一。

我们可以使用思维导图的方式来帮助理解整式的展开公式的结构和演绎过程。

3.1.1 一次方差式的展开以(a+b)2为例，展开公式为a2+2ab+b2。

我们可以用思维导图将展开公式的各个项和系数以图形的形式展示出来，帮助学生直观地理解展开公式的含义。

3.1.2 二次方差式的展开以(a+b)(a−b)为例，展开公式为a2−b2。

同样地，我们可以用思维导图的方式将展开公式的各个项和系数以图形的形式展示出来，便于学生理解和记忆。

初中数学八年级上册思维导图一、数的开方1. 平方根：如果一个正数x的平方等于a，那么x是a的平方根，记作x=√a。

正数a的平方根有两个，它们互为相反数，分别记作+√a 和√a。

0的平方根是0，负数没有平方根。

2. 立方根：如果一个数x的立方等于a，那么x是a的立方根，记作x=³√a。

每个实数都有唯一的立方根。

3. 开方运算：开方运算是求一个数的平方根或立方根的运算。

对于正数a，开方运算可以表示为√a或³√a。

二、实数1. 实数的概念：实数包括有理数和无理数。

有理数是可以表示为两个整数比的数，无理数是不能表示为两个整数比的数。

2. 实数的分类：实数可以分为正实数、负实数和0。

正实数是大于0的实数，负实数是小于0的实数，0既不是正实数也不是负实数。

3. 实数的运算：实数可以进行加法、减法、乘法和除法运算。

在运算过程中，需要遵循实数的运算规律，如交换律、结合律和分配律。

三、勾股定理1. 勾股定理的内容：勾股定理指出，在一个直角三角形中，直角边的平方和等于斜边的平方。

即a²+b²=c²，其中a、b是直角边，c是斜边。

2. 勾股定理的应用：勾股定理可以用来解决直角三角形中的边长问题，也可以用来解决一些与直角三角形相关的实际问题。

3. 勾股定理的证明：勾股定理的证明有多种方法，其中一种常见的证明方法是使用几何图形的面积关系。

四、一次函数1. 一次函数的概念：一次函数是指函数的图像是一条直线，其一般形式为y=kx+b，其中k是斜率，b是截距。

2. 一次函数的性质：一次函数的图像是一条直线，斜率k表示直线的倾斜程度，截距b表示直线与y轴的交点。

3. 一次函数的应用：一次函数可以用来描述一些线性关系，如物体的速度与时间的关系、正比例关系等。

五、不等式1. 不等式的概念：不等式是表示两个数之间大小关系的数学表达式，如a>b、a<b、a≥b、a≤b等。

2. 不等式的性质：不等式可以进行加减、乘除运算，但在乘除运算中需要注意符号的变化。

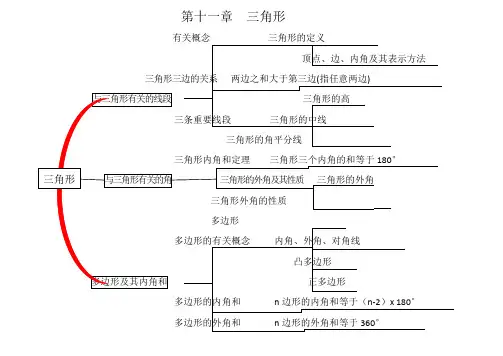
第十一章三角形
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义：式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是，可以先将二次根式化成最简二次根式，再合并同类二次根式
满足下列两个特点的二次根式，叫最简二次根式.
（1）被开方数不含分母，分母
中不含二次根式；
（2）被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b ＞0)
(a ≥0,b ＞0)
第十七章勾股定理
第十八章平行四边形。

初中数学八年级上册思维导图一、数的开方1. 平方根：如果一个正数x的平方等于a，那么x是a的平方根，记作x=√a。

正数a的平方根有两个，它们互为相反数，分别记作√a和√a。

0的平方根是0。

2. 立方根：如果一个数x的立方等于a，那么x是a的立方根，记作x=³√a。

立方根只有一个。

3. 算术平方根：正数a的正的平方根，记作√a，称为a的算术平方根。

4. 立方根的性质：①正数的立方根是正数；②负数的立方根是负数；③0的立方根是0。

二、实数1. 实数的概念：实数包括有理数和无理数。

有理数是可以表示为两个整数比的数，无理数是不能表示为两个整数比的数。

2. 实数的分类：①正实数；②负实数；③零。

3. 实数的运算：实数的加减乘除运算与有理数的运算类似，但需要注意无理数的运算。

三、二次根式1. 二次根式的概念：形如√a的式子，其中a≥0，称为二次根式。

2. 二次根式的性质：①√a²=a（a≥0）；②（√a）²=a（a≥0）；③√ab=√a√b（a≥0，b≥0）；④√a²+b²=√a²+√b²（a≥0，b≥0）。

3. 二次根式的运算：二次根式的加减乘除运算与有理数的运算类似，但需要注意无理数的运算。

四、一元二次方程1. 一元二次方程的概念：形如ax²+bx+c=0（a≠0）的方程，称为一元二次方程。

2. 一元二次方程的解法：①配方法；②求根公式法；③因式分解法。

3. 一元二次方程的根的判别式：判别式△=b²4ac，当△>0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△<0时，方程没有实数根。

五、不等式1. 不等式的概念：表示不相等关系的式子称为不等式。

2. 不等式的性质：①两边同时加上或减去同一个数，不等号方向不变；②两边同时乘以或除以同一个正数，不等号方向不变；③两边同时乘以或除以同一个负数，不等号方向改变。